3544073680

1. Równania różniczkowe zwyczajne rzędu pierwszego

Definicja 1.8. Rozwiązanie odznaczające się tym, że w każdym punkcie jego wykresu zagadnienie Cauchy’ego nie ma jednoznacznego rozwiązania, nazywamy rozwiązaniem osobliwym.

1.2. Równania rzędu pierwszego — istnienie i jednoznaczność

rozwiązania zagadnienia Cauchy’ego

Definicja 1.9. Niech f:R² D Q 3 (x,y) —> f(x,y) G R. Mówimy, że f spełnia warunek Lipschitza ze względu na zmienną y, jeżeli istnieje k > 0, takie że dla dowolnych (x,yi) G Q, (x, 2/2) G Q jest spełniona nierówność

I f(x, Vi) ~ /(at, 1/2)1 < k |j/i - y₂\ •

Rozważmy problem początkowy Cauchy’ego (l.la), (l.lb):

(l.la)

(l.lb)

y' = f(x, y) yM = yo

gdzie: xq G]a, b[, y_Q G [c, d], oraz f: [a, 6] x [c, d] —* R.

Twierdzenie 1.1. Jeżeli f jest ciągła i spełnia warunek Lipschitza ze względu na y w [a,b] x [c,d\, to istnieje ó > 0, takie, że w przedziale [rco — 6, xq + 5] problem początkowy (l.la), (l.lb) posiada dokładnie jedno rozwiązanie.

1.3. Metody rozwiązywania równań różniczkowych rzędu pierwszego

1.3.1. Równania o rozdzielonych zmiennych

Równanie postaci

(1.3)

X(x) dx + Y (y) dy = 0

nazywamy równaniem o rozdzielonych zmiennych. Całką ogólną tego równania jest

J X(x)dx + J Y(y)Ay=0

lub

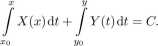
8