Matematyka 2 "1

220 IV Równania ruiniaAtme zwyczajne

y = (C - x)\ C = x₀, x eR Zgodnie z przyjętym określeniem rozwiązanie y = 0. x e R. jest rozwiązaniem osobliwym równania (1).

Natomiast rozwiązanie postaci y = (C-x)\ x eR, dla dowolnej stałej C, nie jest rozwiązaniem regularnym, ani też rozwiązaniem osobliwym.

Zauważmy jeszcze, żc wzory (2) i (3) nie określają wszystkich rozwiązań równania (1) na przedziale I =(-cc,+oo). Rozwiązaniami tego równania będą również funkcje (a będzie ieh nieskończenie wiele) odpowiednio “sklejone" z funkcji (2) i (3), na przykład:

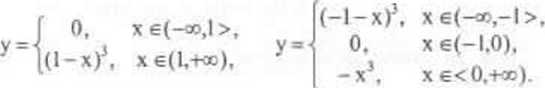
Czytelnikowi pozostawiamy naszkicowanie krzywych całkowych określonych tymi wzorami.

Jak widać problem zapisania wszystkich rozwiązań równania (I) nawet na ustalonym przedziale (-=©.-kc) jest bardziej skomplikowany, niż by się to wydawało na początku.

Można natomiast powiedzieć, że rysunek, na którym znalazłyby się w s z y s t k i e krzywe y = (C- x)\ x eR. C eR, oraz krzywa całkowa y = 0, x eR, przedstawiałby niewątpliwie wszystkie krzywe całkowe równania (l). Na tym rysunku bowiem znajdowałyby się również wykresy wszystkich możliwych rozwiązań sklejonych z rozwiązań (2) i (3).

Na koniec zauważmy, że ograniczenie obszaru, w którym rozwiązujemy równanie (1) pozwala problem uprościć. 7. powyższych rozważań wynika, że:

a) Każde rozwiązanie równania (1) rozważanego na obszarze D, = |(x,y)eR²: y > 0) jest postaci:

y = (C- x)\    xel-oo,C), CeR,

przy czym przez każdy punkt (x₀,y₀)eL)| przechodzi dokładnie jedna krzywa całkowa równania (1) i jest ona określona wzorem

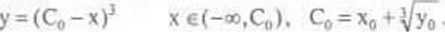
b)    Każde rozwiązanie równania (1) rozważanego na obszarze D,= {(x,y) eR²: y<0} ma postać:

y = (C-x)\    xe(C.+«), CeR,

przy czym przez każdy punkt (x„.y₀) gD, przechodzi dokładnie jedna krzywa całkowa równania (I) i jest ona określona wzorem

y = (C₀-x)³,    X€(C„.+ao), C₀ = x₀ +    .

c)    Ponadto rozwiązaniem równania (1) jest funkcja stała y = 0,

x eR.

Dodajmy, żc rozwiązania przebiegające w obszarach D, i D₂ są rozwiązaniami regularnymi. Mówimy, że w obszarach D, i D₂ dla rozpatrywanego równania ma miejsce jednoznaczność rozwiązań.    ■

Warunki istnienia i jednoznaczności rozwiązań. Niżej podamy dwa twierdzenia o istnieniu i jednoznaczności rozwiązań dla równań różniczkowych pierwszego rzędu w postaci normalnej:

y' = f(x.y).

TWIERDZENIE 1.1 (Pcano). Jeżeli funkcja f jest ciągła na obszarze DcR^:, to przez każdy punkt tego obszaru przechodzi przynajmniej jedna krzywa całkowa równania y' = f(x,y).

TWIERDZENIE 1.2 (Cauchy’ego) Jeżeli funkcja f jest ciągła i ma ciągłą pochodną f' na obszarze D, to przez każdy punkt tego obszaru przechodzi dokładnie jedna krzywa całkowa równania

y'=f(x,y).

PRZYKŁAD 1.4. Weźmy pod uwagę równanie

(1)    /*x(/-l).

Prawa strona tego równania f(x.y) = x(y^: - 1) jest funkcją ciągłą na całej płaszczyźnie, zatem z twierdzenia Peano wynika, żc przez każdy punkt płaszczyzny przechodzi przynajmniej jedna krzywa całkowa równania (I).

Ponieważ pochodna f; = 2xy jest także funkcją ciągłą na płaszczyźnie, więc możemy ponadto stwierdzić, że rozwiązania te są regularne