Rachunek różniczkowy

funkcji jednej zmiennej

Definicja. Zał. że
,
. Ilorazem różnicowym funkcji
w punkcie
nazywamy odwzorowanie
określone równaniem
.
nazywamy pochodną
w punkcie
;

nazywamy pochodną lewostronną w punkcie
;

nazywamy pochodną prawostronną w punkcie
.

Mówimy, że funkcja
jest różniczkowalna
, gdy
istnieje i jest skończona.

Mówimy, że funkcja
jest różniczkowalna na
, gdy

jest różniczkowalna w
.

Mówimy, że funkcja
jest różniczkowalna na
, gdy
jest różniczkowalna w
oraz pochodne jednostronne w punktach
istnieją i są skończone.

Definicja. Zał. że
jest różniczkowalna. Funkcję, która każdemu punktowi
przyporządkowuje
nazywamy pochodną funkcji
.

Mówimy, że
jest pochodną, jeśli istnieje
taka, że
.

Twierdzenie. Jeżeli funkcja
jest różniczkowalna w
, to
jest ciągła w
.

Twierdzenie. Jeżeli
są różniczkowalne w
. Wtedy:

(1)
jest funkcją różniczkowalną w
i
;

(2)
jest funkcją różniczkowalną w
i
;

(3)
jest funkcją różniczkowalną w
i
;

(4)
i
jest funkcją różniczkowalną w
i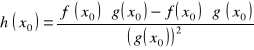
.

Twierdzenie. Funkcja
jest różniczkowalna w
i

istnieje
taka, że
i
jest ciągła w
oraz
.

Twierdzenie. Zał. że
,
,
,
,
jest różniczkowalna w
, a
w
. Wtedy
jest różniczkowalna w
oraz
.

Twierdzenie. Zał. że
jest różnowartościowa, ciągła i różniczkowalna w
,
. Wtedy
jest różniczkowalna w
oraz
.

Definicja. Zał. że
. Wtedy:

(1) funkcja
posiada maksimum lokalne w
, gdy
;

(2) funkcja
ma ścisłe maksimum lokalne w
, gdy
;

(3) funkcja
posiada minimum lokalne w
, gdy
;

(4) funkcja
ma ścisłe maksimum lokalne w
, gdy
.

Twierdzenie. Zał. że
jest różniczkowalna na
. Wtedy, jeżeli
przyjmuje ekstremum lokalne w
, to
.

Twierdzenie Rolle'a. Zał. że
jest ciągła i różniczkowalna na
oraz
. Wtedy
.

Twierdzenie Lagrange'a. Zał. że
jest ciągła i różniczkowalna na
. Wtedy
.

Twierdzenie Cauchy'ego. Zał. że
są ciągłe i różniczkowalne na
. Wtedy
.

Twierdzenie. Zał. że
jest ciągła i różniczkowalna na
. Wtedy:

(1)
jest niemalejąca na
;

(2)
jest rosnąca na
, gdy
;

(3)
jest nierosnąca na
;

(4)
jest malejąca na
, gdy
.

Twierdzenie. Jeżeli
jest różniczkowalna, to
ma własność Darobux, tzn.
.

Reguła d'Hospitala. Zał. że
,
są różniczkowalne na
oraz
. Jeżeli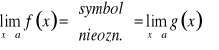
oraz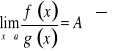
, to
.

Twierdzenie. Zał. że
jest ciągiem funkcji różniczkowalnych,
,
oraz
. Jeżeli
jest funkcją ciągłą oraz
jest jednostajnie zbieżny do
, to
jest różniczkowalna oraz

.

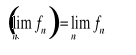
Wniosek. Zał. że
jest różniczkowalna
są ciągłe oraz
,
zbiega jednostajnie do
, to
jest różniczkowalna oraz
,
.

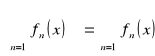
Twierdzenie. Szeregi
,
mają ten sam promień zbieżności
, oraz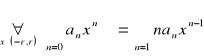
.

Definicja. Zał. że
jest różniczkowalna w
. Jeżeli
posiada pochodną w
, to pochodną tę nazywamy pochodną drugiego rzędu w
i oznaczamy
. Mówimy, że funkcja jest dwukrotnie różniczkowalna na
, gdy
istnieje i jest skończona.

Zał. że
oraz
jest n-krotnie różniczkowalna na
. Jeżeli istnieje pochodna funkcji
w
, to pochodną tę nazywamy pochodną
rzędu w
, oraz
.

Definicja. Mówimy, że funkcja
jest klasy
na
, jeżeli
jest określona i ciągła na
.

Mówimy, że funkcja
jest klasy
(jest „gładka”) na
, gdy
jest klasy
.

Twierdzenie Leibniza. Jeżeli
są funkcjami klasy
, to
oraz
,
.

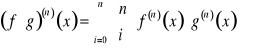
Twierdzenie Taylora. Zał. że
jest klasy
. Wtedy
.

Definicja. Ustalmy
. Wtedy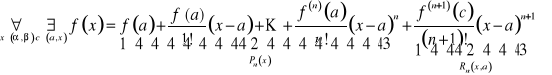
.

to n-ta reszta Taylora w postaci Lagrange'a. Wtedy
.

Jeżeli we wzorze Taylora podstawimy
to otrzymamy wzór MacLaurina
.

Twierdzenie. Jeżeli
oraz
i
, to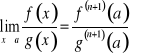
.

Definicja. Zał. że
.
nazywamy szeregiem Taylora (dla funkcji
względem środka
).

Twierdzenie. Jeżeli
, to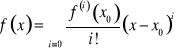
.

Definicja. Zał. że
. Mówimy, że
jest funkcją analityczną, gdy
jest równa sumie swojego szeregu MacLaurina.

Twierdzenie. Jeżeli
oraz
, to
jest funkcją analityczną.

Twierdzenie. Jeżeli
rozwija się w szereg MacLaurina, to istnieje tylko jedno takie rozwinięcie.

Twierdzenie. Jeżeli
jest różniczkowalna na
oraz
i
zmienia znak przechodząc przez
, to
posiada ekstremum lokalne w
.

Definicja. Zał. że
. Mówimy, że
ma punkt przegięcia w
, gdy
taka, że:

(1) na przedziale

leży nad styczną do wykresu
w punkcie

, a na przedziale

leży pod
;

(2) albo zachodzi sytuacja odwrotna.

Twierdzenie. Zał. że
oraz
. Wtedy:

(1) jeżeli
i
, to
posiada maksimum lokalne w
;

(2) jeżeli
i
, to
posiada minimum lokalne w
;

(3) jeżeli
i
dowolna, to
posiada punkt przegięcia w
.

Twierdzenie. Zał. że
. Wtedy:

(1) jeżeli
, to krzywa
jest dla pewnego otoczenia punktu
położona powyżej stycznej do tej krzywej w punkcie
(a więc skierowana wypukłością w dół);

(2) jeżeli
, to krzywa
jest dla pewnego otoczenia punktu
położona poniżej stycznej do tej krzywej w punkcie
(a więc skierowana wypukłością w górę).

1

---