Rachunek różniczkowy
funkcji jednej zmiennej
Definicja. Zał. że![]()
, ![]()
. Ilorazem różnicowym funkcji ![]()
w punkcie ![]()
nazywamy odwzorowanie ![]()
określone równaniem ![]()
. ![]()
nazywamy pochodną ![]()
w punkcie ![]()
;
![]()
nazywamy pochodną lewostronną w punkcie ![]()
;
![]()
nazywamy pochodną prawostronną w punkcie ![]()
.
Mówimy, że funkcja![]()
jest różniczkowalna ![]()
, gdy ![]()
istnieje i jest skończona.
Mówimy, że funkcja![]()
jest różniczkowalna na ![]()
, gdy![]()
![]()
jest różniczkowalna w ![]()
.
Mówimy, że funkcja![]()
jest różniczkowalna na ![]()
, gdy ![]()
jest różniczkowalna w ![]()
oraz pochodne jednostronne w punktach ![]()
istnieją i są skończone.
Definicja. Zał. że ![]()
jest różniczkowalna. Funkcję, która każdemu punktowi ![]()
przyporządkowuje ![]()
nazywamy pochodną funkcji ![]()
.
Mówimy, że ![]()
jest pochodną, jeśli istnieje ![]()
taka, że ![]()
.
Twierdzenie. Jeżeli funkcja ![]()
jest różniczkowalna w![]()
, to![]()
jest ciągła w ![]()
.
Twierdzenie. Jeżeli ![]()
są różniczkowalne w![]()
. Wtedy:
(1) ![]()
jest funkcją różniczkowalną w ![]()
i ![]()
;
(2) ![]()
jest funkcją różniczkowalną w ![]()
i ![]()
;
(3) ![]()
jest funkcją różniczkowalną w ![]()
i ![]()
;
(4) ![]()
i ![]()
jest funkcją różniczkowalną w ![]()
i 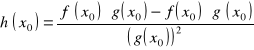
.
Twierdzenie. Funkcja![]()
jest różniczkowalna w ![]()
i ![]()
![]()
istnieje ![]()
taka, że ![]()
i ![]()
jest ciągła w ![]()
oraz ![]()
.
Twierdzenie. Zał. że ![]()
, ![]()
, ![]()
, ![]()
, ![]()
jest różniczkowalna w ![]()
, a ![]()
w ![]()
. Wtedy ![]()
jest różniczkowalna w ![]()
oraz ![]()
.
Twierdzenie. Zał. że ![]()
jest różnowartościowa, ciągła i różniczkowalna w ![]()
, ![]()
. Wtedy ![]()
jest różniczkowalna w ![]()
oraz ![]()
.
Definicja. Zał. że ![]()
. Wtedy:
(1) funkcja ![]()
posiada maksimum lokalne w ![]()
, gdy ![]()
;
(2) funkcja ![]()
ma ścisłe maksimum lokalne w ![]()
, gdy ![]()
;
(3) funkcja ![]()
posiada minimum lokalne w ![]()
, gdy ![]()
;
(4) funkcja ![]()
ma ścisłe maksimum lokalne w ![]()
, gdy ![]()
.
Twierdzenie. Zał. że ![]()
jest różniczkowalna na ![]()
. Wtedy, jeżeli ![]()
przyjmuje ekstremum lokalne w ![]()
, to ![]()
.
Twierdzenie Rolle'a. Zał. że ![]()
jest ciągła i różniczkowalna na ![]()
oraz ![]()
. Wtedy ![]()
.
Twierdzenie Lagrange'a. Zał. że ![]()
jest ciągła i różniczkowalna na ![]()
. Wtedy ![]()
.
Twierdzenie Cauchy'ego. Zał. że ![]()
są ciągłe i różniczkowalne na ![]()
. Wtedy ![]()
.
Twierdzenie. Zał. że ![]()
jest ciągła i różniczkowalna na ![]()
. Wtedy:
(1) ![]()
jest niemalejąca na ![]()
;
(2) ![]()
jest rosnąca na ![]()
, gdy ![]()
;
(3) ![]()
jest nierosnąca na ![]()
;
(4) ![]()
jest malejąca na ![]()
, gdy ![]()
.
Twierdzenie. Jeżeli ![]()
jest różniczkowalna, to ![]()
ma własność Darobux, tzn. ![]()
.
Reguła d'Hospitala. Zał. że ![]()
, ![]()
są różniczkowalne na ![]()
oraz ![]()
. Jeżeli 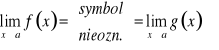
oraz 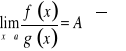
, to ![]()
.
Twierdzenie. Zał. że ![]()
jest ciągiem funkcji różniczkowalnych, ![]()
, ![]()
oraz ![]()
. Jeżeli ![]()
jest funkcją ciągłą oraz ![]()
jest jednostajnie zbieżny do ![]()
, to ![]()
jest różniczkowalna oraz ![]()
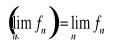
.
Wniosek. Zał. że ![]()
jest różniczkowalna ![]()
są ciągłe oraz ![]()
, ![]()
zbiega jednostajnie do ![]()
, to ![]()
jest różniczkowalna oraz ![]()
, 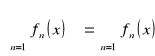
.
Twierdzenie. Szeregi ![]()
, ![]()
mają ten sam promień zbieżności ![]()
, oraz 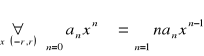
.
Definicja. Zał. że ![]()
jest różniczkowalna w ![]()
. Jeżeli ![]()
posiada pochodną w ![]()
, to pochodną tę nazywamy pochodną drugiego rzędu w ![]()
i oznaczamy ![]()
. Mówimy, że funkcja jest dwukrotnie różniczkowalna na ![]()
, gdy ![]()
istnieje i jest skończona.
Zał. że ![]()
oraz ![]()
jest n-krotnie różniczkowalna na ![]()
. Jeżeli istnieje pochodna funkcji ![]()
w ![]()
, to pochodną tę nazywamy pochodną ![]()
rzędu w ![]()
, oraz ![]()
.
Definicja. Mówimy, że funkcja ![]()
jest klasy ![]()
na ![]()
, jeżeli ![]()
jest określona i ciągła na ![]()
.
Mówimy, że funkcja ![]()
jest klasy ![]()
(jest „gładka”) na ![]()
, gdy ![]()
jest klasy ![]()
.
Twierdzenie Leibniza. Jeżeli ![]()
są funkcjami klasy ![]()
, to ![]()
oraz ![]()
, 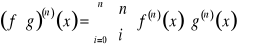
.
Twierdzenie Taylora. Zał. że ![]()
jest klasy ![]()
. Wtedy ![]()
.![]()
Definicja. Ustalmy ![]()
. Wtedy 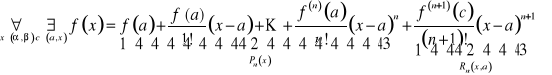
.
![]()
to n-ta reszta Taylora w postaci Lagrange'a. Wtedy ![]()
.
Jeżeli we wzorze Taylora podstawimy ![]()
to otrzymamy wzór MacLaurina ![]()
.
Twierdzenie. Jeżeli ![]()
oraz ![]()
i ![]()
, to 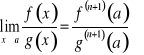
.
Definicja. Zał. że ![]()
. ![]()
nazywamy szeregiem Taylora (dla funkcji ![]()
względem środka ![]()
).
Twierdzenie. Jeżeli ![]()
, to 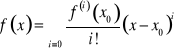
.
Definicja. Zał. że ![]()
. Mówimy, że ![]()
jest funkcją analityczną, gdy ![]()
jest równa sumie swojego szeregu MacLaurina.
Twierdzenie. Jeżeli ![]()
oraz ![]()
, to ![]()
jest funkcją analityczną.
Twierdzenie. Jeżeli ![]()
rozwija się w szereg MacLaurina, to istnieje tylko jedno takie rozwinięcie.
Twierdzenie. Jeżeli ![]()
jest różniczkowalna na ![]()
oraz ![]()
i ![]()
zmienia znak przechodząc przez ![]()
, to ![]()
posiada ekstremum lokalne w ![]()
.
Definicja. Zał. że ![]()
. Mówimy, że ![]()
ma punkt przegięcia w ![]()
, gdy ![]()
taka, że:
(1) na przedziale ![]()
![]()
leży nad styczną do wykresu ![]()
w punkcie ![]()
![]()
, a na przedziale ![]()
![]()
leży pod ![]()
;
(2) albo zachodzi sytuacja odwrotna.
Twierdzenie. Zał. że ![]()
oraz ![]()
. Wtedy:
(1) jeżeli ![]()
i ![]()
, to ![]()
posiada maksimum lokalne w ![]()
;
(2) jeżeli ![]()
i ![]()
, to ![]()
posiada minimum lokalne w ![]()
;
(3) jeżeli ![]()
i ![]()
dowolna, to ![]()
posiada punkt przegięcia w ![]()
.
Twierdzenie. Zał. że ![]()
. Wtedy:
(1) jeżeli ![]()
, to krzywa ![]()
jest dla pewnego otoczenia punktu ![]()
położona powyżej stycznej do tej krzywej w punkcie ![]()
(a więc skierowana wypukłością w dół);
(2) jeżeli ![]()
, to krzywa ![]()
jest dla pewnego otoczenia punktu ![]()
położona poniżej stycznej do tej krzywej w punkcie ![]()
(a więc skierowana wypukłością w górę).
1
Wyszukiwarka
Podobne podstrony:
Rachunek różniczkowy funkcji jednej zmiennej pochodne
5 Rachunek różniczkowy funkcji jednej zmiennej
MATEMATYKA Semestr 2 Rachunek Różniczkowy(1)
C 04,5 Rachunek różniczkowy funkcji wielu zmiennych
11 RACHUNEK RÓŻNICZKOWY FUNKCJI WIELU ZMIENNYCH
G M Fichtenholz Rachunek różniczkowy i całkowy (tom 1)
Zadania rachunek różniczkowy Polutechnika Poznańska PP, Automatyka i Robotyka, Analiza matematyczna
wykład, RACHUNEK ROZNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ 63, 1)
ZME Rachunek rozniczkowy
2011-Rachunek-rozniczkowy-Cwiczenia-4
Rachunek rozniczkowy moodle
Kolokwium rachunek różniczkowy
G M Fichtenholz Rachunek różniczkowy i całkowy (tom 3)
2011 Rachunek rozniczkowy Cwiczenia 4id 27564
Ćwiczenia z analizy matematycznej zadania 4 rachunek różniczkowy
,analiza matematyczna 1, rachunek różniczkowy funkcji jednej zmiennej
rachunek rozniczkowy st
Matematyka III (Ćw) - Lista 05 - Rachunek rózniczkowy funkcji wielu zmiennych, Odpowiedzi
02 rachunek różniczkowy pól wektorowych [feynmana wykl z fizyki tom2 1]fizyka] [www osiolek com] WYV
więcej podobnych podstron