wykład 3

Ruch krzywoliniowy

Krzywa płaska

M τ V

Δs M₁

n Δ*

ρ

0

0₁ Rys.23 Ruch krzywoliniowy punktu

po płaszczyźnie

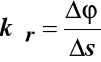
średnia krzywizna (34)

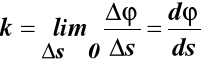
krzywizna toru w punkcie (35)

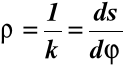
promień krzywizny (36)

Krzywa przestrzenna

pł. normalna

pł. prostująca

pł. ściśle styczna

b

τ

styczna

krzywa n

przestrzenna

normalna główna

ρ binormalna

0

Rys. 24

Prędkość i przyśpieszenie punktu w układzie naturalnym

Ruch płaski

V

M τ a_t

α M₁ Δ*

r Δs

n a

a_n

OM = r

O

Rys.25 Przyśpieszenie styczne i normalne w ruchu

krzywoliniowym punktu na płaszczyźnie

V = V·τ (36)

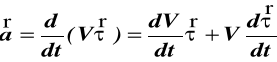
(37)

Pochodna wersora τ

n

τ Δτ

Δ*

A τ Rys.26 Przyrost wersora

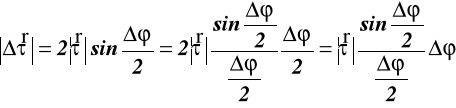
Po przejściu do granicy mamy:

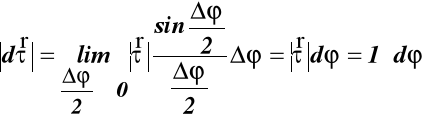
(38)

gdzie: τ = 1

stąd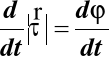
przyrost bezwzględny wersora

Kierunek przyrostu jest zgodny z kierunkiem i zwrotem

wersora n dlatego przyrost wersora τ możemy zapisać

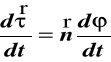
(39)

Podstawiając (39) do (37) otrzymujemy:

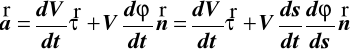
(40)

podstawiając do (40)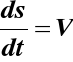
,
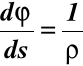
otrzymujemy

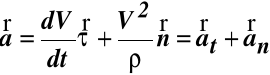
(41)

gdzie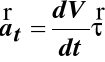

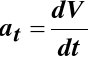
przyśpieszenie styczne

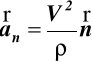
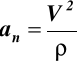
przyśpieszenie normalne (42)

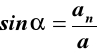
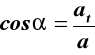
(43)

Przykład 7

Samochód jedzie po moście z prędkością, której wartość

jest stała i wynosi V = 72km/h. Należy wyznaczyć największe przyśpieszenie samochodu, jeżeli wiadomo, że most ma zarys paraboliczny. Wymiary mostu podano na rysunku 27.

Rozwiązanie

Wartość przyśpieszenia stycznego (42)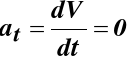

V

h = 1m a_n x

l /2 = 10m l /2 = 10m

ρ

Rys.27 Geometria mostu

Równanie mostu

;
;
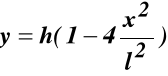
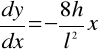
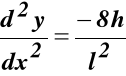
(a)

Z matematyki krzywizna linii płaskiej, wstawiając (a)

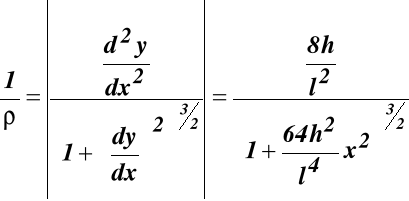
(b)

Z (42) wynika, że a_tmax dla ρ_min czyli dla x = 0 patrz (b)

Wstawiając do (b) x = 0, l = 20m, h = 1m, mamy:

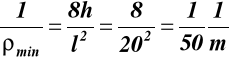
Biorąc pod uwagę, że
, na podstawie

wzoru (42) otrzymujemy

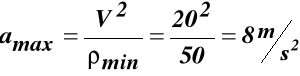
Ruch punktu po okręgu

y

A *

r s

O A₀ x

Rys.28 Ruch punktu po okręgu

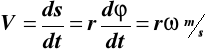
gdzie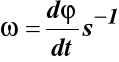

ω prędkość kątowa, n prędkość obrotowa,

jeśli n obr min to

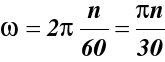
(44)

ponieważ ρ = r to

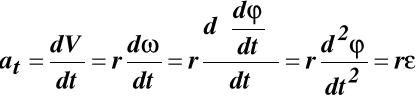
a_t = rε (45)

gdzie: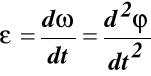
(46)

Przyśpieszenie normalne:

(46)

Przyśpieszenie całkowite:

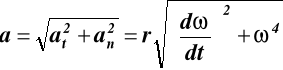
(47)

Prędkość kątowa i przyśpieszenie kątowe jako wektory

z

V A

e

r

*

O A₀

π R

ε

δ

ω

0₁

Rys.29 Ruch punktu po okręgu

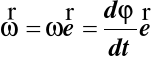
(46)

Prędkość kątowa ω, mająca wartość pochodnej względem

czasu kąta obrotu *, jest wektorem leżącym na osi obrotu.

Moduł wektora prędkości V = ωRsinδ = ωr (47)

V = ω×R (48)

Wektor V jest prostopadły do wektorów ω i R (rys.29).

Przyspieszenie:

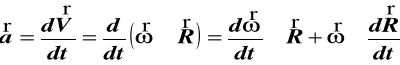
(b)

Przyśpieszenie kątowe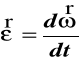
(49)

podstawiamy (49) do (b) i pamiętając że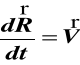

otrzymujemy
(50)

gdzie:
(51)

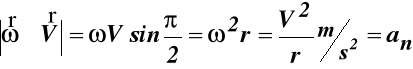
(52)

Przykład 8

Punkt A porusza się po okręgu koła o promieniu r = 0.5m

ze stałą co do wartości prędkością. Promień wodzący OA

tego punktu (rys.30) wykonuje przy tym n = 300 obr/min.

należy wyznaczyć przyśpieszenie punktu A.

Rozwiązanie

Wyznaczamy prędkość kątową ω A

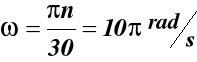
0 a_n

Ponieważ V = const. to a_t = 0 r

z wzoru (52) mamy:

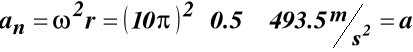
Rys.30

Przejście między układem naturalnym a prostokątnym

na płaszczyźnie.

a_y τ

y

V

n V_y a β a_t

α

A

l a_x V_x

0 x

Rys.31

(c)

Ponieważ: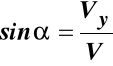
;
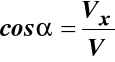
(d)

Wstawiając (d) do (c) otrzymujemy:

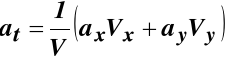
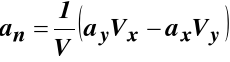
(53)

Przykład 9

Znaleźć przyśpieszenie styczne i normalne dla ruchu określonego równaniami ruchu:

m ;
m

Rozwiązanie

;
(e)

;
(f)

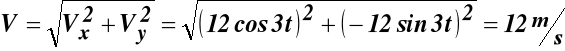
(g)

wstawiając (e), (f) i (g) do (53) otrzymujemy:

a_t = 0; a_n = - 36m/s^-2

18kin

19kin

20kin

21kin

y

22kin

23kin

24kin

25kin

---