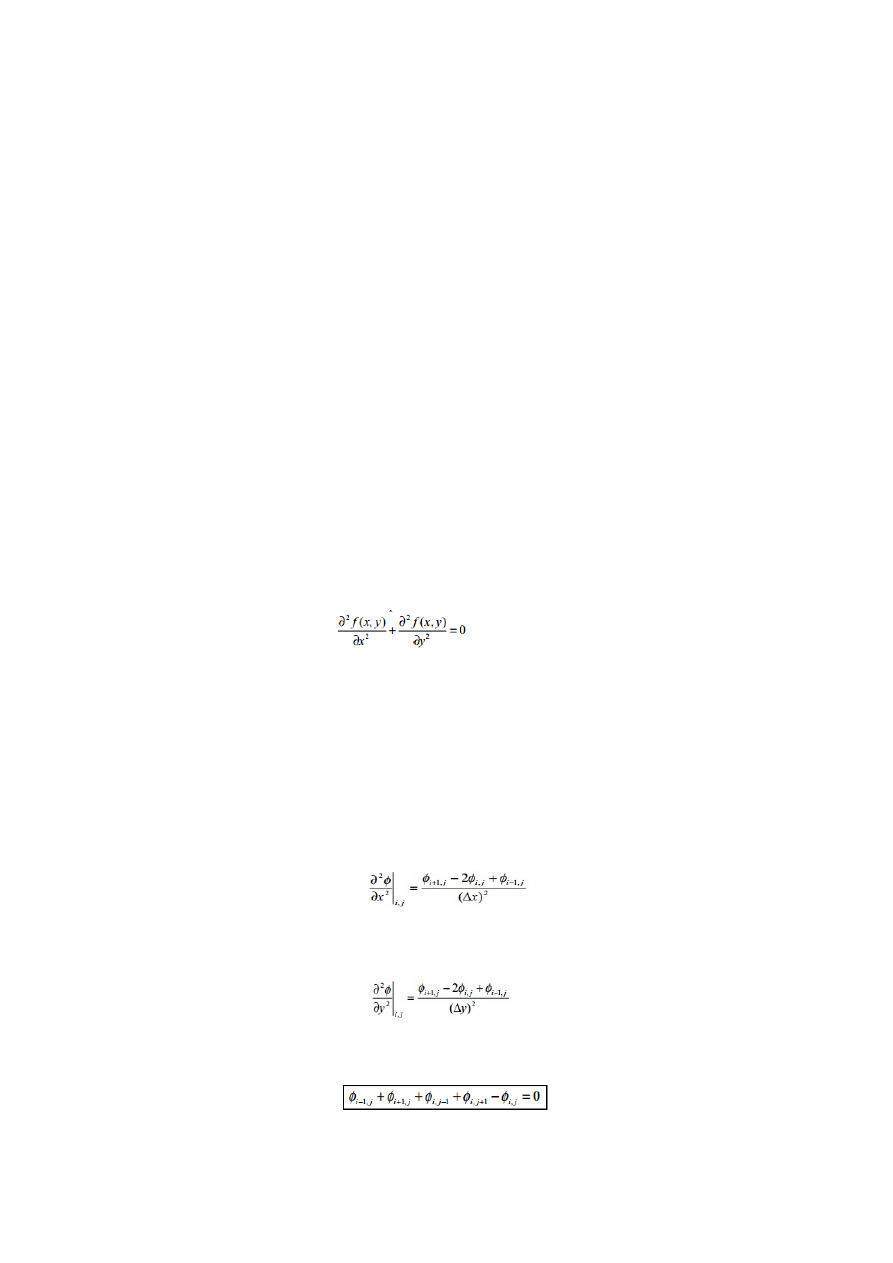
Sprawozdanie

Grupa : Małgorzata Luchter, Anna Duda, Paulina Chłosta, Dominik Bujas

Metoda różnic skończonych jest jedną z najstarszych z metod numerycznych. Pomimo prostoty
niezbędnych obliczeń które trzeba zrobić ich liczba nawet w najprostszym wypadku, jest często
zbyt duża by można wykonać ją ręcznie. Korzystając z komputera można te obliczenia w dość
stosunkowo szybkim czasie wykonać oraz przestawić wynik graficznie.
Klasyczne rozwiązanie metod różnic skończonych jest trudne jeżeli np. : ośrodek jest anizotropowy
lub niejednorodny, region rozwiązania jest dość złożony, warunki brzegowe są mieszanych typów.

Metoda różnic skończonych bazuje na przekształceniu pochodnych cząstkowych, w równania
różnic cząstkowych, opisujące proces fizyczny przy pomocy przybliżeń algebraicznych.
Aby rozwiązać problem za pomocą metody różnic skończonych wystarczą trzy kroki :

1) określenie geometrii modelu oraz jego podział na siatkę węzłów ( to proces dyskretyzacji

modelu ciągłego)

2) znalezienie odpowiedniego równania różniczkowego do opisu problemu oraz jego

przybliżenie przez równoważne równanie różniczkowe

3) rozwiązanie równań różniczkowych przy określonych warunkach początkowych lub

brzegowych

Rozważmy dwuwymiarowe równanie Laplace’a dla dowolnego obszaru z określonymi warunkami
granicznymi :

Cały obszar zostaje podzielony siatką kwadratową o rozmiarach ∆x,∆y lub siatka prostokątna, ale
kwadratowa znacznie ułatwia obliczenia. Wybieramy dowolny punkt na siatce o współrzędnych (i,
j) wraz z jego otoczeniem i określamy potencjał tego punktu.

Teraz to równanie trzeba rozwinąć w otoczeniu punktu (i,j) w szereg Taylora . Ostatecznie po kilku
przekształceniach otrzymujemy :

Postępując analogicznie dla zmiennej y, otrzymujemy:

Dla ułatwienia założyliśmy że siatka jest kwadratowa, więc podstawiamy ∆x = ∆y = h , i
dzielimy przez h. Otrzymujemy w ten sposób równanie:

Wady korzystania z metod różnicowych:

●

Poprawa dokładności obliczeń w zasadzie tylko poprzez zagęszczenie rozmiaru siatki .

●

Trudności z dopasowaniem siatki do skomplikowanych granic obszarów analizyoraz do
krzywoliniowych obiektów w modelu .

●

Kolejnym problemem jest konieczność takiego samego podziału , co jest związane z duża
liczbą węzłów, a zatem duże obciążenie pamięci oraz procesora i wpływa na duży czas
obliczeń .

Georadar (GPR) jest metodą elektromagnetyczną. Fala impulsowa posiadająca określoną
częstotliwość zostaje wyemitowana w głąb ziemi lub struktury badanego obiektu. Spotykając na
drodze kolejne przeszkody lub granice warstw o różnych własnościach dielektrycznych część
niesionej energii odbija się a część przechodzi do drugiego ośrodka. Powstaje fala odbita i fala
załamana. Kąt padania fali jest równy kątowi odbicia. Impuls odbity wracając jest rejestrowany na
powierzchni.

 Metoda georadarowa(GPR) opiera się na zastosowaniu fali mechanicznej wykorzystującej
impuls elektromagnetyczny. Najbardziej typowymi georadarowymi systemami pomiarowymi są
systemy jednokanałowe. Taki system składa się z dwóch anten najczęściej zamkniętych razem w
jednej obudowie. W tym przypadku anteny georadaru zawsze znajdują się w stałej odległości od
siebie (profilowanie).W badaniach georadarowych wykorzystuje częstotliwości fal pomiędzy 10
MHz a kilka GHz.

 W skład systemu do badań georadarowych wchodzą następujące elementy:

•

jednostka sterująca,

•

rejestrator danych,

•

komputer połączony z jednostką sterującą kablem transmisyjnym,

•

urządzenie do pomiaru odległości.
 Pojawiają się również systemy wielokanałowych georadarów, które są używane wtedy
gry pomiar jednokanałowy jest niewystarczający.

•

Zrzut ekranowy geometrii modelu oraz parametrów obliczeniowych przyjętych do
modelowania :

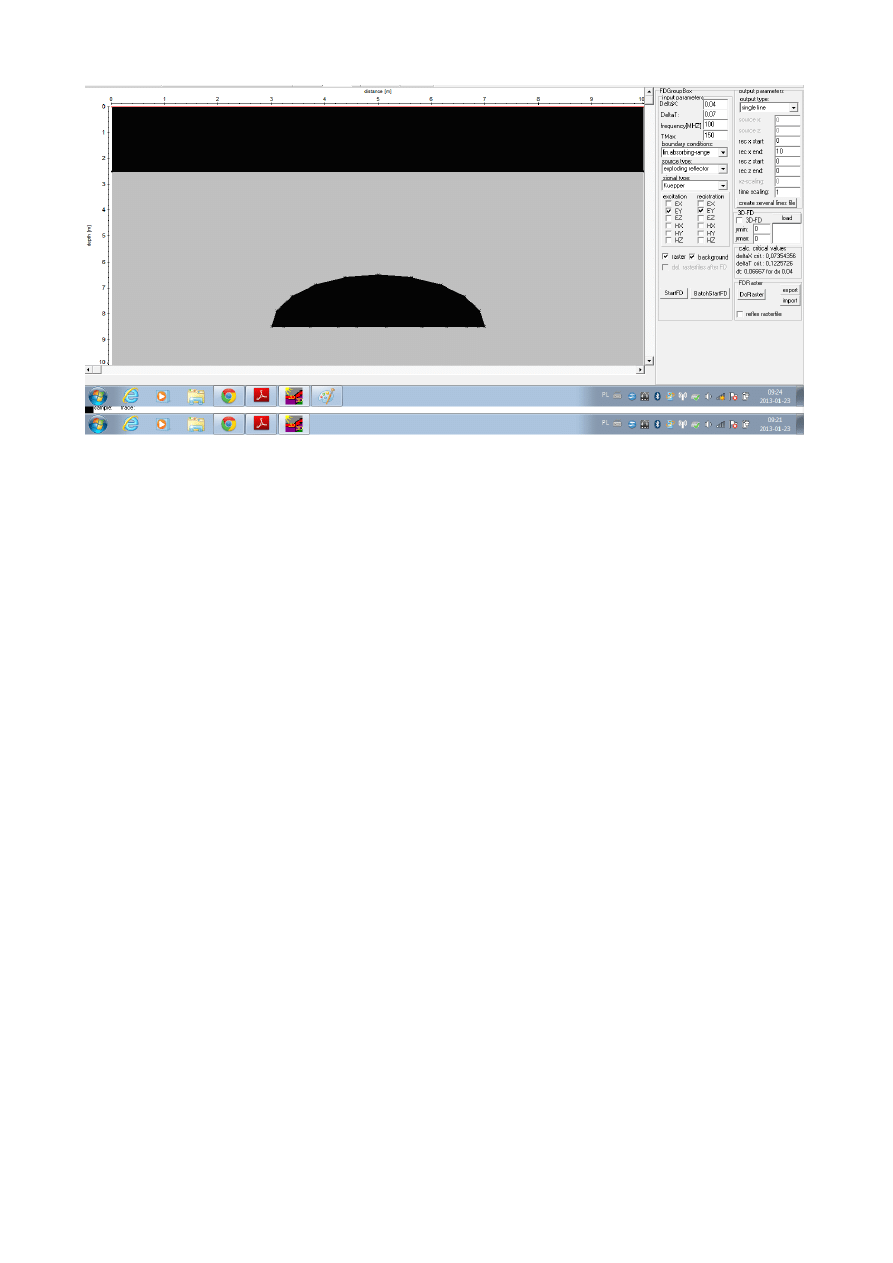
Wiemy z opisu , że badanie było po powierzchni ziemi, częstotliwość wynosi 100 MHz,
profilowania pionowe w standardzie, układ anteny nadawczej i odbiorczej był równoległy w
stosunku do siebie i prostopadły w stosunku profilowym. Hiperbola na echogramie jednoznacznie
wskazuje, zdołaliśmy na profilu 10 metrowym zarejestrować jedna pustkę. Położenie
głębokościowe jest nieznane, więc przyjęliśmy na początku głębokość równą 10m a później
dopasowywaliśmy . Dla pierwszej granicy geologicznej ustawiliśmy parametry materiałowe dla
łupków(epsilon 6,5 , mi zawsze przyjmujemy 1 , sigma 0,002)natomiast drugą granicę jako
wapienie(epsilon 4,5 , sigma 0,001) .Stąd zmienne wielkości deltaX oraz deltaT . Ponadto z
echogramu wynika, że badania były robione w oknie 150 ns .Prędkość rozchodzenia się fali dla
pierwszej warstwy wynosi ok 11,77 cm/ns . Natomiast dla drugiej warstwy ok 14,14 cm/ns .
Warunki brzegowe : przyjmujemy warunek brzegowy tłumiący. Typ źródła : źródło punktowe. Typ
sygnału jaki będzie wysyłany można wywnioskować z echogramu : Kuepper'a Modelujemy
pojedyncza linię profilową, źródło jest na powierzchni terenu czyli jest równe zero, odbiorniki
symulujemy wzdłuż całych linii profilowych .

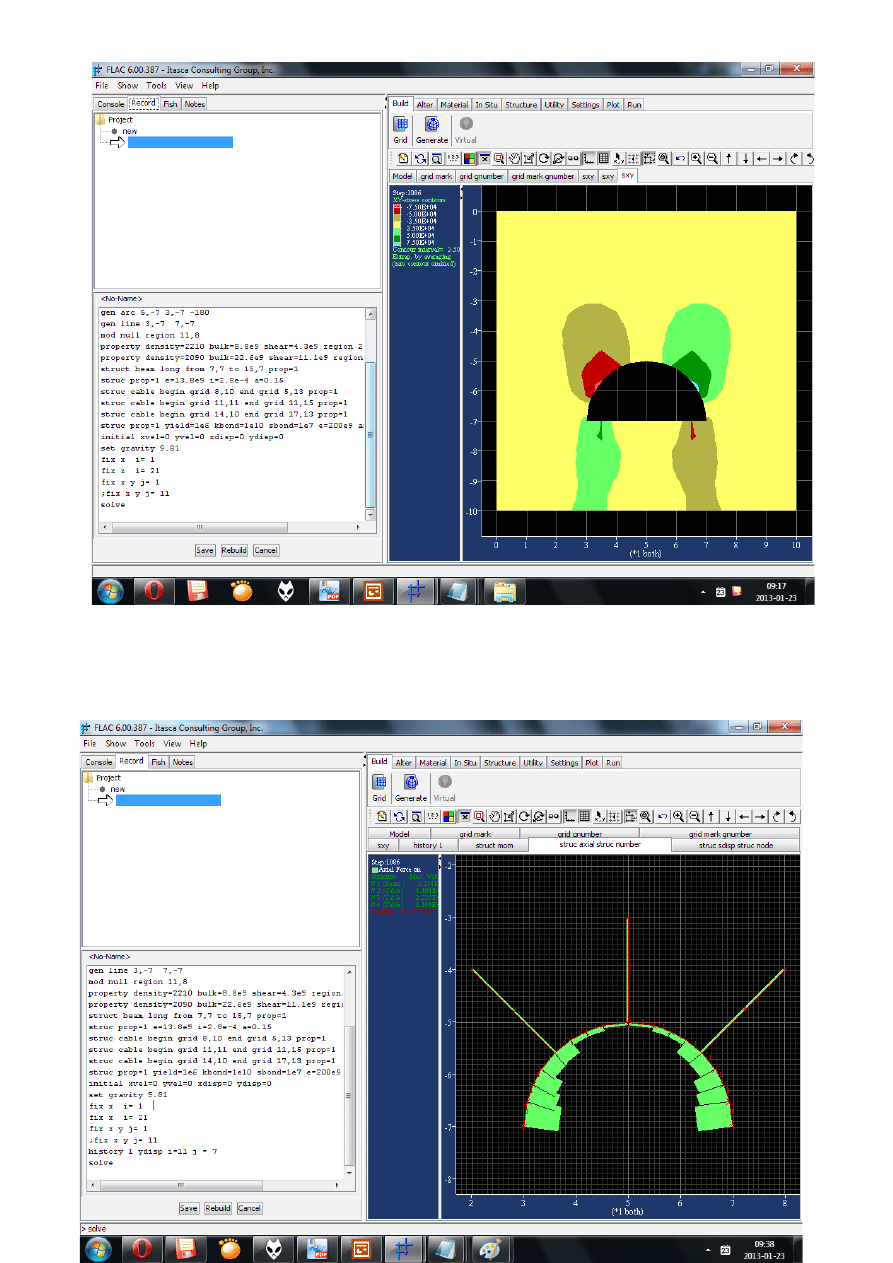
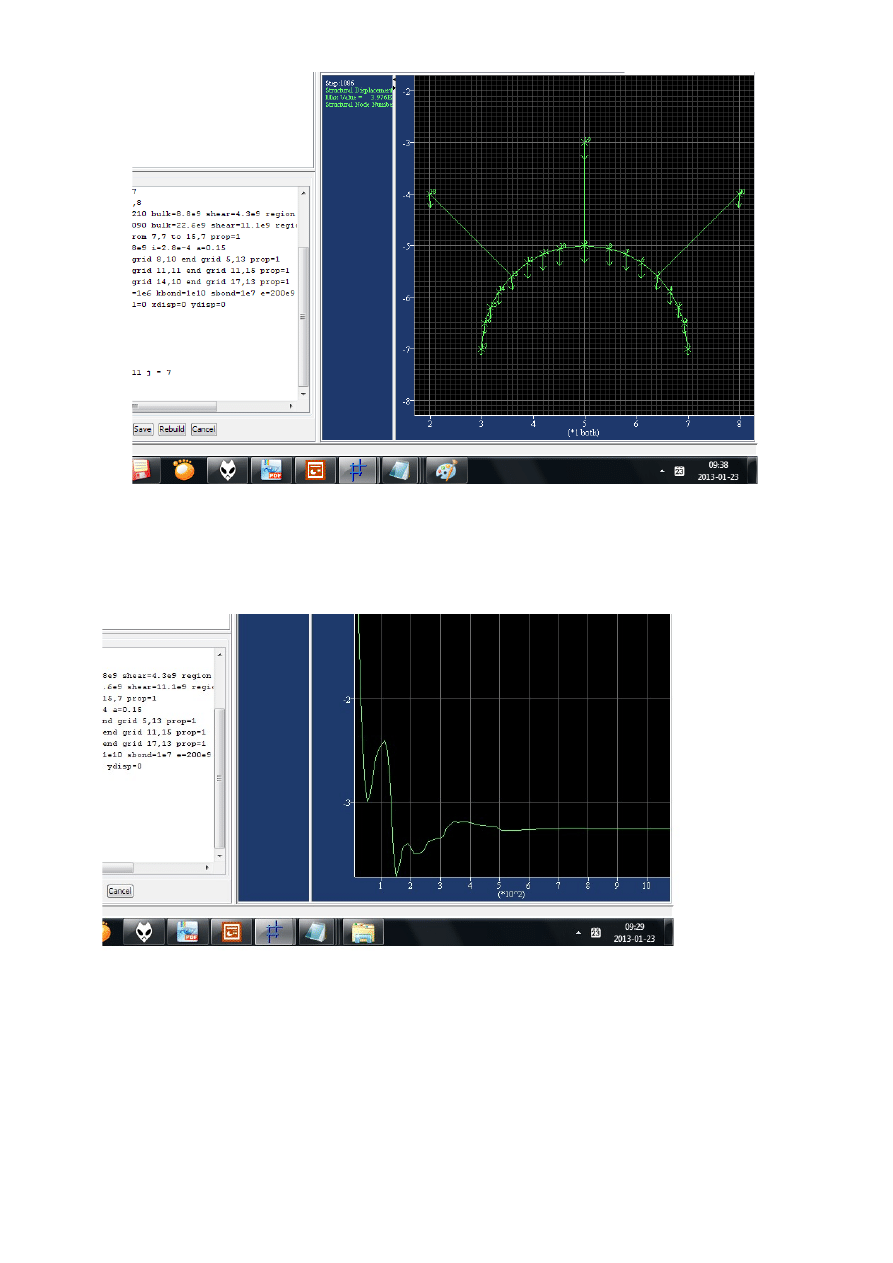
Teoria Geomechaniki :

Zacznijmy od tego, że naprężenie jest wielkością tensorową . Definiowane jest poprzez granicę
stosunku przyrostu siły działającej na powierzchnię , skierowaną do pola tej powierzchni . Można ją
rozłożyć na składowe : styczną i normalną do elementu objętości .
Wartości ujemne naprężeń normalnych określają kompresję , a dodatnie tensję . W przypadku
naprężeń stycznych znak określa kierunek ścinania lub dystorsji .
Wykorzystując naprężenia główne można wyznaczyć wartość naprężeń w dowolnym punkcie
płaszczyzny . Górotwór jako fizyczne ciało może podlegać odkształceniom postaci i objętości . Aby
wyznaczyć z tensora naprężenia składowe odpowiadające za te dwa procesy należy zapisać go w
postaci sumy aksjatora i dewiatora . Związek pomiędzy naprężeniem a odkształceniem ciała zależy
od parametrów materiałowych tego ciała . Kryterium wytrzymałości określa przy jakich
naprężeniach w górotworze następuje przejście systemu sprężystego w stan niesprężysty .
Jednoznaczne wyznaczenie granicy zniszczenia górotworu jest trudne . Plastyczne płynięcie jest
cecha charakterystyczna utworów geologicznych typu gliny , iły, muły .W przypadku skał
zniszczenie jest najczęściej wynikiem pękania poślizgowego przez ścinanie lub przez tensję .