88

Rozdział 7
MODELOWANIE BIOMECHANICZNE

Szczególne zainteresowanie biomechaników skupia się na modelowaniu i metodach rehabilitacji

ruchu. Za pomocą metod teorii sterowania przeprowadza się analizę aparatu szkieletowo-mięśniowo-

stawowego oraz lokomocji człowieka, na podstawie której tworzone są modele biomechaniczne.

Obecnie zauważa się rosnące zainteresowanie modelami obliczeniowymi, które również nazywane są

„eksperymentami obliczeniowymi”, ponieważ przede wszystkim redukują liczbę kontrowersyjnych

badań na zwierzętach.

7.1. Wprowadzenie do modelowania

W analizie biomechanicznej bardzo ważna jest wiedza na temat geometrycznych i wewnętrznych

cech ludzkiego ciała, aby otrzymać statyczne i dynamiczne dane antropometryczne do budowy modelu

biomechanicznego. Ponadto, model musi obejmować dużą liczbę stopni swobody, aby lepiej

symulować rzeczywisty obiekt. W celu uzyskania tego zadania, najodpowiedniejszym modelem jest

model kinematycznych łańcuchów, gdzie segmenty ciała są połączone za pomocą stawów.

Zgodnie z teorią modelowania, model może być zdefiniowany jako obiekt, istniejący lub

abstrakcyjny, który podczas badań dostarcza informacji na temat rzeczywistego obiektu i powiązanych

z nim zjawisk. W ten sposób modelowanie składa się z opracowania reprezentacji własności obiektu

lub zjawiska w odniesieniu do celu jego analizy. Ogólnie, modelowanie polega na przejściu od obiektu

rzeczywistego, poprzez model fizyczny, do opisu matematycznego.

Model fizyczny to pewne uproszczenie konstrukcji rzeczywistej. Powinien dostatecznie dokładnie

odzwierciedlać zjawiska zachodzące w badanym obiekcie, a jednocześnie być możliwie prosty do

opisu matematycznego. Fizyczne modelowanie jest koniecznym pierwszym etapem procedury

modelowania. W inżynierii mechanicznej, ten etap rozpoczyna się projektowaniem cech graficznych

komponentów systemu, przedstawiających szczyty połączone przez łuki reprezentujące ich

wewnętrzne powiązania. W celu uproszczenia analizy podsystemy są przeważnie identyfikowane i

zamodelowane oddzielnie przez odwrócenie ich związków z resztą systemu w działania zewnętrzne.

Ponieważ model fizyczny jest tylko uproszczeniem rzeczywistości, prawdziwe zjawisko różni się od

zachowania modelu. Z tego powodu określenie cech jakościowych modelu powinno być dokonane ze

szczególną ostrożnością i świadomością konsekwencji każdego wyboru oraz uproszczenia.

Model fizyczny stosowany w mechanice ogólnej może między innymi zawierać pojęcia

abstrakcyjne, bryły idealne, punkty materialne, czy siły skupione. Bryła idealna, to ciało, które pod

działaniem dowolnie wielkich sił nie odkształca się., natomiast punkt materialny to taki, który posiada

zerowe wymiary ale ma masę. Siła skupiona to siła, która jest przyłożona do punktu o zerowych

wymiarach.

89

Po ustaleniu modelu fizycznego, drugim etapem procedury modelowania jest opracowanie modelu

matematycznego. Model matematyczny to analityczny opis badanych zjawisk zachodzących w modelu

fizycznym, który za pomocą wzorów matematycznych tworzy algorytm pozwalający rozwiązać

problem. Model matematyczny przeważnie składa się ze zbioru równań z warunkami brzegowymi i

może być otrzymany bezpośrednio przez odniesienie praw fizycznych zarządzających danym

zjawiskiem lub empirycznie przez zastosowanie procedury identyfikacji bazując na pomiarach

eksperymentalnych. Końcowy etap modelowania polega na uwierzytelnieniu modelu przez

porównanie zachowań teoretycznych z rzeczywistymi. W przypadku nieścisłości należy zacząć

procedurę modelowania od początku, rozpoczynając od modyfikacji modelu fizycznego.

Biomechaniczne badania bazują na wyidealizowanej reprezentacji fizycznej systemu mięśniowo-

szkieletowego, dla którego dokonuje się wstępnych założeń (zweryfikowanych na końcu badań).

Jednak naturalny ruch zawsze obejmuje kilka mięśni, a złożone strategie sterowania neuro-mięśniowe

nie są wciąż znane.

W procesie modelowania wykorzystuje się następujące elementy, które można zdefiniować [41]:



Model – obiekt, plan lub teoria, która reprezentuje lub imituje wiele cech obiektu

rzeczywistego (próba reprezentowania rzeczywistości);



Dedukcja – logiczne rozumowanie ze znanego w nieznane, przechodząc od ogółu do

szczegółu;



Indukcja – logiczne rozumowanie na podstawie faktów lub indywidualnych przypadków do

ogólnej konkluzji;



Uwierzytelnianie modelu – dostarczenie dowodów, iż model jest wystarczająco silny i

skuteczny, wykorzystując:

a) pomiary bezpośrednie – porównanie wyników oszacowanych z modelu z wynikami

rzeczywistymi,

b) pomiary pośrednie – pomiary innych zmiennych i porównanie z przewidywanymi

wartościami tej zmiennej z modelu.



Model biomechaniczny – mikroskopowa i makroskopowa reprezentacja systemu

biologicznego;



Diagram ciała swobodnego (wyswobodzonego z więzów) – uproszczony rysunek systemu

mechanicznego, odizolowanego od otoczenia, pokazujący wszystkie wektory sił i momentów

działających na ciało.

Modelowanie biomechaniczne służy do:

1. otrzymania informacji o strukturze i funkcji systemu biologicznego,

2. uproszczenia zrozumienia struktury i funkcji systemu biologicznego,

3. uproszczenia analizy kinematycznej i dynamicznej systemu biologicznego,

90

4. obserwacji zachowania systemu biologicznego pod wpływem działania różnych. Umożliwia

przewidzenie zagrażających warunków obciążenia bez podejmowania rzeczywistego ryzyka.

5. do celów medycznych: monitorowania funkcji fizjologicznych, takich jak: ruch, przepływ

krwi, wzrost lub rekonstrukcja kości, do diagnozowania nieprawidłowego funkcjonowania

organizmu człowieka, leczenia, terapii, rehabilitacji, zastępowania utraconych kończyn i

organów (protetyka, projektowanie implantów),

6. do celów nie-medycznych: badania wytrzymałości człowieka na obciążenia (np. w

ergonomii), w inżynierii projektowania bezpiecznych pojazdów, poprzez zbadanie

zachowania się ludzkiego ciała podczas wypadków i do zapobiegania urazom: projektowanie

kasków, pasów bezpieczeństwa, poduszek powietrznych, bezpieczeństwa produkcyjnego, itd.

Informacja użyta do budowy modelu to:

1. wiedza na temat układu modelowanego – przy użyciu wiedzy na temat modelu modelowanego

można przejść od zasad bardziej ogólnych do szczegółowych (proces dedukcyjny),

2. dane eksperymentalne, które tworzą wejścia i wyjścia układu, na podstawie których można

wysuwać ogólne wnioski na temat działania układu (proces indukcyjny).

Do budowy każdego typu modelu stosuje się uogólnienie, pamiętając jednak, że uproszczenie nie

zawsze jest zgodne z rzeczywistością. Kluczem w modelowaniu jest wiedza, jakie elementy i ich

wzajemne relacje powinno się uwzględnić, a które można pominąć.

Rozróżnia się następujące typy modeli:

1. analityczne, czyli dedukcyjne,

2. pół-analityczne (semi-analityczne) – użycie wielu założeń, ze względu na większą liczbę

niewiadomych w stosunku do równań w celu znalezienia rozwiązania,

3. czarna skrzynka – modele regresyjne, użycie funkcji do określenia zależności pomiędzy

wejściami a wyjściami,

4. koncepcyjne – używane w testowaniu hipotetycznym.

Modele biomechaniczne mogą występować w różnych formach: modele konceptualne, modele

fizyczne, modele matematyczne (zarówno napisane na papierze, jak i przy wykorzystaniu komputera).

Są to modele struktur (takich, jak mięśnie), modele organów, a także modele systemów organizmów.

Te różne systemy modeli mogą być opracowywane oddzielnie, ale wiedza z nich płynąca może być

łączona w tzw. integracji modeli.

Etapy modelowania biomechanicznego są następujące:

1. zdefiniowanie pytań, na które szuka się odpowiedzi,

2. zdefiniowanie układu,

3. przejrzenie istniejącej wiedzy (przegląd literatury),

4. wybranie procedury tworzenia modelu, która ma zostać zastosowana do uzyskania odpowiedzi

na postawione pytanie, a następnie wybranie metody badawczej,

91

5. ustalenie uproszczeń i założeń, czyli podjęcie decyzji, co powinno znaleźć się w modelu, a co

można pominąć,

6. sformułowanie matematycznego podejścia i metody statystycznej, które zostaną zastosowane

do danych,

7. opracowanie rozwiązania matematycznego,

8. oszacowanie modelu,

9. dyskusja, interpretacja i zastosowanie wyników,

10. wnioski.

Modele biomechaniczne dzieli się na statyczne i dynamiczne [41]:

a. Statyka stosuje stałe prędkości liniowe i kątowe (liniowe i kątowe przyspieszenie =0)

Założenia do analizy statycznej:

- znane anatomiczne osie obrotu,

- jedna grupa mięśni przejmuje sterowanie stawem,

- znane miejsca przyczepienia mięśni,

- znane linie działania mięśni,

- znane wagi i środki ciężkości segmentów,

- brak tarcia w stawach, czyli połączeniach segmentów,

- nie jest rozważany dynamiczny aspekt problemu,

- rozważania tylko w dwóch wymiarach,

- ignorowana deformacja mięśni, ścięgien i kości,

- reguła prawej ręki dla określenia momentów sił.

b. Dynamika stosuje zmienną prędkość liniową i kątową (liniowe i kątowe przyspieszenie



0)

1. Wymiary obiektu:

a. punkt – masa (0 wymiarów),

b. linia (1 wymiar),

c. płaszczyzna (2 wymiary),

d. bryła (3 wymiary).

2. Wymiary przestrzeni:

a. jednoosiowa,

b. dwuosiowa,

c. trójosiowa (trójwymiarowy układ współrzędnych kartezjański).

3. Modele mogą być:

a. jednosegmentowe - używają wewnętrznych i zewnętrznych sił oraz momentów sił.

Brak liniowych i kątowych przyspieszeń, co oznacza, że ciało może poruszać się ze

stałą prędkością,

b. wielosegmentowe - stosują siły reakcji oraz momenty sił pomiędzy segmentami.

Parametry wejściowe do modeli biomechanicznych:

92

1. pomiary bezpośrednie – rzeczywiste pomiary parametrów użytych w modelu (np. waga,

wzrost itd.);

2. pomiary pośrednie – pomiary uzyskane z innych źródeł informacji (np. lokalizacja środka

masy segmentów ciała, proporcje segmentów z całej wysokości ciała, oszacowanie gęstości

segmentów ciała);

3. dynamika odwrotna – użycie liniowych i kątowych parametrów przyspieszenia oraz

informacji o masie segmentów i momencie bezwładności do określenia sił i momentów

obrotowych.

Aby powstał model biomechaniczny człowieka, należy wziąć pod uwagę bardzo złożoną analizę

aparatu mięśniowo-szkieletowego, która powinna obejmować: biomechanikę mięśni, biomechanikę

stawów, badanie kończyn, badanie chrząstek, lokomocję, mechanikę tkanek miękkich i przepływy w

arteriach. W celu przeprowadzenia modelowania biomechanicznego należy przeprowadzić

skomplikowaną analizę i syntezę ruchu, do której należy wykorzystać wiedzę z następujących

dziedzin: mechaniki teoretycznej, mechaniki płynów, elektrotechniki teoretycznej, elektroniki, teorii

sterowania, cybernetyki technicznej, informatyki i bioniki, mechatroniki, itd. Złożone partie ludzkiego

aparatu mięśniowo-szkieletowego są trudne do zamodelowania za pomocą tradycyjnych metod

inżynierskich. W ostatnich latach zaczęto na szeroką skalę stosować modelowanie i symulacje

komputerowe bazujące na metodzie elementów skończonych (MES) [35].

Modele biomechaniczne mają kilka praktycznych ograniczeń:

1. liczba zmiennych sterowania rozważanych w tym samym czasie w modelu jest ograniczona ze

względu na ograniczenie czasu;

2. potrzebnych jest wiele kroków przetwarzania do określenia związków pomiędzy zmiennymi

sterowania oraz działaniami EMG (funkcji matematycznych), które mogą być nieliniowe;

3. wiele modeli oszacowań rzadko bierze pod uwagę indywidualne cechy odróżniające osobniki od

siebie, ponieważ matematyczne modele używają tzw. funkcji celowych do optymalizowania

obciążenia np. kręgosłupa.

7.2. Rodzaje modeli biomechanicznych

Modele biomechaniczne ludzkiego ciała są bardzo ważnymi narzędziami w zrozumieniu

funkcjonowania ludzkiego ruchu i jego koordynacji. Tworzenie modeli biomechanicznych ludzkiego

układu mięśniowo-szkieletowego ma szczególne znaczenie dla analizy zjawisk dynamicznych ciała

człowieka. Techniki komputerowego modelowania biomechanicznego zastosowane do ludzkiego ciała

dostarczają bezinwazyjnych możliwości analizy struktury mięśniowo – szkieletowej. Przykłady tych

modeli obejmują [24,35,41]:

- modele połączonych segmentów, używane do oszacowania kinematyki stawów;

- modele mięśni, użyte do oszacowania indywidualnych sił mięśni oraz energetyki;

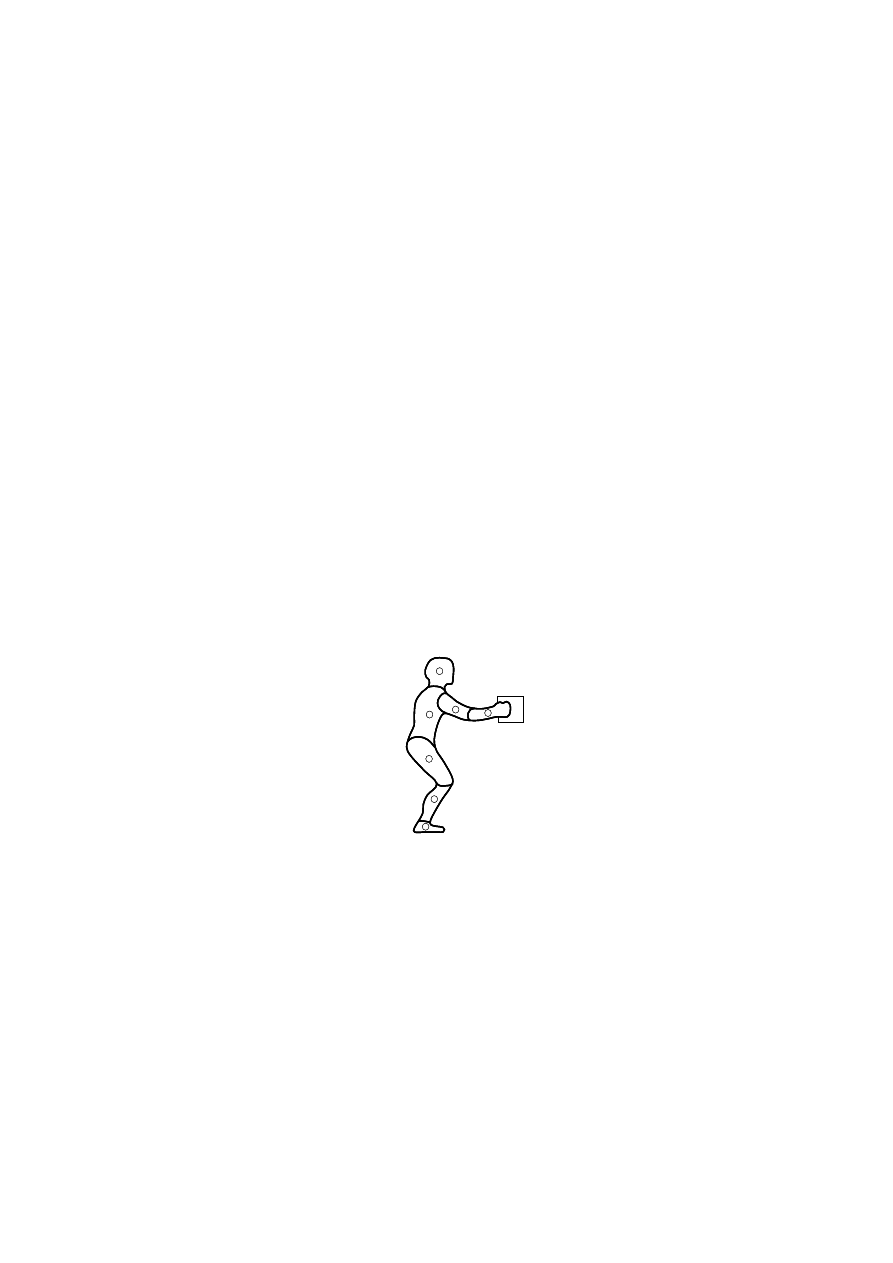
93

- symulację oraz metody dynamiki odwróconej do oszacowania koordynacji i optymalizacji strategii

ruchu,

- modelowanie metodą elementów sztywnych do matematycznego i graficznego opisu

komponentów strukturalnych, takich jak: kości, stawy i więzadła, w celu określenia sił, naprężeń i

ich odkształceń;

- modelowanie metodą elementów skończonych;

- metody sztucznych sieci neuronowych do zamodelowania roli systemu nerwowego w sterowaniu

np. ruchem.

Istnieje kilka rodzajów metod tworzenia modeli biomechanicznych. Do najpopularniejszych należy

metoda podziału ciała na segmenty oraz modelowanie za pomocą elementów sztywnych i

skończonych.

7.2.1. Metoda podziału ciała na segmenty

Model ciała można przedstawić jako bryły połączone przez stawy. Model ten opiera się na

uproszczonych założeniach, takich jak jednorodna gęstość w sekcjach przecięcia oraz wzdłuż osi

wzdłużnych segmentu. Elementy wiotkie ciała są pomijane. Zakłada się pełną symetrię ciała w

odniesieniu do płaszczyzny przyśrodkowej, tzn. całkowitą symetrię strony prawej i lewej.

Przykładowy model segmentowy został przedstawiony na rys. 7.1.

Stopa

Łydka

Udo

Tułów

Głowa/szyja

Przedramię

Ramię górne

Środek ciężkości

Obiekt

Stopa

Łydka

Udo

Tułów

Głowa/szyja

Przedramię

Ramię górne

Środek ciężkości

Obiekt

Rys. 7.1. Podział ciała na segmenty [99]

Kształt geometrycznych brył, które reprezentują segmenty ciała, zależy od kształtu segmentu oraz

lokalizacji środka masy. Niektóre liniowe wymiary segmentów ciała są mierzone, a inne określane z

obliczonych wartości i znanych pozycji środków mas segmentów. Po utworzeniu modelu

segmentowego ciała można przeprowadzić statyczną analizę, która wymaga spełnienia pewnych

założeń, a mianowicie:

- znane są anatomiczne osie obrotu,

- tylko jedna grupa mięśni dominuje sterowaniem połączenia między segmentami (stawu),

- znane są punkty zaczepienia mięśni,

- znane wagi segmentów oraz ich środki ciężkości,

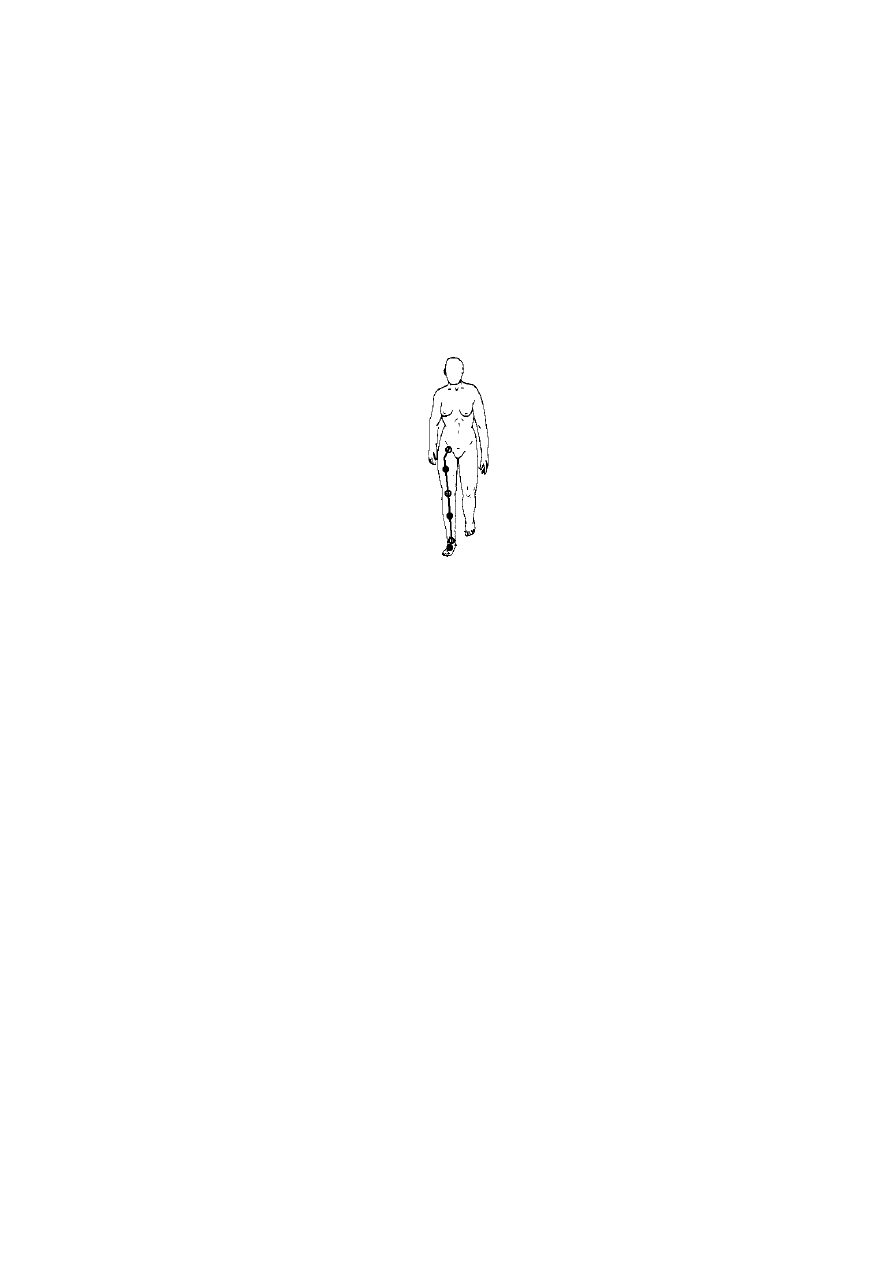
94

- brak tarcia w połączeniach,

- brak rozważenia dynamicznych aspektów,

- pomijanie odkształceń mięśni, ścięgien, kości itd.

7.2.2. Modelowanie metodą elementów sztywnych

Element sztywny, to element, który nie może być deformowany, rozciągany lub ściskany. Na rys.

7.2 został przedstawiony model ciała, którego cechy obejmują stałe pozycje w odniesieniu do siebie

(rys. 7.2).

Rys. 7.2. Przykład podziału kończyny dolnej metodą elementów sztywnych [99]

Techniki modelowania elementami sztywnymi są używane do określenia napięć, deformacji, sił i

ustawień w systemach biomechanicznych, składających się z komponentów strukturalnych takich jak

kości, połączenia i wiązadła. Połączenia między elementami sztywnymi mogą wykonywać

następujące ruchy:

1. ruch translacyjny,

2. obrót wokół ustalonych osi,

3. ogólny ruch płaszczyzny,

4. ruch dokoła ustalonego punktu (ruch w trzech wymiarach),

5. ogólny ruch (poza powyższymi kategoriami).

Model sztywny jest matematycznym i graficznym opisem pewnego obiektu geometrycznego. Po

zbudowaniu modelu sztywnego może on zostać pokryty siatką i przekształcony w model elementów

skończonych.

7.2.3. Modelowanie metodą elementów skończonych

Modelowanie metodą elementów skończonych (MES) jest techniką obliczeniową, która pozwala na

badanie skomplikowanych struktur, posiadająchych złożoną geometrię i parametry materiałowe. Dla

prostych struktur można stosować rozwiązanie analityczne, ale dla złożonych układów dokładne

rozwiązanie nie jest możliwe przy pomocy metod analitycznych. Metoda elementów skończonych to

m

1

, I

1

m

2

, I

2

m

3

, I

3

95

przybliżona metoda rozwiązania, gdzie dyskretyzuje się złożoną strukturę lub dzieli na skończoną

ilość regularnych kształtów, nazywanych elementami. Każdy element jest opisywany za pomocą

węzłów lub punktów i współrzędnych, które ustalają geometrię struktury. Zachowanie całej struktury

jest przybliżane jako suma odpowiednich odpowiedzi każdego z regularnych kształtów. W

biomechanice analizy struktury wykorzystujące metodę elementów skończonych są bardzo popularne.

Badania obejmują: analizę obciążeń i naprężeń w implantach, przy remodelingu kości, patologiach

tkanek itd. Modelowanie elementami skończonymi zostało również wykorzystane w dziedzinie

rehabilitacji, takiej jak protetyka kończyn dolnych.

Metoda analizy MES jest użyta do określenia naprężeń w materiale, wyjaśnienia problemów

związanych z kontaktem różnych materiałów oraz do optymalizacji projektowania. Analiza metodą

elementów skończonych polega na aproksymacji obiektu za pomocą elementów skończonych, gdzie

każdy węzeł jest powiązany z niewiadomą, która ma być rozwiązana. Przykładowo dla bryły 2-

wymiarowej, nieznanymi mogą być przemieszczenia x i y. Zakłada się, że każdy węzeł posiada dwa

stopnie swobody i proces rozwiązania musi rozwiązać 2n stopni swobody. Każdy węzeł może ulec

przemieszczeniu tworząc tzw. pole przemieszczeń. Po obliczeniu przemieszczeń (odkształceń) są one

różniczkowane przez różniczkowanie cząstkowe w funkcji przemieszczenia, a następnie oblicza się

naprężenia z uzyskanych odkształceń.

Jako wejścia do modelu MES używa się:

- obciążenia – mogą być w formie sił, momentów, ciśnienia, temperatury lub przyspieszeń,

- ograniczenia – jako reakcje dla zastosowanego obciążenia. Mogą przeciwdziałać odkształceniom

postępowym lub obrotowym.

Modele biomechaniczne uzyskane za pomocą metody elementów skończonych są bardzo

potężnymi narzędziami do analizowania anatomicznych struktur biomechanicznych i do opracowania

projektów dla implantów, protez oraz konstrukcji mięśniowo-szkieletowych. Zaletą takich modeli jest

zdolność do brania pod uwagę złożonych geometrii i zachowania materiałów