0

TADEUSZ STĘPIEŃ

LOGIKA

(ZARYS -TEMATYKI)

SZKOŁA GŁÓWNA HANDLOWA

Redaktor:
Ewa Heynar – Skowrońska
Redaktor techniczny:
Ewa Łukasiewicz
Skład komputerowy:
Joanna Kowalczyk
Copyright by Oficyna Wydawnicza SGH, Warszawa 1996
ISBN 83-86689-31-5
Oficyna Wydawnicza Szkoły Głównej Handlowej
Warszawa 1996.
Wydanie I. Ark.wyd. 4.40. Ark.druk. 4,25
Zamówienie 15/1/96

Spis treści

Wprowadzenie ........................................................................................ 1

1. Tematyka wykładów ...................................................................... 2

2. Wybrane zagadnienia semantyki .................................................... 4

3. Definicje ......................................................................................... 6

4. Wieloznaczność i nieporozumienia ................................................ 8

5. Podstawowe i pochodne kategorie syntaktyki ............................... 8

6. Funktory ......................................................................................... 9

7. Logika formalna ........................................................................... 11

7. 1 Tautologie rachunku zdań ...................................................... 17

7. 2. Elementy rachunku nazw ...................................................... 20

8. Wnioskowanie pośrednie. Sylogizm kategoryczny ...................... 24

9. Błędy wnioskowania .................................................................... 26

10. Podstawowe wiadomości z teorii relacji ...................................... 28

11. Wypowiedzi modalne ................................................................... 29

12. Elementy metodologii nauki ........................................................ 29

13. Podział logiczny ........................................................................... 36

Zakończenie .......................................................................................... 37

Przykładowe pytania ............................................................................. 37

1

WPROWADZENIE

Każdy z nas spotkał się z różnego rodzaju wyrażeniami językowymi, a więc zdaniami czy

wypowiedziami niepełnymi, które zawierały zwroty: logiczny, logiczne, logika. Niekiedy
spotykamy takie, nieco udziwnione wyrażenia, jak logika dziejów, logika uczuć, logika
działania itp. Te proste obserwacje upoważniają nas do stwierdzenia, iż termin logika zawiera
określenie czegoś stosunkowo ważnego i cenionego w praktyce naszego życia. Uznanie
jakiegoś rozumowania za logicznie poprawne nadaje mówiącemu swoistą nobilitację. I wręcz
przeciwnie, określenie: nielogiczne, pozbawione logiki jest równoznaczne z określeniem
bezwartościowe.

Czym więc jest logika, w jaki sposób można opanować umiejętność logicznego myślenia?

Temu zagadnieniu poświęcony będzie skrypt, a w szczególności wykład z przedmiotu logika.

Należy zaznaczyć, iż logika, jako dyscyplina nauczania może nastręczać słuchaczowi pewne

trudności, które związane są z dużą liczbą nieznanych najczęściej słuchaczom terminów
używanych w czasie wykładu. Trudności sprawiać może również język formalny stosowany w
logice, szczególnie w dziale nazwanym logiką formalną. Większość praw logicznych
występuje w postaci czysto formalnego zapisu, dlatego konieczne jest opanowanie określonej
symboliki logicznej.

Logika nie należy do przedmiotów „spektakularnie” atrakcyjnych dla słuchacza. W tym

względzie jest ona częściowo porównywalna z takimi przedmiotami, jak matematyka,
statystyka itp.

„Atrakcyjność” logiki kryje się w czymś innym niż przyjemny odbiór. Dobre jej

opanowanie i zrozumienie staje się istotnym narzędziem wyrażania naszych myśli, unikania
chaotycznych wypowiedzi, poprawnego wyprowadzania wniosków z uprzednio przyjętych
założeń. Inaczej mówiąc, pozwala nam w sposób najodpowiedniejszy spożytkować wspaniałe
dary człowieka, jakimi są myślenie i mowa.

W procesie uczenia się logiki szczególnego znaczenia nabiera reguła metodyczna, która

mówi o zrozumieniu przyswajanego materiału. Jest to warunek uzyskania korzyści z
uczestnictwa w wykładach z logiki. Nie należy, jak to się zwykło mówić „iść dalej”, jeśli nie
zrozumiałeś materiału poprzedniego. Niektóre formuły trzeba opanować pamięciowo, co
jednocześnie może służyć, jako ćwiczenie pamięci. Szczególnie w logice należy zwracać
uwagę na precyzję i dokładność uczenia się. Pomocą, oprócz wykładów, będą różne
podręczniki, których spis słuchacze znajdą na końcu skryptu.

Jako podstawowy zalecam podręcznik Zygmunta Ziembińskiego „Logika praktyczna”,

który miał siedemnaście wydań, a ostatnie ukazało się w 1994 r. (Należy także wykorzystywać
podręczniki, którymi posługiwali się studenci lat ubiegłych, również w innych niż SGH
uczelniach, np. uniwersytecie).

Zachęcam również do korzystania z konsultacji w czasie moich dyżurów.

Zaliczenie przedmiotu nastąpi w końcu semestru w postaci pisemnej (pytania otwarte i

zamknięte).

śyczę Studentkom i Studentom dużo satysfakcji w czasie pracy nad logiką i korzyści z

praktycznego posługiwania się jej zasadami.

Grudzień 1995. Tadeusz Stępień.

2

1.

TEMATYKA WYKŁADÓW

1.1.

Punktem wyjściu wykładu logiki będzie krótka charakterystyka poglądów na źródła

ludzkiego

poznania.

Poglądy

te

zostały

uporządkowane

w

podręcznikach

filozofii w postaci znanych stanowisk w teorii poznania, zwanej inaczej epistemologią
(episteme – poznanie, logos – nauka). A są to:

−

empiryzm,

−

racjonalizm,

−

fideizm.

Każde z wymienionych tu stanowisk posiada wiele odmian wyrażających poglądy

określonych twórców. Na przykład przedstawiciele empiryzmu, jak: Arystoteles, D. Hume, J.
Locke, J. S. Mill, neopozytywiści - prezentują stanowiska znacznie się różniące. Istnieje jednak
pewien wspólny element ich poglądów, mówiący o istotnej roli doświadczenia w procesie
poznania. Podobnie rzecz ma się z innymi stanowiskami, które będą przedmiotem wykładu.

1.2. Podstawowym instrumentem wyrażania naszej wiedzy o sobie i o świecie

jest język. Ludzki język posiada cechy jemu tylko właściwe, a niewystępujące nigdzie w
świecie zwierzęcym. Jest twórczy, podlega przeobrażeniom, potrafi określić rzeczy, zjawiska,
przeżycia duchowe i fizyczne. Pozwala na wypowiadanie myśli i zrozumienie myśli
wypowiadanych przez innych.

Zagadnieniem szczególnie godnym zainteresowania z punktu widzenia logiki jest sposób

wyrażania treści poznawczych czy emocjonalnych za pomocą znaków – nośników tych treści.
To sprawa przekształcania sygnałów i znaków pojedynczych w bardziej złożone całości a w
końcu w cały system zwany językiem. „Język, – bowiem – to system obejmujący, wyznaczony
przez pewne reguły, zbiór znaków słownych, znaków, z którymi odpowiednie reguły nakazują
wiązać myśli określone go typu, a inne reguły określają dopuszczalny sposób wiązania tych
znaków w wyrażenia złożone”

1

. Natomiast A. Schaff prezentuje taką interesującą myśl: „Jeżeli

jest prawdą, że nie potrafimy myśleć bez słów i że uczymy się myśleć za pomocą słów, tedy
język wyznacza granice i zarys całego ludzkiego poznania”

2

. Wcześniej myśl taką wygłosił

logik, austriacki myśliciel L. Wittgenstein mówiąc, że granice mojego języka oznaczają granice
mojego świata”

3

Ważne jest w tym przypadku rozróżnienie na języki naturalne — gdzie reguły kształtują

się zwyczajowo oraz języki sztuczne — reguły zaprojektowano z góry (esperanto). Na użytek
wykładu będziemy używać określenia języki naturalne dla oznaczenia języka używanego w
codziennej praktyce, choć w nim również występują elementy języków sztucznych.

Język sztuczny wiążę z językiem sformalizowanym, którego zarówno symbolika, jak i

reguły zostały ustalone przez twórców określonych systemów sformalizowanych.

1.3.

Szczególną rolę w procesie poznania pośredniego, a z takim mamy do czynienia w

większości aktów poznawczych, odgrywają znaki. „Znak to wszelki — przedmiot — lub
zespół przedmiotów powiązanych w obustronnym akcie poznania pomiędzy podmiotem
poznającym a przedmiotem poznania”

4

.

Wyróżniamy znaki sztuczne, które są zarazem przedmiotami pośredniczącymi w akcie

porozumiewania się. Są to znaki specjalne utworzone dla przekazywania określonych treści,
np. znaki drogowe, napisy i wypowiedzi zdaniowe. Znaki sztuczne nazywane są niekiedy
znakami właściwymi. Znaki naturalne nie są jednoznacznie przedmiotami pośredniczącymi w
procesie porozumiewania się, np. błyski w czasie burzy, dym, jako znak ognia.

1

Z. Ziembiński: Logika praktyczna. WN PWN Warszaua 1994.

2

A. Schaft. Język a poznanie. PWN. Warszawa 1964.

3

L. Wittgenstein: Tractams Logico-Philosophicus. PWN. Warszawa 1970. s. 66.

4

Z. Kraszewski: Logika — nauka rozumowania. PWN, Warszawa 1984.

3

Jednym i drugim znakom przysługuje funkcja znaczenia. Tak, więc w procesie

porozumiewania się należy umieć odczytywać znaczenie zarówno znaków naturalnych, jak i
znaków sztucznych. Szczególną rolę w procesie poznawania świata natury odgrywa
umiejętność pojmowania znaków, które przekazuje nam świat roślin, zwierząt a również skal,
woda, wiatr.

Warto zaznaczyć pewną charakterystyczną cechę znaków właściwych, czyli sztucznych (np.

nazwa czy zdanie), nazywaną niekiedy przezroczystością semantyczną, co znaczy, że znak
sam nie zatrzymuje na sobie żadnej świadomości, uwagi podmiotu poznającego.

1.4. Po tych uwagach wstępnych należy przejść do próby podania definicji logiki oraz

charakterystyki jej działów. Encyklopedia logiki podaje definicję najbardziej zwięzłą:

Logika to: analiza języka i czynności badawczych (rozumienia, definiowania,

klasyfikowania itp.) w celu podania takich reguł posługiwania się językiem i wykonywania
owych czynności, które uczyniłyby tę, działalność możliwie najbardziej skuteczną.

5

Dla celów niniejszego wykładu tego rodzaju definicja wydaje się wystarczająca, choć można

znaleźć inne, np. logika to nauka o prawach myślenia.

1.5. Najważniejsze działy logiki to:

I. Semiotyka – ogólna teoria znaków ze szczególnym uwzględnieniem znaków tworzących

język, czyli wyrażeń. Semiotyka dzieli się na trzy działy:

a)

Semantyka – opisuje stosunki zachodzące między znakami a rzeczywistością, do której
znaki się odnoszą: konotowanie, denotowanie, prawdziwość.

b)

Syntaktyka – opisuje stosunki zachodzące między znakami wewnątrz języka.
Przedmiotem są stosunki wewnątrz językowe, które mają charakter formalny, czyli żeby
je stwierdzić, nie trzeba znać znaczenia wyrażeń.

c)

Pragmatyka – opisuje stosunki zachodzące między znakami a tymi, którzy te znaki
nadają lub odbierają (rozumienie, komunikowanie się, stwierdzanie).

II. Logika formalna dotyczy schematów rozumowań niezawodnych, tj. takich, które od

prawdziwych przesłanek prowadzą zawsze do prawdziwych wniosków. Podstawowymi
działaniami logiki formalnej są:

a)

Rachunek zdań – wiąże się on z pojęciem formy rozumowania, czyli formy logicznej

(inaczej schematu, struktury).

W rachunku zdań posługujemy się określonymi schematami formalnymi, które powstają przez
zastąpienie elementów stałych w zdaniu symbolami zmiennych i stałych, np. zdanie: jeśli (jest
tak. że) grzmi, to błyska, to: jeśli nie błyska, to nie grzmi, można zapisać w postaci
symbolicznej (p → q) → (~q →~ p).
Ten ostatni zapis nazywamy formą zdania (w tym przypadku wyżej zacytowanego), a
jednocześnie – jak się później okaże – jest to przykład określonego prawa logicznego.

b)

Rachunek kwantyfikatorów – przedmiotem zainteresowań rachunku kwantyfikatorów

są określone twierdzenia z użyciem takich zwrotów, jaki każdy, niektóre, zwanych
kwantyfikatorami. Do działu zwanego logiką formalną można również zaliczyć:

c)

Rachunek nazw – zwany niekiedy sylogistyką zdań asertorycznych. Sylogistyka jest

najstarszym systemem logicznym, którego autorem jest Arystoteles. Jest to teoria czterech
stałych logicznych:
każdy... jest, żaden... nie jest..., niektóre... są, niektóre... nie są, oznaczone symbolami: a, e, i, o.
Są to funktory o trzech zmiennych nazwowych reprezentowanych przez S, M, P, których
wartościami są tylko terminy ogólne i niepuste.

5

Mała encyklopedia logiki. Ossolineum, Wrocław – Warszawa - Kraków, 1988.

4

III. Metodologię nauk można podzielić na dwa działy:

a)

Metodologia ogólna rozważa czynności lub rezultaty poznawcze, występujące we

wszystkich naukach (twierdzenia, definicje, klasyfikowanie).

b)

Metodologia szczegółowa dzieli się na metodologię poszczególnych typów nauki,

różniących się rodzajem zabiegów poznawczych, np. metodologię nauk formalnych, czyli
dedukcyjnych, metodologię nauk empirycznych.

W ramach szeroko pojętej logiki występuje wiele logik szczegółowych, np. logika:

deontyczna, dialogowa, filozoficzna, intuicjonistyczna, kombinatoryczna, matematyczna.

W dalszym toku wykładu zajmiemy się następującymi dziedzinami logiki:

−

wybranymi zagadnieniami semantyki,

−

podstawowymi i pochodnymi kategoriami syntaktyki,

−

głównymi zagadnieniami logiki formalnej,

−

wybranymi tezami rachunku zdań,

−

sylogistyką zdań asertorycznych (logika klasyczna),

−

wybranymi elementami metodologii nauk,

−

rozumowaniem i jego pochodnymi,

−

podziałem logicznym,

−

klasyfikacją,

−

podziałem nauk.

2.

WYBRANE ZAGADNIENIA SEMANTYKI

2.3.

Kluczem do zrozumienia problemów semantycznych jest pojęcie znaczenia, czyli

sposobu rozumienia danego wyrażenia w danym języku.

2.4.

Z punktu widzenia znaczenia możemy wyróżnić tzw. kategorie semantyczne, to

znaczy grupy wyrazów, ich zespołów i całych zwrotów językowych wyróżnionych przez
logikę ze względu na znaczenie.

2.5.

Do podstawowych kategorii semantycznych zaliczamy nazwy i zdania,

2.6.

Należy zwrócić uwagę, że takie same kategorie zostały podane uprzednio, jako

syntaktyczne. Są one jednak w syntaktyce traktowane z punktu widzenia ich funkcji w
strukturze zdaniowej a nie z punktu widzenia znaczenia. Znaczenie wiąże się ściśle z pojęciem
semantyki i dotyczy znaku i rzeczywistości, do której ten znak się odnosi. Oznacza to, że
kategoria nazwa, zdanie, może być traktowana, w ujęciu semantycznym i syntaktycznym.
Rzecz stanie się jaśniejsza w trakcie dalszych wykładów. Należy jednak pamiętać o
powyższych aspektach, aby uniknąć istotnych nieporozumień.

2.7.

Przedmiotem szczególnego zainteresowania semantyki i syntaktyki jest nazwa.

Najczęściej przez pojęcie nazwy rozumiemy wyrażenie językowe, które może wystąpić w
zdaniu w roli podmiotu lub orzecznika.

I tu jest aspekt syntaktyczny tej kategorii, ponieważ wskazuje na jej miejsce w strukturze

wyrażenia złożonego.

Natomiast w analizie semantycznej, a więc zajmującej się związkiem między nazwą, jako

znakiem a rzeczywistością, do której się odnosi, wyróżniamy następujące elementy
semantyczne:

5

Treść nazwy – jest to zespół cech przedmiotu, które dana nazwa wskazuje, określona

niekiedy, jako znaczenie.

Właściwość wskazywania znaczenia nazwy określamy pojęciem konotacja. Na przykład

nazwa krzesło wskazuje na istotne cechy przedmiotu, które pozwalają odróżnić ten przedmiot
od ławki czy stołu. Te właśnie cechy zawarte niejako w nazwie (ze względu na dany język)
nazywamy konotacją. A więc konotacja może być używana zastępczo z treścią bądź
znaczeniem, a może jednocześnie wskazywać na pewien logiczny proces umożliwiający
porozumiewanie się.

Wyróżniamy tzw. cechy konstytutywne i konsekutywne. Cechy konstytutywne to znaczy

takie, bez których nie istnieje dany przedmiot; konsekutywne zaś – to cechy pochodne. Ze
względu na treść mówi się często o trzech różnych tzw. supozycjach nazwy prostej,
formalnej, materialnej. Odróżnić należy pojęcie znaczenia od pojęcia oznaczania. Oznaczać
to nadawać się na orzecznik zdania prawdziwego o tym przedmiocie.

Desygnat nazwy – jest to wszelki przedmiot oznaczony przez tę nazwę przy danym jej

znaczeniu. Desygnatem nazwy koń jest określone zwierzę zajmujące odpowiednie miejsce w
systematyce zwierząt.

Zakres nazwy – przy danym jej znaczeniu to ogól wszystkich jej desygnatów. Zakresy

nazw nazywane są niekiedy denotacjami. Denotować znaczy wskazywać na zakres nazwy.

Wymienione czynniki są podstawowymi elementami semantycznymi nazwy.

2.8.

Podział nazw. Wyrażenia nazwowe mogą występować, jako indywidualne ogólne,

abstrakcyjne.

a)

Wyrażenia nazwowe są przyporządkowane przedmiotom indywidualnym, jako nazwy

indywidualne.

b)

Ogół przedmiotów podobnych do danego pod względem pewnych wyróżnianych cech

określamy, jako nazwy ogólne.

c)

Nazwy własności, relacji, klas, liczb są nazwami abstrakcyjnymi.

Jest to jeden z możliwych podziałów, który można rozwijać do postaci bardzie złożonej. Oto

inny, acz podobny w treści, podział:

nazwy

oznaczające

nieoznaczające

(przedmiotowe, niepuste)

(bezprzedmiotowe)

jednostkowe ogólne

Inny nieco podział nazw znaleźć można u Z. Ziembińskiego

6

, to jest według:

−

liczby wyrazów składowych – proste i złożone,

−

miejsca odniesienia, (do czego się odnoszą) – konkretne i abstrakcyjne,

−

sposobu wskazywania desygnatu – generalne, indywidualne.

−

natury desygnatów — ogólne, jednostkowe, puste,

−

struktury desygnatów — zbiorowe i nie zbiorowe.

Należy jeszcze wyróżnić:

−

nazwy równoważne, czyli takie, które mają ten sam zakres, np. Jan Matejko największy

polski malarz historyczny.

−

nazwy równoznaczne, czyli nazwy mające tą samą treść: np. odwaga i dzielność.

6

Z. Ziembiński: Logika praktyczna. WN PWN, Warszawa 1994.

6

2.9.

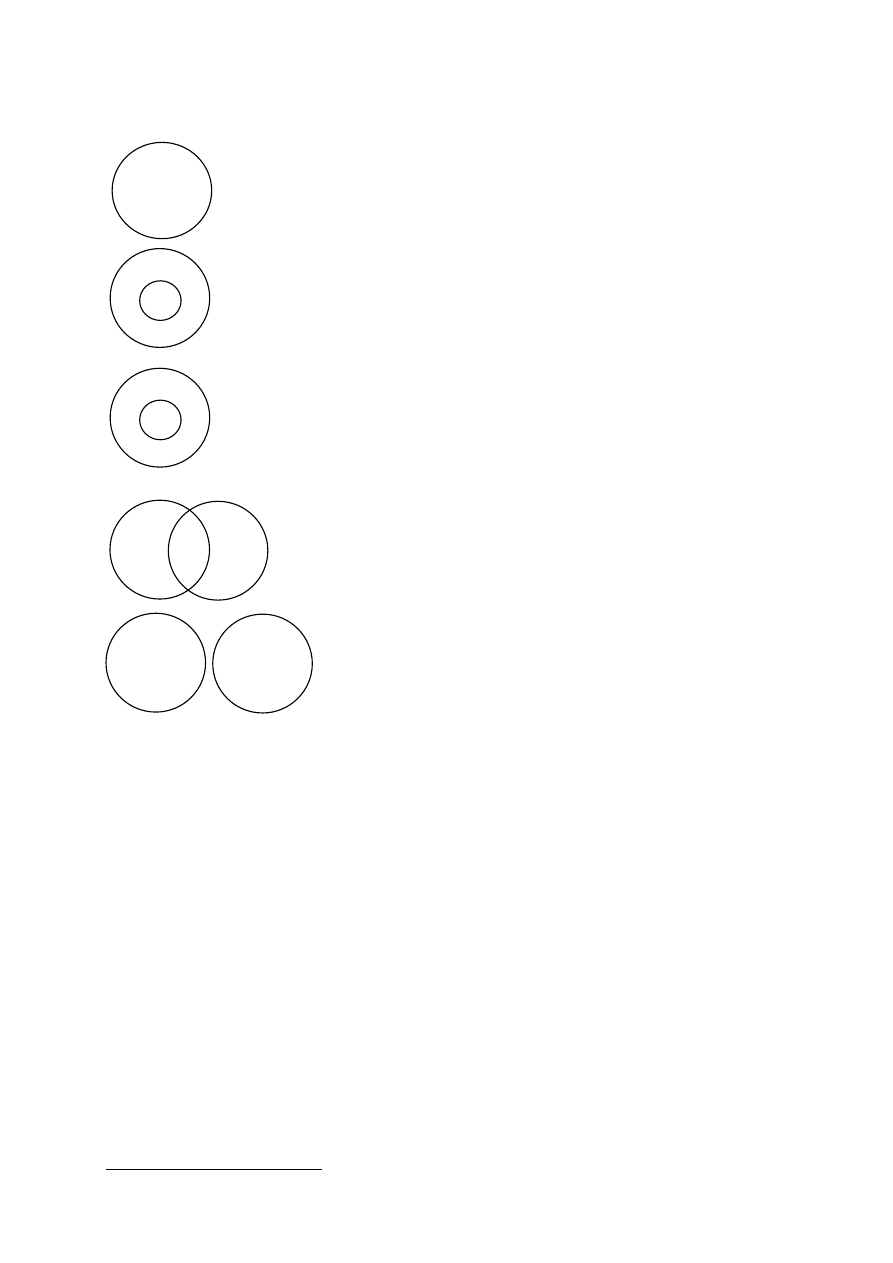
Stosunki miedzy zakresami nazw. Poszczególne stosunki można zilustrować za

pomocą tzw. koła Eulera (logik i matematyk, XVIII w.)

a)

Stosunek

równoważności

(zwany

niekiedy

stosunkiem

zamienności). Zachodzi on między zakresem nazwy 5 i nazwy P wtedy
i tylko wtedy, gdy każdy desygnat nazwy S jest desygnatem nazwy P, a
każdy desygnat nazwy P jest desygnatem nazwy S, np. student (5) i
słuchacz szkoły wyższej (P).

b)

Stosunek podrzędności – każdy desygnat nazwy S jest

desygnatem nazwy P, natomiast nie każdy desygnat nazwy P jest
desygnatem nazwy S, np. ekonomista (S) człowiek (P).

c)

Stosunek nadrzędności – każdy desygnat nazwy P jest

desygnatem nazwy S, nie każdy desygnat nazwy 5 jest desygnatem
nazwy P, np. kobieta (S), mężatka (P).
Czy między zakresem dwóch nazw zachodzi stosunek podrzędności czy
nadrzędności zależy od tego, którą nazwę, do której ustosunkowujemy
(może być stosunek kobieta (S) – mężatka (P) a może być mężatka (5) –
kobieta (P).

d)

Stosunek krzyżowania się. Niektóre desygnaty nazwy S są

desygnatami nazwy P i niektóre desygnaty nazwy P są desygnatami
nazwy S, np. Polak – żołnierz, student – sportowiec.

e)

Stosunek wyłączania się, kiedy żaden desygnat nazwy S

nie jest desygnatem nazwy P, np. stół — krzesło.

f)

Nazwy sprzeczne to takie, z których jedna zaprzecza drugiej, np. człowiek –

nieczłowiek, biały – niebiały. Inaczej mówiąc, że zostaje wydzielona z niej jakaś podklasa, a
pozostała staje się jej zaprzeczeniem.

g)

Nazwy przeciwne, np. dziecko i człowiek dorosły. Suma tych dwóch zbiorów nie da

nam zbioru uniwersalnego, tak jak to ma miejsce przy sumie zbiorów sprzecznych

3.

DEFINICJE

3.1.

Problemy definicji zaliczane są do zagadnień sematycznych. Służą, bowiem

sprecyzowaniu, nadaniu bądź zdaniu sprawy ze znaczenia jakiejś nazwy, pojęcia, terminu
używanego w danym języku. To właśnie definicje są jednym z głównych sposobów
poprawnego porozumiewania się.

3.2.

Dość trudno jest podać określenie definicji głównie ze względów znaczeniowych. W

„Małej encyklopedii logiki” brzmi ona tak:

Termin ten używany bez przydawki, odnoszony bywa z reguły do definicji normalnej, w

którejś z jej postaci (analitycznej lub syntetycznej, słownikowej lub semantycznej itp.)
Ponadto można uważać za zakres nazwy »definicja« sumę zakresów tych wszystkich nazw,
które utworzone są ze słowa »definicja« oraz następującego po nim przymiotnika.

7

7

Mała encyklopedia logiki. Ossolineum. Kraków-Warszawa 1998.

SP

S

P

P

S

SP

P

S

P

S

7

J. Gregorowicz podaje to w sposób następujący:

Wszelka definicja jest wyjaśnieniem znaczenia jakiegoś wyrażenia w jakimś języku, które
polega na podaniu dla tego wyrażenia jego równoważnika.

8

3.3.

W zależności od tego, czy zdanie definiujące określa bezpośrednio jakiś

konkretny przedmiot, czy znaczenia słowa w danym języku, wyróżniamy definicje:

−

realną (podaje charakterystykę przedmiotu),

−

nominalną (podaje informacje o znaczeniu słowa).

3.4.

Ze względu na funkcje, jakie pełnią w procesie porozumiewania się, wyróżniamy

definicje:

−

sprawozdawcze (analityczne) – to znaczy zdaje sprawę ze znaczenia jakiegoś słowa w

danym języku. I w tym sensie ma ona charakter nominalny, choć słowo nominalny nabiera
właściwego znaczenia w zestawieniu ze słowem realny,

−

projektujące (syntetyczne) – mają one zaprojektować znaczenie wyrazu. Są to, więc

propozycje rozumienia jakiegoś słowa. Definicja projektująca może mieć charakter definicji
konstrukcyjnej bądź regulującej.

3.5.

Ażeby zrozumieć dalsze typy definicji niezbędne jest zapoznanie się ze

strukturą definicji. Część definiowaną nazywa się terminem łacińskim definiendum część zaś
definiującą – definiens. Te dwa elementy powiązane są łącznikiem, np. człowiek jest to zwierzę
rozumne. W taki sposób definiuje człowieka Arystoteles. Członem definiującym, czyli
definiendum jest człowiek, natomiast członem definiowanym, czyli definiens – zwierzę
rozumne.

3.6.

Z punktu widzenia budowy możemy mówić o definicji równoważnościowej, to

znaczy, że wyraz definicyjny pokrywa się znaczeniowo z wyrazem definiującym.

3.7.

Szczególnym przykładem definicji równoważnościowej jest definicja klasyczna.

Przykładem może być cytowane określenie człowieka, jako zwierzęcia rozumnego. Definicja ta
polega na podaniu tzw. rodzaju i różnicy gatunkowej. Obydwa te terminy mają znaczenie ściśle
logiczne. Rodzaj oznacza w języku łacińskim – genus a różnica gatunkowa – differentia
specifica. Czyli definitio fit per genus et differentiam specificam. Symbolicznie: A jest BC.

−

Definicje można sformułować w trzech wariantach nazywanych stylizacjami. Mówi się

o stylizacji: słownikowej, semantycznej, przedmiotowej.

3.8.

Wymienia się również definicję przez postulaty.

3.10. Każda poprawna definicja musi spełnić następujące warunki:

−

adekwatność oznacza, że zakresy definiendum i definiens muszą być zamienne,

−

wyrazy występujące w definiens muszą być zrozumiałe dla adresata definicji,

−

w definiens powinny być wymienione te cechy przedmiotów, z powodu których te

przedmioty zostały nazwane tym słowem.

3.11.

Najczęściej popełniane błędy przy definiowaniu:

−

ignotum per ignotum – nieznane przez nieznane, słowo definiujące równie nieznane jak

słowo definiowane;

−

idem per idem to samo przez to samo. Błąd ten nazywany jest niekiedy błędnym,

kołem, które może mieć charakter bezpośredni bądź pośredni;

8

J. Gregorowicz: Zarys logiki dla prawników. PWN, Warszawa 1962, s. 46.

8

−

definicja za szeroka, – o zakres definiens jest nadrzędny w stosunku do zakresu

definiendum;

−

definicja za wąska – sytuacja odwrotna niż w definicji za szerokiej.

3.12.

Znaczenie słów możemy wyjaśniać także przez przykład, odróżnienie, po

równanie, wskazanie. Jest to definicja deiktyczna obiektywna bądź ostensywna.

4.

WIELOZNACZNOŚĆ I NIEPOROZUMIENIA

4.1.Wieloznaczność jest źródłem nieporozumienia i polega na tym, że słowa mają więcej niż

jeden sposób ich rozumienia. Mogą to być:

−

nazwy równobrzmiące o różnych znaczeniach, np. zamek, język, kultura, pranie;

−

znaczenia przeniesione na przedmioty podobne, np. sól;

−

znaczenia przeniesione na inne rzeczy, np. URM — budynek i instytucja polityczna.

4.2.Wieloznaczność może wynikać z pomieszania supozycji prostej i materialnej.

4.3.Specyficzną formą wieloznaczności jest ekwiwokacja – polega ona na dwukrotnym

użyciu jakiegoś słowa w jakiejś wypowiedzi w dwóch różnych znaczeniach.

4.4.Źródłem nieporozumień mogą być również tzw. słowa okazjonalne. Słowa te zmieniają

swoje znaczenie w zależności od tego, kiedy, gdzie i kto je wypowiada, np. dziś, jutro, tam, ja.

4.5.Często spory między ludźmi wynikają z faktu posługiwania się słowami nieostrymi,

tzn. takimi, których zakres nie jest ostatecznie rozstrzygnięty, np. młody, nieletni.

4.6.Do błędów powodujących nieporozumienia zalicza się również amfibologię (spotyka się

również określenie amfibolia, np. część programu całkowicie nie została wykonana; na bal
konie nie chodzą — na balkonie nie chodzą.

4.7.Nieporozumienie powodować może nawet emocjonalne zabarwienie wyrazów.


5. PODSTAWOWE I POCHODNE KATEGORIE SYNTAKTYKI

5.1.Do podstawowych kategorii syntaktyki zalicza się nazwę i zdanie. Ich syntaktyczny

sens wynika z faktu tworzenia wraz z innymi kategoriami znaczących całości. Wzajemne
warunkowania oznaczają ich aspekt syntaktyczny.

Na pytanie, jakie są podstawowe kategorie syntaktyczne, należy odpowiedzieć: nazwa i
zdanie.

Natomiast kategorią pochodną jest funktor.

Dwa wyrażenia należą do tej samej kategorii syntaktycznej, jeśli zastępując w zdaniu jedno

z nich drugim, otrzymamy zdanie.

5.2.Kategoria nazwa została omówiona w rozdziale 2.

5.3.Niezmiernie ważną kategorią syntaktyczną w logice jest zdanie Przez zdanie w logice

rozumiemy wyłącznie zdanie oznajmiające, jak zauważają autorzy „Malej encyklopedii
logiki”.

9

Tak pojęte zdanie określa się:

−

syntaktycznie, czyli strukturalnie,

−

semantycznie,

−

pragmatycznie.

Zdanie w sensie logicznym jest to wyrażenie, które jest bądź prawdziwe, bądź fałszywe.

Takie ograniczenie kategorii rozumienia zdania jest niezbędne dla właściwej analizy procesów
wnioskowania, dowodzenia, sprawdzania czy tłumaczenia, czyli w rozmaitych formach
uzasadniania.

Prawdziwość, czy też fałszywość zdania jest zależna od zgodności treści zdania z

rzeczywistością, do której to zdanie się odnosi. Samo zagadnienie prawdziwości zdań będących
elementami składowymi rozumowania nie jest szczególnym przedmiotem zainteresowań
logiki.

Prawdą poznania zajmuje się specjalny dział teorii poznania. W logice, kiedy mówimy o

prawdziwości lub fałszywości zdania, używamy terminu wartość logiczna zdania i oznaczamy
specjalnymi symbolami i tak: prawdę oznaczamy cyfrą arabską 1 lub literą V (Veritas –
prawda), fałsz cyfrą 0 lub literą F (Falsus – fałsz).

W praktyce przeważa oznakowanie 1 lub 0.

5.4.Podstawowym podziałem zdań jest podział na zdania proste i zdania złożone.

Wyjaśnia się to używając terminologii logicznej, że zdania proste nie zawierają funktora
zdaniotwórczego od argumentów zdaniowych, zdania złożone zaś zawierają taki funktor.

Wyróżnić możemy zdania: podmiotowo-orzecznikowe i podmiotowo-orzeczeniowe, np.: Jan

jest studentem – to zdanie podmiotowo-orzecznikowe, a Jan śpiewa to zdanie podmiotowo-
orzeczeniowe.

Innym rodzajem zdania jest zdanie egzystencjalne, np.: istnieje jeden tylko człowiek, który

pełni funkcją papieża.

Wśród zdań prostych o strukturze a jest b wyróżnić możemy zdania atomimiczne i zdania

subsumpcyjne, np.: Kowalski jest lekarzem to zdanie atomiczne, a zdanie Koń jest ssakiem jest
zdaniem subsumpcyjnym. W pierwszym przypadku mamy indywiduum zaliczone do zbioru, w
drugim zbiór mniejszy do zbioru większego.

Ze względu na rodzaj spójników łączących zdania proste w zdania złożone te ostatnie

dzielimy na zdania: koniunkcyjne, alternatywne, alternatywno-rozłączne, warunkowe,
równoważne, negatywne. Ten podział odgrywa szczególnie doniosłą rolę w logice formalnej.

5.

FUNKTORY

6.1.

Bardzo ważną kategorię syntaktyczną stanowią funktory. Są one z określonego,

omawianego już, punktu widzenia uważane również za dosyć specyficzną kategorię
semantyczną, a to głównie z powodu, że te wyrażenia nie posiadają wyraźnego znaczenia
autonomicznego.

Funktorem nazywamy każde wyrażenie niebędące zdaniem lub nazwą służące do

konstruowania zdań lub nazw, czy też innych funktorów.

Z definicji wynika, więc to, co wyżej powiedziano, że funktor uzyskuje swoje pełne

znaczenie w powiązaniu z innymi kategoriami semantycznymi.

6.2.

Wyrażenia, z którymi funktor tworzy wyrażenie bardziej złożone, nazywamy

argumentami.

10

6.3.

Jeśli w efekcie mamy do czynienia z funktorem łączącym dwa lub więcej zdań w zdanie

złożone, mówimy wówczas o funktorze zdaniowym, a w zależności od liczby zdań
składowych o funktorze zdaniotwórczym od jednego, dwóch lub, więcej argumentów
zdaniowych. Jeśli zaś argumentami są nazwy, które tworzą zdanie, mówimy o funktorze
zdaniotwórczym od jednego, dwóch lub więcej argumentów nazwowych, np.: Kwiatkowski
pracuje. Jest to zdanie złożone z jednej nazwy indywidualnej (Kwiatkowski) i jednego funktora,
który wraz z tą nazwą tworzy zdanie (pracuje), natomiast w zdaniu Kwiatkowski pracuje i
ś

piewa, mamy do czynienia z funktorem zdaniotwórczym (i) od dwóch argumentów

zdaniowych; Kwiatkowski pracuje i Kwiatkowski śpiewa.

6.4.

Jeśli zaś funktor tworzy bardziej złożoną nazwę, nazywamy go funktorem

nazwotwórczym, np. uczony i polityk – wyrażenie i tworzy złożoną nazwę z dwóch
argumentów nazwowych i wówczas mówimy o funktorze nazwotwórczym od dwóch
argumentów nazwowych. W wyrażeniu piękny kwiat mamy do czynienia z funktorem
nazwotwórczym od jednego argumentu nazwowego (piękny).

6.5.

W przypadku, gdy funktorem jest funktor bardziej złożony, to mówimy o funktorze

funktorotwórczym, np. bardzo użyteczny, nadzwyczajnie grzeczny, szalenie pracowity —
bardzo, nadzwyczajnie, szalenie to funktory funktorotwórcze.

6.6.

Każdy z tych funktorów posiada w logice swoją symbolikę i tak:

−

funktor nazwotwórczy od jednego argumentu nazwowego oznacza się często symbolem

gdzie w liczniku mamy do czynienia z określeniem, jaki charakter ma wyrażenie
utworzone z funktorem (w tym przypadku nazwa – n), a w mianowniku z liczbą argumentów
(w tym przypadku jeden argument nazwy).

Wyrażenie uczony i polityk opiszemy symbolicznie , bowiem mamy do czynienia z

dwoma argumentami nazwowymi;

−

funktor zdaniotwórczy od jednego argumentu nazwowego oznaczamy np.

Kwiatkowski pracuje; a od dwóch argumentów zdaniowych np. Kwiatkowski pracuje i
ś

piewa. Może być także funktor zdaniotwórczy od jednego argumentu zdaniowego, np.

nieprawda, że dzisiaj pada deszcz – wyrażenie nieprawda, że... jest funktorem
zdaniotwórczym od jednego argumentu zdaniowego – symbolicznie .

Symbolikę funktorów funktorotwórczych przedstawia się w sposób nieco udziwniony:

bardzo grzeczny oznaczamy .

Mogą być funktory funktorotwórcze od jednego lub więcej argumentów funktorowych.

6.7. Oto przykład rozbioru syntaktycznego zdania z użyciem wspomnianych symboli:

Koń, który pasie się w moim ogrodzie, /pochodzi/ Z bardzo znanej/ stadniny/ janowskiej.
Kreski oznaczają szczegółowe kategorie syntaktyczne.

Koń — n (nazwa),
który pasie się w moim ogrodzie – (funktor nazwotwórczy od jednego argumentu
nazwowego),
pochodzi (funktor zdaniotwórczy od dwóch argumentów nazwowych),

z bardzo znanej (funktor funktorotwórczy),

stadniny – n (nazwa),
janowskiej – (funktor nazwotwórczy od jednego argumentu nazwowego).

n

n

n

n

z

n

z

zz

z

z

n

n

n

n

n

n

z

nn

n

n

n

n

n

n

11

Zestawienie symboliczne przedstawia się następująco:

n n .

7.

LOGIKA FORMALNA

7.1.

Logika formalna jest tym działem logiki, który dotyczy schematów rozumowań

niezawodnych, to jest takich, które od prawdziwych przestanek prowadzą zawsze do
prawdziwych wniosków. A więc, logika zajmuje się tym szczególnym rodzajem rozumowania,
które nazywa się wnioskowaniem. Wnioskowanie, bowiem zajmuje bardzo poczesne miejsce
w naszym opisie świata, jak również w opisie jego przekształceń.

7.2.

Określenie – formalna – wynika z faktu zajmowania się głównie schematami

rozumowania, to znaczy, że przedmiotem zainteresowań nie jest treść zdania a forma, budowa
zdania. Jak się, bowiem okaże, sama budowa zdania może przebiegać według schematu, który
zawsze gwarantuje jego prawdziwość.

7.3.

Należy wyjaśnić, że niektóre schematy zdań prawdziwych dadzą się przedstawić w

postaci reguł wnioskowania. Na przykład dzisiaj jest czwartek, zatem jutro jest piątek. Jest to
zdanie, które można zapisać w innej postaci: jeśli dzisiaj jest zwartek, to jutro jest piątek i
dzisiaj jest czwartek, to jutro jest piątek. W tym drugim przypadku mamy do czynienia z
dwiema częściami rozumowania, mianowicie wiadomościami, które posiadaliśmy przed
rozpoczęciem rozumowania oraz z wiadomościami, które wywodzą się z poprzednich drogą
pewnego rozumowania.

Jeśli dzisiaj jest czwartek, to jutro jest piątek i dzisiaj jest czwartek – to jest informacja,

którą znaliśmy wcześniej. W logice nazywa się ona przesłanką, stanowi bowiem, jeśli można
tak powiedzieć, przesłanie części po niej następującej, która nazywa się wnioskiem i w
przypadku naszego zdania będzie to wyrażenie: to jutro jest piątek.

7.4.

W formule: ponieważ, dzisiaj jest czwartek, to jutro jest piątek: mamy do czynienia ze

stosunkiem wnioskowania. W formule np.: jeśli dzisiaj jest czwartek, to jutro jest piątek
mamy do czynienia z wynikaniem czy też implikacją. Wypowiadając taką implikację, nie
mówimy nic o tym, czy uznajemy zdanie poprzedzacie, czy następne. Natomiast mając do
czynienia z wnioskowaniem, stwierdzamy o związku zdania jednego i drugiego.

7.5.

Wyróżnić, zatem należy schematy formalne zdań i schematy formalne

wnioskowań. Schematy formalne uzyskamy wtedy, gdy w zdaniu złożonym występują zdania
proste i łączące je spójniki zastępujemy odpowiednimi symbolami. Podobnie należy
postępować tworząc schemat zdań kategorycznych. Aby utrzyma składniowa jednoznaczność,
wprowadzamy nawiasy. I lak, np. przyjmując symbole zmiennych zdaniowych p, q, r-a,
odpowiednie znaki spójników np.: → implikacje, /\ koniunkcja, negacja, możemy zdanie typu:
jeżeli 7 dzieli się przez 6, to 7 dzieli się przez 2 oraz 7 dzieli się przez 3, zapisać symbolicznie:
p → (q /\ r)
gdzie: p – 7 dzieli się przez 6,

q – 7 dzieli się przez 2,

r – 7 dzieli się przez 3,

łącznik zaś: jeżeli … to … oznacza symbol →.

Zdanie: Zdanie: każdy pies jest ssakiem, mogę symbolicznie zapisać w postaci: S a P, gdzie:

S — pies,
P — ssak.

Mamy tu do czynienia ze zmiennymi nazwowymi.

7.6.

Schematy zdań zawsze prawdziwych nazywamy tautologiami wnioskowania bądź

niezawodnymi schematami wnioskowania. Już wspomniano, że może zachodzić tożsamość
między tautologią (zwaną niekiedy tezą lub prawem logicznym) a niezawodnym schematem
wnioskowania.

n

n

z

nn n

n

n

n

n

n

12

Z uwagi powyższej wynika, że niekiedy schemat zdaniowy jest schematem zdania

prawdziwego i podobnie jest ze schematem wnioskowania, np. zdanie: Kościuszko był
Polakiem lub Kościuszko nie był Polakiem, jest zdaniem, którego zapis formalny można
przedstawić. P \/ nie p(p \/ p) i czytamy p lub nie p. Schemat ten może być schematem zdania
tylko prawdziwego.

7.7.

Po tych wstępnych wyjaśnieniach należy wprowadzić kilka podstawowych pojęć.

Logika formalna, jak to było wcześniej powiedziane, posiada kilka ważnych działów, takich
jak:

−

rachunek zdań,

−

rachunek nazw,

−

rachunek kwantyfikatorów,

−

rachunek relacji,

−

rachunek zbiorów.

7.8.

W niniejszym wykładzie ograniczymy wykład logiki formalnej do elementów rachunku

zdań i rachunku nazw nawiązując, o ile to będzie potrzebne, do działów pozostałych.

Celem, bowiem tego wykładu nie jest przedstawienie słuchaczom skomplikowanych

problemów logiki, jako dyscypliny naukowej, ale pomoc w poprawnym formułowaniu
własnych myśli, własnych wypowiedzi, najczęściej wygłaszanych w języku naturalnym, w
sposób zgodny z zasadami logiki.

Tak więc, trudne zagadnienia formalne, charakterystyczne dla logiki matematycznej, przy

danym wymiarze godzin nie mogą być przedmiotem wykładu. Nie to, ma na celu niniejszy
wykład, zainteresowani zaś mogą korzystać z wykładów logiki prowadzonych przez
matematyków.

7.9.

Rachunek zdań (logika zdań, teoria zdań, teoria dedukcji) zajmuje się związkami

między zdaniowymi ujmowanymi w zdania złożone, powstające złączenia zdań funktatorami
zdaniotwórczymi od argumentów zdaniowych. Ponieważ w rachunku zdań nie używa się
konkretnych zdań, lecz zmiennych zdaniowych, które reprezentują zdania, dlatego w logice
zdań nie mamy do czynienia ze zdaniem, lecz z funkcjami zdaniowymi. Jeżeli zaś w funkcji
za zmienne podstawimy stałe, to uzyskamy zdanie w sensie logicznym.

7.10.

Język rachunku zdań. W rachunku zdań posługujemy się stałymi logicznymi, które

najczęściej symbolizowane są w sposób następujący:
~ lub niekiedy

– negacja, czytamy nieprawda, że .... nie,

→ lub niekiedy <

– implikacja – czytamy, jeżeli... to.

^ lub niekiedy ·

– koniunkcja – czytamy i (ale jednocześnie można zaliczyć do
koniunkcji wyrażenia typu: oraz, ale, lecz a natomiast
– alternatywa prosta

–

czytamy lub, bądź w sensie: co najmniej jedno z

dwojga,

÷ lub niekiedy

–

alternatywa wyłączająca, zwana niekiedy ekskluzją, czytamy albo,

niekiedy również lub, w sensie do dokładnie jedno z dwojga,

–

dysjunkcja czytamy bądź – bądź, lub w sensie: co najwyżej jedno

z dwojga,

–

równoważność, czytamy zawsze i tylko wtedy ... jeżeli, pod tym

warunkiem i tylko pod tym warunkiem, ze.

–

binegacja

, czytamy ani ... ani

7.11. W rachunku zdań posługujemy się również

zmiennymi logicznymi

, których

symbolem

są najczęściej małe łacińskie litery i to tradycyjnie rozpoczynające się od litery p, q, s, t, ..., ale
można się również spotkać z inną symboliką. Należy wówczas zwracać uwagę czy chodzi o
zmienne zdaniowe, czy nazwowe.

7.12. Zmienne zdaniowe stanowią argumenty, niekiedy nazywane czynnikami.

Argumenty wraz z funktorami tworzą funkcje zdaniowe, a dokładniej funkcje logiczne, jeżeli
funktory przedstawione są w postaci symbolicznej. Przedstawione funktory mogą występować
z jednym bądź dwoma argumentami.

13

Ściślej rzecz biorąc, tylko funktor negacji stanowi funktor jednoargumentowy. Zastępując

zmienne zdaniowe i stałe logiczne odpowiednio zdaniami i spójnikami, otrzymamy zdanie wła-
ś

ciwe. Funkcje zdaniowe same nie posiadają wartości logicznej, uzyskują je po odpowiednim

podstawieniu

7.13. Funktory takie określamy w logice mianem funktorów prawdziwościowych, a

niekiedy funktorów ekstensjonalnych. „Mała encyklopedia logiki” określa funktor
prawdziwościowy, czyli ekstensjonalny następująco: „Jeśli wyrażeniem utworzonym przez
funktory jest zdanie złożone, a denotacją zdania jest wartość logiczna (prawdziwość lub
fałszywość), to funktor jest wówczas ekstensjonalny, gdy wartość logiczna zdania zależy
wyłącznie od wartości logicznej zdań składowych a nie zależy np. od ich treści. Taki funktor
nazywa się prawdziwościowy (ekstensjonalny) z racji zależności pomiędzy prawdziwością
argumentów a prawdziwością całego zdania złożonego”

9

.

Zależność wartości logicznej zdania złożonego od wartości logicznej zdań składowych
(argumentów) przedstawia się w tzw. matrycach (tablicach rachunku zdań).

Konsekwencje tej formuły sprawiają niekiedy słuchaczom spore trudności. Można się,

bowiem spotkać z przykładami zdań, które logika formalna uznaje za zdania prawdziwe, a
potoczne odczucie nie dostrzega związku wynikania między elementami danego zdania
złożonego. Oto przykład podany trafnie przez T. Kotarbińskiego: „Jeśli ptaki mają skrzydła,
to niedziela jest dniem świątecznym”

10

. Implikacja laka wyrażona symbolicznie

p → q jest prawdziwa z punktu widzenia matrycy implikacji, natomiast nie jest prawdziwa,
jeśli użyty spójnik warunkowy rozumieć tak, jak w języku potocznym. Od zdania
warunkowego wymaga się potocznie, aby można było słusznie wnioskować następnik z
poprzednika. Przykład ten wskazuje na pewne rozbieżności w pojmowaniu spójnika
prawdziwościowego w języku potocznym i w logice. Z punktu widzenia logiki te dwa zdania
(w przytoczonym przykładzie) dają nam całość, którą z punktu widzenia zasad logiki uznać
trzeba za prawdziwą, ponieważ prawdziwość tej całości zależy li tylko od prawdziwości zadań
składowych.

7.14. Za pomocą zmiennych i stałych logicznych konstruujemy schematy formalne zdań

zwane funkcjami logicznymi, a z nich te, które przy każdej wartości argumentów (0, 1) (w
logice dwuwartościowej) prowadzą do zdania prawdziwego, nazywają się tautologiami, bądź
prawami logicznymi, czy też tezami rachunku zdań.

7.15. Oto podstawowe funkcje zdaniowe, czyli wyrażenia złożone z argumentów i

funktatorów prawdziwościowych wraz z odpowiednimi matrycami, czyli tabelami. Tabele są
zbudowane w ten sposób, że za poszczególne zmienne, w tym przypadku dwie: p i q,
podstawiamy wartości 1 lub 0. Wartość całości funkcji zdaniowej jest zasadniczą
charakterystyką danego funktora. Stanie się to bardziej zrozumiałe, jeżeli przedstawimy
konkretne przykłady.

a) Oto zapis symboliczny i tablica implikacji (matryca); p → q (czytamy: jeśli p to q).

Tablica implikacji

p

q

p → q

1

1

1

1

0

0

0

1

1

0

0

1

Rubryka p oznacza wartość logiczną jednej zmiennej zdaniowej (oczywiście w skali 0, 1);

rubryka q wartość logiczną drugiej zmiennej zdaniowej. Rubryka trzecia – p → q – oznacza
wartość całości w związku z wartością części składowych.

9

Mała encyklopedia logiki. Ossolineum, Wrocław – Kraków - Warszawa 1988.

10

T. Kotarbiński: Wykłady z dziejów logiki. PWN, Warszawa 1985.

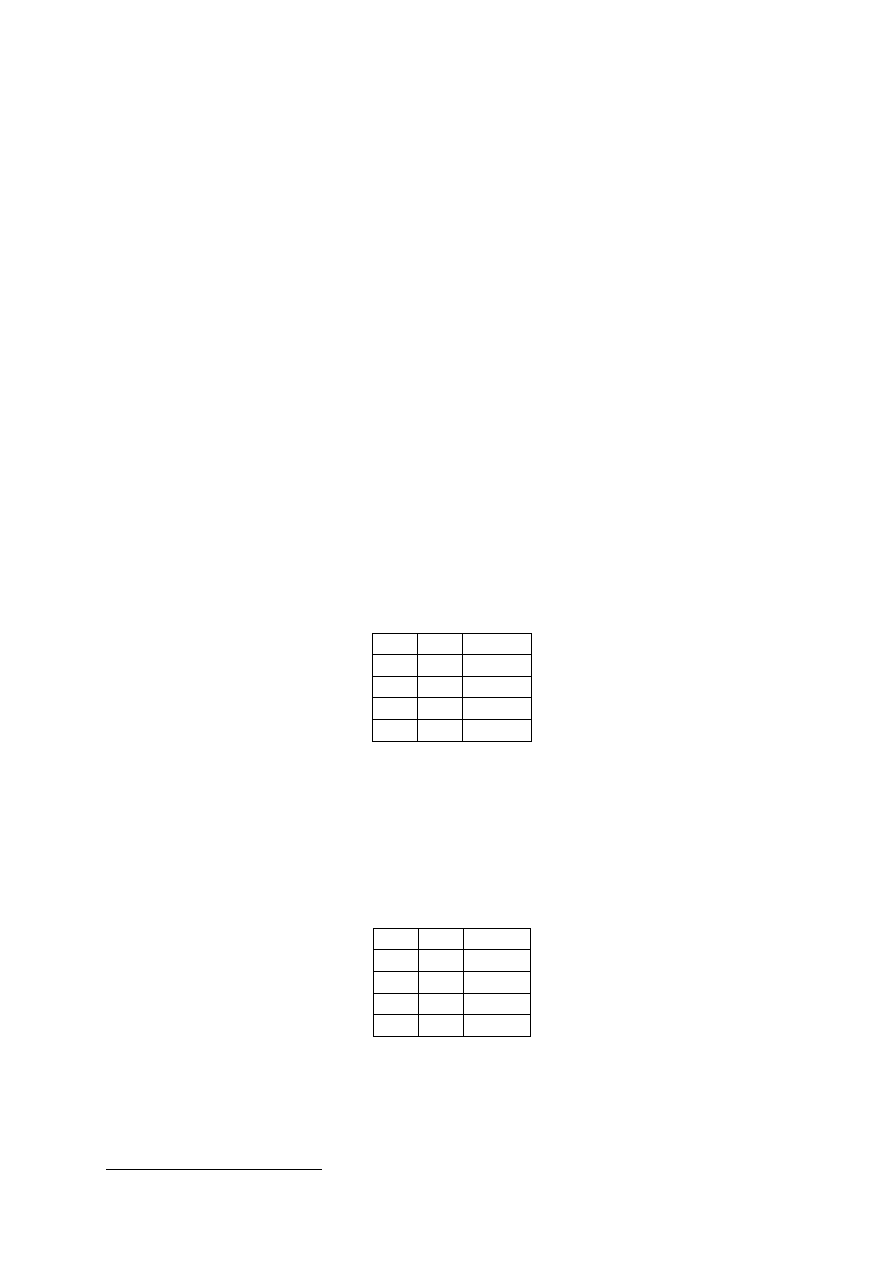
14

Ta część, która występuje, jako pierwsza, czyli przed wyrażeniem „to”, nazywa się

poprzednik, a część następująca po „to” nazywa się następnik. Zgodnie z tabelą możemy
stwierdzić, że implikacja jest zawsze prawdziwa z wyjątkiem, gdy poprzednik jest
prawdziwy a następnik fałszywy.

Przy tej okazji należy teraz, (choć później będziemy o tym jeszcze mówić) wspomnieć o

zależności między związkiem implikacyjnym a związkiem wynikania jednego zdania z
drugiego, czyli związkiem wnioskowania. Te zależności w sposób klarowny wyraża Z.
Ziembiński

11

.

Ze zdania Z

1

wynika zdanie Z

2

wtedy i tylko wtedy, gdy:

1)

implikacja zbudowana ze zdania, Z

1

, jako poprzednika i zdania, Z

2

jako następnika jest

prawdziwa oraz

2)

prawdziwość tej implikacji opiera się na jakimś związku między tym, co głosi zdanie

Z

1

, a tym, co głosi zdanie Z

2

.

O charakterze tych związków będzie mowa później. Warto wspomnieć jeszcze o innej

charakterystyce.

Jeżeli z poprzednika implikacji wynika jej następnik, to poprzednik nazywamy racją, a

następnik implikacji następstwem.

Racja i następstwo są to dwa człony stosunku zwanego wnioskowaniem. Jeżeli używamy,

zatem terminu racja i następstwo, to mówimy tylko o zdaniach składowych implikacji
prawdziwej i zarazem o odpowiednim charakterze związku między jednym a drugim zdaniem.

a)

Funktor koniunkcji połączeniu z argumentami tworzy funkcję zdaniową zwaną

również koniunkcją; symbolicznie: p /\ q (czyt. p i q).

Tablica koniunkcji

p

q

p/\q

1

1

1

1

0

0

0

1

0

0

0

0

Należy pamiętać o tym, że funktor i może również pełnić rolę funktora nazwotwórczego od

dwóch i więcej argumentów nazwowych. W użyciu koniunkcyjnym i występuje w wyrażeniu A
jest B i C, w znaczeniu enumeracyjnym A i B to C.

b)

Funktor alternatywy prostej (symbol v) tworzy funkcję zwaną alternatywą prostą;

symbolicznie: p v q (czyt. p lub q).

Tablica koniunkcji

p

q

p v q

1

1

1

1

0

1

0

1

1

0

0

0

Możemy się spotkać z symbolem, + jako symbolem alternatywy. Jest ona przyrównywana w

rachunku zdań do dodawania w matematyce, tak jak koniunkcja jest czasem oznaczana
symbolem ·, bowiem traktuje się ją na podobieństwo mnożenia.

11

Z. Ziembiński: Logika praktyczna. WN PWN. Warszawa 1994, s. 89.

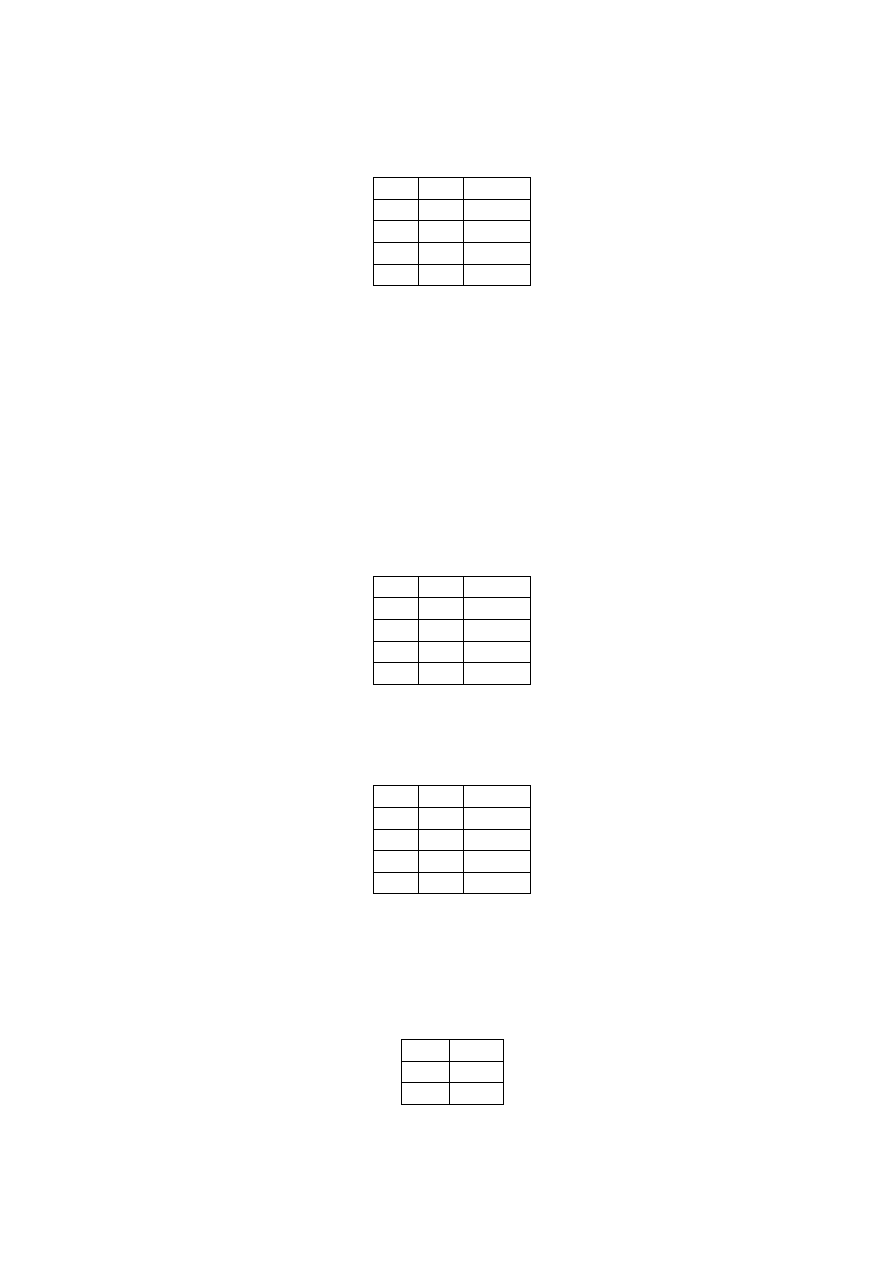
15

c)

Funktor alternatywy rozłącznej lub wyłączającej tworzy funkcję o tej karnej

nazwie; symbolicznie: p ÷ q (czyt. p albo q).

Tablica alternatywy rozłącznej

p

q

p ÷ q

1

1

0

1

0

1

0

1

1

0

0

0

W języku potocznym często nie odróżnia się funkcji znaczeniowych spójnika lub, albo,

bądź. Przykład podany w książce Z. Ziembińskiego może nieco sprawę wyjaśnić, choć dotyczy
problemów prawnych. Na przykład według danego przepisu za pewien czyn przestępca
powinien być ukarany przynajmniej jedną z dwóch kar przy możliwości wymierzeniu obu na
raz, czy też jedną i tylko jedną, czy też, co najwyżej jedną. Jeśli sami wystąpilibyśmy w roli
oskarżonych, znaczenie słowa lub nie byłoby dla nas obojętne. Czasami lub może wystąpić,
jako funktor nazwotwórczy, np. uczony lub szarlatan.

d)

Funktor dysjunkcji tworzy funkcję dysjunkcji; Prawdziwość obu zdań jest

warunkiem wystarczającym do uznania fałszywości dysjunkcji.
symbolicznie: p / q, (czyt. bądź p, bądź q).

Tablica dysfunkcji

p

q

p ÷ q

1

1

0

1

0

1

0

1

1

0

0

1

e)

Funktor równoważności tworzy funkcję równoważności;

symbolicznie: p ≡ q (czytamy: p zawsze i tylko wtedy, gdy q).

Tablica równoważności

p

q

p ≡ q

1

1

1

1

0

0

0

1

0

0

0

1

Przy tworzeniu zdań złożonych z więcej niż dwóch należy stosować nawiasy celem

uniknięcia nieporozumień. Zdania równoważne należy odróżniać od zdań równoznacznych.

g) Funktor negacji tworzy funkcję negacji; symbolicznie: ~p (lub p′) (czyt.: nieprawda, że

p lub nie p).

Tablica negacji

p

~q

1

0

0

1

Wyrażenie nieprawda jest tak, że, synonimiczne nieprawda, że, w języku polskim zaznacza

się umieszczeniem partykuły przeczenia przed odpowiednimi czasownikami np. nieprawda, że
Jan jest ekonomistą, mówimy Jan nie jest ekonomistą.

16

Należy wyraźnie odróżnić zdania sprzeczne od zdań przeciwnych. Zdania typu: Szkoła

Główna Handlowa została zbudowana przed II wojną światową i nieprawda, że Szkoła Główna
Handlowa została zbudowana przed II wojną światową są zdaniami sprzecznymi.

W odniesieniu do zdań sprzecznych można sformułować ważne twierdzenia logiczne,

nazywane także zasadami myślenia. Są to:

−

Zasada sprzeczności (symbolicznie: ~(p/\ ~p)). Dwa zdania względem siebie sprzeczne

nie mogą być zarazem prawdziwe (czytamy: nieprawda, że p i nie p).

−

Zasada wyłączonego środka (symbolicznie: p v ~p; czytamy p lub nie p). Dwa zdania

względem siebie sprzeczne nie mogą być oba fałszywe.

−

Zasada podwójnego przeczenia (symbolicznie: p = ~(~p)) czytamy p jest równoważne

nieprawda, że nie p;).

Zdanie podwójnie zaprzeczone ma wartość logiczną taką samą jak zdanie, które jest

niezaprzeczone.

Wymienione trzy zasady nazywane są w logice również podstawowymi prawami

myślenia.

Należy odróżnić, jak już zaznaczone, zdania sprzeczne od zdań przeczących. Na przykład

para zdań przeczących to: Kwiatkowski jest znakomitym pisarzem i Kwiatkowski jest
analfabetą. Te zdaniu mogą być obydwa prawdziwe i obydwa fałszywe, po nie może się
zdarzyć parze zdań sprzecznych.

f)

Funktor binegacji tworzy funkcję binegacji; symbolicznie: p ↓ q (czyt. ani p ani q).

Tablica binegacji

p

q

p ↓ q

1

1

1

1

0

0

0

1

0

0

0

1

Funktor binegacji ma tę właściwość, że z jego pomocą można zdefiniować wszystkie

pozostałe funktory, podobnie jest z funktorem dysjunkcji.

7.16. Języki naturalne posiadają o wiele więcej spójników prawdziwościowych niż te, o

których mówiliśmy. Chodzi, bowiem o możliwość bardziej adekwatnego zapisu jakiejś
rzeczywistości.

Mówimy

również

o

możliwości

zdefiniowania

jednego

spójnika

prawdziwościowego za pomocą innego, to znaczy, że zastosowanie w zdaniu spójnika b
zamiast spójnika a ni e zmieni sensu tego zdania Powstanie natomiast zdanie równoważne,
które danego spójnika nie zawiera.

Na przykład funktor dysjunkcji można zastąpić funktorami negacji i alternatywy:

p/q = ~p \/ ~q.

Na przykład funktor binegacji może być zastąpiony przez negację i koniunkcje:

p↓q = ~p /\ ~q.

Problem ten nie będzie przedmiotem naszego szczegółowego wywodu, choć należy

wiedzieć, że wszystkie spójniki prawdziwościowe są definiowalne za pomocą odpowiednio
dobranych zbiorów spójników np.: {~, →}. {~, /\}. {~, \/. }

12

. W związku z tym można

stwierdzić, że „każdy schemat prawdziwościowy można, korzystając z odpowiednich definicji,
»przetłumaczyć« na schemat, w którym występują tylko owe wyróżnione spójniki”

13

.

12

B. Stanosz. Wprowadzenie do logiki formalnej. PWN, Warszawa 1985. S. 23

13

Ibidem. S. 23.

17

Ograniczenie do minimum liczby funktorów stosuje się przy konstrukcji tzw. aksjomatycznych
systemów rachunku zdań.

7.17. W zapisach symbolicznych posługujemy się również nawiasami w celu wydzielenia

określonych całości syntaktycznych i uniknięcia tym samym nieporozumień.

7.18. W niektórych przypadkach, np., jeżeli chcemy podkreślić tezowy charakter danej

formuły zdaniowej, korzystamy dodatkowo z symboliki rachunku kwantyfikatorów.

7.19. Rachunek kwantyfikatorów nazywany bywa również rachunkiem predykatów, to

jest nazw odnoszących się do własności lub stosunków, np. wyrażenie zapisane symbolicznie:

/\

(x)

P

(x)

→

Q

(x)

,

czytamy: dla każdego x, jeśli P od x to Q od x. Na przykład dla każdego, przedmiotu, jeśli jest
to przedmiot metalowy, stosuje się prawo mówiące o rozszerzaniu się metalu pod wpływem
wysokiej temperatury. W wyrażeniu tym występują zmienne i symbole stałe wzbogacone w
stosunku do symboli występujących w rachunku zdań.

Symbol /\

x

lub ∏

x

jest to symbol kwantyfikatora dużego lub ogólnego, niekiedy

nazywanego również kwantyfikatorem generalnym. Tak rozumianemu kwantyfikatorowi
odpowiadają w języku naturalnym wyrażenia typu każdy, wszelki, dowolny, dla każdego, dla
dowolnego.

Symbol P reprezentuje predykaty (własności lub stosunki), które przysługują przedmiotom

rozważanego zbioru — nazywamy je symbolami predykatowymi. Predykaty mogą być
wieloargumentowe.

Symbol x, y, z reprezentuje przedmioty (indywidua) danego rodzaju, które nazywane są

symbolami zmiennych indywidualnych.

Symbol V

x

lub Σ

x

jest symbolem kwantyfikatora małego, nazywanego niekiedy

kwantyfikatorem szczegółowym, a także kwantyfikatorem egzystencjalnym. Czytamy: dla
pewnego x istnieje takie x, niektóre x. Oto kilka przykładów formuł zdaniowych z użyciem
symboli rachunku kwantyfikatorów.

/\

x

P

(x)

(dla każdego x P od x) Jest to schemat zdania np. wszyscy jesteśmy omylni.

~/\ P

(x)

(nieprawda, że dla każdego x P od x). Jest to schemat zdania np. nie każdy jest

bezinteresowny.

Użycie kwantyfikatora pozwala podkreślić powszechność określonej właściwości w

stosunku do określonego zbioru przedmiotów czy indywiduów. Inaczej mówiąc pozwala na
osiąganie właściwego stopnia ogólności danego stwierdzenia. Stąd używając w logice
rachunku zdań symboli kwantyfikatorów i wiążąc je z określoną formułą zdaniową,
podkreślamy bądź jej charakter ogólny, czyli, że odnosi się ona do zbioru wszelkich zdań,
które będą zbudowane w taki sam sposób, bądź podkreśla się, że dziedzina zdań prawdziwych
zbudowanych na danej formule ma zasięg ograniczony.

Zagadnienia rachunku kwantyfikatorów, jak sądzę, są słuchaczom znane z racji studiowania

niektórych działów matematyki wykładanej na naszej uczelni.

7.1. TAUTOLOGIE RACHUNKU ZDAŃ

7.1.1. Metoda zero-jedynkowa. Poprawnie zbudowane formuły rachunku zdań, które przy

wszelkich podstawieniach wartości za zmienne zdaniowe stają się zdaniami prawdziwymi,
nazywamy tautologiami, czyli prawami logicznymi, (o czym już mówiliśmy). Czy jakieś
wyrażenie jest tautologią, czy nie, można sprawdzić podstawiając odpowiednie wartości na
miejsce zmiennych i porównując efekt z tablicami odpowiednich funkcji. Należy przy tym
sprawdzić wszystkie możliwości, których liczba odpowiada wzorowi 2

n

, gdzie n oznacza liczbę

zmiennych w formule. I tak w wyrażeniu p → q mamy do czynienie z 2

2

= 4 możliwości, p →

(q → r) mamy 3 zmienne, czyli liczba możliwości wynosi 2

n

= 8.

18

W związku z problemem tautologii B. Stanosz czyni interesującą uwagę: „Celem formalno-

logicznego opisu języka jest wyznaczanie zbioru zdań logicznie prawdziwych. Cel ten osiąga
się poprzez 1° przyporządkowanie zdaniom ich form logicznych 2° ustalenie, które z tych
form są tautologiczne, czyli formami zdań logicznie |prawdziwych”

14

. Pierwsze zdanie wiąże

się z gramatyką i tu jest niewielki udział logiki, głównie w postaci symboliki, drugie zaś jest
całkowicie związane z logiką. Właśnie rachunek zdań wymaga zbioru takich form logicznych.

„Mówiąc, że dane zdanie jest prawdziwe na mocy znaczenia występujących w nim

spójników prawdziwościowych i sposobu, w jaki zostało zbudowane za pomocą spójników ze
zdań prostych, chcemy powiedzieć, że prawdziwe jest każde zdanie zbudowane tak samo za
pomocą tych spójników z dowolnych innych zdań; innymi słowy, – że prawdziwe jest po
prostu każde zdanie, reprezentowane przez schemat prawdziwościowy, pod który podpada
zdanie dane. Takie schematy nazywać będziemy tautologiami rachunku zdań”

15

.

Formuła rachunku zdań (logika zdań) jest tautologią tego działu logiki zawsze i tylko

wtedy, gdy jest schematem wyłącznie prawdziwych zdań.

7.1.2. Wróćmy do przykładów weryfikacji tautologii metodą 0, 1. Zweryfikujemy

metodą 0,1 np. zasado wyłączonego środka: p \/ → p.

I. Za p podstawiamy 1

I. Za p podstawiamy 0

1 \/ ~ 1

0 \/ ~ 0

1 \/ 0

0 \/ 1

1

1

Zapis ten prowadzi zawsze do symbolu 1. Formuła ta jest więc tautologią. A oto przykład:

zasada sprzeczności ~(p /\

~

p)

p/1 ~(1 /\ ~ 1)

p/0 ~(0 /\ ~ 0)

~(1 /\ ~ 0)

~(0 /\ ~ 1)

~ 0

~ 0

1

1

W podobny sposób można sprawdzać formuły logiczne bardziej złożone.

7.1.3. Tautologii rachunku zdań jest bardzo wiele. Poniżej zebrane tautologie są

najbardziej znane wraz z ich symboliką i specjalnymi nazwami, które ustalały się
w ciągu rozwoju logiki.

1.

p → p

zasada tożsamości, (jeżeli p to p)

2.

~(p /\ ~p)

zasada sprzeczności (nieprawda, że p i nie p)

3.

p \/ ~p

zasada wyłącznego środka, (p lub nie p)

4.

p → ~ (~p)

(jeśli p to nieprawda, że nie p)

5.

~ ( ~ p ) → p

prawo podwójnego przeczenia, (jeżeli nieprawda, że nie p, to p)

6.

~ ( p → p) → p

prawo Claviusa

7.

(p → ~p) → ~p

prawo redukcji do absurdu

8.

~p → (p → q)

prawo Dunsa Szkota

9.

~( p \/ q ) ≡ ~p /\ ~q

I prawo De Morgana

10.

~(p /\ q) ≡ ~p \/ ~q

II prawo De Morgana

11.

(~p → ~q) → (q → p)

prawo transpozycji prostej

12.

(p → q) → (~q → ~p)

prawo transpozycji prostej

13.

(p → q) /\ (q → ~p) → ~p

prawo redukcji do absurdu z dwiema zmiennymi

14.

q → (p → q)

prawo symplifikacji

15.

p /\ q ≡ q /\ p

16.

p \/ q ≡ q \/ p

prawo przemienności

17.

(p ≡ q) ≡ (q ≡ p)

14

B. Stanosz: Wprowadzenie do …, Op. Cit., s. 29.

15

Ibidem. S. 29.

19

18.

[(p → q) /\ p] → q

modus ponendo ponens

19.

[(p → q) /\ ~p] → ~p

modus tollendo tollens

20.

[(p \/ q) /\ ~p)] → p

modus tollendo ponens

21.

[(p / q) /\ p)] → ~p

modus ponendo tollens

(czytaj: jeśli bądź p, bądź q i p, to nie q)
22.

~(p → q) → (~q → ~p)

prawo negacji implikacji

23.

[(p → q) /\ (q → r)] → p → r

prawo sylogizmu hipotetycznego

24.

(p /\ q → r) → [p → (q → r)]

prawo eksportacji

25.

[p → (q → r)] → (p /\ q) → r

prawo importacji

26.

(p → q) → [(~p → q) → q]

prawo dylematu konstrukcyjnego

27.

(p → q) → [(p → ~q) → ~p]

prawo dylematu destrukcyjnego

Wiele praw rachunku zdań znano w starożytności, również średniowiecze ma swój wkład w

teorię zdań. W postaci współczesnej rachunek zdań stworzyli G. Frege, który ogłosił rachunek
zdań w wersji implikacyjno-negacyjnej oraz A. Whitehead i B. Russel z negacją i alternatywą.

7.1.4. Posłużymy się funkcją zdaniową bardziej złożoną, o której nie wiemy, czy jest

prawdziwa, czy nie:

[(p \/ q)

→ r] →

[p

→ (q /\ r)]

W celu wydzielenia całości syntaktycznych możemy posłużyć się techniką pomocniczą w

postaci nawiasów.

1

2

3

4

p

q

r

p \/ q

(p \/ q) →

q /\ r

p → (q /\ r)

[(p \/ q) → r] → [p → (q /\ r)]

1

1

1

1

1

1

1

1

1

1

1

1

0

0

0

1

1

0

1

1

1

0

0

0

1

0

0

1

0

0

0

1

0

1

1

1

1

1

1

1

0

1

0

1

0

0

1

1

0

0

1

0

1

0

1

1

0

0

0

0

1

0

1

1

Za pomocą metody zero-jedynkowej wykazaliśmy, że badana funkcja zdaniowa nie jest

tautologią rachunku zdań. Dokładna analiza tego przykładu pozwoli słuchaczowi zrozumieć
samą operację weryfikacyjną.

Metodę zero-jedynkową można skrócić eliminując te sytuacje, kiedy mamy udowodnić

końcową wartość 1.

Jeżeli udowodnimy, że kombinacja wartości, która powinna doprowadzić do wartości 0 (jak

np. w implikacji p → q, jeżeli za p będzie 1, za q będzie 0), zawsze doprowadzi do wartości 1,
tzn., że mamy do czynienia z tautologią.

7.1.5. Nie wnikając bliżej w sprawę, należy stwierdzić, że istnieją jeszcze inne metody

dowodzenia tautologicznego charakteru funkcji.

Jedną z takich metod jest aksjomatyzacja rachunku zdań, która polega na wymienianiu

explicite twierdzeń, które postanawia się przyjąć bez dowodu.

Takie twierdzenia nazywamy aksjomatami lub twierdzeniami pierwotnymi, te natomiast,

które się dowodzi na podstawie tych założeń, nazywają się twierdzeniami pochodnymi. Jest
rzeczą oczywistą, że twierdzenia pochodne czy pierwotne ujawniają się dopiero w ujęciu
całościowym systemu aksjomatycznego. Drugim elementem systemu aksjomatycznego są
zasady dowodzenia zwane regułami inferencyjnymi.

20

Systemy aksjomatyczne logiki formalnej spełniają podstawowe wymogi: to znaczy każda

prawda systemu musi być bądź aksjomatem, bądź twierdzeniem pochodnym. Spełniają one
również wymóg, aby takie twierdzenia, tzn. aksjomaty i pochodne, były prawdziwymi
twierdzeniami systemu. Udowodnienie prawdziwości tych stwierdzeń w odniesieniu do
systemu aksjomatycznego rachunku zdań jest sprawą nieco skomplikowaną. Dlatego też tym
zagadnieniem nie będziemy się zajmować. W trakcie wykładu będzie zademonstrowany jeden
taki przykład.

7.1.6. Rachunek zdań można zbudować również metodą tzw. systemu założeniowego, w

którym istotną rolę odgrywają odpowiednie reguły, np.:

−

odrywania,

−

dołączania koniunkcji,

−

opuszczania koniunkcji,

−

dołączania alternatywy,

−

opuszczania alternatywy,

−

dołączania równoważności,

−

opuszczania równoważności.

7.2. ELEMENTY RACHUNKU NAZW

7.2.1. Najprościej rachunek nazw lub teorię nazw, jak wolą niektórzy, można określić,

jako dział logiki formalnej obejmującej formuły, czyli wzory ze zmiennymi nazwowymi.
Na miejsca zmiennych nazwowych można podstawić tzw. terminy, czyli nazwy ogólne i
niepuste.

7.2.2. Zdania, które są przedmiotem rachunku nazw, nazywają się zdaniami

kategorycznymi, subsumpcyjnymi lub asertorycznymi.

7.2.3. Język rachunku nazw. Symbolika rachunku nazw. Zmienne nazwowe oznaczane są

dużymi literami alfabetu łacińskiego i jest ich trzy: S (łac. Subiectum – podmiot), P (łac.
praedicatum – orzecznik), M (łac., terminus medius – termin średni).

Symbole stałe funktorów zdaniotwórczych od argumentów nazwowych pochodzą od dwóch

łacińskich słów – affirmo – twierdzę i nego – przeczę. Dwie pierwsze samogłoski z tych słów
są symbolami funktorów, czyli a, i, e, o.

7.2.4. Podział zdań kategorycznych. Odpowiednie funktory klasyfikują zdania kategoryczne

na poszczególne grupy, które zgodnie z charakterem funktorów należą do zdań twierdzących
bądź przeczących – podział ze względu, na jakość oraz ogólnych i szczegółowych – podział ze
względu na ilość.

7.2.5. Krzyżując owe kategorie uzyskujemy następujący podział zdań kategorycznych na:

−

ogólnotwierdzące,

−

szczególowotwierdzące.

−

ogólnoprzeczące,

−

szczególowoprzeczące.

Stosując odpowiednią symbolikę możemy poszczególne formuły zdaniowe przedstawić

następująco:

−

ogólnotwierdzące S a P czytamy: każde S jest P,

−

szczegółowotwierdzące S i P czytamy: niektóre S są P,

−

ogólnoprzeczące S e P czytamy: żadne S nie jest P,

−

szczegółowoprzeczące S o P czytamy: niektóre S nie są P.

21

Zdania te można również zapisać używając prostej symboliki rachunku zbiorów i rachunku

zdań:

•

Zdanie S a P może być zapisane:

/\

x

[(x ε S) → (x ε P)],

czytamy: dla każdego x jeśli x jest S, to x jest P.

•

Zdanie S e P:

/\

x

[(x ε S) → (x ε P)′], gdzie znak ′ oznacza przeczenie,

czytamy: dla każdego x, jeśli x jest S, to nie prawda, że x jest P.

•

Zdanie S i P:

Σ

x

[(x ε S) /\ (x ε P)],

czytamy: istnieją takie x, że x jest S i x jest P.

•

Zdanie S o P:

Σ

x

[(x ε S) /\ (x ε P)′],

czytamy: istnieje takie x, że x jest S i nieprawda, że x jest P.

Należy jeszcze zaznaczyć, że wszystkie funkcje zdaniowe sformułowane przez Arystotelesa,

twórcę teorii zdań kategorycznych, zostały sformułowane z użyciem funktora implikacji,
jeśli...to i funktora koniugacji i.

7.2.6. Termin rozłożony. „Przez techniczne określenie »rozłożenie terminu« rozumiemy

użycie terminu w całym zakresie”

16

. Praktycznie rozpoznajemy, czy termin jest rozłożony, czy

nie, po tym czy stoi przed nim jawnie, czy domyślnie słowo każdy, ewentualnie żaden

17

. Można

tutaj przyjąć kilka reguł:

a)

W zdaniach ogólnotwierdzących rozłożony jest podmiot, a nierozłożony orzecznik, np.:

każdy lekarz jest absolwentem Wyższej Szkoły Medycznej. Termin rozłożony – to lekarz.

b)

W zdaniach ogólnoprzeczących rozłożony jest zarówno podmiot, jak i orzecznik.

c)

W zdaniach szczegółowotwierdzących ani podmiot, ani orzecznik nie jest rozłożony, np.

niektórzy ekonomiści są naukowcami.

d)

W zdaniach szczegółowoprzeczących nierozłożony jest podmiot, natomiast rozłożony

jest orzecznik, np. niektóre kobiety nie są matkami, czyli: niektóre kobiety nie należą do klasy
kobiet.

Ogólna formuła na temat rozłożenia terminu brzmi:

W zdaniach kategorycznych rozłożone są terminy figurujące w roli podmiotów zdań

ogólnych oraz terminy będące w zdaniach przeczących orzecznikami.

7.2.7. Prawa rachunku nazw odnoszące się do wnioskowania bezpośredniego. Między

zdaniami kategorycznymi, czyli subsumpcyjnymi, a ściślej między ich wartościami logicznymi
mogą zachodzić różnorodne związki, które mają charakter wnioskowania. W rachunku nazw
wyróżniamy dwa rodzaje wnioskowania i związane z tym prawa logiczne:

a)

wnioskowanie bezpośrednie, które polega na tym, że do wniosku dochodzimy na

podstawie jednej przesłanki;

b)

wnioskowanie pośrednie, kiedy wniosek wyprowadzony jest z dwóch przesłanek, przy

czym odbywa się to z udziałem tzw. terminu średniego. Punkt wyjścia obydwóch wniosków
nazywa się przesłanką, punkt zaś dojścia konkluzją.

16

J. Gregorowicz: Zarys logiki dla prawników. PWN, Warszawa 1962, s. 107.

17

Ibidem.

22

7.2.8. Podstawowymi zasadami wnioskowania bezpośredniego są konwersja, obwersja,

kontrapozycja.

a)

Konwersja polega na wyprowadzaniu z klasycznego zdania kategorycznego tego

odwrócenia i może występować w postaci prostej i z ograniczeniem.

Konwersja prosta polega na zmianie miejsca podmiotu i orzecznika.
Konwersja z ograniczeniem, oprócz zmiany jak w konwersji prostej, wprowadza jeszcze

zmianę ilości zdania odwróconego.

I tak, konwersji prostej podlegają zdania ogólnoprzeczące i szczegółowotwierdzące. Zapis

symboliczny tej zasady:

S e P → P e S

W tych przypadkach możemy użyć również symbolu tożsamości:

S, P → P i S, S e P = P e S, S i P = P i S.

Na przykład:
żaden koń nie jest psem = żaden pies nie jest koniem;
niektórzy ludzie są wegetarianami = niektórzy wegetarianie są ludźmi;
niektórzy studenci są ludźmi wierzącymi zawsze i tylko wtedy, gdy niektórzy ludzie wierzący
są studentami.

b) Obwersja polega na wyprowadzeniu ze zdania twierdzącego równoważnego mu zdania

przeczącego i na odwrót, ze zdania przeczącego wyprowadza się zdanie twierdzące.

Aby dokonać obwersji jakiegoś zdania kategorycznego, musimy zmienić przede wszystkim,
jakość a następnie dodać negację do orzecznika.

Zapis symboliczny: S a P → S e P′ (czytamy: jeśli każde S jest P, to żadne S nie jest nie P).
Na przykład:
jeżeli każda konstytucja jest ustawą, to żadna konstytucja nie jest nie-ustawą – to jest obwersja
zdania ogólnotwierdzącego.
S i P → S o P'
(czytamy: jeżeli niektóre S są P, to niektóre S nie są nie P); jeśli niektórzy ekonomiści nie są
biznesmenami, to niektórzy ekonomiści są nie-biznesmenami.
S e P → S a P' (czytamy: jeżeli żadne S nie jest P, to każde S jest nie P); jeżeli żaden złodziej
nie jest uczciwy, to każdy złodziej jest nieuczciwy.
S o P → S i P' (czytamy: jeżeli niektóre S nie są P, to niektóre S są nie P). Można we
wszystkich wzorach obwersji postawić zamiast znaku implikacji znak równoważności, oznacza
to możliwość wnioskowania w obydwie strony.

J. Gregorowicz pisze, że „Obwersja nie jest jakimś szczególnie płodnym rodzajem

wnioskowania. Może jednak oddać pewne usługi przy rozstrzyganiu np. kwestii czy dwaj
przeciwnicy, wypowiadający swoją tezę różnymi słowami twierdzą to samo, czy też nie”

18

.

c) Kontrapozycja powstaje przez przestawienie i zanegowanie obu terminów zdania

kategorycznego. Może występować w postaci prostej i ograniczonej.

Zapis symboliczny zasady kontrapozycji prostej:

S a P → P' a S' (czytamy: każde S jest P. to każde nie P jest nie S),
S o P → P' o S' (czytamy: jeśli niektóre S nie są P, to niektóre nie P nie są nie S).

Prawa te mogą być zapisane z ujęciem równoważności.

Zapis symboliczny zasady kontrapozycji ograniczonej:
S e P → P' o S' (czytamy: jeżeli żadne S nie jest P, to niektóre nie P nie są nie S).

18

Ibidem. S. 113.

23

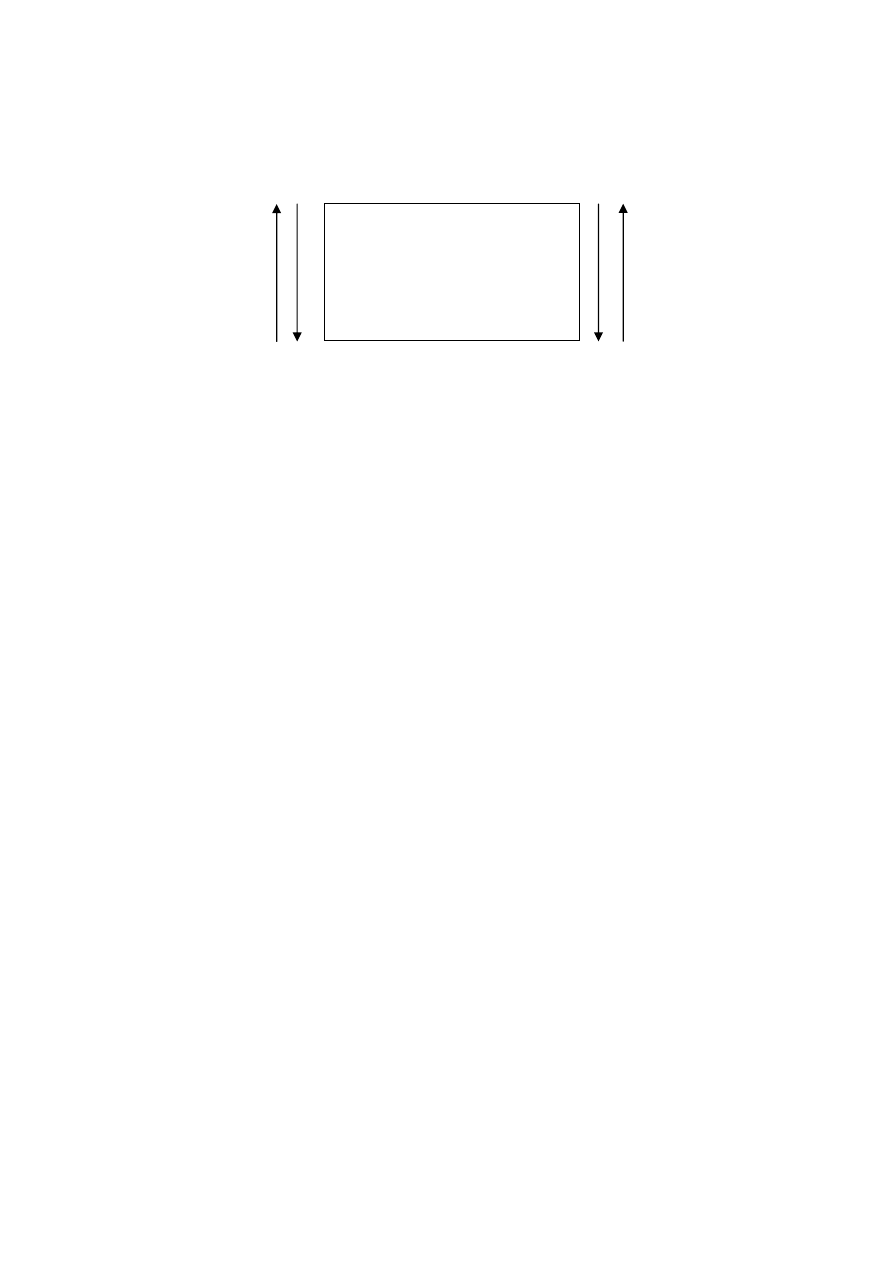
7.2.9. Szczególnym przypadkiem związków między zdaniami kategorycznymi jest kwadrat

logiczny, czyli opozycja zdań. Obraz graficzny kwadratu logicznego:

S a P

Przeciwieństwo

S e P

S i P

Podprzeciwieństwo

S o P

7.2.10. Z przedstawionych tu symbolicznie zależności wynikają bardzo ściśle zasady
wnioskowania.

a) Stosunek przeciwieństwa określają symbolicznie formuły:

S a P → (S e P)', czyli zachodzi tu stosunek równoważności
S e P → (S a P)'.
Niepoprawne są wzory:
(S a P)' → S e P; (S a P)' → (S e P)'; (S e P) → S a P oraz (S e P)' → (S a P)'.

b)

Stosunek podprzeciwieństwa zaś określają takie symboliczne formuły wnioskowania:

(S i P)' → S o P czytamy: jeśli nie jest tak, że niektóre S są P, to niektóre S nie są P.
(S o P)' → S i P czytamy: jeżeli nieprawdą jest, że niektóre S nie są P, to niektóre S są P.
Nieprawidłowe są wzory:
S i P → S o P; S i P → (S o P)';

S o P → S i P, S o P - (S i P)'.

c)

Stosunek sprzeczności zachodzi wtedy, kiedy zdania sprzeczne me mogą być ani

zarazem prawdziwe, ani zarazem fałszywe.

Poprawnych jest osiem wzorów:

S a P → (S o P)'

S e P → (S i P)'

(S a P)' → S o P

(S e P)' → S i P

S o P → (S a P)'

S i P → (S e P)'

(S o P)'→ S a P

(S i P)' → S e P

d) Stosunek nadrzędności. Jeśli zdanie nadrzędne jest prawdziwe, to zdanie podrzędne jest

prawdziwe, natomiast, jeśli zdanie nadrzędne jest fałszywe, to zdanie podrzędne jest
nieokreślone, poprawne są dwie zależności:
S a P → S i P;
S e P → S o P.

e) Stosunek podrzędności jest odwrotnością stosunku nadrzędności. Jeżeli zdane

podrzędne jest prawdziwe, to zdanie nadrzędne jest nieokreślone, a jeśli zdanie podrzędne jest
fałszywe, to nadrzędne jest fałszywe.
Występują, więc dwa wzory:
(S i P)' → (S a P)',
(S o P)1 → (S e P)'.

N

a

d

rz

ę

d

n

o

ść

P

o

d

rz

ę

d

n

o

ść

24

8. WNIOSKOWANIE POŚREDNIE

SYLOGIZM KATEGORYCZNY

8.1. Wnioskowanie sylogistyczne określa się, jako wnioskowanie z dwóch lub więcej

przesłanek. Uważny słuchacz zetknął się już z tym problemem w teorii zdań.

Określa się go również mianem wnioskowania pośredniego właśnie z tego powodu, że

między przesłanką a wnioskiem znajduje się jeszcze jedna przesłanka pośrednia.

Na przykład [(p → q) /\ (q → r)] → (p → r). Można bez trudu zauważyć, że wnioskowanie

sylogistyczne posiada zawsze więcej niż dwie zmienne.

8.2. Sylogizm kategoryczny, jak nie trudno się domyśleć, skonstruowany jest ze zdań

kategorycznych.

Oto przykład konstrukcji zdaniowej:

każda zbrodnia jest przestępstwem;
każdy rabunek jest zbrodnią,

A więc:

każdy rabunek jest przestępstwem.

Można to zdanie zapisać za pomocą znanej już symboliki rachunku nazw:

M a P w postaci implikacji
S a M (M a P /\ S a M) → S a P

A więc:

S a P

Każde zdanie poprzednika tej implikacji nazywa się przesłanką, czyli przesłanką jest M a P

i S a M, następnik zaś jest wnioskiem, który w tym przypadku nazywa się konkluzją. Ta
przesłanka, która zawiera orzecznik konkluzji, nazywa się przesłanką większą, ta zaś, która
zawiera podmiot konkluzji jest przesłanką mniejszą.

Nazwa taka wynika jeszcze ponadto z faktu, iż zakres nazwy będącej orzecznikiem

konkluzji jest szerszy od dwóch pozostałych zakresów nazw. Stąd też termin (nazwa) będący
orzecznikiem konkluzji, czyli w cytowanym przykładzie termin oznaczony symbolem P
nazywamy terminem większym a oznaczony symbolem S – terminem mniejszym.

Natomiast termin, który powtarza się w obydwóch przesłankach, nazywamy terminem

ś

rednim. W trybie sylogistycznym umownie przyjęto najpierw umieszczać przesłankę większą.

Warto podkreślić, że w sylogizmie hipotetycznym elementem wspólnym jest zdanie a w
sylogizmie kategorycznym nazwa.

8.3. Formy sylogizmu kategorycznego mogą być różne i dzielą się na cztery typy zwane

figurami, różniące się od siebie miejscem terminu średniego.

Figura I

Figura II

Figura III

Figura IV

MP

PM

MP

PM

SM

SM

MS

MS

SP

SP

SP

SP

Aby mogło nastąpić wnioskowanie, poszczególne figury muszą być wypełnione

odpowiednimi funktorami, które zamieniają układ symboli w schematy zdań różniących się
ilością i jakością, czyli w zdania bądź to ogólnotwierdzące, ogólnoprzeczące,
szczegółowotwierdzące, szczegółowoprzeczące. Taki zabieg można wykonać wstawiając do
figur znane już litery a, e, i, o.

25

8.4. Tak powstałe schematy wnioskowania nazywają się trybami. Na przykład:
M a P

jest trybem figury I zbudowanym przez wstawienie funktorów,

S a M

symbolizujących zdanie ogólnotwierdzące, między symbole

S a P

zmiennych nazwowych.

Oto przykłady innych trybów zbudowanych na bazie figury I, z użyciem innych funktorów:

M e P

M a P

M e P

S a M

S i M

S i M

S e P

S i P

S o P

8.5. Wszystkich możliwych trybów, a więc schematów wnioskowania opartych a czterech

figurach, jest 256, z tym, że poprawnych jest tylko 24.

Ażeby ułatwić zapamiętanie trybów poprawnych w średniowieczu wymyślono odpowiednie

popomocnicze wyrażenia o charakterze mnemotechnicznym, to znaczy pomagają one
zapamiętać odpowiednią kolejność funktorów, ale same nie posiadają żadnego znaczenia.
Przyporządkowane są odpowiednim figurom po 6 do każdej. Służą pomocą w ten sposób, ze
zawarte w nich symbole funktorów wstawia się kolejno do przesłanki I, II i konkluzji,
przytaczam zapis tych wyrażeń:

−

do figury I

- Barbara, Celarent, Darii, Ferio, Barban, Celaront;

−

do figury II

- Cesare, Camestres, Festino, Baroco, Cesaro, Camestros;

−

do figury III - Darapti, Dismais, Datisi, Felapton, Bocardo, Farison:

−

do figury IV - Bamalip, Calemes, Dimatis, Fesapo, Fresison, Calemos.

8.6. Pośród sylogizmów można wyróżnić tryby doskonałe, których nie trzeba dowodzić i

które pełnią rolę aksjomatów, służąc tym samym do udowadniania pozostałych sylogizmów.
Takie sprawdzanie nazywa się niekiedy redukcją trybów niedoskonałych do doskonałych. Do
trybów doskonałych zaliczamy: Barbara, Celarent.

8.7. Oprócz metody aksjomatycznej weryfikacji poprawności trybów można jeszcze

stosować dwie inne; jedna to tzw. warunki niepoprawności, a druga diagramy Venna.

8.8. Niepoprawny jest sylogizm, który posiada:

a) Więcej niż trzy terminy. Zdarza się to w szczególności, gdy termin szeroki użyty jest w

dwóch znaczeniach

19

.

Każdy zamek jest okazałą budowlą

M

x

a P

Każdy suwak jest zamkiem

S a M

2

Każdy suwak jest okazałą budowlą

S a P

b) Termin środkowy ani razu nierozłożony.

Każdy ptak jest stworzeniem dwunożnym

P a M

Każdy człowiek jest stworzeniem dwunożnym

S a M

Każdy człowiek jest ptakiem

S a P

19

Wszystkie przykłady tu podane pochodzą z pracy J. Gregorowicza: Zarys logiki dla prawników. PWN. Warszawa 1962.

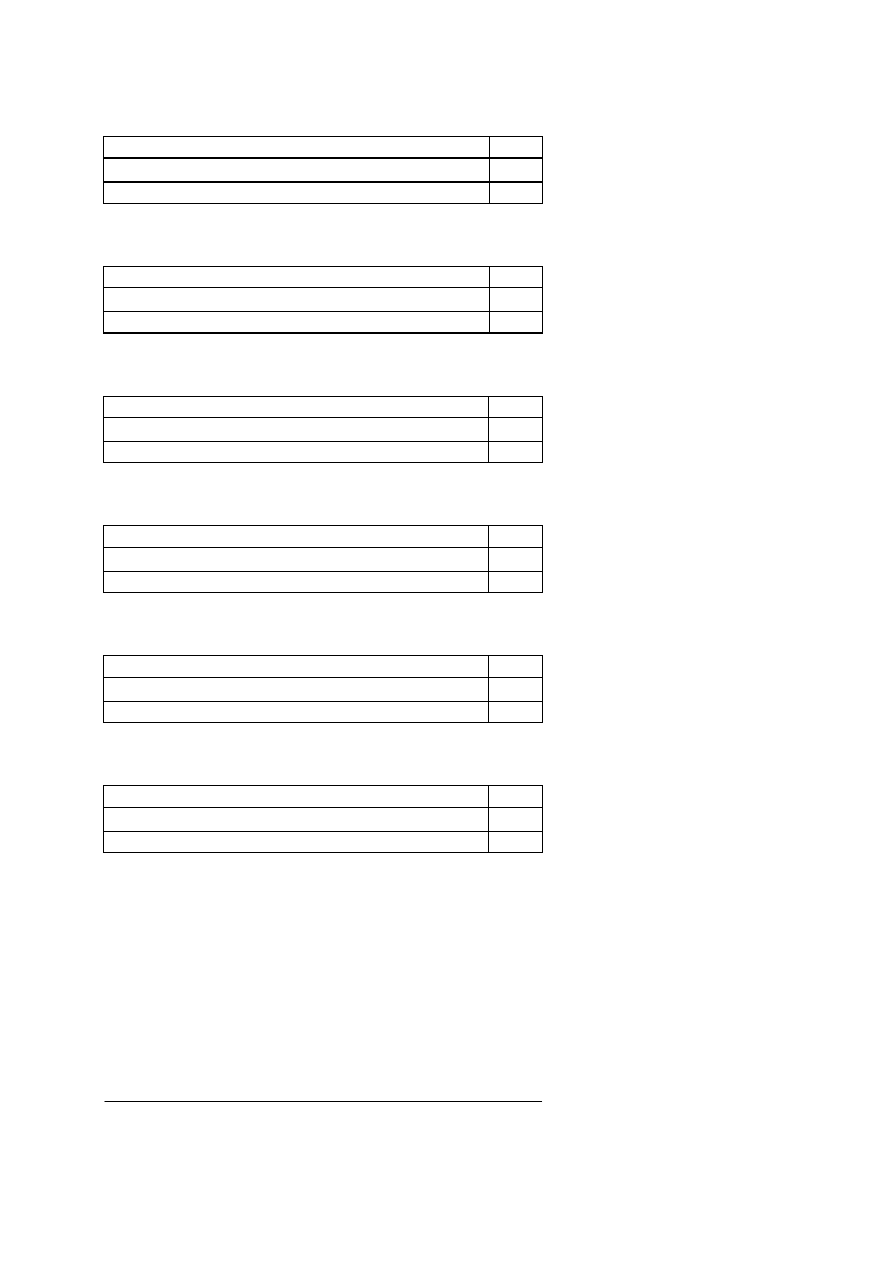
26

c) Obie przesłanki przeczące.

śadna kobieta nie jest mężczyzną

M e P

śadna kobieta nie jest ojcem

M e S

śaden ojciec nie jest mężczyzną

S e P

d) Obie przesłanki szczegółowe.

Niektóre zwierzęta są kotami

M i P

Niektóre zwierzęta są psami

M i S

Niektóre psy są kotami

S i P

e) Termin większy lub mniejszy rozłożony w konkluzji a nierozłożony w przesłankach.

Każde prawo jest związane z interesem społecznym

M a P

śadne społeczeństwo nie jest prawem

S e M

śadne społeczeństwo nie jest związane interesem społecznym

S i P

f) Konkluzję twierdzącą, gdy jedna przesłanka jest przecząca.

Każda zbrodnia jest karalna

M a P

Niektóre czyny ludzkie są zbrodniami

S o M

Każdy czyn ludzki jest karalny

S a P

g) Konkluzję ogólną, gdy jedna z przesłanek jest szczegółowa.

Każdy adwokat jest prawnikiem

M a P

Niektórzy ludzie są prawnikami

S i M

Każdy człowiek jest prawnikiem

S a P

h) Konkluzję przeczącą, gdy ani jedna z przesłanek nie jest przecząca.

Każdy uczciwy człowiek jest zwolennikiem pokoju

M a P

Niektórzy obywatele Polski są ludźmi uczciwymi

S i M

śaden obywatel Polski nie jest zwolennikiem pokoju

S e P

9.

BŁĘDY WNIOSKOWANIA

9.1. Możemy mieć do czynienia z takimi wnioskowaniami, że prawdziwość wniosku nie

będzie przesądzać o poprawności wnioskowania a wniosek fałszywy nie będzie wykluczał
formalnie poprawnego wnioskowania.

9.2. Przykład.

Każdy prokurator jest oskarżycielem publicznym.
Każdy urzędnik państwowy jest prokuratorem.
Każdy urzędnik państwowy jest oskarżycielem publicznym.

Wnioskowanie powyższe przebiega według poprawnego trybu (Barbara) a jednak wniosek

jest fałszywy. Tego rodzaju błąd, gdy mamy do czynienia z fałszywą, choć jedną z przesłanek

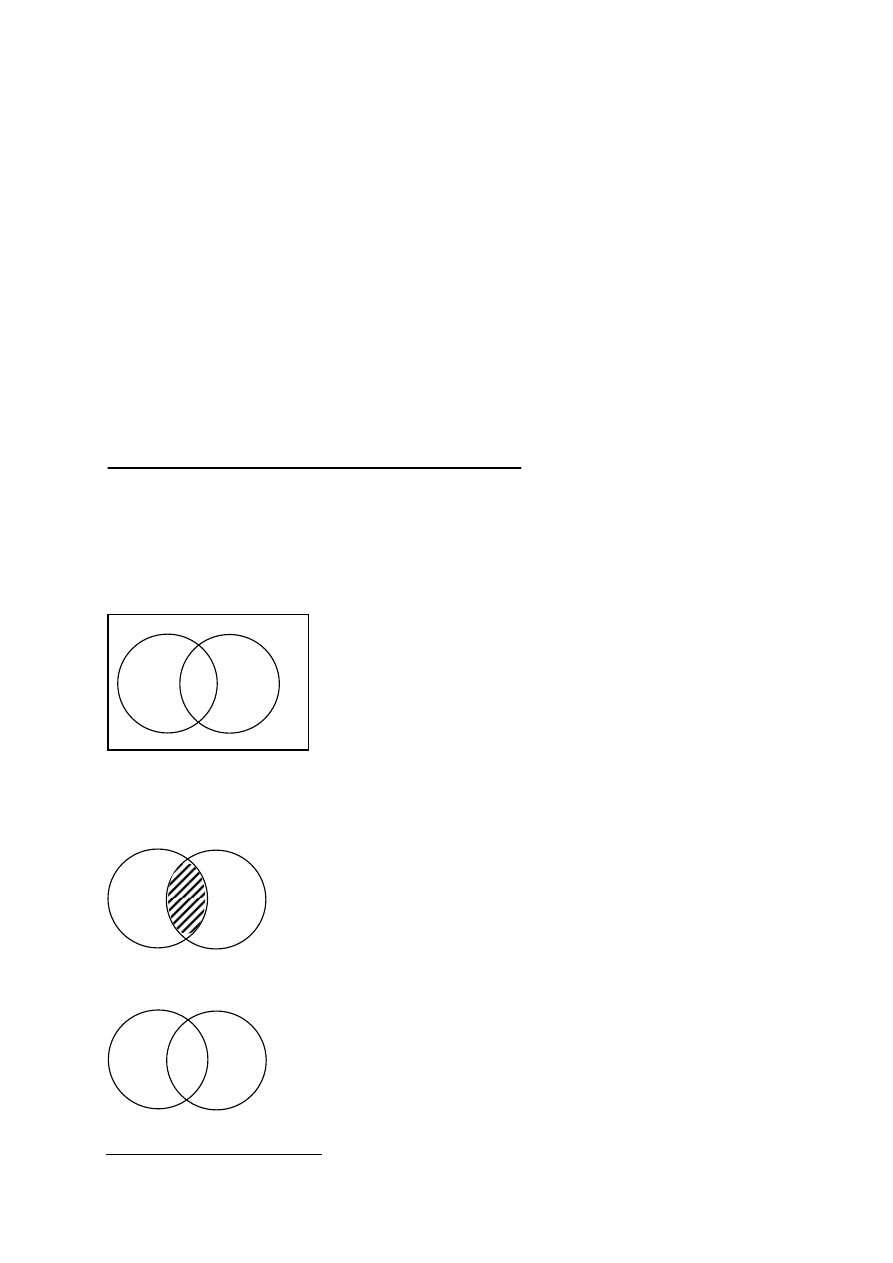
27

(w przytoczonym przykładzie fałszywe jest zdanie: każdy urzędnik państwowy jest
prokuratorem), nazywa się błędem materialnym. Właśnie z takiego błędu materialnego (zdanie
fałszywe) bierze się fałszywy wniosek.

9.3. Innym rodzajem błędu w procesie wnioskowania może być błąd formalny. Mówimy o

błędzie formalnym wtedy, gdy wniosek nie wynika logicznie przesłanek, to znaczy wzór,
według którego przebiega wnioskowanie, nie opiera się na prawie logicznym.

9.4. Należy jeszcze wspomnieć o wnioskowaniu entymematycznym. Nie jest to

wnioskowanie błędne, choć odbiega schematem od sformułowania klasycznego.

Wnioskowanie entymematyczne występuje wtedy, gdy jedna z przesłanek jest założona

milcząco, czyli nie występuje w formie mówionej, bądź pisemnej.
Przykład.
Każdy absolwent SGH jest inteligentem.
Opuszczamy tu aż dwie przesłanki:

Każdy absolwent szkoły wyższej jest inteligentem.
Każdy absolwent SGH jest absolwentem szkoły wyższej.
Każdy absolwent SGH jest inteligentem.

9.5. Uzupełnieniem tematu wnioskowanie pośrednie będzie inna jeszcze metoda

sprawdzania poprawności trybów niż zaprezentowana wcześniej, chodzi o diagramy Venna

20

.

Są to wykresy, za pomocą, których można wykazać prawidłowości konkretnych twierdzeń
rachunku zdań. W przypadku twierdzeń o dwóch terminach podstawą dowodu jest następujący
schemat graficzny:

Na takim schemacie można „zapisać” graficznie poszczególne
zdania, np. S e P, S i P

„Zapisywanie” tych zdań polega na zakreskowaniu pola przedstawiającego zakres pusty,
natomiast oznakowanie krzyżykiem zakresu niepustego.
Przykład. Zdanie S e P oznaczamy:

(pole zakreskowane jest polem pustym, tzn. nie istnieją S, które są P i odwrotnie)

Za pomocą tego schematu sprawdzić formule prostej konwersji prostej S e P → P e S.
Przykład. Formuła podporządkowania S a P → S i P.

20

Opublikował je J. Venn w pracy: Symbolic Logic, 1881.

S P


P

SP′

S′P

SP

S

P

-

P

-

S

+

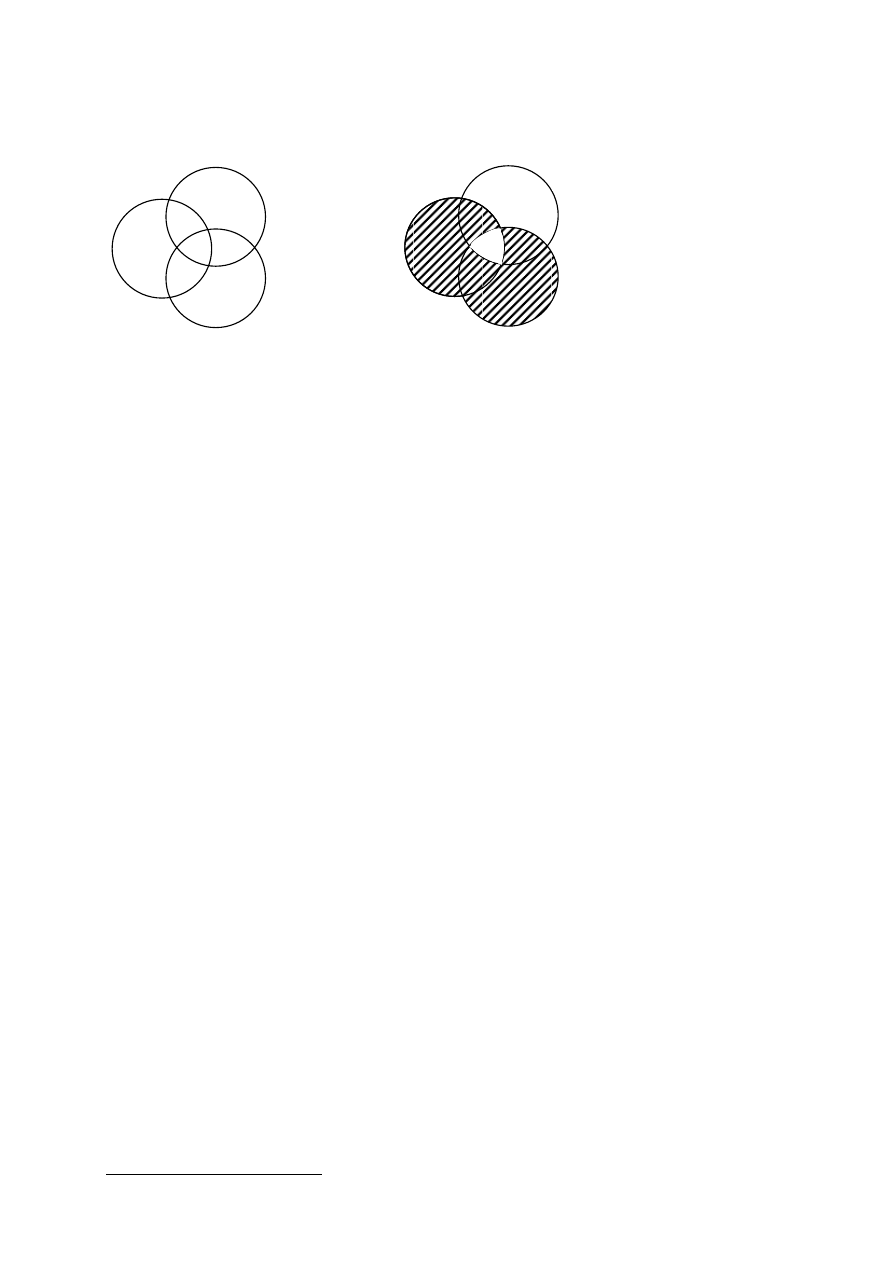
28

Natomiast weryfikacja trybów polega na korzystaniu z następujących schematów:

Weryfikacja typu Barbara: wniosek należy uznać, bo formuła jest sprawdzalna

10.

PODSTAWOWE WIADOMOŚCI Z TEORII RELACJI

10.1 Jednym z ważniejszych działów logiki formalnej jest teoria relacji, która wchodzi

również w zakres teorii mnogości. Z przyczyn wymienionych wcześniej ograniczę się tutaj
tylko do kilku niezbędnych informacji.

10.2. Najprostszą definicję relacji podaje „Mała encyklopedia logiki”:

„...wszelki związek, czy zależność zachodząca między przedmiotami danego (dowolnego)
rodzaju np. równość między liczbami, dłuższość między odcinkami, wynikanie między
zdaniami, różnobarwność między przedmiotami fizycznymi, pokrewieństwo między ludźmi. W
logice współczesnej utożsamia się zwykle relacje ze zbiorami par (trójek itd.)
uporządkowanych, złożonych z przedmiotów, między którymi te zależności zachodzą.”

Autor tego hasła B. Stanosz problem ten wyjaśnia następująco: tak, więc każda relacja

między elementami zbioru A jest pewnym podzbiorem zbioru wszystkich par
uporządkowanych, jakie można utworzyć z przedmiotów należących do A. Relację laką
nazywamy relacją określoną w zbiorze A; (symbolicznie: <a

1

, a

2

> → R)

21

. Zachodzenie

relacji między przedmiotami zaznacza się symbolicznie: x R y.

Wszelkie przedmioty, które są pewnymi elementami par, nazywamy dziedziną relacji R i

oznaczamy symbolicznie Ď(R).

x є D(R) = V

yx

R

y

lub inaczej: ≡ V

y

<x, y>R,

df

np. dziedziną relacji ojcostwo jest zbiór wszystkich dzieci, dla których ktoś jest ojcem.

Te przedmioty, które są drugimi elementami nazywają się przeciwdziedziną relacji R i
oznaczamy je symbolicznie: D(R).

X є Ď (R) = V

yy

R

x

lub inaczej: V

y

(x,x) є R.

df

21

B. Stanosz: Wprowadzenie do logiki formalnej. PWN. Warszawa 1985, s. 99.

S′MP

SM′P

S′M′P′

S′MP′′

SMP′′

SM′P

SMP

P

M

S

29

11.

WYPOWIEDZI MODALNE

11.1. Logikę zdań kategorycznych chciałbym uzupełnić kilkoma uwagami o wypowiedziach

modalnych, do których zalicza się wyrażenia może, musi.

11.2. Dla lepszego zrozumienia sprawy należy wyróżnić podział zdań wedle modalności.

Wyróżniamy zdania:

−

asertoryczne

– między podmiotem a orzecznikiem występuje łącznik jest,

−

problematyczne

– łącznikiem jest może być,

−

apodyktyczne

– łącznik o postaci musi być.

Słowo musi może występować w interpretacji logicznej, np. suma kątów w trójkącie jest

wielkością stałą i wynosi 180°. Jeśli jakaś figura geometryczna jest trójkątem, to suma jej
kątów musi wynieść 180°.

Słowo musi może również występować w interpretacji aksjologicznej, np. temperatura w

salach muzealnych musi być stała.

Występuje także niekiedy w interpretacji etycznej, np. każdy lekarz musi być absolwentem

Akademii Medycznej. Używamy niekiedy wyrażenia musi w interpretacji psychologicznej i
oznacza to swego rodzaju przeświadczenie o konieczności jakiegoś stanu rzeczy.

Analogiczne interpretacje odnoszą się do może, np.:

trójkąt może mieć tylko i wyłącznie 180

o

– interpretacja logiczna;

dla lepszego efektu wychowawczego można posłużyć się:
pochwałą – interpretacja aksjologiczna;
policjant może ukarać mandatem – interpretacja etyczna;
może ten student rzeczywiście chorował a nie tylko udawał? – interpretacja psychologiczna, w
tym przypadku użyta w pytaniu.

11.3. Jeżeli formułujemy zdania z użyciem wyrażenia, że ktoś coś musi ze względu na jakąś

normę, mówimy wówczas o tzw. zdaniu deontycznym.

Zacytuję wypowiedź Z. Ziembińskiego: ,,Zdanie orzekające o kwalifikacji danego czynu

danej osoby ze względu na jakąś normę (zdanie deonetyczne) charakteryzują modalność
normatywną czynów”

22

.

Autor omawia sześć podstawowych modalności normatywnych (deontycznych). Ze względu

na pewną normę rozważamy, czy danej osobie czyn może być nakazany, zakazany, dozwolony,
fakultatywny, indyferentny, czy też może być przedmiotem obowiązku.

12. ELEMENTY METODOLOGII NAUKI

12.1. Metodologia – etymologicznie to nauka o metodach, czyli o sposobach czy drogach

postępowania, w tym przypadku badawczego.

Zakres samego pojęcia jest dość szeroki, obejmuje zarówno procedury badawcze, jak i

efekty tych proce dur, tzn. pojęcia, twierdzenia, teorie.

Inaczej mówiąc, powyższe rozróżnienie refleksji metodologicznej dotyczącej czynności

badawczych i ich metod oraz rezultatów tych czynności wiąże się z dwoma sposobami
pojmowania nauki, jako:

22

Z. Ziembiński: Logika praktyczna. VVN PWN. Warszawa 1994. s. 127.

30

−

ogółu czynności wykorzystywanych przez uczonych w procesach badawczych,

−

ogółu wytworów tych czynności

23

.

12.2. Metodologia dzieli się również na ogólną i szczegółową w zależności od tego, czy

zajmuje się ogółem nauk czy jakąś nauką szczegółową. W tym drugim przypadku można
otrzymać dość obszerną listę różnych metodologii, w tym również metodologię nauk
ekonomicznych. Każdy szanujący się autor podręcznika uważa za stosowne poświęcić jeden
rozdział problemom metodologicznym uprawia-lej przez siebie dyscypliny. Mówimy np. o
metodologii nauk dedukcyjnych czy nauk empirycznych. Każda z nich zawiera wiele ważnych
i interesujących problemów, z których jeden wydaje się mieć znaczenie najważniejsze, jest to
mianowicie prawa uzasadniania twierdzeń. Do tego, więc problemu ograniczę swoje uwagi.

12.3. Co to jest uzasadnianie jakiegoś twierdzenia lub może precyzyjniej, co to znaczy

uzasadnić jakieś twierdzenie?

Wszystkie spotykane definicje podkreślają, że:
Uzasadnić jakieś twierdzenie, to tyle, co podać argumenty, na których to twierdzenie jest

oparte... Uzasadnić jakieś zdanie, ewentualnie uzasadnić uznanie jakiegoś zdania za
prawdziwe, to tyle, co wykazać, ze zostały spełnione warunki wystarczające do uznania tego
zdania za prawdziwe

24

12.4. Rodzaje uzasadnień. W podręczniku logiki wymienia się cztery rodzaje uzasadnień:
a) Odpowiednie spostrzeżenia. Tu możemy zaliczyć np. obserwację rozumianą, jako

postrzeżenie celowe. W ramach obserwacji wyróżnić możemy:

−

obserwacje bezpośrednią – może ona mieć charakter obserwacji zjawisk zewnętrznych

w stosunku do obserwatorów i zjawisk wewnętrznych, psychicznych, w tym przypadku
możemy mówić o tzw. introspekcji;

−

obserwację pośrednią – za pomocą przyrządów lub za pomocą śladów, np.

historycznych.

Oprócz obserwacji stosować możemy również eksperyment.
b) Odwołanie się do odpowiednich konwencji terminologicznych, na przykład, jeśli chcemy

wykazać, że jakaś droga ma trzy kilometry długości.

c) Odwołanie się do intuicji.
d) Odwołanie się do pewnych zdań już uznanych za prawdziwe.

12.5. Pierwsze dwa z wymienionych rodzajów uzasadniania określa się mianem uzasadnień
bezpośrednich i służą one do uzasadniania bądź zdań obserwujących (obserwacja,
eksperyment), bądź zdań analitycznych (konwencja terminologiczna).

Trzeci rodzaj uzasadniania wywołuje wiele dyskusji.
Czwarty rodzaj uzasadniania nazywa się pośrednim. Uzasadnić jakieś zdanie w sposób

pośredni, to znaczy wykazać, że w efekcie jakiegoś rozumowania zdanie to zostało
wywnioskowane z innych zdań uznanych już, jako prawdziwe. To znaczy, że uzasadnienie
pośrednie ma zawsze postać jakiegoś rozumowania. Właśnie rozumowanie jest szczególnym
przedmiotem zainteresowania metodologii nauki a szczególnie tego jej aspektu, który
interesuje się rezultatami badań naukowych. Uzasadnienie pośrednie, jako rozumowanie jest
zawsze operacją na zdaniach. Nawet wtedy, kiedy mamy do czynienia z takim rodzajem
rozumowania, które nazywa się indukcją eliminacyjną, to, jeśli pozostajemy na gruncie
formułowania wniosków, mamy zawsze do czynienia ze zdaniem. Należy jednak pamiętać, że
może być taka metoda postępowania badawczego o charakterze indukcyjnym, ale jest to nieco
inne zagadnienie metodologiczne.

23

Mała encyklopedia logiki. Ossolineum, Wrocław – Warszawa - Kraków, 1988.

24

Ibidem.

31

12.6. Co to jest rozumowanie? Cytuję definicję wybitnego logika J. Łukasiewicza:

Rozumowanie to... taka czynność umysłu, która na podstawie zdań danych, będących

punktem wyjścia rozumowania, szuka zdań innych, będących celem rozumowania a
połączonych z poprzednim stosunkiem wynikania

25

.

Inaczej mówiąc, rozumowanie jest to proces myślowy polegający na dobieraniu dla danego

zdania następstwa albo racji. A jest racją dla zdania B, oznacza, że ze zdania A wynika
logicznie zdanie B.

Aby lepiej zrozumieć pojęcie wynikania logicznego, przytoczę dwie jego definicje:

„Między zdaniem p a zdaniem q istnieje związek wewnętrzny, jeżeli zdanie q wynika ze
zdania p logicznie.
O wyniku logicznym mówimy wtedy, gdy dana implikacja stanowi podstawienie stałych
za zmienne w formule jakiegoś prawdziwego ogólnego twierdzenia logicznego”

26

.

„Ze zdania Z

1

wynika logicznie, Z

2

, gdy implikacja, której poprzednikiem jest Z

1

, jest

podstawieniem prawa logicznego, czyli formuły, która przy wszystkich podstawieniach
przechodzi w zdania prawdziwe.”

27

J. Gregorowicz wymienia jeszcze inne rodzaje związku wewnętrznego między zdaniem, np.:

„Między zdaniem p i q istnieje również związek wewnętrzny, jeżeli istnieje jakieś
empiryczne prawo następstwa zdarzeń gwarantujące nam istnienie tego związku, np.
jeżeli podgrzeję pręt metalowy, to zmieni on swoją długość.”

Oraz:

„Związek wewnętrzny zachodzi między zdaniem p i q także wtedy, gdy istnieje
prawidłowość ogólna ustanowiona przez ustawodawcę, gwarantująca nam zachodzenie
tego związku.”

28

W tych przypadkach należy pamiętać, chociaż nas w tych rozważaniach interesuje głównie

związek wynikania logicznego.

12.7. Klasyfikacja rozumowań. W literaturze polskiej mamy do czynienia różnymi

klasyfikacjami, które łączą się z nazwiskami wybitnych polskich logików. I tak mówimy o
klasyfikacjach Łukasiewicza, Czeżowskiego i Ajdukiewicza.

Z braku czasu ograniczam się głównie do klasyfikacji Czeżowskiego, który dzieli

rozumowanie w sposób następujący:

25

Cytowanie za „Małą encyklopedią... Op. Cit.

26

J. Gregorowicz: Zarys logiki dla prawników. PWN. Warszawa 1962. s. 158.

27

Mała encyklopedia ... Op. cit. Hasło opracowane przez K. Czarnotę.

28

J. Gregorowicz: Zarys logiki.... Op. Cit.

rozumowanie

redukcja

dedukcja

wnioskowanie

dowodzenie

wyjaśnianie

niekiedy tłumaczenie

sprawdzanie

32

12.8. Czym różni się rozumowanie dedukcyjne od redukcyjnego?

Rozumowanie dedukcyjne jest wtedy, gdy kierunek rozumowania zgadza się z kierunkiem

wynikania logicznego, tzn. że dana jest racja a dobiera się następstwo; gdy racja jest zdaniem
już uznanym za prawdziwe i na podstawie tej racji uznaje się następstwo (wnioskowanie,
dowodzenie).

Rozumowanie redukcyjne występuje wtedy, kiedy kierunek rozumowania i kierunek

wynikania są sobie przeciwne, tzn. gdy dane jest następstwo a dobiera się rację; gdy następstwo
jest zdaniem skądinąd uznanym i na podstawie następstwa uznane są racje (sprawdzanie,
wyjaśnianie, tłumaczenie).

12.9. T. Czeżowski dzieli ponadto rozumowanie na:

−

progresywne (wnioskowanie, sprawdzanie) – dana jest racja a szuka się następstwa;

−

regresywne (dowodzenie, wyjaśnianie) – dane jest następstwo a szuka się racji).

12.10. Rozumowanie może być również odkrywcze (wnioskowanie, wyjaśnianie) i

uzasadniające (dowodzenie, sprawdzanie).

12.11. Zapoznamy się teraz z charakterystyką poszczególnych rodzajów rozumowania. I tak:
a)

Wnioskowanie – dobieranie następstwa do racji znanej skądinąd, jako prawdziwa,

dobieranie następstwa do zdań pewnych, np., jeśli będę miał pieniądze, to załatwię bardzo
ważną dla mnie sprawę, b) ( będę miał pieniądze, c) to załatwię sprawę. Zdanie pierwsze i
drugie są przesłankami, są racją dla zdania trzeciego.

b)

Dowodzenie może być różnie definiowane, ale zawsze podkreśla się fakt dobierania

racji pewnej do zdania niepewnego. Inaczej:

Dowodzenie jest to dobieranie racji znanej skądinąd, jako prawdziwa wraz z

wnioskowaniem polegającym na wynikaniu z dobranej racji tego danego następstwa.

29

I na tym tle można zrozumieć podział na rozumowanie regresywne i progresywne. Prof. T.

Kotarbiński pisał:

,,idzie tu raczej o różnicę w dziedzinie dydaktyki niż w dziedzinie metodologii

dowodzenia... Progresywny tok wykładu odpowiada dedukcyjnemu tokowi rozumowania (od
racji do następstwa), regresywny tok wykładu - redukcyjnemu tokowi rozumowania (od
następstw do racji)”.

30

I jeszcze dalszy etap charakterystyki dowodzenia T. Kotarbińskiego:
„Otóż dowodzenie, rozumiane najpełniej, składa się z dwóch stadiów: pierwszego, które

polega na poszukiwaniu dla danej tezy, dla zadanego następstwa, innej tezy, która by była, że
tak powiem, poważną kandydatką na rację, i drugie (stadium), które polega na wysnuwaniu
naszego zadanego następstwa z tej właśnie I wyróżnionej tezy.

31

Przy okazji omawiania dowodzenia należy wyróżnić dowodzenie wprost i dowodzenie nie

wprost, nazywane niekiedy apagogicznym (odwodowym). To drugie polega na tym, że
dowodzi się fałszywości negacji tezy dowodowej i stąd wnosi się o jej prawdziwości. Jeżeli z
negacji dowodzonej tezy wywodzimy jakąś tezę sprzeczną z dowodzoną, to zabieg ten nazywa
się redukcją do absurdu.

29

J Gregorowicz: Zarys logiki..., Op. Cit., s. 161. Ibideem, s. 249.

30

T. Kotarbiński: Elementy teorii poznania, ligiki formalnej i metodologia nauki. W: Dzieła wszystkie. T.1. Ossolineum,

Wrocław – Kraków – Warszawa 1990, s. 249.

31

Ibidem, s. 249.

33

Często przy dowodzeniu nie wprost wykorzystujemy prawo zwane modus tollendo tollens i

zasadę podwójnego przeczenia.

Na przykład: jeżeli egzaminator chce udowodnić, że student nie jest przygotowany dobrze z

logiki, przeprowadza następujący tok rozumowania:
jeżeli pan byłby przygotowany z logiki, – czyli jest to zaprzeczenie tezy wyjściowej brzmiącej:
pan nie jest przygotowany do egzaminu z logiki, – to znałby pan bez problemu formułę zwaną
modus tollendo tollens, ponieważ pan jej nie zna, a przy okazji nie zna pan kilku innych rzeczy
(egzaminator stwierdza sprzeczne następstwa z przyjętą racją), stąd wnioskuję, że pan nie jest
przygotowany do egzaminu z logiki.
Jest to rozumowanie przebiegające według następującego schematu: [(~p → q) /\ → q] → p.

W tym przypadku zmienna p jest zaprzeczeniem tezy: pan nie jest przygotowany do

egzaminu z logiki.

Sens dowodzenia wprost jest zawarty w samej definicji dowodzenia już omawianej.

c)

Sprawdzanie jest to rozumowanie zaliczane do grupy rozumowań redukcyjnych. Mówi

się w sposób zasadny o wnioskowaniu redukcyjnym, rozumiejąc przez wnioskowanie sam tok
rozumowania. Należy pamiętać przy tym. że w rozumowaniu redukcyjnym dane jest
następstwo a dobiera się rację.
Sprawdzanie definiujemy, jako dobieranie następstw pewnych dla zdań nie pewnych. Na
przykład prowadzący ćwiczenia sprawdza czy student przeczytał zadaną literaturę. Poprawna
odpowiedź studenta na zadane pytanie utwierdza pro wadzącego ćwiczenia w przeświadczeniu,
że pytany lekturę przeczytał. A może się okazać, że po prostu przed zajęciami wysłuchał
sprawozdania kolegów, czyli może my powiedzieć, że sprawdzanie to dobieranie następstwa
znanego skądinąd, jako prawdziwe do nieznanej, jako prawdziwa racji.

W nauce sprawdzaniu często poddaje się hipotezy.
Hipotezy są to przypuszczenia (domysły), za pomocą których tłumaczymy dane

faktyczne.

Jest to definicja uproszczona, ale oddaje istotę tego, co należy rozumieć przez hipotezę.
Innym przykładem rozumowania redukcyjnego jest wyjaśnianie lub inaczej tłumaczenie.
Tłumaczenie jest to dobieranie racji do znanego skądinąd, jako prawdziwe następstwa.

Na przykład: zauważyłem, że nie mam portfela w kieszeni. Stwierdzając jego brak,

poszukuję przyczyny, czyli tzw. racji dla znanych następstw. I racji tych może być wiele.
Należy jednak pamiętać, że jeśli jakieś zdanie jest racją dla prawdziwego następstwa, nie
przesądza to sprawy, że ono samo jest prawdziwe. Na przykład twierdzenie, że portfel został
skradziony, może być racją dla opisanego prawdziwego następstwa, ale nie oznacza, że samo
zdanie jest prawdziwe. Portfel mogłem po prostu zostawić w domu.

Szczególnego rodzaju wnioskowaniem redukcyjnym jest indukcja. Odgrywa ona w

naszym postępowaniu poznawczym ogromną rolę. Dlatego też poświęcimy jej nieco uwagi.

Zagadnienie indukcji, jako metody naukowej ma swoją długą tradycję sięgającą

starożytności. Powszechnie wiąże się dwa nazwiska nowożytne z metodyczną refleksją nad
logiką indukcji. Są to F. Bacon ze swoją pracą. „Novum Organum” (1620) i J. S. Mill z
„Systemem logiki dedukcyjnej i indukcyjnej” (1843) Oni to stworzyli teorię indukcji
eliminacyjnej.

D.Hume sformułował swoisty paradoks metodologiczny, który zainspirował do rozważań

nad indukcją. Mianowicie: albo wiedza jest pewna i dotyczy tylko idei skonstruowanych przez,
nasz umysł (matematyka), albo dotyczy faktów realnego świata, ale wtedy pozbawiona jest
pewności. Ten właśnie paradoks zainspirował wielu myślicieli do wysiłku znalezienia lak ich
reguł wnioskowania dotyczących faktów, a ściślej zdań o faktach, które były równoprawne w

34

stosunku do reguł wnioskowania dedukcyjnego. Podobnie jak w innych przypadkach, nie
możemy szczegółowo zajmować się ciekawymi problemami z tym związanymi. Omówimy
jedynie poszczególne przykłady indukcji.

Ogólnie można powiedzieć, że:

„Indukcja jest to wnioskowanie, w którym zdania stwierdzające jakąś ogólną

prawidłowość uznaje się, jako wniosek na podstawie uznanych juz zdań jednostkowych,
stwierdzających poszczególne przypadki tej prawidłowości”

32

.

Inaczej mówiąc, indukcja to tłumaczenie uogólniające, jak stwierdza to słusznie J.

Gregorowicz. Bardzo trafnie definiuje indukcję T. Kotarbiński:

„Przez indukcję rozumiemy częstokroć takie tłumaczenie, (czyli takie dobieranie racji do

danego, skądinąd uznanego następstwa), przy którym jako następstwo występuje koniunkcja
zdań jednostkowych o wspólnym orzeczniku, a jako racja – zdanie ogólne z tymże
orzecznikiem i z podmiotem nadrzędnym do podmiotów tamtych zdań”.
Schematem następstwa jest, przeto:

A

1

jest B, A

2

jest B i A

3

jest B i... A

n

jest B,

natomiast schematem racji jest każde A jest B.

Indukcja jest wyczerpująca (lub zupełna), kiedy desygnaty podmiotów zdań składowych
danego następstwa wyczerpują ogół desygnatów dobranej racji, a jest niewyczerpująca
(niezupełna), kiedy tak nie jest

33

.

Schematycznie indukcję zupełną można przedstawić następująco:

S

l

jest P, S

2

jest P, S

3

jest P... S

n

jest P

S

1

jest S, S

2

jest S, S

3

jest S… S

n

jest S

Każde P jest S, albo S

2

albo S

3

albo S

n

zatem każde S jest P.

Natomiast schemat indukcji niezupełnej wygląda następująco:

S

1

, jest P, S

2

jest P, S

3

jest P… S

n

jest P

S

1

, S

2

, S

3

… jest S

Każde S jest P.

Czyli uznaję jakąś ogólną prawidłowość na podstawie uznanych zdań jednostkowych, lecz

te zdania jednostkowe nie wyczerpują wszystkich desygnatów nazwy S.

Obydwa omówione przykłady indukcji zalicza się do indukcji enumeracyjnej, czyli

indukcji przez proste wyliczanie.

Innego rodzaju indukcją opartą na tym samym schemacie podstawowym jest indukcja

eliminacyjna Milla.

Definiuje się ten przypadek indukcji, jako rozumowanie zmierzające do wykazywania

związków między faktami. Na przykład zawsze ilekroć jest A, to jest B. Inaczej mówiąc, jest to
teoria wnioskowania pozwalająca na podstawie jednostkowych obserwacji dojść do wniosku
stwierdzającego związki przyczynowe. Podkreślam — dojść do wniosku, a nie empirycznie
stwierdzić. Empiryczne stwierdzenie może być podstawą wnioskowania, ale samo nie jest
procesem wnioskowania. Podkreślam ten fakt, bo często mamy do czynienia w odpowiedziach
studentów z uproszczonym pojmowaniem sprawy.

32

Mała encyklopedia... Op. Cit.

33

T. Kotarbiński: Elementy teorii..., Op. Cit., s. 252

35

Przy okazji należy wspomnieć o dwóch sposobach rozumienia terminu przyczyna.
1.

Przyczyną zjawiska B jest takie zjawisko A, po którym B stale następuje (warunek

dostateczny zjawiska B. nie ma A bez B).

2.

Przyczyną zjawiska B jest takie zjawisko A, które stale poprzedza zjawisko B (warunek

konieczny zjawiska B. nie ma B bez A). Poszukiwanie związków przyczynowych sprawdza się
w sposób oczywisty bądź do poszukiwania przyczyn A dla zjawiska B, bądź do poszukiwania
skutków B danego zjawiska A.

Indukcja eliminacyjna zakłada pięć kanonów wnioskowania:

−

jedynej zgodności,

−

jedynej różnicy,

−

zmian towarzyszących.

−

połączonej metody zgodności i różnicy.

−

reszt.

Dla ilustracji posłużę się schematem trzech najważniejszych kanonów w ujęciu

poszukiwania przyczyny i poszukiwania skutków.

Kanon jedynej zgodności. Jeżeli jakaś okoliczność stale towarzyszy występowaniu badanego
zjawiska, to jest albo przyczyną, albo skutkiem.

I. A

1

A

2

A

3

→ B

I. A B

1

B

2

B

3

II. A

1

A

2

Ā

3

→

B

II. A → B

1

B

2

B

3

III. A

1

Ā

2

A

3

→ B

III. A → B

1

B

2

B

3

IV. A

1

Ā

2

Ā

3

→

B

IV. A → B

1

B

2

B

3

Zatem A

l

jest przyczyną B Zatem B

1

jest skutkiem A

Kreska nad literą oznacza brak występowania danego zjawiska. Kanon jedyne, zgodności

upoważnia do stwierdzeń dotyczących warunku koniecznego zjawiska B.

Kanon jedynej różnicy. Jeżeli jakaś okoliczność zachodzi, gdy dane zjawisko występuje a

nie zachodzi, gdy dane zjawisko nie występuje, to okoliczność ta jest skutkiem albo przyczyną
danego zjawiska.

Schematycznie można ten kanon przedstawić następująco:

I. A

1

A

2

A

3

→ B

I. A → B

1

B

2

B

3

II. A

1

A

2

Ā

3

→

B

II. A → B

1

B

2

B

3

Zatem A

l

jest przyczyną B Zatem B

1

jest skutkiem A

Kanon zmian towarzyszących. Jeżeli jedno zjawisko zmienia się równolegle ze zmianą

drugiego, to zachodzi między nimi związek przyczynowy.

I. A

1

A

2

A

3

→ B

I. A → B

1

B

2

B

3

II. zm. A

1

A

2

Ā

3

→

zm. B

II.

zm.

A → zm. B

1

B

2

B

3

Zatem A

l

jest przyczyną B

Zatem B

1

jest skutkiem A

Jest rzeczą zrozumiałą, iż uzyskanie tak „sterylnych” wyników, jak to formułują kanony

indukcji eliminacyjnej, jest niemal niemożliwe. Mimo tego metoda indukcji [eliminacyjnej jest
wielce pożyteczną w nauce a szczególnie w procesie badań nad 'zależnościami przyczynowymi
wielu zjawisk. Kanony te, jak słusznie zauważa Z. Ziembiński, mogą stać się wskazówkami
heurystycznymi, czyli pomagającymi w odkryciach naukowych. Przy zastosowaniu pewnych
zabiegów formalnych te kanony mogłyby się stać dyrektywami inferencyjnymi wnioskowania
dedukcyjnego.

36

12.12. Rozważania o rozumowaniu należy zakończyć omówieniem rozumowania przez

analogię lub inaczej wnioskowaniem przez analogię. „Przesłanki stwierdzają, że każdy z
kolejno napotkanych przedmiotów pewnego rodzaju ma pewną własność. Wniosek stwierdza,
ze i następny napotkany przedmiot tego rodzaju tez będzie posiadał tę własność”

34

. Na

przykład, jeżeli przeczytałem pięć książek autora x i były dla mnie interesujące, wnioskuję, że i
następna też będzie interesująca.

Jest jeszcze jeden aspekt rozumowania przez analogię polegający na tym, że na podstawie

zdań stwierdzających podobieństwo pod względem wielu cech jednego przedmiotu do drugiego
wnioskuję o podobieństwie tych przedmiotów pod względem innych cech, które dotychczas nie
były rozpatrywane.

Jeżeli jakiś przedmiot jest podobny do przedmiotu B pod względem cech a, b, c i przedmiot

A posiada cechę d, to wnioskujemy, że przedmiot B posiada również cechę d.

Ten rodzaj wnioskowania, podobnie jak inne o charakterze redukcyjnym, należy do

wnioskowania zawodnego.

12.13. Na bazie dotychczasowych uwag można poczynić kilka uwag na temat teorii

naukowej, przez którą rozumiemy najogólniej zbiór zdań orzekających o badanej dziedzinie
rzeczywistości. Jest to uporządkowany, według określonych zasad, zbiór zdań. Z racji statusu
ontologicznego przedmiotów badań wyróżniamy:

−

teorię nauk formalnych,

−

teorię nauk empirycznych.

Zagadnienia te dokładniej zostaną omówione na wykładzie.

13. PODZIAŁ LOGICZNY

13.1. Mówiąc o podziale logicznym należy zaznaczyć, że jest to podział zakresu pojęcia

(nazwy), w skrócie mówimy o podziale pojęcia (nazwy). Jest to wydzielanie z zakresu nazwy
jej zakresów podrzędnych, czyli wymienianie pojęć podrzędnych względem tego pojęcia, tak
dobranych, że każdy desygnat dzielonego pojęcia jest desygnatem jednego i tylko jednego z
tych pojęć podrzędnych.

Pojęcie nadrzędne nazywa się pojęciem dzielonym a części powstałe z podziału nazywają

się członami podziału.

13.2. Aby podział był poprawny logicznie, musi spełnić dwa warunki. Powinien być:

−

wyczerpujący (zupełny) – każdy desygnat nazwy dzielonej należy do zakresu któregoś

członu podziału. Suma zakresów członów podziału musi się równać zakresowi pojęcia
dzielonego;

−

rozłączny – każdy desygnat dzielonego pojęcia jest desygnatem (tylko jednego członu

podziału.

13.3. Biorąc pod uwagę sposób dzielenia, wyróżniamy podział dychotomiczny

i podział wedle pewnej zasady.

Z podziałem dychotomicznym mamy do czynienia wtedy, gdy z zakresu pojęcia

dzielonego wydzielamy dwie części, z których jedna powstaje przez dołączenie do niej jakiejś
cechy, a druga przez zanegowanie danej cechy, np. podział ludzi na pełnoletnich i
niepełnoletnich, zdolnych i niezdolnych do wojska itp. Nazwa dychotomiczny pochodzi od
greckiego wyrażenia dichotomos, tzn. podzielony na potowy.

34

Mała encyklopedia… Op. Cit., s 217.

37

13.4. Co oznacza podział wedle określonej zasady lub podstawy podziału?

Podstawą podziału jest właściwość przedmiotów dzielonych, które bierzemy pod uwagę,

kiedy dokonujemy podziału, np. podział ludzi na mężczyzn i kobiety przyjmuje płeć, jako
zasadę podziału. Warunkiem poprawności podziału jest zachowanie jednej i tej samej zasady.
Nie można np. dzielić mieszkańców Warszawy na: kobiety, mężczyzn i osoby duchowne. Taki
podział nie zachowuje jednej zasady podziału.

13.5. Wielostopniowy podział logiczny, polegający na kolejnym dzieleniu członów

podziału, nazywa się klasyfikacja. Jest rzeczą oczywistą, że nie każda klasyfikacja wprowadza
porządek i nie każda jest podziałem naturalnym. Z podziałem naturalnym mamy wtedy do
czynienia, kiedy wydzielone podzakresy pomnażają naszą wiedzę o dzielonym zakresie,
wnoszą coś nowego.

13.6. Można się niekiedy spotkać z pojęciem typowania. Jest to zabieg polegający na

porządkowaniu jakiegoś zbioru wedle pewnego typu idealnego, wzorcowego, tzn. takiego,
który może w rzeczywistości nie występować a stanowi istotę naszego o nim wyobrażenia.
Mówimy wtedy o tzw. typie idealnym.

ZAKOŃCZENIE

Przedstawiona w tym skrypcie charakterystyka tematów jest daleka od „typu idealnego” i

nie pretenduje do roli podręcznika. Ma to być rodzaj pomocy w czasie słuchania wykładów,
które będą rozwinięciem pewnych treści połączonym z analizą przykładów. Dlatego byłoby
wskazane uzupełnienie tezowych ujęć skryptu dobrymi notatkami z wykładu.

Przypominam, że zalecanym podręcznikiem jest „Logika praktyczna” Z. Ziembińskiego

(WN PWN, Warszawa 1994).

Można jednocześnie korzystać z wielu innych podręczników, z których kilka wymienię.
Tadeusz Kotarbiński: Kurs logiki dla prawników. Wyd. 6. PWN, Warszawa 1963.
Kazimierz Ajdukiewicz: Zarys logiki. PWN, Warszawa 1953.
Kazimierz Ajdukiewicz: Logika pragmatyczna. PWN, Warszawa 1965.
Jan Gregorowicz: Zarys logiki dla prawników. PWN, Warszawa 1962.
A. Gregorczyk: Logika popularna. PWN, Warszawa 1955.
Z. Kraszewski: Logika – nauka rozumowania. PWN, Warszawa 1984.
Mała encyklopedia logiki. Ossolineum, Wrocław – Kraków – Warszawa 1988.

Zaliczenie logiki przeprowadzone będzie w formie pisemnej i w postaci określonej liczby

pytań otwartych i zamkniętych.

Otrzymanie określonej liczby punktów będzie warunkiem zaliczenia. Szczegóły zostaną

podane na wykładzie.

Załączone pytania mają charakter kontrolny i wskazują na zakres materiału

egzaminacyjnego. Nie są to przykłady pytań egzaminacyjnych.

38

PRZYKŁADOWE PYTANIA

1.

Podać jedną z definicji logiki.

2.

Co rozumiemy przez pojęcie logiki formalnej?

3.

Co to jest denotacja i konotacja?

4.

Co to jest nazwa i co to jest jej funkcja?

5.

Przytocz znany ci podział nazw.

6.

Co to jest desygnat nazwy, a co zakres?

7.

Co to jest treść nazwy?

8.

Co to są nazwy jednostkowe, ogólne i puste?

9.

Co to jest nazwa ostra i nazwa nieostra?

10.

Wymień i przedstaw graficznie stosunki między zakresami nazw.

11.

Co to są nazwy okazjonalne?

12.

Co jest źródłem wieloznaczności?

13.

Co to jest definicja i jakie są jej funkcje?

14.

Omów strukturę definicji.

15.

Wyjaśnij pojęcie definicji klasycznej.

16.

Co to jest definicja analityczna, inaczej sprawozdawcza?

17.

Co to jest definicja syntetyczna?

18.

Co to jest definicja regulująca?

19.

Co to jest zdanie w sensie logicznym?

20.

Jaki jest stosunek zdań logicznych do zdań w sensie gramatycznym?

21.

Co to są funktory i jakie są ich rodzaje?

22.

Podaj przykład funktora od dwóch argumentów zdaniowych.

23.

Podaj przykład funktora nazwotwórczego.

24.

Co to są zmienne zdaniowe?

25.

Wymień podstawowe znaki stałe używane w rachunku zdań.

26.

Co to jest funkcja zdaniowa?

27.

Wymień podstawowe funkcje rachunku zdań.

28.

Scharakteryzuj funkcję implikacji.

29.

Scharakteryzuj funkcję koniunkcji.

30.

Przy jakiej wartości argumentów alternatywa będzie fałszywa?

31.

Omów znaczenie i podaj zapis formalny następujących zasad:

−

sprzeczności,

−

wyłącznego środka,

−

podwójnego przeczenia.

32.

Przedstaw sposoby sprawdzania tez logicznych.

33.

Co to jest zdanie kategoryczne?

34.

Wymień cztery zasadnicze zdania kategoryczne. Zapisz je w symbolice rachunku zbiorów.