
9
PRZEKSZTAŁCENIE LAPLACE’a
str.
117
8
PRZEKSZTAŁCENIE LAPLACE’A
Przekształcenie Laplace’a jest stosowane do opisu stanów nieustalonych w liniowych ukła-
dach regulacji. Najważniejszą zaletą przekształcenia Laplace’a jest możliwość zapisania równania
różniczkowego liniowego w postaci transmitancji operatorowej. Transmitancja operatorowa opi-
suje właściwości dynamiczne elementów automatyki tworzących schemat blokowy układu regu-
lacji oraz umożliwia obliczanie charakterystyk czasowych i częstotliwościowych.
8.1.
Definicja przekształcenia Laplace’a
W teorii regulacji jest stosowane jednostronne przekształcenie Laplace’a L[f(t)], przyporząd-
kowujące funkcji czasowej f(t), zwanej oryginałem, funkcję operatorową F(s), zwanej transfor-
matą, określoną wzorem:
∫
∞
−
⋅
=
=
0
t
s
dt
e
)
t
(
f
)]
t
(
f
[
L
)
s
(
F
(8.1)
Funkcja f(t) jest funkcją rzeczywistą zmiennej rzeczywistej t. Funkcja F(s) jest funkcją zespo-
loną zmiennej zespolonej s, (s = σ + i ω). Warunkiem istnienia transformaty jest zbieżność całki
Laplace’a.
Niezależnie od tego, jakie nieregularności cechują funkcję f(t), jej transformata jest zawsze w
obszarze zbieżności funkcją holomorficzną, to znaczy funkcja F(s) ma pochodną
ds
)
s
(
dF
w każdym punkcie obszaru zbieżności.
8.2.
Przykłady obliczania transformat Laplace’a
8.2.1.
Funkcja czasowa
t
a
e
f(t)
−
=
, wykładnik ”a” jest liczbą rzeczywistą.
∫
∫
∞
+
−
∞
−
−
−
=
⋅
=
=
0
t
)
a
s
(
0
t
s
t
a
t
a
dt
e
dt
e
e
]
e
[
L
)
s
(
F
[
]
0
)
a
s
(
)
a
s
(
t
)
a
s
(
e
e
)
a
s
(
1
e
)
a
s
(
1
)
s
(
F
t
0
t
+
−
∞
+
−
+
−
−
⋅
+
−
=
⋅
+
−
=
∞
=
=
Transformata funkcji
t
a
e
−
istnieje dla tych wartości zmiennej „s”, dla których granica funkcji
0
e
lim
t
)
a
s
(
t
=
+
−
∞
→
,
czyli dla
0
a
s
>
+
,
a
s
−
>
.
[ ]
[ ]
t
a
e
L
)
a
s
(
1
1
0
)
a
s
(
1
)
s
(
F
−
=
+
=
−
⋅
+
−
=
(8.2)
9
PRZEKSZTAŁCENIE LAPLACE’a
str.
118
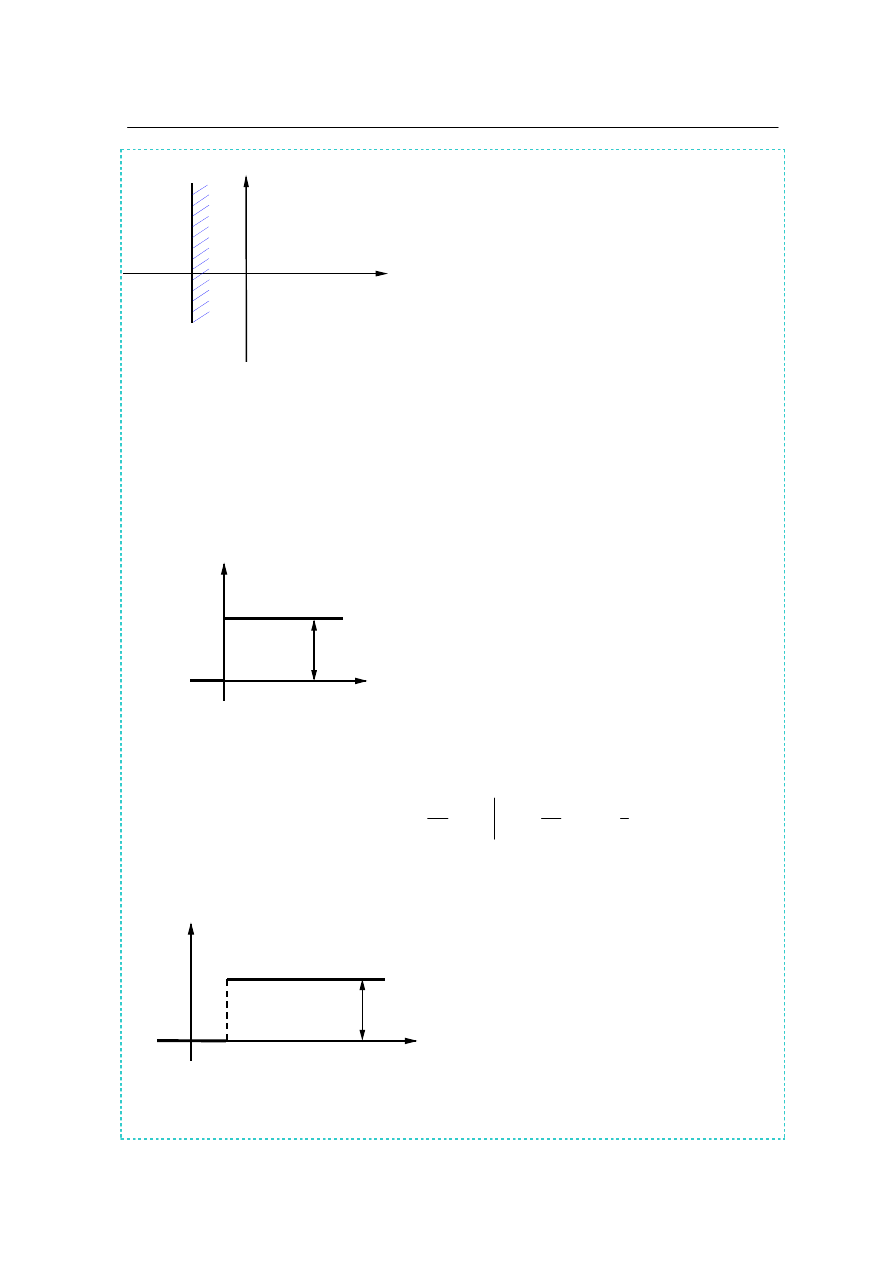
Rys. B.1 Obszar zbieżności całki Laplace'a
funkcji wykładniczej e
-at
Obszar zbieżności
całki Laplace'a
Re[s]
> - a
Re[s]
Im[s]
Prosta
Re[s] = - a
Obszar zbieżności całki Laplace’a dla funkcji
wykładniczej przedstawiono na rys. B.1. Całka
Laplace’a funkcji
t
a
e
−
jest zbieżna we wszyst-
kich punktach s = σ + i ω płaszczyzny liczb ze-
spolonych leżących na prawo od prostej
a
s
−
=
,
czyli w punktach spełniających warunek
a
]
s
Re[
−
>
.
8.2.2
Funkcja skokowa jednostkowa 1(t).
Funkcja skokowa jednostkowa, której wykres przedstawiono na rys. B.2 służy do opisu pro-
cesów nieciągłych. Definicja funkcji
1(t):
1(t) =
<
>
0
t
dla
0
0
t
dla
1
(8.3)
Dla t = 0 funkcja
1(t) nie ma żadnej wartości.
Transformata Laplace’a funkcji
1(t) jest równa
s
1
)
1
0
(
s
1
e
s
1
dt
e
1
dt
e
)
t
(
1
)
s
(
F
t
0
t
t
s
0
t
)
s
(
0
t
s
=
−
−
=
⋅
−
=
⋅
=
⋅
=
∞
=
=
⋅
−
∞
⋅
−
∞
⋅
−
∫
∫
(8.4)
8.2.3
Funkcja skokowa jednostkowa przesunięta w czasie 1(t-T).
Wykres funkcji jednostkowej przesuniętej w czasie przedstawiono na rys. B.3
Definicja funkcji
1(t-T):
1(t-T) =
<
>
T
t
dla
0
T
t
dla
1
(8.5)
Dla t = T funkcja
1(t-T) nie przyjmuje żadnej
wartości.
t
Rys. B.2. funkcja skokowa jednostkowa 1(t)
1
f(t)
f(t) = 1(t)
t
Rys. B.3. funkcja skokowa jednostkowa 1(t - T)
1
f(t)
f(t) = 1(t - T)
T
9
PRZEKSZTAŁCENIE LAPLACE’a
str.
119
Transformata Laplace’a funkcji
1(t-T) jest równa
∫
∫
∫
∞
−
−
∞
−
−
+
−
=
−
=
T
t
s
T
0
t
s
0
t
s
dt
e
)
T
t
(
1
dt
e
)
T
t
(
1
dt
e
)
T
t
(
1
)
s
(
F
T
s
T
s
t
T
t
t
s
T
t
s
T
0
t
s
e
s
1
)
e
0
(
s
1
e
s
1
0
dt
e
1
dt
e
0
)
s
(
F
⋅
−
⋅
−
∞
=
=
−
∞
−
−
⋅
=
−
−
=
⋅
−
+
=
⋅
+
⋅
=
∫
∫
(8.6)
8.2.4
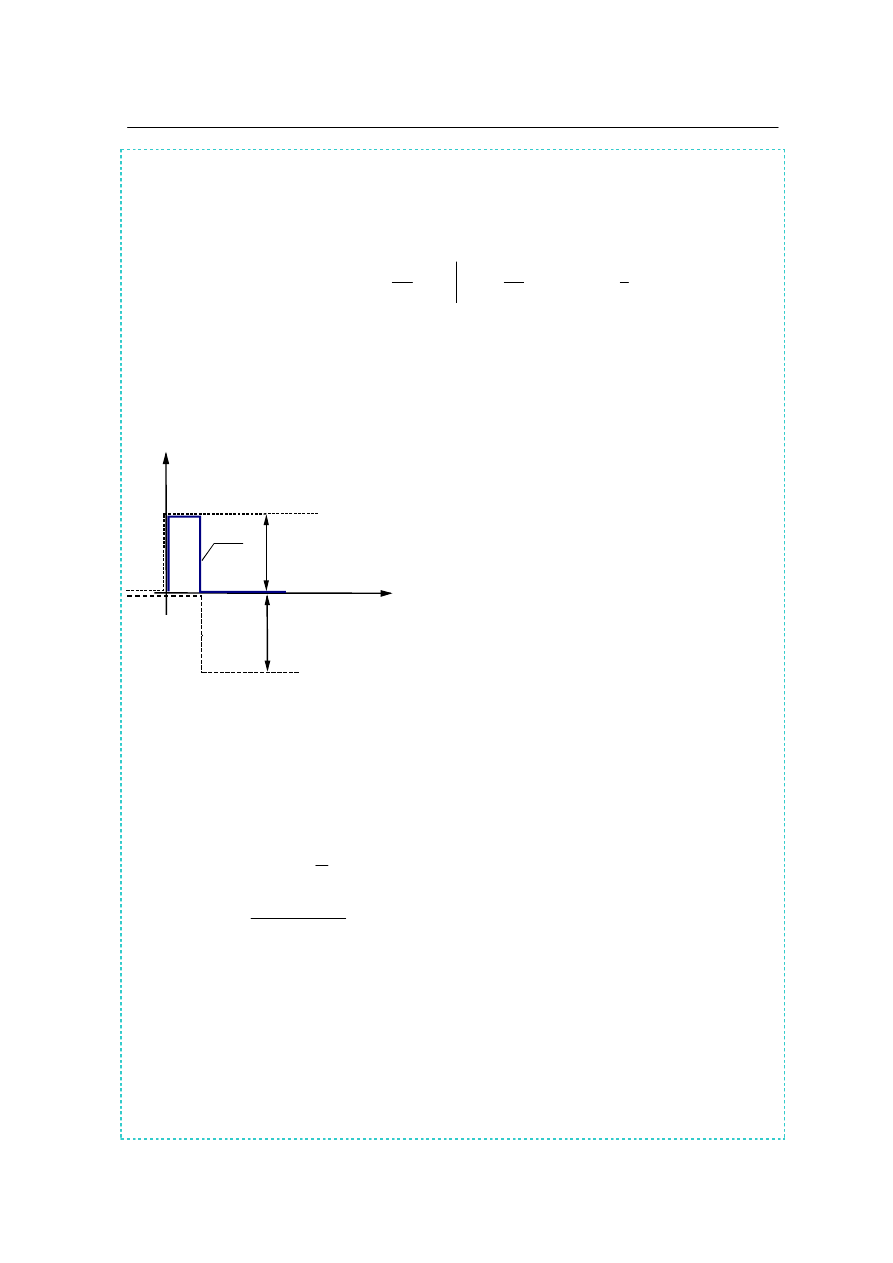
Funkcja impulsowa δ(t) Diraca.
Funkcja impulsowa δ(t) służy do przedstawienia sygnałów w postaci krótkotrwałych impulsów.
Przyjmuje się następującą skróconą definicje funk-
cji δ(t)
δ(t) =
>
=
∞
<
0
dla
0
0
t
dla
0
t
dla
0
(8.7)
przy czym całka funkcji δ(t) jest równa 1.
1
t
d
)
t
(
=
δ
∫
+∞
∞
−
(8.8)
Mimo, iż w definicji użyto sowa „funkcja”, δ(t) nie
jest funkcją w tradycyjnym znaczeniu.
W teorii dystrybucji funkcję δ(t) określa jako gra-
nicę, do której zbliża się funkcja opisująca impuls
rzeczywisty niosący pewną skończoną energię, gdy
czas trwania impulsu maleje do zera.
Jeżeli jako funkcję aproksymującą przyjmiemy impuls prostokątny przedstawiony na rys. B.4, o
szerokości „T” i wysokości
T
1
, to definicja funkcji δ(t) jest następująca:
T
)
T
t
(
)
t
(
lim
)
t
(
T
−
−
=
δ
→
1
1
0
(8.9)
Gdy czas trwania impulsu maleje do zera, jego wysokość rośnie do nieskończoności, a pole
pod wykresem przedstawiające wykonaną pracę jest równe Transformata Laplace’a funkcji δ (t)
jest równa 1.
Zestawienie wybranych funkcji czasowych i odpowiadających im transformat Laplace’a
podano w tabeli 8.1.
t
Rys. B.4. Aproksymacja funkcji
δ
(t)
funkcjami skokowymi
f(t)
T
1
T
__
1
T
__
1
T
__
δ
(t)
1(t)
T
__
1
1(t - T)
_
T
__
1
9
PRZEKSZTAŁCENIE LAPLACE’a
str.
120
8.
3.
Podstawowe własności przekształcenia Laplace’a
8.3.1
Transformata sumy funkcji (liniowość transformacji Laplace’a)
Przekształcenie Laplace’a ma następujące własności:
T
WIERDZENIE
1,
Jeśli funkcje czasowe f
1
(t), f
2
(t) mają transformaty F
1
(s), F
2
(s), to sumie
tych funkcji czasowych pomnożonych przez stałe współczynniki a
1
, a
2
od-
powiada suma funkcji operatorowych pomnożonych przez te współczynni-
ki.
Jeżeli
f(t) = a
1
f
1
(t) + a
2
f
2
(t)
To
F(s) = a
1
F
1
(s) + a
2
F
2
(s)
(8.10)
Twierdzenie to wynika z własności całki. Całka sumy funkcji jest równa sumie całek
z tych funkcji.
8.3.2
Transformata całki
T
WIERDZENIE
2
Jeśli funkcja czasowa f(t) ma transformatę F(s), to całce oznaczonej tej
funkcji czasowej odpowiada funkcja operatorowa F(s) podzielona przez
operator Laplace’a „s”.
Jeżeli
∫
∞
⋅
−
⋅
=
0
t
s
dt
e
)
t
(
f
)
s
(
F
To
s
)
s
(
F
dt
)
t
(
f
L
t
0
=
∫
(8.11)
Całce oznaczonej n – krotnej odpowiada dzielenie funkcji operatorowej przez
s
n
.
n
n
2
t
0
1
1
t
0
t
0
s
)
s
(
F
dt
dt
dt
)
t
(
f
L
n
2
=
∫ ∫
∫
L
L
(8.12)
Twierdzenie 2 można odnosi się również do całki nieoznaczonej, ponieważ
C
dt
)
t
(
f
dt
)
t
(
f
t
0
+
=
∫
∫
(8.13)
gdzie C jest stałą całkowania równą wartości funkcji
∫
dt
)
t
(
f
dla t = 0
∫
∞
−
=
0
dt
)
t
(
f
C
(8.14)
Jeżeli w przedziale
0
t
<
<
∞
−
funkcja f(t) = 0, to C = 0.

9
PRZEKSZTAŁCENIE LAPLACE’a
str.
121
8.3.4
Transformata pochodnej
T
WIERDZENIE
3
Jeśli funkcja czasowa f(t) ma dla t > 0 pochodną
)
t
(
'
f
i istnieje transfor-
mata
[
]
)
t
(
'
f
L
tej pochodnej, to istnieje również transformata funkcji f(t).
L[f(t)] = F(s) i zachodzi wzór
[
]
∫
∞
−
+
−
=
=
0
t
s
)
0
(
f
)
s
(
F
s
dt
e
)
t
(
'
f
)
t
(
'
f
L
(8.15)
gdzie
)
t
(
f
)
f(0
m
i
l
0
t
+
→
=
+
jest prawostronną granicą funkcji f(t) dla t → 0+.
Transformata drugiej pochodnej jest równa
[
]
∫
∞
−
+
−
+
−
=
⋅
=
0
2
t
s
2
2
)
0
(
f
s
)
0
(
'
f
)
s
(
F
s
dt
e
t
d
)
t
(
f
d
)
t
(
'
'
f
L
(8.16)
Transformata n – tej pochodnej jest równa
[
]
)
0
(
f
s
)
s
(
F
s
)
t
(
f
L
)
k
(
1
n
0
k
k
1
n
n
)
n
(
+
⋅
−
=
∑
−
=
−
−
(8.17)
8.3.5
Mnożenie i dzielenie przez t funkcji f(t)
T
WIERDZENIE
4.
Jeśli
[
]
)
s
(
F
)
t
(
f
L
=
, to
[
]
ds
)
s
(
dF
)
t
(
f
t
L
−
=
⋅
(8.18)
[
]
( )
n
n
n
ds
)
s
(
F
d
1
)
t
(
f
t
L
−
=
⋅
(8.19)
8.3.6
Twierdzenie o przesunięciu w dziedzinie zespolonej
T
WIERDZENIE
5.
Jeśli
[
]
)
s
(
F
)
t
(
f
L
=
, to
[
]
ds
)
a
s
(
dF
)
t
(
f
e
L
t
a
+
−
=
⋅
−
(8.20)
8.3.7
Twierdzenie o przesunięciu w dziedzinie rzeczywistej
T
WIERDZENIE
6.
Jeśli
[
]
)
s
(
F
)
t
(
f
L
=
, to dla
0
t
o
≥
[
]
)
s
(
F
e
)
t
t
(
)
t
t
(
f
L
o
t
s
o
o
⋅
=
−
⋅
−
−
1
(8.21)

9
PRZEKSZTAŁCENIE LAPLACE’a
str.
122
[
]
∫
⋅
−
⋅
=
+
−
+
dt
)
t
(
f
e
)
s
(
F
e
)
t
t
(
f
L
o
o
t
0
t
s
t
s
o
(8.22)
8.3.8
Twierdzenie o zmianie skali
T
WIERDZENIE
7.
Jeśli
[
]
)
s
(
F
)
t
(
f
L
=
, oraz
0
a
>
,
0
t
o
≥
, stała a przyjmuje dowolną
wartość, to:
[
]
)
a
s
(
F
e
a
)
t
t
a
(
)
t
t
a
(
f
L
o
t
a
s
o
o
⋅
=
−
⋅
−
−
1
1
(8.23)
Dla
0
t
o
=
otrzymamy
[
]
)
a
s
(
F
a
)
t
a
(
f
L
⋅
=
1
(8.24)
8.3.9
Twierdzenie o wartościach granicznych
T
WIERDZENIE
8.
Jeśli
[
]
)
s
(
F
)
t
(
f
L
=
, oraz istnieje granica
)
(
f
)
t
(
f
m
i
l
t
∞
=
+∞
→
(8.25)
to
)
(
f
)
s
(
f
s
m
i
l
0
s
∞
=
⋅
→
(8.26)
T
WIERDZENIE
9.
Jeśli
[
]
)
s
(
F
)
t
(
f
L
=
, oraz istnieje granica
)
0
(
f
)
t
(
f
m
i
l
0
t
+
=
+
→
(8.27)
to
)
0
(
f
)
s
(
F
s
m
i
l
s
+
=
+∞
→
(8.28)
8.3.10
splot funkcji
Splotem funkcji
)
t
(
f
1
i
)
t
(
f
2
w przedziale
+∞
<
<
t
0
nazywamy funkcję
)
t
(
ϕ
okre-
śloną dla
0
t
≥
następująco
∫
τ
τ
−
⋅
τ
=
∗
=
ϕ
t
0
2
1
2
1
d
)
t
(
f
)
(
f
)
t
(
f
)
t
(
f
)
t
(
(8.29)
Splot jest funkcją określoną przez całkę (29), przy czym całka ta zależy od t zarówno po-
przez górną granicę całkowania, jak i poprzez parametr podcałkowy. Ta podwójna zależność splo-
tu od czasu t powoduje, iż splot, ogólnie biorąc, nie ma takich własności regularnościowych, jakie

9
PRZEKSZTAŁCENIE LAPLACE’a
str.
123
ma każda całka zależna tylko od górnej granicy. Splot nie musi istnieć dla każdego
0
t
≥
i nie
musi być dla każdego
0
t
≥
ciągły. Splot nie musi dążyć do zera dla t → 0+, (jest to źródło popu-
larnych błędów. Prawdziwe jest jednakże następujące twierdzenie
T
WIERDZENIE
10.
Jeśli chociaż jedna z funkcji
)
t
(
f
1
lub
)
t
(
f
2
jest ograniczona w każdym
przedziale [0, T], T>0, to splot
)
t
(
f
)
t
(
f
2
1
∗
:
1)
istnieje i jest ciągły dla każdego
0
t
≥
,
2)
dąży do zera, dla t → 0+.
Właściwości 1), 2) zachodzą wówczas, gdy chociaż jedna z funkcji
)
t
(
f
1
lub
)
t
(
f
2
jest dla
0
t
≥
ciągła.
8.4
Transformata splotu funkcji
T
WIERDZENIE
10.
Jeśli funkcje
)
t
(
f
1
i
)
t
(
f
2
są bezwzględnie transformowalne, istnieją
transformaty
[ ]
)
s
(
F
)
t
(
f
L
1
1
=
,
[
]
)
s
(
F
)
t
(
f
L
2
2
=
oraz chociaż jedna z
nich jest ograniczona w każdym przedziale [0, T], T > 0, to
[
]
)
s
(
F
)
s
(
F
)
t
(
f
)
t
(
f
L
2
1
2
1
⋅
=
∗
(8.30)
Transformata splotu dwóch funkcji jest równa iloczynowi transformat splatanych funkcji.
8.3.11
Transformata iloczynu funkcji
T
WIERDZENIE
11.
Jeśli funkcje
)
t
(
f
1
i
)
t
(
f
2
są bezwzględnie transformowalne oraz istnieją
całki
∫
∞
−
⋅
0
2
1
t
c
2
dt
)
t
(
f
e
1
;
∫
∞
−
⋅
0
2
2
t
c
2
dt
)
t
(
f
e
2
(8.31)
to istnieje transtormata iloczynu
)
t
(
f
)
t
(
f
2
1
⋅
dla
2
1
c
c
]
s
Re[
+
≥
, określona
wzorem (32) przy warunku (33) oraz wzorem (34) przy warunku (35).
[
]
∫
ω
+
ω
−
σ
σ
−
⋅
σ
π
=
⋅
i
c
i
c
2
1
2
1
1
1
d
)
s
(
F
)
(
F
i
2
1
)
t
(
f
)
t
(
f
L
(8.32)
przy czym
2
a
1
1
a
x
]
s
Re[
c
x
−
<
<
(8.33)
lub analogicznie przy zmianie kolejności funkcji pod całką

9
PRZEKSZTAŁCENIE LAPLACE’a
str.
124
[
]
∫
ω
+
ω
−
σ
σ
⋅
σ
−
π
=
⋅
i
c
i
c
2
1
2
1
2
2
d
)
(
F
)
s
(
F
i
2
1
)
t
(
f
)
t
(
f
L
(8.34)
przy czym
1
a
2
2
a
x
]
s
Re[
c
x
−
<
<
(8.35)
8.4
Odwrotne przekształcenie Laplace’a
Zasadnicze znaczenie w zastosowaniach ma zagadnienie odwrotne: d a n a j e s t fu n kc j a
z mi e n n e j ze s p o l o n e j F ( s ) , n a l e ży w y z n a c z yć f u n kc j ę f ( t ) , d l a kt ó r e j F( s ) j e s t
t r a n s f o r ma t ą La p l a c e ’ a .
T
WIERDZENIE
12.
Jeśli funkcja f(t):
a)
jest bezwzględnie transformowalna, tj.
+∞
≠
a
x
i L[f(t)] = F(s),
b)
w każdym przedziale [0, T], T>0, ma ograniczoną zmienność, to dla dowolnej ustalo-
nej wartości
a
x
c
>
, to:
<
=
+
⋅
>
=
⋅
π
∫
∞
+
∞
−
0
t
dla
0
0
t
dla
)
0
(
f
2
1
0
t
dla
)
t
(
f
s
d
)
s
(
F
e
i
2
1
i
c
i
c
t
s
(8.36)
Wzór (36) nosi nazwę wzoru Riemanna-Mellina i określa analitycznie odwrotne przekształ-
cenie Laplace’a oznaczane symbolem
1
L
−
.
[ ]
∫
∞
+
∞
−
−
⋅
π
=
=
i
c
i
c
t
s
1
s
d
)
s
(
F
e
i
2
1
)
s
(
F
L
)
t
(
f
(8.36a)

9
PRZEKSZTAŁCENIE LAPLACE’a
str.
125
8.5
Rozkład funkcji operatorowej na ułamki proste
W układach liniowych występują funkcje operatorowe wymierne w postaci ułamka, w któ-
rych licznik i mianownik są wielomianami o stałych współczynnikach. Funkcję wymierną można
rozłożyć na ułamki proste, a odpowiadające im funkcje czasowe znaleźć w tablicach funkcji ope-
ratorowych. Najpierw należy obliczyć pierwiastki mianownika, następnie mianownik funkcji ope-
ratorowej rozłożyć na czynniki i w zależności od tego czy pierwiastki są rzeczywiste lub zespolo-
ne, pojedyncze lub wielokrotne, należy zaproponować odpowiednie wyrażenie zawierające ułam-
ki proste pomnożone przez współczynniki. Wartości tych współczynników obliczamy z warunku,
aby wyrażenie złożone z ułamków prostych było równoważne danej funkcji operatorowej F(s). Z
tablic funkcji operatorowych znajdujemy funkcje czasowe odpowiadające poszczególnym ułam-
kom prostym występującym w znalezionym wzorze na F(s). Zestawienie wybranych funkcji cza-
sowych i odpowiadających im transformat Laplace’a podano w tabeli 8.1).
Sposoby znajdywania rozkładu funkcji operatorowych na ułamki proste są przedstawione w
załączonych rozwiązaniach zadań.
8.6
Związek między transformatami Laplace’a i Fouriera
Jeżeli funkcja f(t) jest funkcją bezwzględnie całkowalną w przedziale
)
,
0
(
∞
+
i równą zeru
dla t<0 oraz istnieje co najmniej w obszarze
0
]
s
Re[
≥
jej L-transformata oraz F-transformata, to
transformatę Fouriera otrzymuje się z transformaty Laplace’a przez podstawienie s = i ω. Zwią-
zek między przekształceniem Fouriera i przekształceniem Laplace’a przybiera postać
[
] [ ]
=
=
⋅
ω
=
i
s
)
t
(
f
L
)
t
(
)
t
(
f
F
1
t
d
e
)
t
(
f
0
t
i
∫
∞
ω
−
(8.37)
Jednostronne przekształcenie Fouriera można uważać za przypadek szczególny jednostronne-
go przekształcenia Laplace’a.
Dla funkcji
t
a
e
f(t)
−
=
, mającej transformatę Laplace’a
[ ]
)
a
s
(
1
e
L
)
s
(
F
t
a
+
=
=
−
transformata Fouriera jest równa:
[
] [ ]
=
=
⋅
ω
=
−
−
i
s
t
a
t
a
e
L
)
t
(
e
F
1
ω
+
i
a
1
(8.38)
9
PRZEKSZTAŁCENIE LAPLACE’a
str.
126
Jeżeli weźmiemy funkcję f(t) równą zeru dla t<0 oraz taką, że dla
0
a
≥
funkcja
f(t)
e
t
a
−
jest bezwzględnie całkowalna w przedziale
)
,
0
(
∞
+
, wówczas zachodzą następujące związki
między przekształceniami Fouriera i Laplace’a.
[
]
∫
∫
∞
ω
+
−
∞
−
ω
−
−
=
=
0
t
)
i
a
(
0
t
a
t
i
t
a
t
d
)
t
(
f
e
t
d
)
t
(
f
e
e
)
t
(
f
e
F
(8.39)
Porównując z wzorem (B.1) widzimy, że
[
]
[ ]
a
s
Re
t
a
)
t
(
f
L
)
t
(
f
e
F
=
−
=
(8.40)
Tabela 8.1
Transformaty Laplace’a wybranych funkcji
Lp.
Funkcja f(t)
Funkcja F(s)
1
)
t
(
δ
1
2
1
s
1
3
1
(t)
s
1
4
t
2
s
1
5
n
t
)
1
n
(
s
!
n
+
6
t
1
s
π
7
t
2
3
s
2
−
⋅
π
8
t
a
e
⋅
−
a
s
1
+
9
t
a
e
⋅
a
s
1
−
10
)
e
1
(
T
t
−
−
)
1
s
T
(
s
1
+
11
−
−
⋅
−
)
e
1
(
T
t
k
T
t
)
1
s
T
(
s
k
2
+
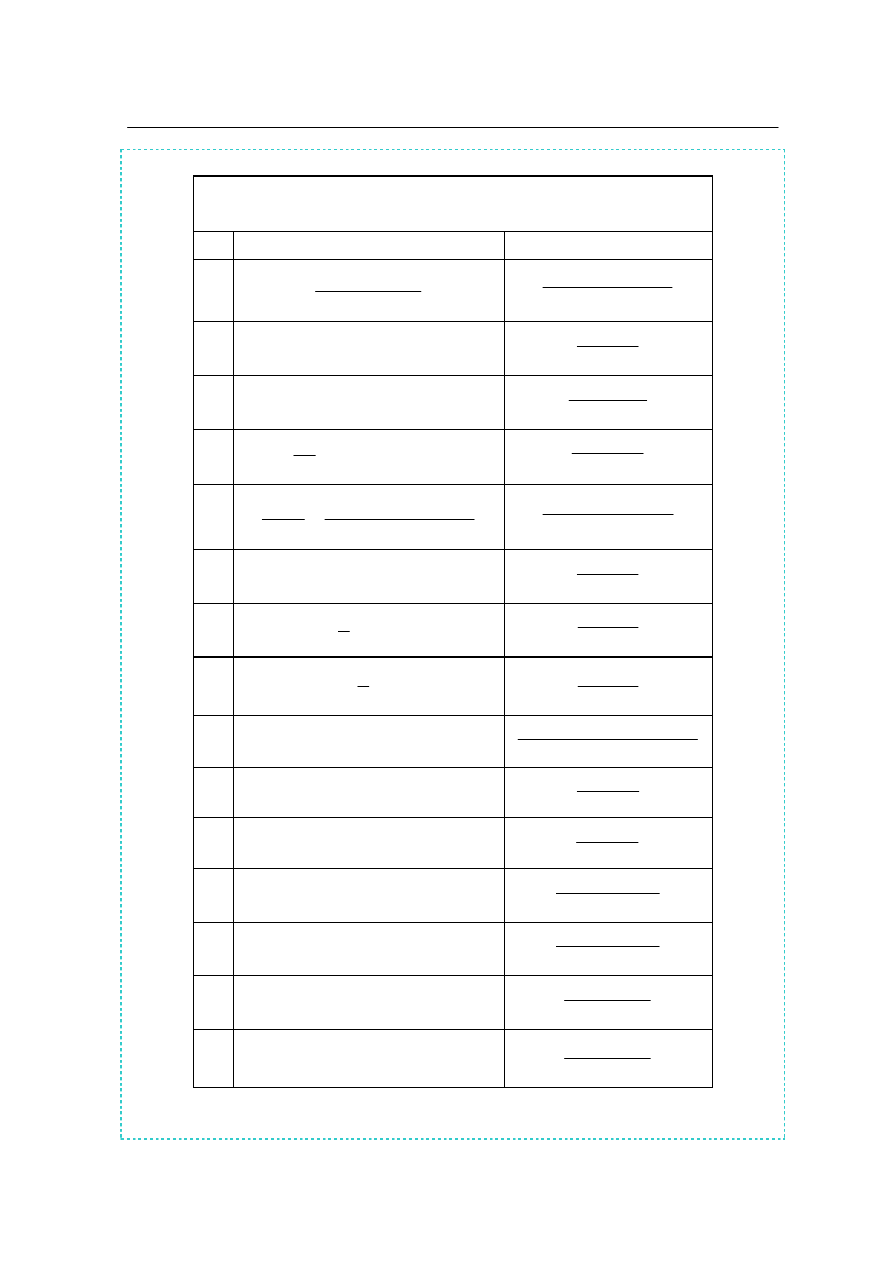
9
PRZEKSZTAŁCENIE LAPLACE’a
str.
127
Tabela 8.1
Transformaty Laplace’a wybranych funkcji
Lp.
Funkcja f(t)
Funkcja F(s)
12
1
2
t
a
t
a
a
a
e
e
2
1
−
−
−
−
)
a
s
(
)
a
s
(
1
2
1
+
⋅
+
13
t
a
e
t
⋅
−
2
)
a
s
(
1
+
14
t
a
n
e
t
⋅
−
1
n
)
a
s
(
!
n
+
+
15
[
]
t
a
2
e
)
t
a
1
(
1
a
1
−
+
−
2
)
a
s
(
s
1
+
16
)
a
a
(
a
a
e
a
e
a
a
a
1
1
2
2
1
t
a
2
t
a
1
2
1
1
2
−
−
+
−
−
)
a
s
(
)
a
s
(
s
1
2
1
+
+
17
t
a
e
)
t
a
1
(
⋅
−
−
2
)
a
s
(
s
+
18
t
a
2
e
)
t
a
2
1
t
(
⋅
−
−
3
)
a
s
(
s
+
19
t
a
2
2
e
)
t
a
2
1
t
a
2
1
(
⋅
−
+
−
3
2
)
a
s
(
s
+
20
n
t
)
e
1
(
−
−
)
n
s
(
)
2
s
(
)
1
s
(
s
!
n
+
+
+
L
21
t
sin
ω
2
2
s
ω
+
ω
22
t
cos
ω
2
2
s
s
ω
+
23
t
sin
e
t
a
ω
−
2
2
)
a
s
(
ω
+
+
ω
24
t
cos
e
t
a
ω
−
2
2
)
a
s
(
a
s
ω
+
+
+
25
t
sin
t
ω
2
2
2
)
s
(
s
2
ω
+
ω
26
t
cos
t
ω
2
2
2
2
2
)
s
(
s
ω
+
ω
−
9
PRZEKSZTAŁCENIE LAPLACE’a
str.
128
Tabela 8.1
Transformaty Laplace’a wybranych funkcji
Lp.
Funkcja f(t)
Funkcja F(s)
27
)
t
cos
1
(
1
2
ω
−
ω
)
s
(
s
1
2
2
ω
+
28
)
t
cos
t
t
(sin
2
1
2
ω
ω
−
ω
ω
2
2
2
)
s
(
1
ω
+
29
t
sin
2
ω
)
4
s
(
s
2
2
2
2
ω
+
ω
30
t
cos
2
ω
)
4
s
(
s
2
s
2
2
2
2
ω
+
ω
+
31
)
t
cos
t
t
(sin
2
1
2
ω
ω
+
ω
ω
2
2
2
2
)
s
(
s
ω
+
32
t
sin
2
t
t
cos
ω
ω
−
ω
2
2
2
3
)
s
(
s
ω
+
33
t
t
sin
ω
s
tg
arc
ω
Wyszukiwarka
Podobne podstrony:
Przekształcenia Laplacea cz1
Przekształcenie Laplace
Przekształcenie Laplace'a
4 Przeksztalcenie Laplacea
Przekszta?nie Laplace 1
Przekształcenie Laplace-tabela
03 przeksztalcenie laplace
Przeksztalcenie%20Laplace
4 Przeksztalcenie Laplacea CW
02 Przeksztalcenie Laplace, MiBM Politechnika Poznanska, IV semestr, automatyka, egzamin, pierdoly,
Rozwiazywanie rownan rozniczkowych Przeksztalcenia Laplacea, Nauka i Technika, Automatyka, Teoria st
Przekształcenia Laplace'a, Matematyka
Przekształcenie Laplace
02 Przeksztalecenie Laplace
02 Przeksztalecenie Laplace
4 Przeksztalcenie Laplacea
więcej podobnych podstron