P r z e k s z t a ł c e n i a L a p l a c e ’ a
Przekształcenie Laplace'a
Przekształcenie Laplace’a jest stosowane do opisu stanów nieustalonych w liniowych układach regulacji. Największą zalet
przekształcenia Laplace’a jest mo
zapisania
ą
żliwość
równania różniczkowego liniowego w postaci transmitancji operatorowej. Transmitancja operatorowa opisuje właściwości dynamiczne elementów automatyki tworzących schemat blokowy układu regulacji oraz umożliwia obliczanie charakterystyk czasowych i częstotliwościowych.
• Definicja
Przekształcenie Laplace'a jest operatorem przekształcającym sygnał x(t) na pewną funkcję zespoloną X(s)
Dziedzinę funkcji X(s) (L-transformaty) tworzą te wartości zmiennej zespolonej s, dla których całka we wzorze jest zbieżna.
• Warunki istnienia transformacji Laplace'a
1
dla t ≥
f (t) =
0
0 dla t < 0
W zagadnieniach opisu układów fizykalnych występują zawsze takie funkcje dla których przekształcenie Laplace'a jest wykonalne.
• Zastosowania
Transformata Laplace'a oddaje nieocenione usługi w wielu dziedzinach nauki i techniki. Jej zasadnicze zastosowanie to rozwiązywanie równań różniczkowych. Dokładnie rzecz ujmując, dla wielu klas równań różniczkowych zastosowanie transformaty Laplace'a sprowadza problem rozwiązania równania różniczkowego do problemu rozwiązania pewnego liniowego równania algebraicznego.
• Równania różniczkowe zwyczajne
Najwdzięczniejszym obiektem zastosowań transformacji Laplace'a jest rozwiązywanie równań różniczkowych zwyczajnych o stałych współczynnikach. Równania takie pojawiają się często podczas opisu układów elektrycznych, mechanicznych czy też układów automatyki.
• Równania różniczkowe cząstkowe
Przekształcenie Laplace'a może być użyte do rozwiązywania niektórych równań różniczkowych cząstkowych. W elektrotechnice sztandarowym przykładem są linie długie -
w w w . c h o m i k u j . p l / M a r W a g 9 8 7











































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































P r z e k s z t a ł c e n i a L a p l a c e ’ a
obwody elektryczne, których rozmiary geometryczne powodują opóźnienia istotnie wpływające na zachowanie układu.
• Równania całkowe
Transformacja Laplace'a ma zastosowanie dla rozwiązywania pewnych klas równań całkowych czy też różniczkowo całkowych. W postaci takiego równania mogą być sformułowane np. równania opisujące linię długą.
• Transmitancja
Cechą charakterystyczną liniowych obwodów elektrycznych jest fakt, że transformata Laplace'a dowolnego napięcia lub prądu w układzie jest liniowa kombinacją transformat napięć (prądów) wymuszających oraz warunków początkowych występujących na pojemnościach (napięcia) i indukcyjności (prądów). Własność ta jest konsekwencją liniowości równań opisujących obwód oraz niezmienności w czasie parametrów obwodu (wartości pojemności, indukcyjności, oporności itd.). Cecha ta jest własnością nie tylko obwodów elektrycznych. Mają ją np. liczne układy mechaniczne czy układy automatycznego sterowania. Ogólnie układy takie tworzą klasę układów liniowych niezmiennych ze względu na przesunięcia w dziedzinie czasu. Transformatę Laplace’a stosuje się także do badania odpowiedzi impulsowej układu oraz badania stabilności układu.
• Twierdzenia (właściwości) dotyczące przekształcenia Lapace’a
• Liniowość
Podstawową własnością przekształcenia Laplace'a jest liniowość; innymi słowy przekształcenie Laplace'a spełnia zasadę superpozycji.
• Transformata całki funkcji
Jeśli funkcja czasu f(t) ma transformatę F(s) , to całce oznaczonej tej funkcji czasowej odpowiada funkcja operatorowa F(s) podzielona przez operator Laplace’a „s”
∞
Jeżeli :
F(s) = ∫
−
f (t) ⋅ st
e dt
0
To:
t
L[
∫ f (t d
) t]=
0
F(s)
s
w w w . c h o m i k u j . p l / M a r W a g 9 8 7

















































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































P r z e k s z t a ł c e n i a L a p l a c e ’ a
1
(
φ s) = F(s)
s
• Transformata pochodnej funkcji
Jeśli funkcja czasu f(t)ma dla t>0 pochodną f’(t) i istnieje transformata L[f’(t)]tej pochodnej, to istniej również transformata funkcji f(t) L[f’(t)]=F(s)
gdzie
jest prawostroną granicą funkcji f(t) dla
• Transformata drugiej pochodnej jest równa
• Transformata n-tej pochodnej jest równa
• Twierdzenie o przesunięciu rzeczywistym, czyli o opóźnieniu Funkcję czasu f(t) transformowalną według Laplace'a możemy zawsze przedstawić w postaci f(t)=f(t)*1(t) w celu uwypuklenia, że funkcja ta zanika dla chwil ujemnych.
• Twierdzenie o przesunięciu zespolonym
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
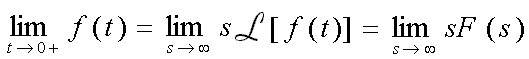




















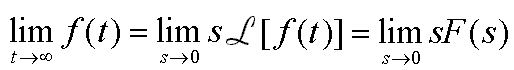






















































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































P r z e k s z t a ł c e n i a L a p l a c e ’ a
gdzie a jest w przypadku ogólnym wielkością zespoloną.
• Twierdzenie o wartości początkowej
Jeśli istnieje granica funkcji f(t) dla t
0+, to wartość początkowa wyraża się zależnością:
• Twierdzenie o wartości końcowej
Jeśli istnieje granica funkcji f(t) dla t
, to wartość końcowa wyraża się zależnością:
• Transformata splotu - twierdzenie Borela
• Twierdzenie o zmianie skali, czyli o podobieństwie
Przy liczbie k rzeczywistej i dodatniej:
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
P r z e k s z t a ł c e n i a L a p l a c e ’ a
• Tabela Transformat Laplace'a
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
P r z e k s z t a ł c e n i a L a p l a c e ’ a
• DODATEK
L i c z b a Π = 3 . 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6
Limeryk: Źle w mgle i snach bolejącym do wiedzy progu iść.
L i c z b a „ e ” = 2 . 7 1 8 2 8 1 8 2 8 4 5 9
Literatura:
• http://www.kmg.ps.pl/to/przeksztalcenie_laplacea/index.html
• Notatki kolegi z starszego roku
• http://www.it.pw.edu.pl/~zab/wyklad003/wyklad003.htm
• http://www.math.edu.pl/liczba-e
• http://pl.wikipedia.org/wiki/Pi
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Wyszukiwarka
Podobne podstrony:
Przekształcenia Laplacea cz1
Przekształcenie Laplace'a
4 Przeksztalcenie Laplacea
Przekszta?nie Laplace 1
Przekształcenie Laplace-tabela
03 przeksztalcenie laplace
Przekształcenie Laplace'a
Przeksztalcenie%20Laplace
4 Przeksztalcenie Laplacea CW
02 Przeksztalcenie Laplace, MiBM Politechnika Poznanska, IV semestr, automatyka, egzamin, pierdoly,
Rozwiazywanie rownan rozniczkowych Przeksztalcenia Laplacea, Nauka i Technika, Automatyka, Teoria st
Przekształcenia Laplace'a, Matematyka
Przekształcenie Laplace
02 Przeksztalecenie Laplace
02 Przeksztalecenie Laplace
4 Przeksztalcenie Laplacea
więcej podobnych podstron