
Opis wielowymiarowego układu sterowania
– we współrzędnych uogólnionych
u
B
f
Kq
q
L
q
M
u
+
=
+
+
&
&
&
– we współrzędnych stanu (pominięcie macierzy przejść)
+
=
+
+
=
w
Cx
y
Bu
Dz
Ax
x
&
gdzie:
=
q
q
x
&
–
wektor współrzędnych stanu,
−
−
=
−
−
0
I
K
M
L
M
A
1
1
– macierz stanu układu,
=
−
0
M
D
1
– macierz zakłóceń,
=
−
0
B
M
B
u
1
– macierz wejść,
C
– macierz wyjść,
f
z
≡
– wektor zakłóceń,
y
– wektor wyjść, którego składowe są zarejestrowanymi odpowiedziami układu,
w
– wektor zakłóceń pomiarowych.
W szczególnym przypadku, gdy rejestrowane są wartości wszystkich składowych
wektora przemieszczeń uogólnionych q, spełniony jest warunek:
q
y
≡
. Należy również
zauważyć, że wszystkie niepotencjalne siły uogólnione, których oddziaływanie nie jest
związane z efektem sterowania (tzn. wektor f), traktowane są jako zakłócenie.
Optymalny sygnał sterujący względem zadanej trajektorii
x

(
)
x
x
K
B
R
u
−
⋅
=
−
T
1
W przypadku, gdy nie są znane wartości wszystkich współrzędnych stanu, zachodzi
konieczność odtworzenia (estymacji) wektora x. Niech zarejestrowane odpowiedzi układu
stanowią składowe wektora wyjść y. W celu odtworzenia wektora współrzędnych stanu na
podstawie zarejestrowanych odpowiedzi, podajemy równanie obserwatora typu Luenbergera:
(
)
x
C
y
K
Bu
x
A
x
ˆ
ˆ
ˆ
−
+
+
=
e
&
,
gdzie:
xˆ
– estymata wektora współrzędnych stanu,
K
e
– macierz wzmocnień obserwatora.
Wyznaczanie estymaty xˆ wektora współrzędnych stanu x w warunkach „prawie”
stacjonarnych (A=const, C=const)
Rozwiązanie algebraicznego równania Riccatiego:
0
V
CS
C
S
A
S
AS
=
+
−
+
e
T
e
T
e
e
,
gdzie:
(
)
T
T
E
D
Dzz
V
=
jest macierzą kowariancji zakłóceń.
W rezultacie otrzymujemy:
T
e
e
C
S
K
=
.
Ponieważ macierz wzmocnień obserwatora
K
e
=const, jej elementy można wyznaczyć przed
rozpoczęciem procesu sterowania w trybie
off–line.
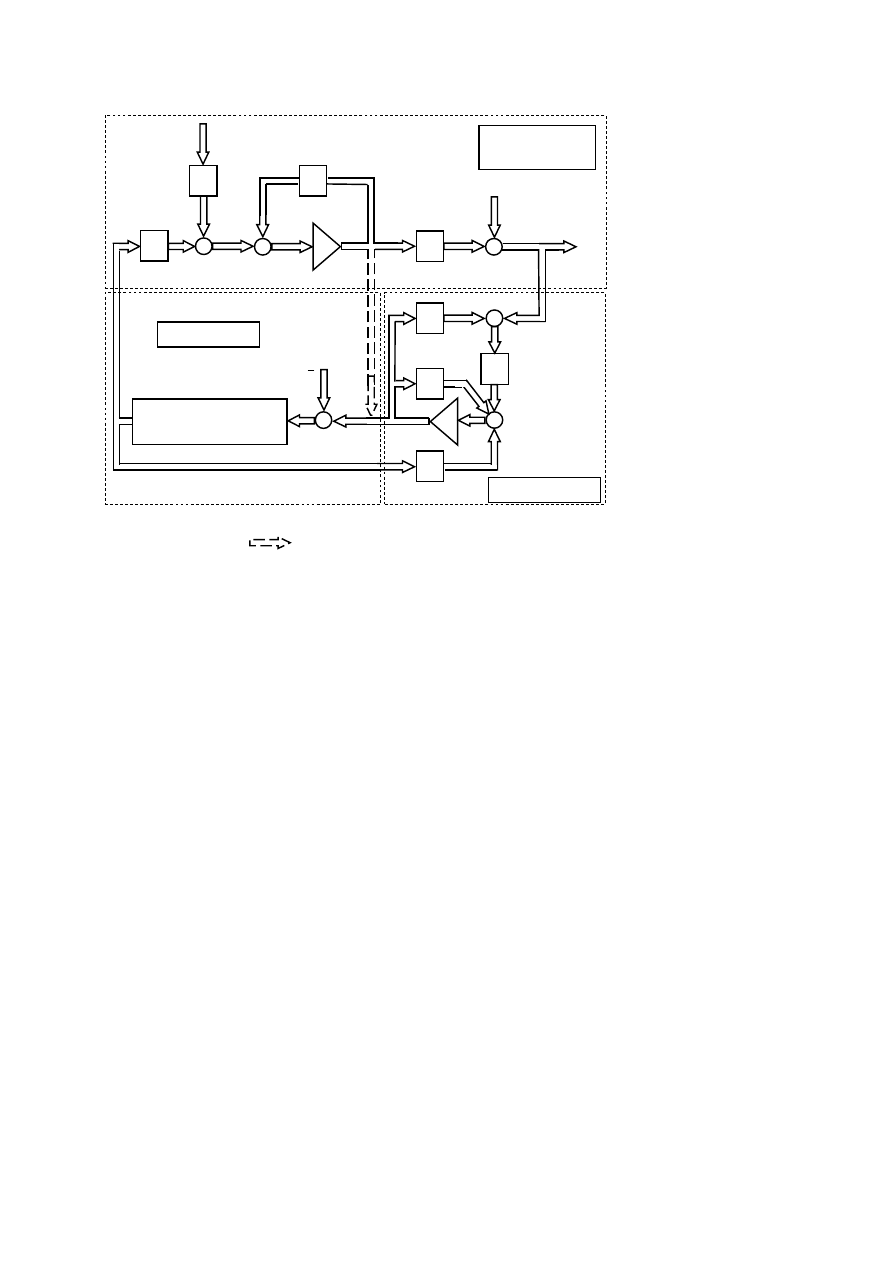
Schemat sterowania optymalnego we współrzędnych stanu: sygnał
x
x
≡
ˆ
w układzie ze sterowaniem z pominięciem obserwatora
y
x
K
B
R
T
1
−
K
e
∫
OBIEKT
STEROWANIA
STEROWNIK
z
w
x
xˆ
u
A
C
B
B
OBSERWATOR
–
+
A
C
∫
+
+
+
+
+
+
–
+
+
+
D
+
Wyszukiwarka
Podobne podstrony:
MUM wykład12
MUM wykład10
MUM wykład7
MUM-wykład6
MUM wykład1
MUM wykład4
MUM wykład3
MUM wykład6
MUM wykład4a
MUM Wykład8a
Napęd Elektryczny wykład
więcej podobnych podstron