Przedmiot: MODELOWANIE UKŁADÓW

MECHATRONICZNYCH

Prowadzący: dr hab. inż. Krzysztof KALIŃSKI, prof. nadzw. PG

Katedra Mechaniki i Mechatroniki

109 WM,

[e-mail]

Konsultacje:

wtorek 13:00–14:00

czwartek 11:00–12:00

Wiadomości organizacyjne

1.Wykład

15 godzin – zalecana obecność

2.Ćwiczenia laboratoryjne 15 godzin – obecność obowiązkowa
3.Ćwiczenia projektowe 15 godzin – obecność obowiązkowa
4.

Zaliczenie ćwiczeń laboratoryjnych i projektowych

5.

Egzamin:

– obejmuje materiał wykładów
– warunek konieczny –

zaliczone laboratorium oraz 2 projekty

Materiały z wykładów:

https://sites.google.com/a/mech.pg.gda.pl/krzysztof-kalinski/

Literatura:

1. Heimann B., Gerth W., Popp K.: Mechatronika. Komponenty – metody –

przykłady. Warszawa: Wyd. Nauk. PWN 2001.

2. Gawrysiak M.: Mechatronika i projektowanie mechatroniczne. Białystok: Wyd.

Polit. Białostockiej 1997.

(jest dostępna w internecie)

3. Metoda elementów skończonych w dynamice konstrukcji. Gawroński W.,

Kruszewski J., Ostachowicz W., Tarnowski J., Wittbrodt E. Warszawa: Arkady
1984.

4. Cannon H. C.: Dynamika układów fizycznych. Warszawa: WNT 1973.
5. Kaczorek T.: Teoria sterowania i systemów. Warszawa: Wyd. Nauk. PWN 1993.
6. Grzegożek W., Adamiec-Wójcik I., Wojciech S.: Komputerowe modelowanie

dynamiki pojazdów samochodowych. Kraków: Politechnika Krakowska im. T.
Kościuszki 2003.

(literatura uzupełniająca)

Sprawy porządkowe:

1.We wszystkich budynkach i pomieszczeniach obowiązuje całkowity

zakaz palenia tytoniu

2.Zabrania się wnoszenia na salę wykładową wszelkiego rodzaju

urządzeń, które swoim działaniem mogłyby zakłócić przebieg zajęć.
Dotyczy to m.in. uaktywnionych telefonów komórkowych

3.W salach wykładowych zabrania się spożywania posiłków oraz picia

wszelkiego rodzaju napojów

W trakcie wykładu na sali obowiązuje cisza

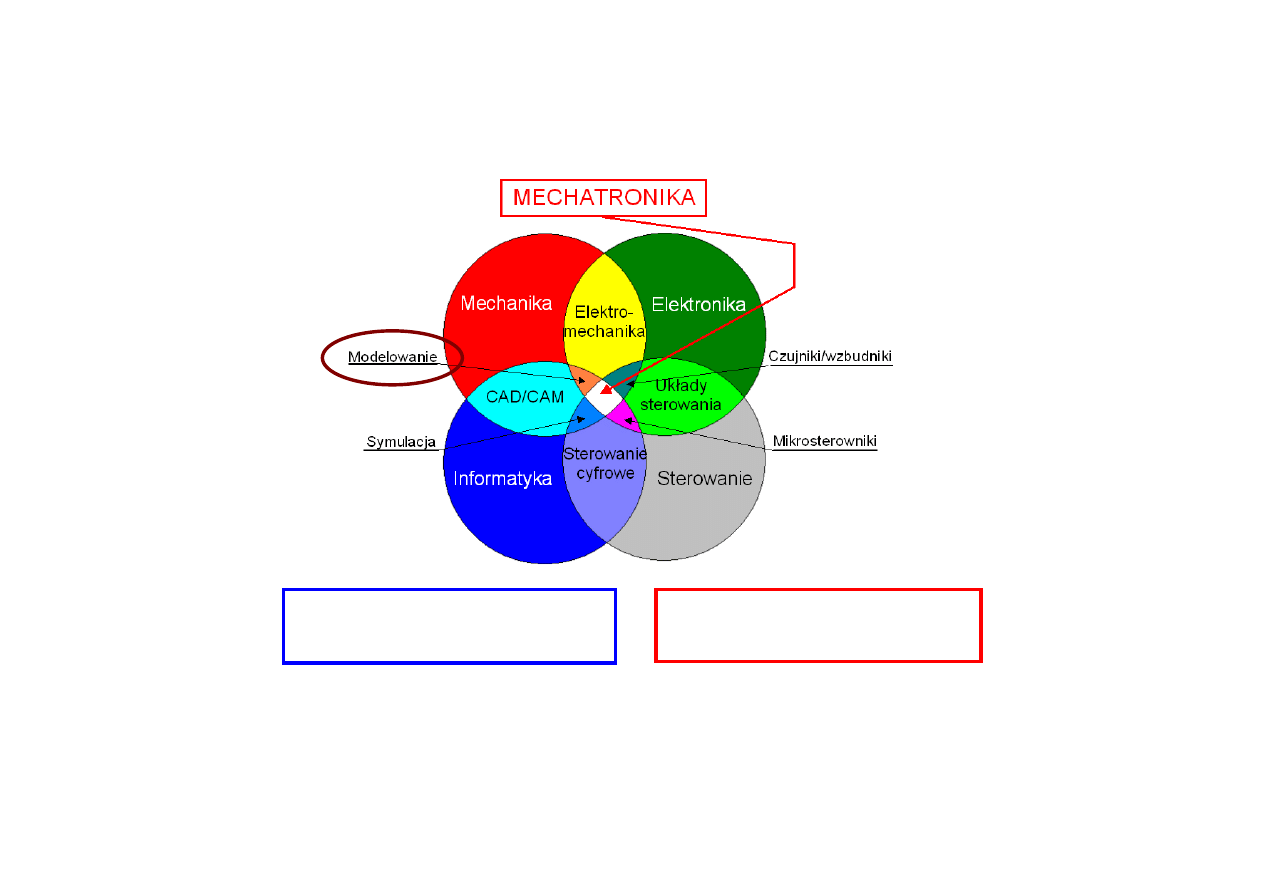
Modelowanie układów mechatronicznych – pojęcia podstawowe

Multidyscyplinarność ⇒

⇒

⇒

⇒

Interdyscyplinarność

wiele dyscyplin

wiele dyscyplin

istniejących oddzielnie

zintegrowanych w całość

Spójne podejście do modelowania wszystkich elementów składowych

Modelowanie w mechatronice polega na:

⇒

umiejętności zastępowania obiektów rzeczywistych
(mechatronicznych) odpowiednimi układami abstrakcyjnymi

⇒

umiejętności pomijania mniej istotnych czynników

⇒

umiejętności opisywania danego problemu za pomocą równań
matematycznych

⇒

umiejętności rozwiązywania zdefiniowanego problemu

Trudności matematyczne ⇒ prawa opisujące tzw. „fizykę zjawisk” w
swojej użytkowej formie podlegają znacznym ograniczeniom i
uproszczeniom, a mimo to są zwykle jednymi z najogólniejszych praw
przyrody stosowanymi przez inżynierów.

Definicja: Rzeczywisty obiekt mechatroniczny jest to obiekt

istniejący w rzeczywistości lub możliwy do zrealizowania

Definicja: Model fizyczny jest to myślowo uproszczony obiekt

rzeczywisty zapewniający dostatecznie dokładne
odzwierciedlenie zjawisk zachodzących w obiekcie
rzeczywistym, umożliwiający zastosowanie prostego opisu
zachodzących zjawisk

Definicja: Model matematyczny jest to matematyczny opis zjawisk

zachodzących w modelu fizycznym, podany w formie
usystematyzowanych wzorów lub równań – algorytm

Definicja: Modelowanie jest to czynność polegająca na przejściu od

obiektu rzeczywistego, poprzez model fizyczny, do modelu
matematycznego

Sztuka inżynierska ⇒ dobieranie takich modeli, aby:

- błędy były jak najmniejsze
- można było przewidzieć wielkość błędów

Podejście deterministyczne

– aktualnie dominujące na świecie

opis własności układów mechatronicznych (wraz z wartościami

parametrów modeli), z jednoczesnym spełnieniem warunku

powtarzalności

Inne podejścia – dopuszczają niepewność modelowania

Weryfikacja negatywna ⇒ zmienić model tak, aby zmniejszyć błędy z

niego wynikające

⇒

zmiana modelu fizycznego na obiekt bardziej odzwierciedlający
rzeczywistość

⇒

mniejsze uproszczenia w modelu matematycznym

⇒

dokładniejsze obliczenia modelu matematycznego

Problemy szczegółowe modelowania układów mechatronicznych

Tworzenie modeli obliczeniowych
– modele elementów składowych układów mechatronicznych

(elementy mechaniczne, elektryczne, hydrauliczne, termiczne)

– modele układów wielomasowych.

– modele strukturalne – uwzględniają podatność elementów

mechanicznych
(modele metody elementów skończonych)

– modele modalne – alternatywna forma opisu własności

strukturalnych układów

Opis matematyczny
– analogie między środowiskami fizycznymi.
– równania dynamiki we współrzędnych uogólnionych
– równania dynamiki we współrzędnych stanu.

Sterowanie układów mechatronicznych
– Wielowymiarowe układy sterowania.

– Sterowanie modalne.

– Optymalne sterowanie liniowe.

Podział układów mechatronicznych z uwagi na zmienność parametrów
modeli obliczeniowych:
– liniowe układy stacjonarne – parametry niezmienne w czasie
– liniowe układy niestacjonarne – zmiany w czasie parametrów opisane

znanymi funkcjami czasu

– układy nieliniowe – zmiany parametrów opisane nieznanymi

funkcjami czasu

W modelowaniu układów mechatronicznych można wyróżnić:
– modelowanie obiektów (opis matematyczny, parametry modeli)
– modelowanie sygnałów

Zadania modelowania układów mechatronicznych

1. Modelowanie otwartych układów sterowania

– definiowanie własności elementów składowych w postaci

równań

różniczkowych,

transmitancji

operatorowych,

charakterystyk

częstotliwościowych,

charakterystyk

statycznych

2. Modelowanie układów ze sprzężeniem zwrotnym

– synteza układów funkcjonalnych, w konwencji schematów

blokowych układów automatyki

– uwzględnienie sprzężeń opóźniających
– zwrócenie szczególnej uwagi na problemy stabilności i jakości

układów

Do rozwiązywania zadań modelowania układów mechatronicznych
zaleca się oprogramowanie AMESim (dostępne w Katedrze
Mechaniki i Mechatroniki)

Modelowanie sygnałów

Sygnał jest określoną wielkością fizyczną oddziaływującą na obiekt.

Rozróżniamy sygnały:

Wejściowe, które są najczęściej znanymi wielkościami fizycznymi
i stanowią formę oddziaływania środowiska na badany obiekt.

Wyjściowe (odpowiedzi) są to wielkości fizyczne, które stanowią reakcję
badanego obiektu na określone wejście.

Zakłócenia są to sygnały, które nie są ani wejściem ani odpowiedzią.

OBIEKT

WE

WY

Z

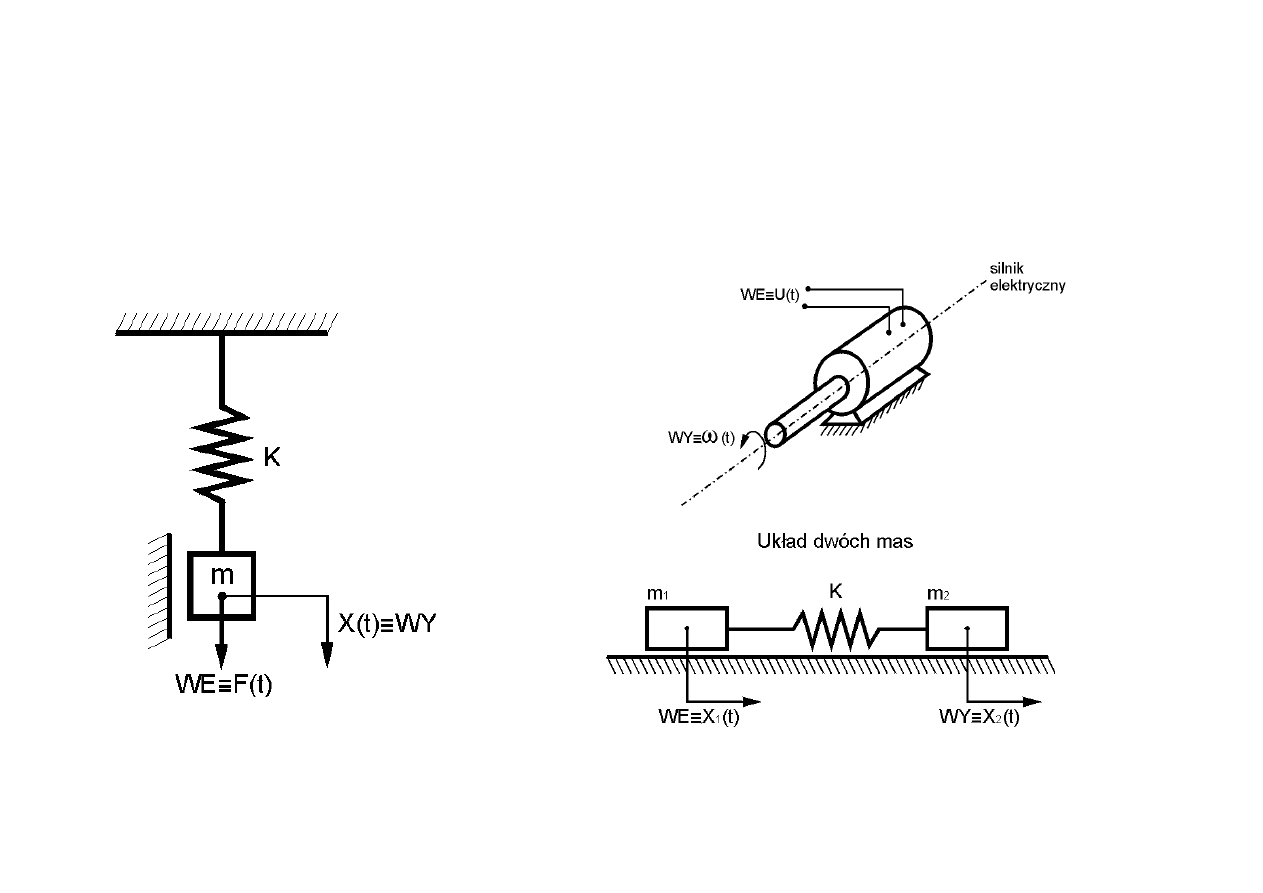
Pomimo, że wejściem oraz wyjściem mogą być dowolne wielkości fizyczne
należy je dobierać tak, aby wyjście było skutkiem zaś wejście przyczyną
oddziaływania.
Przykłady: