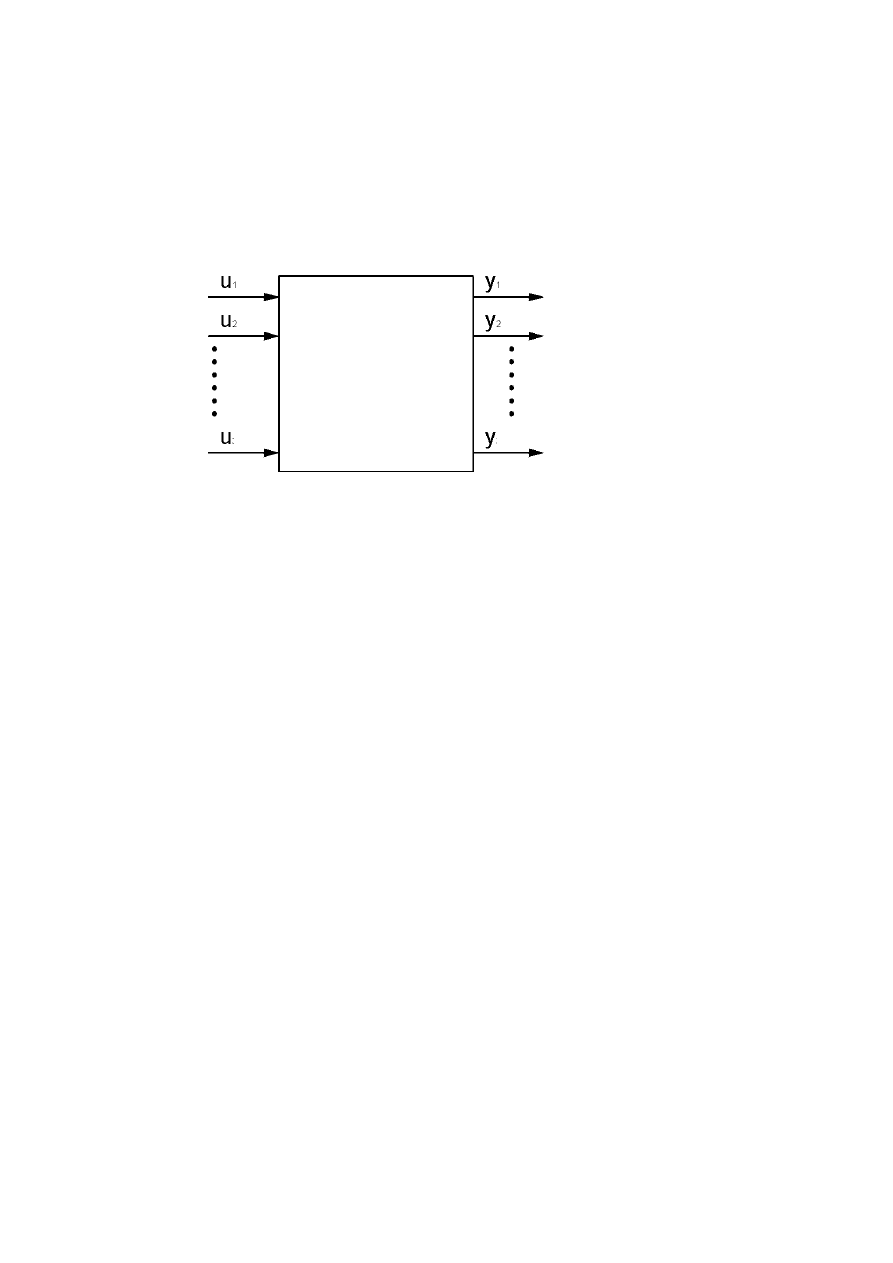
Wielowymiarowe układy sterowania
Układem wielowymiarowym nazywamy układ, dla którego zdefiniowano
skończoną liczbę wejść oraz w przypadku którego obserwujemy skończoną
liczbę odpowiedzi.
Wejścia oraz odpowiedzi możemy przedstawić w postaci wektorów:
)
,...,
,
(
2
1
2
1
p
p
u
u
u
col
u
u
u
=
=
M
u
)
,...,
,
(
2
1
2
1
k
k
y
y
y
col
y
y
y
=
=
M
y
Dokonujemy przekształcenia Laplace’a obu wektorów (przy zerowych
warunkach początkowych) otrzymując ich transformaty tzn.
)
(
)
(
)
(
)
(
s
t
s
t
y
y
u
u
→
→
Macierzą transmitancji operatorowych nazywamy macierz, która opisuje
zależność pomiędzy wektorem wejść a wektorem odpowiedzi zgodnie z
następującym równaniem:
)
(
)
(
)
(
s
s
s
u
K
y
⋅
=
Macierz K(s) jest macierzą transmitancji operatorowych o wymiarach:
k
p
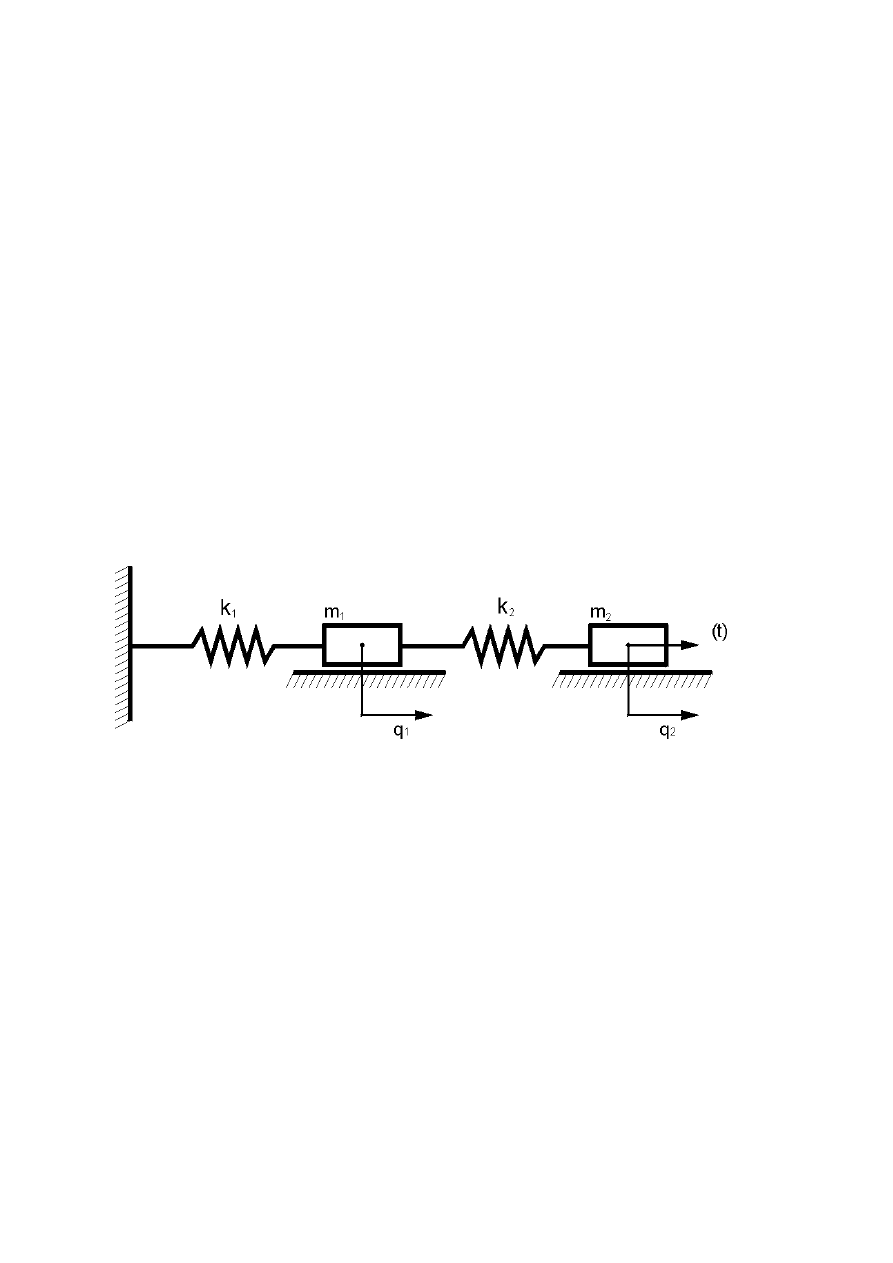
p
k
kp
k
k
p
p
s
K
s
K
s
K
s
K
s
K
s
K
s
K
s
K
s
K
s
×
=
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
1
2
22
21
1
12
11
L
M
M
M
L
L
K
Element macierzy
)
(s
K
ij
oznacza transmitancję operatorową pomiędzy
wejściem nr j a odpowiedzią nr i.
Sens fizyczny elementu tej macierzy jest taki, że opisuje wpływ wejścia j na
odpowiedź i.
Wyznaczenie macierzy transmitancji operatorowych prześledzimy na
następującym przykładzie:
Definiujemy wektory wejść i odpowiedzi:
{ }
2
,
1
,
)
(
2
1
=
=
=
=
k
q
q
p
t
F
y
u
Na podstawie znanych metod wyprowadzania równań dynamiki (np. równania
Lagrange’a II rodzaju) otrzymujemy:
=
+
−
=
−
+
+
)
(
0
)
(
2
2
1
2
2
2
2
2
1
2
1
1
1
t
F
q
k
q
k
q
m
q
k
q
k
k
q
m
&
&
&
&
F

Po dokonaniu przekształcenia Laplace’a otrzymujemy:
*
=
+
+
⋅
−
=
−
+
+
)
(
)
(
)
(
)
(
0
)
(
)
(
)
(
2
2
2
2
1
2
2
2
1
2
1
2
1
s
F
s
q
k
s
m
s
q
k
s
q
k
s
q
k
k
s
m
Sposoby wyznaczania macierzy transmitancji operatorowych
1. układ równań zapisujemy w postaci macierzowej.
{
)
(
)
(
1
0
)
(
)
(
)
(
)
(
2
1
2
2
2
2
2
2
1
2
1
s
s
F
s
s
q
s
q
s
k
s
m
k
k
k
k
s
m
u
y
G
⋅
=
⋅
+
−
−
+
+
3
2
1
4
4
4
4
4
3
4
4
4
4
4
2
1
albo:
)
(
1
0
)
(
)
(
s
s
s
u
y
G
⋅
=
⋅
Przekształcamy to równanie do następującej postaci:
Po wykonaniu odpowiednich obliczeń otrzymamy:
1
2
2
2
2
2
2
2
1
2
1
2
1
2
1
2
2
2
2
2
2
1
2
1
2
)
)(
(
)
)(
(
)
(
×
−
+
+
+
+
+
−
+
+
+
=
k
k
s
m
k
k
s
m
k
k
s
m
k
k
s
m
k
k
s
m
k
s
K
2. Polega na wyznaczeniu z układu równań (* ), zapisanych w postaci
operatorowej poszczególnych składowych wektora odpowiedzi, w zależności
od składowych wektora wejść.
)
(
)
(
1
0
)
(
)
(
1
s
s
s
s
u
K
G
y
⋅
⋅
=
−
43
42
1

Współczynniki w tych wyrażeniach stanowią elementy macierzy
transmitancji:
)
(
)
)(
(
)
(
)
(
)
)(
(
)
(
2
2
2
2
2
2
1
2
1
2
1
2
1
2
2
2
2
2
2
2
1
2
1
2
1
s
F
k
k
s
m
k
k
s
m
k
k
s
m
s
q
s
F
k
k
s
m
k
k
s
m
k
s
q
⋅
−
+
+
+
+
+
=
⋅
−
+
+
+
=
Po ustawieniu zaznaczonych współczynników jako elementów macierzy K(s)
otrzymamy identyczną postać, jak w przypadku macierzy uzyskanej sposobem
1.
Opis wielowymiarowych układów automatyki we współrzędnych stanu.
Wprowadzamy wektor stanu x. Liczba jego składowych m jest równa liczbie
warunków początkowych, niezbędnych do rozwiązania różniczkowych równań
dynamiki. W ogólnym przypadku jest ona różna od liczby stopni swobody
układu wielowymiarowego n. W rezultacie, otrzymujemy równania stanu, które
przyjmują następującą postać:
1. równanie podstawowe
Bu
Ax
x
+
=
&
2. równanie wyjść
Du
Cx
y
+
=
A – macierz stanu
B – macierz wejść
C – macierz wyjść
D – macierz przejść
Dla układu o p wejściach, k wyjściach i liczbie współrzędnych stanu m,
poszczególne macierze mają następujące wymiary:
p
k
m
k
p
m
m
m
x
x
x
x
,
,
,
D
C
B
A
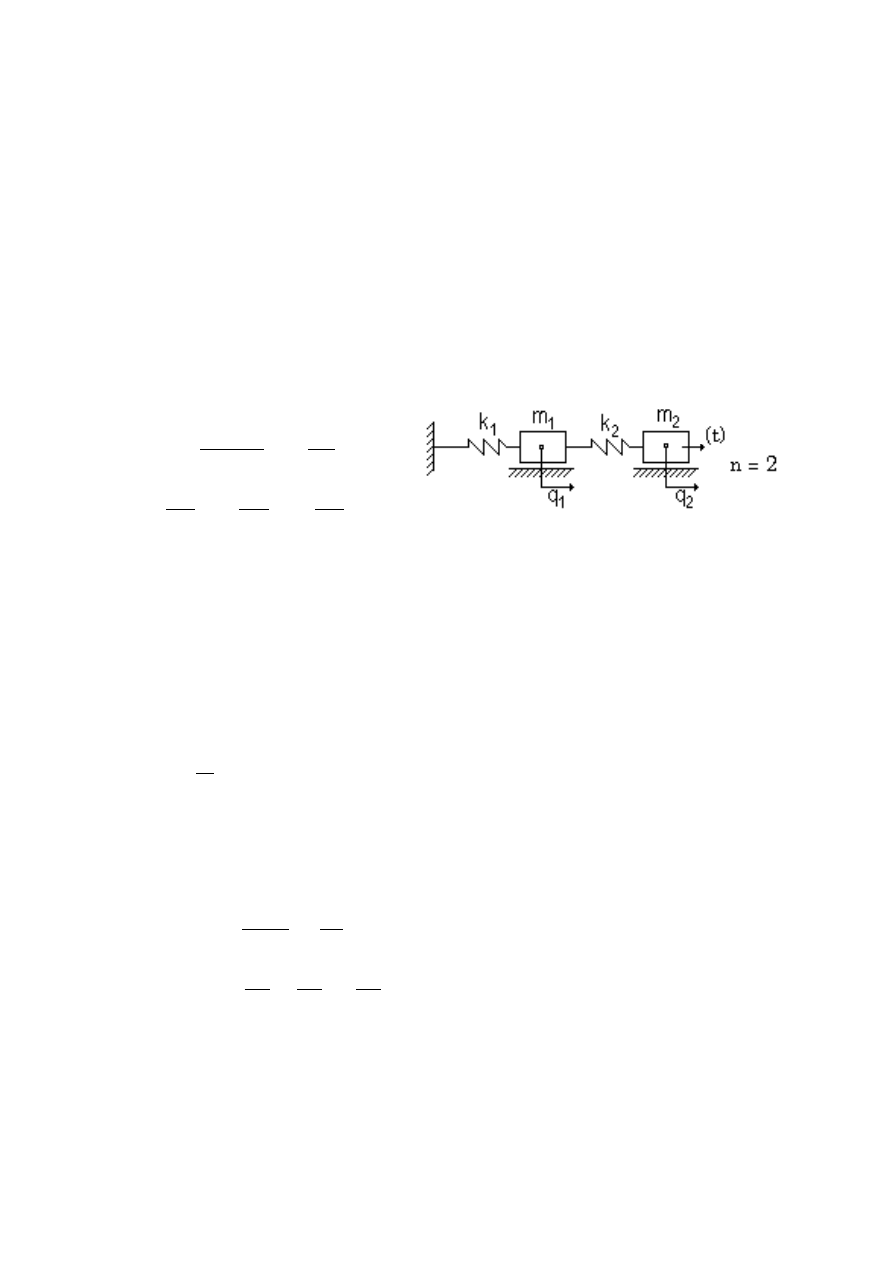
Przykład:
( )
{ }
(
)
( )
4
=
0
2
=
=
1
=
t
=
2
2
1
2
2
2
2
2
1
2
1
1
1
2
1
m
t
=F
q
k
q
-k
q
m
q
k
q
k
k
q
m
k
q
q
p
F
+
=
−
+
+
&
&
&
&
y
u
Układ równań dynamiki zapisujemy w postaci:
( )
+
−
=
+
+
=
t
F
m
q
m
k
q
m
k
q
q
m
k
q
m
k
k
-
q
2
2
2
2
1
2
2
2
2
1
2
1
1
2
1
1
1
&
&
&
&
Aby rozwiązać układ równań, należy podać następujące warunki początkowe:
( )
( ) ( )
( )
0
,
0
,
0
,
0
2
1
2
1
q
q
q
q
&
&
Otrzymujemy zatem następujący wektor oraz równania stanu.
( )
( )
( )
( )
t
F
q
+
q
+
q
+
q
q
t
F
q
+
q
+
q
+
q
q
t
F
m
+
q
m
k
-
q
m
k
+
q
+
q
q
t
F
+
q
m
k
+
q
m
+k
k
+
q
+
q
q
q
q
q
q
=
dt
d
q
q
q
q
=
⋅
+
⋅
⋅
⋅
⋅
=
⋅
+
⋅
⋅
⋅
⋅
=
⋅
⋅
=
⋅
⋅
⋅
=
→
0
0
0
1
0
0
0
0
0
1
1
0
0
0
0
0
2
1
2
1
2
2
1
2
1
1
2
2
2
2
1
2
2
2
1
2
2
1
2
1
1
2
1
2
1
1
2
1
2
1
2
1
2
1
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
X
X
W zapisie macierzowym układ równań przyjmie postać:
F

{
{
( )
{ }
3
2
1
3
2
1
&
&
4
4
4
4
3
4
4
4
4
2
1
&
&
&
&
&
&
&
u
B
X
A
X
↓
+
=
t
F
m
q
q
q
q
m
k
-
m
k
m
k
m
+k
k
-
q
q
q
q
0
0
1
0
0
0
1
0
0
0
0
1
0
0
0
0
2
2
1
2
1
2
2
2
2
1
2
1
2
1
2
1
2
1
i jest on podstawowym równaniem stanu.
W podobny sposób otrzymujemy równanie wyjść:
{
{
{
( )
{ }
3
2
1
&
&
4
4 3
4
4 2
1
u
D
x
C
y
t
F
q
q
q
q
q
q
+
=
0
0
1
0
0
0
0
1
0
0
2
1
2
1
2
1
W opisie układu wielowymiarowego we współrzędnych stanu macierze A, B, C,
D określają, podobnie jak macierz transmitancji, własności układu, z tą różnicą,
ż
e elementami tych macierzy są liczby rzeczywiste, a w macierzy transmitancji
były funkcje zmiennej zespolonej s.
Związek pomiędzy macierzą transmitancji, a macierzami występującymi w
równaniach stanu
Rozważmy ponownie macierzowe równania stanu, tzn.:
( )
( )
( )
( )
( )
( )
+
=
+
=
↓
s
s
s
s
s
s
s
Du
Cx
y
Bu
Ax
x
Du
+
Cx
=
y
Bu
+
Ax
=
x&
Przekształcenie Laplace’a przy zerowych warunkach
początkowych
W przypadku układu liniowego (stacjonarnego), elementami macierzy stanu są
stałe współczynniki. Z powyższego układu należy wyrugować wektor x(s).
Pierwsze z równań przekształcamy do postaci:
( ) ( )
( )
(
) ( )
( )
s
s
-
s
s
=
s
-
s
s
Bu
x
A
I
Bu
Ax
x
=
I – macierz jednostkowa o wymiarach m
×
m, a następnie
( ) (
)
( )
s
-
s
s
-1
Bu
A
I
x
=
- wstawiamy do II z równań stanu.
W rezultacie otrzymujemy:
( ) (
)
( )
( )
(
)
(
)
( )
( )
s
s
-
s
s
+
s
-
sI
s
1
-1
u
K
D
B
A
I
C
Du
Bu
A
C
y
4
4
4
3
4
4
4
2
1
+
=
=
−
Przykład:
Dla analizowanego poprzednio układu wykazać prawdziwość związku
pomiędzy macierzami w równaniach stanu, a macierzą transmitancji
operatorowych.
Na podstawie wcześniejszych rozważań otrzymujemy:
(
)
{
(
)(
)
(
)(
)
( )
4
4
4
4
4
3
4
4
4
4
4
2
1
3
2
1
4
4
4
4
3
4
4
4
4
2
1
4
4 3
4
4 2
1
s
0
0
+
0
0
1
0
-
0
1
0
0
0
1
0
0
1
0
0
0
0
1
0
0
2
2
2
2
2
2
1
2
1
2
1
2
1
2
2
2
2
2
2
1
2
1
2
2
1
1
-
1
2
2
2
1
2
1
2
1
K
D
B
A
Ι
C
=
⋅
−
−
⋅
−
-k
+k
s
m
+k
+k
s
m
+k
+k
s
m
-k
+k
s
m
+k
+k
s
m
k
m
s
s
s
m
k
m
-k
s
m
-k
m
+k
k
s

Sterowalność i obserwowalność układów mechatronicznych
Układ zdefiniowany macierzami A, B, C nazywamy sterowalnym, jeżeli
możliwe jest jego przeprowadzenie z dowolnego stanu początkowego x
0
do
dowolnego stanu końcowego x
k
przez odpowiedni dobór sterowania u.
Pojęcie sterowalności wykorzystywane jest w teorii sterowania optymalnego.
Układ zdefiniowany macierzami A, B, C nazywamy obserwowalnym, jeżeli na
podstawie znajomości wektora wyjść y można określić stan początkowy układu
x
0
.
Pojęcie obserwowalności wykorzystuje się w projektowaniu obserwatorów oraz
rozwiązywaniu zagadnień minimalnej realizacji.
Rząd macierzy (przypomnienie) – najwyższy stopień różnego od zera minora
wyznacznika głównego tej macierzy
Warunek sterowalności układu dynamicznego
[
]
m
rząd
rząd
m
mp
m
=
=
−
×
B
A
B
A
AB
B
S
1
2
M
K
M
M
M
gdzie:
S jest macierzą sterowalności układu o wymiarach m
×
mp
Warunek obserwowalności układu dynamicznego
m
rząd
rząd
m
m
km
=
=
−
×
1
2
CA
CA
CA
C
O
L
M
L
L
L
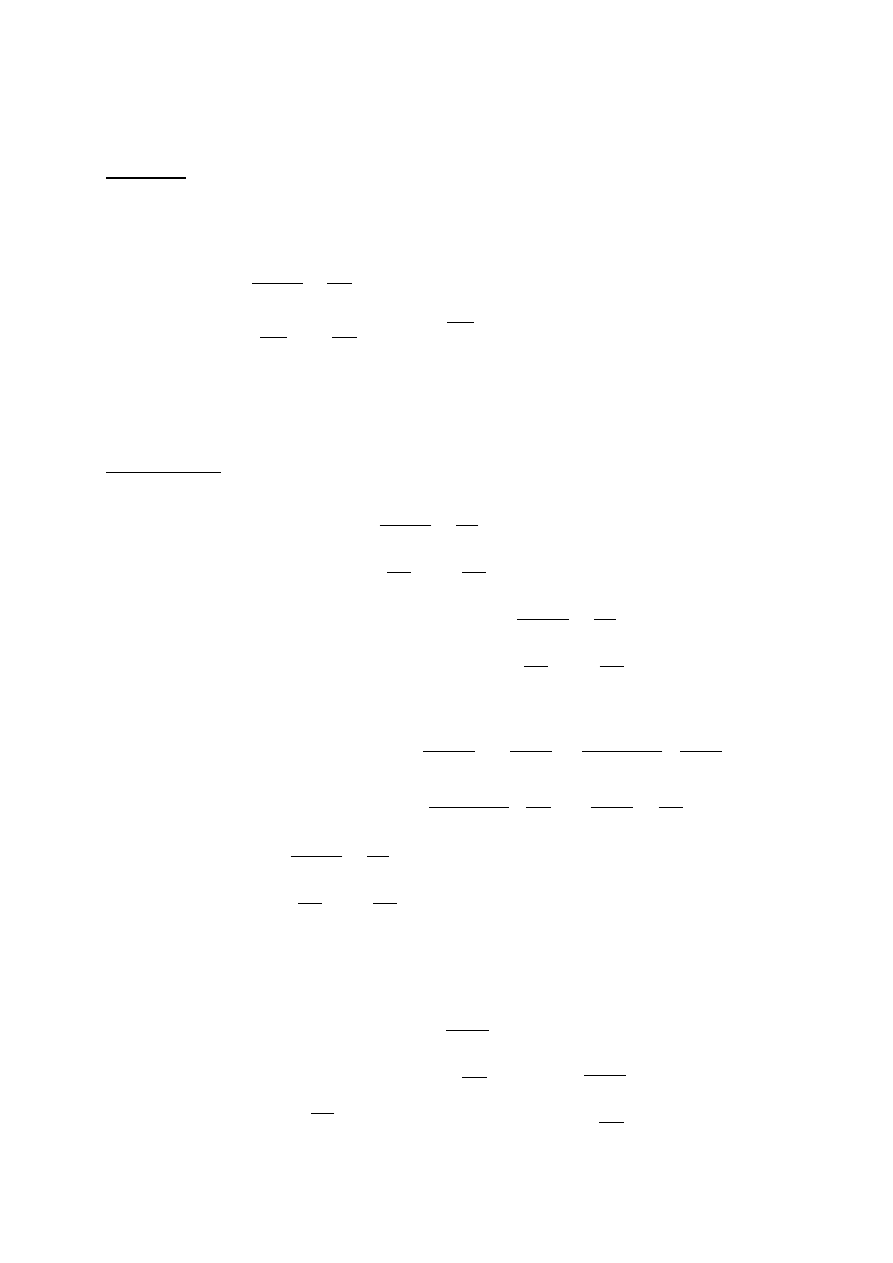
gdzie:
O jest macierzą obserwowalności układu o wymiarach km
×
m
Przykład. Zbadać sterowalność i obserwowalność układu sterowanego,
zdefiniowanego macierzami:
=
0
0
1
0
0
0
0
1
0
0
0
0
1
2
2
2
1
2
1
2
1
m
k
-
m
k
m
k
m
+k
k
-
A
,
=
0
0
1
0
2
m
B
,
=
1
0
0
0
0
1
0
0
C
, m=4
Rozwiązanie. Wyznaczamy macierze:
−
+
−
−
+
−
=
⋅
=
2
2
2
2
1
2
1
2
1
2
2
2
2
1
2
1
2
1
2
0
0
0
0
0
0
0
0
m
k
m
k
m
k
m
k
k
m
k
m
k
m
k
m
k
k
A
A
A
(
)
(
)
−
+
−
+
−
+
−
−
+
−
+
+
=
⋅
=
0
0
0
0
0
0
0
0
2
2
2
2
1
2
1
2
1
2
2
2
2
1
2
2
2
2
2
2
2
1
2
2
1
2
1
2
2
2
1
2
2
1
2
1
2
2
2
1
2
1
2
3
m
k
m
k
m
k
m
k
k
m
k
m
m
k
m
k
m
m
k
k
k
m
m
k
m
k
k
k
m
m
k
m
k
k
A
A
A
a następnie podmacierze macierzy sterowalności:
=
2
1
0
0
0
m
AB
−
=
0
0
2
2
2
2
1
2
2
m
k
m
m
k
B
A
−
=
2
2
2
2
1
2
3
0
0
m
k
m
m
k
B
A
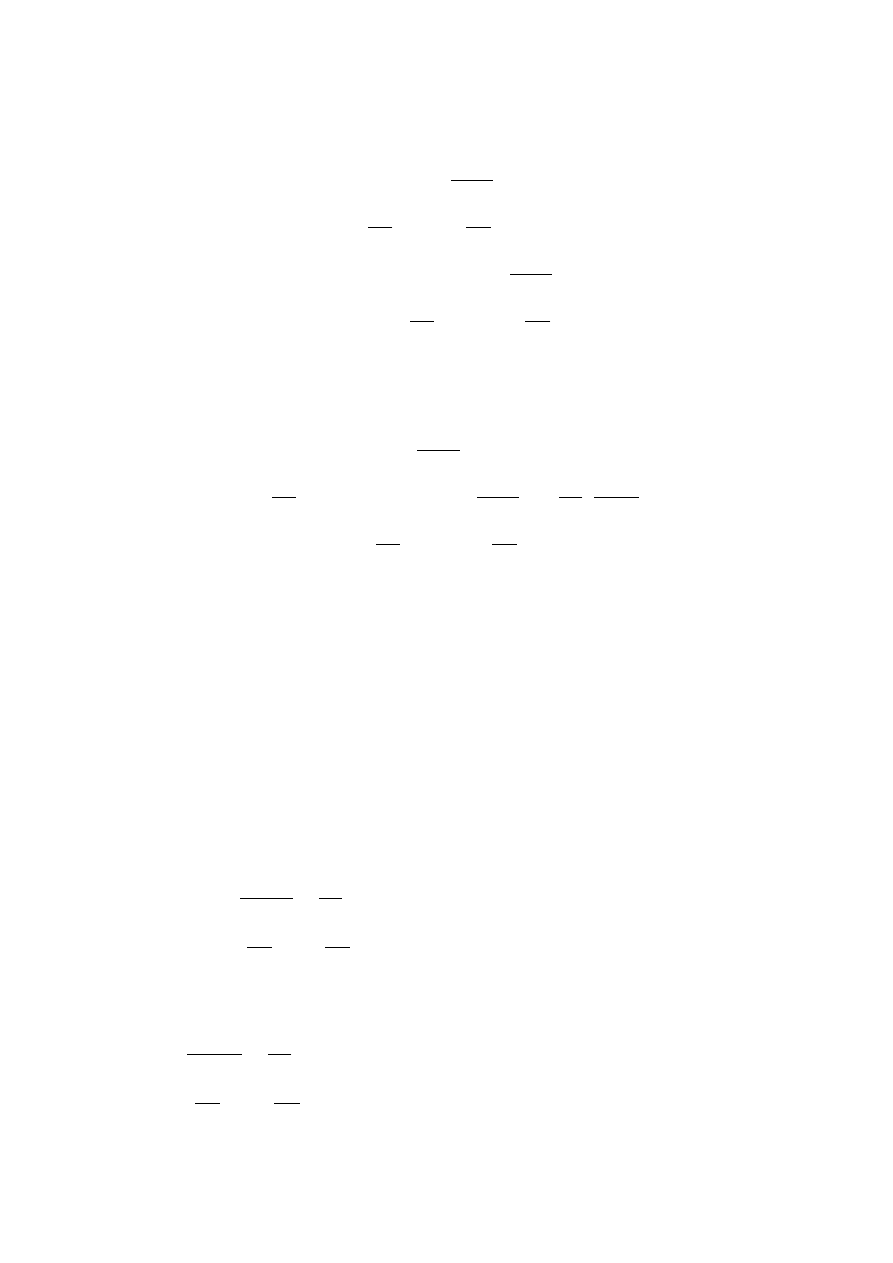
Macierz sterowalności przyjmie postać:
−
−
=
2
2
2
2
2
1
2
2
2
2
2
2
1
2
0
1
0
0
0
0
0
0
1
0
0
0
m
k
m
m
m
k
m
k
m
m
m
k
S
Obliczamy jej wyznacznik (minor rzędu 4):
( )
0
1
0
1
0
0
0
0
det
1
1
det
3
2
2
1
2
2
2
2
2
2
2
2
1
2
2
1
2
2
≠
−
=
−
⋅
−
⋅
=
m
m
k
m
m
k
m
m
m
k
m
m
k
m
S
Ponieważ rząd S = 4 = m, układ jest sterowalny.
Wyznaczamy podmacierze macierzy obserwowalności:
=
0
0
1
0
0
0
0
1
CA
−
+
−
=
2
2
2
2
1
2
1
2
1
2
0
0
0
0
m
k
m
k
m
k
m
k
k
CA
−
+
−
=
0
0
0
0
2
2
2
2
1
2
1
2
1
3
m
k
m
k
m
k
m
k
k
CA

W rezultacie, macierz obserwowalności przyjmie postać:
−
+
−
−
+
−
=
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
1
0
0
0
0
1
0
0
2
2
2
2
1
2
1
2
1
2
2
2
2
1
2
1
2
1
m
k
m
k
m
k
m
k
k
m
k
m
k
m
k
m
k
k
O
Obliczamy jej minor rzędu 4, czyli:
0
1
0
0
1
1
0
0
0
1
0
1
0
0
1
0
0
0
0
1
1
0
0
0
0
1
0
0
4
≠
=
⋅
=
=
∆
Poniewa
ż
rząd O
=4=
m
, układ jest obserwowalny.
Optymalne sterowanie liniowe
Rozwa
ż
my równanie stanu sterowanego układu parametrycznego (
A
=
A
(
t
),
B
=
B
(
t
)) w postaci:
( )
( )
u
B
x
A
x
t
t
+
=
&
•
Pomijamy wpływ zakłóce
ń
•
Definiujemy całkowy wska
ź
nik jako
ś
ci – problem Lagrange’a
( )
( )
[
]
∫
+
=
r
t
T
T
dt
t
t
J
0
2
1
u
R
u
x
P
x
t
r
- znany czas ko
ń
ca procesu

P(t) - macierz wagowa stanu
R(t) - macierz efektu sygnału sterującego
•
Sterowanie u nie podlega żadnym ograniczeniom – może zmieniać się w
sposób nieograniczony
Definicja
Sterowaniem optymalnym (minimalno-całkowym bez ograniczeń)
( )
t
uˆ
nazywamy takie sterowanie u(t), które minimalizuje zdefiniowany wskaźnik
jakości J.
Można wykazać (Kaczorek), że:
( )
( ) ( ) ( ) ( )
t
t
t
t
t
T
x
K
B
R
u
1
ˆ
−
=
gdzie:
macierz K(t)
m
×
m
jest rozwiązaniem różniczkowego równania Riccatiego:
( )
( ) ( )
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
t
t
t
t
t
t
t
t
t
t
t
T
T
P
K
B
R
B
K
K
A
A
K
K
+
−
−
−
=
−
1
&
przy znanym warunku końcowym: K(t
r
)=0
Jest to skomplikowany, trudny do rozwiązania problem numeryczny
W przypadku obiektu stacjonarnego: t
r
→∞
(A=const, B=const, P=const)
otrzymamy:
( )
( )
t
t
T
Kx
B
R
u
1
ˆ
−
=
gdzie:
macierz K
m
×
m
jest rozwiązaniem algebraicznego równania Riccatiego (ARE):
0
P
K
B
KBR
K
A
KA
=
+
+
+
−
T
T
1

Nowoczesne środowiska komputerowe (np. MATLAB) posiadają procedurę
rozwiązywania
algebraicznego
równania
Riccatiego,
która
ponadto
każdorazowo bada sterowalność układu.
Przykład. Rozważmy stacjonarny proces sterowania obiektem o transmitancji
operatorowej:
( ) ( )
Ts
s
k
s
G
+
=
1
przy całkowym wskaźniku jakości:
(
)
dt
bu
ax
J
∫
∞
+
=
0
2
2
2
1
Rozwiązanie:
Po przekształceniach, równanie dynamiki układu sterowanego przedstawiamy w
postaci:
ku
x
x
T
=
+
&
&
&
Wprowadzamy wektor współrzędnych stanu:
=
x
x
&
x
Otrzymujemy równanie stanu w postaci:
Bu
Ax
x
+
=
&
przy czym:
−
=
T
1
0
1
0
A
=
T
k
0
B
=
0
0
0
a
P
[ ]
b
=
R
.
Ponieważ:
=
22
21
12
11
k
k
k
k
K
jest macierzą symetryczną (k
12
=k
21
), oraz:
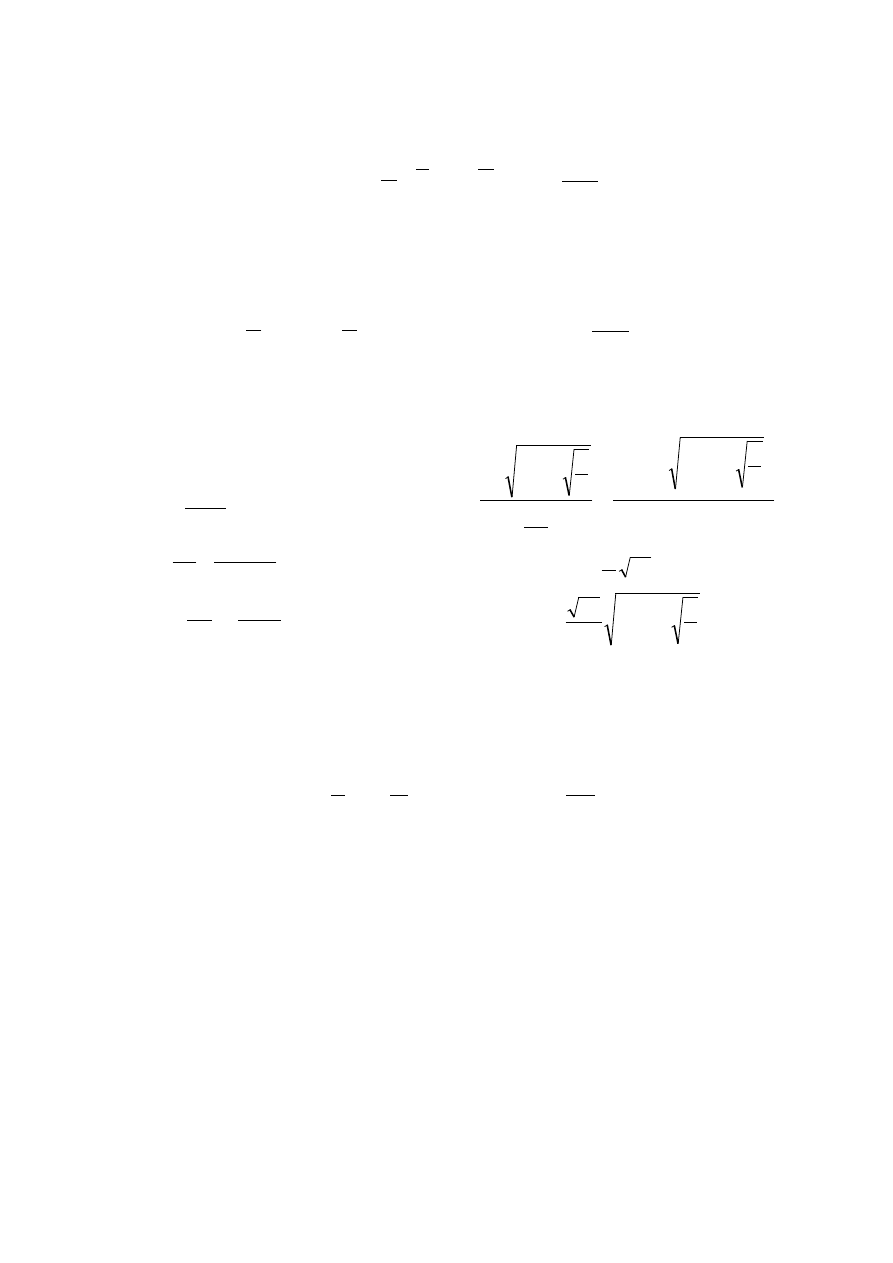
=
⋅
⋅
=
−
2
2
1
0
0
0
0
1
0
bT
k
T
k
b
T
k
T
B
BR
możemy zapisać algebraiczne równanie Riccatiego :
=
+
−
+
−
0
0
0
0
0
0
1
1
0
0
1
0
1
0
22
12
12
11
2
2
22
12
12
11
22
12
12
11
22
12
12
11
a
k
k
k
k
bT
k
k
k
k
k
k
k
k
k
T
T
k
k
k
k
Otrzymujemy układ równań:
=
+
−
=
+
−
=
0
2
0
2
2
2
22
22
12
2
2
22
12
12
11
2
2
2
12
bT
k
k
T
k
k
bT
k
k
k
T
k
k
a
bT
k
k
skąd:
−
±
=
=
−
±
=
−
±
=
b
a
kT
k
ab
k
ab
k
T
k
k
b
a
kT
bT
bT
k
b
a
kT
k
2
1
2
1
1
1
1
11
12
2
2
22
Optymalny sygnał sterujący:
(
)
x
k
x
k
bT
k
x
x
k
k
k
k
T
k
b
T
&
&
22
12
22
12
12
11
1
0
1
ˆ
+
=
=
=
−
Kx
B
R
u
Prosta postać – możliwość uzyskania rozwiązania analitycznego
Wyszukiwarka
Podobne podstrony:
MUM wykład12
MUM wykład10
MUM-wykład6
MUM wykład1
MUM wykład4
MUM wykład3
MUM wykład8
MUM wykład6
MUM wykład4a
MUM Wykład8a
Napęd Elektryczny wykład
więcej podobnych podstron