Elementy układów mechatronicznych – opis matematyczny 1. Elementy rozpraszające energię
a) opór tarcia wiskotycznego (płynnego) w ruchu postępowym.
FT – siła tarcia, z – przemieszczenie, Cv– współczynnik tarcia wiskotycznego z& – prędkość liniowa
b) opór tarcia wiskotycznego (płynnego) w ruchu obrotowym.
MT – moment tarcia, ϕ – kąt obrotu, Cω – współczynnik rozproszenia energii ϕ& – prędkość kątowa
c) opór przepływu laminarnego w układach hydraulicznych i pneumatycznych.
∆ p – spadek ciśnienia, Q – objętość medium, Rp – współczynnik oporu przepływu Q& – objętościowe natężenie przepływu
d) opór elektryczny
U – napięcie, q – ładunek elektryczny, Re – opór omowy q& – natężenie prądu
Równanie ogólne procesu rozpraszania energii:
y = R ⋅ x&
y – „siła” uogólniona (w rzeczywistości, jest to siła jedynie przez analogię) x – współrzędna uogólniona
z
FT
C
v
ϕ
MT
x ≡
ω
y ≡
R ≡ C
Q
∆ p
Rp
q
U
Re
Funkcja rozproszenia energii jest zdefiniowana zależnością : 1
2
D =
R ⋅ x&
2
Uwaga. Nie jest to energia !!!
2. Elementy magazynujące energię potencjalną.
a) magazynowanie energii w ruchu postępowym
Fs – siła sprężystości, ks – współczynnik sztywności liniowej b) magazynowanie energii w ruchu obrotowym
Ms – moment skręcający, ks – współczynnik sztywności skrętnej c) kondensator w układzie elektrycznym
C – pojemność kondensatora
d) napełnianie zbiornika płynem nieściśliwym.
p – ciśnienie, Ch – stała hydrauliczna, V( Q) – objętość medium Ogólne równanie procesu magazynowania energii potencjalnej t
y t
( ) = ∫ & d
x
k
t + y(0)
0
gdzie:
k
Fs
l
z
k
S
M s
ϕ
1
y ≡
k ≡
x ≡
U
C
q
1
p
V ( Q)
Ch
Ogólne równanie energii potencjalnej:
1
2
U =
k ⋅ x
2
3. Elementy magazynujące energię kinetyczną.
a) masa w ruchu postępowym
F – siła zewnętrzna wywołująca ruch postępowy b) bryła sztywna w ruchu obrotowym
M – moment sił zewnętrznych wywołujący ruch obrotowy c) cewka indukcyjna włączona w obwód elektryczny
L – indukcyjność cewki
Równanie ogólne procesu magazynowania energii kinetycznej d
y = k
( x&)
dt
gdzie:
F
z
m
y ≡ M
x ≡ ϕ
k ≡ I
0
U
q
L
Energia kinetyczna magazynowana w poszczególnych elementach opisana jest zależnością:
1
2
T =
k( x&)
2
Równania dynamiki we współrzędnych uogólnionych
1. metody szczegółowe
W celu utworzenia równań dynamiki wykorzystujemy znane prawa fizyczne np.
zasady dynamiki Newtona, prawo zachowania ładunku, prawo zachowania energii, równanie ciągłości strugi.
2. metoda z wykorzystaniem równań Lagrange’a drugiego rodzaju.
Jeżeli w układzie fizycznym wyodrębniono współrzędne uogólnione xi możemy wówczas zapisać następujące wyrażenie:
d T
∂
T
∂
U
∂
D
∂
−
+
+
= fi
dt x
∂&
x
∂
x
∂
x
∂&
i
i
i
i
Oznacza ono równanie Lagrange’a drugiego rodzaju, sformułowane dla współrzędnej uogólnionej xi ; fi oznacza pobudzenie (siłę uogólnioną) w kierunku współrzędnej xi.
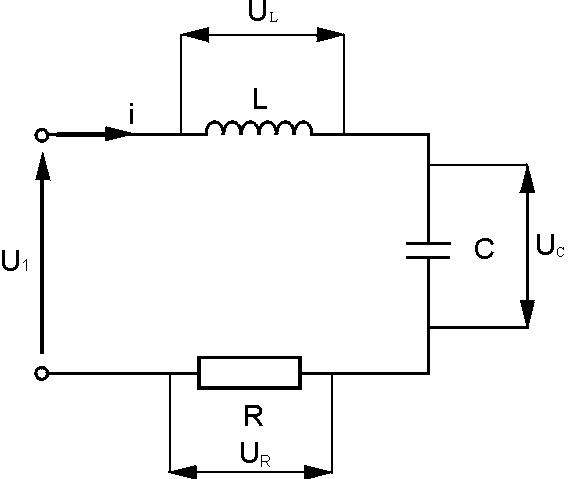
Przykład 1.
W układzie przedstawionym na rysunku należy sformułować równanie dynamiki wykorzystując metody szczegółowe oraz metodę równań Lagrange’a drugiego rodzaju.
di
U = L
L
dt
1
UC =
∫ idt
C
U = R ⋅ i
R
Korzystając z drugiego prawa Kirchhoffa :
1
U 1 =
di
L
+ ∫ idt + Ri
dt
C
Uwzględniając
i = q&
1
otrzymamy:
U = Lq&
& + q
R & +
q
1
C
• metoda równania Lagrange’a drugiego rodzaju
współrz
= ≡
ędna uogólniona:
x
x
q
i
Funkcja rozproszenia energii:
1
1
2
2
D =
R( x&) =
Rq&
2
2
Energia potencjalna układu:
1 1
1 1
2
2
U =
( x) =
q
2 C
2 C
Energia kinetyczna układu:
1
1
2
2
T =
L( x&) =
L( q&)
2
2
∂
∂ T
D
∂
U
∂
1
d
T
= 0
= q
R &
= q
= Lq&
&
∂ q
&
q
q
∂
∂
C
dt q
∂ &
f ≡ U
1
i
1
U = Lq&
& + q
R & + q
1
c
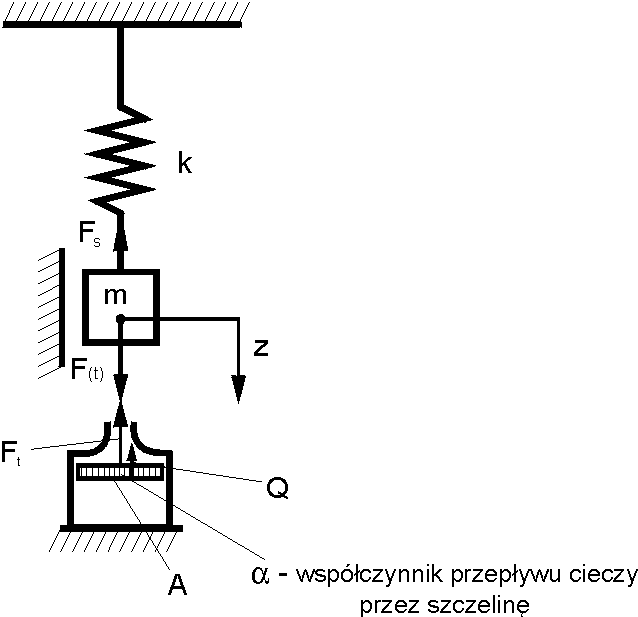
Przykład 2.
FS − siła oporu sprężyny
Ft − siła oporu tłumika
Q – przepływ medium przez szczelinę, objętość płynu.
• metoda szczegółowa
Na podstawie obserwacji ruchu masy m możemy zapisać równanie dynamiki w postaci:
z
m &
& = F t
( ) − F − F
S
t
F = k ⋅ z
S
Q = A ⋅ z – objętość płynu przepływającego przez szczelinę wynika z przemieszczenia tłoczka, określonego współrzędną z Różnica ciśnień między komorami tłoczka wynika z zależności:
∆
Różniczkując względem czasu pierwsze równanie, a następnie porównując stronami, otrzymujemy :
Az& = α ⋅ p
∆
Mnożąc obustronnie przez powierzchnię A i dzieląc przez α otrzymamy: A 2 ⋅ z& = A⋅ p
∆ = Ft
α
Podstawiając do równania dynamiki oraz porządkując to równanie otrzymamy: 2
A
mz&
& +
z& + kz = F ( t) α
• metoda równań Lagrange’a
Energia kinetyczna:
1
2
T =
z
m&
2
Energia potencjalna:
1
2
U =
kz
2
Funkcja rozproszenia energii:
1
2
D
R Q&
= 2 p
1
p
∆ = R Q& ⇒ Q& =
p
∆
1
p
Rp
= α
RP
1 1
2
D =
Q&
α
2
Związek między współrzędnymi Q i z: Q= A z 1 A 2
D =
z&2
2 α
d
T
∂
∂
=
U
mz&
&
= kz
dt
z
∂&
z
∂
∂ T
2
=
D
∂
A
0
=
∂
z&
z
z
∂&
α
2
A
z
m &
& +
z& + kz = F ( t) α
Przykład 3. Wyznaczyć równanie dynamiki układu hydraulicznego.
Q 1= QS+ Q 2 – Stosujemy równanie ciągłości strugi Q 1 – ilość cieczy dopływająca przez rurociąg Q 2 – ilość cieczy przepływająca przez zwężkę Q S – ilość cieczy gromadzona w zbiorniku
1
Funkcja rozproszenia energii:
& 2
D =
R ⋅ Q
p
2
2
1 ρ ⋅ g
2
1
1
2
A
Energia potencjalna: U =
⋅
⋅ Q = ⋅
⋅ Q
gdzie: C =
S
S
h
ρ ⋅
2
A
2 C
g
h
otrzymamy:
1
2
Q 2 = Q 1 − QS
D =
⋅ R ⋅ ( Q& − Q& )
p
1
2
s
Stosujemy metodę równań Lagrange’a drugiego rodzaju różniczkując względem
„współrzędnej” QS , gdyż Q 1 jest wielkością zadaną.
Q& ≡ q
1
1
D
∂ = − R Q
( &
&
1 − Q )
p
S
Q
∂ & S
U
∂
ρ ⋅ g
=
QS
Q
∂
A
S
Otrzymujemy:
ρ ⋅ g
R ⋅ Q& +
Q = R ⋅ Q&
p
S
A
S
p
1
Q = A⋅ h
S
Q& = A⋅ h&
S
Po podstawieniu do równania różniczkowego otrzymamy:
ρ ⋅ g
R ⋅ A ⋅ h& +
⋅ A ⋅ h = R ⋅ q
p
p
1
A
R ⋅ A ⋅ h& + ρ ⋅ g ⋅ h = R ⋅ q
: ρ ⋅ g
p
p
1
R ⋅ A
R
p
p
⋅ h& + h =
⋅ q 1
ρ ⋅ g
ρ ⋅ g
3
2
1
3
2
1
T
k
T – wielkość stała (stała czasowa)
k –stały współczynnik
Przykład 4. W skład układu wchodzą:
- bęben dwuwalcowy (masy i wymiary geometryczne podane na rysunku)
- sprężyna liniowa (sztywność k)
- tłumik hydrauliczny
-
Bęben 2-walcowy toczy się bez poślizgu po poziomej płaszczyźnie.
Masy krążka nie uwzględniamy
Współrzędne przyjęte do opisu ,
ϕ z , z ,Q, z, y
1
2
.
Przedstawić równanie dynamiki układu
U – energia potencjalna
T – energia kinetyczna
D – funkcja rozproszenia energii
1
1 1
1
1 1
U=
kz 2
T=
ϕ
1
( M+m) y& +
2
⋅ ( MR +
2
mr 2 ) 2
R =
D=
⋅ Q&
&
2
p
α
2
2
2 2
2 α
y
y&
=
ϕ
⇒ &
ϕ =
z
ϕ 2 2
ϕ
1 =
⋅ R= y z 2 = ( R+r)
R+r
= y
R
R
R
Q= (
A z-z 2 )
R+r
R+r
= A z-
y ⇒ & =
Q A z-
&
y&
R
R
1
1
1
1
1
1
U=
k ⋅ 4 y 2 =
k* ⋅ y 2
T= M+m+ ( MR +
2
mr 2 )
2
2
{
y& = m* ⋅ y&
2
2
2
2
R 2
k*
2
1
4
4
4
4
2
4
4
4
4
3
m*
1 1
2
δ
δ
2
R+r
d
T
T
D=
A z-
&
y&
= m y
* &
&
= 0 ( T=T ( &) δU
y
= k*y
α
δ
2
&
δ
δ
R
dt
y
y
y
2
δD
A 2
R+r
R+r
A 2 R+r
A 2 R+r
=
-
z&
y&
-
=
& -
y
z&
δ &
α
α
α
y
R
R
R
R
Po wstawieniu uzyskanych wyrażeń otrzymujemy równanie dynamiki w następującej postaci:
2
A 2 R+r
A 2 R+r
m* +
y&
&
& +
y k*y=
⋅
z&
α
α
R
R
Wyszukiwarka
Podobne podstrony:
MUM wykład12
MUM wykład10
MUM wykład7
MUM wykład1
MUM wykład4
MUM wykład3
MUM wykład8
MUM wykład6
MUM wykład4a
MUM Wykład8a
Napęd Elektryczny wykład
więcej podobnych podstron