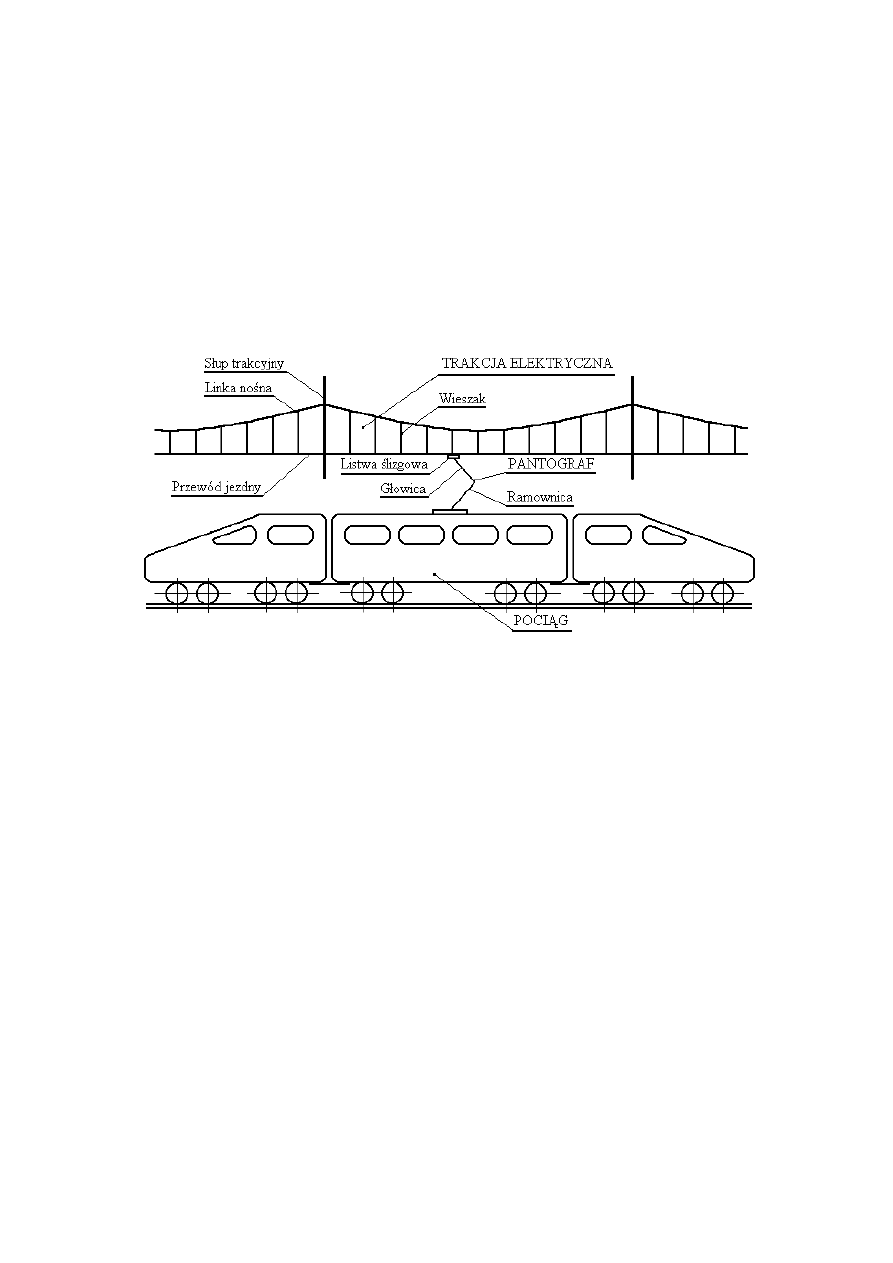
Przykład. Modelowanie nadzorowania drgań pantografów pojazdów
szynowych o dużych prędkościach
W przypadku pojazdów szynowych (pociągów) poruszających się z
prędkościami do ok. 200 km/godz. dostrzeżono niebezpieczny problem utraty
kontaktu pomiędzy listwą ślizgową pantografu a przewodem jezdnym trakcji
naziemnej. Jego konsekwencją jest powstanie łuku elektrycznego, który
przerywa doprowadzenie zasilanie pociągu, a ponadto niszczy elementy trakcji.
Główne przyczyny tego zjawiska:
– zbyt duża wartość siły dociskającej listwę do przewodu. Staje się ona
wówczas źródłem drgań wymuszonych o zauważalnym poziomie, albo
– zbyt małą wartość siły dociskającej listwę do przewodu.
Modelowanie dynamiki pantografu pojazdów szynowych
Model pierwszy uwzględnia:
- masy: ramownicy m
1
oraz głowicy pantografu m
2
,
- sztywność k
l
struktury głowicy pantografu oraz strefy kontaktu listwa-
przewód jezdny,
- sztywność k
2
połączenia ramownicy i głowicy,
- sztywności słupów trakcyjnych k
s
,
- sztywności wieszaków k
w
,
- siłę docisku statycznego listwy F
0
.
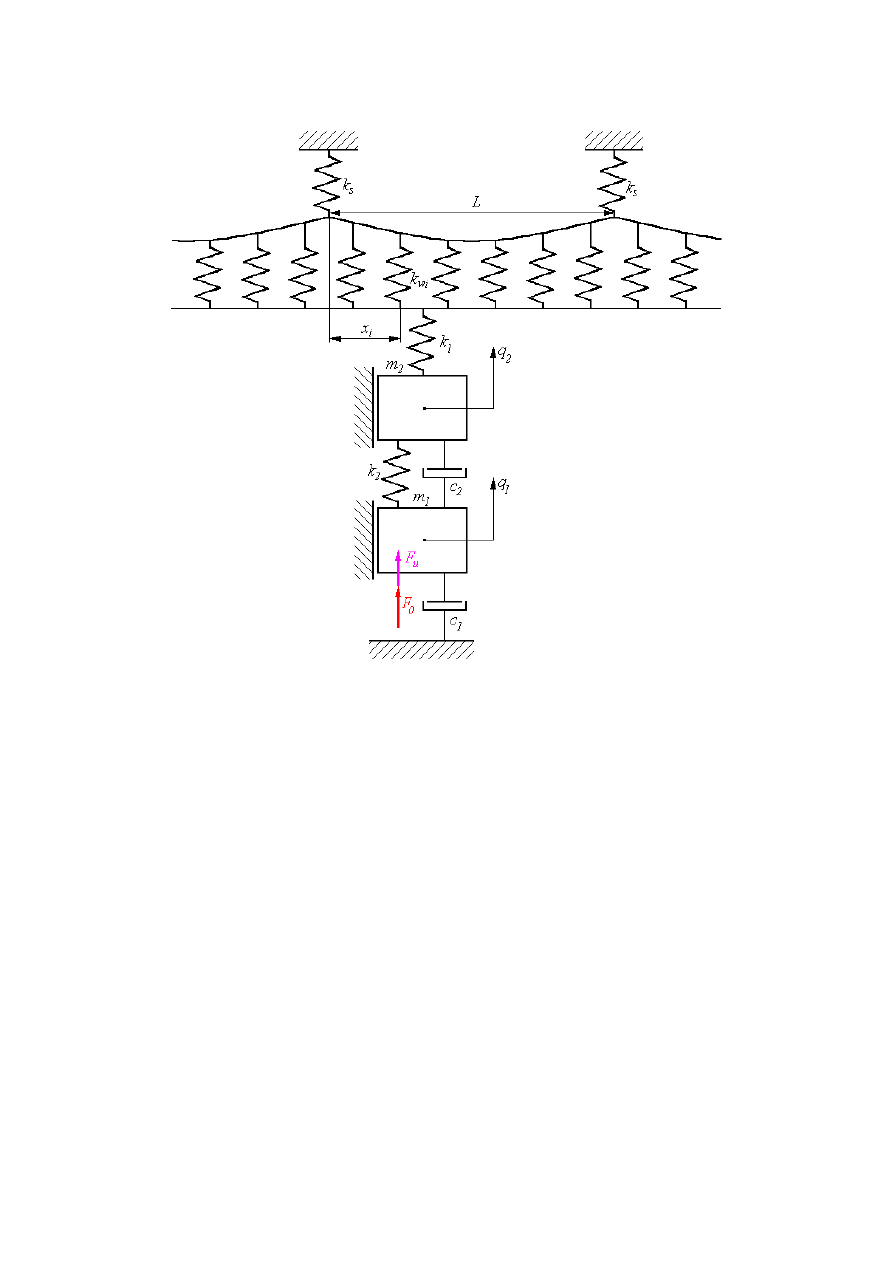
– Uwzględniono efekt oddziaływania wzbudnika, który generuje sygnał
sterujący w postaci siły F
u
.
– Z uwagi na obserwowane niskie częstości drgań (do kilkudziesięciu Hz) oraz
niski poziom sił wzbudnika (kilkadziesiąt N), w rozwiązaniach praktycznych
stosuje się wzbudniki pneumatyczne.
– Przedstawiony model uwzględnia ponadto wpływ prędkości ruchu v na
dynamikę pantografu.
W rezultacie, zdefiniowano macierze układu sterowanego w postaci:
=
2
1
0
0
m
m
M
−
−
+
=
2
2
2
2
1
c
c
c
c
c
L

+
−
−
=
)
(
2
2
2
2
*
t
k
k
k
k
k
K
=
2
1
q
q
q
=
0
0
F
f
=
0
1
u
B
u
F
≡
u
.
Występująca we wzorze funkcja czasu k(t) jest kombinowaną sztywnością
elementów trakcji oraz strefy kontaktu, którą wyznaczamy na podstawie niżej
podanych zależności:
)
(
)
(
)
(
t
k
k
t
k
k
t
k
t
l
t
l
+
=
)
(
)
(
)
(
)
(
)
(
2
1
2
1
t
k
t
k
t
k
t
k
t
k
t
t
t
t
t
+
=
,
(
)
(
)
(
)
1
1
2
1
1
)
(
)
(
)
(
−
−
+
=
T
xl
s
s
xl
t
t
t
t
k
T
K
K
T
,
(
)
1
1
1
2
)
(
)
(
)
(
−
−
=
=
∑
T
xl
i
i
wi
xl
t
t
t
t
k
w
T
K
T
−
−
=
4
2
2
2
1
L
k
L
k
L
k
k
s
s
s
s
s
K
=
4
2
2
2
2
L
k
L
k
L
k
k
s
s
s
s
s
K
−
−
−
=
2
2
2
2
L
x
k
L
x
k
L
x
k
k
i
wi
i
wi
i
wi
wi
wi
K
−
=
−
=
2
1
2
1
)
(
L
vt
L
x
t
l
xl
T

Zadaniem układu sterowania jest minimalizacja odchylenia wartości
rzeczywistej siły kontaktu listwa-przewód jezdny od jej wartości ustalonej,
wynikającej z zadanej siły docisku F
0
.
Zdefiniowano wskaźnik jakości:
(
)
(
)
Ru
u
q
q
q
q
T
T
t
k
Q
J
2
1
)
(
0
0
0
2
1
2
+
−
−
=
który uwzględnia energię potencjalną sprężystości elementów trakcji oraz strefy
kontaktu, a także efekt sygnału sterującego. Podane sformułowanie spełnia
zatem cechy sterowania minimalno-energetycznego w dziedzinie czasu
(współczynnik Q
1
=0). Należy zauważyć, że do określenia wskaźnika jakości
oraz optymalnego sygnału sterującego wystarcza znajomość jedynie
przemieszczenia q
2
głowicy pantografu (pozostałe współrzędne stanu są
nieistotne), co ułatwia realizację sterowania w trybie on-line.
Konieczność znajomości metod rozwiązywania zagadnień sterowania
optymalnego w
układach niestacjonarnych
.
Model drugi uwzględnia uproszczenie w postaci zastąpienia zmiennej funkcji
sztywności kombinowanej k(t) jej wartością uśrednioną. Jest to zatem model
stacjonarny, który ułatwia analizę problemu sterowania z punktu widzenia
możliwości doboru stałych wzmocnień regulatora. Uniemożliwia natomiast
przeprowadzenie, na etapie symulacji komputerowej, analizy wpływu prędkości
jazdy na dynamikę pantografu.
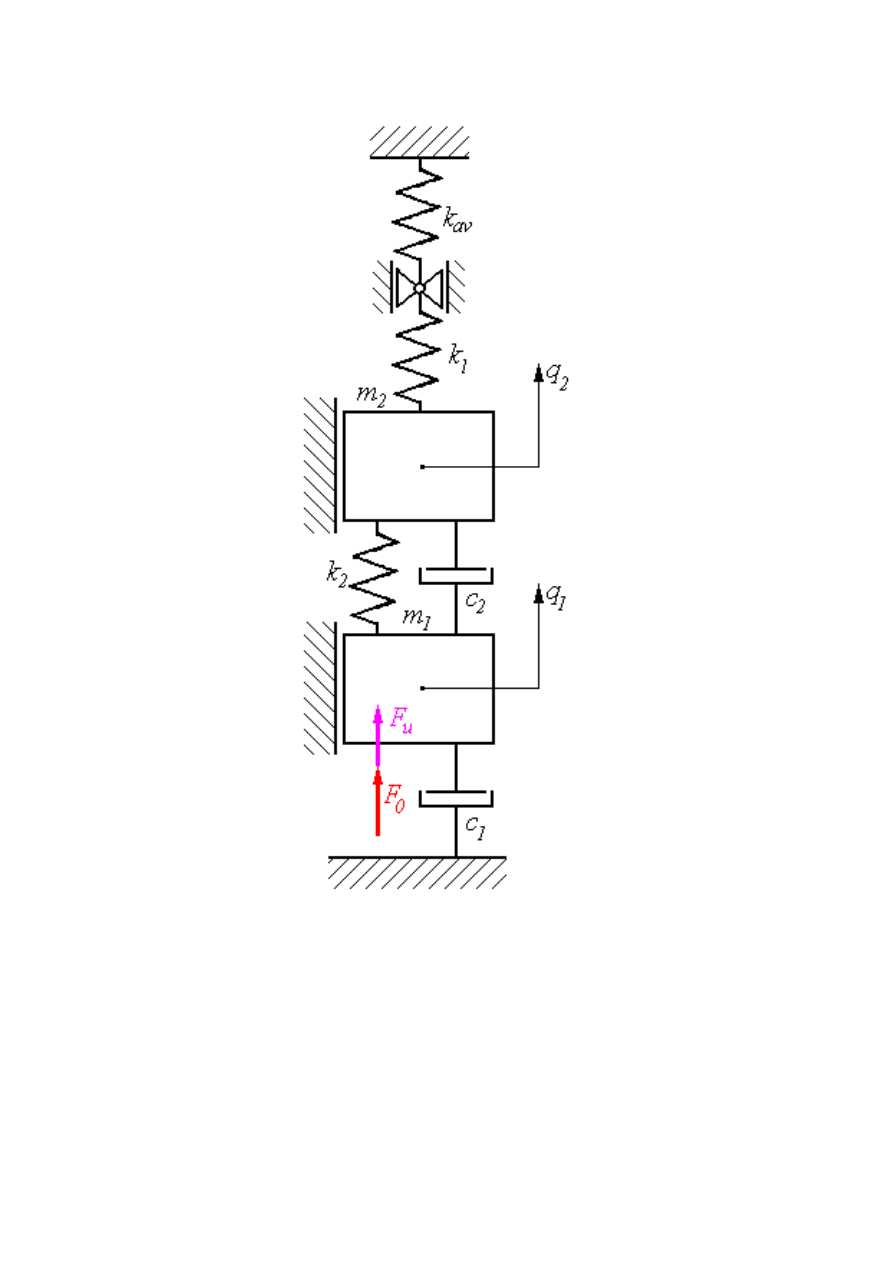
Wówczas rozwiązanie można uzyskać, definiując:
– problem sterowania optymalnego przy całkowym wskaźniku jakości –
rozwiązanie algebraicznego równania Riccatiego, albo
– problem sterowania modalnego przy energetycznym wskaźniku jakości

Wówczas równanie dynamiki układu sterowanego ma postać
u
av
l
av
l
F
F
q
q
k
k
k
k
k
k
k
k
q
q
c
c
c
c
c
q
q
m
m
+
=
+
+
−
−
+
−
−
+
+
0
1
0
0
0
0
2
1
2
2
2
2
2
1
2
2
2
2
1
2
1
2
1
&
&
&
&
&
&
Wyszukiwarka
Podobne podstrony:
MUM wykład10
MUM wykład7
MUM-wykład6
MUM wykład1
MUM wykład4
MUM wykład3
MUM wykład8
MUM wykład6
MUM wykład4a
MUM Wykład8a
Napęd Elektryczny wykład
więcej podobnych podstron