Metoda elementów skończonych – zagadnienia przestrzenne
początek: M. T. Turner (1956)
rozwinięcie: O.C. Zienkiewicz (Swansea, UK)
J. Szmelter (WAT – Warszawa)
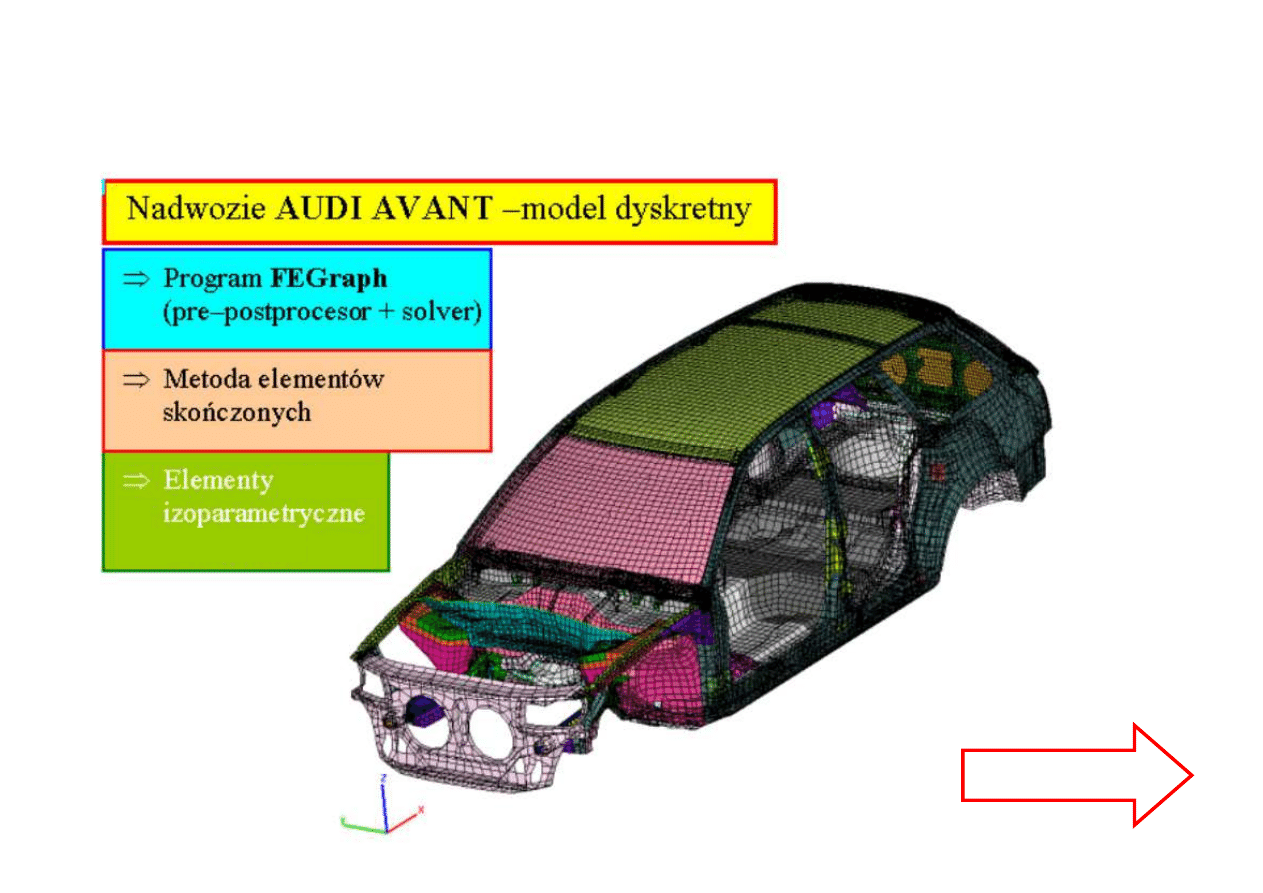
KSZTAŁTOWANIE
PROTOTYPU KONSTRUKCJI
METODĄ ELEMENTÓW
SKOŃCZONYCH
(MES)
•
odwzorowanie własności stereomechanicznych konstrukcji
geometria, własności masowo–sprężysto–tłumiące
•
typy elementów skończonych
Metoda sztywnych elementów skończonych
(J. Kruszewski, Katedra Mechaniki i Wytrzymałości Materiałów, 1969-1980)
– sztywne elementy skończone (SES)
– elementy sprężysto–tłumiące (EST)
Metoda odkształcalnych elementów skończonych
Katedra Mechaniki i Wytrzymałości Materiałów, od 1970
– elementy izoparametryczne 2–wymiarowe
– elementy izoparametryczne 3–wymiarowe
Metody hybrydowe
(E. Wittbrodt, od 1972, K. Kaliński, od 1983)
•
zastosowania
•
nowoczesne techniki obliczeniowe
– aspekty techniczne i ekonomiczne
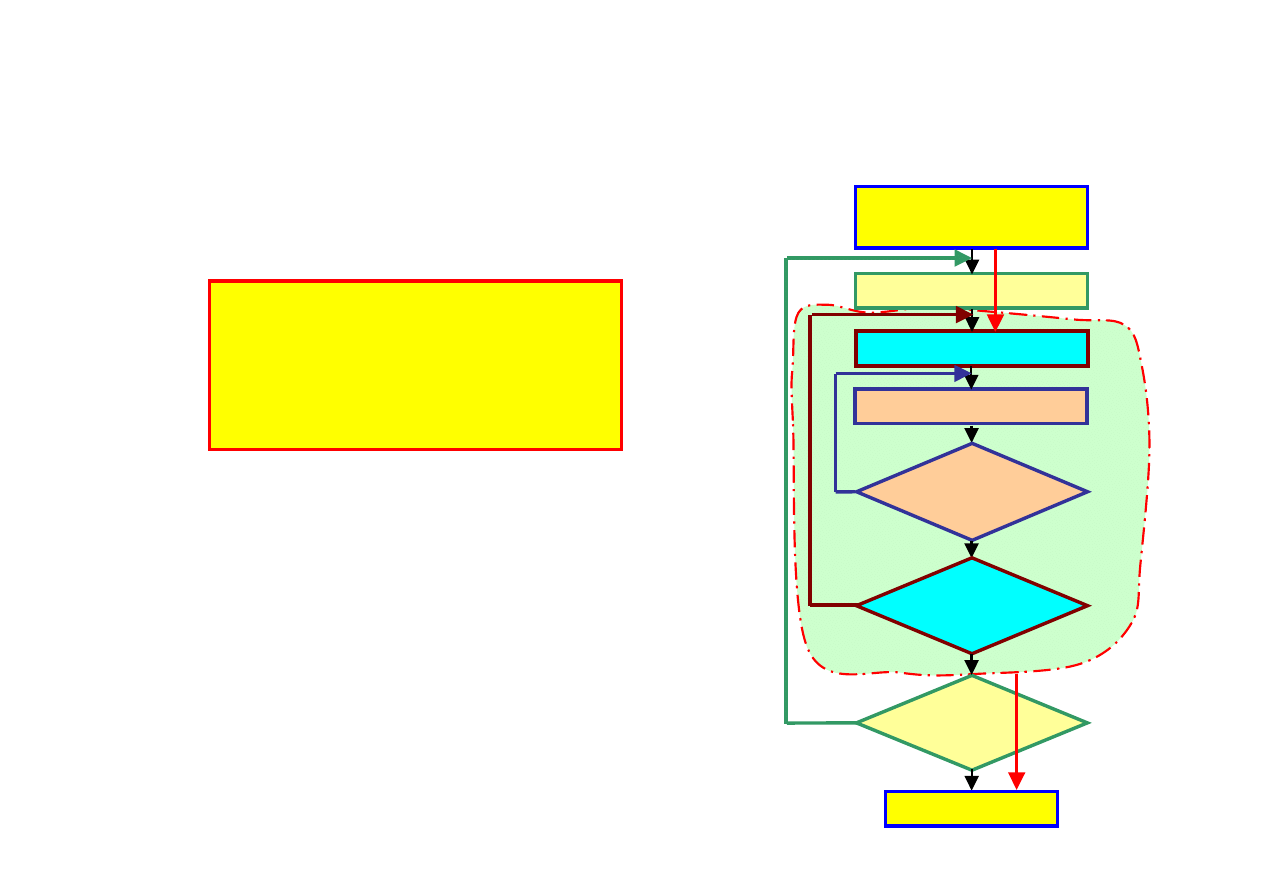
Faza projektowania
Obiekt rzeczywisty
(koncepcja)
Model fizyczny
Model dyskretny
Model obliczeniowy
PROTOTYP
Poprawność modelu
obliczeniowego
Poprawność modelu
dyskretnego
Poprawność modelu
fizycznego
TAK
TAK
TAK
model
strukturalny
MES
TENDENCJA
TENDENCJA
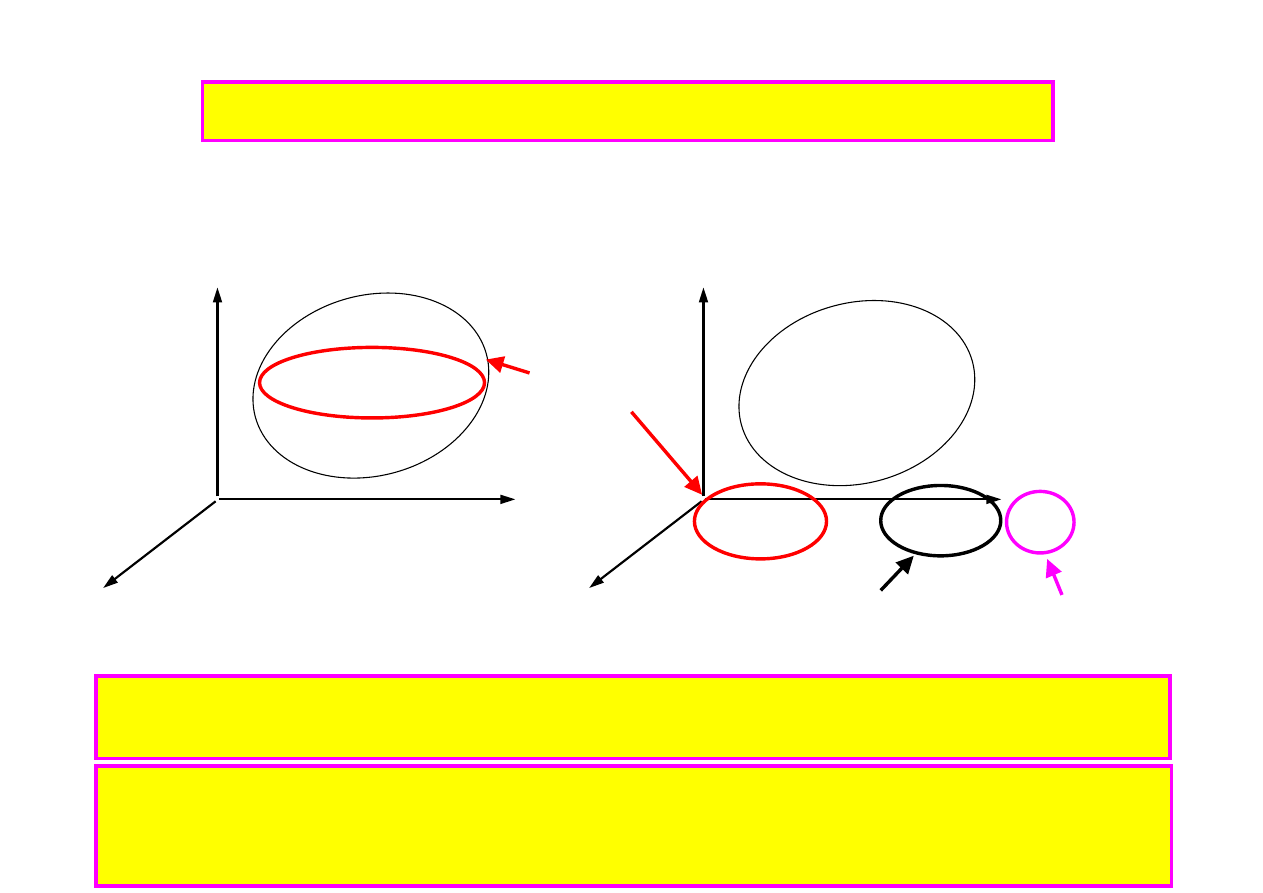
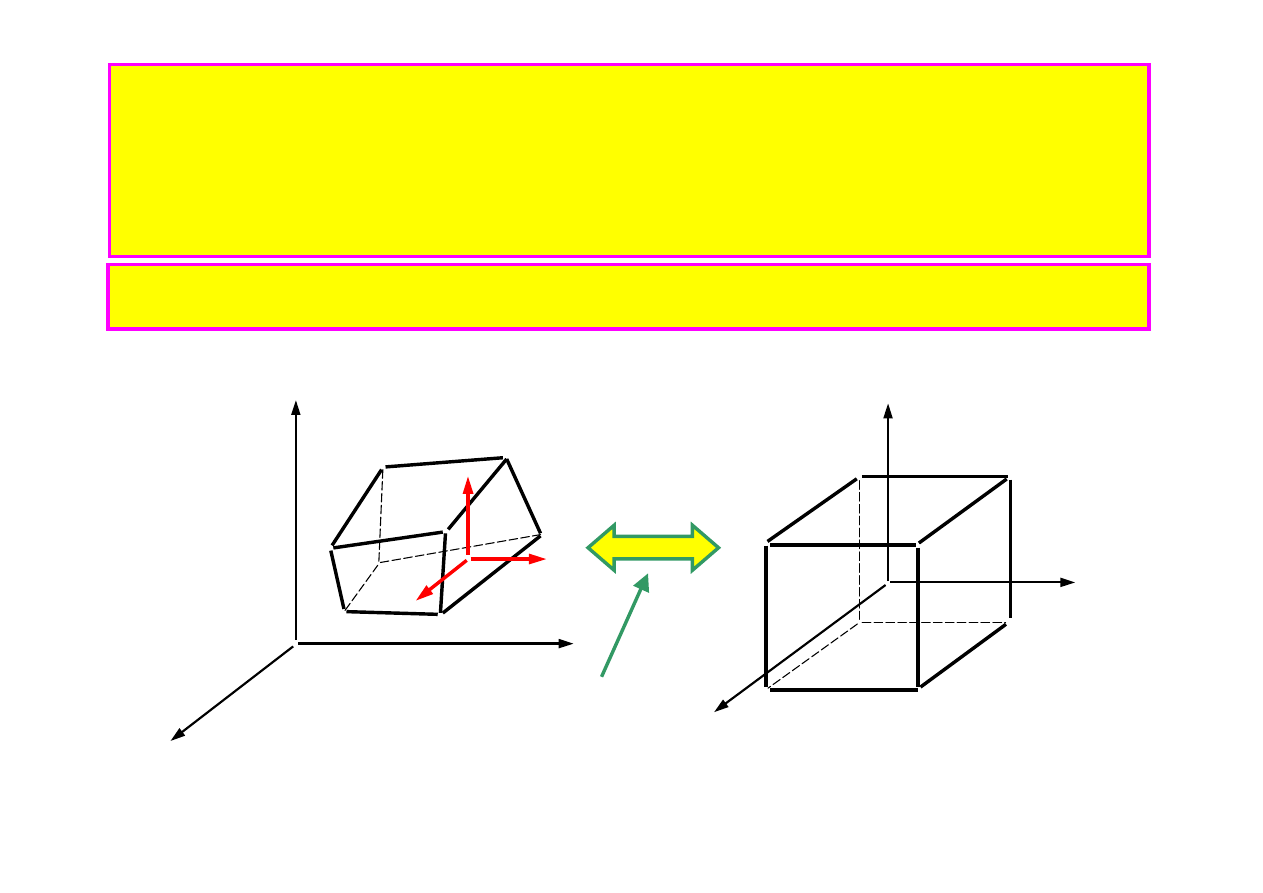
Koncepcja elementu skończonego
w przemieszczeniach
Ośrodek ciągły
Założenie: węzły A
i
(x
i
, y
i
, z
i
)
wartości węzłowe
φ
i
(t), i=1, ... , n.
Element skończony
– idealizacja ośrodka ciągłego w ten sposób, że wartości funkcji
wnętrza wyrażone są za pomocą wartości węzłowych
A
°
φ
(t) =
φ
(x, y, z, t)
x
y
z
°
x
y
z
°
A
°
A
1
°
A
3
°
A
4
°
A
2
°
(
)
(
) ( )
∑
=
⋅
=
n
i
i
i
t
z
y
x
N
t
z
y
x
1
,
,
,
,
,
φ
φ
funkcja
kształtu
wartość
węzłowa i
funkcja
wnętrza
φ
i
(t) –
przemieszczenia
,
naprężenia
siły, temperatura
Rezultat:
model strukturalny
dyskretyzacja przemieszczeń i obciążeń – wartości węzłowe
zróżnicowane własności materiałowe – zredukowane do węzłów elementu
O
O

Wymagania dotyczące funkcji kształtu
– zachowanie ciągłości funkcji wnętrza wewnątrz elementu oraz jej
zgodność w węzłach
Element zgodny
– możliwość opisania stałych składowych funkcji wnętrza (np.
przemieszczeń niezależnych od punktu wnętrza – ruch ciała
sztywnego)
– Element zupełny
– możliwość opisania stałych pochodnych funkcji wnętrza (np. stałych
odkształceń i naprężeń)
– Element zupełny
Ponieważ ciągłość funkcji wnętrza jest spełniona tylko w węzłach,
dla spełnienia warunku zgodności modelu MES z ośrodkiem
ciągłym wymagana bardzo duża gęstość podziału
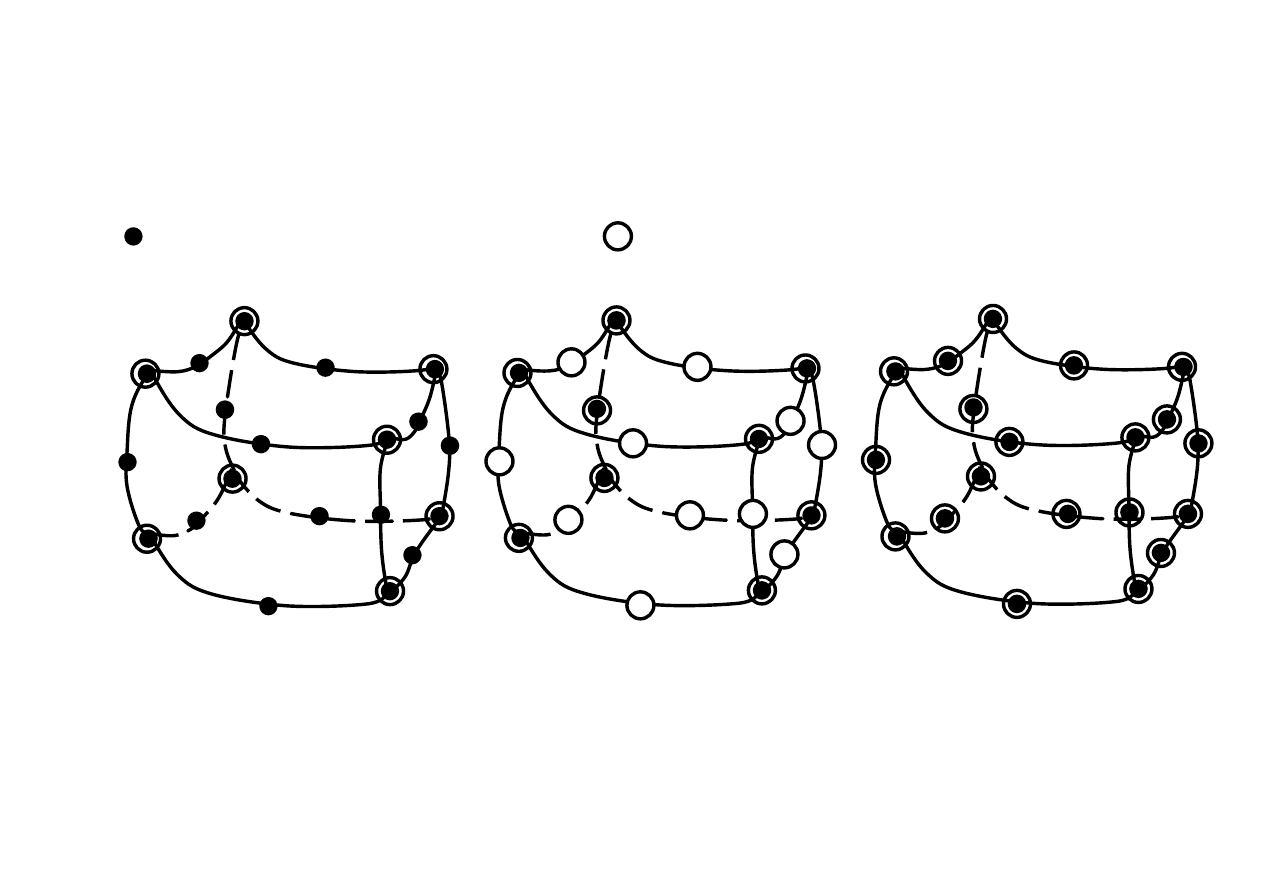
Odwzorowanie geometryczne – elementy zakrzywione
węzły definiujące geometrię (n
g
)
węzły definiujące wartości węzłowe (n
w
)
Element superparametryczny
Element subparametryczny
Element izoparametryczny
n
g
> n
w
n
g
< n
w
n
g
= n
w
°
°
°
°
°
°
°
°
°
q
x
q
y
q
z
x
y
z
1
2
3
4
5
6
7
8
°
°
°
°
°
°
°
°
°
ξ
η
ζ
°
1
2
3
4
5
6
7
8
Bryła izoparametryczna 8–węzłowa – element 3–wymiarowy
Jakobian
przekształcenia
Element izoparametryczny
odwzorowanie złożonej geometrii konstrukcji
możliwość zróżnicowania własności materiałowych
Rezultat: modele dyskretne powyżej
kilkuset tysięcy
stopni swobody
wymagane duże moce obliczeniowe systemów komputerowych
współrzędne znormalizowane
współrzędne kartezjańskie
O
S

Przykład. Przedmiot podatny, materiał: brąz CC331G (BA1032) zamocowano na stole
frezarki Mikron VCP 600
Rezultat. Model MES 23760 elementów 8-węzłowych, 33717 węzłów, po 3 stopnie
swobody w węźle. Długość boku elementu skończonego – 2 mm.
Przedmiot podatny
Szcz
ę
ki mi
ę
kkie
MEDINA – tworzenie
modelu obliczeniowego
(pre-procesor)
PERMAS – rozwiązanie
„w przemieszczeniach”
(solver)
FeGraph – wizualizacja
stanu przemieszczeń
(kolorystyka)
Ź
ródło: prace Katedry
Mechaniki i Wytrzymałości
Materiałów PG

Dla wybranego punktu o współrzędnych x, y, z wektor przemieszczeń q
ma składowe q
x
, q
y
, q
z
, co zapisujemy w postaci
(
)
(
)
z
y
x
q
q
q
col
z
y
x
,
,
,
,
=
q
.
Stosujemy transformację ze współrzędnych kartezjańskich x, y, z do
współrzędnych znormalizowanych
ξ
,
η
,
ζ
Znormalizowane współrzędne węzłów elementu 8–węzłowego
i
ξ
i
η
i
ζ
i
1
1
–1
–1
2
1
1
–1
3
–1
1
–1
4
–1
–1
–1
5
1
–1
1
6
1
1
1
7
–1
1
1
8
–1
–1
1
Współrzędne kartezjańskie x, y, z wybranego punktu elementu są
definiowane przez odpowiadające współrzędne znormalizowane
ξ
,
η
,
ζ
∑
=
=
8
1
i
i
i
x
c
x
∑
=
=
8
1
i
i
i
y
c
y
∑
=
=
8
1
i
i
i
z
c
z
gdzie:
(
)(
)(
)
ζ
ζ
η
η
ξ
ξ
i
i
i
i
c
+
+
+
=
1
1
1
8
1
Macierz transformacji (Jakobian)
(
)
⋅
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
8
8
8
2
2
2
1
1
1
8
1
8
1
8
1
,
,
z
y
x
z
y
x
z
y
x
c
c
c
c
c
c
z
y
x
z
y
x
z
y
x
M
M
M
L
L
L
ζ
ζ
η
η
ξ
ξ
ζ
ζ
ζ
η
η
η
ξ
ξ
ξ
ζ
η
ξ
J

gdzie:
(
)(
)
(
)(
)
(
)(
)
8
,...,
1
,
1
1
8
1
,
1
1
8
1
,
1
1
8
1
=
+
+
=
∂
∂
+
+
=
∂
∂
+
+
=
∂
∂
i
c
c
c
i
i
i
i
i
i
i
i
i
i
i
i
ζ
ξ
ξ
η
η
ζ
η
ζ
ζ
ξ
ξ
η
ξ
ζ
ζ
η
η
ξ
.
Macierz funkcji kształtu elementu
Wektor przemieszczeń, dla punktu o współrzędnych x, y, z
(
) (
)
a
X
q
⋅
=
z
y
x
z
y
x
,
,
,
,
gdzie:
(
)
(
)
(
)
(
)
=
z
y
x
z
y
x
z
y
x
z
y
x
,
,
,
,
,
,
,
,
X
0
0
0
X
0
0
0
X
X
(
)
[
]
xyz
yz
xz
xy
z
y
x
z
y
x
1
,
,
=
X
[
]
T
a
a
24
1
K
=
a
jest wektorem nieznanych stałych współczynników.
Wektor nieznanych współczynników a jest określany z równania:
a
X
q
⋅
=
nod
e
gdzie:
(
)
(
)
(
)
8
8
8
1
1
1
,
,
,...,
,
,
z
y
x
z
y
x
col
e
q
q
q
=
- warunki brzegowe
wektor przemieszczeń węzłowych elementu skończonego (ES) nr e

(
)
(
)
=
8
8
8
1
1
1
,
,
,
,
z
y
x
z
y
x
nod
X
X
X
M
Stąd:
(
)
(
)
e
e
z
y
x
z
y
x
q
N
q
⋅
=
,
,
,
,
,
gdzie:
(
) (
)
1
,
,
,
,
−
⋅
=
nod
e
z
y
x
z
y
x
X
X
N
jest macierzą funkcji kształtu elementu skończonego nr e.
Pozwala ona opisać przemieszczenia dla dowolnie wybranego punktu
elementu, jako funkcję jego przemieszczeń węzłowych.
Macierz sztywności elementu skończonego
W elemencie skończonym nr e jest magazynowana energia potencjalna
sprężystości.
∫
=
V
T
e
dV
U
ε
σ
2
1
Uwzględniając macierzowy operator różniczkowania liniowego
T
l
x
y
z
z
x
y
z
y
x
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
0
0
0
0
0
0
0
0
0
Γ

oraz macierz sprężystości dla trójwymiarowego stanu naprężeń
(
)(
)
−
−
−
−
−
−
−
+
=
2
2
1
.
0
2
2
1
0
0
2
2
1
0
0
0
1
0
0
0
1
0
0
0
1
2
1
1
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
sym
E
D
otrzymamy
(
)
(
)
(
)
e
l
e
e
l
l
z
y
x
z
y
x
z
y
x
l
q
B
q
N
Γ
q
Γ
ε
B
,
,
,
,
,
,
=
=
=
4
43
4
42
1
oraz
(
)
e
l
z
y
x
q
DB
Dε
σ
,
,
=
=
( )
(
)
(
)
(
)
(
)
(
)
(
)
(
) (
)
e
e
T
e
e
V
l
T
l
T
e
V
e
e
l
T
e
e
l
V
l
T
l
V
T
V
T
e
e
l
dxdydz
z
y
x
z
y
x
dxdydz
z
y
x
z
y
x
dxdydz
z
y
x
z
y
x
dV
dV
U
q
K
q
q
DB
B
q
q
N
Γ
D
q
N
Γ
q
DΓ
q
Γ
Dε
ε
ε
Dε
K
B
2
1
,
,
,
,
2
1
,
,
,
,
2
1
,
,
,
,
2
1
2
1
2
1
=
⋅
⋅
=
=
=
=
=
=
=
∫
∫
∫
∫
∫
4
4
4
4
4
3
4
4
4
4
4
2
1
4
43
4
42
1
e
e
e
U
f
q
=
∂
∂
równanie statyki liniowej ES nr e
e
e
e
f
q
K
=
Macierz sztywności elementu skończonego opisuje zdolność elementu
do magazynowania energii potencjalnej sił sprężystości
(
) (
)
∫
=
V
l
T
l
e
dxdydz
z
y
x
z
y
x
,
,
,
,
DB
B
K

Macierz sztywności w dziedzinie współrzędnych znormalizowanych
(
) (
) (
)
(
)
(
) (
) (
)
(
)
(
)
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
d
d
d
z
y
x
z
y
x
l
T
l
e
,
,
det
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
1
1
1
1
1
1
J
DB
B
K
∫ ∫ ∫
+
−
+
−
+
−
⋅
=
Macierz B
l
wyznaczamy z zależności
(
)
(
)
(
)
1
,
,
,
,
,
,
−
⋅
=
=
nod
l
e
l
l
z
y
x
z
y
x
z
y
x
X
X
Γ
N
Γ
B
(
)
′
′
′
′
′
′
′
′
′
=
9
8
7
6
5
4
3
2
1
,
,
X
0
X
X
X
0
0
X
X
X
0
0
0
X
0
0
0
X
X
Γ
z
y
x
l

Natomiast
[
]
yz
z
y
0
0
0
1
0
1
=
′
X
[
]
xz
z
x
0
0
1
0
0
2
=
′
X
[
]
xy
y
x
0
1
0
0
0
3
=
′
X
[
]
xz
z
x
0
0
1
0
0
4
=
′
X
[
]
yz
z
y
0
0
0
1
0
5
=
′
X
[
]
xy
y
x
0
1
0
0
0
6
=
′
X
[
]
xz
z
x
0
0
1
0
0
7
=
′
X
[
]
xy
y
x
0
1
0
0
0
8
=
′
X
[
]
yz
z
y
0
0
0
1
0
9
=
′
X
Macierz sztywności K
e
wyznaczana poprzez całkowanie numeryczne
np. metodą kwadratury Gaussa-Legendre’a.
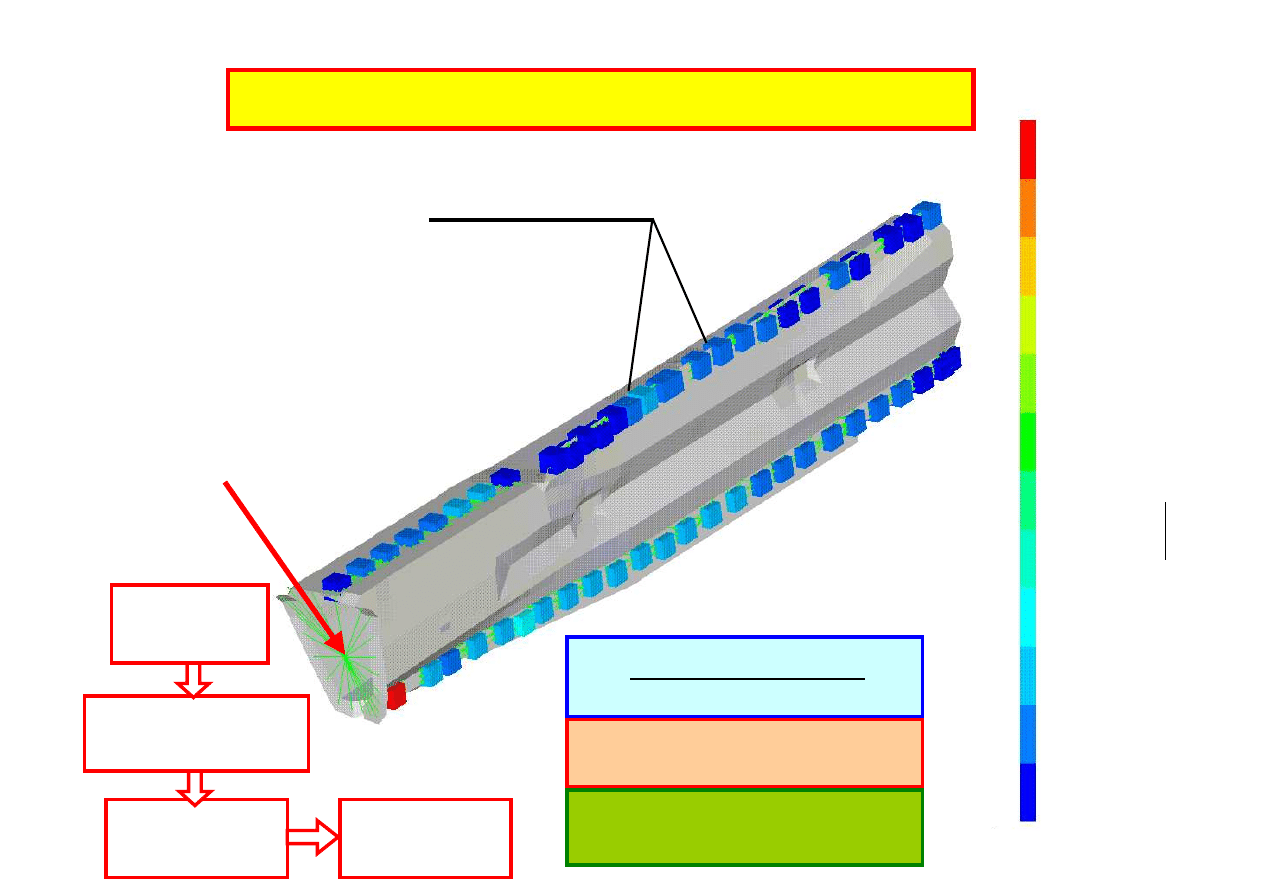
BMW – samochód osobowy – prototyp (2002)
K. Kaliński (współpraca)
Podłużnica
– długość 940 mm
– wysokość 180 mm
– szerokość 70 – 80 mm
Obciążenie w miejscu
mocowania do zderzaka
59.83
54.95
15.91
20.79
25.67
50.07
30.55
35.43
40.31
45.19
11.03
6.156
1.276
Siły wewnętrzne w połączeniach zgrzewanych
S
ił
a
[N
]
•
Program FEGraph
–
rozbudowany
–
•
Metoda elementów
skończonych
•
Bryły
izoparametryczne 8–
węzłowe
bryły 8–węzłowe
izoparametryczne
Obciążenia
zewnętrzne
Przemieszczenia
węzłów
Naprężenia
w elementach
Siły w
przekrojach
Macierz bezwładności elementu skończonego
W elemencie skończonym nr e jest magazynowana energia kinetyczna
∫
=
V
T
e
dV
T
q
q &
&
ρ
2
1
(
)
e
e
T
e
e
V
e
T
e
T
e
V
e
e
T
e
e
e
e
dV
dV
T
q
M
q
q
N
N
q
q
N
q
N
M
&
&
&
43
42
1
&
&
&
2
1
2
1
2
1
=
=
=
∫
∫
ρ
ρ
Macierz bezwładności elementu skończonego opisuje zdolność
elementu do magazynowania energii kinetycznej
(
) (
) (
)
∫
=
V
e
T
e
e
dV
z
y
x
z
y
x
z
y
x
,
,
,
,
,
,
N
N
M
ρ

Macierz bezwładności w dziedzinie współrzędnych znormalizowanych
(
) (
) (
)
(
)
(
) (
) (
)
(
)
(
) (
) (
)
(
)
(
)
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ζ
η
ξ
ρ
d
d
d
z
y
x
z
y
x
z
y
x
e
T
e
e
,
,
det
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
1
1
1
1
1
1
J
N
N
M
⋅
⋅
⋅
=
∫ ∫ ∫
+
−
+
−
+
−
Zbiór elementów skończonych jako układ zachowawczy (pominięcie
rozproszenia energii) – macierzowe równanie Lagrange’a II rodzaju
f
q
q
q
=
∂
∂
+
∂
∂
−
∂
∂
⋅
U
T
T
dt
d
&
Energia kinetyczna układu
Energia potencjalna(sprężysta)
∑
∑
=
=
=
=
e
e
i
e
e
e
T
e
i
e
e
T
T
1
1
2
1
q
M
q
&
&
∑
∑
=
=
=
=
e
e
i
e
e
e
T
e
i
e
e
U
U
1
1
2
1
q
K
q
∑
=
×
=
e
i
e
n
n
e
1
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
M
M
∑
=
×
=
e
i
e
n
n
e
1
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
K
K
1
×
=
n
e
L
L
L
L
q
q
1
×
=
n
e
K
K
K
K
f
f
Uwaga:
1. Ten sam układ współrzędnych Oxyz dotyczy każdego elementu
skończonego nr e. Nie ma potrzeby stosowania
transformacji
2. Liczba stopni swobody układu n=3
×
i
w
(liczba węzłów)

Dla
0
f
=
równanie drgań swobodnych nietłumionych (własnych)
0
Kq
q
M
=
+
&
&
Równanie różniczkowe jednorodne – rozwiązanie ogólne
( )
( )
( )
t
t
ω
sin
0
q
q
=
( )
0
q
– wektor maksymalnych wychyleń (z uwzględnieniem znaku) z
położenia równowagi. Interpretacja: postać drgań własnych
Po podstawieniu otrzymamy, symetryczne zagadnienie własne:
(
)
( )
0
q
M
K
=
−
0
2
ω

z którego wyznaczamy:
w
i
i
i
⋅
=
3
,
,
1
,
0
K
ω
– częstości kołowe drgań własnych. Sens
obliczeniowy: pierwiastek z wartości własnej nr i
( )
w
i
i
i
⋅
=
3
,
,
1
,
0
K
q
– postacie drgań własnych odpowiadające
poszczególnym częstościom kołowym.
Sens obliczeniowy: wektory własne, których składowe są wyznaczane z
dokładnością do stałego czynnika. Konieczność
normowania
WYKŁAD 4A
Wyszukiwarka
Podobne podstrony:
MUM wykład12
MUM wykład10
MUM wykład7
MUM-wykład6
MUM wykład1
MUM wykład3
MUM wykład8
MUM wykład6
MUM wykład4a
MUM Wykład8a
Napęd Elektryczny wykład
więcej podobnych podstron