Modelowanie układów wielomasowych
Układy wielomasowe:
1. Skończona liczba brył sztywnych i
r
2. Bryły sztywne połączone są:
– biernymi elementami mechanicznymi lub elektromechanicznymi
(sprężyny, tłumiki)
– aktywnymi elementami mechanicznymi lub elektromechanicznymi
(napędy nastawcze, wzbudniki)
3. Na bryły sztywne mogą być nałożone więzy:
– geometryczne
– kinematyczne
4. Na bryłę sztywną nr r mogą działać siły zewnętrzne lub momenty sił
Założenia:
1. Ruch każdej bryły sztywnej opisywany jest w przestrzeni 3-wymiarowej za
pomocą 6 współrzędnych
2. Współrzędne opisujące ruch bryły sztywnej są mierzone w układzie
głównych centralnych osi bezwładności. Są one liniowo niezależne, mogą
być zatem uznane jako współrzędne uogólnione
Bryły sztywne zdefiniowane w ten sposób noszą nazwę: sztywne elementy
skończone (SES)
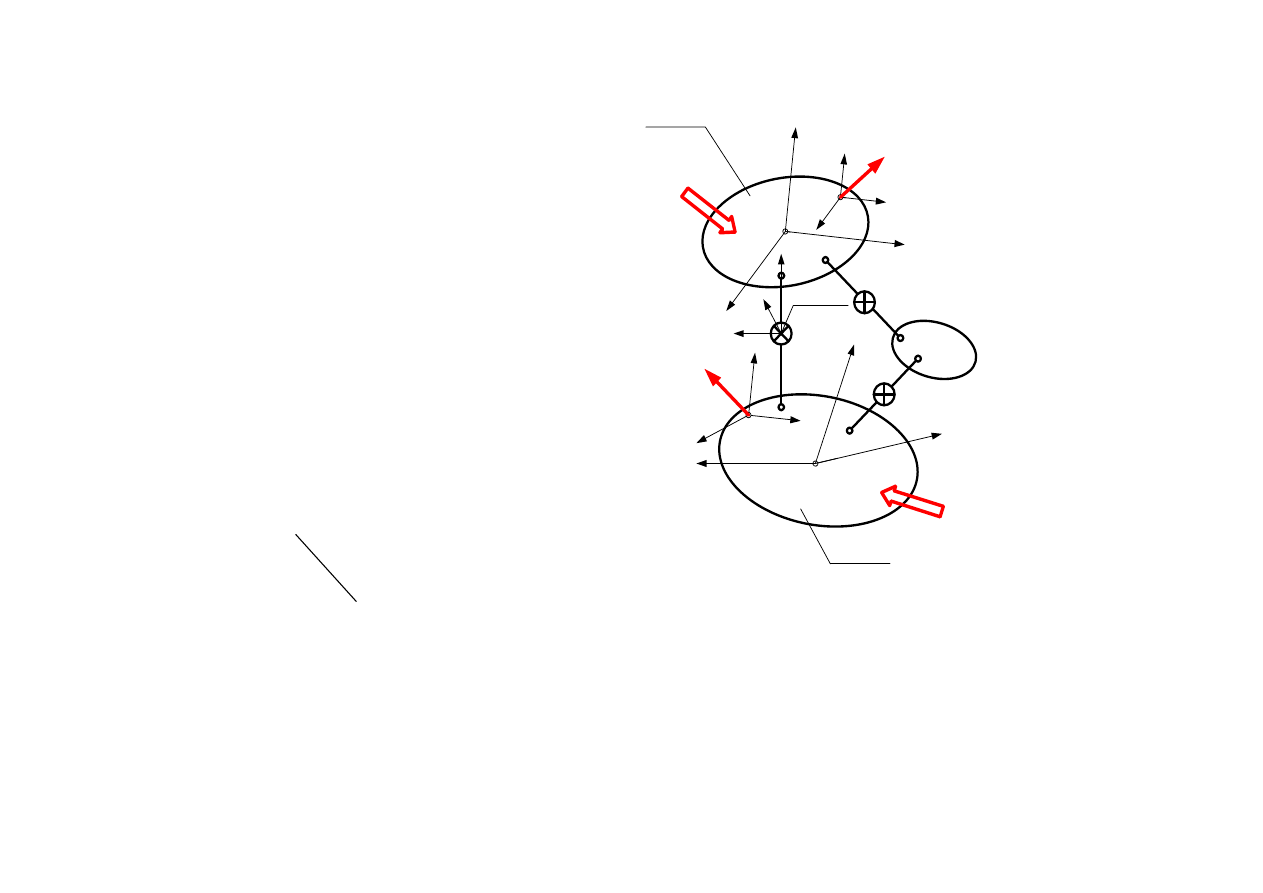
x
r1
SES nr r
x
r2
x
r3
O
r
z
r
κ
2
2
z
r
κ
2
3
z
r
κ
2
1
O
r
κ
F
r
κ
u
r
χ
z
p
κ
2
2
z
p
κ
2
3
z
p
κ
2
1
O
p
κ
F
p
κ
x
p2
x
p1
x
p3
u
p
χ
SES nr p
O
p
y
k1
y
k2
y
k3
EST nr k
O
k
Podobnie, wektor sił zewnętrznych
( )
6
,
...
,
1
,
=
==
i
f
col
ri
r
κ
F
x
r1
, x
r2
, x
r3
- układ głównych centralnych
osi bezwładności
q
r1
, q
r2
, q
r3
– przemieszczenia wzdłużne
q
r4
, q
r5
, q
r6
- kąty obrotu odpowiednio
wokół osi x
r1
, x
r2
, x
r3
Współrzędne uogólnione tej bryły
możemy zapisać w postaci wektora o
sześciu składowych:
( )
6
,
...
,
1
,
6
5
4
3
2
1
=
=
=
i
q
col
q
q
q
q
q
q
ri
r
r
r
r
r
r
r
q
Macierz kolumnowa (wektor)

Dla SES nr r definiujemy diagonalną macierz współczynników bezwładności
W przypadku bryły sztywnej o własnościach izotropowych otrzymamy:
m
r1
=m
r2
=m
r3
=m
r
masa SES nr r
m
r4
=I
r1
masowe momenty bezwładności względem
m
r5
=I
r2
poszczególnych głównych centralnych osi
m
r6
=I
r3
bezwładności SES nr r
[ ]
6
...,
,
1
,
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
6
6
6
5
4
3
2
1
=
=
=
×
i
m
diag
m
m
m
m
m
m
ri
r
r
r
r
r
r
r
M
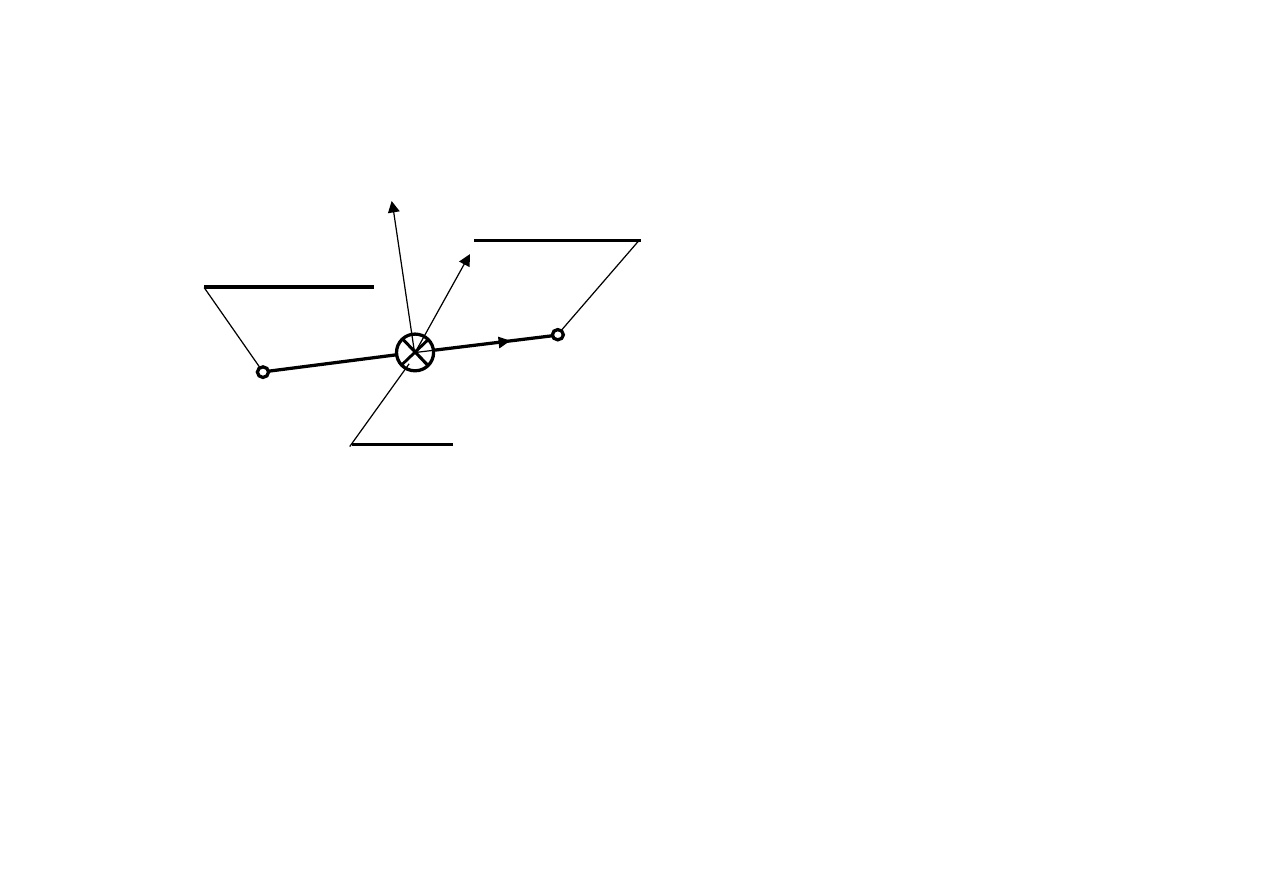
3. W układzie drgającym występuje i
k
elementów sprężysto–tłumiących
(EST) o następujących własnościach:
- dla EST nr k określamy diagonalną macierz współczynników sztywności
- dla EST nr k określamy diagonalną macierz współczynników tłumienia
[ ]
6
...,
,
1
,
=
=
i
L
diag
ki
k
L
- EST nr k łączy SES nr r z SES nr p
-
EST doznaje odkształceń w
sześciu kierunkach uogólnionych
mierzonych zgodnie z przyjętym
układem współrzędnych y
k1
y
k2
y
k3
[ ]
6
...,
,
1
,
=
=
i
K
diag
ki
k
K
EST nr k
Punkt zamocowania
do SES nr r
Punkt zamocowania
do SES nr p
y
k3
y
k2
y
k1

- punkt EST nr k dołączony do SES nr r doznaje przemieszczeń (mierzonych
w układzie y
k1
y
k2
y
k3
), których stan możemy określić za pomocą wektora
w
rk
= col (w
rki
) i= 1, …, 6
Podobnie definiujemy wektor przemieszczeń punktu zamocowania do SES
nr p:
w
pk
= col (w
pki
) i=1, …, 6
- dla EST nr k określamy macierz współrzędnych zamocowania do SES nr r,
mierzonych w układzie współrzędnych x
r1
x
r2
x
r3
tego SES:
−
−
−
=
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
1
2
1
3
2
3
rk
rk
rk
rk
rk
rk
rk
s
s
s
s
s
s
S

oraz, w sposób analogiczny, macierz współrzędnych zamocowania do SES
nr p.
- dla EST nr k określamy macierz kosinusów kierunkowych kątów między
osiami układu współrzędnych y
k1
y
k2
y
k3
a osiami x
r1
x
r2
x
r3
:
=
*
*
rk
rk
rk
Θ
0
0
Θ
Θ
gdzie:
[
]
.
3
,
2
,
1
,
,
cos
3
3
*
=
=
×
j
i
rkij
rk
α
Θ
jest macierzą kosinusów kątów między osiami: y
ki
i x
rj
.
Dla EST nr k określony wektor różnic przemieszczeń końców:

[
]
−
=
−
=
p
r
pk
pk
rk
rk
pk
rk
k
q
q
S
Θ
S
Θ
w
w
∆w
M
oraz wektor różnic prędkości jego końców:
[
]
−
=
−
=
p
r
pk
pk
rk
rk
pk
rk
k
q
q
S
Θ
S
Θ
w
w
w
∆
&
&
M
&
&
&
Wektor sił zewnętrznych SES nr r zredukowanych do środka masy
,
1
)
(
∑
=
=
κ
κ
κ
κ
κ
r
i
r
T
r
T
r
Z
r
F
Θ
S
F
W SES nr r magazynowana jest energia kinetyczna, którą możemy opisać
zależnością:
Forma kwadratowa
r
r
T
r
r
T
q
M
q
&
&
2
1
=

Energia potencjalna sił sprężystości magazynowana jest w EST nr k. Energię tę
Funkcję rozproszenia energii (dyssypacji) w EST wyrażamy zależnością:
Można wykazać (patrz literatura), że dla układu o skończonej liczbie stopni
swobody = n, poszczególne funkcje energetyczne są opisane zależnościami:
k
k
T
k
k
U
∆w
K
∆w
2
1
=
q
L
q
Kq
q
q
M
q
&
&
&
&
T
T
T
D
U
T
2
1
2
1
2
1
=
=
=
k
k
T
k
k
D
w
∆
L
w
∆
&
&
2
1
=

M – macierz bezwładności układu wielomasowego
L – macierz tłumienia układu wielomasowego
K – macierz sztywności układu wielomasowego
q – wektor współrzędnych uogólnionych układu wielomasowego
przy czym:
∑
=
×
=
r
i
r
n
n
r
1
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
M
M
,
n
n
i
k
pk
pk
k
T
pk
T
pk
rk
rk
k
T
pk
T
pk
pk
pk
k
T
rk
T
rk
rk
rk
k
T
rk
T
rk
k
×
=
∑
−
−
=
1
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
S
Θ
L
Θ
S
S
Θ
L
Θ
S
S
Θ
L
Θ
S
S
Θ
L
Θ
S
L
,

n
n
i
k
pk
pk
k
T
pk
T
pk
rk
rk
k
T
pk
T
pk
pk
pk
k
T
rk
T
rk
rk
rk
k
T
rk
T
rk
k
×
=
∑
−
−
=
1
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
S
Θ
K
Θ
S
S
Θ
K
Θ
S
S
Θ
K
Θ
S
S
Θ
K
Θ
S
K
1
×
=
n
p
r
L
L
L
q
q
q
,
,
1
)
(
∑
=
=
r
i
r
Z
r
K
K
K
K
F
f
Stosując równania Lagrange’a II rodzaju
,
f
q
q
q
q
=
∂
∂
+
∂
∂
+
∂
∂
−
∂
∂
U
D
T
T
dt
d
&
&
otrzymamy
f
Kq
q
L
q
M
=
+
+
&
&
&

Uwagi dotyczące wyznaczania macierzy M, L oraz K:
– w prostych przypadkach możemy korzystać z zależności matematycznych
podawanych w literaturze
– w przypadkach znacznej liczby stopni swobody korzystamy ze
specjalistycznego oprogramowania (np. AMESim). Wówczas rola
użytkownika sprowadza się jedynie do podania parametrów poszczególnych
SES oraz EST, oraz sposobu ich połączenia.
Wyszukiwarka
Podobne podstrony:
MUM wykład12
MUM wykład10
MUM wykład7
MUM-wykład6
MUM wykład1
MUM wykład4
MUM wykład8
MUM wykład6
MUM wykład4a
MUM Wykład8a
Napęd Elektryczny wykład
więcej podobnych podstron