
Wybrane zagadnienia projektowania układów sterowania
Projektowanie układu sterowania polega na takim doborze biegunów układu
sterowanego opisanego równaniem:
(
)
(
)
Dz
x
BR
I
A
y
−
⋅
−
≡
−
−
sT
R
e
s
1
przy czym macierz stanu układu sterowanego ma postać
A
BR
A
+
=
−
sT
R
e
aby układ sterowania spełniał określone kryteria jakości.
Problem matematyczny: zadanie odwrotne do rozwiązania równania
(
)
0
det
=
−
s
R
I
A
umożliwiającego wyznaczenie wartości własnych macierzy stanu układu
sterowanego A
R
Sformułowanie ogólne: optymalizacja dynamiczna
Dobór biegunów układu sterowania na podstawie
wybranych kryteriów oceny jakości
1. Ocena stanów ustalonych:
a) stabilność
b) dokładność statyczna (uchyb statyczny)
2. Ocena stanów nieustalonych sygnałów UAR.
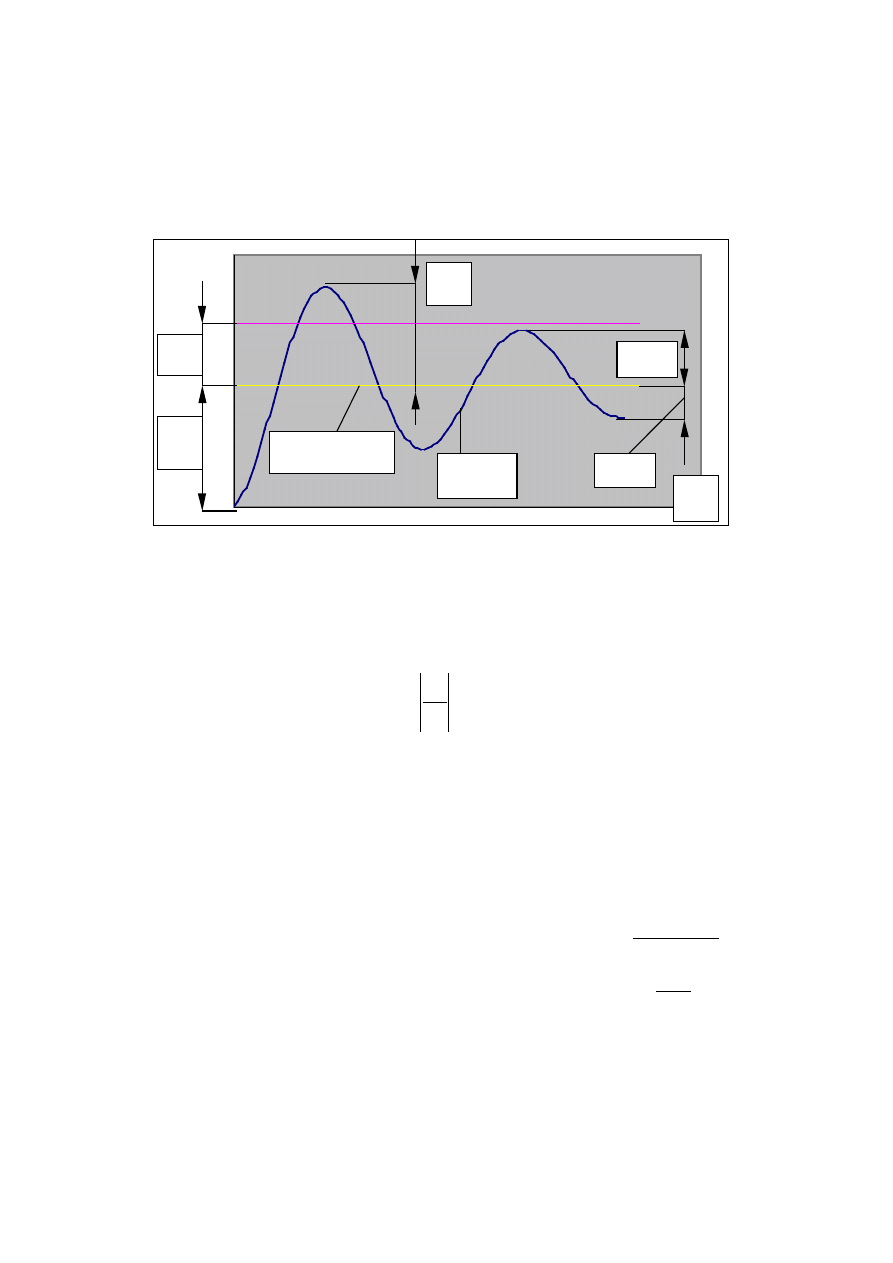
Rozważmy proces nieustalony układu sterowania, w trakcie którego, w wyniku
sterowania sygnałem
)
(
)
(
t
t
u
σ
≡
obserwujemy przebieg zmienny w czasie x(t).
Wartość ustalona tego przebiegu
S
x
.
a) przesterowanie (przeregulowanie ) – określamy jako bezwzględną wartość z
ilorazu pierwszej amplitudy przebiegu nieustalonego i wartości ustalonej
tego przebiegu.
%
100
1
⋅
=
S
x
x
κ
b) czas regulacji (sterowania) – jest to czas po którym warto
ść
ε
ε
+
<
<
−
S
S
x
t
x
x
)
(
.
ε
- bł
ą
d sterowania przyjmowany arbitralnie.
Przykład. Dla obiektu sterowania o transmitancji operatorowej
( )
10
4
1
2
+
+
=
s
s
s
K
S
zaprojektować sterownik PID o transmitancji operatorowej
⋅
+
⋅
+
=
s
T
s
T
k
s
K
d
i
p
R
1
1
)
(
tak, aby:
– uchyb statyczny
e
s
= 0
– przesterowanie
05
,
0
≤
κ
– czas sterowania
t
s
< 1,5 s, przy błędzie
ε
nie przekraczającym 2 %.
x
S
e
S
x
1
ε
+
ε
−
x(t)
)
(
)
(
t
t
u
σ
≡
t

Rozwiązanie. Transmitancja operatorowa układu zamkniętego
+
+
⋅
+
+
+
+
+
⋅
+
+
=
s
T
s
T
k
s
s
s
T
s
T
k
s
s
s
K
d
i
p
d
i
p
z
1
1
10
4
1
1
1
1
10
4
1
)
(
2
2
Po uporządkowaniu i dokonaniu podstawień
i
p
i
T
k
k
=
d
p
d
T
k
k
=
otrzymujemy
(
)
(
)
i
p
d
i
p
d
z
k
k
s
k
s
s
k
s
k
s
k
s
K
+
+
+
+
+
+
+
=
10
4
)
(
2
3
2
Mianownik transmitancji K
z
(s) jest wielomianem 3-go stopnia, który posiada 3 pierwiastki
będące biegunami s
1
, s
2
, s
3
transmitancji K
z
(s). Możemy zatem zapisać:
(
)
(
)
(
)(
)(
)
3
2
1
2
3
10
4
s
s
s
s
s
s
k
k
s
k
s
s
i
p
d
−
−
−
=
+
+
+
+
+
Pierwsze dwa bieguny wyznaczymy z odpowiedzi skokowej układu, tzn.
(
)
0
2
2
2
2
2
1
sin
1
1
1
1
sin
1
1
0
ϕ
ω
ζ
ζ
ζ
ζ
ω
ζ
ζ
ζω
ϕ
ζω
+
−
⋅
−
−
=
−
+
−
⋅
−
−
=
−
−
t
e
arctg
t
e
y
n
t
n
t
n
n
4
4 3
4
4 2
1
Przyjmując czas osiągnięcia 1-go maksimum (przesterowanie)
2
1
ζ
ω
π
κ
−
=
′
n
t
oraz
κ
=
−
1
1
y
, otrzymamy
κ
ζ
κ
ζω
=
−
′
−
2
1
t
n
e
K
R
(s)
K
S
(s)
•
+
–
Następnie
κ
ζ
ζ
ω
π
ζω
=
−
−
−
2
1
1
2
n
n
e
κ
ζ
πζ
≅
−
−
2
1
e
a po przekształceniu
κ
π
κ
ζ
2
2
ln
ln
+
=
Podstawiając dane liczbowe
69
,
0
05
,
0
ln
05
,
0
ln
2
2
=
+
=
π
ζ
n
s
s
arctg
t
t
ω
ζ
ζ
ζ
2
2
1
1
−
−
+
=
′
ε
ζ
ζω
=
−
′
−
2
1
s
n
t
e
−
=
′
2
1
1
ln
ζ
ε
ζω
s
n
t
−
′
=
2
1
1
ln
1
ζ
ε
ζ
ω
s
n
t
Ponieważ
s
s
t
t
>
′
, przyjęcie
s
t
s
5
,
1
=
′
oznacza, że
t
s
<1,5 s.
s
rad
n
/
09
,
4
69
,
0
1
02
,
0
1
ln
5
,
1
69
,
0
1
2
=
−
⋅
=
ω
Bieguny mają postać:
2
2
/
1
1
ζ
ω
ζω
−
±
−
=
n
n
j
s
czyli:
s
rad
j
s
rad
s
/
96
,
2
/
82
,
2
2
/
1
±
−
=
Obliczamy wyrażenie
(
)(
)
74
,
16
65
,
5
2
2
1
+
+
=
−
−
s
s
s
s
s
s
Trzeci biegun przyjmujemy arbitralnie tak, aby jego część rzeczywista była znacznie mniejsza
od dwóch pozostałych, np. s
3
= –10. Wówczas nie wpływa on w istotny sposób na własności
układu sterowania.
A zatem
(
)(
)(
)
(
)
(
)
4
,
167
24
,
73
65
,
15
10
74
,
16
65
,
5
2
3
2
3
2
1
+
+
+
=
+
+
+
=
−
−
−
s
s
s
s
s
s
s
s
s
s
s
s

Następnie, należy porównać współczynniki mianownika transmitancji K
z
(s) oraz otrzymanego
wielomianu 3-go stopnia
(
)
(
)
4
,
167
24
,
73
65
,
15
10
4
2
3
2
3
+
+
+
=
+
+
+
+
+
s
s
s
k
k
s
k
s
s
i
p
d
Stąd otrzymujemy
k
d
=11,65
k
p
=63,24
oraz k
i
=167,4
oraz transmitancję operatorową sterownika
( )
s
s
s
s
K
R
4
,
167
24
,
63
65
,
11
2
+
+
=
Układ z zaprojektowanym sterownikiem spełnia warunki zadania, ponieważ:
– uchyb statyczny
( )
0
1
0
1
=
−
=
−
=
i
i
z
s
k
k
K
e
– przesterowanie
κ
= 4,9 %
– t
s
= 0,605 s
Obiekt sterowania (układ otwarty) bieguny: –2
±
2,45j
Układ ze statycznym sprzężeniem zwrotnym k=1 bieguny: –2
±
2,65j
Układ ze statycznym sprzężeniem zwrotnym k=90 bieguny: –2
±
9,8j
Układ ze sterownikiem PID
bieguny: –2,82
±
2,96j, –10
zera:
–2,71
±
2,65j
(miejsca zerowe licznika transmitancji K
z
(s))
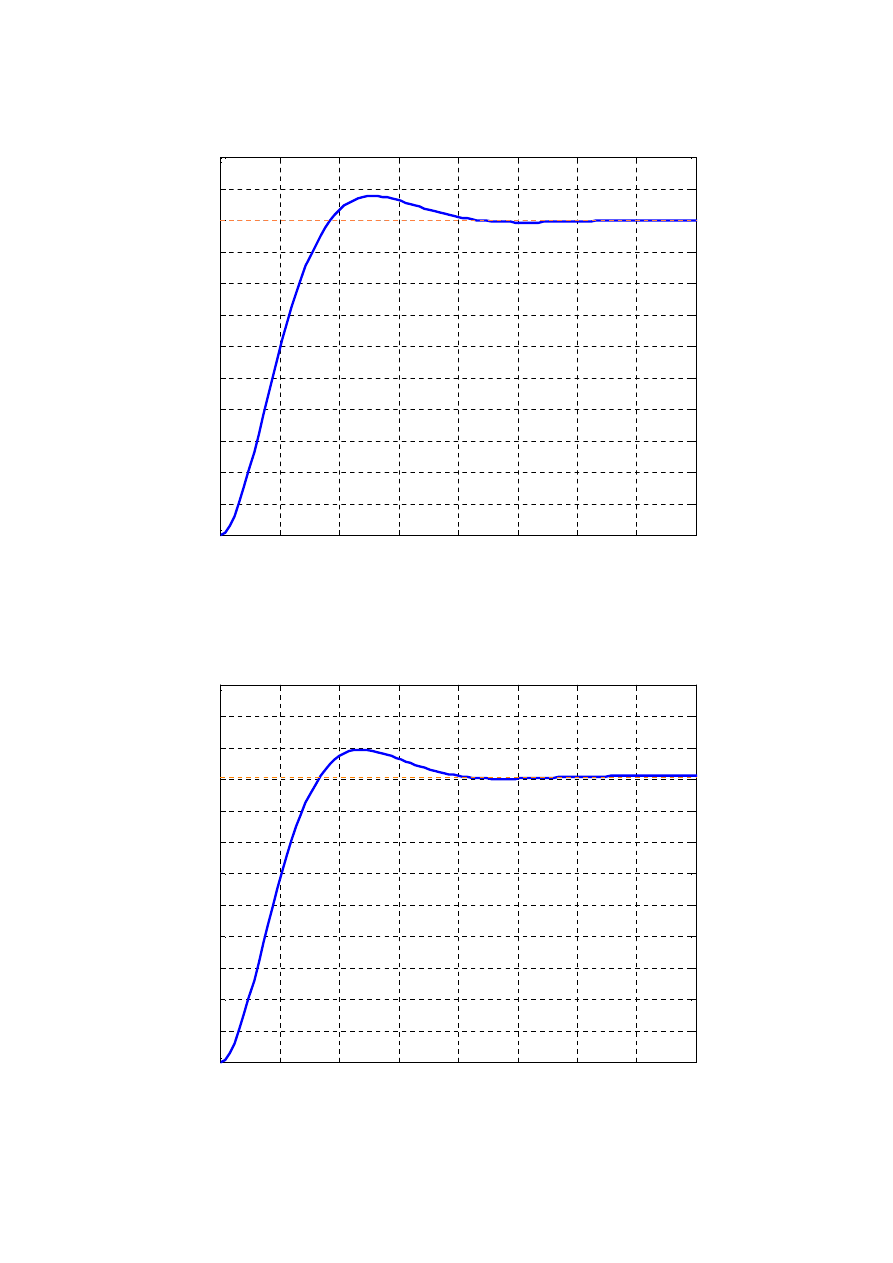
Odpowiedz skokowa obiektu
0
0.5
1
1.5
2
2.5
3
3.5
4
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
0.11
0.12
t [s]
Odpowiedz skokowa ukladu ze sprzezeniem zwrotnym, K=1
0
0.5
1
1.5
2
2.5
3
3.5
4
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
0.11
0.12
t [s]
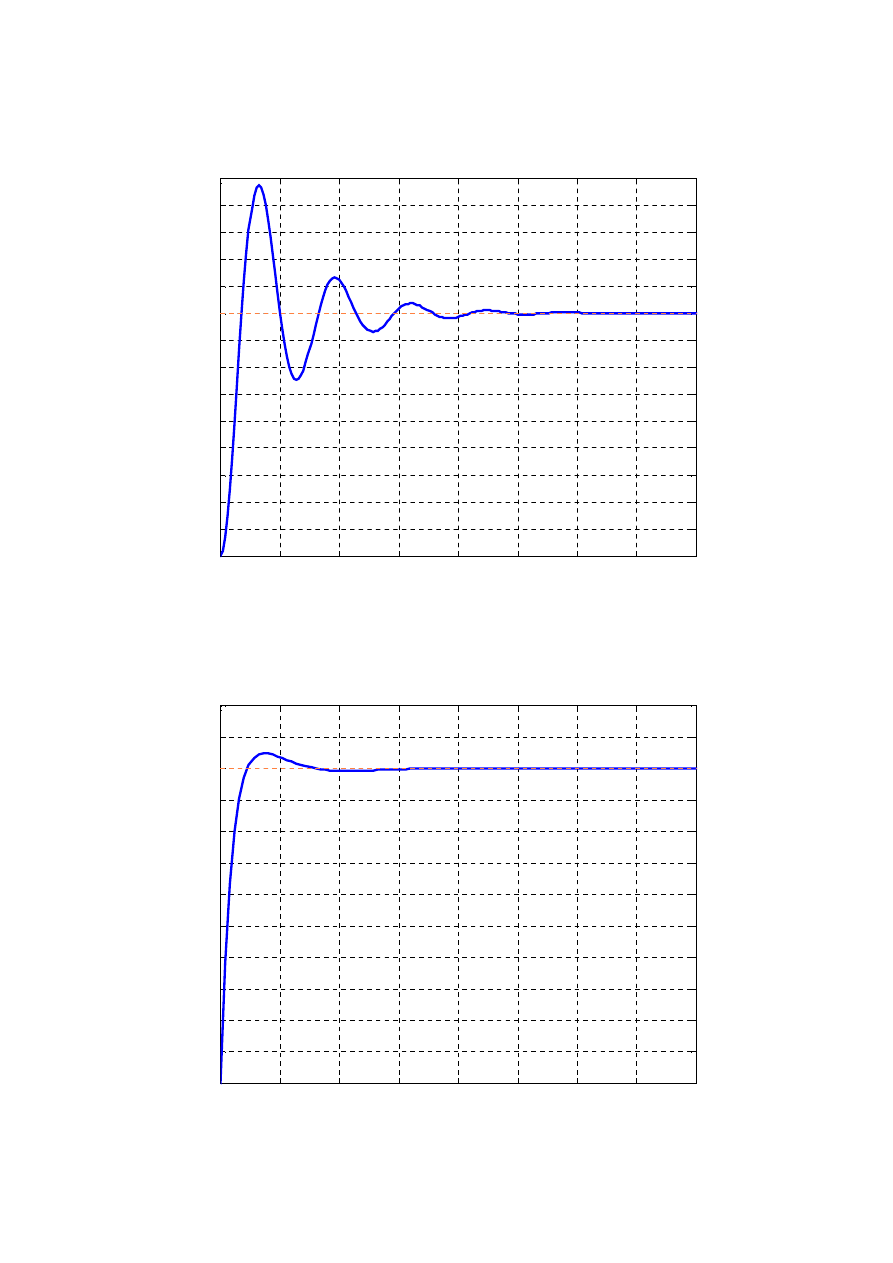
Odpowiedz skokowa ukladu ze sprzezeniem zwrotnym, K=90
0
0.5
1
1.5
2
2.5
3
3.5
4
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
t [s]
Odpowedz skokowa ukladu zamknietego ze sterownikiem PID
0
0.5
1
1.5
2
2.5
3
3.5
4
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
t [s]
Wyszukiwarka
Podobne podstrony:
MUM wykład12
MUM wykład7
MUM-wykład6
MUM wykład1
MUM wykład4
MUM wykład3
MUM wykład8
MUM wykład6
MUM wykład4a
MUM Wykład8a
Napęd Elektryczny wykład
więcej podobnych podstron