WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.1

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

3.1. Zasady dynamiki Newtona

Siłą nazywamy wektorową wielkość, która jest miarą mechanicznego oddziaływania na ciało ze

strony innych ciał. W dalszej części będziemy rozpatrywać tylko oddziaływanie pomiędzy ciałami będącymi
w bezpośrednim kontakcie. Siły, tak jak wielkości wektorowe, będziemy oznaczać czcionką pogrubioną
natomiast wartości sił czcionką normalną.

Siła, podobnie jak wektor, jest określona jednoznacznie przez swoją wartość bezwzględną (długość),

kierunek w przestrzeni, zwrot i punkt przyłożenia. Dla obliczeń nie będzie jednak miało większego znacze-
nia to, że siła może się poruszać na prostej pokrywającej się się z kierunkiem jej działania.

Pierwsza zasada Newtona mówi, że jeżeli na ciało nie działa żadna siła lub jeżeli siły się równoważą

(ich suma wektorowa wynosi zero) to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym
prostoliniowym.

Druga zasada dynamiki Newtona jest podstawowym prawem dynamiki. Orzeka ona jak zmienia się

ruch ciała pod wpływem przyłożonych do niego sił. W sensie matematycznym możemy je zapisać w postaci

a

=

F

m

,

(3.1)

w którym F oznacza siłę działającą na ciało, m oznacza masę ciała natomiast a oznacza przyśpieszenie ciała.
Przyśpieszenie ciała możemy zapisać jako

a

=

d v

dt

,

(3.2)

w którym v oznacza prędkość ciała natomiast t oznacza czas. Warto zauważyć, że prędkość oraz
przyśpieszenie ciała są wielkościami wektorowymi. Jeżeli siła działająca na ciało jest wektorem zerowym to
i przyśpieszenie tego ciała wynosi zero. Jak widać jest to treść pierwszej zasady dynamiki.

Trzecia zasada dynamiki Newtona mówi, że dwa ciała oddziaływują ze sobą siłami, które są sobie

równe co do wartości i działające na tej samej prostej, lecz mają przeciwne zwroty. Jeżeli F

12

jest siłą

wywieraną przez pierwsze ciało na drugie, a F

21

jest siłą wywieraną przez drugie ciało na pierwsze to trzecią

zasadę dynamiki możemy zapisać w postaci wektorowej

F

12

=−

F

21

.

(3.3)

której graficzną interpretację przedstawia rysunek 3.1

1

2

F

21

F

12

Rys. 3.1. Graficzna interpretacja trzeciej zasady dynamiki Newtona

3.2. Siła wypadkowa układu sił nierównoległych na płaszczyźnie

W dalszej części naszego kursu Wytrzymałości materiałów z podstawami Mechaniki budowli będzie-

my rozpatrywali siły, które działają na jednej płaszczyźnie.

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.2

Dwie dowolne nierównoległe siły P

1

i P

2

możemy sprowadzić do siły wypadkowej, która jest ich

sumą wektorową

W

=

P

1



P

2

.

(3.4)

Kierunek działania siły wypadkowej W przechodzi przez punkt przecięcia się kierunków sił P

1

i P

2

natomiast jej długość jest równa przekątnej równoległoboku zbudowanego na siłach P

1

i P

2.

Położenie,

kierunek, wartość i zwrot siły wypadkowej W przedstawia rysunek 3.2.

P

1

P

2

P

2

P

1

W

W

Rys. 3.2. Siła wypadkowa z dwóch nierównoległych sił

Jeżeli mielibyśmy układ trzech nierównoległych sił P

1

, P

2

i P

3

. To najpierw możemy znaleźć siłę

wypadkową W

1

z sił P

1

i P

2

w sposób opisany powyżej a następnie znaleźć siłę wypadkową z sił W

1

i P

3

.

Możemy więc zapisać wektorowo

W

1

=

P

1



P

2

,

(3.5)

W=P

1



P

2



P

3

=

W

1



P

3

.

(3.6)

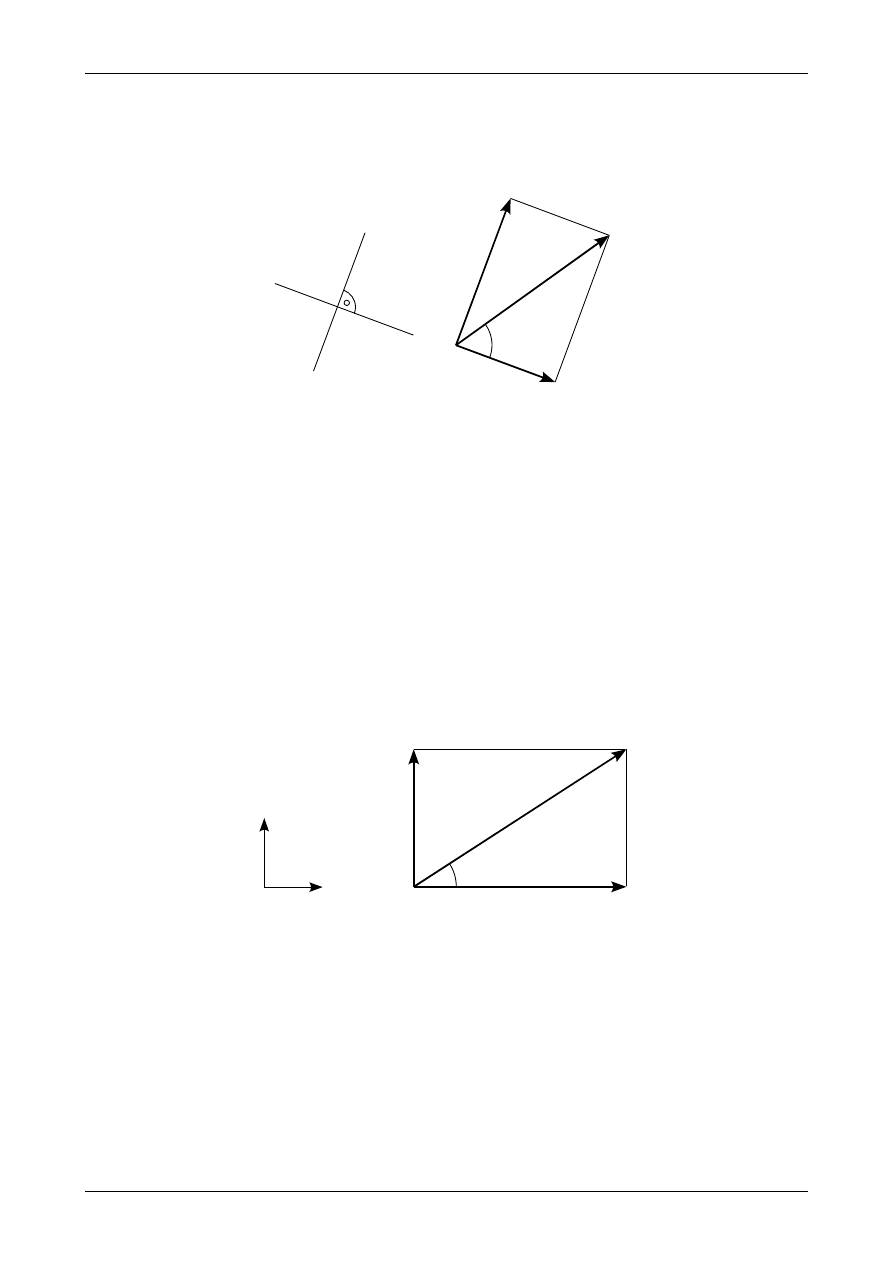
Graficzną interpretację siły wypadkowej z układu trzech nierównoległych sił P

1

, P

2

i P

3

przedstawia

rysunek 3.3.

W

P

1

P

2

P

2

P

1

W

1

W

1

W

1

P

3

W

P

3

Rys. 3.3. Siła wypadkowa z układu trzech nierównoległych sił

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.3

Jeżeli układ sił składałby się z więcej niż trzech nierównoległych sił aby znaleźć siłę wypadkową

najpierw składamy dwie dowolne siły a następnie ich wypadkową składamy z trzecią siłą i tak dalej.

3.3. Analityczne rozkładanie sił

P

a

b

α

P

b

P

a

Rys. 3.4. Składowe siły P

Najczęściej będziemy rozkładali siły na dwa kierunki, które są wzajemnie do siebie prostopadłe. Ry-

sunek 3.4 przedstawia siłę P, którą rozkładamy na dwie siły składowe po kierunkach a i b. Wartości sił
składowych wynoszą

P

a

=

P

⋅

cos







,

(3.7)

P

b

=

P⋅sin







.

(3.8)

Jako dodatnią siłę składową określimy tą siłę, której zwrot jest zgodny z przyjętym dodatnim kierun-
kiem.

P

X

Y

P

X

P

Y

α

Rys. 3.5. Rozkład siły P na składową poziomą i pionową

Rysunek 3.5 przedstawia najczęściej występujący rozkład siły P na dwa kierunki: poziomy zgodny ze

zwrotem osi X oraz pionowy zgodny ze zwrotem osi Y. Wartości składowych siły P wyznaczymy ze wzorów

P

X

=

P⋅cos







,

(3.9)

P

Y

=

P⋅sin







.

(3.10)

Ponieważ obie składowe mają zwroty zgodne ze zwrotami osi X i Y więc obie będą dodatnie.

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.4

3.4. Moment siły względem punktu

P

r

M

O

Π

O

P

r

O

M

O

α

180

O

-

α

a

a)

b)

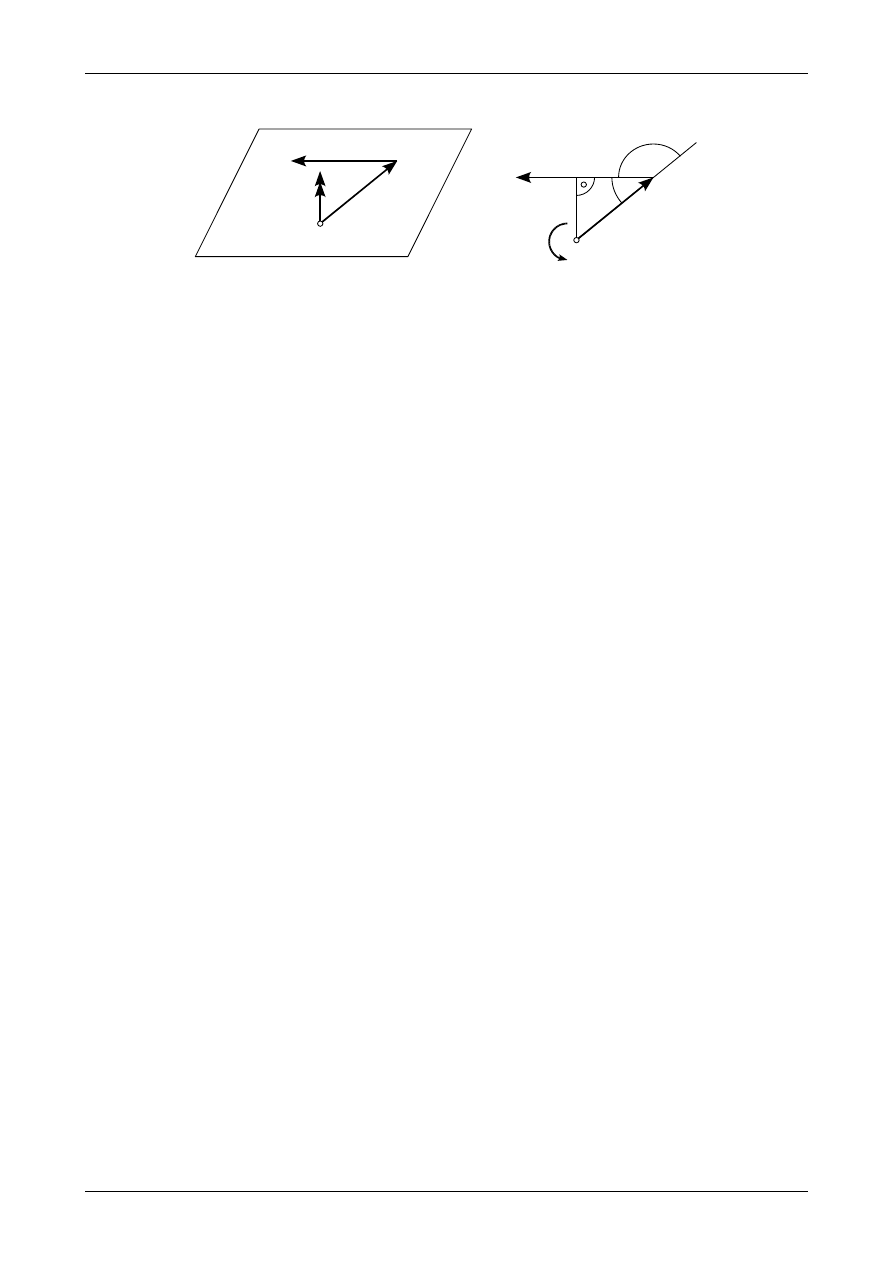
Rys. 3.6. Moment siły P względem punktu O

Zakładamy, że siła P działa na płaszczyźnie

Π

przedstawionej na rysunku 3.6. Na płaszczyźnie tej

znajduje się punkt O nie leżący na prostej działania siły P. Statycznym momentem siły P względem
punktu O nazywamy iloczyn wektorowy

M

O

=

r

×

P

,

(3.11)

w którym wektor r jest wektorem wodzącym siły P. Jak widać na rysunku 3.6 a) wektor M

O

jest prostopadły

do płaszczyzny

Π

a jego zwrot jest zgodny z kierunkiem wkręcania się śruby prawoskrętnej kręcącej się od

wektora wodzącego r do wektora siły P. Rysunek 3.6 b) przedstawia widok z góry na płaszczyznę

Π

. Wektor

momentu siły M

O

został zastąpiony strzałką. Wartość momentu siły względem punktu O wynosi

M

O

=

r

⋅

P

⋅

sin



180 °

−





=

r

⋅

P

⋅

sin







,

(3.12)

którą możemy zapisać jako

M

O

=

P

⋅

a

,

(3.13)

w którym a oznacza odległość siły P od punktu O na płaszczyźnie natomiast P oznacza wartość siły. O tym
czy jest to moment dodatni czy ujemny decyduje kierunek obrotu siły względem punktu. Jeżeli obrót
następuje zgodnie z ruchem wskazówek zegara to będziemy taki moment przyjmować jako dodatni.
Jeżeli przeciwnie do ruchu wskazówek zegara będziemy taki moment przyjmować jako moment
ujemny.

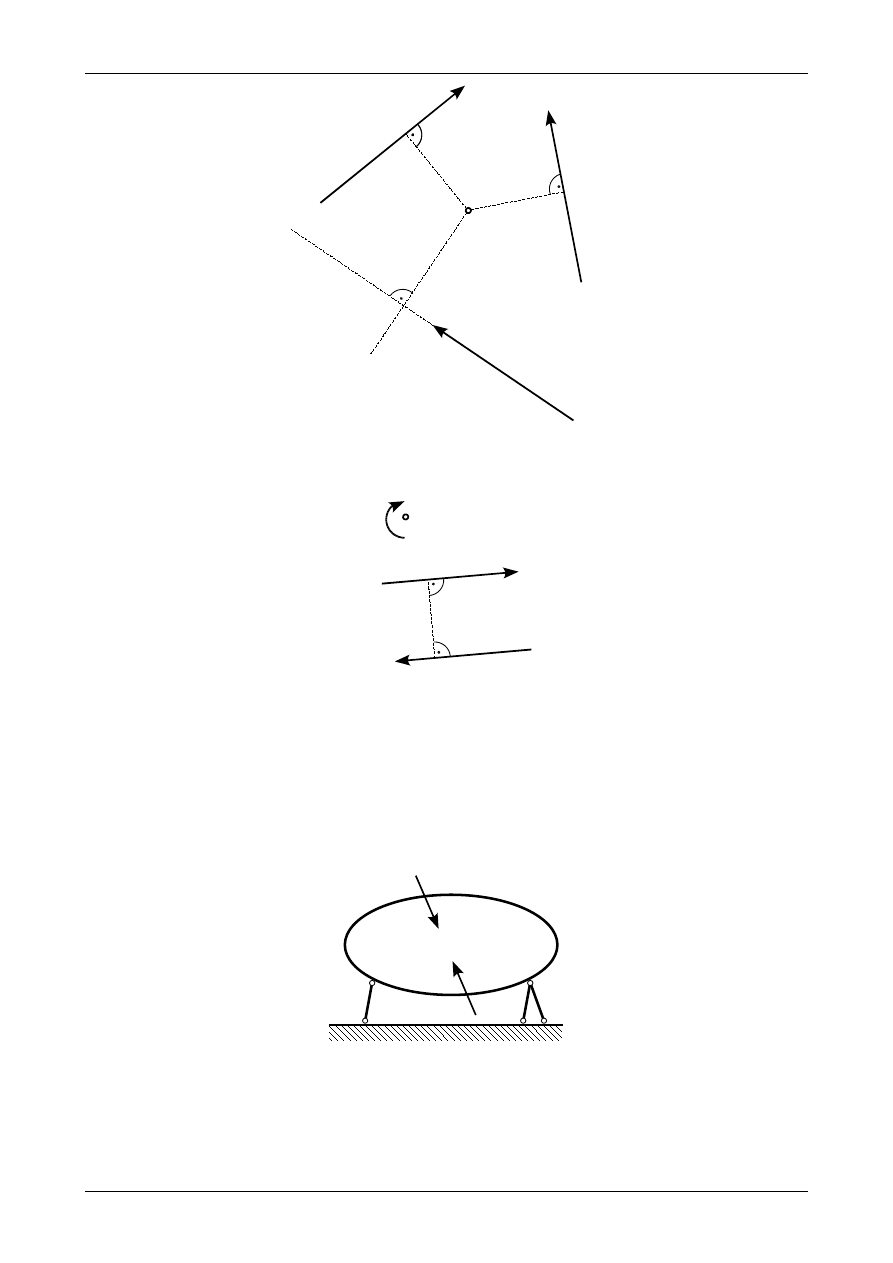
Moment kilku sił względem punktu jest sumą momentów od poszczególnych sił. Na rysunku 3.7

przedstawione są trzy siły, których moment względem punktu O ma wartość

M

O

=

P

1

⋅

a

1

−

P

2

⋅

a

2



P

3

⋅

a

3

.

(3.14)

Siła P

2

obraca się przeciwnie do ruch wskazówek zegara względem punktu O więc jej moment jest ujemny.

Parą sił nazywamy układ dwóch sił o takich samych wartościach, kierunkach równoległych do siebie

lecz przeciwnych zwrotach. Wartość momentu pary sił względem dowolnego punktu O wynosi

M

O

=

P⋅a

,

(3.15)

w którym a jest odległością sił od siebie. Jak widać moment pary sił nie zależy od położenia punktu O.
Rysunek 3.8 przedstawia parę sił. Moment M

O

jest dodatni.

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.5

O

P

1

P

2

P

3

a

1

a

2

a

3

Rys. 3.7. Moment układu trzech sił

P

P

O

a

M

O

Rys. 3.8. Moment pary sił

3.5. Reakcje w więzach

Rysunek 3.9 przedstawia geometrycznie niezmienną i statycznie wyznaczalną tarczę sztywną, na którą

działa siła P. Siła ta może być wypadkową wielu sił działających na daną tarczę. Siły działające na tarczę,
których wypadkową może być siła P nazywamy siłami czynnymi.

P

R

1

2

3

I

Rys. 3.9. Siły działające na tarczę sztywną

Tarcza sztywna jest geometrycznie niezmienna, czyli nie porusza się więc zgodnie z pierwszą zasadą

dynamiki siły działające na tarczę muszą się równoważyć czyli ich siła wypadkowa musi się równać zero.
Wynika z tego, że na tarczę sztywną musi działać jeszcze jedna siła. Wynika to także z trzeciej zasady
dynamiki. Jeżeli tarcza sztywna działa na tarczę podporową siłą P to tarcza podporowa musi działać na

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.6

tarczę sztywną siłą działającą na tej samej prostej, o tej samej wartości lecz przeciwnym zwrocie. Siły,
którymi tarcza podporowa działa na tarczę sztywną nazywamy siłami biernymi lub reakcjami. Wartość
reakcji R musi więc spełniać warunek

R=P

.

(3.16)

Reakcje przekazują się z tarczy podporowej poprzez więzy. Reakcja R jest więc wypadkową z reakcji

działających we wszystkich więzach tarczy sztywnej.

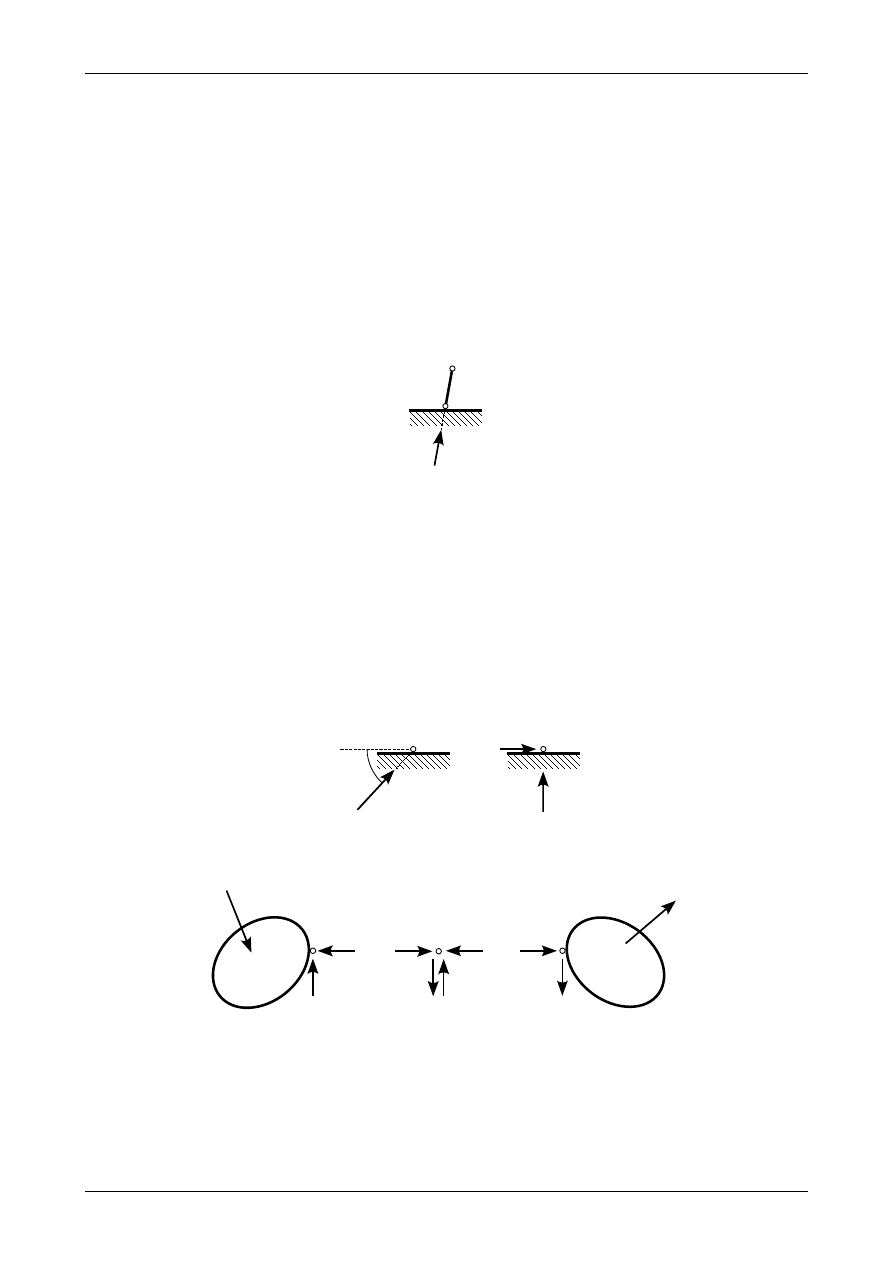
W pręcie podporowym będzie działała jedna reakcja, przedstawiona na rysunku 3.10, której kierunek

pokrywa się z prętem podporowym. Jedyną niewiadomą jest w tym przypadku wartość reakcji w tym więzie.
Ma to związek z tym, że pręt podporowy odbiera tarczy sztywnej jeden stopnień swobody.

1

R

1

Rys. 3.10. Reakcja w pręcie podporowym

W przegubie rzeczywistym działa także jedna reakcja, której kierunek przechodzi przez ten przegub

jednak w przeciwieństwie do pręta podporowego nie znamy jego kąta nachylenia. Możemy więc stwierdzić,
że w przegubie rzeczywistym będziemy mieli dwie niewiadome: wartość reakcji oraz kąt nachylenia
kierunku tej reakcji. Ma to związek z tym, że przegub odbiera tarczy sztywnej dwa stopnie swobody.
Przedstawia to rysunek 3.11 a). Ze względów obliczeniowych korzystniej jest rozłożyć reakcję w przegubie
rzeczywistym na dwie składowe H

A

oraz V

A

i wyznaczenie wartości i zwrotów obu składowych. Przedstawia

to rysunek 3.11 b).

A

R

A

α

A

V

A

H

A

a)

b)

Rys. 3.11. Reakcja w przegubie rzeczywistym

A

I

II

P

1

P

2

A

V

A

(I)

V

A

(II)

H

A

(I)

H

A

(II)

A

H

A

(I)

V

A

(I)

H

A

(II)

V

A

(II)

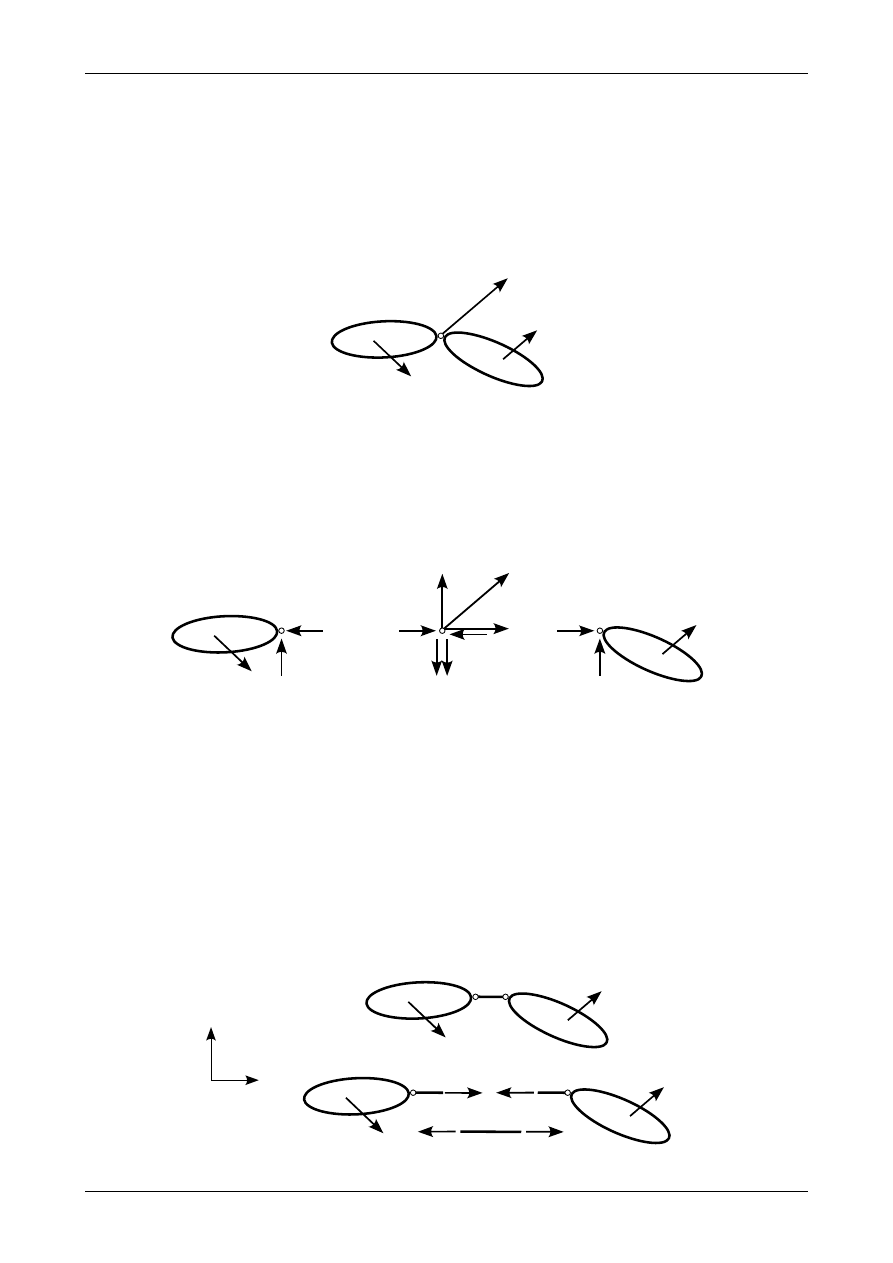
Rys. 3.12. Reakcje w przegubie rzeczywistym łączącym dwie tarcze sztywne nie będące podporowymi

Jeżeli przegub rzeczywisty łączy dwie tarcze sztywne, z których żadna nie jest tarczą podporową to

w przegubie na każdą z tarcz sztywnych działają dwie składowe reakcji mające parami te same wartości
i kierunek ale przeciwne zwroty. Przedstawia je rysunek 3.12. Ich suma wektorowa wynosi oczywiście zero.
Czyli jeżeli rozpatrujemy obie tarcze razem to w przegubie nie działa żadna reakcja, jeżeli rozdzielimy je to
w przegubie mamy po dwie składowe reakcji. Wartości ich spełniają warunki

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.7

{

H

A



I



−

H

A



II



=

0⇒ H

A



I



=

H

A



II



−

V

A



I





V

A



II



=

0⇒V

A



I



=

V

A



II



.

(3.17)

Rysunek 3.13 przedstawia przegub rzeczywisty A łączący dwie tarcze sztywne, nie będące podporo-

wymi, numer I i II. Na tarczę sztywną numer I działa siła czynna P

1

natomiast na tarczę sztywną numer II

działa siła czynna P

2

. Ponadto w przegubie rzeczywistym działa siła czynna P.

I

II

P

1

P

2

A

P

Rys. 3.13. Siła czynna działająca w przegubie rzeczywistym

W takim przypadku musimy osobno rozpatrywać równowagę tarcz sztywnych numer I i II oraz

równowagę przegubu rzeczywistego A. Rysunek 3.14 przedstawia siły czynne i bierne działające na każdą
z tarcz sztywnych oraz na przegub rzeczywisty.

A

A

V

A

(I)

V

A

(II)

H

A

(I)

H

A

(II)

I

II

P

1

P

2

A

P

H

A

(I)

V

A

(I)

H

A

(II)

V

A

(II)

P

X

P

Y

Rys. 3.14. Reakcje działające na tarcze sztywne i przegub rzeczywisty

Siłę czynną P rozkładamy na dwie siły składowe: poziomą P

X

oraz pionową P

Y

. Wartości sił działa-

jących w przegubie, zgodnie z rysunkiem 3.14, spełniają warunki sumy rzutów wszystkich sił działających
w przegubie rzeczywistym na kierunek poziomy i pionowy w postaci

H

A



I



−

H

A



II





P

X

=

0

,

(3.18)

V

A



I





V

A



II



−

P

Y

=

0

.

(3.19)

I

P

1

II

P

2

1

I

P

1

1

II

P

2

1

R

1

(I)

R

1

(II)

R

1

(I)

R

1

(II)

X

Y

1

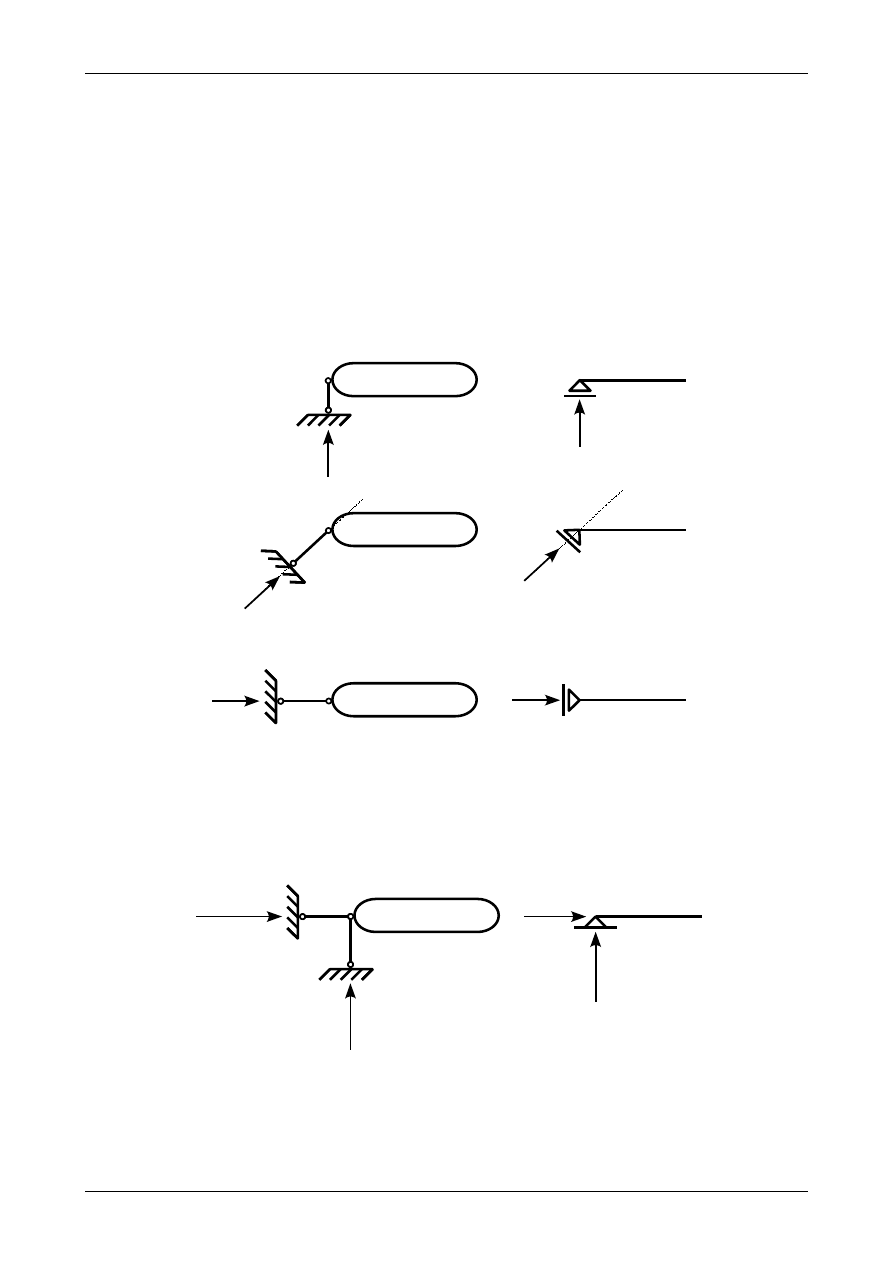
Rys. 3.15. Reakcja w pręcie podporowym łączącym tarcze sztywne numer I i II

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.8

Rysunek 3.15 przedstawia pręt podporowy numer 1 łączący dwie tarcze sztywne, nie będące podporo-

wymi, numer I i II. Pręt taki nazywamy ściągiem. Na tarczę sztywną numer I działa siła czynna P

1

natomiast

na tarczę sztywną numer II działa siła czynna P

2

. Jeżeli rozpatrujemy obie tarcze sztywne razem to w pręcie

nie działa żadna siła. Jeżeli natomiast będziemy rozpatrywali każdą z tarcz sztywnych z osobna to w pręcie
podporowym działać będą dwie reakcje, których wartości spełniają warunek



X =−R

1



I





R

1



II



=

0⇒ R

1



I



=

R

1



II



.

(3.20)

Na podporze przegubowo-przesuwnej, która odpowiada prętowi podporowemu, działa jedna reakcja.

Kierunek tej reakcji pokrywa się z kierunkiem pręta podporowego. Reakcje w pręcie podporowym oraz
w podporze przegubowo-przesuwnej przedstawia rysunek 3.16.

R

R

R

R

R

R

Rys. 3.16. Reakcja na podporze przegubowo-przesuwnej

Podpora przegubowo-nieprzesuwna odbiera prętowi dwa stopnie swobody więc na tej podporze wys-

tąpią dwie reakcje. Najczęściej przyjmuje się, że jedna z nich jest pionowa a druga pozioma. Rysunek 3.17
przedstawia reakcje na podporze przegubowo-nieprzesuwnej.

H

V

H

V

Rys. 3.17. Reakcja na podporze przegubowo-nieprzesuwnej

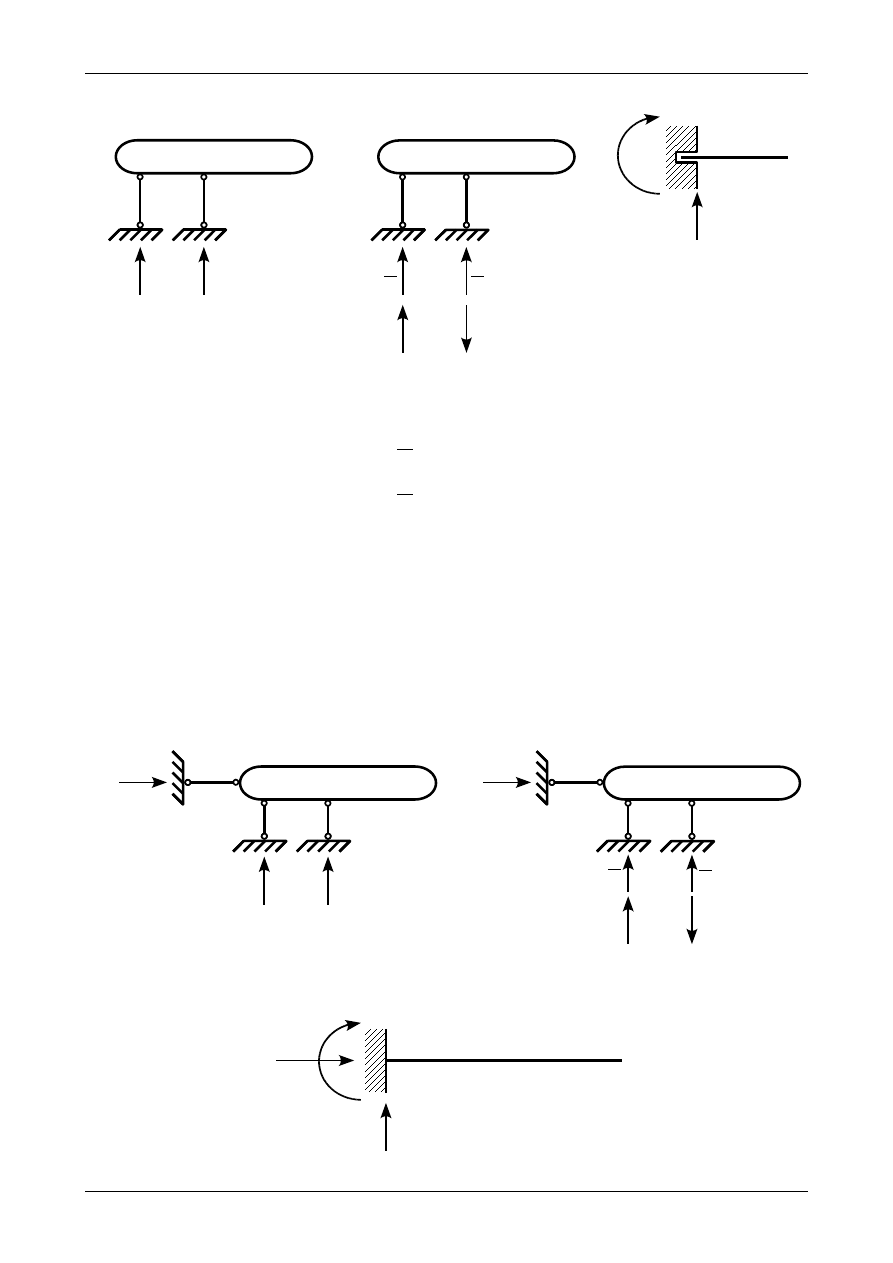
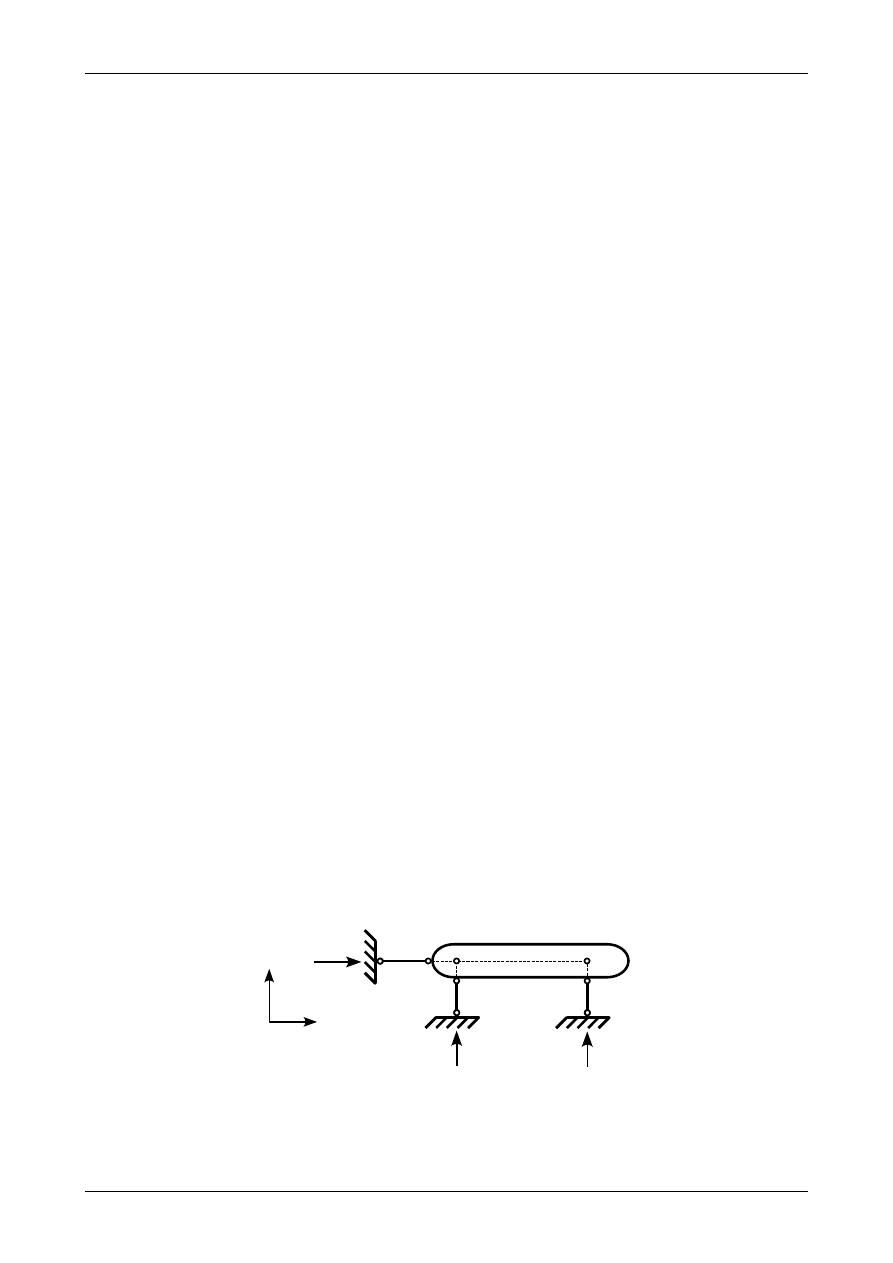
Podpora ślizgowa odbiera także dwa stopnie swobody więc na tej podporze muszą wystąpić dwie

reakcje. Na rysunku 3.18 a) w każdym z prętów podporowych tej podpory występuje pojedyncza reakcja.
Wartości tych reakcji można zapisać w sposób przedstawiony na rysunku 3.18 b) jako

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.9

R

1

R

2

R

R

V

M

a)

b)

c)

V

2

V

2

Rys. 3.18. Reakcje na podporze ślizgowej

R

1

=

V

2



R

R

2

=

V

2

−

R

.

(3.21)

Reakcje V/2 razem dają nam reakcję pionową V. Natomiast reakcje R stanowią parę sił, którą można
zastąpić odpowiednim momentem M. Ostatecznie na podporze ślizgowej występują dwie reakcje zaznaczo-
ne na rysunku 3.18 c).

Utwierdzenie odbiera prętowi trzy stopnie swobody. Na podporze tej wystąpią więc trzy reakcje.

Rysunek 3.19 a) przedstawia wszystkie trzy reakcje. Reakcje R

1

oraz R

2

zapisujemy zgodnie ze wzorem

(3.21) natomiast reakcję R

3

oznaczamy jako reakcję poziomą H. W wyniku tych działań otrzymamy reakcje

przedstawione na rysunku 3.20.

R

1

R

2

R

R

R

3

R

3

a)

b)

V

2

V

2

Rys. 3.19. Reakcje w utwierdzeniu

M

V

H

Rys. 3.20. Reakcje w utwierdzeniu

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.10

Porównując rysunki 3.16, 3.17, 3.18 c) oraz 3.20 widać, że na każdej z tych podpór występują reakcje

o kierunkach, które blokuje dana podpora. Podpora przegubowo-przesuwna nie pozwala na przesuw w pew-
nym kierunku i ten sam kierunek ma reakcja na tej podporze. Podpora przegubowo-nieprzesuwna blokuje
przesuw w poziomie i pionie i takie kierunki mają obie reakcje. Podpora ślizgowa blokuje przesuw w pionie
oraz obrót. Reakcje na tej podporze to reakcja pionowa oraz moment. Wreszcie utwierdzenie blokuje
przesuw w poziomie i w pionie oraz obrót. Stąd na tej podporze mamy reakcję poziomą, pionową i moment.

P

1

A

I

O

R

R

1

R

A

R

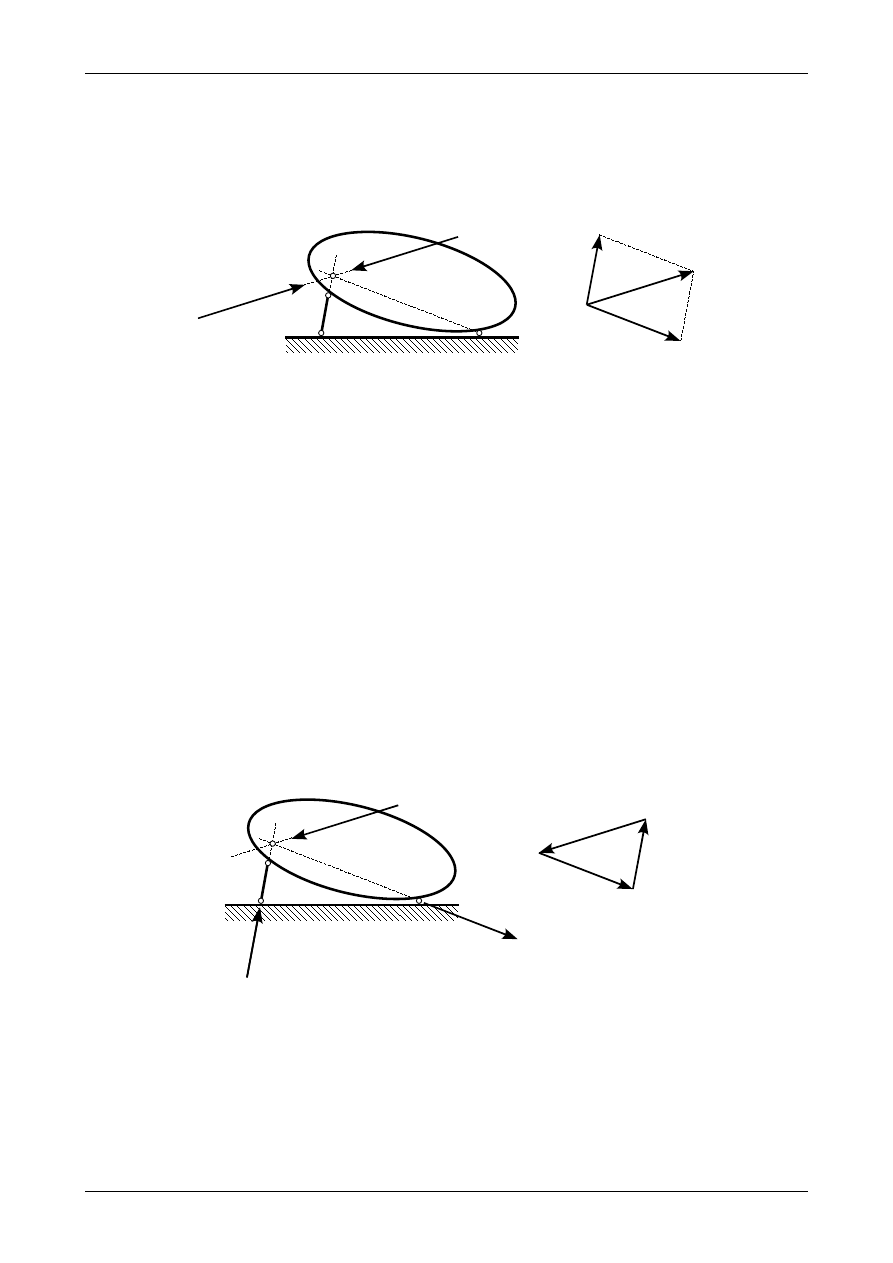
Rys. 3.21. Wypadkowa reakcja działająca na tarczę sztywną

Wyznaczanie reakcji w więzach nazywamy analizą statyczną. Rysunek 3.21 przedstawia geometrycz-

nie niezmienną tarczę sztywną na którą działa siła czynna P. Wypadkowa reakcja R leży na prostej działania
siły czynnej P i ma ona tą samą wartość ale przeciwny zwrot. Reakcja ta jest wypadkową z reakcji w pręcie
podporowym R

1

oraz w przegubie R

A

. Wektorowo możemy to zapisać jako

R

=

R

1



R

A

.

(3.22)

Kierunek wypadkowej reakcji R musi przejść przez punkt przecięcia się kierunków reakcji składo-

wych R

1

oraz R

A

. Jednak na razie nie znamy drugiego punktu na prostej działania reakcji w przegubie A,

znamy natomiast punkt przecięcia kierunków siły czynnej P oraz reakcji R

1

, którym jest punkt O przed-

stawiony na rysunku 3.21. Kierunek reakcji w przegubie A musi więc przechodzić przez ten punkt. W ten
sposób znamy kierunek reakcji R

A

. Na koniec możemy wyznaczyć reakcje R

1

i R

A

. Na rysunku 3.22

przedstawione są wszystkie siły działające na tarczę sztywną. Jeżeli wykonamy ich sumę wektorową to
otrzymamy trójkąt przedstawiony na tym rysunku. Trójkąt ten nazywa się wielobokiem sił. Jak widać siła
wypadkowa w wieloboku sił jest wektorem zerowym. Taki układ sił nazywamy układem w równo-
wadze.

P

R

1

1

A

I

O

R

A

P

R

1

R

A

Rys. 3.22. Siły działające na tarczę sztywną

Siły działające na tarczę sztywną: wypadkowa siła czynna oraz reakcje w więzach, będą

w równowadze, jeżeli ich kierunki będą się przecinać w jednym punkcie oraz siła wypadkowa z tych
wszystkich sił będzie wektorem zerowym. Innymi słowy siły w wieloboku sił muszą się „gonić”.

Rysunek 3.23 przedstawia tarczę sztywną obciążoną tylko dwiema siłami. Jeżeli na tarczę sztywną

działają dwie siły R

1

i R

2

to aby tarcza była w równowadze siły te muszą działać na tej samej prostej,

mieć te same wartości ale przeciwne zwroty czyli ich wartości muszą spełniać warunek wektorowy

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.11

R

1

R

2

Rys. 3.23. Dwie siły w równowadze działające na tarczę sztywną

R

1

=−

R

2

.

(3.23)

Przedstawione powyżej dwie zasady, kiedy siły działające na tarczę sztywną znajdują się w równo-

wadze mają zastosowanie przy metodzie wykreślnej wyznaczania reakcji. Metody tej nie będziemy tutaj
omawiać.

W dalszej części niniejszego kursu skupimy się na metodzie analitycznej wyznaczania reakcji

podporowych, którą zastosujemy do płaskich układów prętowych.

P

R

1

1

A

I

R

A

X

Y

Rys. 3.24. Siły działające na tarczę sztywną

W metodzie tej zerowanie się sił w wieloboku sił zastępujemy dwoma warunkami sumy rzutów

wszystkich działających na tarczę sztywną na dwa nierównoległe kierunki. Zgodnie z rysunkiem 3.24 mogą
to być sumy rzutów wszystkich sił działających na tarczę sztywną na oś poziomą X oraz pionową Y. Sumy
tych rzutów muszą wynosić zero. Są to najczęściej wykorzystywane kierunki.

W metodzie analitycznej warunek przecinania się kierunków wszystkich sił działających na tarczę

sztywną w jednym punkcie zastępujemy warunkiem sumy momentów wszystkich sił działających na tarczę
sztywną względem dowolnego punktu na płaszczyźnie. Suma momentów musi wynosić zero.

Równania sumy rzutów oraz sumy momentów nazywamy równaniami równowagi. Zapisujemy je

w następującej postaci

{



X

=

0



Y

=

0



M

=

0

,

(3.24)

w którym dwa pierwsze równania to sumy rzutów, trzecie to suma momentów.

Możemy także wykorzystywać jedno równanie sumy rzutów oraz dwa równania sumy momentów

względem dwóch dowolnych punktów na płaszczyźnie. Będą one miały postać

{



X =0



M

1

=

0



M

2

=

0

,

(3.25)

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.12

{



Y =0



M

1

=

0



M

2

=

0

.

(3.26)

Równania równowagi (3.25) lub (3.26) są najczęściej wykorzystywanymi równaniami przy obliczaniu

reakcji podporowych w układach prętowych.

Istnieje także trzecia postać równań równowagi. Będą to trzy sumy momentów względem trzech

dowolnych punktów. Jednak punkty te nie mogą leżeć na jednej prostej. Równania te będą miały postać

{



M

1

=

0



M

2

=

0



M

3

=

0

.

(3.27)

Płaski układ prętowy zastępujemy płaskim układem tarcz sztywnych. Dla każdej tarczy sztywnej

określamy kierunki reakcji w więzach oraz zakładamy ich zwroty. W dalszej kolejności dla każdej tarczy
sztywnej zapisujemy trzy równania równowagi. Jeżeli mamy t tarcz sztywnych to otrzymujemy w ten sposób
układ 3t równań z 3t niewiadomymi, którymi są reakcje w więzach. Układ ten ma postać

{



X



1



=

0



Y



1



=

0



M



1



=

0

⋮



X



t



=

0



Y



t



=

0



M



t



=

0

.

(3.28)

Aby układ równań (3.28) miał rozwiązania wyznacznik główny tego układu musi być różny od zera.

Płaski układ prętowy, dla którego wyznacznik główny układu (3.28) jest różny od zera jest układem
geometrycznie niezmiennym i statycznie wyznaczalnym. Stanowi to więc warunek konieczny i dostatecz-
ny geometrycznej niezmienności. Po rozwiązaniu układu równań (3.28) otrzymamy wartości i zwroty reakcji
we wszystkich podporach. Jeżeli dana reakcja jest dodatnia to ma ona zwrot zgodny z przyjętym na
początku obliczeń. Jeżeli dana reakcja jest ujemna to ma ona zwrot przeciwny do przyjętego na
początku obliczeń. W praktyce najczęściej nie trzeba rozwiązywać całego układu równań (3.28), ponieważ
da się tak zapisać równania równowagi aby z pojedynczego równania wyznaczyć jedną reakcję.

1

2

3

A

B

X

Y

R

2

R

1

R

3

Rys. 3.25. Tarcza sztywna

Rysunek 3.25 przedstawia przykładową tarczę sztywną. Zakładamy zwroty reakcji w prętach podporo-

wych. Punkt A jest punktem przecięcia kierunków reakcji w prętach numer 1 i 2 natomiast punkt B jest

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.13

punktem przecięcia kierunków reakcji w prętach numer 1 i 3. Wartości reakcji wyznaczymy z następujących
warunków równowagi.

{



X =0



M

B

=

0



M

A

=

0

.

(3.29)

Drugie równanie stanowi sumę momentów względem punktu B a trzecie względem punktu A. Z pierwszego
równania wyznaczymy wartość reakcji R

1

. Z drugiego równania wyznaczymy wartość reakcji R

2

, ponieważ

momenty pozostałych reakcji względem punktu B wynoszą zero. Z trzeciego równania wyznaczymy wartość
reakcji R

3

, ponieważ momenty pozostałych reakcji względem punktu A wynoszą zero. Równanie sumy

rzutów wszystkich sił działających na tarczę sztywną na oś pionową Y posłuży nam do sprawdzenia popraw-
ności obliczeń wartości reakcji R

2

i R

3

.

A

B

C

V

A

H

A

V

C

H

C

A

B

C

V

A

H

A

V

C

H

C

B

H

B

(I)

V

B

(I)

V

B

(II)

H

B

(II)

I

II

I

II

X

Y

B

H

B

(I)

V

B

(I)

H

B

(II)

V

B

(II)

Rys. 3.26. Układ trójprzegubowy z przegubami A i C na jednym poziomie

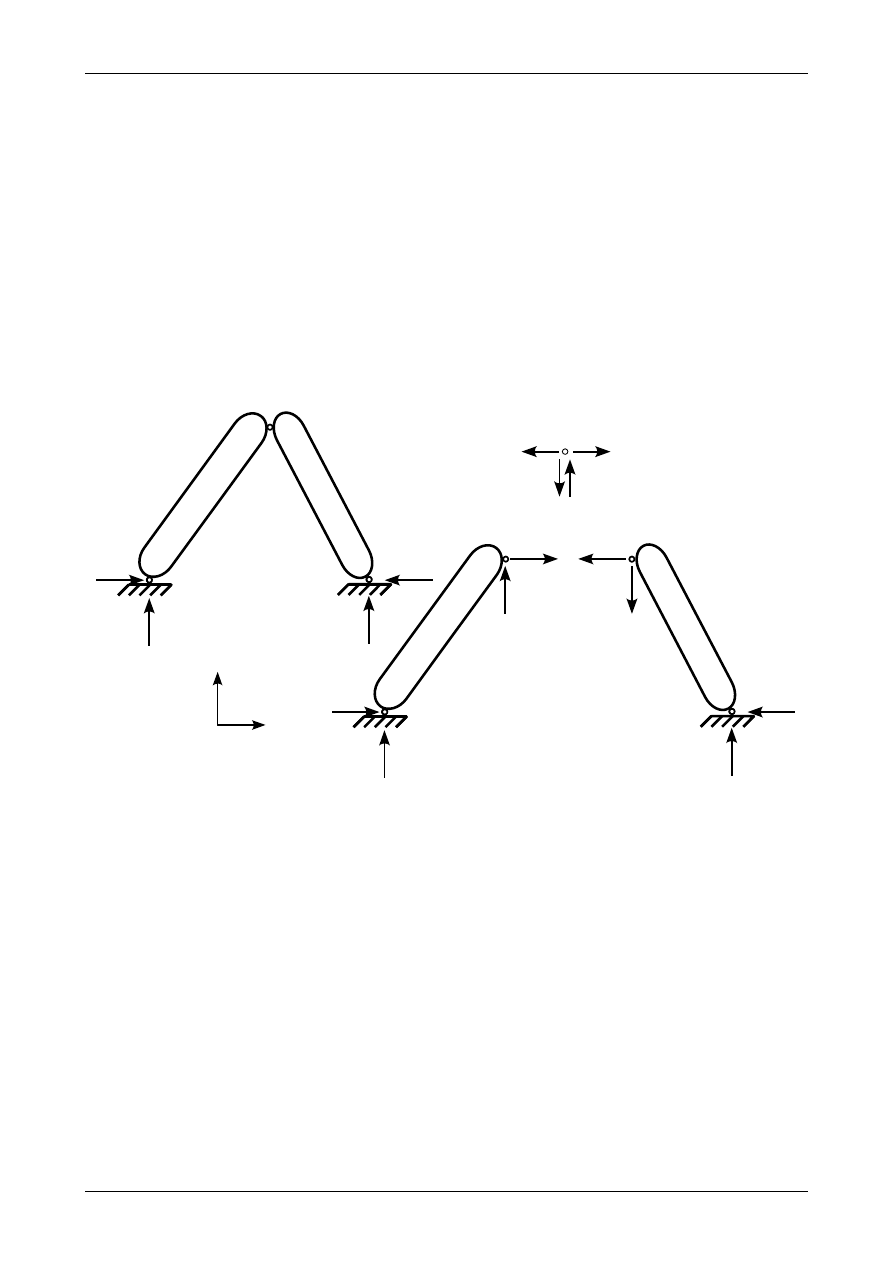
Rysunek 3.26 przedstawia układ trójprzegubowy z przegubami A i C na jednym poziomie. Zakładamy

zwroty reakcji we wszystkich przegubach. Należy pamiętać o tym, że w przegubie B na każdą z tarcz
sztywnych będą działały dwie reakcje, których wartości spełniają warunek

{

−

H

B



I





H

B



II



=

0⇒ H

B



I



=

H

B



II



−

V

B



I





V

B



II



=

0⇒V

B



I



=

V

B



II



.

(3.30)

Wartości pionowych reakcji w przegubach A i C wyznaczymy z następujących równań równowagi dla

całego układu trójprzegubowego (tarcze sztywne I+II)

{



M

C



I II



=

0



M

A



I II



=

0

.

(3.31)

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.14

Z pierwszego równania otrzymamy wartość reakcji V

A

, ponieważ momenty pozostałych trzech reakcji,

działających na cały układ trójprzegubowy, względem punktu C wynoszą zero. Z drugiego równania otrzy-
mamy wartość reakcji V

C

, ponieważ momenty pozostałych trzech reakcji, działających na cały układ trój-

przegubowy, względem punktu A wynoszą zero. Następnie wykorzystamy sumę rzutów wszystkich sił
działających na cały układ trójprzegubowy na oś pionową Y w celu sprawdzenia poprawności obliczenia
wartości reakcji V

A

i V

C

.

Wartość poziomej reakcji w przegubie A wyznaczymy z warunku sumy momentów wszystkich sił

działających na tarczę sztywną numer I względem punktu B czyli



M

B



I



=

0

.

(3.32)

Wartość poziomej reakcji w przegubie C wyznaczymy z warunku sumy momentów wszystkich sił działa-
jących na tarczę sztywną numer II względem punktu B czyli



M

B



II



=

0

.

(3.33)

Następnie wykorzystamy sumę rzutów wszystkich sił działających na cały układ trójprzegubowy na oś
poziomą X w celu sprawdzenia poprawności obliczenia wartości reakcji H

A

i H

C

.

Wartość reakcji w przegubie B działających na tarczę sztywną numer I wyznaczymy z następujących

równań równowagi

{



X



I



=

0



Y



I



=

0

.

(3.34)

Z pierwszego równania wyznaczymy wartość reakcji H

B

(I)

natomiast z drugiego wartość reakcji V

B

(I)

.

Wartość reakcji w przegubie B działających na tarczę sztywną numer II wyznaczymy z następujących
równań równowagi

{



X



II



=

0



Y



II



=

0

.

(3.35)

Z pierwszego równania wyznaczymy wartość reakcji H

B

(II)

natomiast z drugiego wartość reakcji V

B

(II)

.

Wartości reakcji H

B

(I)

i H

B

(II)

oraz V

B

(I)

i V

B

(II)

muszą spełniać zależność (3.30). Stanowi to sprawdzenie pop-

rawności obliczenia wartości tych reakcji.

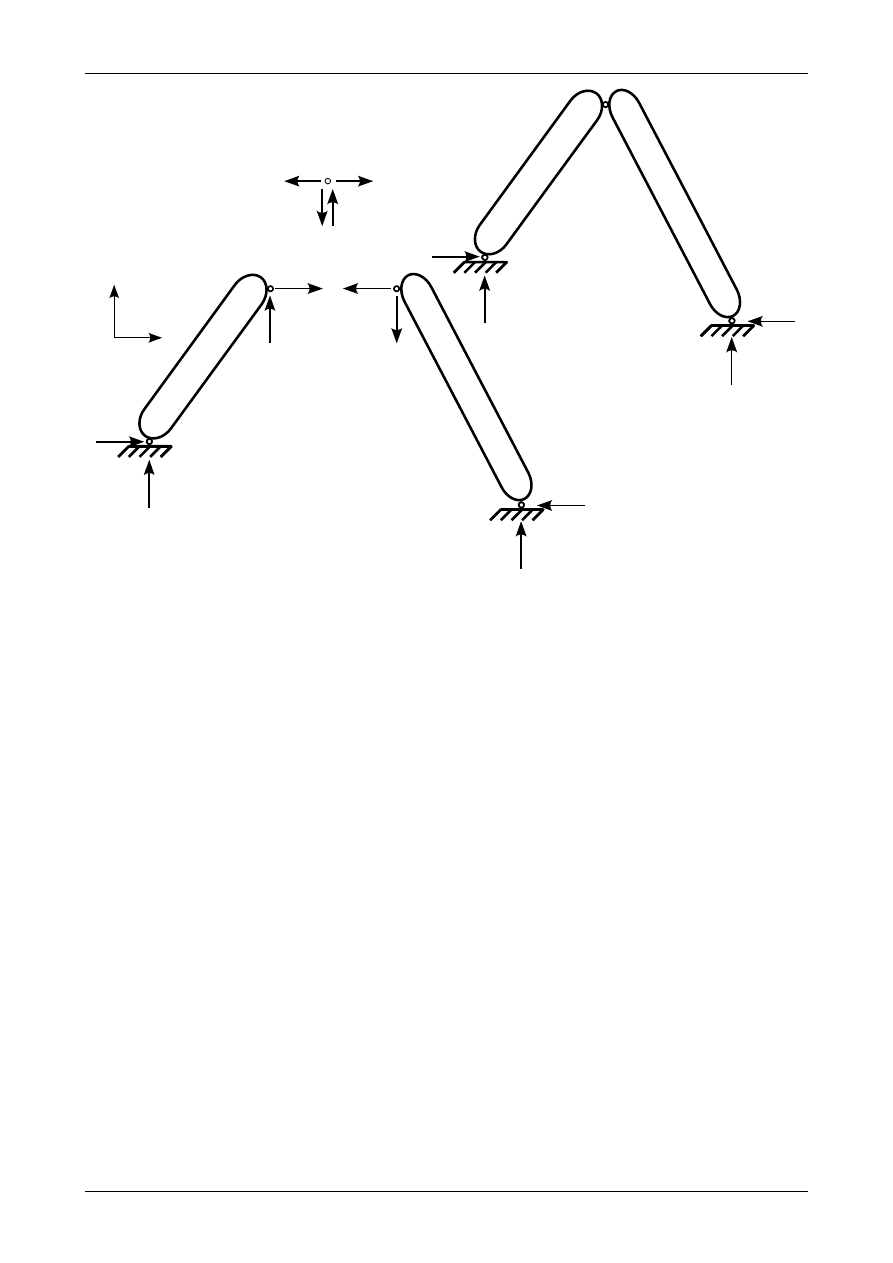
Rysunek 3.27 przedstawia układ trójprzegubowy z przegubami A i C na różnych poziomach. Zakłada-

my zwroty reakcji we wszystkich przegubach. Należy pamiętać o tym, że w przegubie B na każdą z tarcz
sztywnych będą działały dwie reakcje, które wartości spełniają warunek (3.30).

Wartości reakcji w przegubie A wyznaczymy z następujących równań równowagi

{



M

C



I II



=

0



M

B



I



=

0

.

(3.36)

Pierwsze równanie dotyczy całego układu trójprzegubowego natomiast drugie tylko tarczy sztywnej numer
I. Równania te stanowią układ równań, z którego wyznaczymy wartości reakcji V

A

i H

A

.

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.15

A

B

C

V

A

H

A

V

C

H

C

A

B

C

V

A

H

A

V

C

H

C

B

H

B

(I)

V

B

(I)

V

B

(II)

H

B

(II)

I

II

I

II

X

Y

B

H

B

(I)

V

B

(I)

H

B

(II)

V

B

(II)

Rys. 3.27. Układ trójprzegubowy z przegubami A i C na różnych poziomach

Wartości reakcji w przegubie C wyznaczymy z następujących równań równowagi

{



M

A



I II



=

0



M

B



II



=

0

.

(3.37)

Pierwsze równanie dotyczy całego układu trójprzegubowego natomiast drugie tylko tarczy sztywnej numer
II. Równania te stanowią układ równań, z którego wyznaczymy wartości reakcji V

C

i H

C

.

W celu sprawdzenia poprawności obliczenia wartości reakcji w przegubach A i C zastosujemy

równania dotyczące całego układu trójprzegubowego

{



X



I II



=

0



Y



I II



=

0

.

(3.38)

Wartość reakcji w przegubie B działających na tarczę sztywną numer I wyznaczymy z następujących

równań równowagi

{



X



I



=

0



Y



I



=

0

.

(3.39)

Z pierwszego równania wyznaczymy wartość reakcji H

B

(I)

natomiast z drugiego wartość reakcji V

B

(I)

.

Dr inż. Janusz Dębiński

WM

3. PODSTAWY STATYKI NA PŁASZCZYŹNIE

R3.16

Wartość reakcji w przegubie B działających na tarczę sztywną numer II wyznaczymy z następujących
równań równowagi

{



X



II



=

0



Y



II



=

0

.

(3.40)

Z pierwszego równania wyznaczymy wartość reakcji H

B

(II)

natomiast z drugiego wartość reakcji V

B

(II)

.

Wartości reakcji H

B

(I)

i H

B

(II)

oraz V

B

(I)

i V

B

(II)

muszą spełniać zależność (3.30). Stanowi to sprawdzenie

poprawności obliczenia wartości tych reakcji.

Zastosowanie metody analitycznej do wyznaczania reakcji w więzach płaskiego układu tarcz sztyw-

nych omówimy na konkretnych przykładach załączonych do niniejszego rozdziału.

Dr inż. Janusz Dębiński