Statystyki opisowe (Arkusz1)
N ważnych Średnia
Minimum
Maksimum
Odch.std
Ocena
219
3,310502
2,000000
6,000000
1,126995
Po co przeprowadza się badania empiryczne w psychologii?
Jakie oceny otrzymaliby studenci z egzaminu ze statystyki,
gdyby wszyscy mieli takie same oceny?
Co to znaczy, że ocena studenta X jest różna od średniej?
Jak można liczbowo przedstawić odchylenie od średniej?
Dlaczego oceny jednych są wyższe od średniej a innych niższe?
Od czego zależy wielkość różnicy w stosunku do średniej?
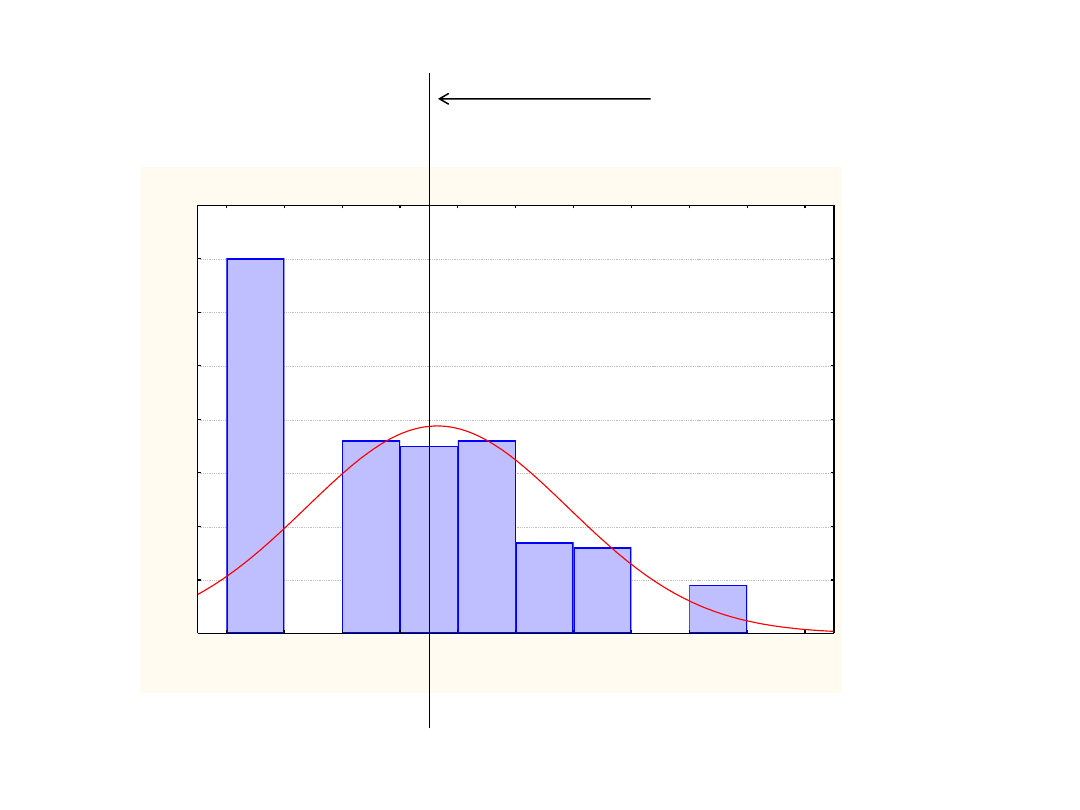
Ocena = 219*0,5*normal(x; 3,3105; 1,127)
1,5
2,0
2,5
3,0
3,5
4,0
4,5
5,0
5,5
6,0
6,5
Ocena
0
10
20
30
40
50
60
70
80
L
icz
b
a
o
b
s.
średnia arytmetyczna
Badania empiryczne polegają na poszukiwaniu przyczyn
różnic od średniej
Od czego zależy wielkość odchylenia od średniej w przypadku
wyników egzaminu?
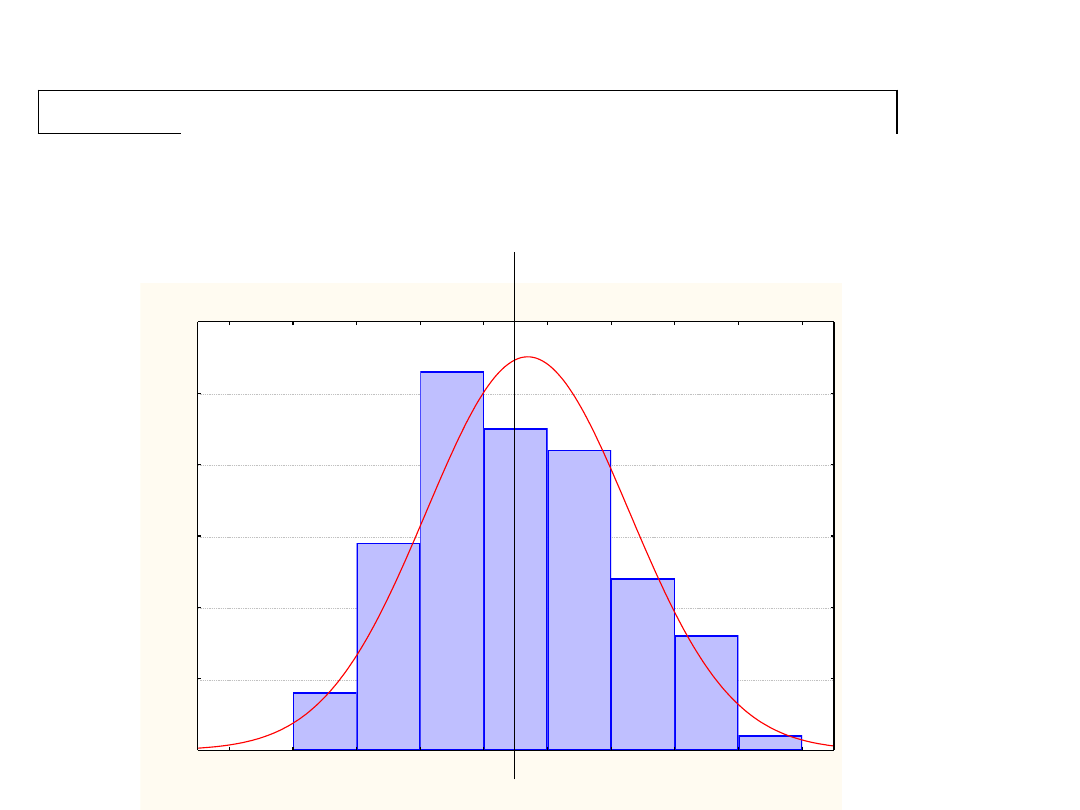
Odpowiedź – od liczby zdobytych punktów
suma punktów = 219*5*normal(x; 23,3196; 7,9291)
0
5
10
15
20
25
30
35
40
45
suma punktów
0
10
20
30
40
50
60
L
icz
b
a
o
b
s.
Statystyki opisowe (Arkusz1)
N
ważnych
Średnia
Minimum
Maksimu
m
Odch.std
suma
punktów
219
23,31963
8,000000
41,00000
7,929051
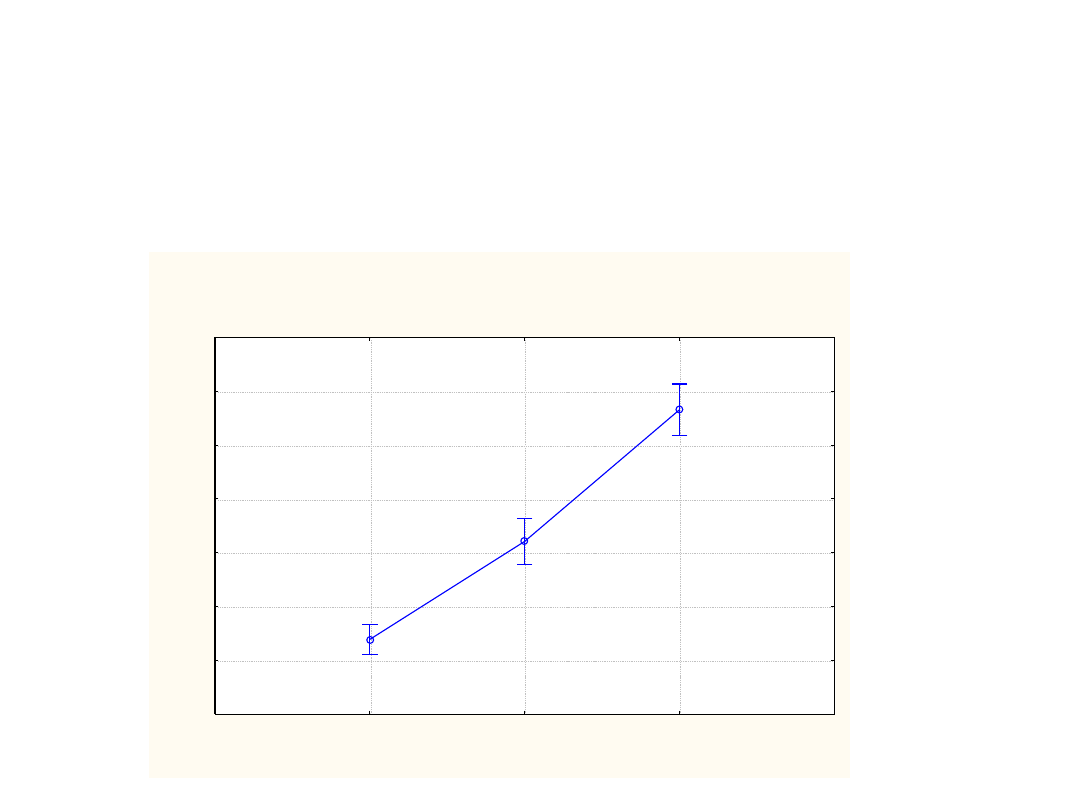
Bieżący efekt: F(2, 216)=122,10, p=0,0000
Dekompozycja efektywnych hipotez
Pionowe słupki oznaczają 0,95 przedziały ufności
1
2
3
Zmn5
2,0
2,5
3,0
3,5
4,0
4,5
5,0
5,5
O
ce
n
a
Badanie różnicowe – czy podział osób badanych na jakieś grupy po
badaniu pozwala na znalezienie przyczyny odchyleń od średniej
Badanie eksperymentalne – podział osób na grupy przed badaniem i
manipulacja sytuacją
W jakich przypadkach na podstawie oceny łatwiej jest
przewidzieć sumę punktów i poziom aktywności a w jakich
trudniej?
Przestrzeń probabilistyczna to przestrzeń wszystkich
możliwych zdarzeń, które mogą wystąpić i których nie można z
góry przewidzieć
Przestrzeń taka może być skończona (na przykład zbiór liczby
oczek przy rzucie kostką)
lub nieskończona (na przykład czas reakcji w eksperymencie
psychologicznym, który można mierzyć z dowolną dokładnością)
Przestrzeń probabilistyczna – intuicyjnie – to przestrzeń
wszystkich możliwych zdarzeń, np. wszystkie możliwe oceny z
egzaminu.
Wyniki eksperymentów psychologicznych można opisać za
pomocą pojęcia przestrzeni probabilistycznej
Przykłady przestrzeni probabilistycznej:
1. Rzut monetą – dwa zdarzenia może wypaść orzeł lub
reszka
2. Rzut dwoma monetami (kolejność nieistotna) – trzy
zdarzenia:
(orzeł, orzeł) (reszka, reszka) (orzeł, reszka)
3. Losowanie (bez zwracania)6 kuleczek ze zbioru 49 różnych
kuleczek, jeżeli kuleczki te się ponumerują to zdarzenia
mogą wyglądać tak:
(1,2,3,4,5,6) (28, 45, 36, 2, 6, 19) itd.
z 49 kuleczek można wylosować 6 na 13 983 816
sposobów
4. Zaznaczenie jednej z odpowiedzi: zdecydowanie nie lubię,
nie lubię, nie mam zdania, lubię, zdecydowanie lubię
dla pytania „Czy lubisz wykłady ze statystyki?”
Definicja prawdopodobieństwa
Klasyczna (częstościowa) definicja
prawdopodobieństwa:
Ω = {X
1
, X
2
, ..., X
N
} -
Ω - zbiór wszystkich możliwych zdarzeń,
sytuacji, itp. Na przykład zbiór wszystkich
możliwych wyników rzutu kostką, wyników na
egzaminie, itp. Zbiór Ω nie musi być zbiorem
liczb, może to być zbiór różnych obiektów.
X - to pewien podzbiór zdarzeń ze zbioru Ω
(inaczej zbiór zdarzeń sprzyjających albo zbiór
sukcesów) – na przykład zbiór liczb parzystych
na kostce albo zbiór ocen nie gorszych niż 4,0
)
(
)
(
)
(
n
X
n
X
P
,
Pierre Simon de
Laplace
ur. 23 marca 1749 w
Beaumont-en-Auge, zm. 5
marca 1827 w Paryżu)
Ile wynosi prawdopodobieństwo dla następujących
zdarzeń?
1. Orzeł przy jednym rzucie monetą?
2. Co najmniej dwa orły przy rzucie dwoma monetami?
3. Trafienie 6 w lotto, jeżeli skreśliło się cyfry:
(1,2,3,4,5,6)
4. Trafienie 6 w lotto jeżeli skreśliło się cyfry (28, 45, 36,
2, 6, 19)
5. Wybranie odpowiedzi „zdecydowanie lubię wykład ze
statystyki” przez wszystkie osoby obecne na
wykładzie?
Definicja zdarzeń niezależnych
Zdarzenia ze zbioru Ω mogą być podzielone na różne typy
zdarzeń. Jeżeli prawdopodobieństwo wystąpienia zdarzenia
typu X jest niezależne od wystąpienia zdarzenia typu Y to
mówimy, że zdarzenia X i Y są od siebie niezależne.
Dla zdarzeń niezależnych zachodzi: P(X i Y) = P(X) P(Y)
Przykład zdarzeń niezależnych – rzut wieloma monetami,
rzut monetą i rzut kostką
Jakie są psychologiczne przykłady zdarzeń niezależnych?
Zdarzenia niezależne to także błędy pojawiające się w
eksperymentach psychologicznych
Zmienna losowa
Ze zmienną losową mamy do czynienia wtedy, gdy
wszystkim zdarzeniom ze zbioru Ω przypisane są liczby
według tej samej zasady.
Y1
Y2
Y3
.
.
.
YN
Przykłady zmiennych losowych
1. Rzut monetą – dwa zdarzenia może wypaść orzeł lub reszka –
jeżeli orzeł to zapisujemy 1, jeżeli reszka to 0
2. Rzut dwoma monetami (kolejność nieistotna) – trzy zdarzenia:
(orzeł, orzeł) (reszka, reszka) (orzeł, reszka) jako wartości
zmiennej podajemy liczbę orłów
3. Losowanie (bez zwracania) 6 kuleczek ze zbioru 49 różnych
kuleczek. Możemy jako wartości zmiennych zapisać sumę na
sześciu kuleczkach
4. Zaznaczenie jednej z odpowiedzi: zdecydowanie nie lubię, nie
lubię, nie mam zdania, lubię, zdecydowanie lubię
dla pytania „Czy lubisz wykłady ze statystyki?”
Możemy odpowiedzi kodować przy pomocy liczb: 1, 2, 3, 4, 5
Zmienna losowa jest funkcją
Funkcja to przepis pozwalający jednoznacznie łączyć w pary
liczby z jednego zbioru z liczbami z drugiego zbioru. Każda
liczba z pierwszego zbioru może mieć przyporządkowaną tylko
jedną liczbę z drugiego zbioru.
Czy ta zasada obowiązuje w drugą stronę?
Zbiory te można nazwać zbiorem wartości niezależnych
(dziedziną funkcji - pierwszy zbiór) i zbiorem wartości
zależnych (drugi zbiór)
Przykłady funkcji:
Funkcja Stała: Dla każdego X, Y = 3,0 (np. cena kawy w barze)
co mogłoby być zmienną X?
Funkcja Liniowa: Dla każdego X, Y = 102 X,
X to na przykład ceny w barku w dniu wczorajszym
Zmienna losowa jest funkcją, dla której dziedziną są zdarzenia
elementarne (czyli zdarzenie opisane w przestrzeni
probabilistycznej)
Przepis na łączenie zdarzeń z liczbami może być dowolny, aby
tylko jednemu zdarzeniu przypisywano jedną liczbę
Na tym samym zbiorze zdarzeń elementarnych można
zdefiniować różne zmienne losowe – nie można ich jednak
„mylić” między sobą w tej samej analizie
Przykład – nie można jako wartości zmiennych zależnych
wpisywać na zmianę wzrostu i ilorazu inteligencji, bo są to
różne zmienne losowe
Zmienne losowe mogą przybierać wartości ze
skończonego zbioru – są to wtedy zmienne skokowe lub
inaczej dyskretne
Wszystkie przykłady zmiennych losowych (1-4) wyżej to
zmienne tego typu.
Intuicyjnie – zmienne dyskretne to takie, dla których nie da
się podać wartości pośrednich (nie można wyrzucić 3,5
oczka na kostce do gry)
Zmienne losowe mogą też przyjmować wartości z
nieskończonego zbioru – są to wtedy zmienne ciągłe.
Intuicyjnie – nieskończony zbiór to taki, który nie ma
granicy dolnej lub górnej (na przykład zbiór liczb
rzeczywistych od -
do + ) lub taki (co jest w sumie
jednoznaczne), w którym między każdymi dowolnymi
wartościami znajduje się wartość pośrednia.
Ciągłość zmiennych – paradoksy Zenona z Elei
Czy Achilles dogoni żółwia?
Czy strzała może lecieć bez czasu?
Czy można trafić z łuku w jeden konkretny punkt na tarczy
Liczby losowe z przedziału od 0 do 1
Zenon z Elei
Wartośd oczekiwana
E= X
1
p
1
+ X
2
p
2
+ ... + X
n
p
n
X - stany rzeczy,
p - prawdopodobieństwo wystąpienia tych stanów
Przykład:
Rzucam kostką. Jeżeli wypadnie parzysta liczby oczek dostajesz 1 zł,
jeżeli nieparzysta - płacisz 2 zł. Ile wynosi wartośd oczekiwana w tej
grze?
Przykład: Oceny w szkole
Oceny w grupie A
1
1
2
3
5
wartość oczekiwana
2,4
Oceny w grupie B
2
3
4
4
6
wartość oczekiwana
3,8
Jak obliczyć wartość oczekiwaną dla wszystkich 10
uczniów?
Jakie wartości oczekiwane możemy przypisać każdej
osobie?
Oceny
w.oczek
grupy
całkowita
w. oczek
Ocena -
w.oczek
grupa
w_ocze
k gr - w
oczek
całk
Oceny w grupie A
1
2,4
3,1
-1,4
-0,7
1
2,4
3,1
-1,4
-0,7
2
2,4
3,1
-0,4
-0,7
3
2,4
3,1
0,6
-0,7
5
2,4
3,1
2,6
-0,7
wartość
oczekiwana
2,4
Oceny w grupie B
2
3,8
3,1
-1,8
0,7
3
3,8
3,1
-0,8
0,7
4
3,8
3,1
0,2
0,7
4
3,8
3,1
0,2
0,7
6
3,8
3,1
2,2
0,7
wartość
oczekiwana
3,8
Wynik osoby 1.: 1 = 3,1 + (-0,7) + (-1,4)
Wynik pojedynczej osoby badanej jest sumą
-całkowitej wartości oczekiwanej
-odchylenia od wartości oczekiwanej w grupie
-odchylenia wartości oczekiwanej grupy od całkowitej
wartości oczekiwanej
Projektowanie eksperymentu polega na
•ustaleniu jakie wartości oczekiwane można przypisać
każdej osobie
•ocenie skąd się biorą różnice pomiędzy wynikiem danej
osoby a każdym typem wartości oczekiwanej
•ustaleniu, które różnice można wyjaśnić i w jaki sposób
•ocenie w jakim stopniu na podstawie wyniku
pojedynczej wybranej losowo osoby można przewidzieć
przyporządkowane tej osobie wartości oczekiwane
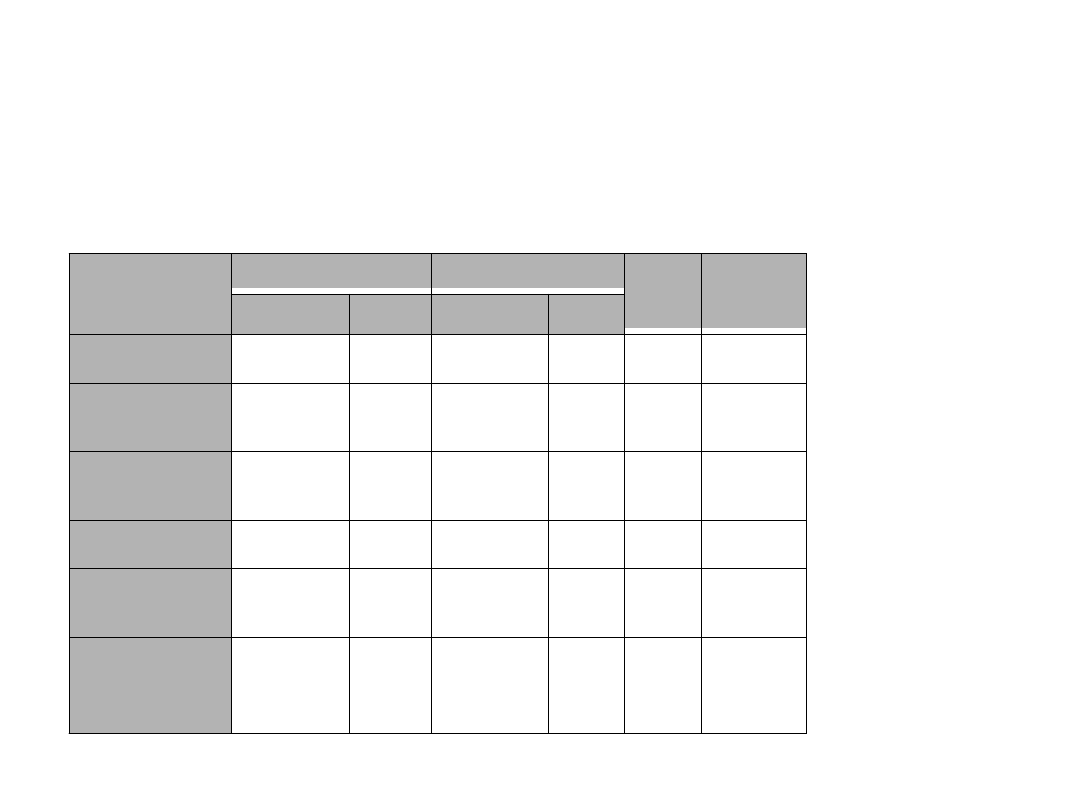
Tabela X. Różnice w zakresie częstości niewerbalnych zachowań współmałżonków
M
SD
Rodzaj
zachowania
Mężowie Żony Mężowie Żony
df
t
a
Uśmiechy
2,65
3,83
2,30
3,78
39
–2,72*
Głośny
śmiech
0,80
1,78
1,16
2,28
39
–3,40*
Marszczenie
czoła
0,36
0,31
0,81
0,66
38
0,29
Zaskoczenie
0,00
0,03
0,00
0,16
38
–1,00
Liczba
spojrzeń
10,83
10,76
6,11
7,05
39
0,05
Długość
spojrzenia w
sek. (średnia)
4,61
7,50
2,81
5,95
39
–3,27*
* p.<0,05
Wyniki w grupie można przedstawić krócej za pomocą
statystyk opisowych
Najważniejszą statystyką opisową jest średnia arytmetyczna,
która ogólnie nazywa się wartością oczekiwaną
Jak oblicza się średnią?
Co to jest średnia ważona
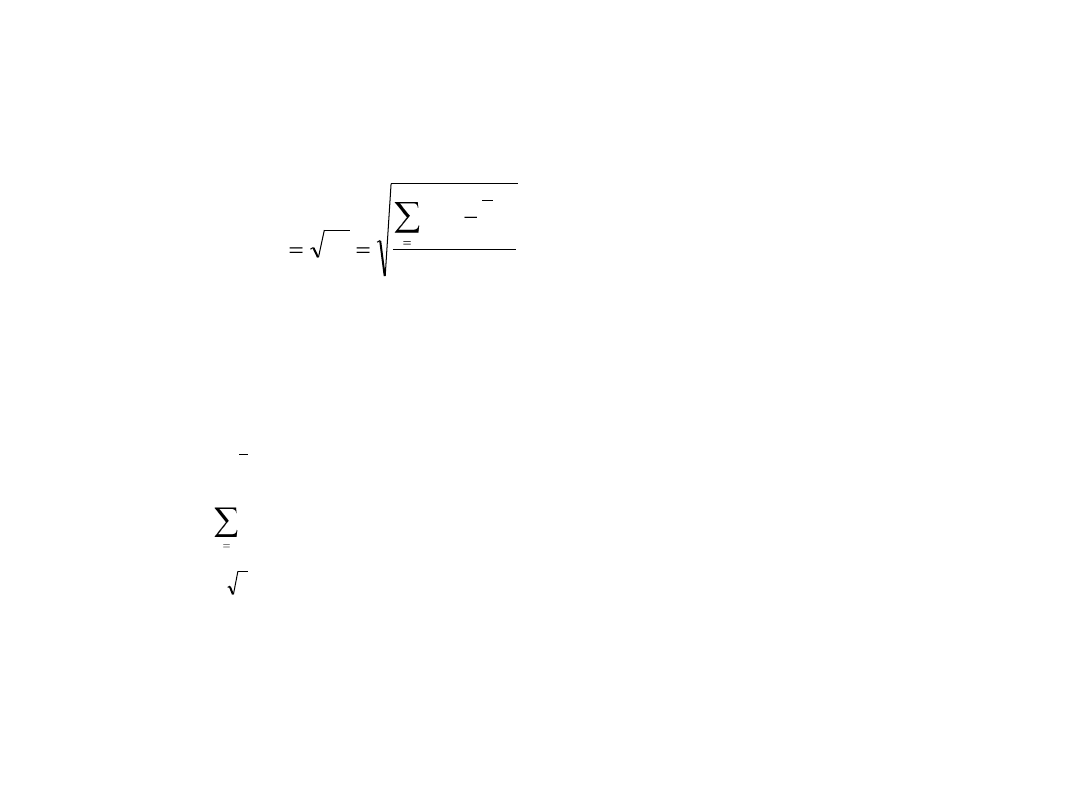
n
x
X
s
s
n
i
i
1
2
2
)
(
s odchylenie standardowe,
n liczba wszystkich obserwacji w zbiorze,
X
i
wartość kolejnego, i-tego pomiaru,
x
średnia arytmetyczna,
n
i 1
suma n wartości danych,
pierwiastek kwadratowy.
Odchylenie standardowe jest średnią geometryczną z różnic w
stosunku do Wartości oczekiwanej
Statystyki opisowe (Dane_egzamin_semestr_zimowy)
N ważnych Średnia
Minimum
Maksimum Odch.std
dotk
punkty
217
2,59908
-1,00000
8,00000
2,678895
suma
punktów
219
23,31963
8,00000
41,00000
7,929051
Ocena
219
3,31050
2,00000
6,00000
1,126995
Wskaźnik zmienności:
odchylenie standardowe
średnia arytmetyczna
1,03071
0,340016
0,34043