Drgania termiczne atomów

Fale zwi

ą

zan

ą

z drganiami atomów o cz

ę

sto

ś

ci kołowej rozchodz

ą

c

ą

si

ę

w krysztale mo

ż

na opisa

ć

poni

ż

szym wzorem, którego cz

ęść

rzeczywista lub

urojona mo

ż

e opisywa

ć

wychylenie z poło

ż

enia równowagi atomów

znajduj

ą

cych si

ę

w poło

ż

eniu :

( )

(

)

(

)

t

R

q

i

e

A

R

R

n

i

i

n

ω

−

⋅

=

∆

r

r

r

r

r

exp

Składowe wektora falowego s

ą

wielko

ś

ciami o quasi-ci

ą

głym zbiorze warto

ś

ci,

jednak

ż

e liczba dozwolonych wektorów falowych opisuj

ą

cych mo

ż

liwe rodzaje

fal jest sko

ń

czona i zale

ż

y od liczby atomów w krysztale. Dowolne drganie w

krysztale mo

ż

na opisa

ć

jako zło

ż

enie tzw. 3N drga

ń

normalnych (N-liczba

atomów w krysztale) scharakteryzowanych przez cz

ę

sto

ść

kołow

ą

ω

,

wektor falowy

oraz wektor

okre

ś

laj

ą

cy kierunek drga

ń

( kierunek ten

mo

ż

e by

ć

równoległy do

–drgania podłu

ż

ne lub prostopadły do

-drgania

poprzeczne) . Istnieje ograniczenie na maksymaln

ą

warto

ść

wektora falowego .

W krysztale 1 DIM zło

ż

onym z atomów poło

ż

onych wzgl

ę

dem siebie w stałej

odległo

ś

ci a jedyna niezerowa składowa wektora falowego przyjmuje warto

ś

ci z

zakresu

Temu samemu

mo

ż

e odpowiada

ć

kilka ró

ż

nych cz

ę

sto

ś

ci

drga

ń

pochodz

ą

cych z ró

ż

nych gał

ę

zi drga

ń

. Dla opisu drga

ń

istotne jest

wyznaczenie zale

ż

no

ś

ci cz

ę

sto

ś

ci kołowej drga

ń

od wektora falowego dla

ka

ż

dej z gał

ę

zi

.

)

(q

r

ω

ω

=

ω

-

wektor falowy okre

ś

laj

ą

cy kierunek rozchodzenia si

ę

fali ,

wersor okre

ś

laj

ą

cy kierunek drga

ń

q

r

i

e

r

n

R

r

q

r













−

a

a

π

π

,

i

e

r

q

r

q

r

q

r

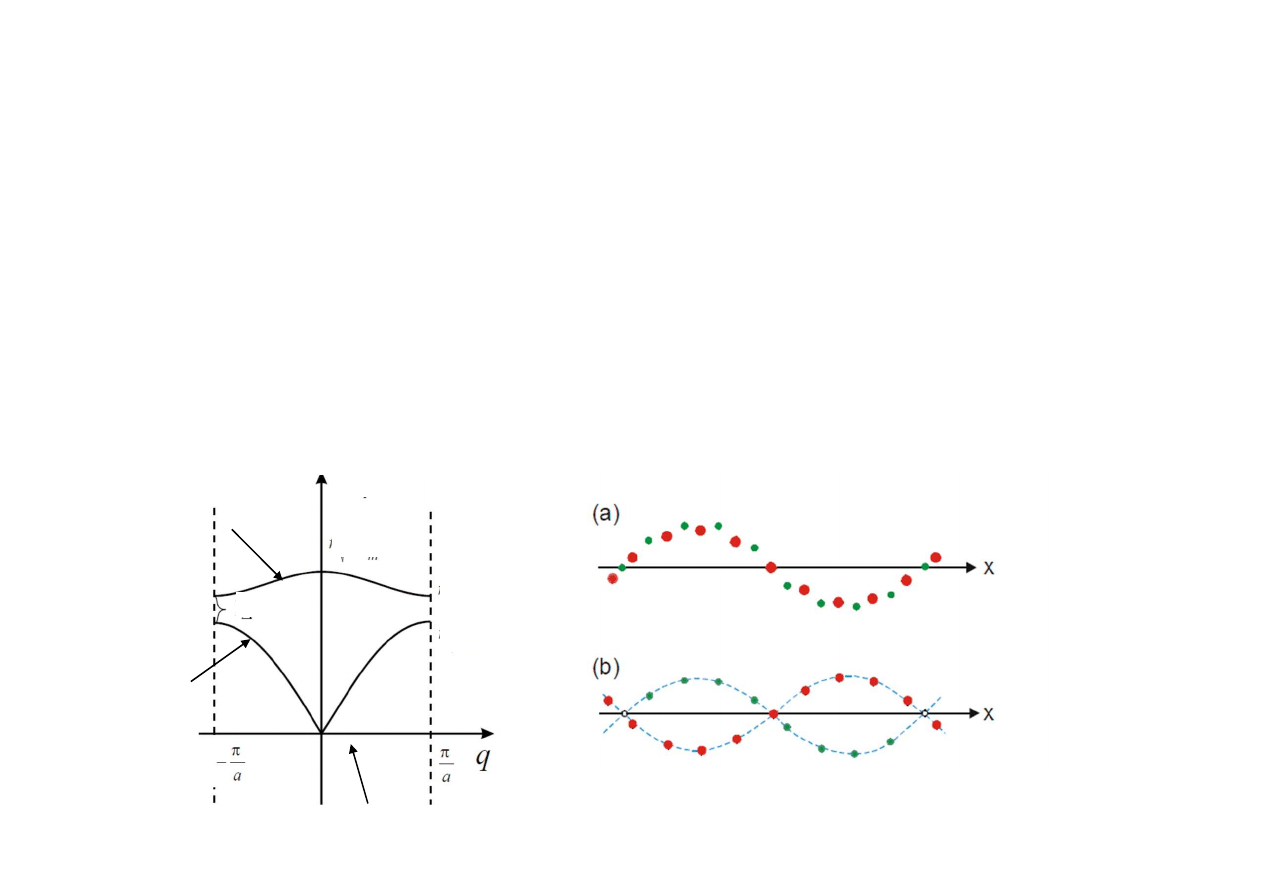
Analiza zale

ż

no

ś

ci wskazuje na to z w dowolnym krysztale 3

wymiarowym wyst

ę

puj

ą

3 gał

ę

zie akustyczne dla których

W przypadku bardziej zło

ż

onych kryształów zło

ż

onych np. z ró

ż

nych

atomów wyst

ę

puj

ą

tak

ż

e gał

ę

zie optyczne dla których

W przypadku drga

ń

z gał

ę

zi optycznej dla s

ą

siednie atomy drgaj

ą

w

przciwfazie, za

ś

dla drga

ń

z gał

ę

zi akustycznej w fazie.

0

)

(

lim

0

=

→

q

q

r

ω

0

)

(

lim

0

≠

→

q

q

r

ω

ω

drgania akustyczne

drgania optyczne

Drgania akustyczne i optyczne

0

→

q

Zale

ż

no

ść

cz

ę

sto

ś

ci drga

ń

od wektora falowego w

przypadku kryształu jednowymiarowego zawieraj

ą

cego dwa

ró

ż

ne rodzaje atomów

q

∝

gał

ąź

akustyczna

gał

ąź

optyczna

)

(q

r

ω

Fonony-kwanty energii drga

ń

atomów w krysztale

Dla fononów można wprowadzić funkcję gęstości stanów D(ω) określającą ilość
drgań normalnych o częstości kołowej z zakresu

w krysztale

( )

∑∑













+

=

i

q

i

q

n

q

U

r

r

r

h

2

1

,

ω

Energie zwi

ą

zan

ą

z drganiami atomów w krysztale mo

ż

na zapisa

ć

jako

sum

ę

energii tzw. drga

ń

normalnych reprezentuj

ą

cych kolektywne drgania

wszystkich atomów w krysztale opisywanych przez fale. Do okre

ś

lenia

energii drgania normalnego wykorzystujemy wzór na energie drga

ń

kwantowego oscylatora harmonicznego

gdzie okre

ś

la stopie

ń

wzbudzenia danego drgania, równy ilo

ś

ci

quasi-cz

ą

stek zwanych fononami, b

ę

d

ą

cych bezspinowymi bozonami o

energii i quasi-p

ę

dzie

Sumowanie po i dotyczy sumowania po ró

ż

nych modach drga

ń

opisanych przez ten sam wektor falowy

ω

h

=

fon

E

q

p

fon

r

h

r

=

(

)

ω

ω

ω

d

+

,

q

r

Funkcja g

ę

sto

ś

ci stanów dla fononów

i

q

n

,

r

W najprostszym przybli

ż

eniu zakładaj

ą

c i

ż

zachodzi zale

ż

no

ść

(V- pr

ę

dko

ść

rozchodzenia si

ę

fal opisuj

ą

cych drgania atomów) obowi

ą

zuj

ą

ca

w rzeczywisto

ś

ci dla fononów akustycznych dla małych q funkcja g

ę

sto

ś

ci

stanów wyra

ż

a si

ę

dla wzorem V

ob

-obj

ę

to

ść

kryształu

N-liczba atomów

w krysztale

przy czym wyznaczamy z warunku

co prowadzi do wniosku i

ż

q

V

r

=

ω

max

ω

ω

<

max

ω

N

d

D

3

)

(

max

0

=

∫

ω

ω

ω

ob

V

V

D

3

2

2

2

3

)

(

π

ω

ω

=

Poniewa

ż

fonony mo

ż

na traktowa

ć

jako bozony o potencjale chemicznym

µ

=0 to

ś

redni

ą

energi

ę

zwi

ą

zan

ą

z drganiami atomów mo

ż

emy wyznaczy

ć

z

równania (pomijamy energie drga

ń

zerowych)

gdzie

-

wzór wynikaj

ą

cy z rozkładu

Bosego-Einsteina okre

ś

laj

ą

cy

ś

redni

ą

liczb

ę

fononów w temperaturze T w

konkretnym stanie o energii , k

B

-stała Boltzmanna

( ) ( )

∫

=

max

0

ω

ω

ω

ω

ω

d

N

D

U

h

1

exp

1

)

(

−













=

T

k

N

B

ω

ω

h

ω

h

3

3

2

max

/

6

ob

V

NV

π

ω

=

Wyznaczenie

ś

redniej energii termicznej drga

ń

i ciepła molowego

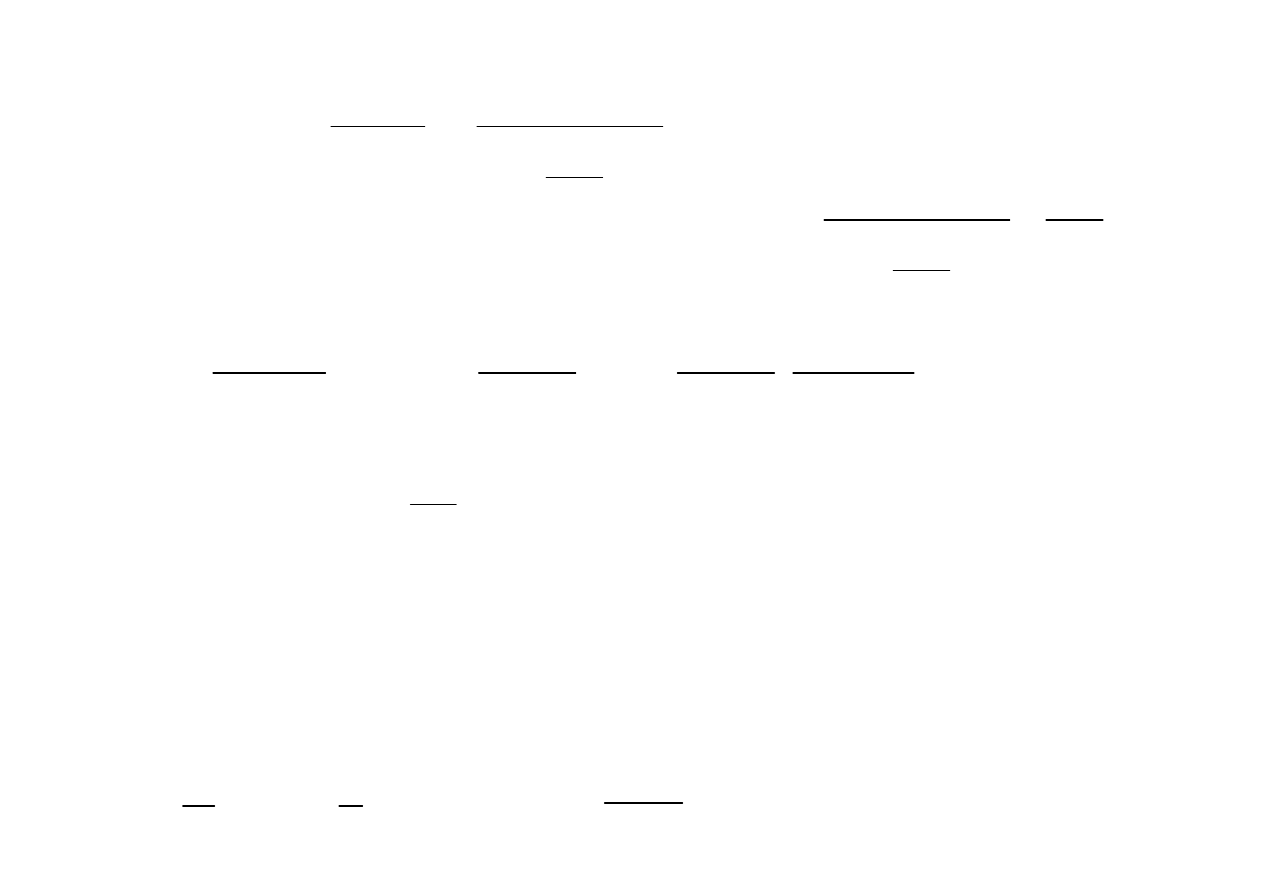
W granicy wysokich temperatur można przyjąć iż

i wówczas można pokazać iż

A zatem zgodnie z zasadą ekwipartycji energii ciepło molowe przy stałej
objętości

jest niezależne od temperatury i równe

N

A

-liczba Avogadro

W niskich temperaturach można przy liczeniu U zastąpić
przez i wówczas można pokazać iż

gdzie temperatura Debye’a

A

B

v

N

k

C

3

=

3

4

5

12













=

θ

π

T

N

k

C

A

B

v

θ

<<

T

B

k

max

ω

θ

h

=

dT

dU

C

v

=

∫

−













=

max

0

0

3

2

2

1

exp

1

2

3

ω

ω

ω

π

ω

ω

d

T

k

h

V

V

U

B

b

h

ω

ω

h

h

T

k

T

k

B

B

≈

−













1

exp

1

max

ω

∞

T

Nk

V

NV

V

TV

k

V

TV

k

d

V

TV

k

U

B

ob

ob

B

ob

B

ob

B

3

6

2

2

2

3

3

2

3

2

3

max

3

2

0

2

3

2

max

=

⋅

=

=

=

∫

π

π

ω

π

ω

ω

π

ω

Po zró

ż

niczkowaniu obustronnym powy

ż

szej zale

ż

no

ś

ci otrzymujemy

relacj

ę

:

Liczba drga

ń

normalnych o energiach o cz

ę

sto

ś

ciach z zakresu

jest proporcjonalna do obj

ę

to

ś

ci cienkiej warstwy kulistej w przestrzeni

wektorów falowych o promieniu i grubo

ś

ci

Uzupełnienie-Wyznaczenie funkcji g

ę

sto

ś

ci stanów dla

fononów akustycznych przy zało

ż

eniu liniowej relacji dyspersji

Vq

=

ω

Vdq

d

=

ω

(

)

ω

ω

ω

d

+

,

V

q

ω

=

ω

d

V

dq

1

=

Objętość tej warstwy jest równa

ω

ω

π

π

d

V

dq

q

3

2

2

4

4

⋅

=

W celu obliczenia liczby drga

ń

normalnych trzeba podzieli

ć

t

ą

obj

ę

to

ść

przez obj

ę

to

ść

przypadaj

ą

c

ą

na jeden wektor falowy w rozwa

ż

anej

przestrzeni równ

ą

i pomno

ż

y

ć

przez 3 ze wzgl

ę

du na to i

ż

zakładamy i

ż

ka

ż

demu

wektorowi mog

ą

odpowiada

ć

3 mody drga

ń

Ostatecznie otrzymujemy

( )

ob

q

V

V

3

2

~

π

=

r

ob

ob

V

V

V

V

D

3

2

2

3

3

2

2

3

3

8

4

)

(

π

ω

π

ω

π

ω

=

⋅

⋅

⋅

=