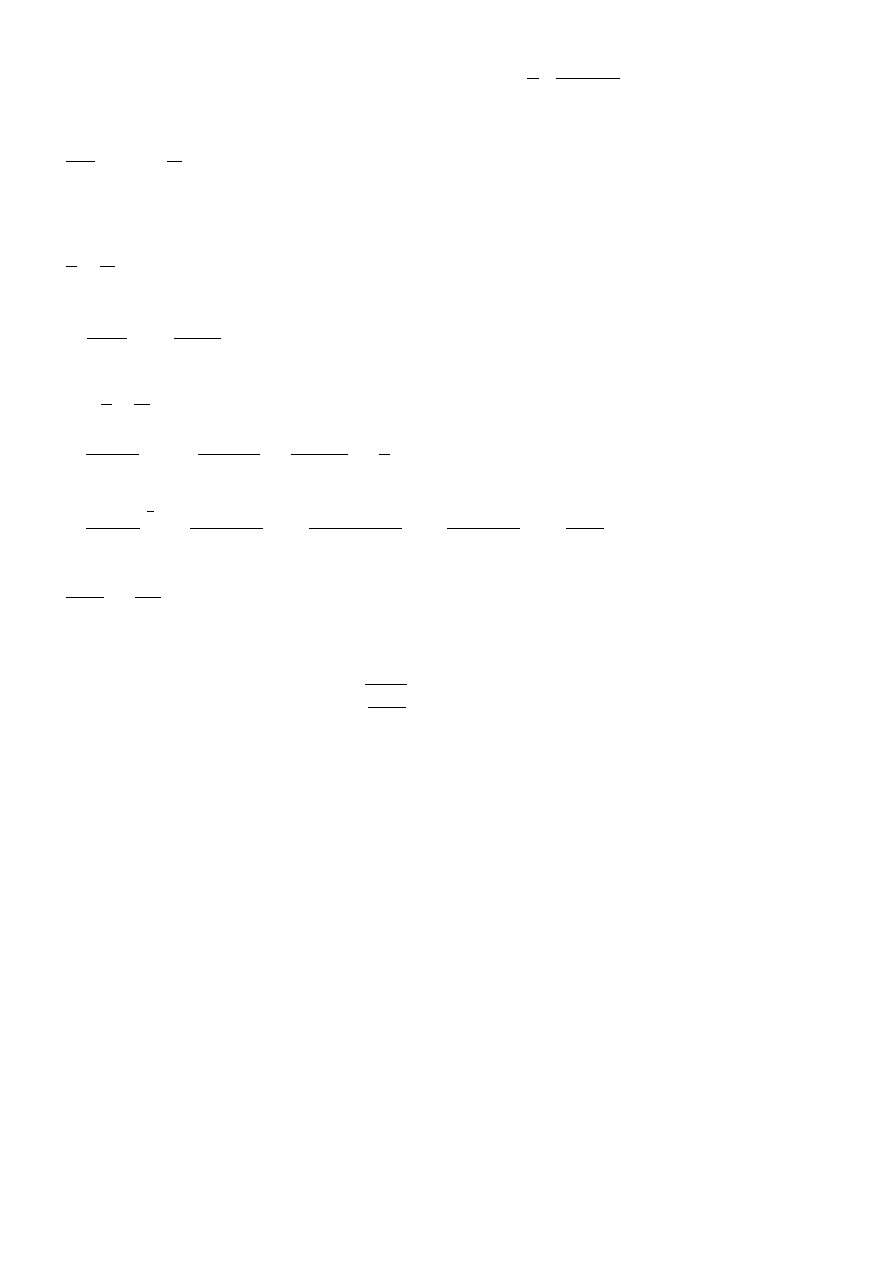
Pochodne:

f (g ( x))= f ' ( g (x ))∗g ' (x)

cos(lnx)=cos (lnx)∗

1

x

=

cos (lnx)

x

Reguła De L'Hospitala

[

A

±∞

]

=

0

[

A
0

]

=±∞

ln 0 →−∞
ln 1=0
ln e=1
ln ∞ →∞

jeżeli występuje któryś z pierwszych dwóch symboli nie oznaczonych:

[

0
0

]

,

[

∞

∞

]

,

[

0⋅∞

]

,

[

∞−∞

]

,

[

1

∞

]

,

[

∞

0

]

,

[

0

0

]

to:

lim

x →

❑

f ( x)

g (x )

=

H

↑

❑

lim

x →

❑

f ' ( x)

g ' (x )

Przykład:

dla:

[

0
0

]

,

[

∞

∞

]

;

lim

x →0

2 e

x

−

2

sin x

[

2∗e

0

−

2

sin 0

]

=

[

2∗1−2

0

]

=

[

0
0

]

lim

x →0

2 e

x

−

2

sin x

=

H

[

0
0

]

lim

x → 0

(

2 e

x

−

2)'

(

sin x)'

=

lim

x → 0

(

2 e

x

)

'−(2)'

cos x

=

lim

x→ 0

2(e

x

)

'−0

cos x

=

lim

x → 0

2 e

x

cos x

=

2

[

2 e

0

cos0

]

=

[

2⋅1

1

]

=

[

2

]

dla:

[

∞−∞

]

w 90% sprowadzenie do wspólnego mianownika

dla:

[

0⋅∞

]

f (x )⋅g ( x)=

f ( x)

1

g (x )

dla:

[

1

∞

]

,

[

∞

0

]

,

[

0

0

]

a

b

=

e

bln a

lim

x →

❑

f ( x)

g (x)

=

lim

x →

❑

e

g (x)ln f (x)

=

e

∇

lim

x →

❑

g (x)ln f (x )=∇

Całkowanie przez części:
np.

∫

xsin x dx=

∣

U =x

V '=sin x

U ' =1 V =

∫

V '

∣

=

U⋅V −

∫

U '⋅Vdx