1

ODPOWIEDZI DO ZADA

Ń

SAMODZIELNYCH

BLOK 1 odpowiedzi do zada

ń

do samodzielnego rozwi

ą

zania

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

Odpowiedzi do zestawu do samodzielnego rozwi

ą

zania:

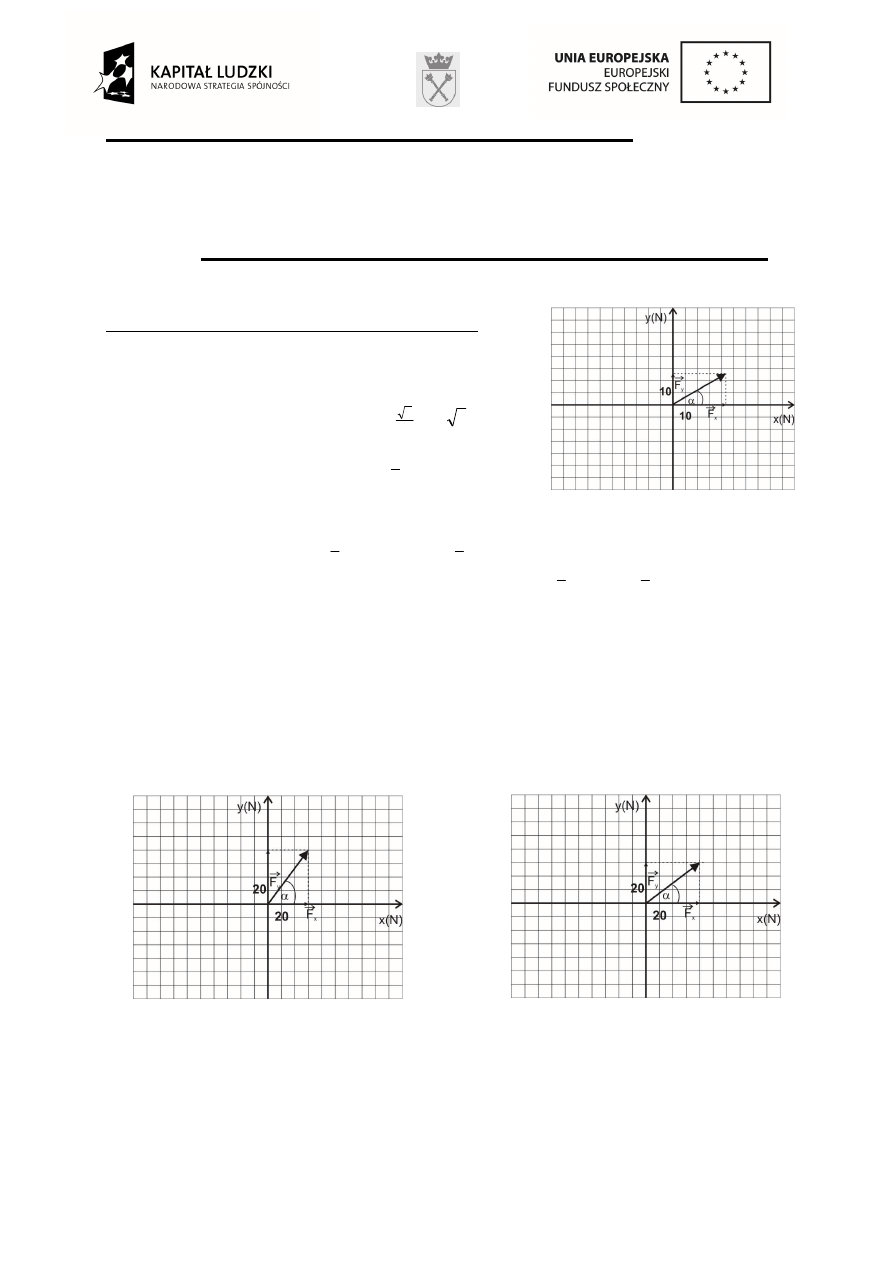
1. Składowe danego wektora to wektory równoległe do osi

układu współrz

ę

dnych, których suma jest równa danemu

wektorowi.

Współrz

ę

dne siły:

N

3

25

N

50

30

cos

N

50

cos

|

F

|

F

2

3

o

x

=

⋅

=

⋅

=

α

⋅

=

r

N

25

N

50

30

sin

N

50

sin

|

F

|

F

2

1

o

y

=

⋅

=

⋅

=

α

⋅

=

r

Obie współrz

ę

dne s

ą

dodatnie, poniewa

ż

obie składowe

wektora maj

ą

ten sam zwrot, co odpowiadaj

ą

ce im osi współrz

ę

dnych.

2.

N

100

|

F

|

=

r

,

4

3

y

x

|

F

|

/

|

F

|

=

r

r

lub

4

3

x

y

|

F

|

/

|

F

|

=

r

r

α

⋅

=

cos

|

F

|

|

F

|

x

r

r

, a

α

⋅

=

sin

|

F

|

|

F

|

y

r

r

, dlatego

4

3

y

x

ctg

|

F

|

/

|

F

|

=

α

=

r

r

lub

4

3

tg

=

α

.

K

ą

t:

=

∠

)

F

,

F

(

x

r

r

o

13

,

53

=

α

albo

o

13

,

233

=

α

Lub

=

∠

)

F

,

F

(

x

r

r

o

87

,

36

=

α

albo

o

87

,

216

=

α

Warto

ś

ci składowych:

N

60

6

,

0

N

100

|

cos

|

|

F

|

|

F

|

x

=

⋅

=

α

⋅

=

r

r

i

N

80

8

,

0

N

100

|

sin

|

|

F

|

|

F

|

y

=

⋅

=

α

⋅

=

r

r

lub

N

80

8

,

0

N

100

|

cos

|

|

F

|

|

F

|

x

=

⋅

=

α

⋅

=

r

r

i

N

60

6

,

0

N

100

|

sin

|

|

F

|

|

F

|

x

=

⋅

=

α

⋅

=

r

r

lub

3. Wektory niezerowe

a

r

i

b

r

s

ą

do siebie prostopadłe

⇔

0

b

a

=

r

o

r

Spr.

⇒

=

⋅

+

⋅

=

+

=

4

2

1

1

2

b

a

b

a

b

a

y

y

x

x

r

o

r

te wektory nie s

ą

prostopadłe do siebie.

4. E

Blok 1:

Podstawowe wielko

ś

ci fizyczne w kinematyce.

Rachunek wektorowy i jego zastosowanie w fizyce. Ruch
wzgl

ę

dny.

2

ODPOWIEDZI DO ZADA

Ń

SAMODZIELNYCH

BLOK 1 odpowiedzi do zada

ń

do samodzielnego rozwi

ą

zania

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

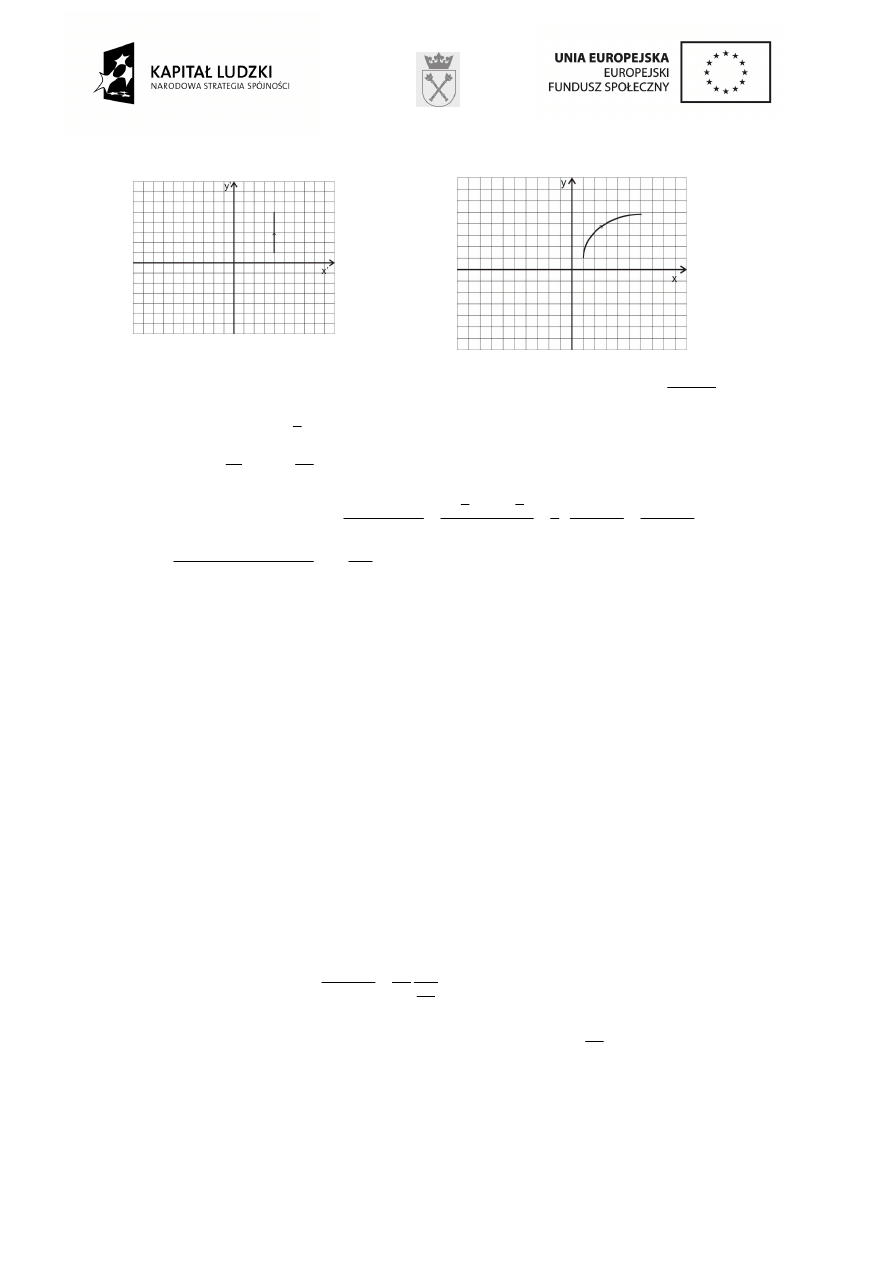
5. Tor piłki w układzie odniesienia

Tor piłki w układzie odniesienia zwi

ą

zanym z Ziemi

ą

:

zwi

ą

zanym z wagonem:

6. Szybko

ść

ś

rednia w ruchu, który składa si

ę

z dwóch etapów dana jest:

2

1

2

1

ś

r

t

t

s

s

v

+

+

=

.

Jednocze

ś

nie

t

t

t

2

1

2

1

=

=

. Ruch w ka

ż

dym etapie jest ruchem jednostajnym prostoliniowym,

dlatego:

1

1

1

t

s

v

=

i

2

2

2

t

s

v

=

. St

ą

d:

1

1

1

t

v

s

⋅

=

i

2

2

2

t

v

s

⋅

=

.

Zatem szybko

ść

ś

rednia:

2

v

v

t

v

v

t

t

t

v

t

v

t

t

v

t

v

v

2

1

2

1

2

1

2

1

2

2

1

1

2

2

1

1

ś

r

+

=

+

=

+

=

+

=

.

h

km

55

2

h

/

km

70

h

/

km

40

v

ś

r

=

+

=

7.

d

s

wyp

v

v

v

r

r

r

+

=

Dziecko idzie po ruchomych schodach w stron

ę

ruchu schodów

⇒

obie pr

ę

dko

ś

ci maj

ą

ten sam

zwrot. Obieramy tak o

ś

OX układu współrz

ę

dnych, aby była równoległa do obu pr

ę

dko

ś

ci i miała

ten sam zwrot, co one. Wówczas równanie na współrz

ę

dnych iksowych:

s

m

s

m

s

m

h

km

v

v

v

d

s

wyp

/

5

,

3

/

)

3

5

,

0

(

/

3

/

8

,

1

|

|

|

|

=

+

=

+

=

+

=

r

r

Dziecko idzie po ruchomych schodach w stron

ę

przeciwn

ą

do ruchu schodów

⇒

pr

ę

dko

ść

schodów ma zwrot przeciwny do zwrotu pr

ę

dko

ś

ci dziecka . Obieramy tak o

ś

OX układu

współrz

ę

dnych np. tak, aby była równoległa do obu pr

ę

dko

ś

ci i miała ten sam zwrot, co pr

ę

dko

ść

schodów. Wówczas równanie na współrz

ę

dnych iksowych:

s

m

s

m

s

m

h

km

v

v

v

d

s

wyp

/

5

,

2

/

)

3

5

,

0

(

/

3

/

8

,

1

|

|

|

|

−

=

−

=

−

=

−

=

r

r

. W równaniu tym obliczona

współrz

ę

dna pr

ę

dko

ś

ci wypadkowej jest ujemna, co oznacza,

ż

e iksowa składowa pr

ę

dko

ś

ci

wypadkowej nie jest zgodna ze zwrotem wybranej przez nas wcze

ś

niej osi OX. Zatem ma ona

zwrot zgodny ze zwrotem pr

ę

dko

ś

ci dziecka.

8. Najłatwiej obliczy

ć

czas, przechodz

ą

c do układu współrz

ę

dnych zwi

ą

zanego z jednym z

pojazdów. W tym układzie suma dróg, które musz

ą

pokona

ć

skutery wynosi

km

20

L

=

, a

szybko

ść

wzgl

ę

dna skuterów:

h

/

km

80

v

v

v

2

1

wzgl

=

+

=

. St

ą

d czas, który minie do chwili

spotkania skuterów:

h

25

,

0

km

80

20

v

v

L

t

h

km

2

1

=

=

+

=

.

Czas ten jest równy tak

ż

e całkowitemu czasowi lotu pszczoły. Pszczoła leci z szybko

ś

ci

ą

h

/

km

60

u

=

, dlatego w sumie pokona ona drog

ę

;

km

15

h

25

.

0

60

t

u

s

h

km

=

⋅

=

⋅

=

.

3

ODPOWIEDZI DO ZADA

Ń

SAMODZIELNYCH

BLOK 1 odpowiedzi do zada

ń

do samodzielnego rozwi

ą

zania

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

9. D

Wszystkie łódki przepłyn

ą

w tym samym czasie na drugi brzeg, poniewa

ż

decyduj

ą

o tym tylko

składowe ich pr

ę

dko

ś

ci prostopadłe do linii brzegowej. Z rysunku wynika,

ż

e składowe te s

ą

dla

wszystkich łódek identyczne.

10. To zadanie najłatwiej rozwi

ą

za

ć

w układzie odniesienia zwi

ą

zanym z nurtem rzeki, czyli takim,

który wzgl

ę

dem brzegów porusza si

ę

z pr

ę

dko

ś

ci

ą

rzeki.

Załó

ż

my,

ż

e pocz

ą

tkowo motorówka płyn

ę

ła z nurtem rzeki.

W tym etapie ruchu , w czasie

s

30

t

1

=

motorówka przebyła w wybranym przez nas układzie

współrz

ę

dnych drog

ę

równ

ą

1

M

1

t

v

s

⋅

=

(w układzie zwi

ą

zanym z nurtem rzeki musimy wzi

ąć

pod uwag

ę

pr

ę

dko

ść

motorówki wzgl

ę

dem rzeki). Po zawróceniu: w tym samym układzie

współrz

ę

dnych: droga przebyta przez motorówk

ę

:

2

M

2

t

v

s

⋅

=

, a droga przebyta przez

płyn

ą

ce z nurtem rzeki koło jest równa zeru (wzgl

ę

dem nurtu koło si

ę

nie porusza).

Dodatkowo drogi s

ą

sobie równe (bo liczymy je wzgl

ę

dem nurtu rzeki). St

ą

d wida

ć

,

ż

e

2

1

t

t

=

.

Analogiczne rozumowanie mo

ż

na przeprowadzi

ć

zakładaj

ą

c,

ż

e pocz

ą

tkowo motorówka

poruszała si

ę

pod pr

ą

d rzeki.