1

BLOK 5 odpowiedzi do zada

ń

do samodzielnego rozwi

ą

zania

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

Odpowiedzi do zada

ń

do samodzielnego rozwi

ą

zania:

1. Wskazanie wagi spr

ęż

ynowej jest równe co do warto

ś

ci sile reakcji powierzchni wagi.

Poniewa

ż

masa człowieka jest równa 80 kg, to wskazanie wagi w windzie spoczywaj

ą

cej

powinno by

ć

równe:

N

800

10

kg

80

mg

|

F

|

|

R

|

2

s

m

c

=

⋅

=

=

=

r

r

. Ale w zadaniu wskazanie wagi jest

wi

ę

ksze ni

ż

ta warto

ść

. Oznacza to,

ż

e warto

ść

reakcji podło

ż

a jest wi

ę

ksza ni

ż

w windzie

spoczywaj

ą

cej i wynosi 1000 N. Zadanie to mo

ż

na rozwi

ą

za

ć

w dwóch układach:

•

W układzie inercjalnym. Siły działaj

ą

ce na człowieka nadaj

ą

mu przyspieszenie równe

przyspieszeniu windy:

II zasada dynamiki Newtona:

m

a

F

R

c

⋅

=

+

r

r

r

. Niech pionowa o

ś

układu współrz

ę

dnych

b

ę

dzie zwrócona ku górze. Wówczas algebraiczne równanie ruchu przyjmuje posta

ć

:

m

a

mg

R

F

R

y

c

⋅

=

−

=

−

, przy czym nie wiemy jeszcze, czy

0

a

y

>

, czy

0

a

y

<

.

2

2

s

m

s

m

y

5

,

2

kg

80

N

200

kg

80

10

kg

80

N

1000

m

mg

R

a

=

=

⋅

−

=

−

=

. Współrz

ę

dna ta jest dodatnia,

zatem przyspieszenie windy jest równe co do warto

ś

ci

2

s

m

5

,

2

a

=

i skierowane pionowo w

gór

ę

, zgodnie z kierunkiem i zwrotem wybranej przez nas osi układu współrz

ę

dnych.

Oznacza to mo

ż

liwo

ść

zaistnienia dwóch przypadków: albo winda porusza si

ę

pionowo w

gór

ę

i przyspiesza, albo porusza si

ę

pionowo w dół i hamuje.

•

W układzie nieinercjalnym, zwi

ą

zanym z wind

ą

.

Ż

eby móc stosowa

ć

II zasad

ę

dynamiki Newtona, musimy uwzgl

ę

dni

ć

sił

ę

bezwładno

ś

ci działaj

ą

c

ą

na człowieka w

tej windzie.

0

F

F

R

b

c

=

+

+

r

r

r

, gdy

ż

człowiek nie porusza si

ę

w swoim własnym układzie

współrz

ę

dnych (inaczej mówi

ą

c: w układzie windy). Korzystamy z wektorowej definicji siły

bezwładno

ś

ci:

m

a

F

b

⋅

−

=

r

r

.

Uwaga: minus jest tutaj istotny!

Czyli:

0

m

a

F

R

c

=

⋅

−

+

r

r

r

m

a

F

R

c

⋅

=

+

⇒

r

r

r

.

Od tego miejsca rozwi

ą

zanie zadania jest analogiczne jak w układzie inercjalnym:

Niech pionowa o

ś

układu współrz

ę

dnych b

ę

dzie zwrócona ku górze. Wówczas

algebraiczne równanie ruchu przyjmuje posta

ć

:

m

a

mg

R

F

R

y

c

⋅

=

−

=

−

, przy czym nie

wiemy jeszcze, czy

0

a

y

>

, czy

0

a

y

<

.

2

2

s

m

s

m

y

5

,

2

kg

80

N

200

kg

80

10

kg

80

N

1000

m

mg

R

a

=

=

⋅

−

=

−

=

. Współrz

ę

dna ta jest dodatnia,

zatem przyspieszenie windy jest równe co do warto

ś

ci

2

s

m

5

,

2

a

=

i skierowane pionowo w

gór

ę

, zgodnie z kierunkiem i zwrotem wybranej przez nas osi układu współrz

ę

dnych.

Oznacza to mo

ż

liwo

ść

zaistnienia dwóch przypadków: albo winda porusza si

ę

pionowo w

gór

ę

i przyspiesza, albo porusza si

ę

pionowo w dół i hamuje.

Odp. B i C

Blok 5:

Układy nieinercjalne.

Siły bezwładno

ś

ci

2

BLOK 5 odpowiedzi do zada

ń

do samodzielnego rozwi

ą

zania

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

2. Wskazanie wagi jest równe co do warto

ś

ci sile reakcji powierzchni wagi na człowieka. Je

ż

eli

jednak winda urwała si

ę

, to zarówno winda, jak i waga, jak i człowiek – wszystkie te ciała

poruszaj

ą

si

ę

z tym samym przyspieszeniem równym przyspieszeniu ziemskiemu. II zasada

dynamiki Newtona w układzie inercjalnym (laboratoryjnym, zwi

ą

zanym z Ziemi

ą

):

m

a

R

F

c

⋅

=

+

r

r

r

, ale

g

a

r

r

=

, jak to poprzednio zauwa

ż

yli

ś

my. Zatem:

0

R

m

g

R

g

m

=

⇒

⋅

=

+

r

r

r

r

.

Zatem wskazanie wagi tak

ż

e jest równe zeru.

3. Naci

ą

g nici nie jest dla danej nici warto

ś

ci

ą

uniwersaln

ą

. Siła naci

ą

gu nici dostosowuje si

ę

bowiem (a

ż

do pewnej warto

ś

ci granicznej zwanej wytrzymało

ś

ci

ą

nici) do warto

ś

ci sił

napr

ęż

aj

ą

cych ni

ć

. Sił

ą

napr

ęż

aj

ą

c

ą

ni

ć

jest wypadkowa sił działaj

ą

cych na ni

ć

od strony kulki

wahadła matematycznego, a ta z kolei jest równa składowej wzdłu

ż

nici siły wypadkowej

działaj

ą

cej na kulk

ę

. Rozpatrujemy wahadło w pozycji (stanie) równowagi. Gdy autobus stoi

na przystanku, wahadło matematyczne wisi w pozycji pionowej. Gdy autobus rusza z
przystanku, mo

ż

na przyj

ąć

,

ż

e od pierwszej chwili jego przyspieszenie jest stałe i wynosi

a

r

.

Na kulk

ę

wahadła zaczyna wi

ę

c działa

ć

siła bezwładno

ś

ci zwrócona w stron

ę

przeciwn

ą

do

przyspieszenia autobusu,

a

r

. Wahadło matematyczne zaczyna si

ę

odchyla

ć

w pierwszych

chwilach jazdy i znajduje now

ą

pozycj

ę

równowagow

ą

– w odchyleniu o pewien k

ą

t

α

od

pionu. K

ą

t ten jest

ś

ci

ś

le ustalony i jego tangens wynosi

g

a

|

F

|

|

F

|

tg

c

b

=

=

α

r

r

.

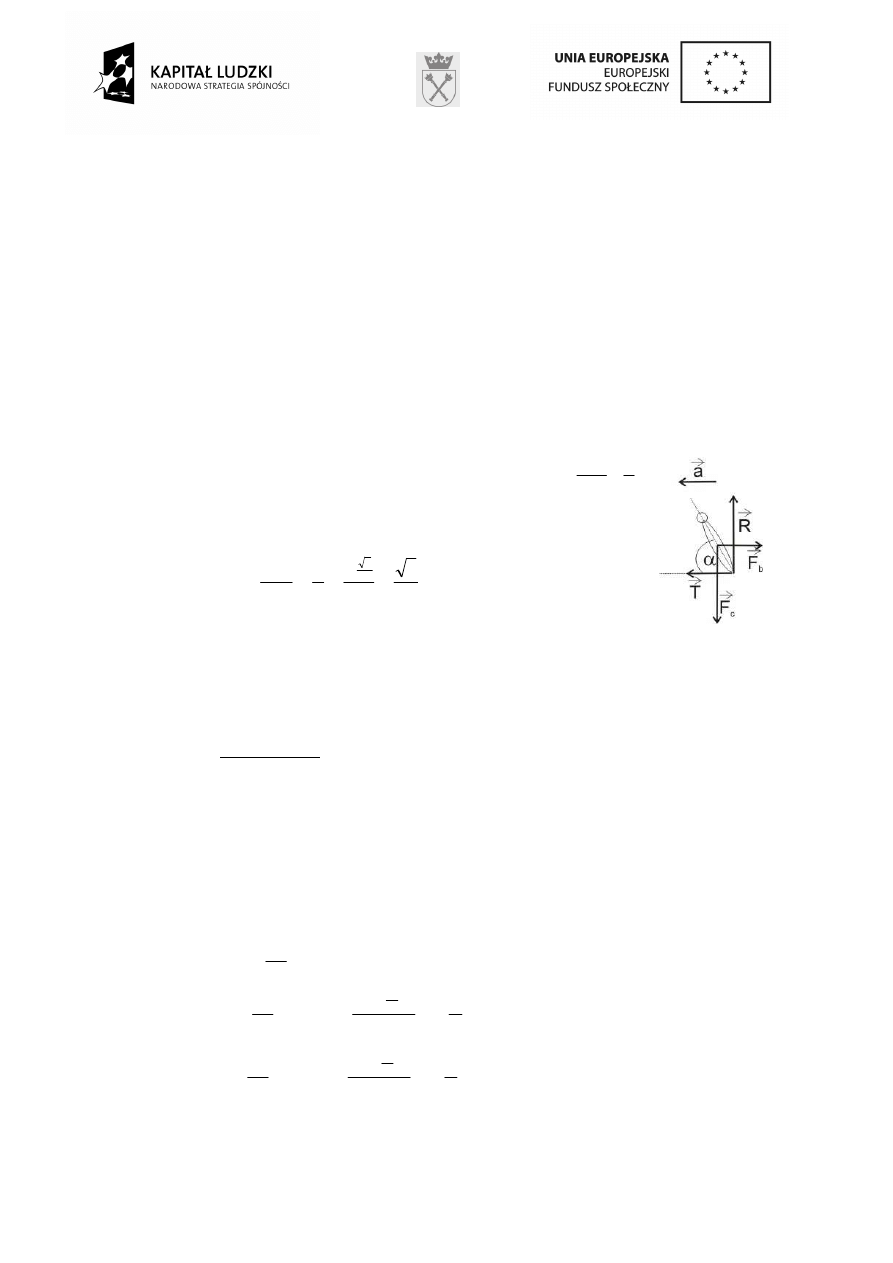
4. Zadanie to mo

ż

na rozwi

ą

za

ć

np. w układzie nieinercjalnym. Siły

działaj

ą

ce na człowieka (autobus przyspiesza w lewo):

Zatem

o

3

3

c

b

60

α

3

3

g

g

g

a

|

F

|

|

F

|

ctgα

=

⇒

=

=

=

=

r

r

5. Warto

ść

siły nacisku pilota na fotel jest równa warto

ś

ci siły reakcji fotela na pilota. Zadanie

mo

ż

emy rozwi

ą

za

ć

np. w układzie nieinercjalnym:

I zasada dynamiki Newtona w obu przypadkach (pilot w maksymalnym lub minimalnym
poło

ż

eniu) jest dana:

0

R

F

F

b

c

=

+

+

r

r

r

Uwaga: Sił

ą

bezwładno

ś

ci w ruchu jednostajnym po okr

ę

gu jest siła od

ś

rodkowa.

Mo

ż

emy nie korzystaj

ą

c z wektorowej definicji siły bezwładno

ś

ci, od razu zapisa

ć

I zasad

ę

dynamiki Newtona w składowych igrekowych (o

ś

OY wybieramy pionow

ą

, zwrócon

ą

do

ś

rodka okr

ę

gu).

Pilot porusza si

ę

tak,

ż

e jego głowa jest stale zwrócona do

ś

rodka p

ę

tli, a zatem porusza si

ę

po wewn

ę

trznej stronie tej p

ę

tli.

Pilot w najwy

ż

szym punkcie toru:

0

F

R

mg

b

najwyzszy

=

−

+

mg

m

a

mg

F

R

d

b

najwyzszy

−

⋅

=

−

=

⇒

Pilot w najni

ż

szym punkcie toru:

0

F

R

mg

b

najnizszy

=

−

+

−

mg

m

a

mg

F

R

d

b

najnizszy

+

⋅

=

+

=

⇒

Poniewa

ż

R

v

a

2

d

=

, to:

N

3200

kg

80

10

m

200

)

100

(

m

g

R

v

R

2

s

m

2

s

m

2

najwyzszy

=

⋅















−

=

⋅















−

=

N

4800

kg

80

10

m

200

)

100

(

m

g

R

v

R

2

s

m

2

s

m

2

najnizszy

=

⋅















+

=

⋅















+

=

3

BLOK 5 odpowiedzi do zada

ń

do samodzielnego rozwi

ą

zania

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

6. Siła nacisku roweru na mostek jest jak zawsze równa sile reakcji powierzchni mostka na

rower.

I zasada dynamiki Newtona:

0

R

F

F

b

c

=

+

+

r

r

r

Teraz sytuacja jest jednak inna ni

ż

w poprzednim zadaniu, poniewa

ż

rower porusza si

ę

po

zewn

ę

trznej stronie zakrzywionego mostka. Ponownie wybieramy o

ś

OY, tym razem np.

zwrócon

ą

pionowo w dół:

0

F

R

mg

b

=

−

−

N

400

kg

80

m

20

)

10

(

10

m

R

v

g

R

2

s

m

s

m

2

2

=

⋅















−

=

⋅















−

=

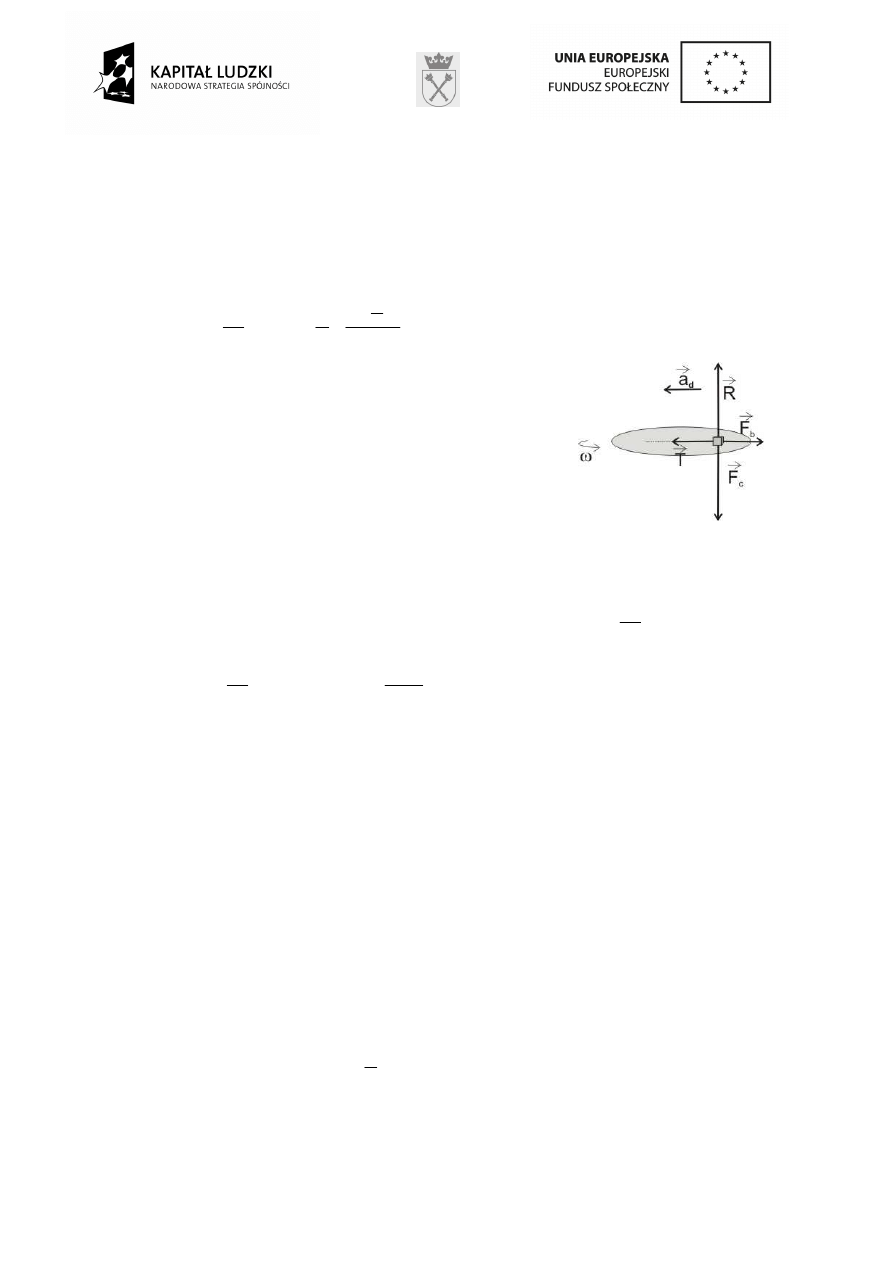
7. Zadanie to mo

ż

emy rozwi

ą

za

ć

np. w układzie

nieinercjalnym, zwi

ą

zanym z tarcz

ą

. O

ś

OY tego układu jest

prostopadła do powierzchni tarczy, a o

ś

OX jest równoległa

do powierzchni tarczy i zwrócona do

ś

rodka tarczy; pocz

ą

tek

układu współrz

ę

dnych znajduje si

ę

np. w punkcie poło

ż

enia

klocka.

Siły reakcji i ci

ęż

ko

ś

ci równowa

żą

si

ę

(klocek nie porusza

si

ę

, a tym bardziej nie przyspiesza w pionie):

(*)

c

c

F

R

0

F

R

=

⇒

=

−

Składowa pozioma siły wypadkowej, w układzie klocka tak

ż

e jest równa zeru i w przypadku

granicznym (tu

ż

przed zerwaniem przyczepno

ś

ci):

0

F

T

b

max

s

=

−

m

a

R

d

s

=

µ

⇒

.

Korzystaj

ą

c z wzoru na warto

ść

przyspieszenia do

ś

rodkowego:

r

v

a

2

d

=

oraz z równania (*),

otrzymujemy:

2

s

2

2

s

g

r

m

r

m

r

v

mg

ω

⋅

µ

=

⇒

⋅

⋅

ω

=

=

⋅

µ

8. Tak, jest to mo

ż

liwe. Wystarczy,

ż

eby siła docisku klocka do pionowej

ś

ciany (a tym samym

siła reakcji

ś

ciany,

R

r

) miała na tyle du

żą

warto

ść

, aby tarcie statyczne powstałe pomi

ę

dzy

ś

cian

ą

a klockiem zrównowa

ż

yło sił

ę

ci

ęż

ko

ś

ci klocka.

Zatem spełnione musz

ą

by

ć

dwa warunki:

c

s

F

T

=

, czyli w przypadku granicznym

mg

R

s

=

µ

.

Siła docisku jest równa co do warto

ś

ci sile bezwładno

ś

ci działaj

ą

cej na klocek (je

ś

li

rozpatrujemy sytuacj

ę

klocka w nieinercjalnym układzie współrz

ę

dnych zwi

ą

zanym z pionow

ą

ś

cian

ą

platformy. Czyli

m

a

R

⋅

=

. Ostateczny warunek na spoczywanie klocka po pionowej

ś

cianie:

g

a

s

=

⋅

µ

.

9. Zadanie mo

ż

na rozwi

ą

za

ć

np. w układzie nieinercjalnym zwi

ą

zanym z kartk

ą

. I zasada

dynamiki Newtona dla kredy:

0

F

T

R

F

b

max

s

c

=

+

+

+

r

r

r

r

, przy czym w układzie współrz

ę

dnych, w którym o

ś

OY jest

prostopadła do powierzchni kartki, a o

ś

OX jest równoległa do tej powierzchni i ma kierunek i

zwrot zgodny z kierunkiem i zwrotem przyspieszenia kartki:
dla osi OX:

0

F

T

b

max

s

=

−

dla osi OY:

g

m

F

R

0

F

R

c

c

⋅

=

=

⇒

=

−

Poniewa

ż

R

T

s

max

s

µ

=

oraz

m

a

F

b

⋅

=

otrzymujemy warunek na maksymaln

ą

warto

ść

przyspieszenia:

2

s

m

s

2

g

µ

a

=

⋅

=

.