1

BLOK 4 odpowiedzi do zada

ń

do samodzielnego rozwi

ą

zania

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

Odpowiedzi do zada

ń

do samodzielnego rozwi

ą

zania:

1. II zasada dynamiki Newtona dla całego układu:

)

m

m

(

a

R

R

F

F

F

2

1

2

1

2

c

1

c

+

⋅

=

+

+

+

+

r

r

r

r

r

r

Poniewa

ż

ruch odbywa si

ę

w poziomie, to interesuje nas

tylko równanie na iksow

ą

składow

ą

siły wypadkowej działaj

ą

cej na ten układ klocków:

2

1

2

1

m

m

F

a

)

m

m

(

a

F

+

=

⇒

+

=

.

Uwaga: siła reakcji podło

ż

a przyło

ż

ona do ka

ż

dego z klocków równowa

ż

ona jest przez sił

ę

ci

ęż

ko

ś

ci tego klocka, bo

ż

aden z klocków nie porusza si

ę

(a tym bardziej nie przyspiesza) w

kierunku pionowym.

II zasada dynamiki Newtona dla klocka o masie

1

m

:

⇒

⋅

=

1

m

a

N

r

r

1

2

1

1

m

m

m

F

m

a

N

⋅

+

=

⋅

=

5

F

4

N

=

⇒

odp. D

2. II zasada dynamiki Newtona dla całego układu:

m

3

a

)

m

m

m

(

a

R

R

R

F

F

F

F

C

B

A

C

B

A

cC

cB

cA

⋅

⋅

=

+

+

⋅

=

+

+

+

+

+

+

r

r

r

r

r

r

r

r

r

(bo ka

ż

dy z klocków ma t

ę

sam

ą

mas

ę

m).

Pami

ę

taj: w wyra

ż

eniu na sił

ę

wypadkow

ą

działaj

ą

c

ą

na cały układ nie uwzgl

ę

dniamy sił

wewn

ę

trznych, czyli tych działaj

ą

cych pomi

ę

dzy elementami układu (czyli np. siły napi

ę

cia nici).

Uwaga: siła reakcji podło

ż

a przyło

ż

ona do ka

ż

dego z klocków równowa

ż

ona jest przez sił

ę

ci

ęż

ko

ś

ci tego klocka, bo

ż

aden z klocków nie porusza si

ę

(a tym bardziej nie przyspiesza) w

kierunku pionowym.
Poniewa

ż

ruch odbywa si

ę

w poziomie, to interesuje nas tylko równanie na iksow

ą

składow

ą

siły

wypadkowej działaj

ą

cej na ten układ klocków:

m

a

3

F

⋅

⋅

=

m

3

/

F

a

=

⇒

.

Wypadkowa siła działaj

ą

ca na klocek B nadaje temu klockowi przyspieszenie o warto

ś

ci a

obliczonej powy

ż

ej. Zatem warto

ść

tej siły

3

F

m

3

F

B

m

ma

F

=

⋅

=

=

Uwaga: zauwa

ż

,

ż

e nie musieli

ś

my zna

ć

warto

ś

ci poszczególnych sił działaj

ą

cych na klocek B, a i

tak mogli

ś

my obliczy

ć

warto

ść

siły wypadkowej.

Odp. B

3. II zasada dynamiki dla klocka (1):

a

m

N

F

1

1

1

c

r

r

r

⋅

=

+

, czyli wzdłu

ż

nici:

a

m

N

F

1

1

1

c

⋅

=

−

II zasada dynamiki dlaklocka (2):

a

m

T

N

R

F

2

2

2

2

c

r

r

r

r

r

⋅

=

+

+

+

Prostopadle do nici:

0

F

R

2

c

=

−

. Wzdłu

ż

nici:

a

m

T

N

2

2

⋅

=

−

i

R

F

T

N

µ

=

µ

=

, a poniewa

ż

z

równania w kierunku prostopadłym wiemy,

ż

e

2

c

F

R

=

, to wnioskujemy,

ż

e

2

c

F

T

µ

=

. Wiemy

tak

ż

e,

ż

e

2

1

N

N

=

.

Zatem przekształcaj

ą

c, otrzymujemy:

)

m

m

(

a

F

T

2

1

1

c

+

−

=

)

m

m

(

a

g

m

g

m

2

1

1

2

+

−

=

µ

⇒

g

m

)

m

m

(

a

g

m

2

2

1

1

+

−

=

µ

⇒

.

Blok 4:

Dynamika ruchu post

ę

powego

.

Równia,

wielokr

ąż

ki, układy ciał

2

BLOK 4 odpowiedzi do zada

ń

do samodzielnego rozwi

ą

zania

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

Zatem współczynnik tarcia kinetycznego:

75

,

0

10

kg

2

kg

)

2

3

(

3

10

kg

3

2

2

2

s

m

s

m

s

m

=

⋅

+

−

⋅

=

µ

a

m

N

F

1

1

1

c

⋅

=

−

N

21

kg

3

)

3

10

(

m

)

a

g

(

m

a

F

N

2

s

m

1

1

1

c

1

=

−

=

−

=

⋅

−

=

⇒

.

Odp. Współczynnik tarcia kinetycznego wynosi

75

,

0

=

µ

, a siła naci

ą

gu nici ma warto

ść

N

21

F

N

=

.

4. Odp. D

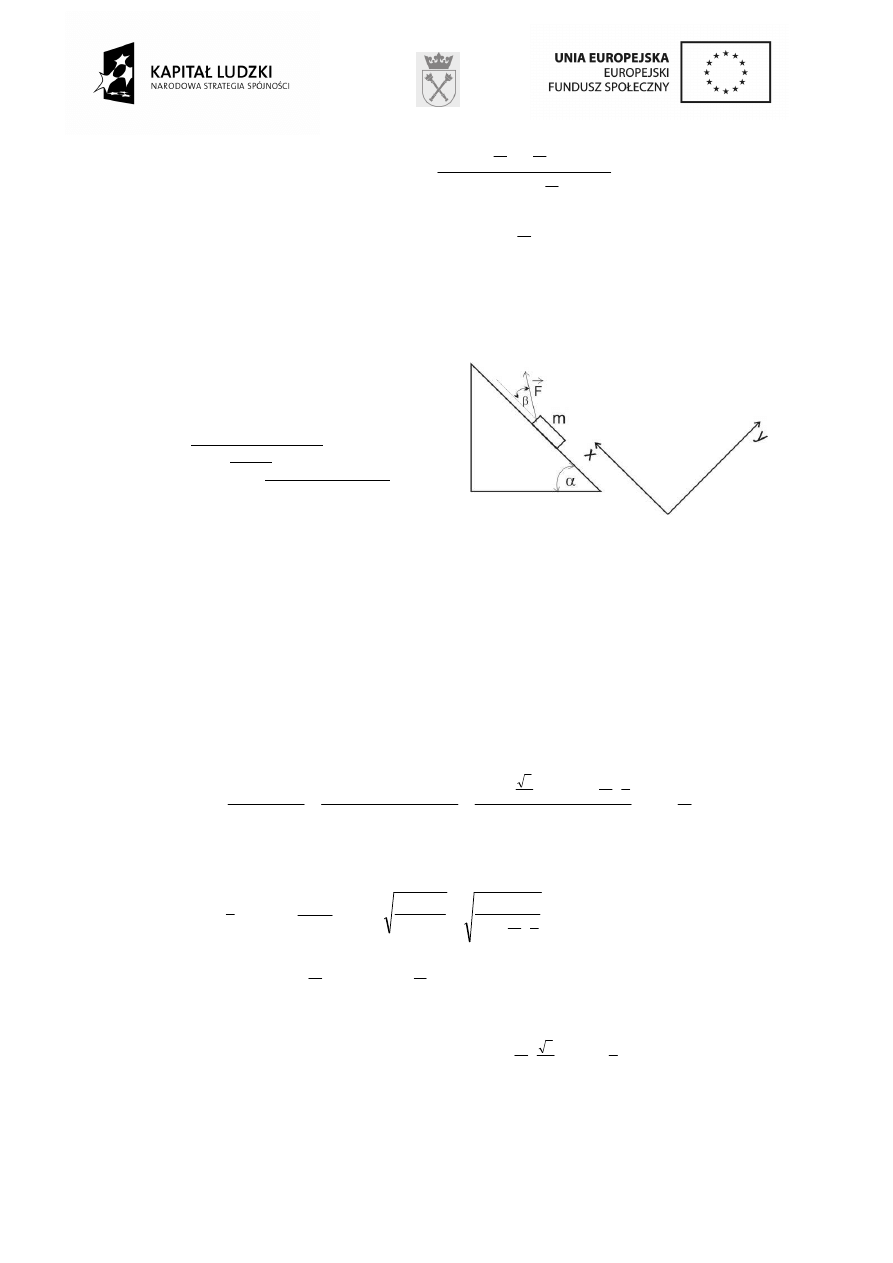
5. II zasada dynamiki Newtona dla klocka:

m

a

R

F

F

c

⋅

=

+

+

r

r

r

r

. Korzystnie jest wybra

ć

układ

współrz

ę

dnych jak pokazano na rysunku (ale

mo

ż

na tak

ż

e wybra

ć

inny układ współrz

ę

dnych).

Uwaga: sposób rozwi

ą

zania przedstawiony w

dalszej cz

ęś

ci zale

ż

y od wyboru układu

współrz

ę

dnych, ale wyniki – nie zale

żą

od tego

wyboru.

W układzie współrz

ę

dnych przedstawionym na rysunku dynamiczne równania ruchu

przedstawiaj

ą

si

ę

nast

ę

puj

ą

co:

)

(

∗

Wzdłu

ż

osi OX:

m

a

|

F

|

|

F

|

cx

x

⋅

=

−

)

(

∗∗

Wzdłu

ż

osi OY:

0

|

F

|

R

|

F

|

cy

y

=

−

+

Gdzie:

β

⋅

=

cos

F

|

F

|

x

,

β

⋅

=

sin

F

|

F

|

y

- s

ą

warto

ś

ciami składowych siły

F

r

w wybranym układzie

współrz

ę

dnych,

α

⋅

=

sin

F

|

F

|

c

cx

,

α

⋅

=

cos

F

|

F

|

c

cy

- s

ą

warto

ś

ciami składowych siły ci

ęż

ko

ś

ci

c

F

r

w wybranym

układzie współrz

ę

dnych,

a R – jest warto

ś

ci

ą

siły reakcji podło

ż

a.

Zatem z równania

)

(

∗

, mamy:

•

Warto

ść

przyspieszenia klocka:

2

2

s

m

2

1

s

m

2

3

cx

x

66

,

3

kg

1

10

kg

1

N

10

m

sin

g

m

cos

F

m

|

F

|

|

F

|

a

≈

⋅

⋅

−

⋅

=

α

⋅

⋅

−

β

⋅

=

−

=

•

Czas potrzebny do osi

ą

gni

ę

cia szczytu równi mo

ż

na obliczy

ć

z kinematycznego

równania ruchu w ruchu jednostajnie przyspieszonym (klockowi nie nadano pr

ę

dko

ś

ci

pocz

ą

tkowej, czyli

0

v

0

=

r

):

2

2

1

at

s

=

i

α

=

sin

H

s

s

48

,

1

66

,

3

m

2

2

sin

a

H

2

t

2

1

s

m

2

≈

⋅

⋅

=

α

⋅

=

⇒

.

•

Szybko

ść

ko

ń

cow

ą

nale

ż

y obliczy

ć

z drugiego kinematycznego równania ruchu:

s

m

s

m

k

42

,

5

s

48

,

1

66

,

3

t

a

v

2

=

⋅

=

⋅

=

•

Siła nacisku klocka na równi

ę

jest równa co do warto

ś

ci sile reakcji podło

ż

a na klocek,

zatem z równania

)

(

∗∗

otrzymujemy:

N

66

,

3

N

10

10

kg

1

sin

F

cos

g

m

|

F

|

|

F

|

R

2

1

2

3

s

m

y

cy

2

≈

⋅

−

⋅

⋅

=

β

⋅

−

α

⋅

⋅

=

−

=