Blok 4: Dynamika ruchu postępowego.

Równia, wielokrążki, układy ciał

Odpowiedzi do zadań do samodzielnego rozwiązania:

1. II zasada dynamiki Newtona dla całego układu: r

r

r

r

r

F +

r

F + F + R + R = a ⋅ (m + m )

1

c

c2

1

2

1

2 Ponieważ ruch odbywa się w poziomie, to interesuje nas tylko równanie na iksową składową siły wypadkowej działającej na ten układ klocków: F

F = a(m

⇒

+

=

1

m 2 )

a

.

m +

1

m 2

Uwaga: siła reakcji podłoża przyłożona do każdego z klocków równoważona jest przez siłę ciężkości tego klocka, bo żaden z klocków nie porusza się (a tym bardziej nie przyspiesza) w kierunku pionowym.

II zasada dynamiki Newtona dla klocka o masie m1 : r

r

F

⇒

N = a ⋅ m

= ⋅

=

⋅

4F

⇒

1

N

a m1

m1

N =

m +

5

1

m 2

odp. D

2. II zasada dynamiki Newtona dla całego układu: r

r

r

r

r

r

r

r

F +

r

F

+ F + F + R + R + R = a ⋅(m + m + m ) = a ⋅3⋅ m cA

cB

cC

A

B

C

A

B

C

(bo każdy z klocków ma tę

samą masę m).

Pamiętaj: w wyrażeniu na siłę wypadkową działającą na cały układ nie uwzględniamy sił

wewnętrznych, czyli tych działających pomiędzy elementami układu (czyli np. siły napięcia nici).

Uwaga: siła reakcji podłoża przyłożona do każdego z klocków równoważona jest przez siłę ciężkości tego klocka, bo żaden z klocków nie porusza się (a tym bardziej nie przyspiesza) w kierunku pionowym.

Ponieważ ruch odbywa się w poziomie, to interesuje nas tylko równanie na iksową składową siły wypadkowej działającej na ten układ klocków: F = 3 ⋅ a ⋅ m ⇒ a = F / m 3

.

Wypadkowa siła działająca na klocek B nadaje temu klockowi przyspieszenie o wartości a obliczonej powyżej. Zatem wartość tej siły F

F

=

= ⋅

=

B

F

ma

m

3m

3

Uwaga: zauważ, że nie musieliśmy znać wartości poszczególnych sił działających na klocek B, a i tak mogliśmy obliczyć wartość siły wypadkowej.

Odp. B

r

r

r

3. II zasada dynamiki dla klocka (1): F + N = m ⋅ a

−

=

⋅

1

c

1

1

, czyli wzdłuż nici: F

N

m a

1

c

1

1

r

r

r

r

r

II zasada dynamiki dlaklocka (2): F

+ R + N + T = m ⋅a

c2

2

2

2

Prostopadle do nici: R − F

= 0

− =

⋅

= µ

= µ

c2

. Wzdłuż nici: N

T

m

a

2

2

i T

F

R

N

, a ponieważ z

równania w kierunku prostopadłym wiemy, że R =

=

c

F 2 , to wnioskujemy, że T µ c

F 2 . Wiemy

także, że

1

N = N2 .

Zatem przekształcając, otrzymujemy: T = F − a(m + m ) ⇒ µ

=

−

+

1

c

1

2

m g

m g

a(m

m )

2

1

1

2

m g − a(m + m )

1

1

2

⇒ µ =

.

m g

2

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego w ramach programu operacyjnego KAPITAŁ LUDZKI 1

BLOK 4 odpowiedzi do zadań do samodzielnego rozwiązania

3 kg ⋅10 m − 3 m 3

( + )

2 kg

2

2

Zatem współczynnik tarcia kinetycznego:

s

s

µ =

= ,

0 75

2 kg ⋅10 m2

s

F − N = m ⋅ a

m

⇒

=

− ⋅

= −

=

−

=

1

c

1

1

N

F

a m

(g

a)m

1

( 0

)

3

3 kg

21 N

1

1

c

1

1

.

2

s

Odp. Współczynnik tarcia kinetycznego wynosi µ = , 0 75 , a siła naciągu nici ma wartość

F = 21 N

N

.

4. Odp. D

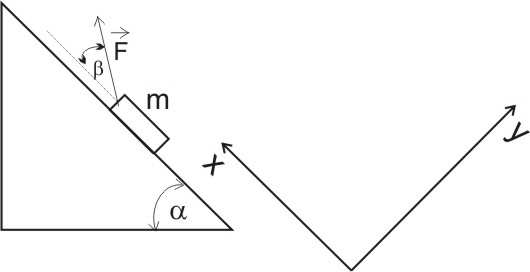
5. II zasada dynamiki Newtona dla klocka: r

r

r

F +

r

F + R = a ⋅ m

c

. Korzystnie jest wybrać układ

współrzędnych jak pokazano na rysunku (ale można także wybrać inny układ współrzędnych).

Uwaga: sposób rozwiązania przedstawiony w dalszej części zależy od wyboru układu

współrzędnych, ale wyniki – nie zależą od tego wyboru.

W układzie współrzędnych przedstawionym na rysunku dynamiczne równania ruchu przedstawiają się następująco:

( )

∗ Wzdłuż osi OX: | F | − | F |= a ⋅ m

x

cx

(∗ )

∗ Wzdłuż osi OY: | F | +R− | F |= 0

y

cy

Gdzie:

r

| F

| Fy =

| F ⋅

x =

| F ⋅ cos β ,

sin β - są wartościami składowych siły F w wybranym układzie współrzędnych,

r

| F

| Fcy =

| Fc ⋅

cx =

| Fc ⋅ sin α ,

cos α - są wartościami składowych siły ciężkości c F w wybranym

układzie współrzędnych,

a R – jest wartością siły reakcji podłoża.

Zatem z równania ( )

∗ , mamy:

• Wartość przyspieszenia klocka:

3

m

1

10 N ⋅

−1 kg ⋅10 ⋅

2

|

−

⋅

β − ⋅ ⋅

α

x

F | | c

F x |

F cos

m g sin

2

s

2

m

a =

=

=

≈ ,

3 66

2

s

m

m

1 kg

• Czas potrzebny do osiągnięcia szczytu równi można obliczyć z kinematycznego równania ruchu w ruchu jednostajnie przyspieszonym (klockowi nie nadano prędkości r

początkowej, czyli v = 0

0

):

H

⋅

1

2

2H

2 2 m

s = at i s =

⇒ t =

=

≈ ,

1 48 s .

2

sin α

a ⋅ sin α

,

3 66 m 1

⋅

s2

2

• Szybkość końcową należy obliczyć z drugiego kinematycznego równania ruchu: m

m

v = ⋅ =

⋅

=

k

a t

,

3 66

,

1 48 s

,

5 42

2

s

s

• Siła nacisku klocka na równię jest równa co do wartości sile reakcji podłoża na klocek, zatem z równania (∗ )

∗ otrzymujemy:

R |

= F | − | F |= m ⋅g ⋅cosα − F⋅sinβ =1 kg ⋅10 m 3

⋅

−10 N 1

⋅ ≈ ,

3 66 N

cy

y

s 2

2

2

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego w ramach programu operacyjnego KAPITAŁ LUDZKI 2

BLOK 4 odpowiedzi do zadań do samodzielnego rozwiązania