1
BLOK 3 odpowiedzi do zada
ń
do samodzielnego rozwi
ą
zania
Projekt jest współfinansowany z Europejskiego Funduszu Społecznego
w ramach programu operacyjnego KAPITAŁ LUDZKI
Odpowiedzi do zada
ń
do samodzielnego rozwi
ą
zania:
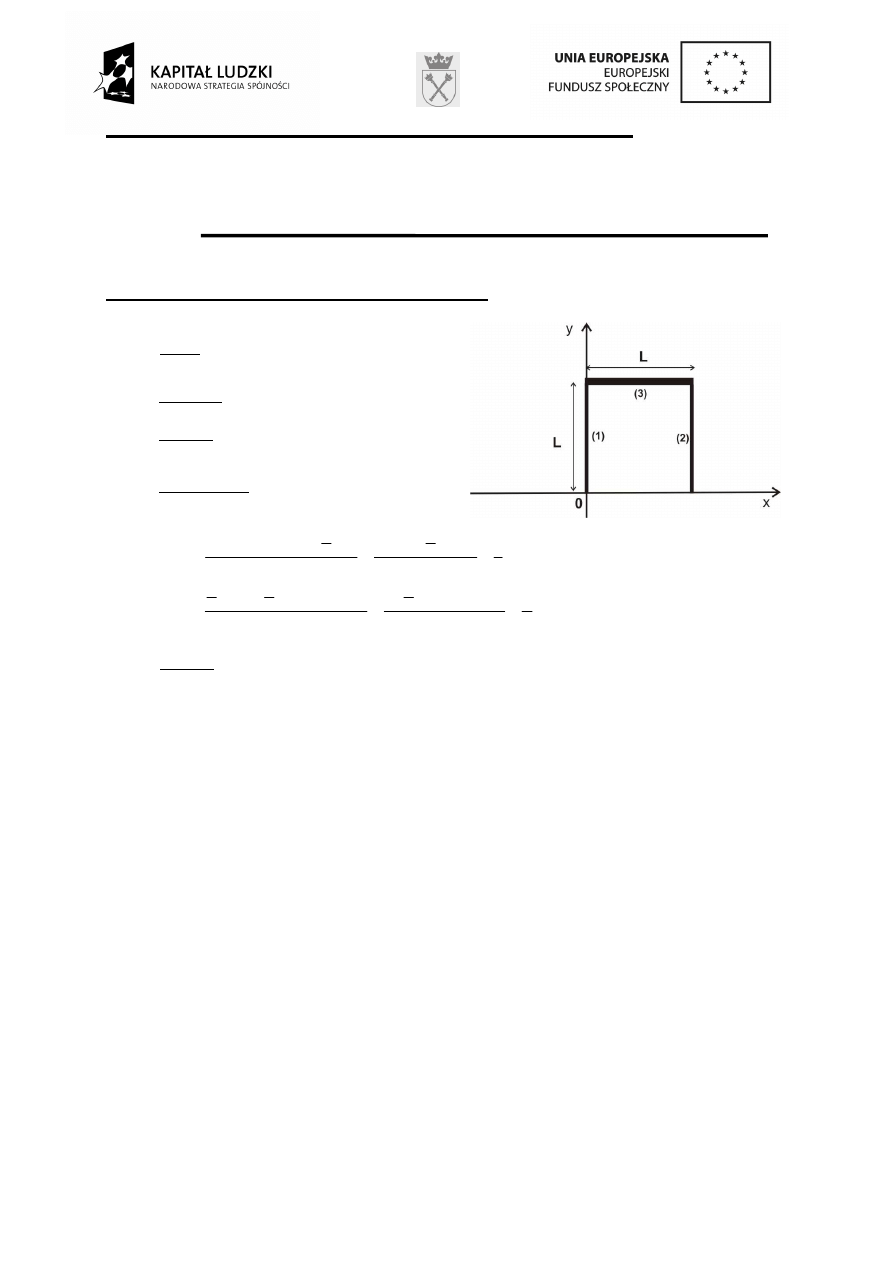
1. Dane:
L
L
L
L
3
2
1
=
=
=
m
3
m
,
m
m
m
3
2
1
=
=
=
Szukane:
?
r
ś
m
=
r
Analiza: Zadanie rozwi
ą
zujemy w
przestrzeni dwuwymiarowej (pomini
ę
to
grubo
ść
pr
ę
tów).
Rozwi
ą
zanie:
L
m
3
m
m
m
3
m
L
m
m
m
m
m
L
m
0
x
2
1
2
L
3
2
1
3
2
L
2
1
ś
m
=
⋅
+
+
⋅
⋅
+
⋅
=
+
+
+
⋅
+
⋅
=
L
5
4
m
3
m
m
m
3
L
m
2
m
m
m
m
L
m
m
y
2
L
3
2
1
3
2
2
L
1
2
L
ś
m
=
⋅
+
+
⋅
⋅
+
⋅
⋅
=
+
+
⋅
+
⋅
+
⋅
=
2. Analiza: Z wykresu wynika,
ż
e współrz
ę
dna wypadkowej siły jest dodatnia, a zatem ( na mocy
II zasady dynamiki Newtona) tak
ż
e i współrz
ę
dna przyspieszenia jest dodatnia. Współrz
ę
dna
pr
ę
dko
ś
ci jest natomiast ujemna (co wynika z tre
ś
ci zadania). Zatem pr
ę
dko
ść
i
przyspieszenie maj
ą
przeciwne zwroty. St
ą
d wiadomo,
ż
e ruch ten jest opó
ź
niony. Poniewa
ż
w ruchu tym współrz
ę
dna siły nie jest stała, to tak
ż
e współrz
ę
dna przyspieszenia nie jest stała
w czasie (z wykresu wynika,
ż
e współrz
ę
dna siły ro
ś
nie liniowo z czasem, zatem tak
ż
e
współrz
ę
dna przyspieszenia ro
ś
nie liniowo z czasem).
Zatem odp. D – ruch niejednostajnie opó
ź
niony
3. Warto
ść
siły napr
ęż
enia jest równa warto
ś
ci siły, z jak
ą
sznur działa na chłopca, a ta z kolei
jest równa warto
ś
ci siły, z jak
ą
chłopiec działa na sznur, czyli 100 N.
4. Obaj chłopcy działaj
ą
na sznur siłami o takich samych warto
ś
ciach i co wa
ż
ne
ś
rodek masy
liny nie przemieszcza si
ę
. Ale de facto jeden chłopiec ci
ą
gnie, a drugi tylko przytrzymuje
sznur, zatem sytuacja ta nie ró
ż
ni si
ę
od sytuacji z poprzedniego zadania, w której chłopiec
ci
ą
gnie za jeden koniec sznura, a drugi jego koniec jest przymocowany do
ś
ciany. Zatem
napr
ęż
enie sznura wynosi tak
ż
e 100 N.
Mo
ż
na to tak
ż
e wyja
ś
ni
ć
w inny sposób. Sił
ę
napr
ęż
enia sznura wyznaczamy do
ś
wiadczalnie:
przecinamy lin
ę
w dowolnym miejscu i wpinamy w to miejsce siłomierz. Napr
ężę
nie to siła,
któr
ą
wskazałby ten siłomierz. Wybierzmy jeden z kawałków sznura – jest on ci
ą
gni
ę
ty z
jednej strony przez chłopca, a z drugiej przez siłomierz. Poniewa
ż
sznur pozostaje w
spoczynku, to (zgodnie z I zasad
ą
dynamiki Newtona) siły działaj
ą
ce na sznur musz
ą
si
ę
równowa
ż
y
ć
, a zatem siła, któr
ą
ci
ą
gnie chłopiec ma tak
ą
sam
ą
warto
ść
, jak siła z drugiej
strony (wskazana przez wpi
ę
ty siłomierz). Czyli warto
ść
napr
ęż
enia tego sznura wynosi tak
ż
e
100 N.
Blok 3:
Zasady dynamiki Newtona. Siły.
2
BLOK 3 odpowiedzi do zada
ń
do samodzielnego rozwi
ą
zania
Projekt jest współfinansowany z Europejskiego Funduszu Społecznego
w ramach programu operacyjnego KAPITAŁ LUDZKI
5. Podwieszaj
ą
c belk
ę
nie mo
ż
emy doprowadzi
ć
do zerwania sznurów, czyli nie mo
ż
emy
przekroczy
ć
obci
ąż
enia równego wytrzymało
ś
ci sznura na zerwanie. Całkowita siła ci
ęż
ko
ś
ci
działaj
ą
ca na belk
ę
jest równowa
ż
ona przez sum
ę
sił spr
ęż
ysto
ś
ci wszystkich lin:
zerw
c
F
n
g
m
F
⋅
=
⋅
=
, gdzie n – liczba wszystkich kawałków sznura.
25
N
20
10
kg
50
F
g
m
n
2
s
m
zerw
=
⋅
≈
⋅
=
Belk
ę
nale
ż
y zawiesi
ć
za pomoc
ą
25 kawałków takiego sznura.
6. Dane:
2
,
0
,
N
10
|
F
|
,
kg
1
m
=
µ
=
=
r
Szukane:
?
a
=
r
Analiza: Aby obliczy
ć
a
r
, nale
ż
y poda
ć
jego składowe. Ruch jest jednowymiarowy, wi
ę
c tylko
jedna składowa przyspieszenia mo
ż
e mie
ć
warto
ść
ró
ż
n
ą
od zera. Poszukujemy zatem
x
a
.
Rozwi
ą
zanie:
II zasada dynamiki dla klocka:
m
a
T
R
F
F
c
⋅
=
+
+
+
r
r
r
r
r
Dla osi OX zwróconej zgodnie ze zwrotem
F
r
i osi OY zwróconej zgodnie ze zwrotem
R
r
,
otrzymujemy:
x:
m
a
T
F
x
⋅
=
−
y:
0
F
R
c
=
−
(ciało nie porusza si
ę
w kierunku pionowy, a zatem tak
ż
e w tym kierunku
nie przyspiesza)
2
2
s
m
s
m
k
c
k
k
x
8
kg
1
10
kg
1
0,2
N
10
m
g
m
µ
F
m
F
µ
F
m
R
µ
F
m
T
F
a
=
⋅
⋅
−
=
⋅
⋅
−
=
⋅
−
=
⋅
−
=
−
=
Odp. Klocek porusza si
ę
z przyspieszeniem o warto
ś
ci
2
8
s
m
zgodnie ze zwrotem siły
F
r
.
7. Dane:
0
v
,
m
100
s
,
10
36
v
k
s
m
h
km
0
=
=
=
=
Szukane:
?
k
=
µ
Rozwi
ą
zanie:
To zadanie mo
ż
na rozwi
ą
za
ć
dwoma sposobami:
I – z zasad dynamiki Newtona i kinematycznych równa
ń
ruchu:
m
a
T
F
z
⋅
=
=
r
r
r
R
T
i
m
a
T
F
k
z
⋅
µ
=
⋅
=
=
, gdzie R – warto
ść
siły reakcji podło
ż
a; w tym
zadaniu
g
m
F
R
c
⋅
=
=
oraz:
s
2
v
a
a
2
v
s
t
a
v
v
i
at
t
v
s
2
0
2
0
0
k
2
2
1
0
⋅
=
⇒
⋅
=
⇒
⋅
−
=
−
⋅
=
Czyli:
05
,
0
10
m
100
2
)
10
(
g
s
2
v
g
a
m
a
g
m
2
s
m
2
s
m
2
0
k
k
=
⋅
⋅
=
⋅
⋅
=
=
µ
⇒
⋅
=
⋅
⋅
µ
LUB
II – z zasady zachowania energii mechanicznej:
Praca wykonana przez sił
ę
tarcia jest równa zmianie energii kinetycznej ciała:
⇒
−
=
∆
⇒
∆
=
2
mv
2
mv
x
T
E
W
2
0
2
k
k
o
⇒
−
=
⋅
⋅
2
mv
)
180
cos(
s
T
2
0
o
2
mv
s
T
2
mv
s
T
2
0
2
0
=
⋅
⇒
−
=
⋅
−
oraz
3
BLOK 3 odpowiedzi do zada
ń
do samodzielnego rozwi
ą
zania
Projekt jest współfinansowany z Europejskiego Funduszu Społecznego
w ramach programu operacyjnego KAPITAŁ LUDZKI
R
T
k
⋅
µ
=
i w tym zadaniu
g
m
F
R
c
⋅
=
=
.
Zatem:
05
,
0
10
m
100
2
)
10
(
s
g
2
v
2
mv
s
g
m
2
s
m
2
s
m
2
0
k
2
0
k
=
⋅
⋅
=
⋅
⋅
=
⋅
µ
⇒
=
⋅
⋅
⋅
µ
Odp. Współczynnik tarcia kinetycznego wynosi 0,05
8. Wypadkowa siła jest równa zeru na mocy I zasady dynamiki Newtona, poniewa
ż
, jak
stwierdzono w tre
ś
ci zadania, ciało to porusza si
ę
ruchem prostoliniowym (kierunek pr
ę
dko
ś
ci
nie ulega zmianie), stale w t
ę
sam
ą
stron
ę
(zwrot pr
ę
dko
ś
ci nie ulega zmianie) i warto
ść
pr
ę
dko
ś
ci tego ciała tak
ż
e pozostaje stała (jak to wida
ć
na wykresie). Zatem pr
ę
dko
ść
jako
cały wektor pozostaje stały, dlatego wypadkowa siła działaj
ą
ca na to ciało jest równa zeru.
Czyli odp. D
9. Je
ż
eli ciało porusza si
ę
po okr
ę
gu, to jedynie warto
ść
pr
ę
dko
ś
ci tego ciała nie ulega zmianie
(zgodnie z wykresem), natomiast kierunek i zwrot pr
ę
dko
ś
ci nieustannie si
ę
zmieniaj
ą
w
trakcie ruchu. Zatem musi istnie
ć
niezerowa siła, która powoduje zmian
ę
tych dwóch cech
wektora pr
ę
dko
ś
ci. Sił
ą
t
ą
jest siła do
ś
rodkowa. Siła ta jest zawsze skierowana prostopadle do
pr
ę
dko
ś
ci. Dodatkowo, poniewa
ż
ruch jest jednostajny (warto
ść
pr
ę
dko
ś
ci nie ulega zmianie),
to i warto
ść
siły do
ś
rodkowej dana wzorem:
r
v
m
a
m
F
2
d
d
⋅
=
⋅
=
jest stała. Ale stale zmienia
si
ę
kierunek i zwrot tej siły, dlatego
ż
adna z podanych w zadaniu 8 odpowiedzi szczegółowych
(A-F) nie jest w tym przypadku prawdziwa i prawidłowa jest odp. G.
10. Dane:
Hz
3
,
13
f
,
m
25
,
0
cm
25
r
,
kg
1
m
min
1
obr
800
≈
=
=
=
=
Szukane:
?
F
d
=
Rozwi
ą
zanie:
N
1746
f
m
4π
r
(2π2π
m
r
ω
m
r
r
ω
m
r
v
m
a
m
F
2
2
2
2
2
2
2
d
d
≈
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
=
⋅
=
Odp. Warto
ść
siły do
ś
rodkowej działaj
ą
cej na bielizn
ę
wynosi ok. 1,75 kN.
11. Przyspieszenie do
ś
rodkowe dane jest wzorem:
r
r
v
a
2
2
d
⋅
ω
=
=
. Na pocz
ą
tku zatem
przyspieszenie do
ś
rodkowe:
1
2
1
1
d
r
a
⋅
ω
=
, a na ko
ń
cu:
( )
1
2
1
9
2
1
2
3
2
2
2
2
d
r
r
2
r
a
1
⋅
ω
=
⋅
⋅
=
⋅
ω
=
ω
, czyli
9
2
a
a
1
d
2
d
=
.
Odp. E
12. Analiza: W równaniu fizycznym jednostki po obu jego stronach musz
ą
by
ć
sobie równe.
x
x
v
F
b
=
, st
ą
d: jednostk
ą
b jest
s
kg
kg
N
s
m
s
m
s
m
2
=
⋅
=
4
BLOK 3 odpowiedzi do zada
ń
do samodzielnego rozwi
ą
zania
Projekt jest współfinansowany z Europejskiego Funduszu Społecznego
w ramach programu operacyjnego KAPITAŁ LUDZKI
13. Dane:
m
2
r
,
m
5
,
1
r
2
1
=
=
Szukane:
?
f
f
1
2
=
Analiza:
Je
ż
eli dwa koła ( w tym przypadku dwie szpule) poł
ą
czone s
ą
sznurkiem (ta
ś
m
ą
, paskiem)
ś
ci
ś
le przylegaj
ą
cym do punktów na obrze
ż
ach tych kół (szpul) oraz sznurek (ta
ś
ma, pasek)
jest nierozci
ą
gliwy, to aby si
ę
nie zerwał, musi by
ć
spełniona zale
ż
no
ść
:
2
1
v
v
=
(czyli
pr
ę
dko
ść
punktów le
żą
cych na obwodzie jednego koła musi by
ć
równa pr
ę
dko
ś
ci punktów
le
żą
cych na obwodzie drugiego koła).
Rozwi
ą
zanie:
r
f
2
r
v
⋅
⋅
π
⋅
=
⋅
ω
=
, gdzie f – jest cz
ę
stotliwo
ś
ci
ą
obrotu koła.
Czyli
2
2
1
1
r
f
2
r
f
2
⋅
⋅
π
⋅
=
⋅
⋅
π
⋅
4
3
m
2
m
5
,
1
r
r
f
f
2
1
1
2
=
=
=
⇒
.
Odp. Stosunek cz
ę
stotliwo
ś
ci wynosi 3/4.