
Przemysław Gawłowski
127086
06.11.2012
Metody probabilistycze i statystyka
Laboratorium
Sprawozdanie 4
2FDI grupa L04
Zadanie 1:
Na podstawie szeregu szczegółowego wyników egzaminu z pewnego przedmiotu (punkty skala od
0 do 100) wyznaczyć średnią arytmetyczną. Obliczenia i odpowiednie wykresy wykonać
wykorzystując arkusz kalkulacyjny Excel. Wyniki egzaminu: 14, 16, 24, 24, 28, 36, 36, 36, 36, 36,
40, 40, 42, 44, 44, 44, 44, 44, 44, 48, 48, 48, 48, 48, 48, 50, 50, 50, 50, 50, 50, 52, 52, 56, 56, 56,
56, 56, 56, 56, 58, 58, 58, 58, 58, 58, 58, 60,
60, 60, 60, 60, 60, 60, 60, 60, 60, 60, 64, 64, 64, 68, 68, 68, 68, 68, 68, 72, 72, 72.
Obliczyć miary asymetrii i koncentracji osobno dla szeregu szczegółowego i osobno dla szeregu
rozdzielczego.
Dane:
Zbiorowość generalna:
wyniki
Zbiorowość próbna:
wyniki z pewnego przedmiotu
Cecha statystyczna:
punkty
Liczba próby n =
70
Liczba wariantów cechy:
k>12
Wartość minimalna:
14
Wartość maksymalna
72
Rozstęp R =
58
Ustalenie liczby przedziałów:
9
Rozpiętość h =
7
Wyznaczenie szeregu rozdzielczego:
Nr wariantu
Wariant cechy
Obliczenia pomocnicze
1
14
37.97
2
16
35.97
3
24
27.97
4
24
27.97
5
28
23.97
6
36
15.97
7
36
15.97
8
36
15.97
9
36
15.97
10
36
15.97
11
40
11.97
12
40
11.97
13
42
9.97
14
44
7.97

15
44
7.97
16
44
7.97
17
44
7.97
18
44
7.97
19
44
7.97
20
48
3.97
21
48
3.97
22
48
3.97
23
48
3.97
24
48
3.97
25
48
3.97
26
50
1.97
27
50
1.97
28
50
1.97
29
50
1.97
30
50
1.97
31
50
1.97
32
52
0.03
33
52
0.03
34
56
4.03
35
56
4.03
36
56
4.03
37
56
4.03
38
56
4.03
39
56
4.03
40
56
4.03
41
58
6.03
42
58
6.03
43
58
6.03
44
58
6.03
45
58
6.03
46
58
6.03
47
58
6.03
48
60
8.03
49
60
8.03
50
60
8.03
51
60
8.03
52
60
8.03
53
60
8.03
54
60
8.03
55
60
8.03
56
60
8.03
57
60
8.03
58
60
8.03
59
64
12.03
60
64
12.03
61
64
12.03
62
68
16.03
63
68
16.03
64
68
16.03
65
68
16.03
66
68
16.03
67
68
16.03
68
72
20.03
69
72
20.03
70
72
20.03
Suma =
702.23
r wariantu
wartość
liczebność
częstość
l. skumulowana
cz. skumulowana
1
14-20
2
0.29
2
0.03
2
21-27
2
0.29
4
0.06
3
28-34
1
0.14
5
0.07
4
35-41
7
1.00
12
0.17
5
42-48
13
1.86
25
0.36
6
49-55
8
1.14
33
0.47
7
56-62
25
3.57
58
0.83
8
63-69
9
1.29
67
0.96
9
70-76
3
0.43
70
1.00
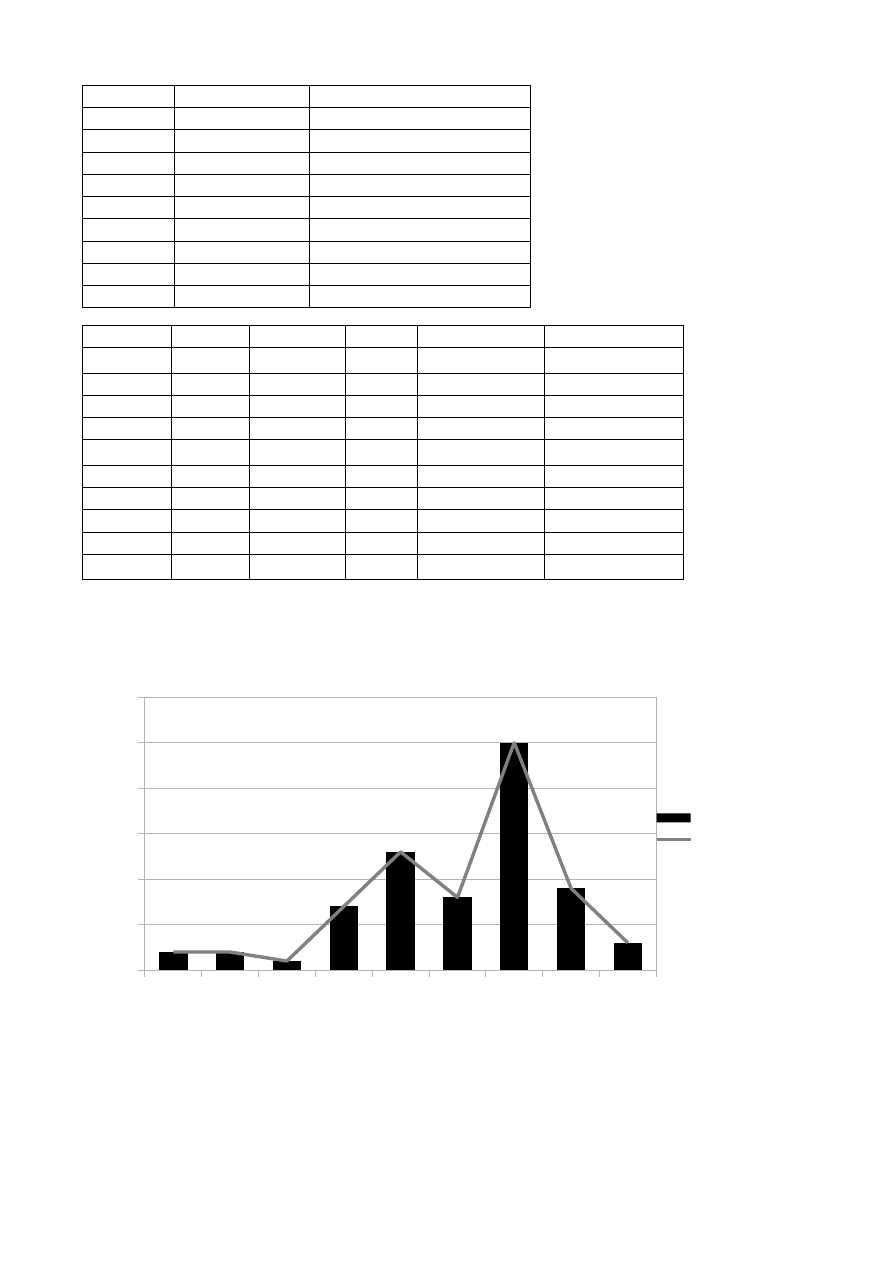
Wykresy:
14-20
21-27
28-34
35-41
42-48
49-55
56-62
63-69
70-76
0
5
10
15
20
25
30
Histogram i diagram liczebności
liczebność
liczebność
14-20
21-27
28-34
35-41
42-48
49-55
56-62
63-69
70-76
0.00
0.50
1.00
1.50
2.00
2.50
3.00
3.50
4.00
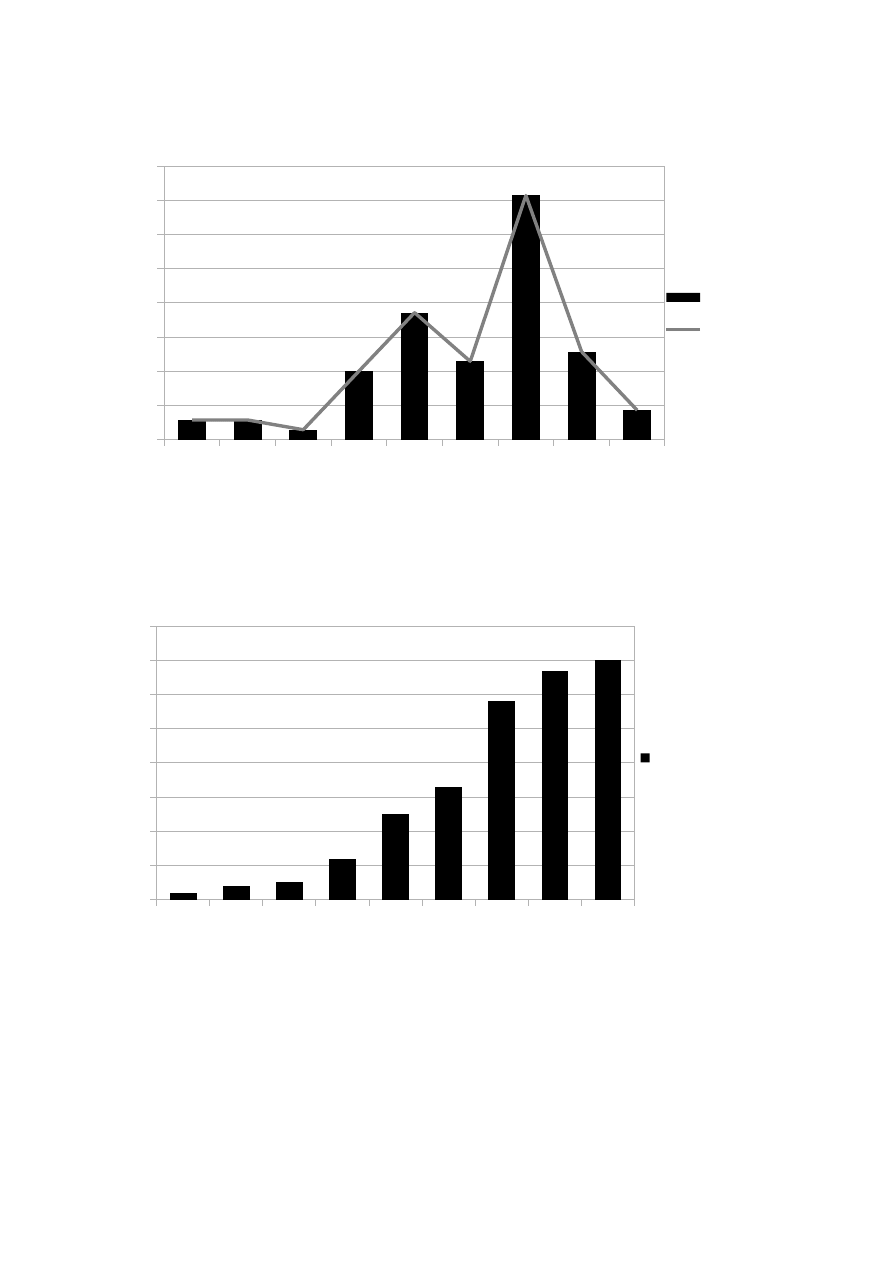
Histogram i diagram częstości
częstość
częstość
14-20
21-27
28-34
35-41
42-48
49-55
56-62
63-69
70-76
0
10
20
30
40
50
60
70
80
Dystrybuanta empiryczna liczebności
l. skumulowana
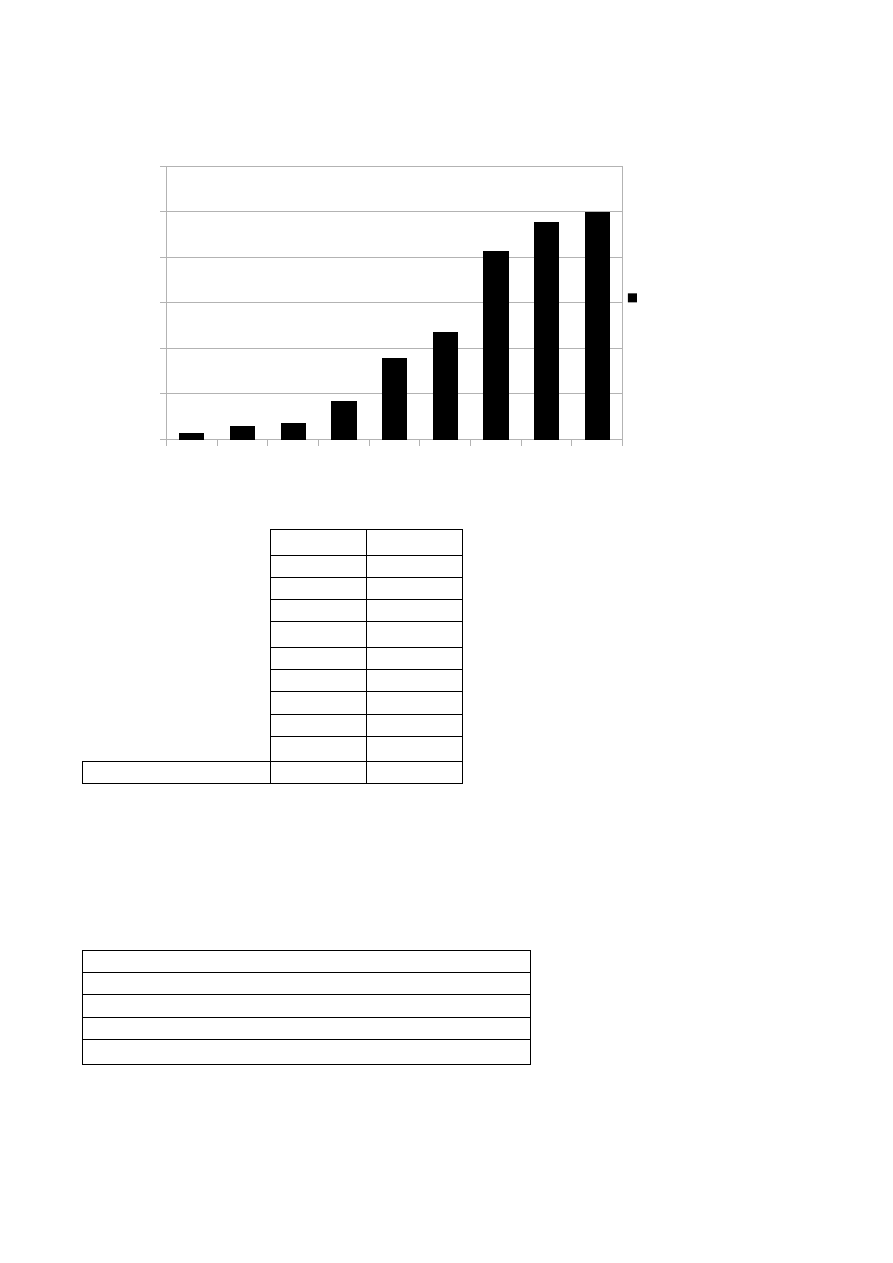
x
i
∗
n
i
(
x
i
∗
n
i
)
2
∗
n
i
34.00
578.00
48.00
1152.00
31.00
961.00
266.00
10108.00
585.00
26325.00
416.00
21632.00
1475.00
87025.00
594.00
39204.00
219.00
15987.00
Suma =
3668.00
202972.00
Średnia arytmetyczna
Dla szeregu szczegółowego:
̄x
=
51.97
Dla szeregu rozdzielczego przedziałowego:
̄x
=
52.40
Kwadryle
minimum
Q0 =
14
dolny
Q1 =
44
drugi
Q2 =
56
górny
Q3 =
60
maximum
Q4 =
72
Współczynnik skośności =
-8.03
14-20
21-27
28-34
35-41
42-48
49-55
56-62
63-69
70-76
0.00
0.20
0.40
0.60
0.80
1.00
1.20
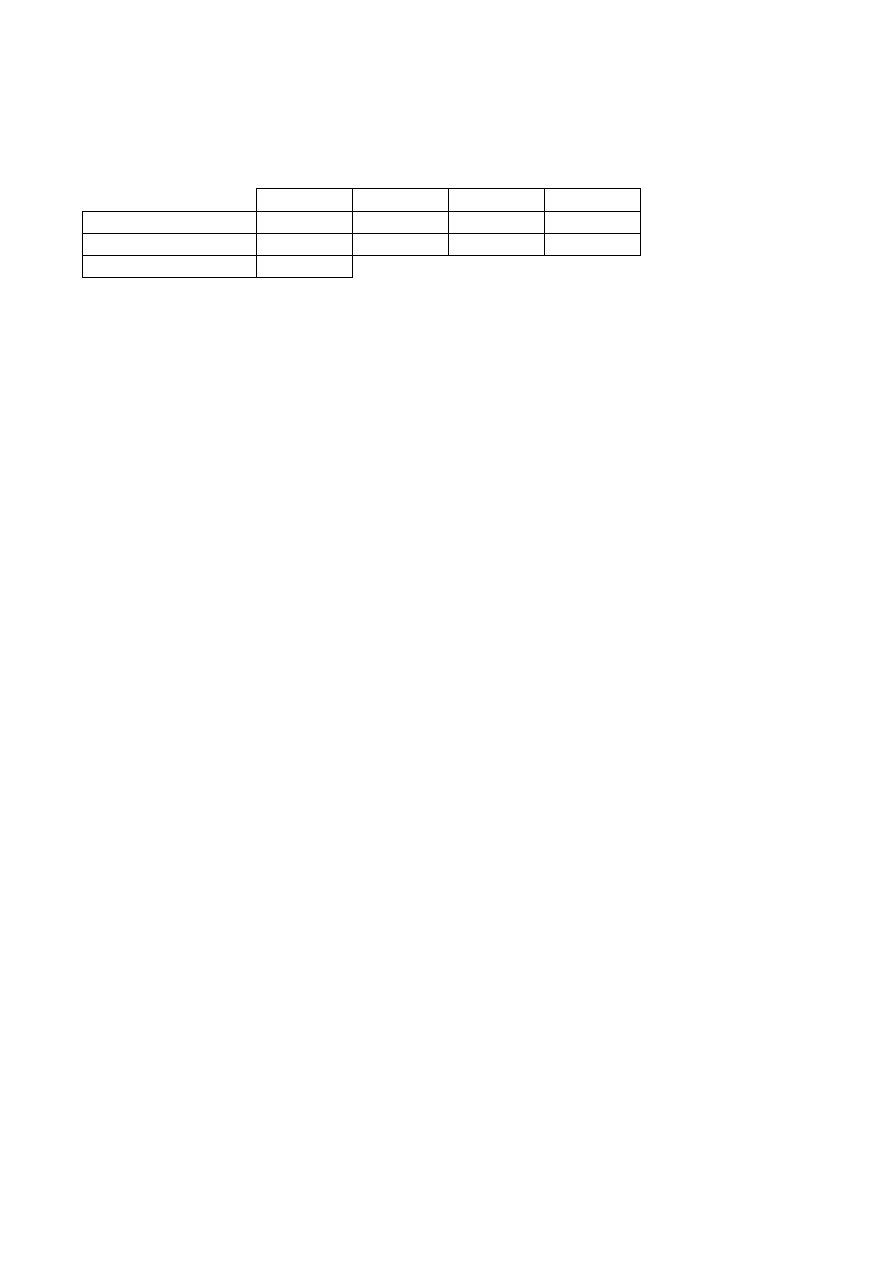
Dystrybuanta empiryczna częstości
cz. skumulowana

Wariancja
Dla szeregu szczegółowego:
s
2
=
161.31
Dla szeregu rozdzielczego przedziałowego:
s
2
=
2899.6
Odchylenie standardowe
Dla szeregu szczegółowego:
s
=
12.70
Dla szeregu rozdzielczego przedziałowego:
s
=
53.85
Współczynnik asymetrii
Dla szeregu szczegółowego:
As =
-0.63
Dla szeregu rozdzielczego przedziałowego:
As =
-0.14
Dla szeregu szczegółowego:
Ad =
-0.80
Dla szeregu rozdzielczego przedziałowego:
Ad =
-0.15
Odchylenie przeciętne
Dla szeregu szczegółowego:
d =
10.03
Dla szeregu rozdzielczego przedziałowego:
d =
52.40
Miary koncentracji
Dla szeregu szczegółowego:
m4 =
95830.86
K =
3.68
Dla szeregu rozdzielczego przedziałowego:
m4 =
39233.55
K =
0.01
Zadanie 2:
Załóżmy, że gęstość zaludnienia w dwóch 100-tysięcznych miastach wynosiła w 2010 roku
odpowiednio 1100 osób/km^2 I 900 osób/km^2. Jaka była przeciętna gęstość zaludnienia tych
miast?
Gęstość zaludnienia
1100
900
Średnia harmoniczna =
990
Zadanie 3
W ciągu 4 kolejnych lat ceny pewnego elementu elektronicznego zwiększyły się w stosunku do
roku poprzedniego kolejno o 6%, 19%, 10% i 7%.
Obliczyć średni roczny wzrost cen tego elementu.
Rok 1
Rok 2
Rok 3
Rok 4
Element elektryczny
0.06
0.19
0.1
0.07
Indeks dynamiczny
3.1666666667 0.5263157895
0.7
Średni wzrost cen =
0.7
Wyszukiwarka
Podobne podstrony:
MPiS Sprawozdanie 7
MPiS Sprawozdanie 1
MPiS Sprawozdanie 5
MPiS Sprawozdanie 9
MPiS Sprawozdanie 3
MPiS Sprawozdanie 8
Tomasz Zięba L16 MPiS sprawozdanie 7 docx
Dawid Zięba L16 MPiS sprawozdanie 7 docx
sprawozdanie VII MPiS
2 definicje i sprawozdawczośćid 19489 ppt
PROCES PLANOWANIA BADANIA SPRAWOZDAN FINANSOWYC H
W 11 Sprawozdania
Wymogi, cechy i zadania sprawozdawczośći finansowej
Analiza sprawozdan finansowych w BGZ SA
W3 Sprawozdawczosc
1 Sprawozdanie techniczne
Karta sprawozdania cw 10
więcej podobnych podstron