Przemysław Gawłowski
127086

18.12.2012

Metody probabilistycze i statystyka

Laboratorium

Sprawozdanie 9

2FDI grupa L04

Zadanie 1

Test 1

Test 2

Rangi x

i

Rangi y

i

200

190

1

2

190

200

2

1

180

170

3

4

170

150

4

6

160

160

5

5

150

180

6

3

Para

1.4

1.6

1.5

1.3

2.1

Nota

1

1

1

1

-1

Para

2.6

2.5

2.3

4.6

4.5

Nota

1

1

1

1

1

Para

5.3

6.5

6.3

Nota

-1

-1

-1

∑

Nota =

5

V =

4

r

KEN

=

0.33

Odpowiedź: Otrzymany wynik świadczy o przeciętnym skorelowaniu wyników Testu 1 z
uporządkowaniem według wyników Testu 2. Otrzymany w wyniku obliczeń współczynnik

r

KEN

mieści się w przedziale

0.3<r

KEN

<

0.5

.

140

150

160

170

180

190

200

0

50

100

150

200

250

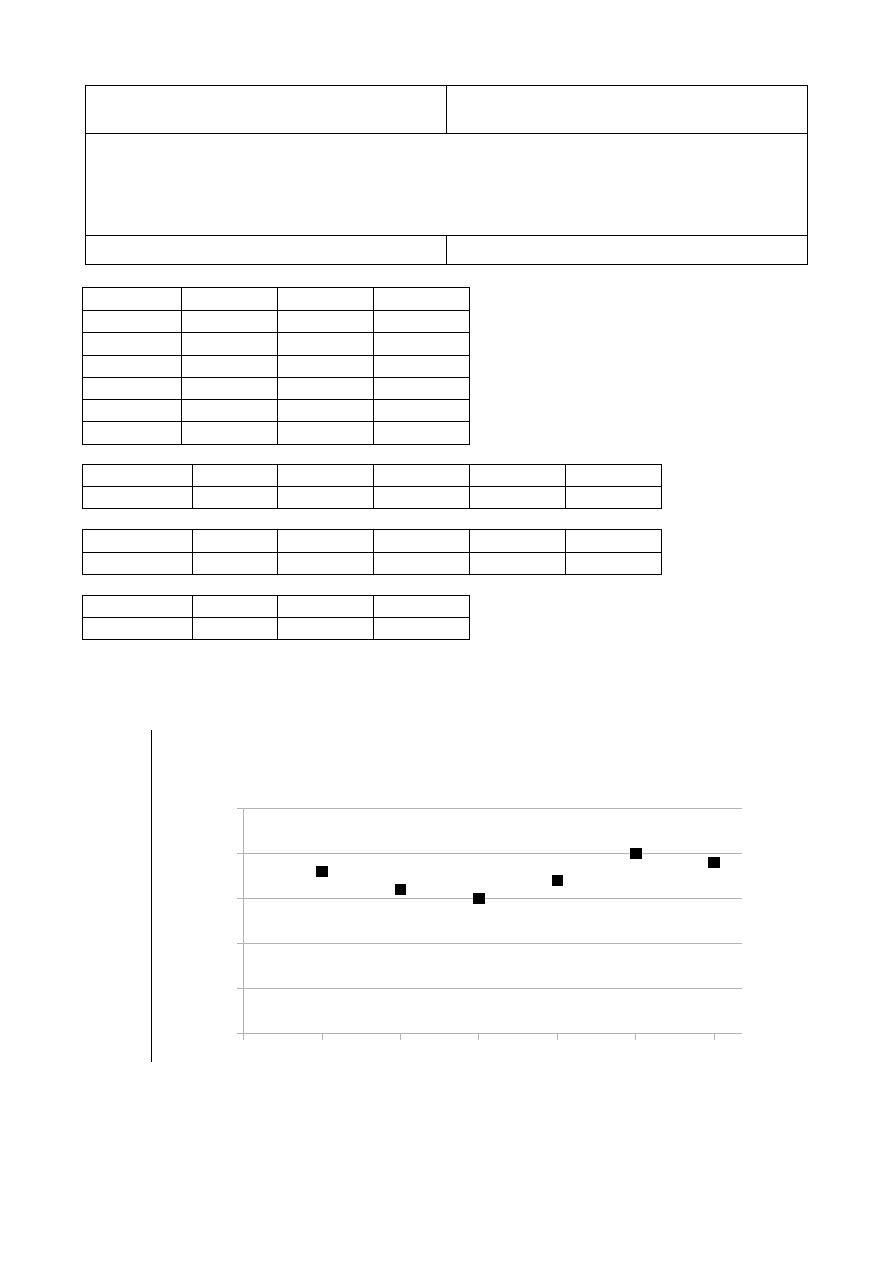
Diagram korelacyjny

T

e

s

t 2

Zadanie 2

Lp

x

i

y

i

x

i

−̄x

y

i

−̄y

(

x

i

−̄x)

2

(

y

i

−̄y )

2

(

x

i

−̄x)∗( y

i

−̄y)

1

5436

506

956.18

-13.82

914283.67

190.94

-13212.69

2

5252

526

772.18

6.18

596264.76

38.21

4773.49

3

5220

633

740.18

113.18

547869.12 12810.12

83775.12

4

5205

503

725.18

-16.82

525888.67

282.85

-12196.24

5

5167

598

687.18

78.18

472218.85

6112.40

53725.12

6

5120

561

640.18

41.18

409832.76

1695.94

26363.85

7

4956

585

476.18

65.18

226749.12

4248.67

31038.40

8

4526

459

46.18

-60.82

2132.76

3698.85

-2808.69

9

4231

451

-248.82

-68.82

61910.49

4735.94

17123.21

10

3672

459

-807.82

-60.82

652570.21

3698.85

49130.03

11

493

437

-3986.82

-82.82 15894719.21

6858.85

330181.03

̄x = 4479.82 519.82 Suma = -1.82E-012 -5.68E-013 20304439.64 44371.64

567892.64

S

x

=

1845858.15

S

x

2

=

3407192305344.91

S

y

=

4033.79

S

y

2

=

16271422.43

cov ( X , Y ) =

51626.60

r

xy

=

0.60

r

xy

2

=

0.36

Odpowiedź: Między cechami występuje pełna zależność korelacyjna. Okazuje się, że 35%
zmienności liczby stypendystów jest wyjaśnion przez zmienności liczby studentów.

0

1000

2000

3000

4000

5000

6000

0

100

200

300

400

500

600

700

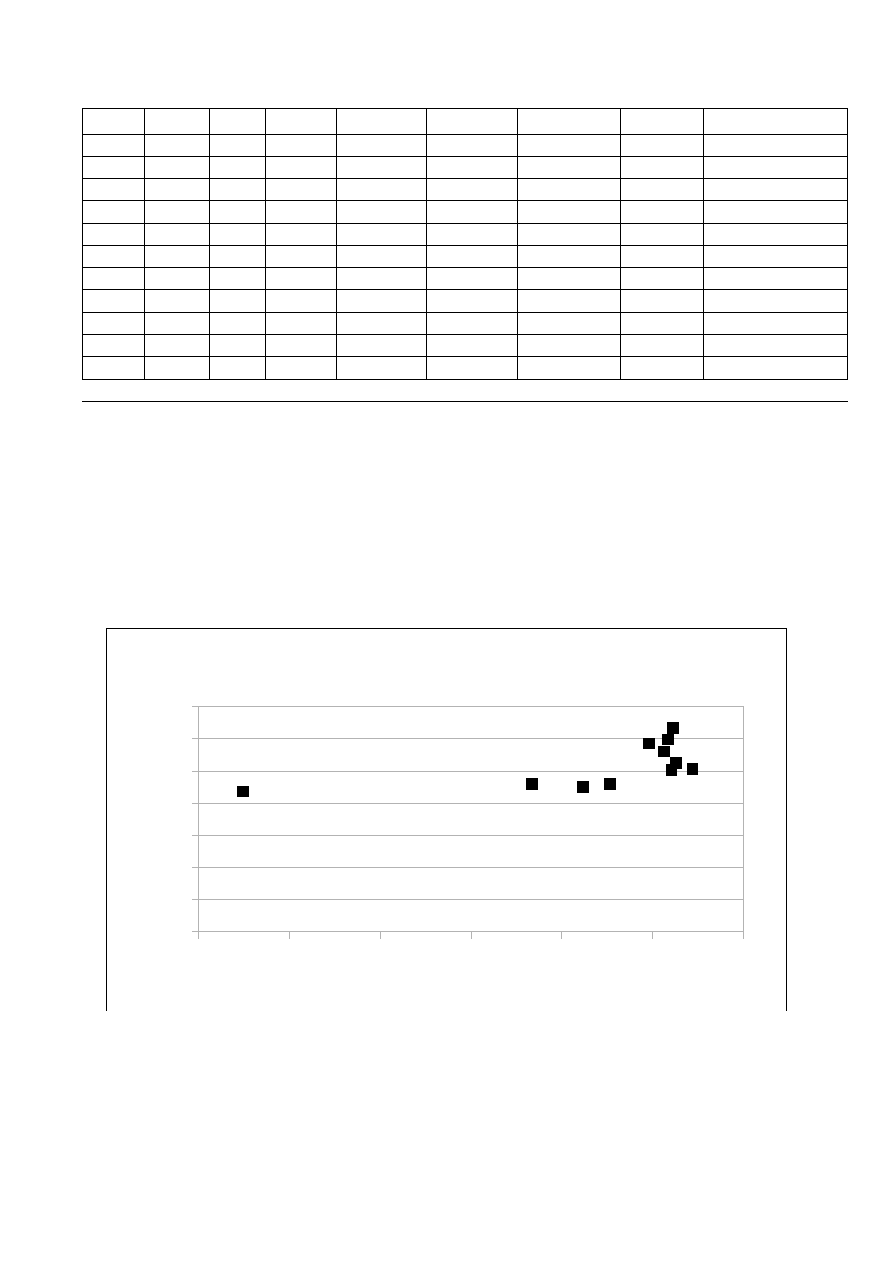
Diagram korelacyjny

xi

yi