14.12.2012

Politechnika Rzeszowska

Wydział Elektrotechniki i Informatyki

Metody probabilistyczne

i statystyka

Laboratorium 7

Wnioskowanie statystyczne – weryfikacja hipotez statystycznych

Dawid Zięba

L16, II EF-DI

Zadanie 1

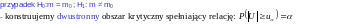
n	100
Xsr	12,5	tys. km
s	2,4	tys. km
α	0,03

ETAP I - FORMUŁOWANIE TEZY
H0	m =	12	tys. km
H1	m !=	12	tys. km

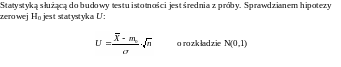
U = 2,083333333

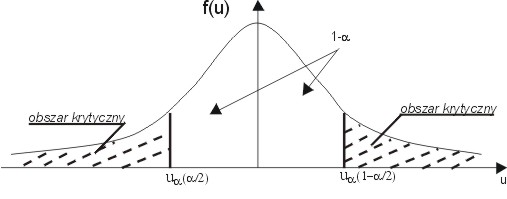
ETAP III - OKREŚLENIE OBSZARU KRYTYCZNEGO
a/2	0,015
u(a/2)	-2,170090378
u(1-a/2)	2,170090378

(-∞;-2,17009) u (2,17009; +∞)

Odp. Wartość statystyki sprawdzającej znajduje się w obszarze krytycznym, więc tezę mówiącą o tym, że przeciętna ilość kilometrów przebytych przez samochód to 12000km należy odrzucić.

Zadanie 2

Dane:
nA	60
X1Sr	23,8	mg
s1	1,2	mg
s1^2	1,44
α	0,05

nB	50
X2sr	24,1	mg
s2	1,4	mg
s2^2	1,96

ETAP I – Formułowanie tezy
H0:	m1=m2
H1:	m1<m2

Etap II – Wybór statystyki sprawdzającej

U= -1,193335926

Etap III – Obszar krytyczny

u(a) = -1,644853627

(-∞;-1,64485)

Odp. Wartość statystyki sprawdzającej nie mieści się w obszarze krytycznym więc nie ma podstaw, aby wnioskować, że przeciętna zawartość nikotyny w papierosach gatunku A jest mniejsza niż w papierosach gatunku B

Zadanie 3

Staż pracy	Liczba pracowników (ni)	xsr ni	xsr*ni	(Xsr-xsr)^2*ni
0 - 4	4	2	8	213,764566
4 - 8	9	6	54	98,6254459
8 - 12	8	10	80	3,804994055
12 - 16	4	14	56	87,97146254
16 - 20	4	18	72	302,0404281
suma	29		270	706,2068966

α	0,02
n	29
Xsr	9,310344828

Etap I

wariancja=20

wariancja>20

Etap II CHI , n-1 35,31034483

Etap III

a	0,02
n-1	28

chi , a; n-1

45,41884738

wariancja	(45,4188	; +∞)

Odp: Nasza statystyka sprawdzająca nie zawiera się w obszarze krytycznym, dlatego nie ma podstaw wnioskować, że wariancja stażu pracy w zakładzie jest większa niż 20.