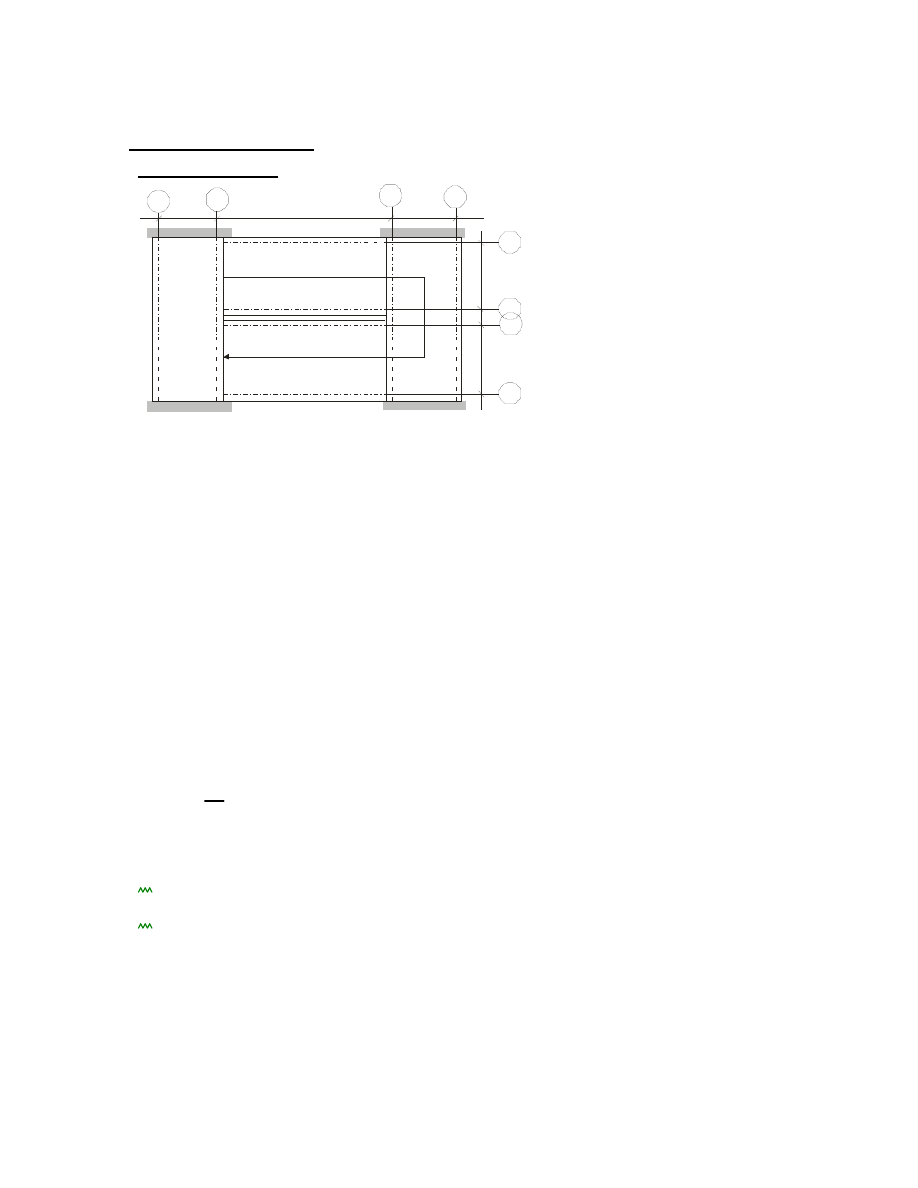
1.1. Ogólny opis konstrukcji stropu.

Projekt konstrukcyjny obejmuje obliczenia statyczne zinwentaryzowanego stropu drewnianego
belkowego według wymagań normy PN-EN-1995-1-1:2010. Konstrukcja budynku nie wchodzi w
zakres opracowania. Budynek o konstrukcji tradycyjnej: ściany murowane z elementów
ceramicznych.

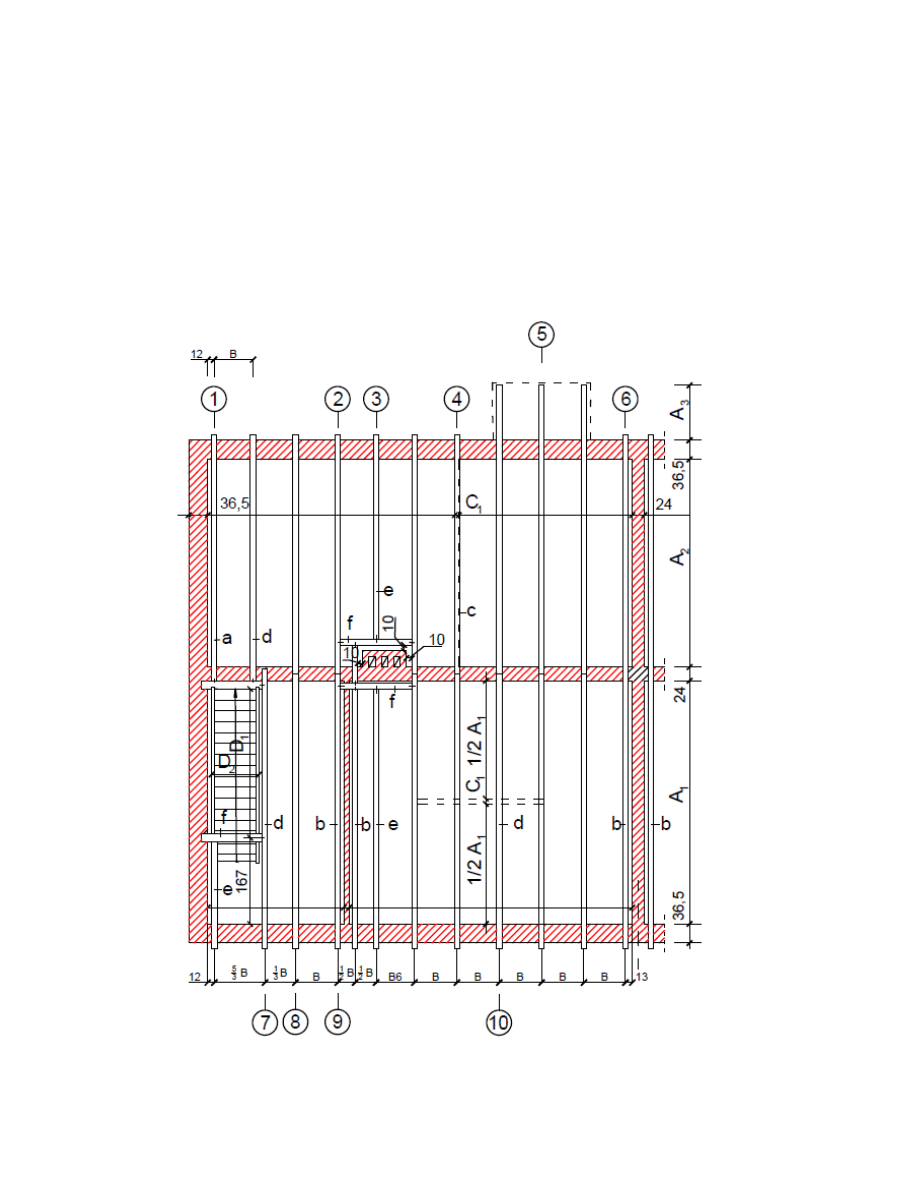
1.2. Rzut stropu

1.3 Dane zinwentaryzowanego stropu

-Numer belki objętej opracowaniem : 5
-Typ stropu: F
-Wymiary belki:

b=24 cm
h=24 cm

-Rozpiętość stropu w świetle: A2=550 cm
-Rozpiętość balkonu w świetle: A3=95 cm
-Rozstaw osiowy belek: B=65 cm
-Klasa drewna: C30
-Kategoria użytkowania [PN-EN 1991-1-1] = B
-Typ pomieszczenia : pokój

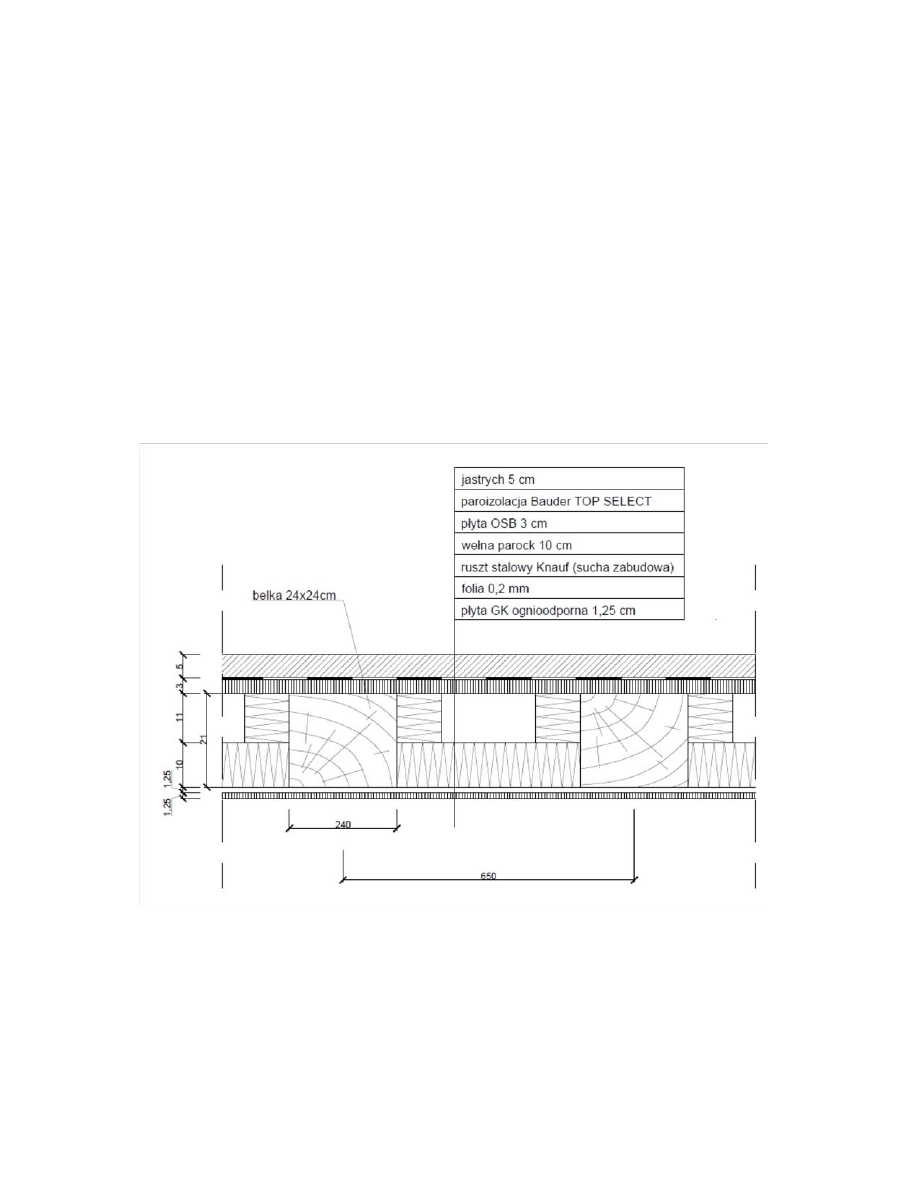
1.4 Przekrój przez strop

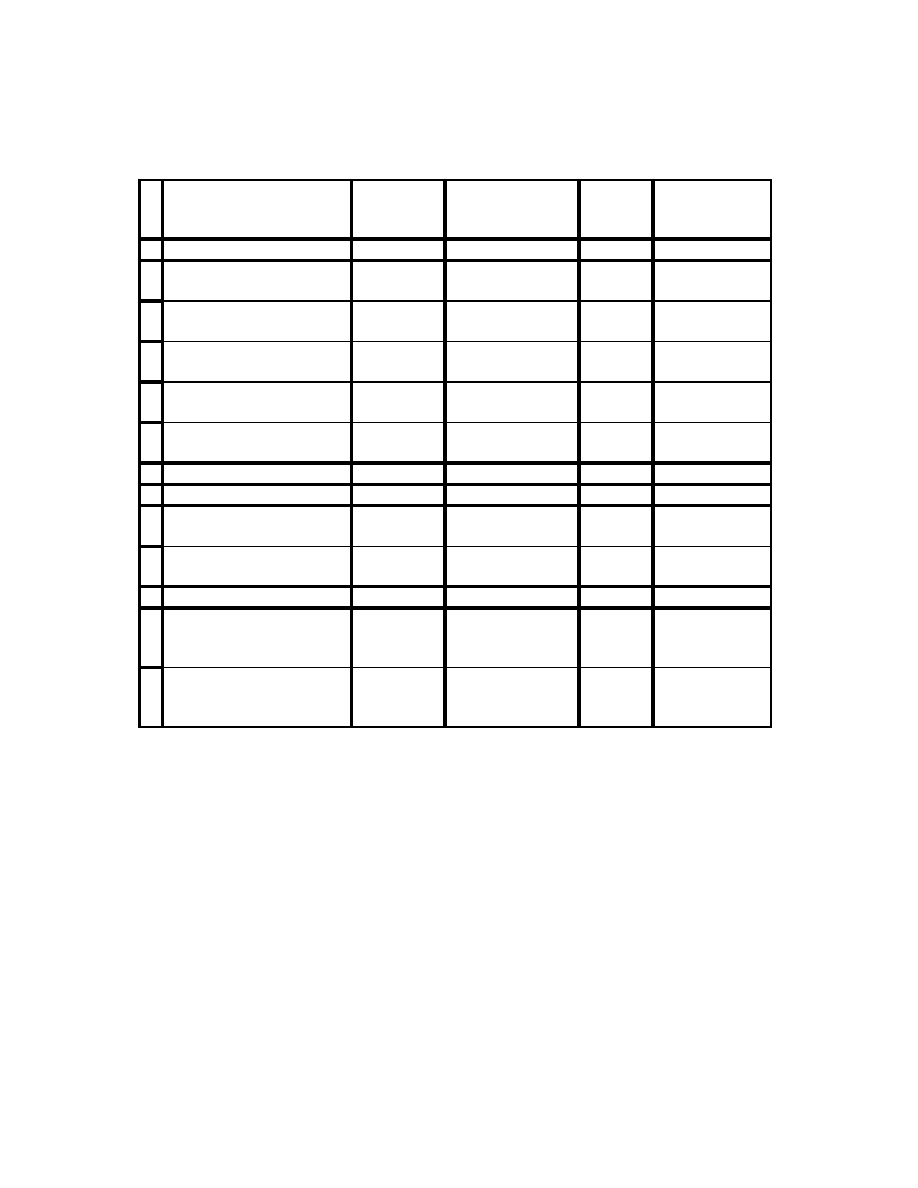
2.1 Zestawienie obciążeń

Lp.

Rodzaj obciążenia

ciężar

objętościowy

Wartość

charak terystyczna

[k N/m]



Warość

obliczeniowa

[k N/m]

obciążenie własne stropu

1

jastrych 0.05

(*0.65m*0.05m)

23[kN/m^3]

0.748

1.35

1.009

2

płyta OSB 0.03m

(*0.65m*0.03m)

5[kN/m^3]

0.098

1.35

0.132

3

wełna mineralna 0.03m

(*0.65m*0.1m)

1.7[kN/m^3]

0.111

1.35

0.149

4

sufit podwieszany

(*0.65m)

15[kN/m^2]

0.098

1.35

0.132

5

belka

(*0.25m*0.25m)

4.5[kN/m^3]

0.265

1.35

0.358

-

Suma

-

q

k

=1.318

-

q

d

=1.779

obciążenie własne balkonu

6

belka

(*0.25m*0.25m)

4.5[kN/m^3]

0.265

1.35

0.358

7

pokrycie drewniane 0.032

(*0.0.65m*0.032m)

4.5[kN/m^3]

0.096

1.35

0,129

-

Suma

-

q

k.w sp

=0.361

-

qd.wsp=0.487

8

obc zmienne stropu dla kat.

B

(*0.65m)

1.5[kN/m^2]

1.950

1.5

2.925

9

obc zmienne balkonu dla

kat. B

(0.65m)

2.5[kN/m^2]

1.625

1.5

2.438

Paroizolację Bauder Top Select oraz folię pominięto w zestawieniu obciążeń.

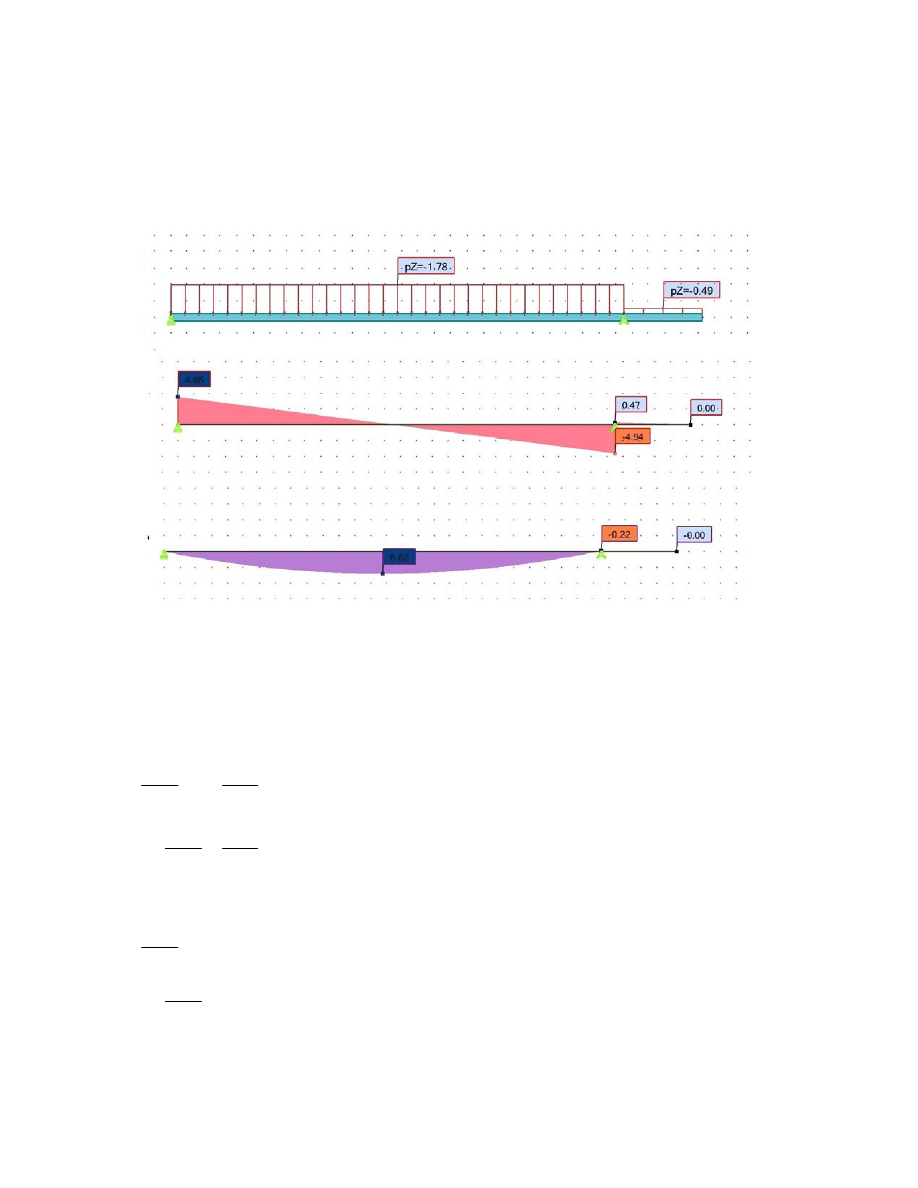
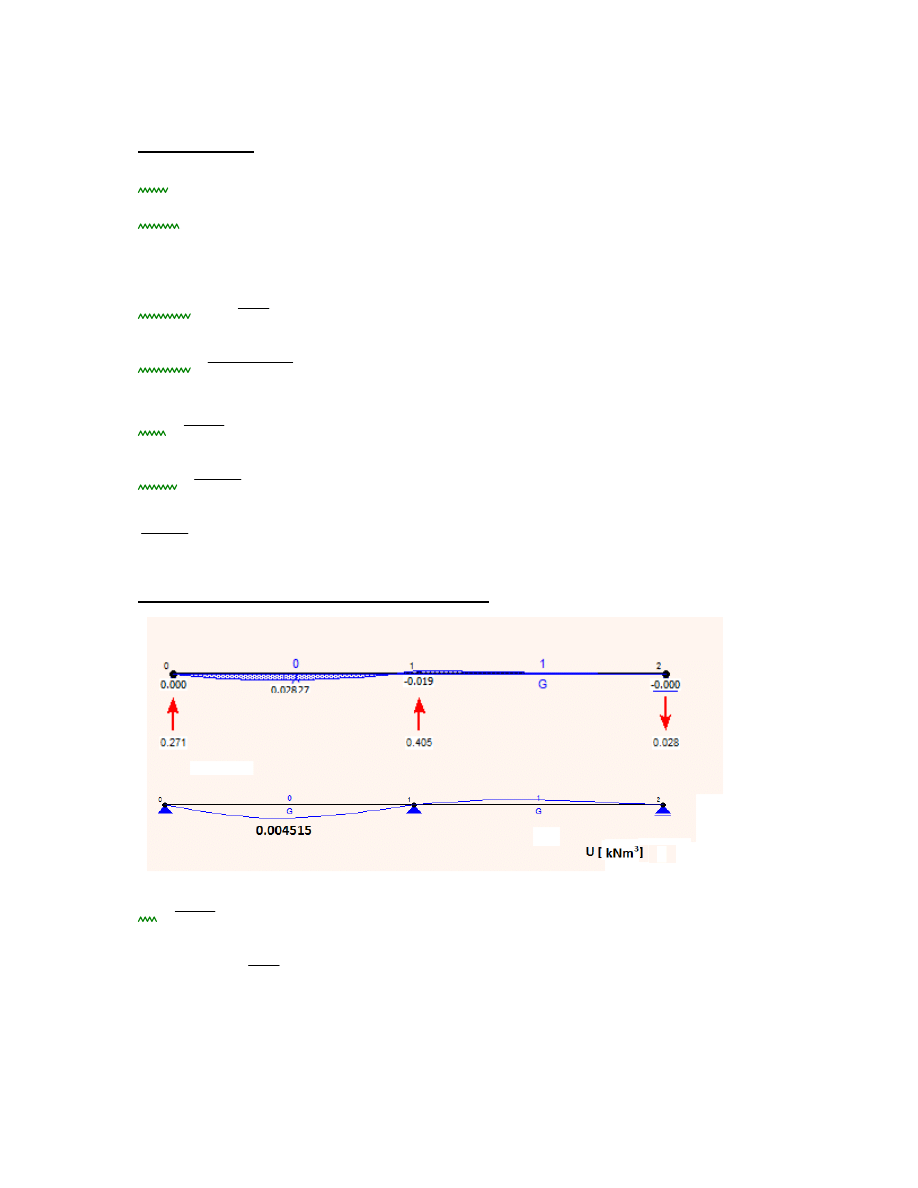
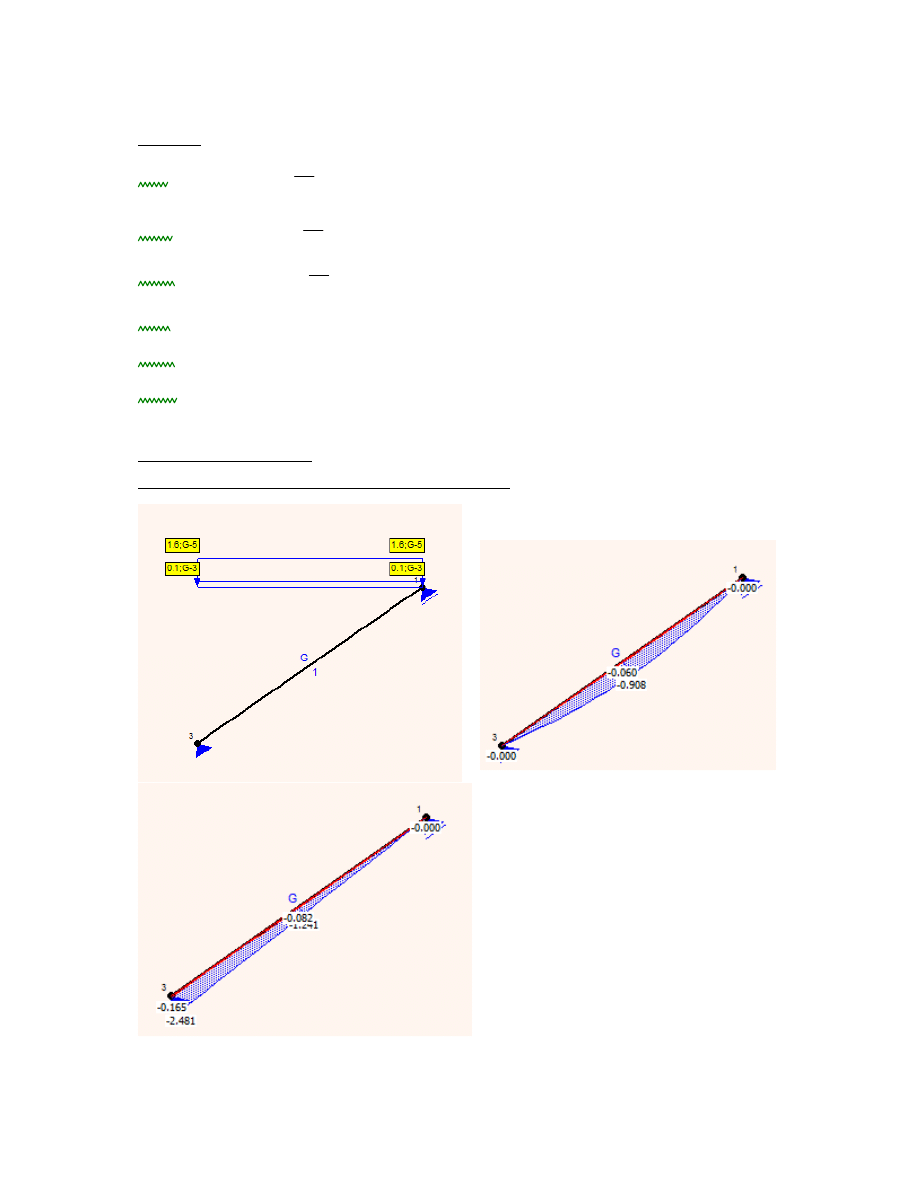
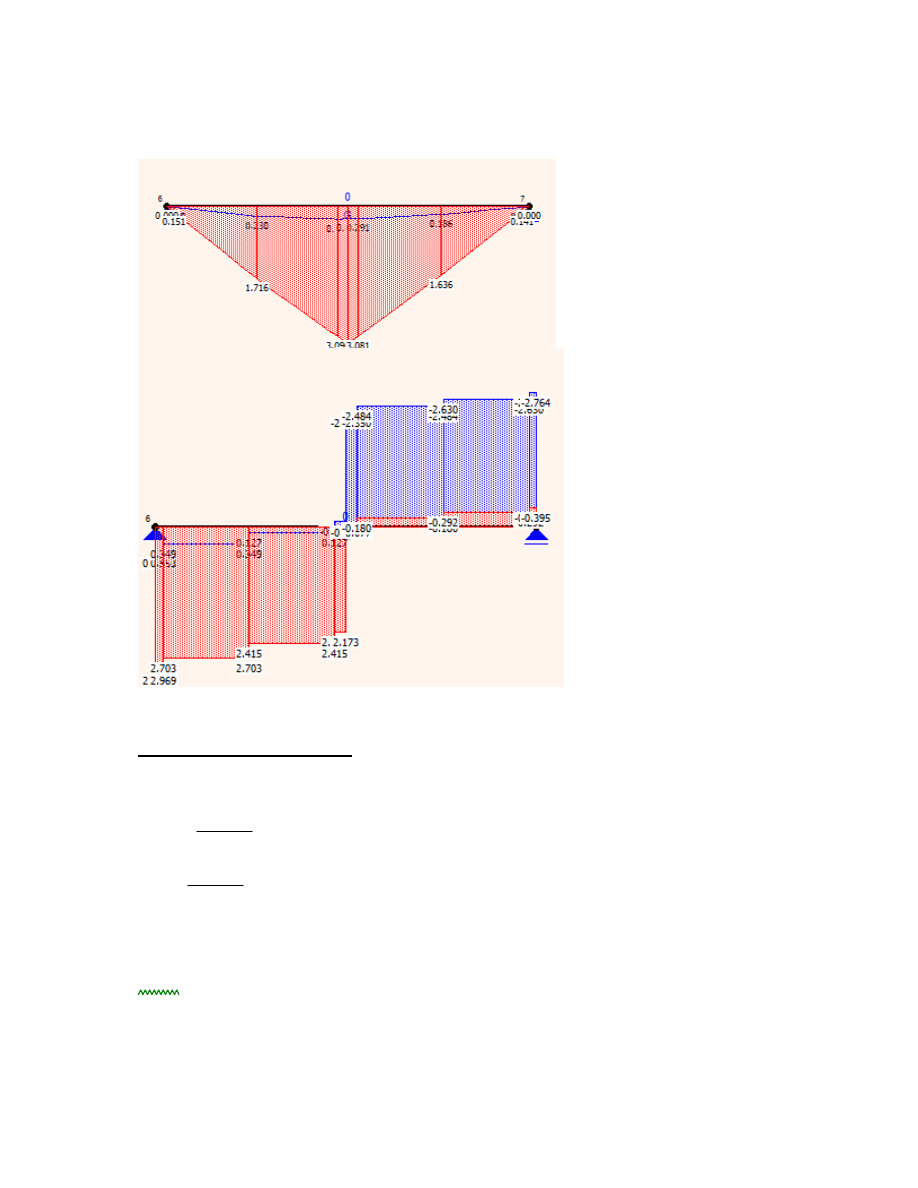
2.2. Schemat statyczny, geometria układu, wykresy sił wewnętrznych kombinacji K1

kombinacja K1: ciężar własny

Md

6.62kN m





2.3 Analiza stanu granicznego nośności SGN dla kombinacji obciążenia K1

σmyd

fmyd

km

σmzd

fmzd





1



km

σmyd

fmyd



σmzd

fmzd



1



ponieważ σmzd =0 powyższe wzory przyjmują postać

σmyd

fmyd

1



km

σmyd

fmyd



1



dane przekroju belki

rozpiętość stropu w świetle

leff.s 550cm



wysięg wspornika w świetle

leff.w 95cm



długość obliczeniowa belki

leff

leff.s leff.w



6.45 m





szerokość belki

b

24cm



wysokość belki

h

24cm



pole przekroju

A

b h



576 cm

2







wskaźnik wytrzymałości

Wy

b h

2



6

2.304

10

3



cm

3







moment bezwładności

Iy

b h

3



12

2.765

10

4



cm

4







przyjęte współczynniki

częściowy współczynnik bezpieczeństwa właściwości materiału

γM

1.3



współczynnik modyfikujący, uwzględniający efekt
czasu trwania obciążenia i wilgotności - obciążenie
stałe:

kmod 0.6



współczynnik k.h nie uwzględniony

wytrzymałość charakterystyczna drewna C30 na zginanie

fmyk 30

N

mm

2



wytrzymałośc materiału:

zginanie

fmyd

fmyk kmod



γM

13.846 MPa







obliczeniowe naprężenia:

naprężenia

σmyd

Md
Wy

2.873 MPa







sprawdzenie warunków normowych:

σmyd

fmyd

1



1



warunek stanu graniczenego nośności SGN dla kombinacji K1 jest spełniony

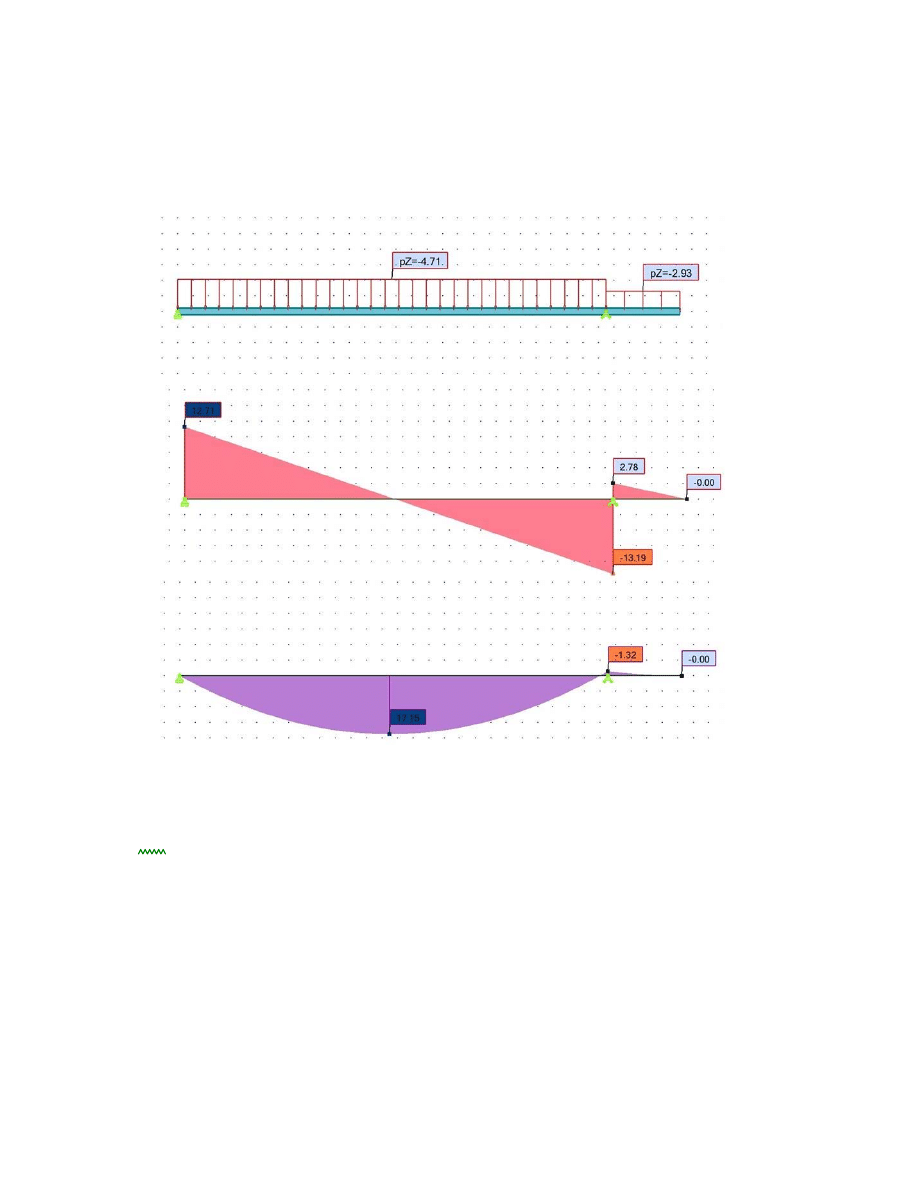
2.4. Schemat statyczny, geometria układu, wykresy sił wewnętrznych kombinacji K2

K2: ciężar własny + obc. użytkowe

Md

17.15kN m





2.5 Analiza stanu granicznego nośności SGN dla kombinacji obciążenia K2

przyjęte współczynniki

częściowy współczynnik bezpieczeństwa właściwości materiału

γM

1.3



współczynnik modyfikujący, uwzględniający efekt
czasu trwania obciążenia i wilgotności - obciążenie
stałe:

kmod 0.8



współczynnik k.h nie uwzględniony

wytrzymałość charakterystyczna drewna C30 na zginanie

fmyk 30

N

mm

2



wytrzymałośc materiału:

fmyd

fmyk kmod



γM

18.462 MPa







zginanie

obliczeniowe naprężenia:

naprężenia

σmyd

Md
Wy

7.444 MPa







sprawdzenie warunków normowych:

σmyd

fmyd

1



1



warunek stanu graniczenego nośności SGN dla kombinacji K2 jest spełniony

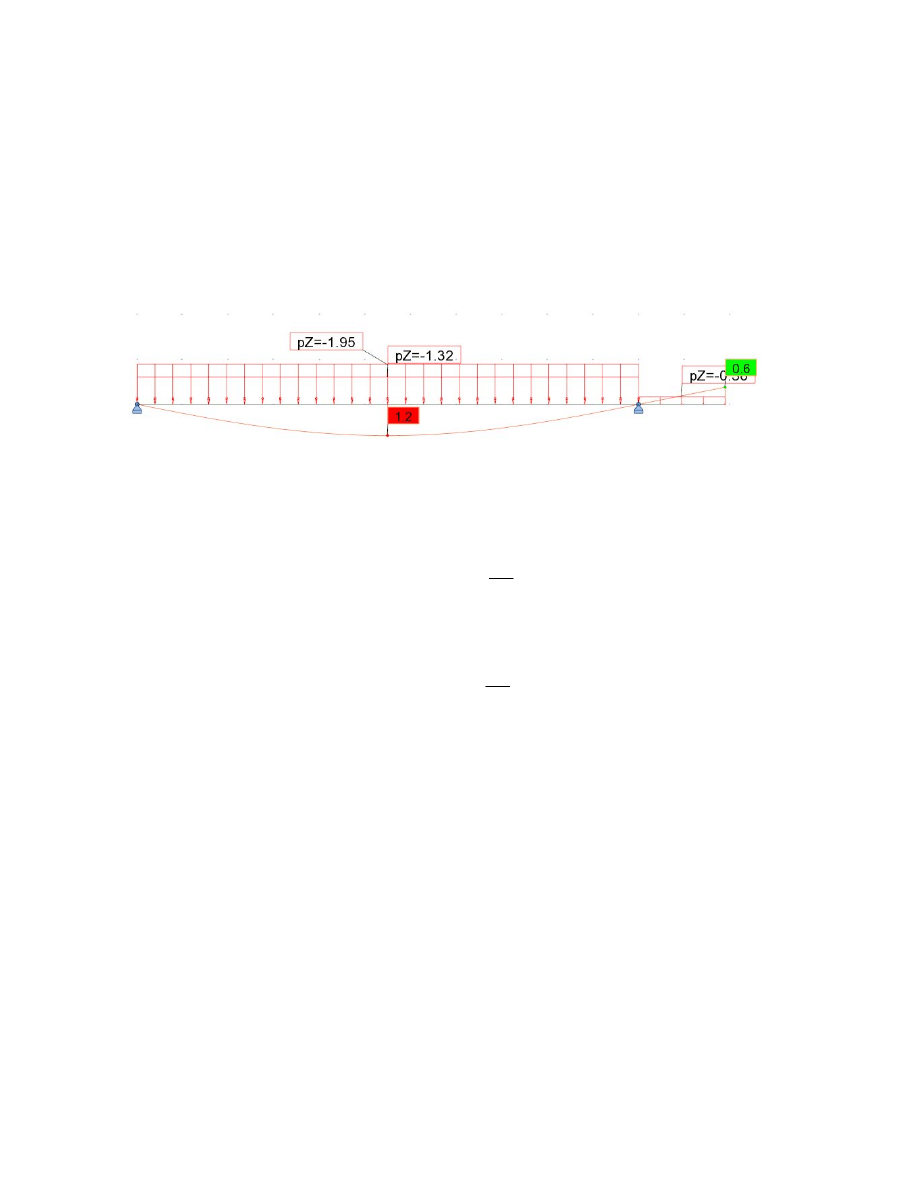
2.6 Analiza stanu granicznego użytkowalności

wybór najbardziej niekorzystnej kombinacji obciążeń

największe ugięcie belki występuje w przypadku kombinacji obciążenia stałego na całej długości
oraz obciążenia zmiennego stropu

obciążenia stałe + obciążenie zmienne stropu

ugięcie belki

ub

1.2cm



ugięcie wspornika

uw 0.6cm



ugięcia maksymalne dla wspornika

umax.w

leff
150

4.3 cm







zwiększenie maksymalnego ugięcia
stropu z uwagi na strop istniejący

umax.w.p umax.w 2



8.6 cm







ugięcia maksymalne dla belki

umax.b

leff
300

2.15 cm







zwiększenie maksymalnego ugięcia
belki z uwagi na strop istniejący

umax.b.p umax.b 2



4.3 cm







sprawdzenie warunków

ub umax.b.p



1



uw umax.w.p



1



obliczenia programu ROBOT zostały sprawdzone z obliczeniami "ręcznymi"

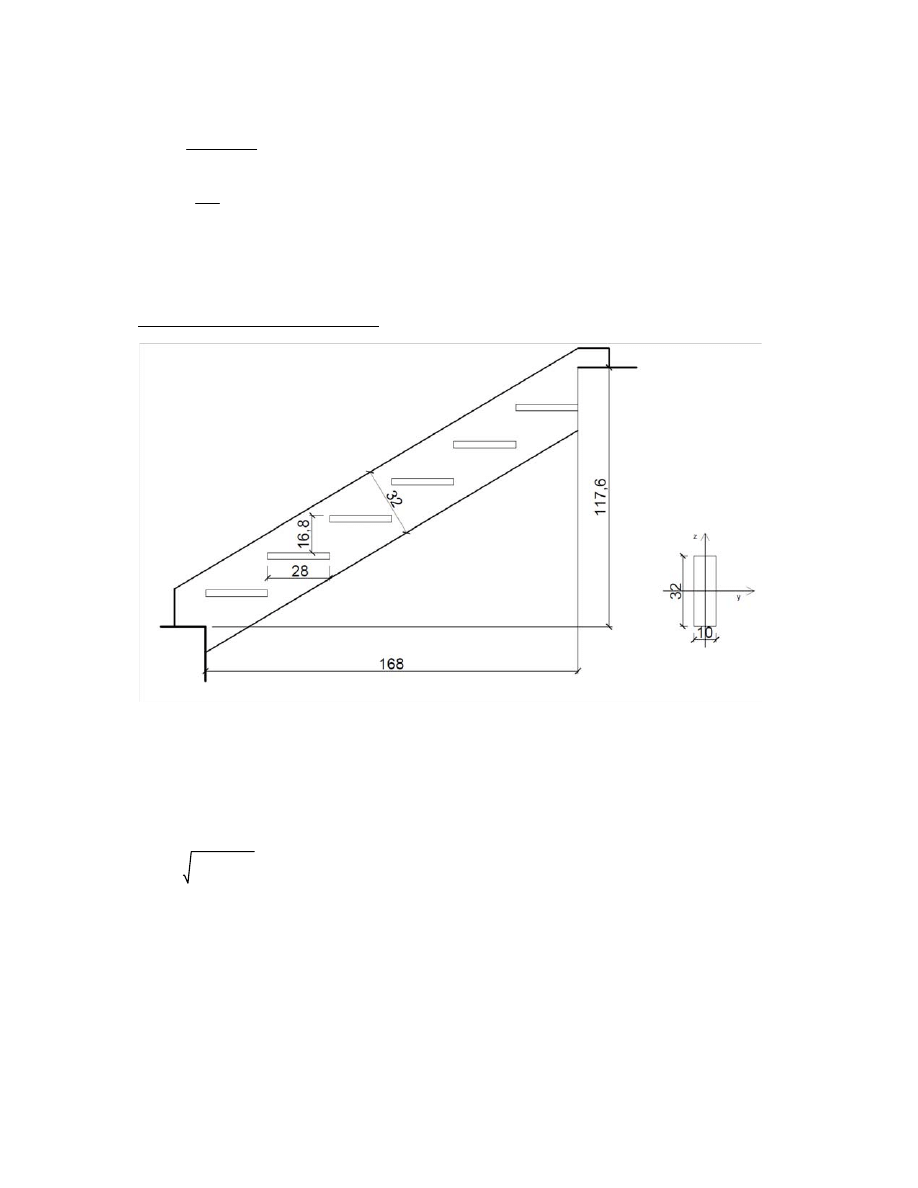
3. Obliczenia dla schodów

3.1 dane projektowe

 

n x h

s

s

n x h

s

s

1

2

3

4

A

B

C

D

a

1

a =(n-1) x s

3

a

1

a

4

a

2

nośna podpora

sp

o

czn

ik

2

sp

o

cz

n

ik

1

bieg

bieg

typ konstrukcji

schody wsuwane

drewno klasy

C24

kategoria użytkowania

B

materiał stopnia

sklejka mieszana

hs 16.8cm



wysokość stopnia

a1

105cm



szerokość biegu

a2

95cm



rozstawy osiowe
belek spocznikowych

a4

150cm



ss 28cm



głębokość stopnia

war

2 hs



ss



0.616 m





warunek szerokości stopnia

60cm

war



65cm



1



szerokość jest właściwa

ρsk

6.2

kN

m

3



gęstość średnia sklejki mieszanej

h1

30mm



grubość stopnia

b

10cm



wstępne wymiary belki policzkowej

h

32cm



bsp

16cm



wstępne wymiary belki spocznikowej

hsp

28cm



n

7



liczba stopni

3.1.2 Rysunek schematyczny konstrukcji

3.2 Zestawienie obciążeń dla stopnia

Ciężar własny
stopnia

g1k ρsk h1



ss



0.052

kN

m







Obciążenie
zmienne

q1k 4.5

kN

m

2

ss



1.26

kN

m







Obciążenie zmienne
skupione

Q1k 3kN



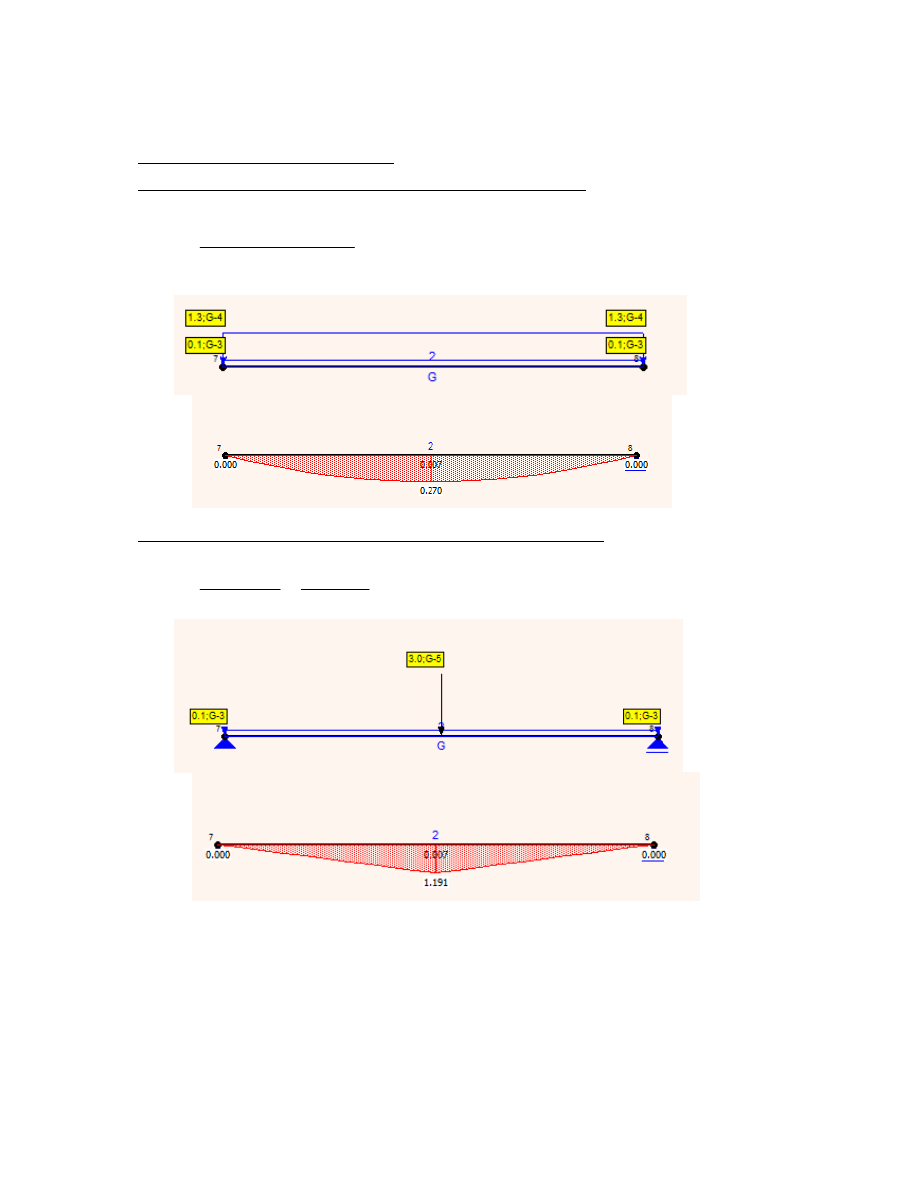
3.3 kombinacje obciążeń dla stopnia

3.3.1 kombinacja I (ciężar własny + obciążenie zmienne liniowe)

MEd1

g1k 1.35



q1k 1.5









a1

2



8

0.27 kN m









maksymalny moment przęsłowy

3.3.2 kombinacja II (ciężar własny + obciążenie zmienne skupione)

MEd2

g1k a1

2



1.35



8

Q1k a1



1.5



4



1.191 kN m









maksymalny moment przęsłowy

3.4 Sprawdzenie warunku SGN

σmyd

fmyd

km

σmzd

fmzd





1



wz. 6.11

km

σmyd

fmyd



σmzd

fmzd



1



wz. 6.12

ponieważ σmzd =0 powyższe wzory przyjmują postać

σmyd

fmyd

1



km

σmyd

fmyd



1



km 1.0



dla elementów drewnopochodnych, dla wszystkich przekrojów

dla kombinacji 1

γM

1.2



częściowy współczynnik bezpieczeństwa właściwości materiału

współczynnik modyfikujący, uwzględniający efekt czasu trwania obciążenia
wilgotności - działanie średniotrwałe

kmod 0.8



współczynnik nie uwzględniany

kh

fm.90.k 34.6

N

mm

2





wytrzymałość charakterystyczna sklejki na zginanie

fm.90.d

fm.90.k kmod



γM

23.067 MPa







wytrzymałość obliczeniowa materiału na zginanie

Wy

ss h1

2



6

42 cm

3







wskaźnik wytrzymałości przekroju

σm.d

MEd1

Wy

6.432 MPa







obliczeniowe naprężenia

σm.d

fm.90.d

0.279



<1

warunek stanu granicznego nośności został spełniony

dla kombinacji 2

γM

1.2



częściowy współczynnik bezpieczeństwa właściwości materiału

tab 2.3

współczynnik modyfikujący, uwzględniający efekt czasu trwania obciążenia i
wilgotności - działanie krótkotrwałe

kmod 0.9



współczynnik nie uwzględniany

kh

fm.90.k 34.6

N

mm

2





wytrzymałość charakterystyczna sklejki na zginanie

fm.90.d

fm.90.k kmod



γM

25.95 MPa







wytrzymałość obliczeniowa materiału na zginanie

Wy

ss h1

2



6

42 cm

3







wskaźnik wytrzymałości przekroju

σm.d

MEd2

Wy

28.356 MPa







obliczeniowe naprężenia

σm.d

fm.90.d

1.093



<1

warunek stanu granicznego nośności nie został spełniony

3.5 zmiana konstrukcji

w związku z niespełnieniem warunków stanu granicznego nośności dla stopnia, w środku biegu
zostaje zaprojektowana dodatkowa belka podpierająca stopnie.

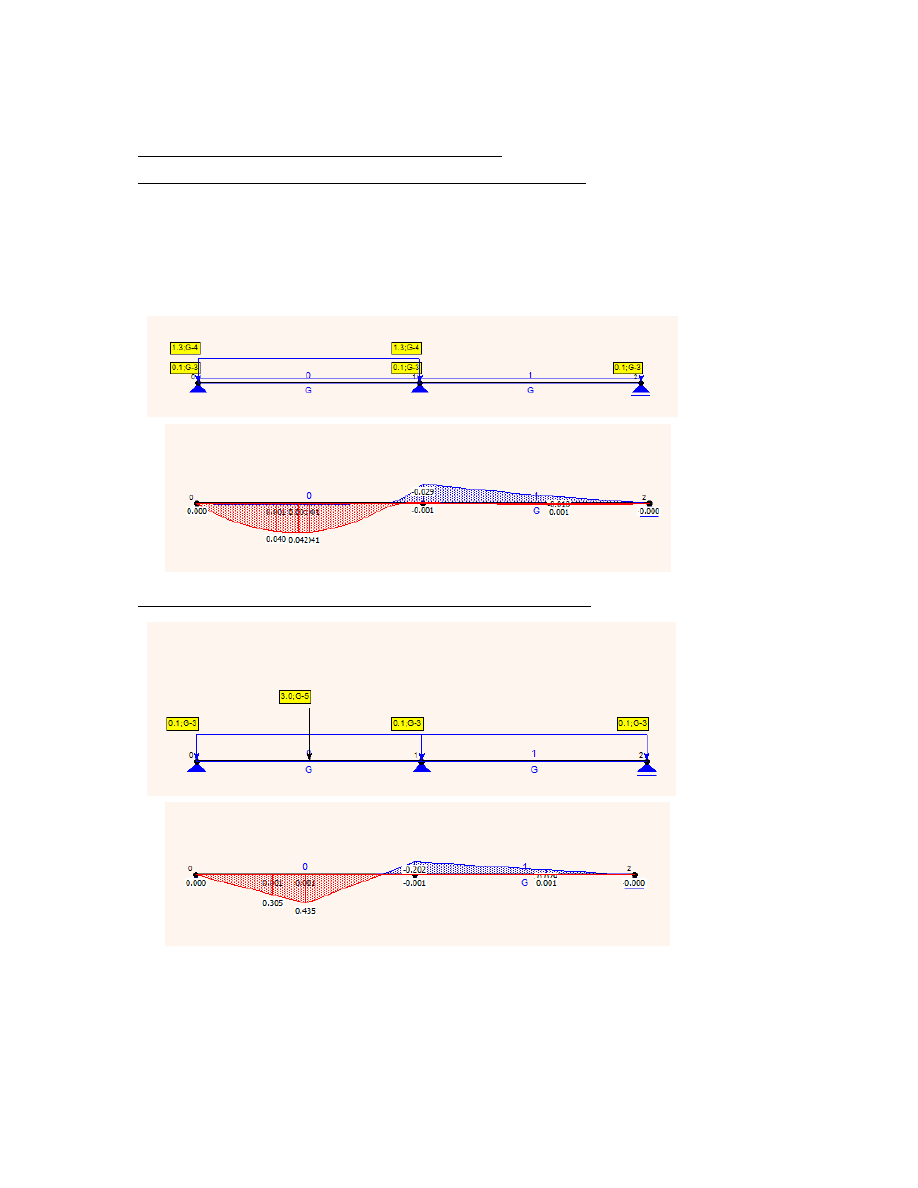
3.5 kombinacje obciążeń dla zmienionej konstrukcji

3.5.1 kombinacja I (ciężar własny + obciążenie zmienne liniowe)

a1p 47.5cm



szerokość przęsła belki

MEd1p

0.042kN m





maksymalny moment przęsłowy

3.5.2 kombinacja II (ciężar własny + obciążenie zmienne liniowe)

MEd2p

0.435kN m





maksymalny moment przęsłowy

3.6 Sprawdzenie warunku SGN dla zmienionej konstrukcji

σmyd

fmyd

km

σmzd

fmzd





1



wz. 6.11

km

σmyd

fmyd



σmzd

fmzd



1



wz. 6.12

ponieważ σmzd =0 powyższe wzory przyjmują postać

σmyd

fmyd

1



km

σmyd

fmyd



1



km 1.0



dla elementów drewnopochodnych, dla wszystkich przekrojów

dla kombinacji 1

γM

1.2



częściowy współczynnik bezpieczeństwa właściwości materiału

współczynnik modyfikujący, uwzględniający efekt czasu trwania
obciążenia i wilgotności - działanie średniotrwałe

kmod 0.8



współczynnik nie uwzględniany

kh

fm.90.k 34.6

N

mm

2





wytrzymałość charakterystyczna sklejki na zginanie

fm.90.d

fm.90.k kmod



γM

23.067 MPa







wytrzymałość obliczeniowa materiału na zginanie

Wy

ss h1

2



6

42 cm

3







wskaźnik wytrzymałości przekroju

σm.d

MEd1p

Wy

1 MPa







obliczeniowe naprężenia

σm.d

fm.90.d

0.043



<1

warunek stanu granicznego nośności został spełniony

dla kombinacji 2

γM

1.2



częściowy współczynnik bezpieczeństwa właściwości materiału

współczynnik modyfikujący, uwzględniający efekt czasu
trwania obciążenia i wilgotności - działanie krótkotrwałe

kmod 0.9



współczynnik nie uwzględniany

kh

fm.90.k 34.6

N

mm

2





wytrzymałość charakterystyczna sklejki na zginanie

fm.90.d

fm.90.k kmod



γM

25.95 MPa







wytrzymałość obliczeniowa materiału na zginanie

Wy

ss h1

2



6

42 cm

3







wskaźnik wytrzymałości przekroju

σm.d

MEd2p

Wy

10.357 MPa







obliczeniowe naprężenia

σm.d

fm.90.d

0.399



<1

warunek stanu granicznego nośności został spełniony

3.7 sprawdzenie SGU dla stopnia dla kombinacji 2

Iy

ss h1

3



12

63 cm

4







moment bezwładności stopnia

E0.mean 9519

N

mm

2





średni moduł sprężystości (zginanie)

u

4.515 10

3





kN



m

3





ugięcia belki

ufin

u

E0.mean Iy



0.075 cm







umax

a1

250

0.42 cm







ugięcie maksymalne

ufin umax



1



warunek został spełniony

4. obliczenia dla belki policzkowej

hb

n hs



1.176 m





wysokość biegu

a3

n

1



(

) ss



1.68 m





długość biegu w planie

lb

hb

2

a3

2



2.051 m





długość biegu

α

35deg



kąt nachylenia schodów

sin α

( )

0.574



4.1 zestawienie obciążeń

wartości charakterystyczne

stałe

ciężar objętościowy drewna klasy C24

ρb

4.2

kN

m

3





pk

ρb h

 b



0.134

kN

m







ciężar własny belki policzkowej (pionowo po długości belki)

pk.r pk sin α

( )



0.077

kN

m







ciężar własny belki policzkowej (równolegle do osi belki)

pk.p pk cos α

( )



0.11

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

ρsk 6.2

kN

m

3





cięzar objętościowy sklejki

pks

ρsk

1
4

 a1



h1



0.049

kN

m







cięzar własny stopni (pionowo po długości belki)

pks.r pks sin α

( )



0.028

kN

m







ciężar własny belki policzkowej (równolegle do osi belki)

pks.p pks cos α

( )



0.04

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

zmienne

qp

3

kN

m

2

1
4

 a1



0.788

kN

m







obciążenie zmienne użytkowe (pionowo po długości belki)

obciążenie zmienne użytkowe (równolegle do osi belki)

qpr qp sin α

( )



0.452

kN

m







obciążenie zmienne użytkowe (prostopadle do osi belki)

qpp qp cos α

( )



0.645

kN

m







Qp

4.5kN



obciążenie montażowe (pionowo po długości belki)

Qpr Qp sin α

( )



2.581 kN







obciążenie montażowe (równolegle do osi belki)

Qpp Qp cos α

( )



3.686 kN







obciążenie montażowe (prostopadle do osi belki)

wartości obliczeniowe

stałe

współczynnik bezpieczeństwa właściwości materiałów dla
drewna litego

γM.d

1.3



γM 1.2



współczynnik bezpieczeństwa materiałów dla sklejki

γM.z

1.5



współczynnik bezpieczeństwa dla obciążeń zmiennych

pkdd

pk γM.d



0.175

kN

m







ciężar własny belki policzkowej (pionowo po długości belki)

pk.r.d pk.r γM.d



0.1

kN

m







ciężar własny belki policzkowej (równolegle do osi belki)

pk.p.d pk.p γM.d



0.143

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

pksd pks γM



0.059

kN

m







cięzar własny stopni (pionowo po długości belki)

pks.rd

pks.r γM



0.034

kN

m







ciężar własny belki policzkowej (równolegle do osi belki)

pks.pd pks.p γM



0.048

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

zmiennne

qpd qp γM.z



1.181

kN

m







obciążenie zmienne użytkowe (pionowo po długości belki)

obciążenie zmienne użytkowe (równolegle do osi belki)

qprd qpr γM.z



0.678

kN

m







obciążenie zmienne użytkowe (prostopadle do osi belki)

qppd

qpp γM.z



0.968

kN

m







Qpd Qp γM.z



6.75 kN







obciążenie montażowe (pionowo po długości belki)

Qprd Qpr γM.z



3.872 kN







obciążenie montażowe (równolegle do osi belki)

Qppd

Qpp γM.z



5.529 kN







obciążenie montażowe (prostopadle do osi belki)

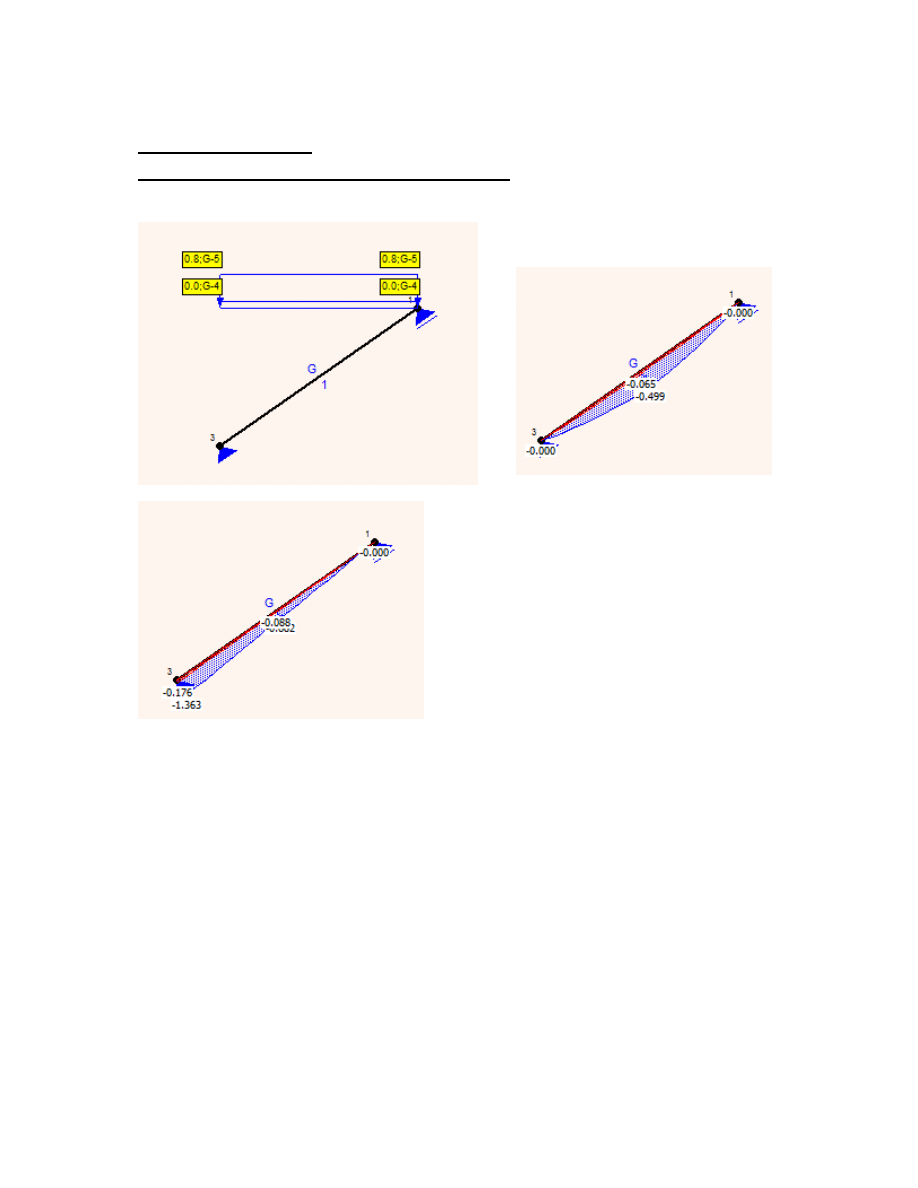
4.2 kombinacje obciążeń

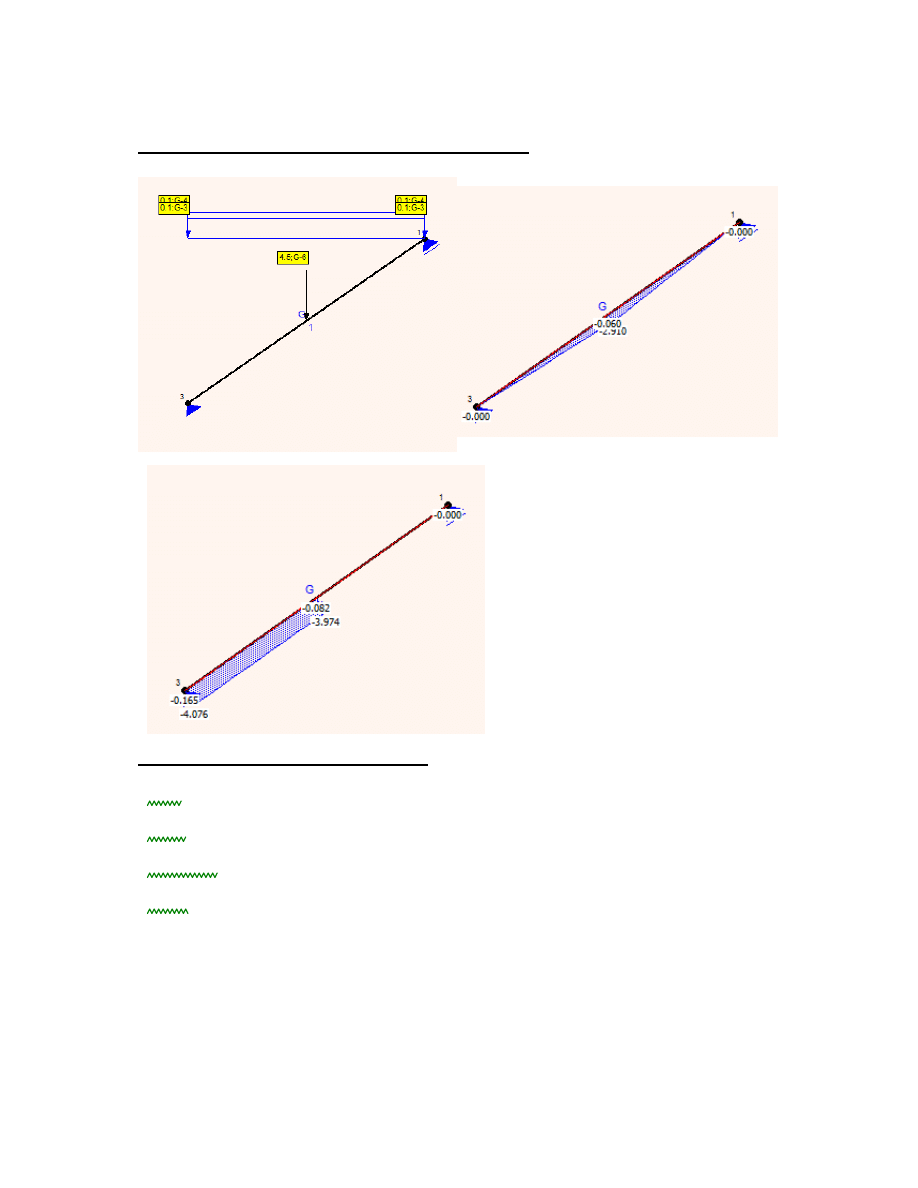
4.2.1 kombinacja I (obc. stałe + obciążenie użytkowe)

momenty [kNm]

schemat

siły podłużne [kN]

4.2.2 kombinacja II (obc. stałe + obciążenie montażowe)

schemat

momenty [kNm]

siły podłużne [kN]

4.3 Wymiarowanie SGN belki policzkowej

fm.k 24MPa



wytrzymałość na zginanie

fc.0.k 21MPa



wytrzymałość na ściskanie wzdłuż włókien

E0.mean.p 11GPa



średni modłuł sprężystości wzdłuż włókien

E0.05 7.4GPa



5% kwantyl modułu sprężystości wzdłuż włókien

4.3.1 zestawienie miarodajnych obciążeń (warości obliczeniowe)

kombinacja I

Md1 0.499kN m





Nd1 0.682kN



Md2 2.917kN m





kombinacja II

Nd2 3.984kN



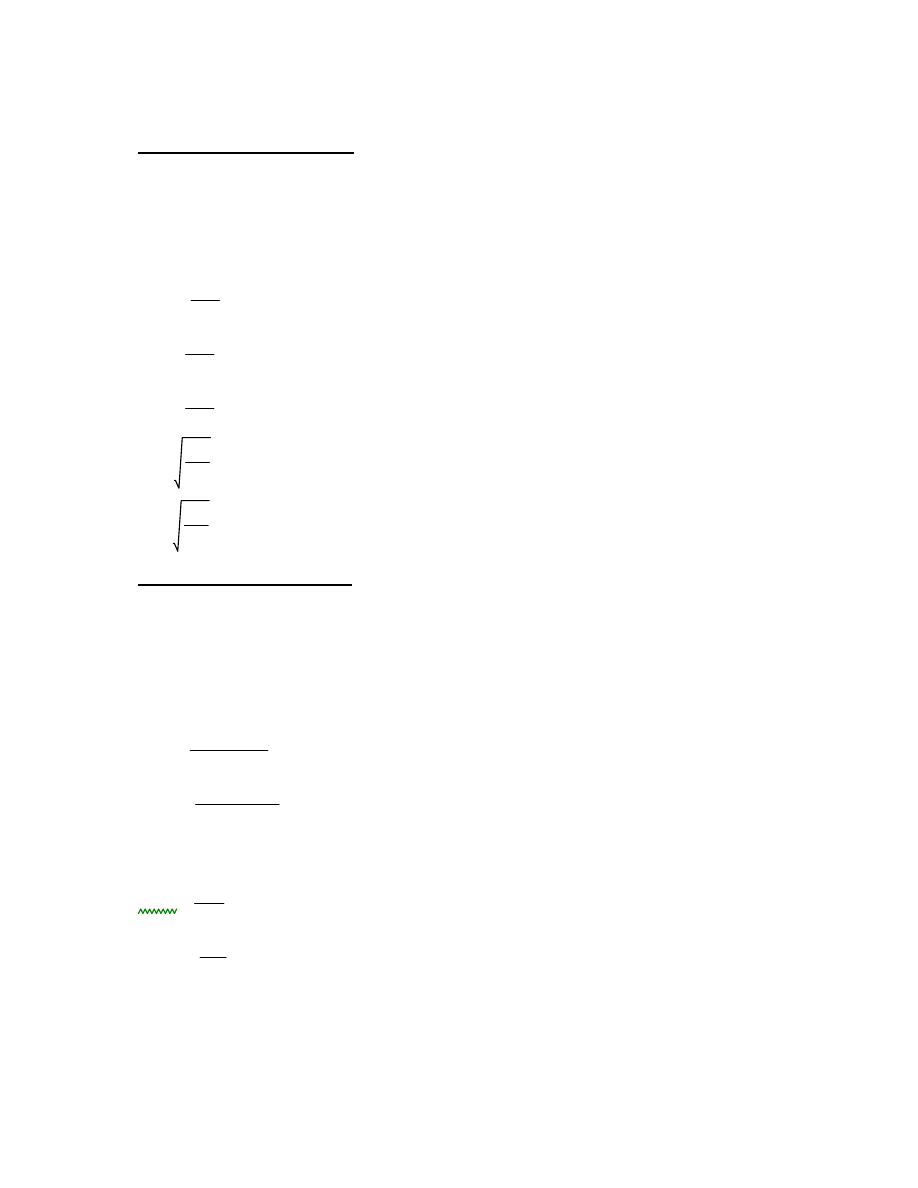
4.3.2 dane dotyczące przekroju

b

0.1 m



szerokość belki

h

0.32 m



wysokość belki

lef

1.05 lb



2.153 m





efektywna długość belki

Ab

b h



0.032 m

2





pole przekroju belki

Wyb

b h

2



6

1.707

10

3



cm

3







wskaźnik wytrzymałości

moment bezwładności względem osi y

Iy.b

b h

3



12

2.731

10

4



cm

4







moment bezwładności względem osi z

Iz.b

h b

3



12

2.667

10

3



cm

4







iy

Iy.b

Ab

9.238 cm







promień bezwładności względem osi y

iz

Iz.b

Ab

2.887 cm







promień bezwładności względem osi y

4.4 obliczenia dla kombinacji I

γM.d 1.3



częściowy współczynnik bezpieczeństwa materiału dla drewna

współczynnik modyfikujący uwględniający efekt czasu
trwania obciążenia i wilgotności - obciążenie średniotrwałe

kmod.d 0.8



wartości obliczeniowe wytrzymałości potrzebne do wymiarowania

fm.d

fm.k kmod.d



γM.d

14.769 MPa







zginanie

fc.0.d

fc.0.k kmod.d



γM.d

12.923 MPa







ściskanie wzdłuż włókien

obliczeniowe naprężenia:

σm.d

Md1
Wyb

0.292 MPa







zginanie

σc.0.d

Nd1

Ab

0.021 MPa







ściskanie

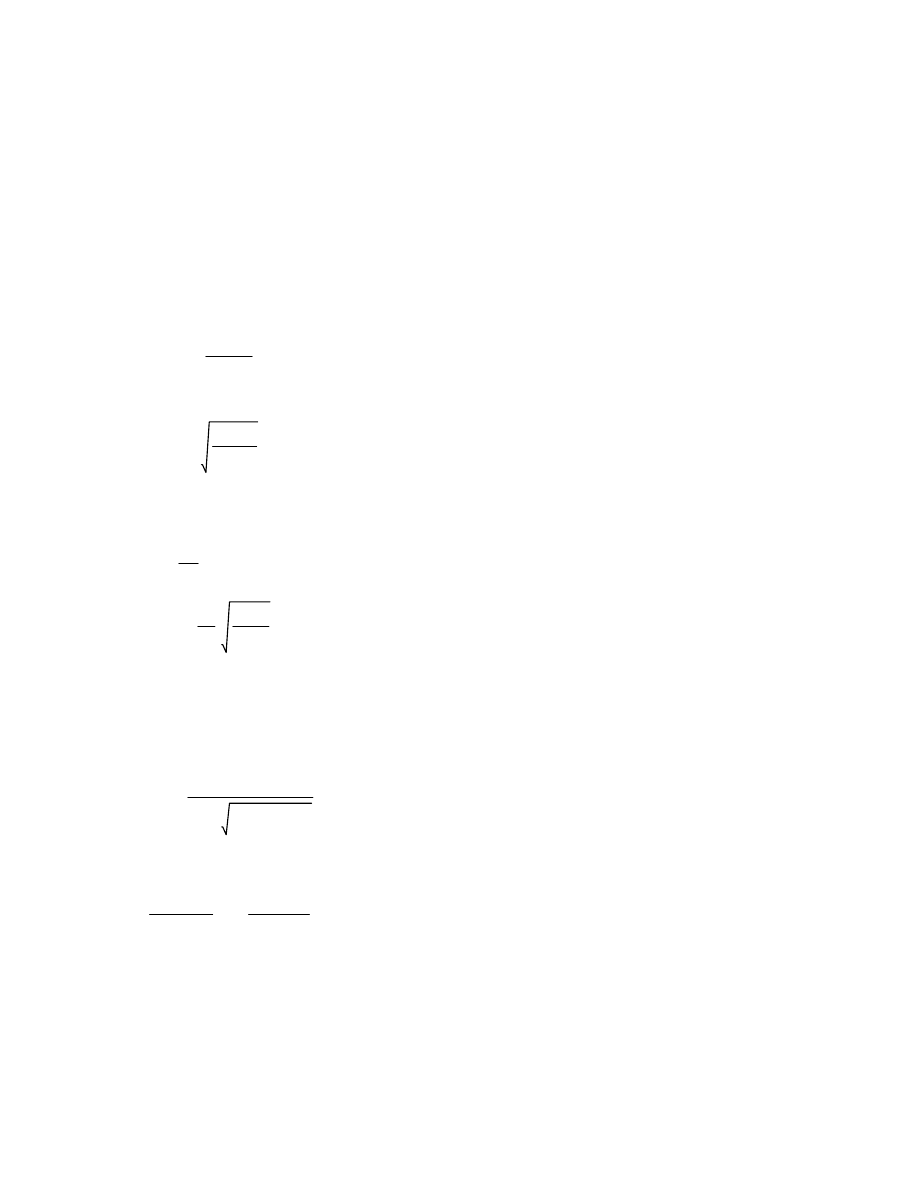
sprawdzenie stanu graniczenego nośności przekroju na zginanie ze ściskaniem

naprężenia:

σm.y.d

σm.d 0.292 MPa







σm.z.d.

0Pa



fm.y.d fm.d 14.769 MPa







naprężenie krytyczne przy zginaniu

σm.crit

0.78 b

2



h lef



E0.05



83.769 MPa







belka z drewna litego o przekroju prostokątnym

smukłość względna przy zginaniu

λrel.m

fm.k

σm.crit

0.535





współczynnik uwzględniający redukcje wytrzymałości
ze względu na zwichrowanie elementu

kkrit 1



λz

lef

iz

74.59





smukłość względem osi z

λrel.z

λz

π

fc.0.d

E0.05



0.992





współczynnik dotyczący prostoliniowości elementów (drewno lite)

βc

0.2



kz 0.5 1 βc λrel.z 0.5











λrel.z

2













1.041





kc.z

1

kz

kz

2

λrel.z

2





0.403





sprawdzenie warunku normowego

warunek jest spełniony

σc.0.d

kc.z fc.0.d















2

σm.d

kkrit fm.d





1.981 %





4.4 obliczenia dla kombinacji II

γM.d 1.3



częściowy współczynnik bezpieczeństwa materiału dla drewna

współczynnik modyfikujący uwględniający efekt czasu
trwania obciążenia i wilgotności - obciążenie średniotrwałe

kmod.d 0.9



wartości obliczeniowe wytrzymałości potrzebne do wymiarowania

fm.d

fm.k kmod.d



γM.d

16.615 MPa







zginanie

fc.0.d

fc.0.k kmod.d



γM.d

14.538 MPa







ściskanie wzdłuż włókien

obliczeniowe naprężenia:

σm.d

Md2
Wyb

1.709 MPa







zginanie

σc.0.d

Nd2

Ab

0.125 MPa







ściskanie

sprawdzenie stanu graniczenego nośności przekroju na zginanie ze ściskaniem

naprężenia:

σm.y.d

σm.d 1.709 MPa







σm.z.d.

0Pa



fm.y.d fm.d 16.615 MPa







naprężenie krytyczne przy zginaniu

σm.crit

0.78 b

2



h lef



E0.05



83.769 MPa







belka z drewna litego o przekroju prostokątnym

smukłość względna przy zginaniu

λrel.m

fm.k

σm.crit

0.535





współczynnik uwzględniający redukcje wytrzymałości
ze względu na zwichrowanie elementu

kkrit 1



λz

lef

iz

74.59





smukłość względem osi z

λrel.z

λz

π

fc.0.d

E0.05



1.052





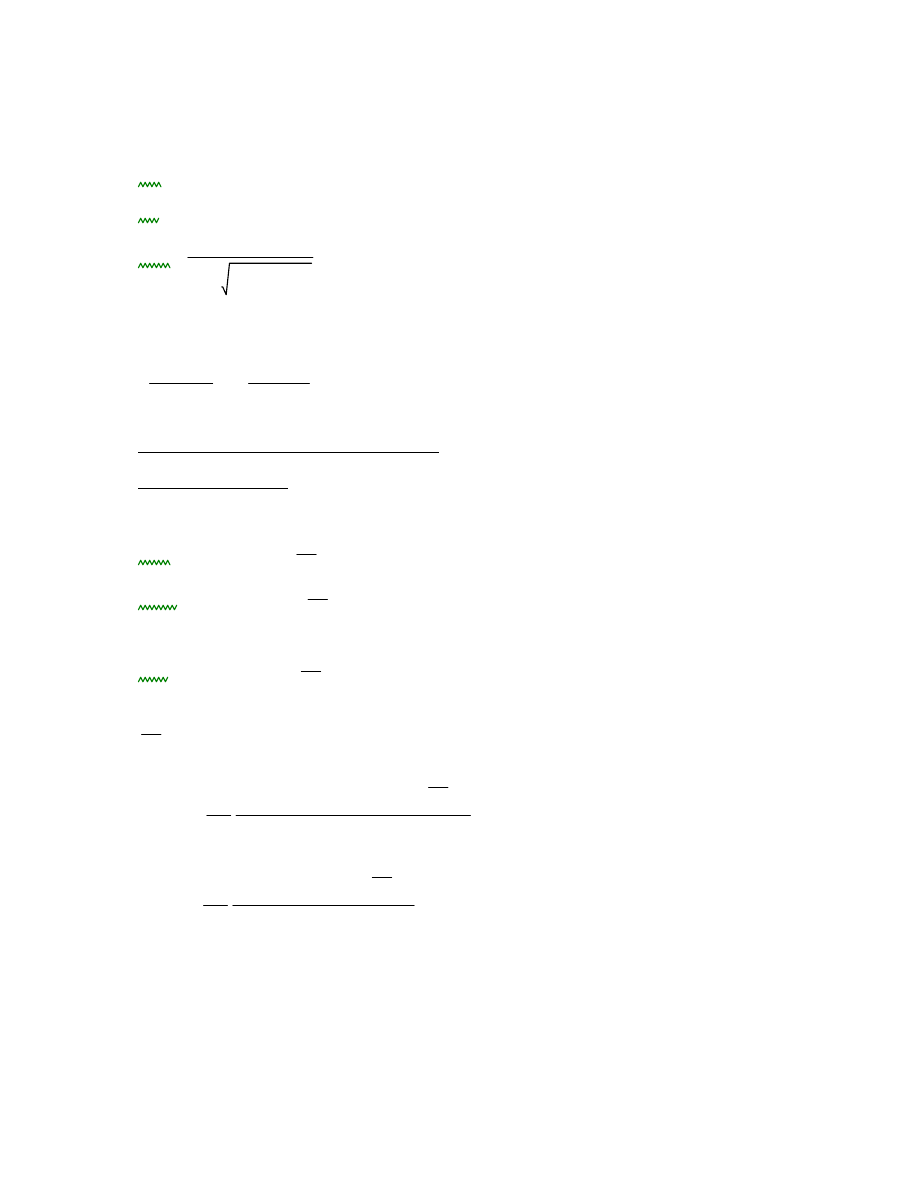
współczynnik dotyczący prostoliniowości elementów (drewno lite)

βc

0.2



kz 0.5 1 βc λrel.z 0.5











λrel.z

2













1.109





kc.z

1

kz

kz

2

λrel.z

2





0.379





sprawdzenie warunku normowego

σc.0.d

kc.z fc.0.d















2

σm.d

kkrit fm.d





10.338 %





warunek jest spełniony

4.5 sprawdzenie SGU dla belki policzkowej

4.5.1 dla kombinacji I

obciążenia stałe

pk.p pk cos α

( )



0.11

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

pks.p pks cos α

( )



0.04

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

obciążenia zmienne

obciążenie zmienne użytkowe (prostopadle do osi belki)

qpp qp cos α

( )



0.645

kN

m







lef

h

6.729



<20

sprawdzenie warunku

ugięcie od obciążeń stałych

uinst.G

5

384

pk.p pks.p







lef

4



1

19.2

h

lef













2















E0.mean.p Iy.b



0.02 mm







ugięcie od obciążeń zmiennych

uinst.q

5

384

qpp

 

lef

4



1

19.2

h

lef













2















E0.mean.p Iy.b



0.086 mm







kdef

0.6



dla drewna litego, 1szej klasy użytkowania

ψ2

0.3



dla kategorii B

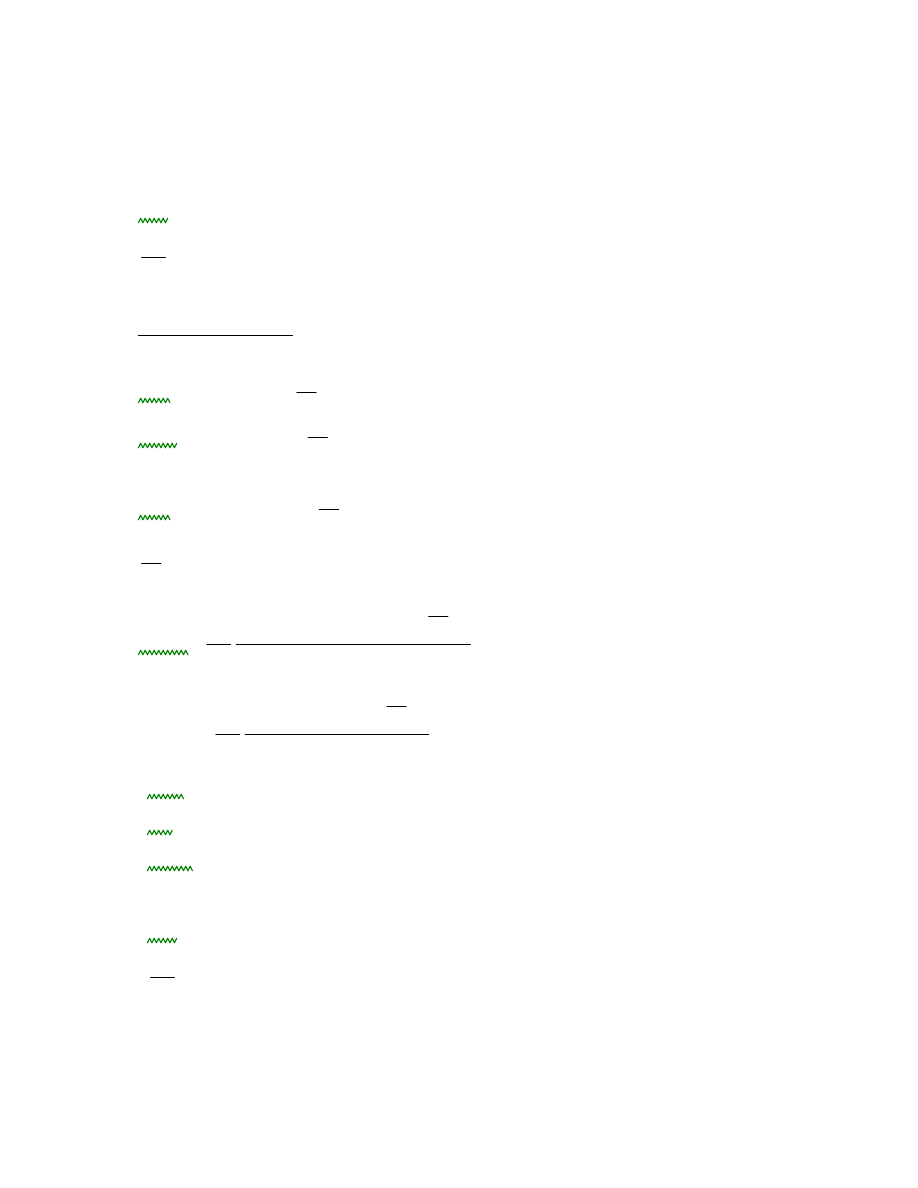
ufin.G uinst.G 1 kdef









0.032 mm







ugięcie od oddziaływania stałego

ufin.q uinst.q 1 ψ2 kdef











0.101 mm







ugięcie od oddziaływań zmiennych

ufin ufin.G ufin.q



0.133 mm







przemieszczenie końcowe

lef

250

8.613 mm





graniczne ugięcie belki

warunek został spełniony

4.5.1 dla kombinacji II

obciążenia stałe

pk.p pk cos α

( )



0.11

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

pks.p pks cos α

( )



0.04

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

obciążenia zmienne

obciążenie zmienne użytkowe (prostopadle do osi belki)

Qpp Qp cos α

( )



3.686 m

kN

m







lef

h

6.729



<20

sprawdzenie warunku

ugięcie od obciążeń stałych

uinst.G

5

384

pk.p pks.p







lef

4



1

19.2

h

lef













2















E0.mean.p Iy.b



0.02 mm







ugięcie od obciążeń zmiennych

uinst.Q

5

384

Qpp

 

lef

3



1

19.2

h

lef













2















E0.mean.p Iy.b



0.227 mm







kdef

0.6



dla drewna litego, 1szej klasy użytkowania

ψ2

0.3



dla kategorii B

ufin.G uinst.G 1 kdef









0.032 mm







ugięcie od oddziaływania stałego

ufin.Q uinst.Q 1 ψ2 kdef











0.268 mm







ugięcie od oddziaływań zmiennych

ufin ufin.G ufin.Q



0.3 mm







przemieszczenie końcowe

lef

250

8.613 mm





graniczne ugięcie belki

warunek został spełniony

5. obliczenia dla dodatkowej belki pod biegiem

b

10cm



wstępne wymiary belki policzkowej

h

10.06cm



5.1 zestawienie obciążeń

wartości charakterystyczne

stałe

ciężar objętościowy drewna klasy C24

ρb

4.2

kN

m

3





pk

ρb

24.49cm

10.08cm


2



b



0.073

kN

m







ciężar własny belki policzkowej (pionowo po długości)

pk.r pk sin α

( )



0.042

kN

m







ciężar własny belki policzkowej (równolegle do osi belki)

pk.p pk cos α

( )



0.059

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

ρsk 6.2

kN

m

3





cięzar objętościowy sklejki

pks

ρsk

1
2

 a1



h1



0.098

kN

m







cięzar własny stopni (pionowo po długości belki)

pks.r pks sin α

( )



0.056

kN

m







ciężar własny belki policzkowej (równolegle do osi belki)

pks.p pks cos α

( )



0.08

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

zmienne

qp

3

kN

m

2

1
2

 a1



1.575

kN

m







obciążenie zmienne użytkowe (pionowo po długości belki)

obciążenie zmienne użytkowe (równolegle do osi belki)

qpr qp sin α

( )



0.903

kN

m







obciążenie zmienne użytkowe (prostopadle do osi belki)

qpp qp cos α

( )



1.29

kN

m







Qp

4.5kN



obciążenie montażowe (pionowo po długości belki)

Qpr Qp sin α

( )



2.581 kN







obciążenie montażowe (równolegle do osi belki)

Qpp Qp cos α

( )



3.686 kN







obciążenie montażowe (prostopadle do osi belki)

wartości obliczeniowe

stałe

współczynnik bezpieczeństwa właściwości materiałów dla
drewna litego

γM.d

1.3



γM 1.2



współczynnik bezpieczeństwa materiałów dla sklejki

γM.z

1.5



współczynnik bezpieczeństwa dla obciążeń zmiennych

pkdd

pk γM.d



0.094

kN

m







ciężar własny belki policzkowej (pionowo po długości belki)

pk.r.d pk.r γM.d



0.054

kN

m







ciężar własny belki policzkowej (równolegle do osi belki)

pk.p.d pk.p γM.d



0.077

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

pksd pks γM



0.117

kN

m







cięzar własny stopni (pionowo po długości belki)

pks.rd

pks.r γM



0.067

kN

m







ciężar własny belki policzkowej (równolegle do osi belki)

pks.pd pks.p γM



0.096

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

zmiennne

qpd qp γM.z



2.362

kN

m







obciążenie zmienne użytkowe (pionowo po długości belki)

obciążenie zmienne użytkowe (równolegle do osi belki)

qprd qpr γM.z



1.355

kN

m







obciążenie zmienne użytkowe (prostopadle do osi belki)

qppd

qpp γM.z



1.935

kN

m







Qpd Qp γM.z



6.75 kN







obciążenie montażowe (pionowo po długości belki)

Qprd Qpr γM.z



3.872 kN







obciążenie montażowe (równolegle do osi belki)

Qppd

Qpp γM.z



5.529 kN







obciążenie montażowe (prostopadle do osi belki)

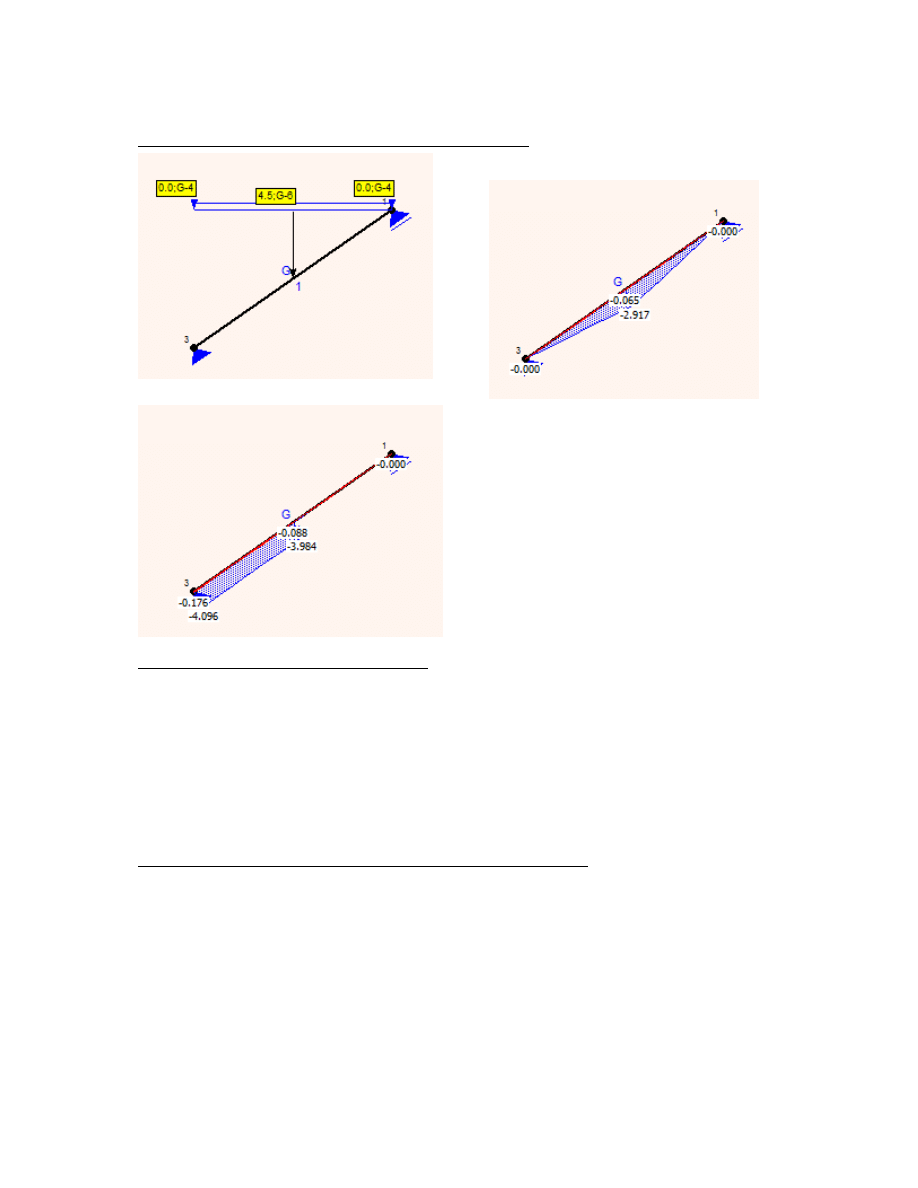
5.2 kombinacje obciążeń

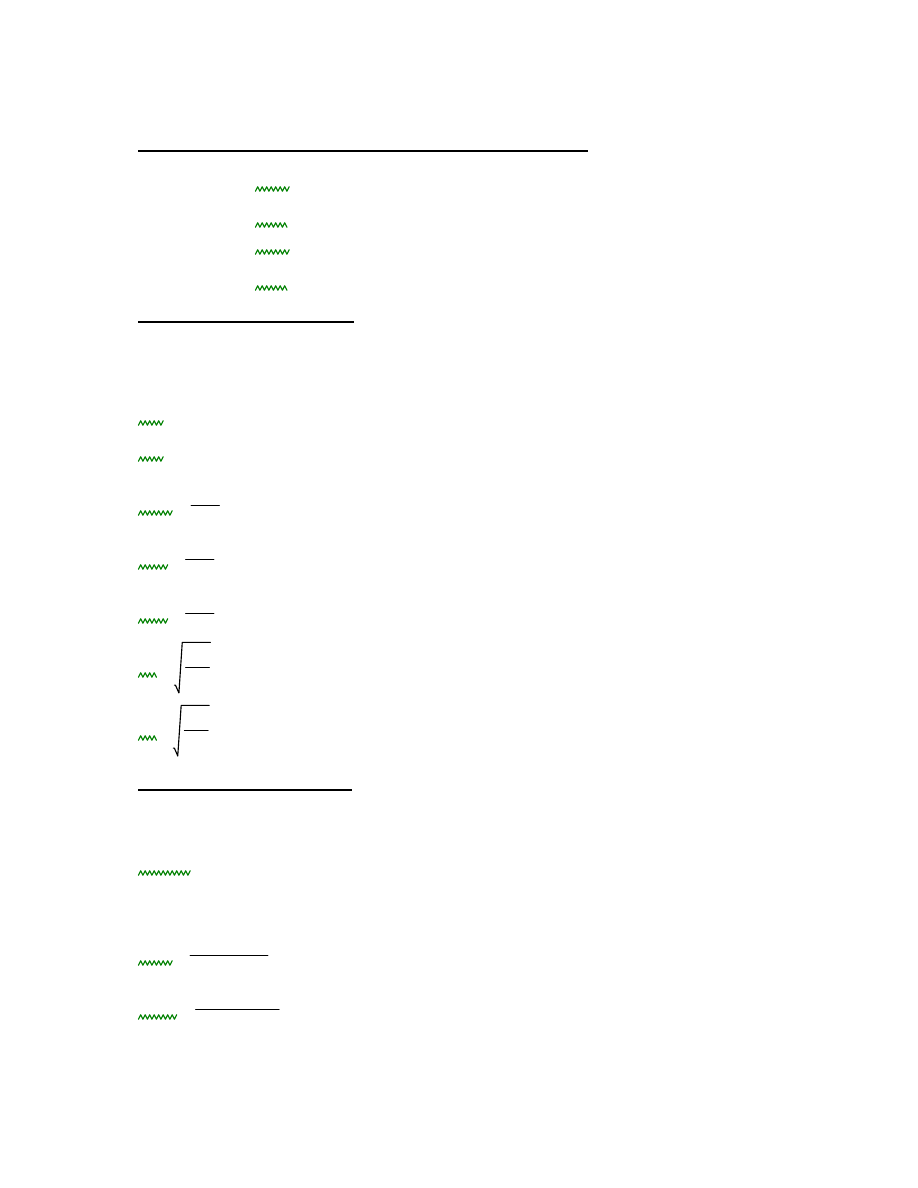
5.2.1 kombinacja I (obc. stałe + obciążenie użytkowe)

schemat

momenty [kNm]

siły podłużne [kN]

5.2.2 kombinacja II (obc. stałe + obciążenie montażowe)

schemat

momenty [kNm]

siły podłużne [kN]

5.3 Wymiarowanie SGN belki policzkowej

fm.k 24MPa



wytrzymałość na zginanie

fc.0.k 21MPa



wytrzymałość na ściskanie wzdłuż włókien

E0.mean.p 11GPa



średni modłuł sprężystości wzdłuż włókien

E0.05 7.4GPa



5% kwantyl modułu sprężystości wzdłuż włókien

5.3.1 zestawienie miarodajnych obciążeń (warości obliczeniowe)

kombinacja I

Md1 0.908kN m





Nd1 1.241kN



kombinacja II

Md2 2.910kN m





Nd2 3.974kN



5.3.2 dane dotyczące przekroju

b

0.1 m



szerokość belki

h

0.101 m



wysokość belki

lef

1.05 lb



2.153 m





efektywna długość belki

Ab

b h



0.01 m

2





pole przekroju belki

Wyb

b h

2



6

168.673 cm

3







wskaźnik wytrzymałości

Iy.b

b h

3



12

848.424 cm

4







moment bezwładności względem osi y

Iz.b

h b

3



12

838.333 cm

4







moment bezwładności względem osi z

iy

Iy.b

Ab

2.904 cm







promień bezwładności względem osi y

iz

Iz.b

Ab

2.887 cm







promień bezwładności względem osi y

5.4 obliczenia dla kombinacji I

γM.d 1.3



częściowy współczynnik bezpieczeństwa materiału dla drewna

współczynnik modyfikujący uwględniający efekt czasu
trwania obciążenia i wilgotności - obciążenie średniotrwałe

kmod.d 0.8



wartości obliczeniowe wytrzymałości potrzebne do wymiarowania

fm.d

fm.k kmod.d



γM.d

14.769 MPa







zginanie

ściskanie wzdłuż włókien

fc.0.d

fc.0.k kmod.d



γM.d

12.923 MPa







obliczeniowe naprężenia:

σm.d

Md1
Wyb

5.383 MPa







zginanie

σc.0.d

Nd1

Ab

0.123 MPa







ściskanie

sprawdzenie stanu graniczenego nośności przekroju na zginanie ze ściskaniem

naprężenia:

σm.y.d

σm.d 5.383 MPa







σm.z.d.

0Pa



fm.y.d fm.d 14.769 MPa







naprężenie krytyczne przy zginaniu

σm.crit

0.78 b

2



h lef



E0.05



266.463 MPa







belka z drewna litego o przekroju prostokątnym

smukłość względna przy zginaniu

λrel.m

fm.k

σm.crit

0.3





współczynnik uwzględniający redukcje wytrzymałości
ze względu na zwichrowanie elementu

kkrit 1



λz

lef

iz

74.59





smukłość względem osi z

λrel.z

λz

π

fc.0.d

E0.05



0.992





współczynnik dotyczący prostoliniowości elementów (drewno lite)

βc

0.2



kz 0.5 1 βc λrel.z 0.5











λrel.z

2













1.041





kc.z

1

kz

kz

2

λrel.z

2





0.403





sprawdzenie warunku normowego

σc.0.d

kc.z fc.0.d















2

σm.d

kkrit fm.d





36.505 %





warunek jest spełniony

5.4 obliczenia dla kombinacji II

γM.d 1.3



częściowy współczynnik bezpieczeństwa materiału dla drewna

współczynnik modyfikujący uwględniający efekt czasu
trwania obciążenia i wilgotności - obciążenie średniotrwałe

kmod.d 0.9



wartości obliczeniowe wytrzymałości potrzebne do wymiarowania

fm.d

fm.k kmod.d



γM.d

16.615 MPa







zginanie

ściskanie wzdłuż włókien

fc.0.d

fc.0.k kmod.d



γM.d

14.538 MPa







obliczeniowe naprężenia:

σm.d

Md2
Wyb

14.822 MPa







zginanie

σc.0.d

Nd2

Ab

0.395 MPa







ściskanie

sprawdzenie stanu graniczenego nośności przekroju na zginanie ze ściskaniem

naprężenia:

σm.y.d

σm.d 14.822 MPa







σm.z.d.

0Pa



fm.y.d fm.d 16.615 MPa







naprężenie krytyczne przy zginaniu

σm.crit

0.78 b

2



h lef



E0.05



266.463 MPa







belka z drewna litego o przekroju prostokątnym

smukłość względna przy zginaniu

λrel.m

fm.k

σm.crit

0.3





współczynnik uwzględniający redukcje wytrzymałości
ze względu na zwichrowanie elementu

kkrit 1



λz

lef

iz

74.59





smukłość względem osi z

λrel.z

λz

π

fc.0.d

E0.05



1.052





współczynnik dotyczący prostoliniowości elementów (drewno lite)

βc

0.2



kz 0.5 1 βc λrel.z 0.5











λrel.z

2













1.109





kc.z

1

kz

kz

2

λrel.z

2





0.379





sprawdzenie warunku normowego

σc.0.d

kc.z fc.0.d















2

σm.d

kkrit fm.d





89.718 %





warunek jest spełniony

5.5 sprawdzenie SGU dla belki policzkowej

5.5.1 dla kombinacji I

obciążenia stałe

pk.p pk cos α

( )



0.059

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

pks.p pks cos α

( )



0.08

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

obciążenia zmienne

obciążenie zmienne użytkowe (prostopadle do osi belki)

qpp qp cos α

( )



1.29

kN

m







lef

h

21.404



<20

sprawdzenie warunku

ugięcie od obciążeń stałych

uinst.G

5

384

pk.p pks.p







lef

4



1

19.2

h

lef













2















E0.mean.p Iy.b



0.436 mm







ugięcie od obciążeń zmiennych

uinst.q

5

384

qpp

 

lef

4



1

19.2

h

lef













2















E0.mean.p Iy.b



4.032 mm







kdef

0.6



dla drewna litego, 1szej klasy użytkowania

ψ2

0.3



dla kategorii B

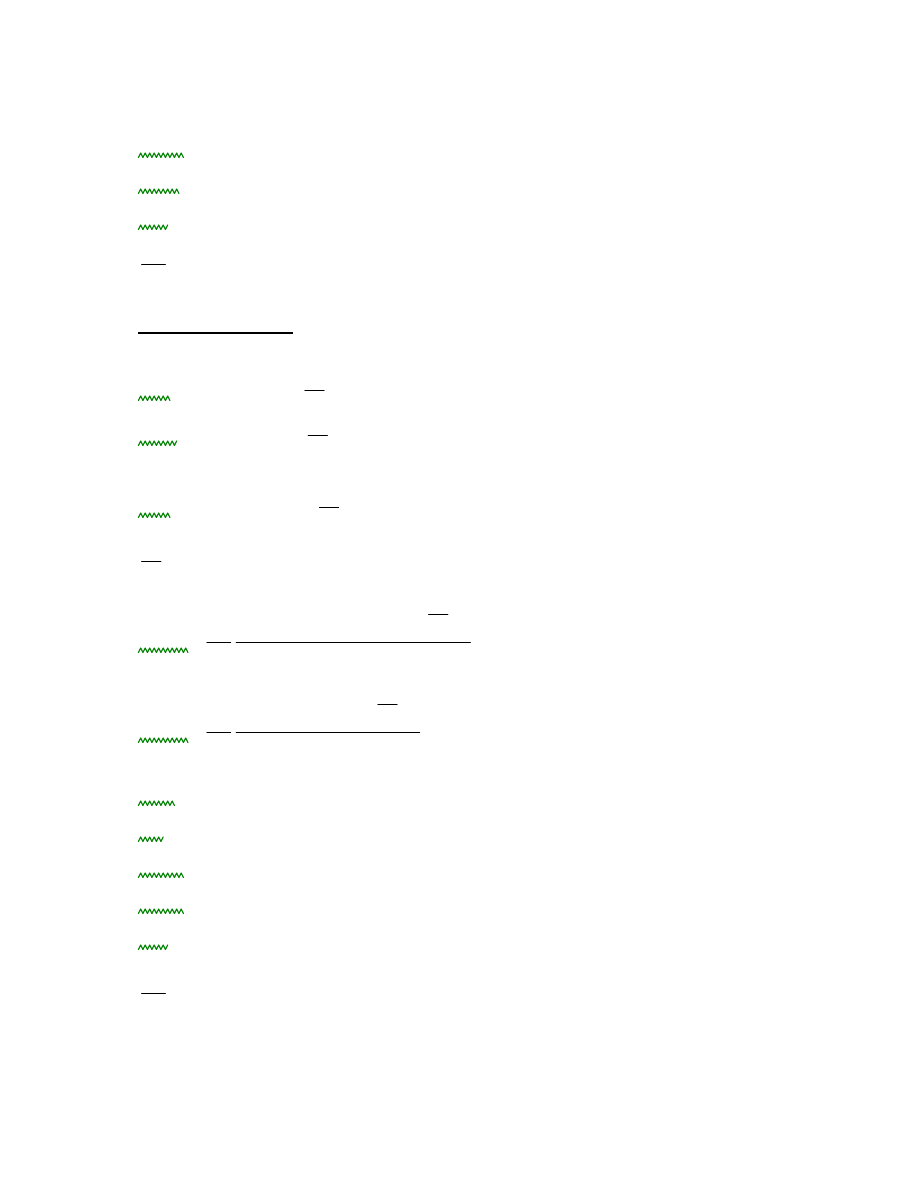
ufin.G uinst.G 1 kdef









0.697 mm







ugięcie od oddziaływania stałego

ufin.q uinst.q 1 ψ2 kdef











4.757 mm







ugięcie od oddziaływań zmiennych

ufin ufin.G ufin.q



5.455 mm







przemieszczenie końcowe

lef

250

8.613 mm





graniczne ugięcie belki

warunek został spełniony

5.5.1 dla kombinacji II

obciążenia stałe

pk.p pk cos α

( )



0.059

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

pks.p pks cos α

( )



0.08

kN

m







ciężar własny belki policzkowej (prostopadle do osi belki)

obciążenia zmienne

obciążenie zmienne użytkowe (prostopadle do osi belki)

Qpp Qp cos α

( )



3.686 m

kN

m







lef

h

21.404



<20

sprawdzenie warunku

uinst.G

5

384

pk.p pks.p







lef

4



1

19.2

h

lef













2















E0.mean.p Iy.b



0.436 mm







ugięcie od obciążeń stałych

uinst.Q

5

384

Qpp

 

lef

3



1

19.2

h

lef













2















E0.mean.p Iy.b



5.35 mm







ugięcie od obciążeń zmiennych

kdef

0.6



dla drewna litego, 1szej klasy użytkowania

ψ2

0.3



dla kategorii B

ufin.G uinst.G 1 kdef









0.697 mm







ugięcie od oddziaływania stałego

ufin.Q uinst.Q 1 ψ2 kdef











6.312 mm







ugięcie od oddziaływań zmiennych

ufin ufin.G ufin.Q



7.01 mm







przemieszczenie końcowe

lef

250

8.613 mm





graniczne ugięcie belki

warunek został spełniony

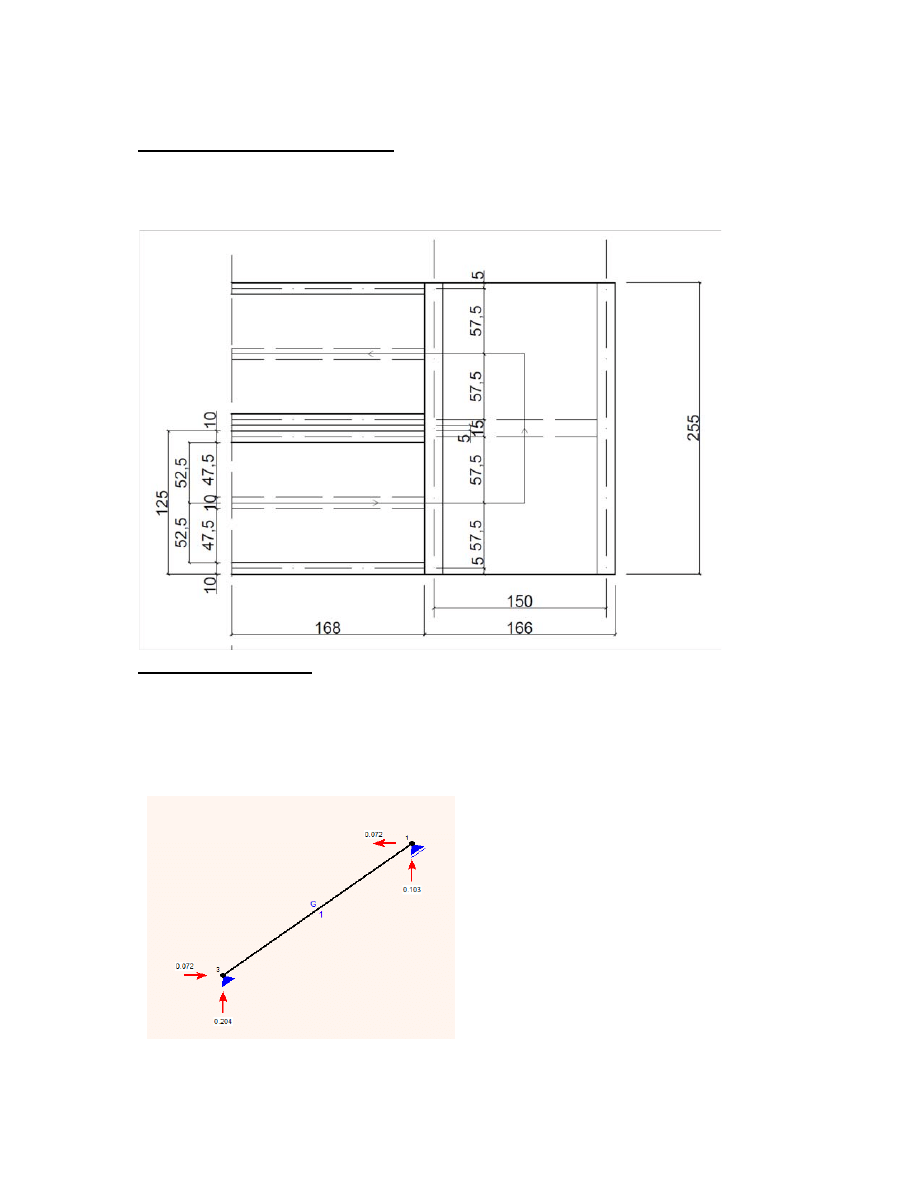
6. Obliczenia dla belki spocznikowej

z uwagi na zastosowanie belki w środku rozpiętości spocznika, zablokowane zostało jej
ugięcie w płaszczyźnie poziomej. belka ta nie zbiera obciążenia od pokrycia spocznika
(zamocowana poniżej)

6.1 zestawienie obciążeń

hsp 0.28 m



wysokość belki spocznikowej

bsp 0.16 m



grubość belki spocznikowej

stałe:

ciężar stopni (1/4 szerokości) + ciężar belki policzkowej:

w kierunku pionowym

wbp2

0.204kN



wbp3

0.103kN



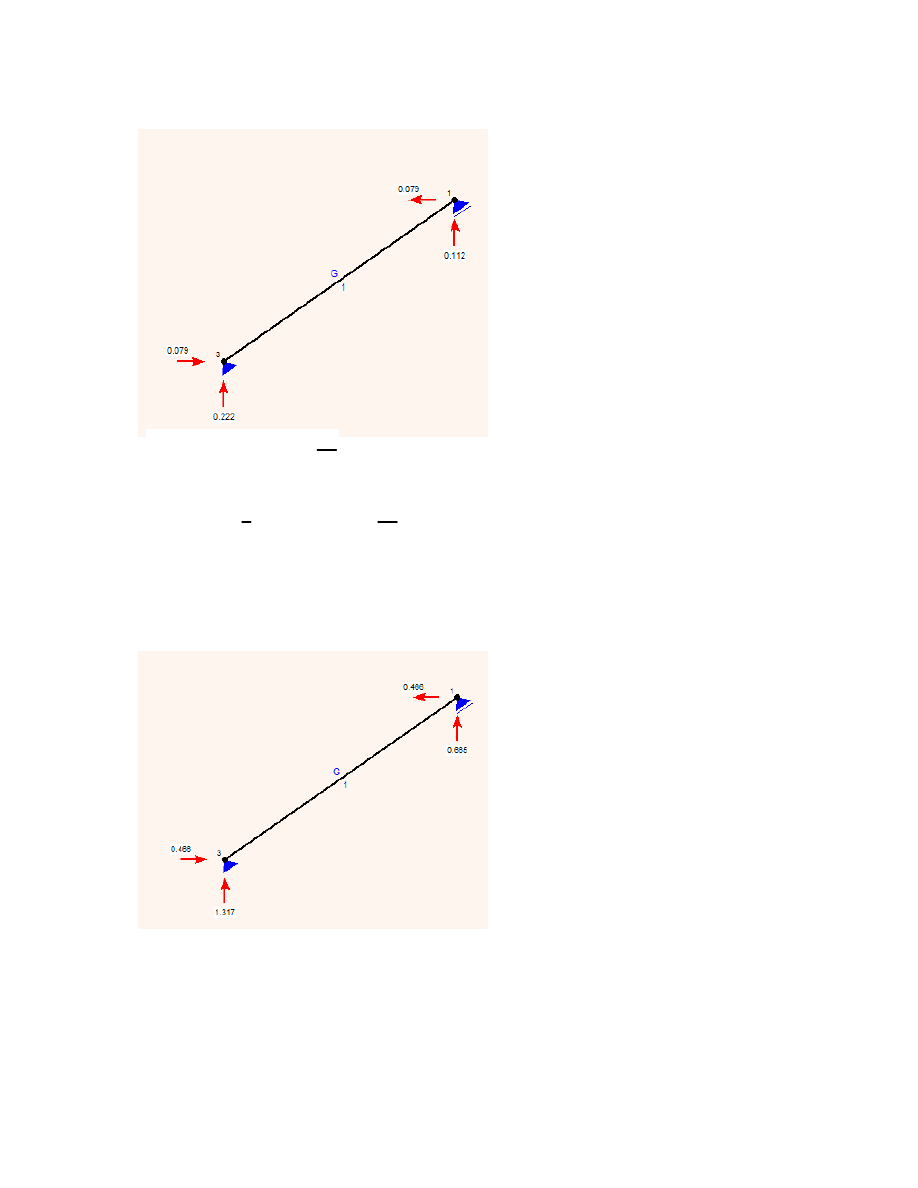
ciężar stopni (1/2 szerokości) + ciężar belki dodatkowej:

w kierunku pionowym

wbp4

0.222kN



wbp5

0.112kN



psp

ρb hsp



bsp



0.188

kN

m







ciężar własny belki spocznikowej

ppsp 1.66m

1
2

 ρsk



0.03



m

0.154

kN

m







ciężar pokrycia spocznika - zbierany z połowy
spocznika (sklejka 30mm)

obciążenia zmienne:

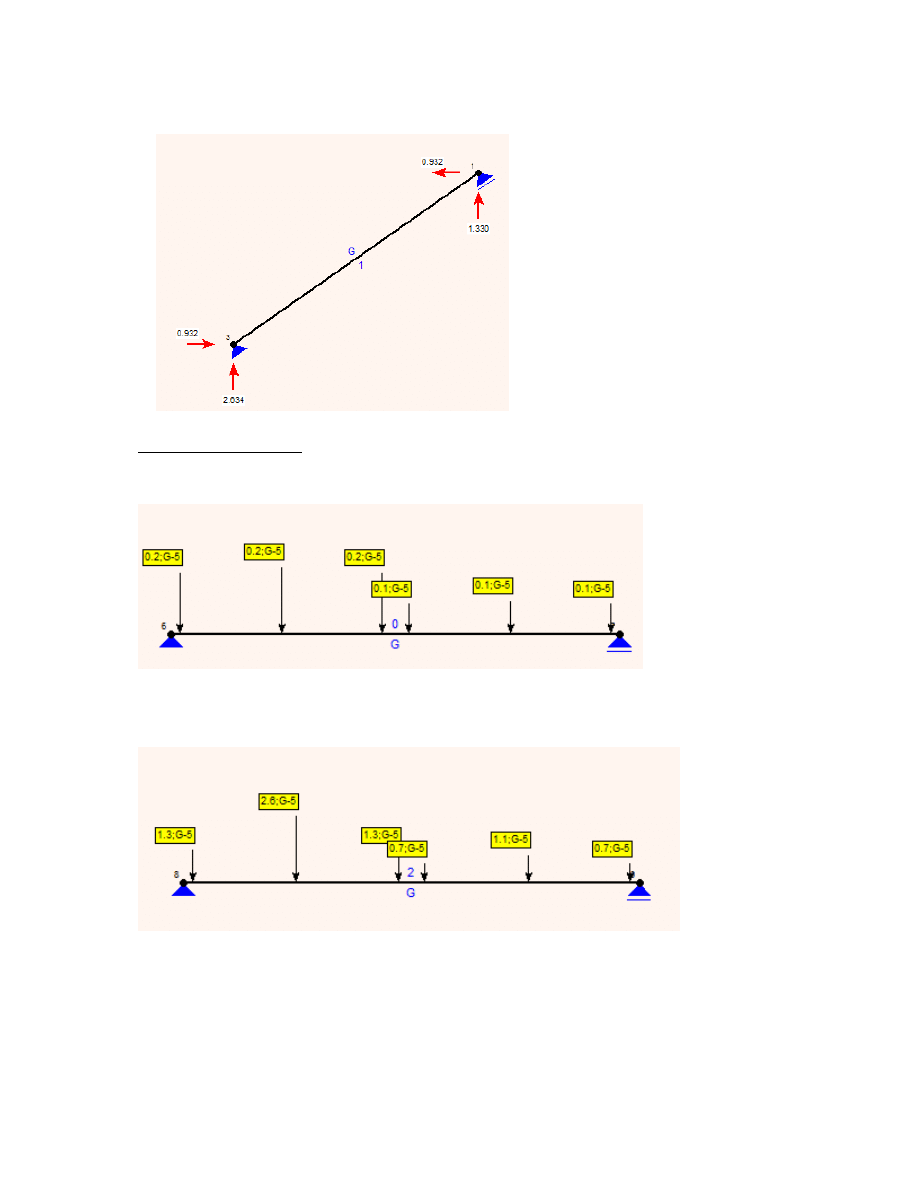
obciążenie użytkowe , zbierane z belki policzkowej (3kN/m)

w kierunku pionowym

wbp6

1.317kN



wbp7

0.665kN



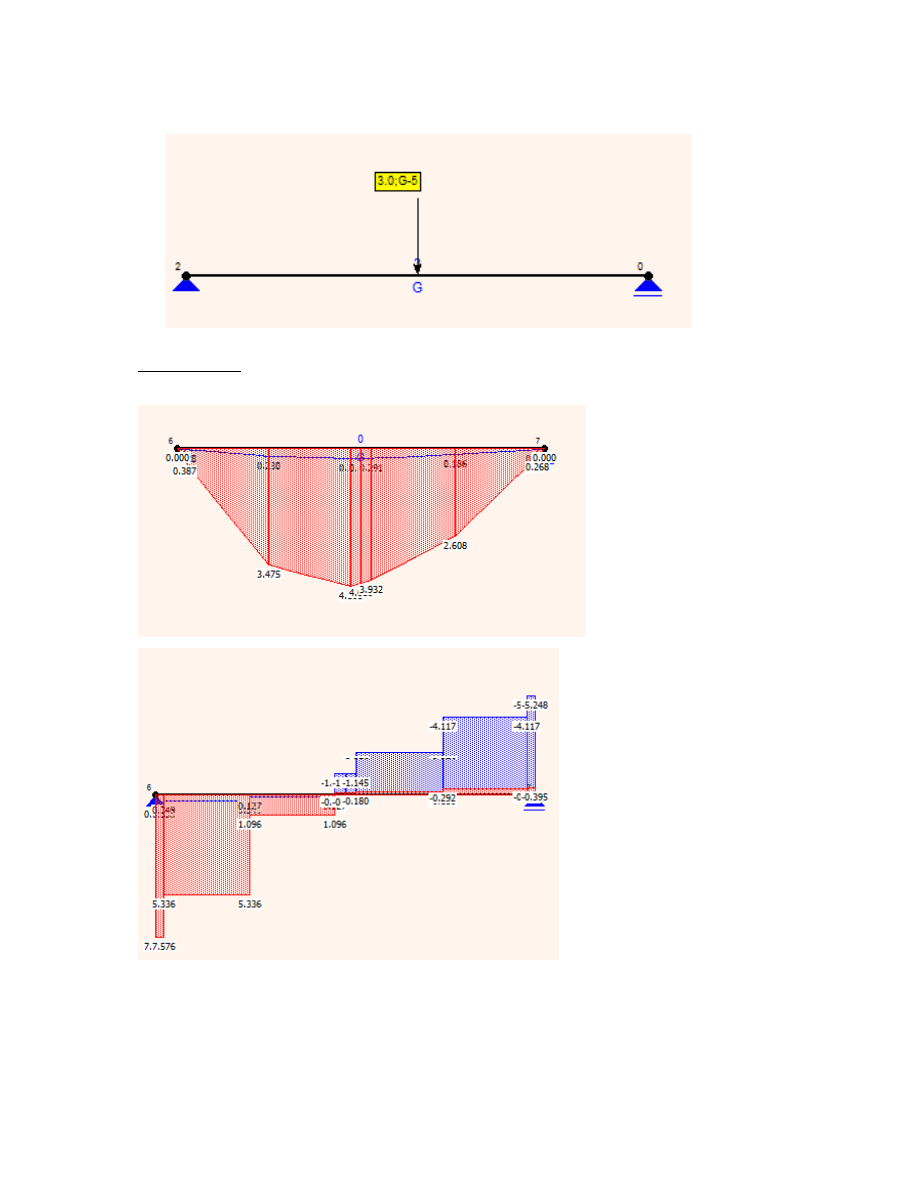
obciążenie użytkowe , zbierane z dodatkowej belki podbiegowej (3kN/m)

w kierunku pionowym

wbp8

2.634kN



wbp9

1.330kN



6.2. schematy obciążeń

stałe

użytkowe

technologiczne

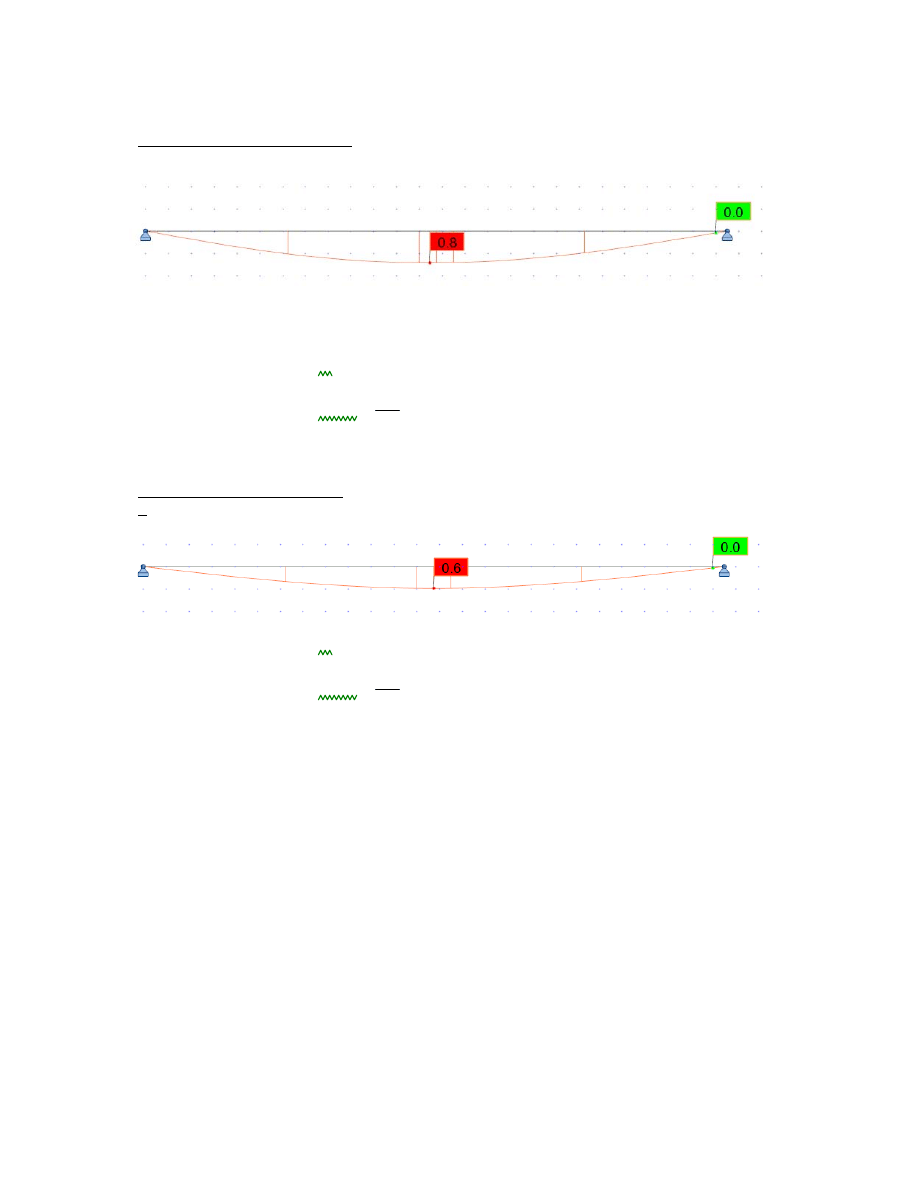
6.3 wykresy sił

kombinacja I (stałe + użytkowe) [kNm]

Myd.1 4.102kN m





momenty [kNm]

siły poprzeczne [kN]

kombinacja II (stałe + technologiczne) [kN]

momenty [kNm]

Myd.2 3.255kN m





siły poprzeczne [kN]

6.3. Stan SGN dla kombinacji I

Asp

bsp hsp



0.045 m

2





pole przekroju belki

Wysp

bsp hsp

2



6

2.091

10

3



cm

3







wskaźnik wytrzymałości

Iysp

bsp hsp

3



12

2.927

10

4



cm

4







moment bezwładności

γM.d 1.3



częściowy spółczynnik bezpieczeństwa właściowości
materiału

kmod 0.8



współczynnik modyfikujący, uwzględniający efekt czasu
trwania obciążenia i wilgotności - obciązenie średniotrwałe

wartości obliczeniowe wytrzymałości potrzebne do wymiarowania

fm.d

fm.k kmod



γM.d

14.769 MPa







zginanie

km 0.7



dla przekroju prostokątnego, litego drewna

σm.y.d

Myd.1

Wysp

1.962 MPa







fm.y.d fm.d 14.769 MPa







sprawdzenie warunków normowych:

km

σm.y.d

fm.y.d



9.299 %





warunek został spełniony

6.4. Stan SGN dla kombinacji II

Asp

bsp hsp



0.045 m

2





pole przekroju belki

Wysp

bsp hsp

2



6

2.091

10

3



cm

3







wskaźnik wytrzymałości

Iysp

bsp hsp

3



12

2.927

10

4



cm

4







moment bezwładności

γM.d 1.3



częściowy spółczynnik bezpieczeństwa właściowości
materiału

kmod 0.9



współczynnik modyfikujący, uwzględniający efekt czasu
trwania obciążenia i wilgotności - obciązenie średniotrwałe

wartości obliczeniowe wytrzymałości potrzebne do wymiarowania

fm.d

fm.k kmod



γM.d

16.615 MPa







zginanie

km 0.7



dla przekroju prostokątnego, litego drewna

σm.y.d

Myd.2

Wysp

1.557 MPa







fm.y.d fm.d 16.615 MPa







sprawdzenie warunków normowych:

km

σm.y.d

fm.y.d



6.559 %





warunek został spełniony

6.5. Stan SGU dla kombinacji I

długość belki spocznikowej ls 2.55m



u

0.8cm



ugięcie
belki
maksymalne ugięcie
belki

umax

ls

250

1.02 cm







sprawdzenie
warunku

u

umax



1



6.6. Stan SGU dla kombinacji
II

u

0.6cm



ugięcie
belki
maksymalne ugięcie
belki

umax

ls

250

1.02 cm







sprawdzenie
warunku

u

umax



1

