Wymiarowanie schodów drewnianych

ze wzgl

ę

du na SGN i SGU.

(Cz

ęść

obliczeniowa).

1. Sprawdzenie SGN dla stopnia.

(na podstawie EC0 EC5).

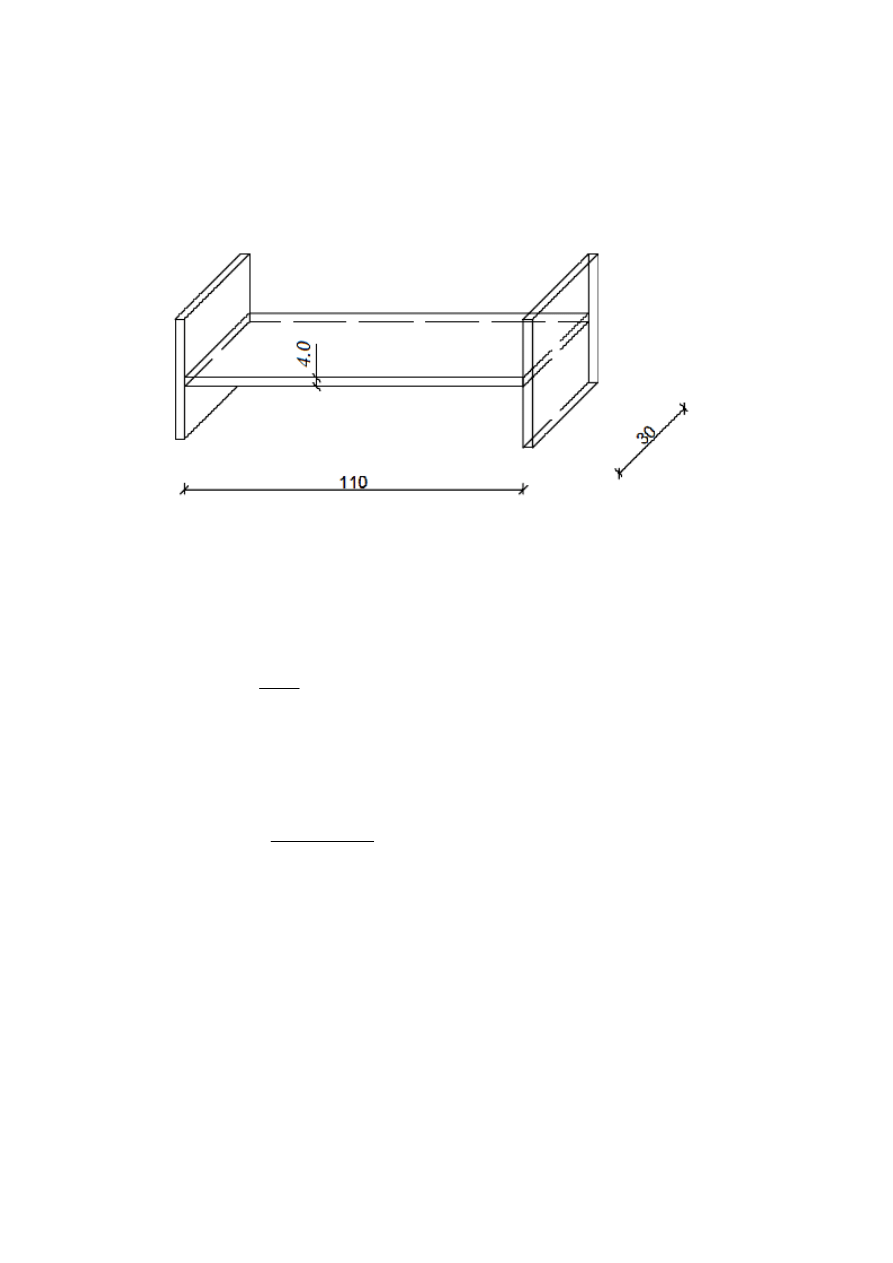
1.1 Schemat stopnia.

1.2 Charakterystyki geometryczne przekroju.

bs

30cm

:=

hs

4cm

:=

Wy_s

bs hs

2

⋅

6

80 cm

3

⋅

=

:=

1.3 Współczynniki potrzebne do wyznaczenie wytrzymało

ś

ci obliczeniowej.

stopie

ń

wykonany z drewna litego C20

fmd90k

20MPa

:=

(tab.1 EN:338:2009)

fmd90d

fmd90k kh

⋅

kmod

⋅

γM

:=

kh

kh

1.3

:=

EC 5 pkt 3.2 str 28

Współczynniki

kmod

okre

ś

lone przy zało

ż

eniu pierwszej klasy u

ż

ytkowania dla

drewna litego EC5 tab. 3.1

kmod1

0.6

:=

Działanie stałe

kmod2

0.9

:=

Działanie stałe + zmienne krótkotrwałe

kmod3

1.1

:=

Działanie stałe + zmienne chwilowe

Cz

ęś

ciowy współczynnik bezpiecze

ń

stwa dla drewna litego na podst. EC5 tab. 2.3

γM

1.3

:=

1.4 Obliczenie wytrzymało

ś

ci obliceniowej dla trzech wariantów obci

ążę

nia stopnia

Wariant 1
Oddziaływanie od ci

ęż

aru własnego

Wariant 2
Suma oddziaływa

ń

od ci

ęż

aru własnego i

zmiennego - tłum

fmd90d1

fmd90k kh

⋅

kmod1

⋅

γM

12 MPa

⋅

=

:=

fmd90d2

fmd90k kh

⋅

kmod2

⋅

γM

18 MPa

⋅

=

:=

Wariant 2
Suma oddziaływa

ń

od ci

ęż

aru własnego i

zmiennego - monta

ż

owego

fmd90d3

fmd90k kh

⋅

kmod3

⋅

γM

22 MPa

⋅

=

:=

1.5 Masymalne napr

ęż

enia w zale

ż

no

ś

ci od przypadku obci

ąż

eniowego.

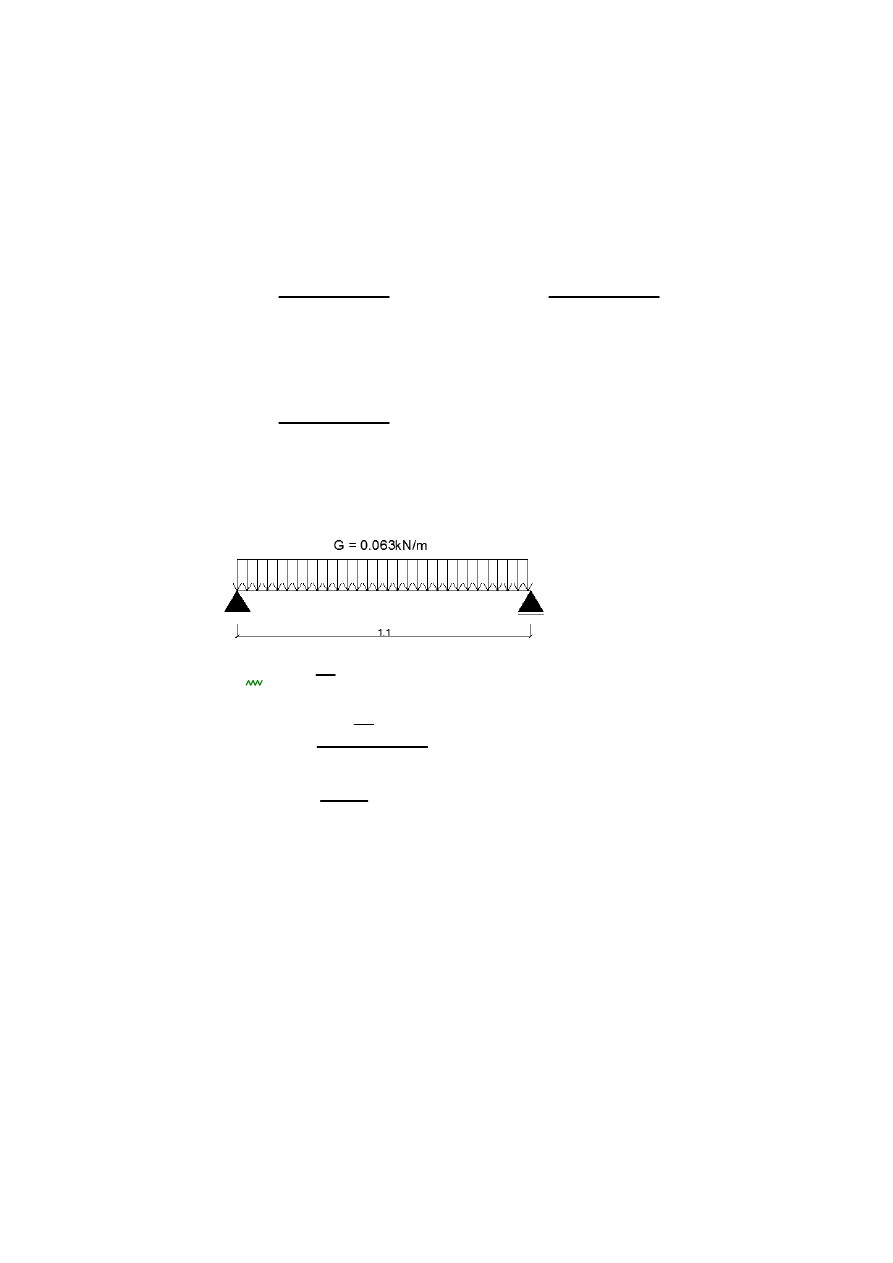
1.5.1 Przypadek 1 - obci

ąż

enie ci

ęż

arem własnym.

G

0.063

kN

m

:=

obci

ąż

enie stałe

Mmax1

0.063

kN

m

1.1m

(

)

2

⋅

8

0.01 kN m

⋅

⋅

=

:=

σmd901

Mmax1

Wy_s

0.119 MPa

⋅

=

:=

σmd901 fmd90d1

<

warunek SGN spelniony.

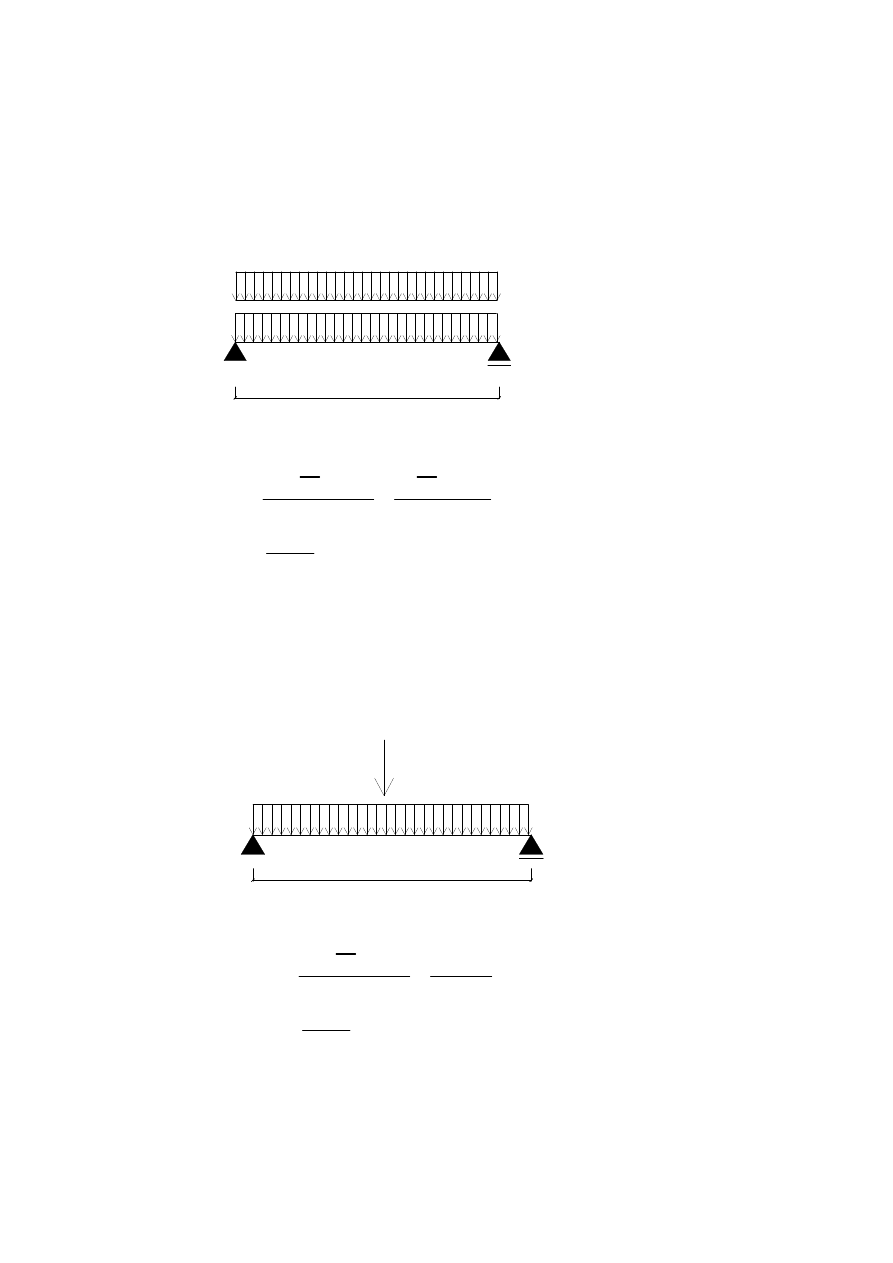
1.5.2 Przypadek 2 - obci

ąż

enie ci

ęż

arem własnym oraz Q1 - ci

ęż

ar tłumu.

G = 0.063kN/m

Q

1

= 0.9kN/m

1.1

Mmax2

0.063

kN

m

1.1m

(

)

2

⋅

8

0.9

kN

m

1.1m

(

)

2

⋅

8

+

0.146 kN m

⋅

⋅

=

:=

σmd902

Mmax2

Wy_s

1.821 MPa

⋅

=

:=

G = 0.063kN/m

Q

1

= 3kN/m

1.1

σmd902 fmd90d2

<

warunek SGN spelniony.

1.4.3 Przypadek 3 - obci

ąż

enie ci

ęż

arem własnym G oraz Q2 - obci

ąż

enie monta

ż

owe.

Mmax3

0.063

kN

m

1.1m

(

)

2

⋅

8

3kN 1.1

⋅

m

4

+

0.835 kN m

⋅

⋅

=

:=

σmd903

Mmax3

Wy_s

10.432 MPa

⋅

=

:=

σmd902 fmd90d2

<

warunek SGN spelniony.

2. Sprawdzenie SGU dla stopnia.

(na podstawie EC0 EC5).

2.1 Warto

ś

ci charakterystyczne oddziaływan.

qG

0.05

kN

m

:=

oddzialywanie od ciezaru wlasnego stopnia

qQ.1

0.6

kN

m

:=

oddzialywanie od obc. uzytkowego Q1

qQ.2

2kN

:=

oddziaływanie od obc. uzytkowego Q2

2.2 Okreslenie warto

ś

ci liczbowych potrzebnych do wyznaczenia ugi

ę

c.

kdef

0.6

:=

(EC 5 tab. 3.2) - przyjmujemy klas

ę

u

ż

ykowania 1, drewno lite

ψ21

0.3

:=

ψ01

0.7

:=

ψ02

0.7

:=

(EC 0 tab.A 1.1)

l

1.1m

:=

l

hs

27.5

=

> 20

E0mean

10

kN

mm

2

:=

E0mean 1 10

4

×

MPa

⋅

=

2.3 Obliczenie ugi

ę

cia belki.

Iy

bs hs

3

⋅

12

160 cm

4

⋅

=

:=

l

hs

20

>

dla obliczenia

uinst

stosujemy wzór

EC5 - NA.1

uM1

5

384

qG l

4

⋅

E0mean Iy

⋅

⋅

0.06 mm

⋅

=

:=

uinstG

uM1

:=

uM2

5

384

qQ.1 l

4

⋅

E0mean Iy

⋅

⋅

0.071 cm

⋅

=

:=

uinstQ1

uM2

:=

uinstQ2

1

48

qQ.2 l

3

⋅

E0mean Iy

⋅

⋅

0.347 cm

⋅

=

:=

ufinG

uinstG

:=

ufinQ1

uinstQ1 ψ01 ψ21 kdef

⋅

+

(

)

⋅

0.063 cm

⋅

=

:=

ufinQ2

uinstQ2 ψ02 ψ21 kdef

⋅

+

(

)

⋅

0.305 cm

⋅

=

:=

2.3 Obliczenie ugi

ę

cia belki.

warunek na dopuszczalne ugiecie bleki stropowej l/150<wfin

(EC5 tab. 7.2)

ufin

ufinG ufinQ1

+

ufinQ2

+

0.374 cm

⋅

=

:=

wfin.lim

l

250

0.44 cm

⋅

=

:=

wfin wfin.lim

<

Warunek SGU spełniony

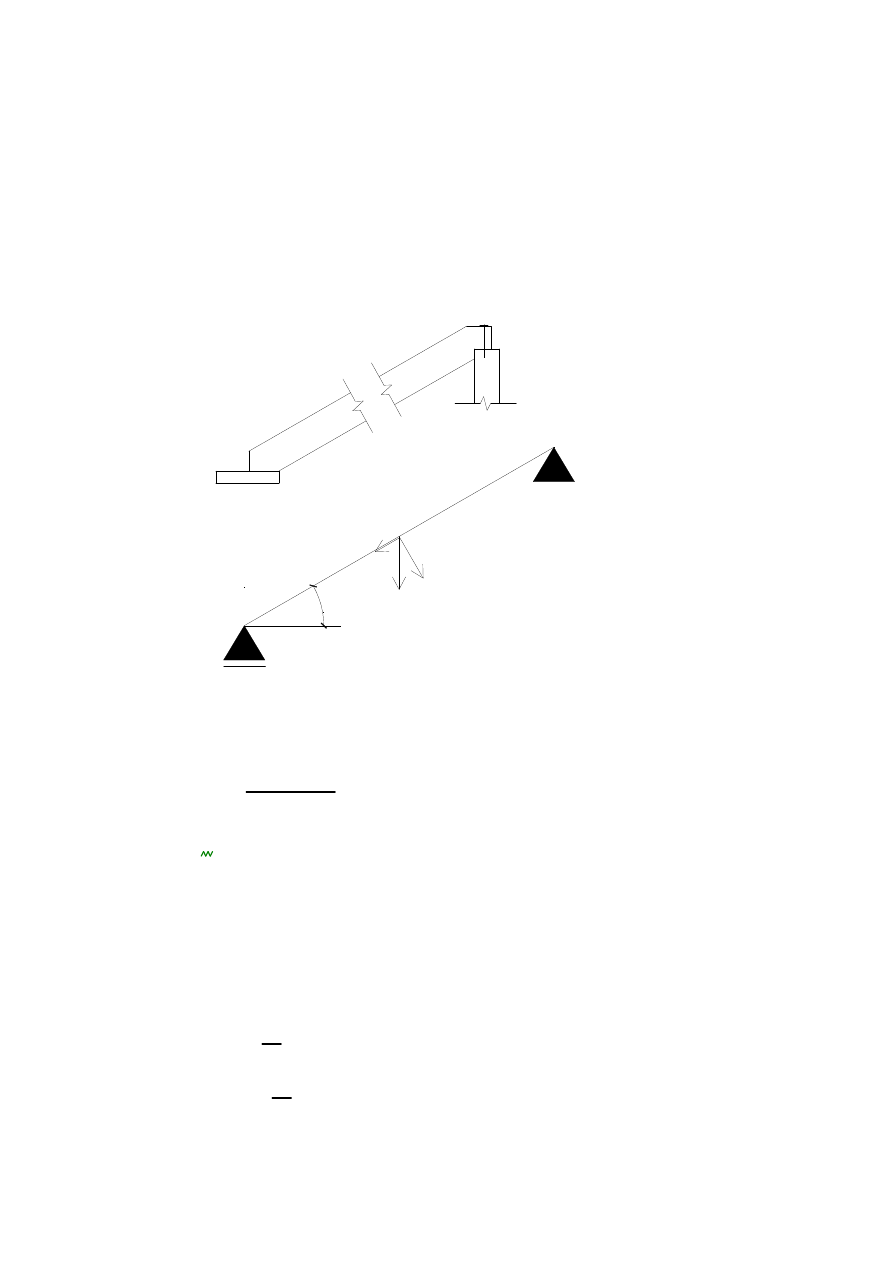
3. Sprawdzenie SGN dla belki policzkowej

Przyjmujemy schemat statyczny z przesuwem na dole, co powoduje,

ż

e mamy zginanie z

rozci

ą

ganiem osiowym

3

0

°

A

B

C

3.1. Charakterystyki geoetryczne pzekroju:

bp

10cm

:=

hp

32cm

:=

Wy

10cm 32cm

(

)

2

⋅

6

1706.667 cm

3

⋅

=

:=

hs 0.04 m

=

- wysoko

ść

stopnia

s

30cm

:=

- szeroko

ść

stopnia

n

7

:=

- ilo

ść

stopni

lrz

n

1

−

(

) s

⋅

1.8 m

=

:=

- długo

ść

rzutu belki policzkowej

l0

2.1m

:=

długo

ść

belki policzkowej

3.2 Składowa obci

ąż

e

ń

prostopadła i podłu

ż

na do belki, wyznaczenie max. momentów

zginaj

ą

cych, oraz napr

ęż

e

ń

w

ś

rodku rozpi

ę

to

ś

ci belki i przy zamocowaniu do belki

spocznikowej

q

0.24

kN

m

:=

obci

ąż

enie stałe, składowa prostopadła do belki

Q1

1.22

kN

m

:=

obci

ąż

enie zmienne - tłum składowa prostopadła do belki

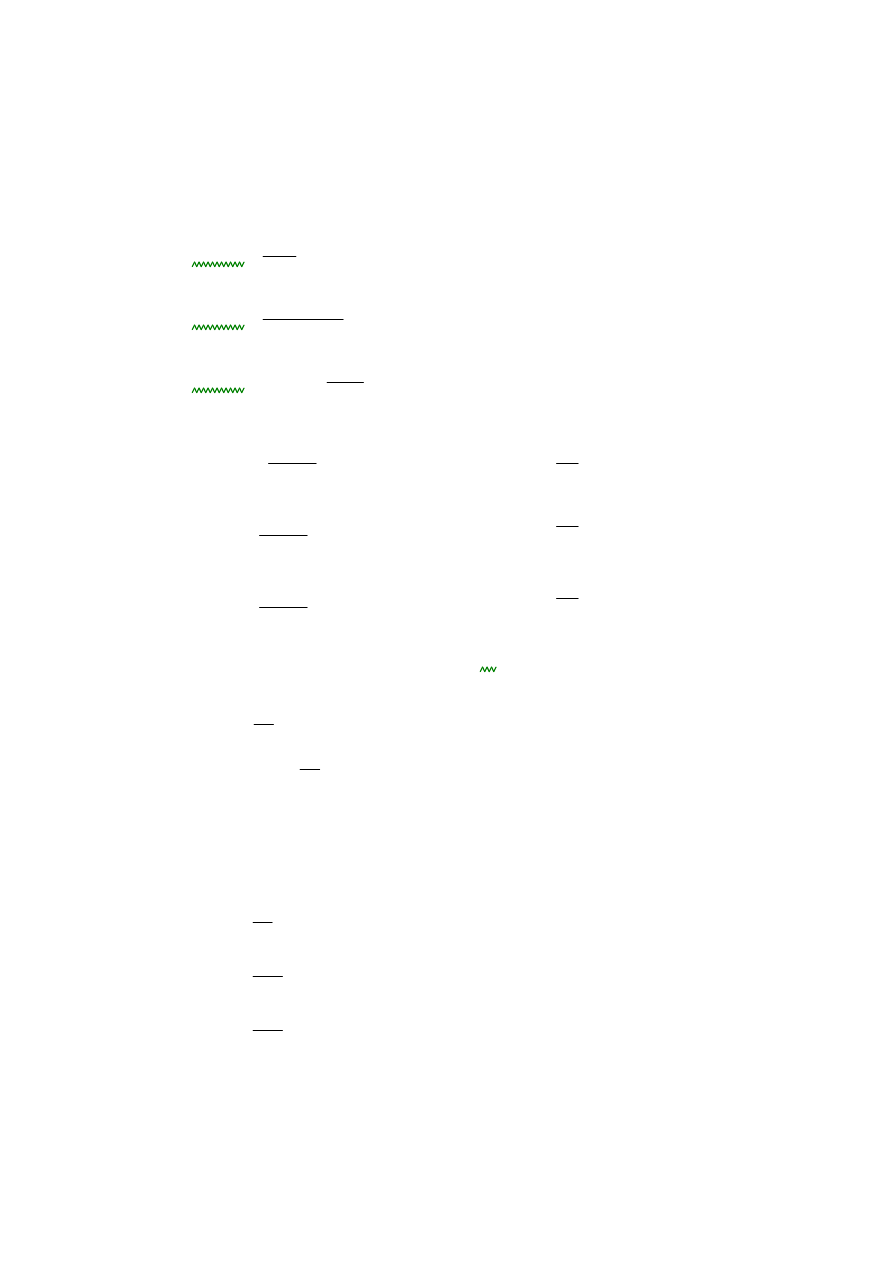
Q2

2.58kN

:=

obci

ąż

enie zmienne - monta

ż

owe, składowa prostopadła do belki

Mmax1

q l0

2

⋅

8

0.132 kN m

⋅

⋅

=

:=

Mmax2

Q1 q

+

(

)

l0

2

⋅

8

0.805 kN m

⋅

⋅

=

:=

Mmax3

Mmax1

Q2 l0

⋅

4

+

1.487 kN m

⋅

⋅

=

:=

Napr

ęż

enia w

ś

rodku ozpi

ę

to

ść

i od

momentów zginaj

ą

cych

Napr

ęż

enia przy poł

ą

czeniu z belk

ą

spocznikow

ą

od momentów zginaj

ą

cych

σmyd1B

Mmax1

Wy

77.52 kPa

⋅

=

:=

σmyd1C

0

Wy

0 kPa

⋅

=

:=

σmyd2C

0

Wy

0 kPa

⋅

=

:=

σmyd2B

Mmax2

Wy

471.577 kPa

⋅

=

:=

σmyd3C

0

Wy

0 kPa

⋅

=

:=

σmyd3B

Mmax3

Wy

871.172 kPa

⋅

=

:=

Siła rozci

ą

gaj

ą

ca przy poł

ą

czeniu z belk

ą

spocznikow

ą

od sił podłu

ż

nych

A

10cm 32

⋅

cm

0.032 m

2

=

:=

Nq

0.13

kN

m

l0

⋅

0.273 kN

⋅

=

:=

NQ1

Nq 0.71

kN

m

l0

⋅

+

1.764 kN

⋅

=

:=

NQ2

Nq 1.5kN

+

1.773 kN

⋅

=

:=

Nap

ęż

enia przy poł

ą

czeniu z belk

ą

spocznikow

ą

od sił podłu

ż

nych

σt0d1C

Nq

A

8.531 kPa

⋅

=

:=

σt0d2C

NQ1

A

55.125 kPa

⋅

=

:=

σt0d3C

NQ2

A

55.406 kPa

⋅

=

:=

Siła rozci

ą

gaj

ą

ca w

ś

rodku rozpi

ę

to

ś

ci belki od sił podłu

ż

nych

σt0d1B

Nq

2

A

4.266 kPa

⋅

=

:=

σt0d2B

NQ1

2

A

27.563 kPa

⋅

=

:=

σt0d3B

NQ2

2

A

27.703 kPa

⋅

=

:=

bp 0.1m

=

bp 15cm

<

uwzgl

ę

dniamy dodatkowo współczynnik wysoko

ś

ci

kh

kh

min

150

100













0.2

1.3

,













1.084

=

:=

ft0c

12MPa

:=

wytrzymało

ść

charakterystyczna na rozci

ą

ganie

fmyc

20MPa

:=

wytrzymało

ść

charakterystyczna na zginanie

Wyznaczenie wytrzymało

ś

ci obliczeniowych - współczynniki

kmod

jak dla stopni

ft0d1

kh kmod1

⋅

ft0c
γM

⋅

6.006 MPa

⋅

=

:=

ft0d2

kh kmod2

⋅

ft0c
γM

⋅

9.009 MPa

⋅

=

:=

ft0d3

kh kmod3

⋅

ft0c
γM

⋅

11.012 MPa

⋅

=

:=

fmyd1

kmod1

fmyc

γM

⋅

9.231 MPa

⋅

=

:=

fmyd2

kmod2

fmyc

γM

⋅

13.846 MPa

⋅

=

:=

fmyd3

kmod3

fmyc

γM

⋅

16.923 MPa

⋅

=

:=

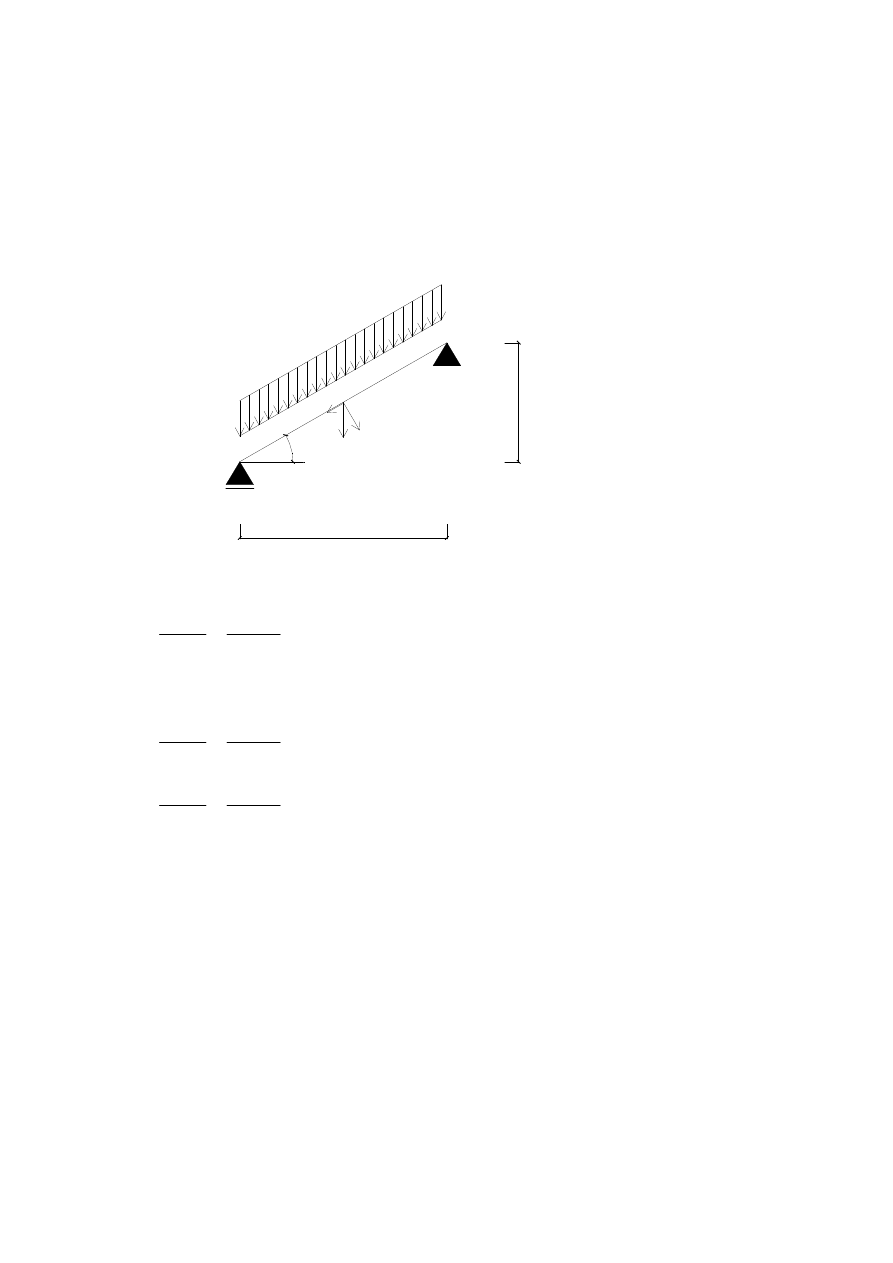
1.5 Masymalne napr

ęż

enia w zale

ż

no

ś

ci od przypadku obci

ąż

eniowego.

1.5.1 Przypadek 1 - obci

ąż

enie ci

ęż

arem własnym.

3

0

°

180

1

2

2

.5

G = 0.09kN/m

A

B

C

Do oblicznia SGN stosujemy wzór EC5 6.17, który ze wzgl

ę

du na brak zginania belki

policzkowej wzgl

ę

dem osi z ulega znacznemu uproszczeniu:

σt0d1C

ft0d1

σmyd1C

fmyd1

+

1

<

Obliczenia przeprowadzono dla

ś

rodka rozpi

ę

to

ś

ci belki policzkowej (punkt B) i punktu

oparcia (C):

σt0d1C

ft0d1

σmyd1C

fmyd1

+

0.001

=

σt0d1B

ft0d1

σmyd1B

fmyd1

+

0.009

=

1.5.1 Przypadek 2 - obci

ąż

enie ci

ęż

arem własnym oraz obci

ąż

eniem zmiennym - ci

ęż

ar

tłumu

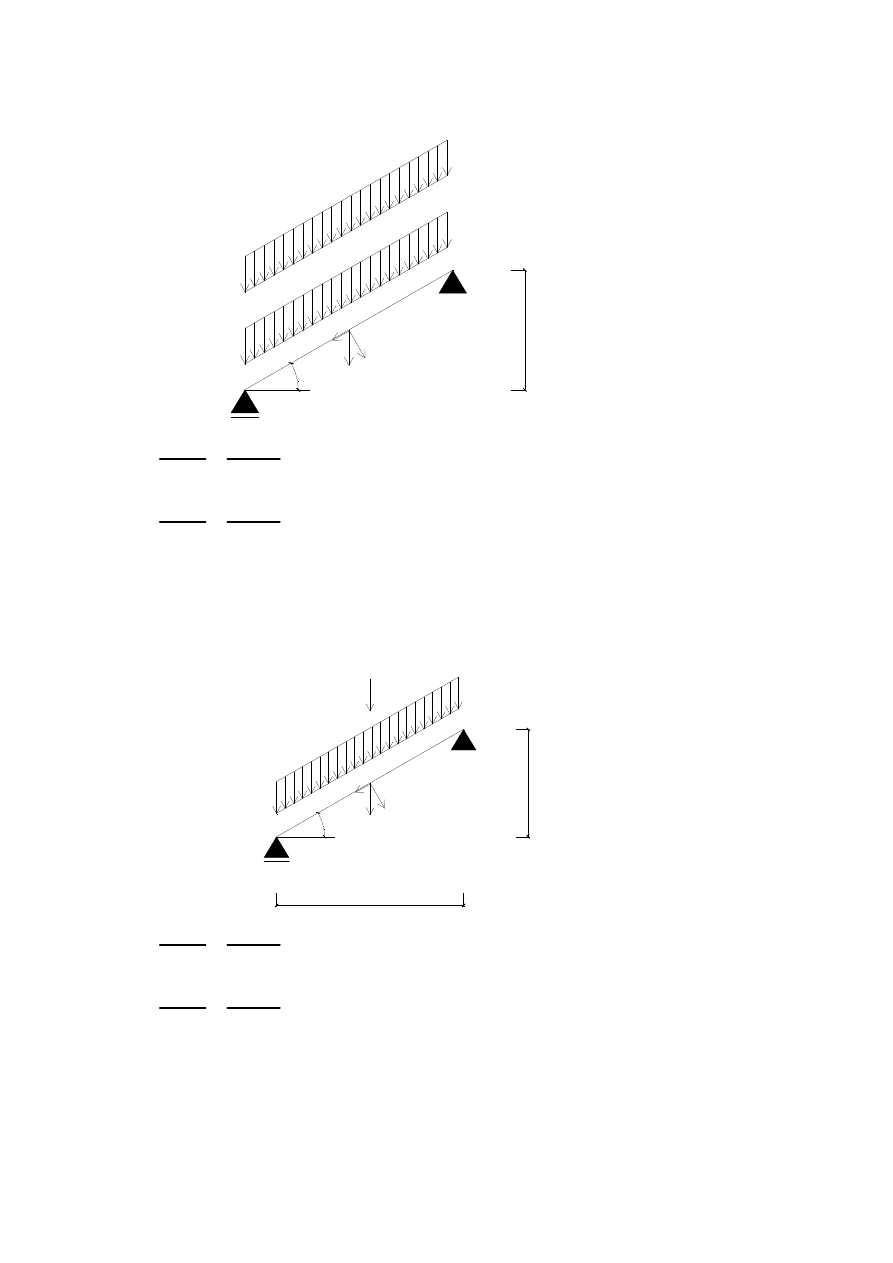
3

0

°

1

2

2

.5

G = 0.09kN/m

Q

1

= 3kN/m

A

B

C

σt0d2C

ft0d2

σmyd2C

fmyd2

+

0.006

=

σt0d2B

ft0d2

σmyd2B

fmyd2

+

0.037

=

1.5.1 Przypadek 3 - obci

ąż

enie ci

ęż

arem własnym oraz obci

ąż

eniem zmiennym -

monta

ż

owym

3

0

°

180

1

2

2

.5

G = 0.09kN/m

Q

2

= 3kN

A

B

C

σt0d3C

ft0d3

σmyd3C

fmyd3

+

0.005

=

σt0d3B

ft0d3

σmyd3B

fmyd3

+

0.054

=

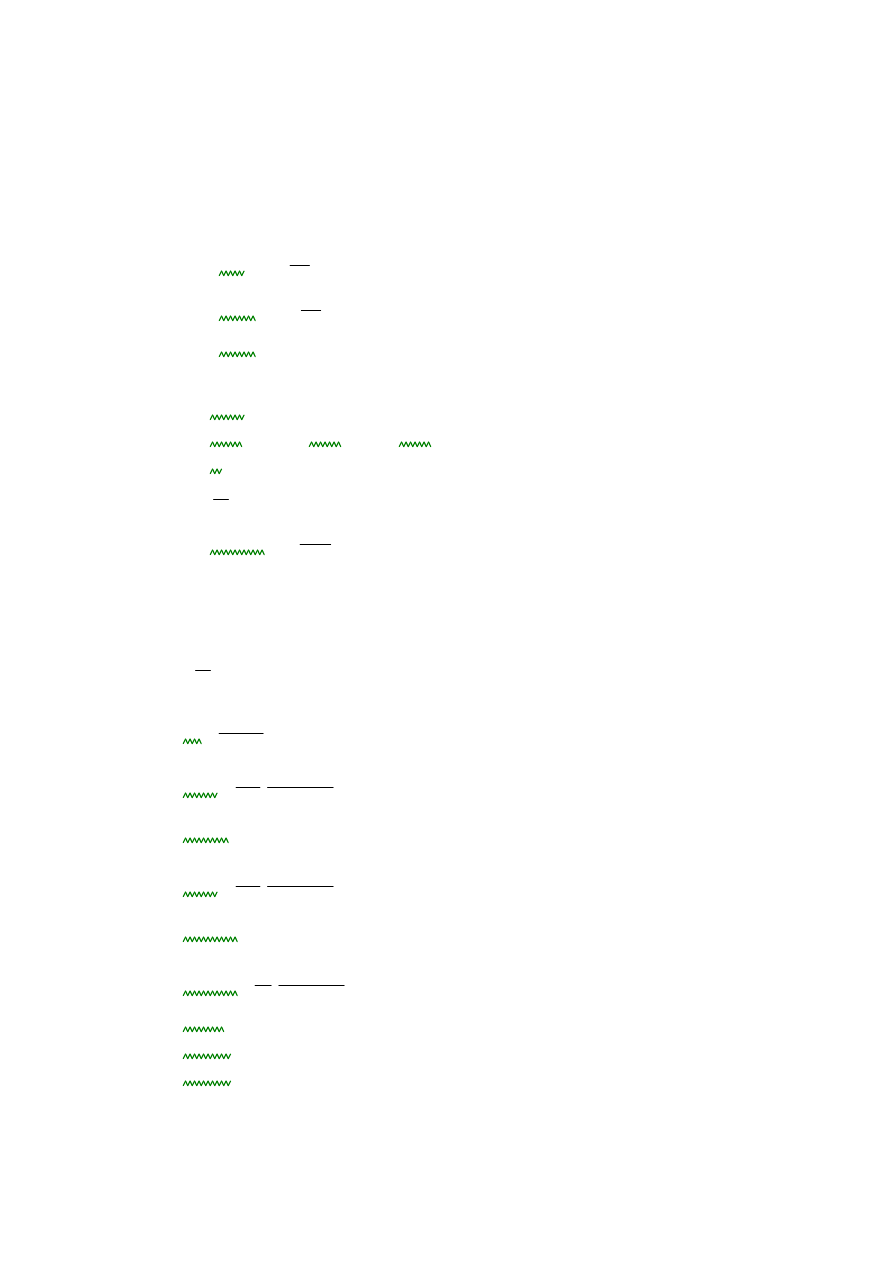
4. Sprawdzenie SGU dla belki policzkowej.

(na podstawie EC0 EC5).

3.1 Warto

ś

ci charakterystyczne oddziaływan, składowe prostopadłe do belki polic zkowej.

qG

0.17

kN

m

:=

oddzialywanie od ciezaru wlasnego stopnia

qQ.1

0.81

kN

m

:=

oddzialywanie od obc. uzytkowego Q1

qQ.2

1.72kN

:=

oddziaływanie od obc. uzytkowego Q2

3.2 Okreslenie warto

ś

ci liczbowych potrzebnych do wyznaczenia ugi

ę

c.

kdef

0.6

:=

(EC 5 tab. 3.2 - 1 klasa u

ż

ytkowania dla drewna litego

ψ21

0.3

:=

ψ01

0.7

:=

ψ02

0.7

:=

(EC 0 tab.A 1.1)

l

2.1m

:=

l

hs

52.5

=

> 20

E0mean

10

kN

mm

2

:=

E0mean 1 10

4

×

MPa

⋅

=

3.3 Obliczenie ugi

ę

cia belki.

l

hs

20

>

dla obliczenia

uinst

stosujemy wzór

EC5 - NA.1

Iy

bp hp

3

⋅

12

27306.667 cm

4

⋅

=

:=

uM1

5

384

qG l

4

⋅

E0mean Iy

⋅

⋅

0.016 mm

⋅

=

:=

uinstG

uM1

:=

uM2

5

384

qQ.1 l

4

⋅

E0mean Iy

⋅

⋅

0.075 mm

⋅

=

:=

uinstQ1

uM2

:=

uinstQ2

1

48

qQ.2 l

3

⋅

E0mean Iy

⋅

⋅

0.122 mm

⋅

=

:=

ufinG

uinstG

:=

ufinQ1

uinstQ1 ψ01 ψ21 kdef

⋅

+

(

)

⋅

0.066 mm

⋅

=

:=

ufinQ2

uinstQ2 ψ02 ψ21 kdef

⋅

+

(

)

⋅

0.107 mm

⋅

=

:=

3.4 Obliczenie ugi

ę

cia belki.

warunek na dopuszczalne ugiecie bleki stropowej l/150< wfin

ufin

ufinG ufinQ1

+

ufinQ2

+

0.189 mm

⋅

=

:=

wfin.lim

l

250

8.4 mm

⋅

=

:=

wfin wfin.lim

<

Warunek SGU spełniony

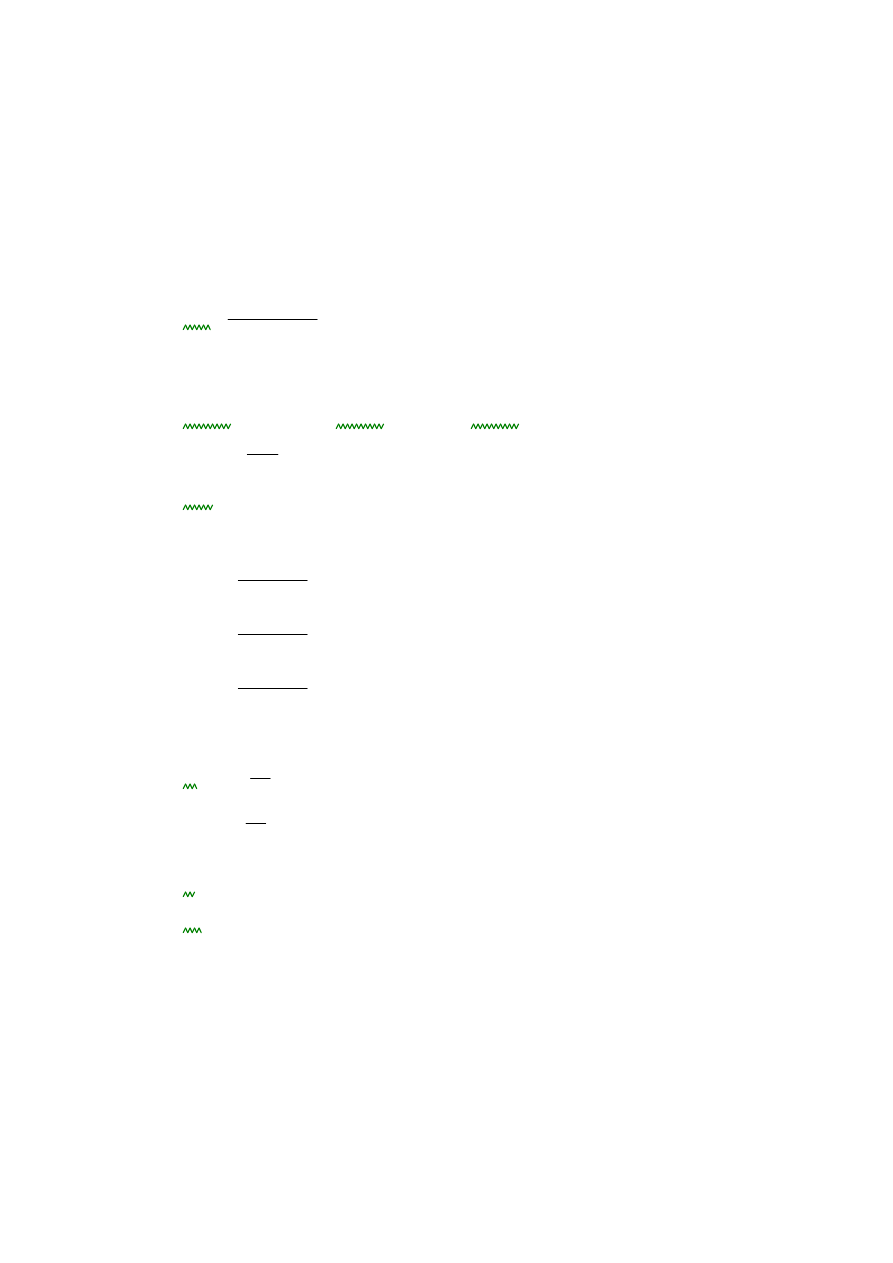
Belka spocznikowa SGN

.

1. Charakterystyki geometryczne przekroju.

b

16cm

:=

h

28cm

:=

Wy

16cm 28cm

(

)

2

⋅

6

2090.667 cm

3

⋅

=

:=

2. Wytrzymało

ść

obliczeniowa na zginanie.

Współczynniki

kmod

i

γM

przyjmujemy jak dla stopnia:

kmod1

0.6

:=

kmod2

0.9

:=

kmod3

1.1

:=

fmk

20

N

mm

2

20 MPa

⋅

=

:=

γM

1.3

:=

Wyznaczenie wytrzymało

ś

ci obliczeniowych:

fmd1

kmod1 fmk

⋅

γM

9.231 MPa

⋅

=

:=

fmd2

kmod2 fmk

⋅

γM

13.846 MPa

⋅

=

:=

fmd3

kmod3 fmk

⋅

γM

16.923 MPa

⋅

=

:=

3. Wyznaczenie maksymalnych napreze

ń

. (w zaleznosci od przypadku).

P

2.2 2

⋅

kN

:=

siła stał

ą

od schodów

q

0.477

kN

m

:=

obci

ąż

enie stałe spocznika

Q

1.65

kN

m

:=

obci

ąż

enie zmiene - tłum

Pq

3kN

:=

obci

ąż

enie zmienne - monta

ż

owe

l

265cm

:=

l0

1.05 l

⋅

:=

Przypadek 1 - obci

ąż

enie stałe - siły skupione od obci

ąż

enia stałego schodów +

obci

ąż

enie stałe socznika

Zakładamy uproszczenie - cztery siły od belek policzkowych, zast

ę

pujemy jedn

ą

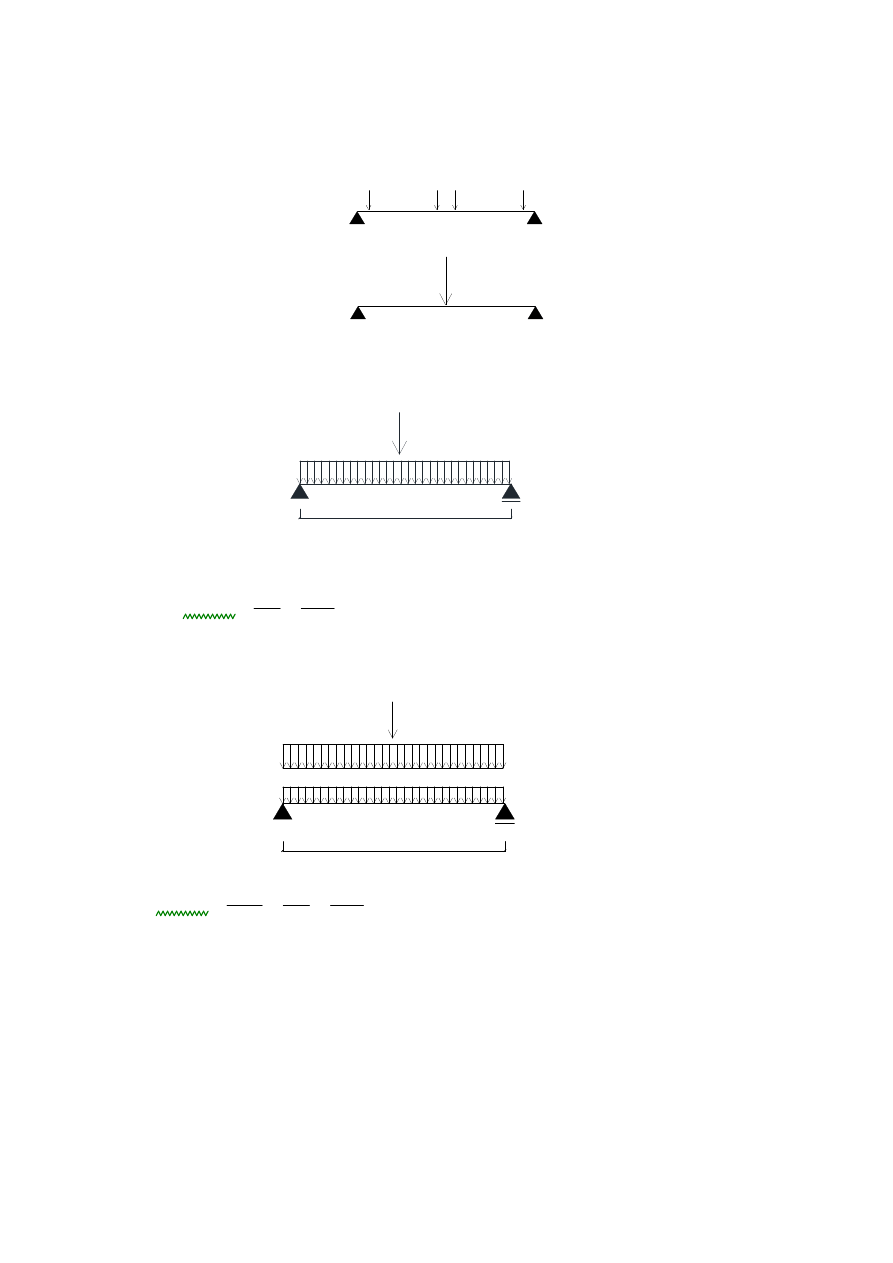
umieszczon

ą

w

ś

rodku rozpi

ę

to

ś

ci belki spocznikowej równ

ą

co do warto

ś

ci podwojonej

sile od pojedynczego spocznika

G = 0.477kN/m

Q1 = 2x(2.2kN)=4.4kN

2.65

Schemat statyczny dla wariantu 1:

2.65

G = 0.477kN/m

Q

1

= 1.65kN/m

Mmax1

P l0

⋅

4

q l0

2

⋅

8

+

3.522 kN m

⋅

⋅

=

:=

Przypadek 2 - obci

ąż

enie stałe jak dla przypadku 1 + obci

ąż

enie zmienne u

ż

ytkowe -

tłum:

Mmax2

Q l0

2

⋅

8

P l0

⋅

4

+

q l0

2

⋅

8

+

5.119 kN m

⋅

⋅

=

:=

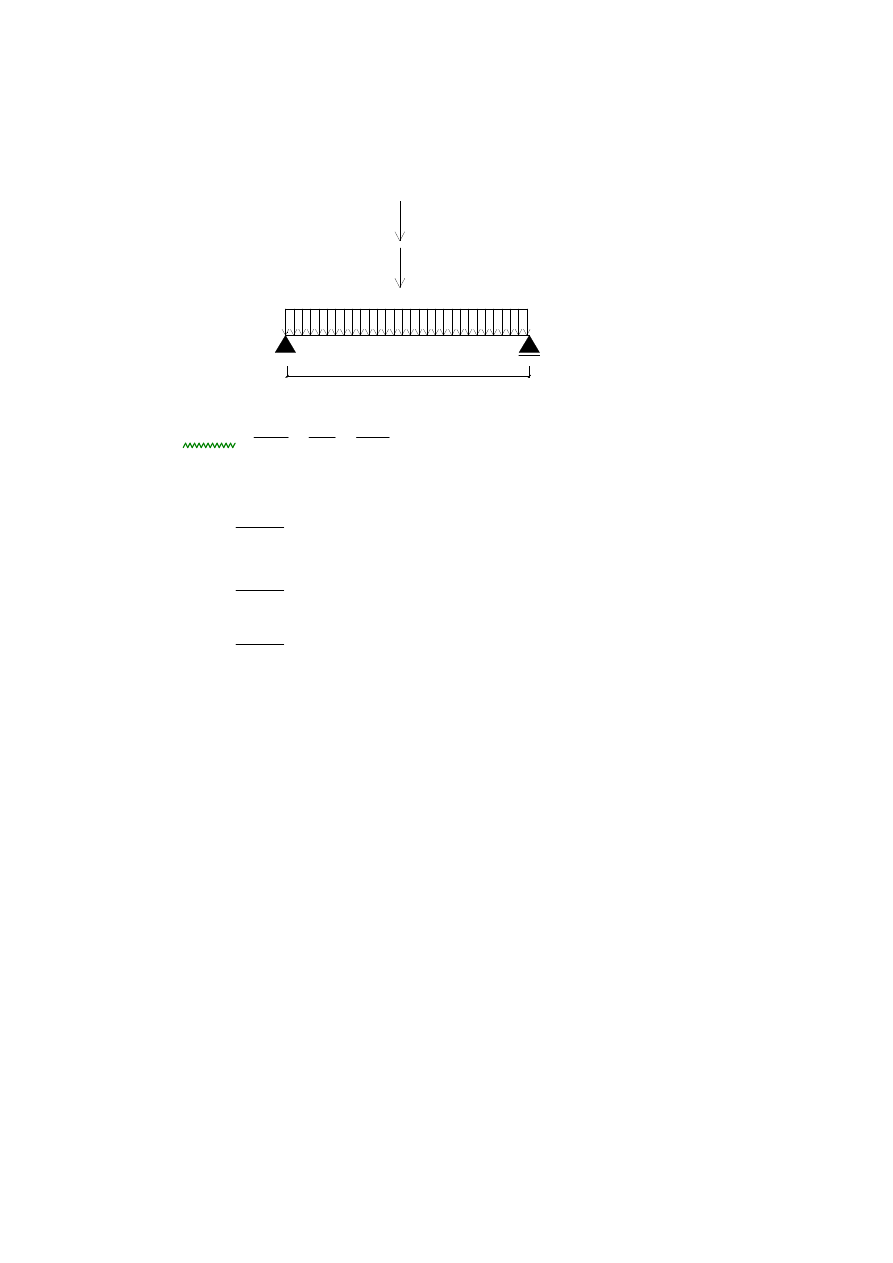
Przypadek 3 - obci

ąż

enie stałe jak dla przypadku 1 + obci

ąż

enie zmienne - monta

ż

owe:

Q1 = 2x(2.2kN)=4.4kN

P

q

= 3kN

G = 0.477kN/m

2.65

Mmax3

Pq l0

⋅

4

P l0

⋅

4

+

q l0

2

⋅

8

+

5.609 kN m

⋅

⋅

=

:=

Sprawdzenie warunku SGN:

σ1m

Mmax1

Wy

1.685 MPa

⋅

=

:=

σ1m fmd1

<

warunek SGN spelniony

σ2m fmd2

<

warunek SGN spelniony

σ2m

Mmax2

Wy

2.449 MPa

⋅

=

:=

σ3m fmd3

<

warunek SGN spelniony

σ3m

Mmax3

Wy

2.683 MPa

⋅

=

:=

SPRAWDZENIE SGU

.

1.1 Warto

ś

ci charakterystyczne oddziaływan.

qG

0.353

kN

m

:=

oddzialywanie od ciezaru wlasnego belki

qGS

2.2 2

⋅

kN

:=

oddziaływanie od belek policzkowych

qQ.1

1.1

kN

m

:=

oddzialywanie od obc. uzytkowego Q1

qQ.2

2kN

:=

oddziaływanie od obc. uzytkowego Q2

1.2 Okreslenie warto

ś

ci liczbowych potrzebnych do wyznaczenia ugi

ę

c.

kdef

0.6

:=

(EC 5 tab. 3.2 dla drewna litego, klasa u

ż

ytkowania 1)

ψ21

0.3

:=

ψ01

0.7

:=

ψ02

0.7

:=

(EC 0 tab.A 1.1)

l

2.65m

:=

l

h

9.464

=

< 20

E0mean

10

kN

mm

2

:=

E0mean 10000 MPa

⋅

=

1.3 Obliczenie ugi

ę

cia belki.

l

hs

20

>

dla obliczenia

uinst

stosujemy wzór

EC5 - NA.1

Iy

b h

3

⋅

12

2.927

10

4

×

cm

4

⋅

=

:=

uM1

5

384

qG l

4

⋅

E0mean Iy

⋅

⋅

1

48

qGS l

3

⋅

E0mean Iy

⋅

⋅

+

0.66 mm

⋅

=

:=

uinstG

uM1

:=

uM2

5

384

qQ.1 l

4

⋅

E0mean Iy

⋅

⋅

0.024 cm

⋅

=

:=

uinstQ1

uM2

:=

uinstQ2

1

48

qQ.2 l

3

⋅

E0mean Iy

⋅

⋅

0.026 cm

⋅

=

:=

ufinG

uinstG

:=

ufinQ1

uinstQ1 ψ01 ψ21 kdef

⋅

+

(

)

⋅

0.021 cm

⋅

=

:=

ufinQ2

uinstQ2 ψ02 ψ21 kdef

⋅

+

(

)

⋅

0.023 cm

⋅

=

:=

warunek na dopuszczalne ugiecie bleki stropowej l/150<wfin

ufin

ufinG ufinQ1

+

ufinQ2

+

1.106 mm

⋅

=

:=

l

250

10.6 mm

⋅

=