Materia wspó finansowany ze !rodków Unii Europejskiej
w ramach Europejskiego Funduszu Spo ecznego
Centralna
Komisja
Egzaminacyjna
Miejsce
na naklejk
ARKUSZ ZAWIERA
INFORMACJE
PRAWNIE CHRONIONE
DO MOMENTU
ROZPOCZ CIA
EGZAMINU!
MMA-P1_1P-095
PRÓBNY EGZAMIN
MATURALNY
Z MATEMATYKI
POZIOM PODSTAWOWY
Czas pracy 170 minut
Instrukcja dla zdaj!cego
1. Sprawd", czy arkusz egzaminacyjny zawiera 17 stron (zadania
1 – 34). Ewentualny brak zg o! przewodnicz#cemu zespo u
nadzoruj#cego egzamin.
2. Rozwi#zania zada$ i odpowiedzi zamie!% w miejscu na to
przeznaczonym.
3. Odpowiedzi do zada$ zamkni&tych przenie! na kart&
odpowiedzi, zaznaczaj#c je w cz&!ci karty przeznaczonej dla
zdaj#cego. Zamaluj
pola do tego przeznaczone. B &dne
zaznaczenie otocz kó kiem
i zaznacz w a!ciwe.
4. Pami&taj, 'e pomini&cie argumentacji lub istotnych oblicze$
w rozwi#zaniu zadania otwartego mo'e spowodowa%, 'e za to
rozwi#zanie mo'esz nie dosta% pe nej liczby punktów.
5. Pisz czytelnie. U'ywaj d ugopisu lub pióra tylko z czarnym
tuszem lub atramentem.
6. Nie u'ywaj korektora, a b &dne zapisy przekre!l.
7. Pami&taj, 'e zapisy w brudnopisie nie podlegaj# ocenie.
8. Mo'esz korzysta% z zestawu wzorów matematycznych, cyrkla
i linijki oraz kalkulatora.
9. Na karcie odpowiedzi wpisz swoj# dat& urodzenia i PESEL.
Nie wpisuj 'adnych znaków w cz&!ci przeznaczonej
dla egzaminatora.
!yczymy powodzenia!
LISTOPAD
ROK 2009
Za rozwi#zanie
wszystkich zada$
mo'na otrzyma%
#cznie
50 punktów
Wype"nia zdaj!cy
przed rozpocz ciem pracy
PESEL ZDAJ#CEGO
KOD
ZDAJ#CEGO
Próbny egzamin maturalny z matematyki
Poziom podstawowy
2
ZADANIA ZAMKNI$TE
W zadaniach od 1. do 25. wybierz i zaznacz na karcie odpowiedzi jedn"
poprawn" odpowied#.
Zadanie 1. (1 pkt)
Wska' nierówno!%, która opisuje sum& przedzia ów zaznaczonych na osi liczbowej.
x
6
–2
A.
2
4
x
!
B.
2
4
x
"
C.
4
2
x
"
D.
4
2
x
!
Zadanie 2. (1 pkt)
Na seans filmowy sprzedano 280 biletów, w tym 126 ulgowych. Jaki procent sprzedanych
biletów stanowi y bilety ulgowe?
A. 22%
B. 33%
C. 45%
D. 63%
Zadanie 3. (1 pkt)
6% liczby x jest równe 9. Wtedy
A.
240
x #
B.
150
x #
C.
24
x #
D.
15
x #
Zadanie 4. (1 pkt)
Iloraz
4
3
1
32 :
8
$ %
& '
( )
jest równy
A.
27
2
B.
3
2
C.
3
2
D.
27
2
Zadanie 5. (1 pkt)
O liczbie
x
wiadomo, 'e
3
log
9
x #
. Zatem
A.
2
#
x
B.
2
1
#
x
C.
9
3
#
x
D.
3
9
#
x
Zadanie 6. (1 pkt)
Wyra'enie
3
3
27x
y
*
jest równe iloczynowi
A.
+
,
+
,
2
2
3
9
3
x
y
x
xy
y
*
*
B.
+
,
+
,
2
2
3
9
3
x
y
x
xy
y
*
*
*
C.
+
,
+
,
2
2
3
9
3
x
y
x
xy
y
*
*
D.
+
,
+
,
2
2
3
9
3
x
y
x
xy
y
*
Zadanie 7. (1 pkt)
Dane s# wielomiany:
+ ,
3
3
1
W x
x
x
#
*
oraz
+ ,
3
2
V x
x
#
. Wielomian
+ , + ,
W x V x
-
jest równy
A.
5
4
3
2
6
2
x
x
x
*
B.
6
4
3
2
6
2
x
x
x
*
C.
5
2
3
1
x
x
*
*
D.
5
4
3
2
6
2
x
x
x
*
*
Próbny egzamin maturalny z matematyki
Poziom podstawowy
3
BRUDNOPIS
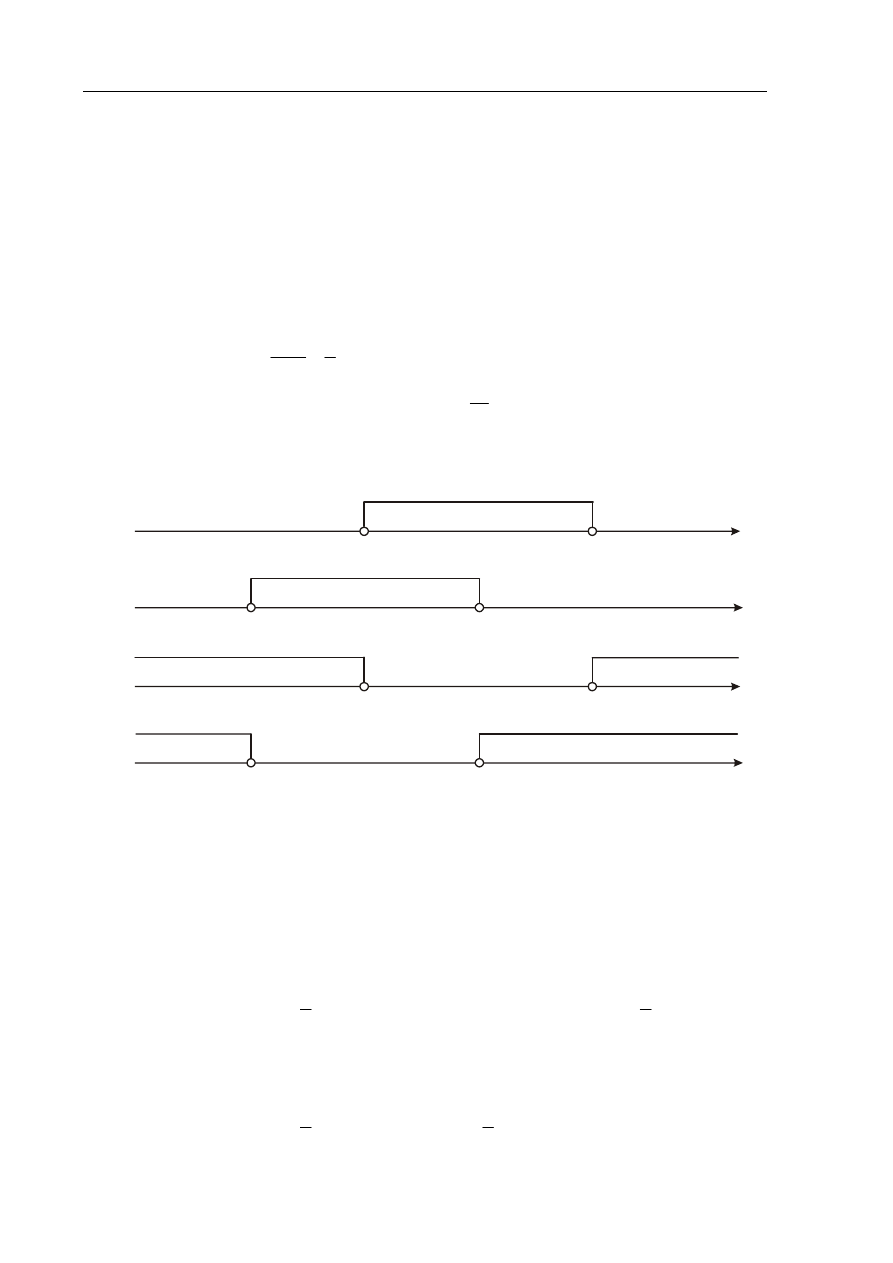
Próbny egzamin maturalny z matematyki
Poziom podstawowy
4
Zadanie 8. (1 pkt)
Wierzcho ek paraboli o równaniu
+
,
2
3
1
y
x
#
*
ma wspó rz&dne
A.
+
,
1, 0
B.
+
,
0, 1
C.
+ ,
1, 0
D.
+ ,
0,1
Zadanie 9. (1 pkt)
Do wykresu funkcji
+ ,
2
2
f x
x
x
#
*
nale'y punkt
A.
+
,
1, 4
B.
+
,
1, 1
C.
+
,
1, 1
D.
+
,
1, 2
Zadanie 10. (1 pkt)
Rozwi#zaniem równania
5
2
3
3
x
x
#
*
jest liczba
A.
21
B.
7
C.
17
3
D.
0
Zadanie 11. (1 pkt)
Zbiór rozwi#za$ nierówno!ci
+
,+
,
1
3
0
x
x
*
!
przedstawiony jest na rysunku
A.
3
x
–1
B.
1
x
–3
C.
3
x
–1
D.
1
x
–3
Zadanie 12. (1 pkt)
Dla
1, 2, 3,...
n #
ci#g
+ ,
n
a
jest okre!lony wzorem:
+ , +
,
1
3
n
n
a
n
#
-
. Wtedy
A.
3
0
a "
B.
3
0
a #
C.
3
1
a #
D.
3
1
a !
Zadanie 13. (1 pkt)
W ci#gu arytmetycznym trzeci wyraz jest równy 14, a jedenasty jest równy 34. Ró'nica tego
ci#gu jest równa
A.
9
B.
5
2
C.
2
D.
2
5
Zadanie 14. (1 pkt)
W ci#gu geometrycznym
+ ,
n
a
dane s#:
1
32
a #
i
4
4
a # . Iloraz tego ci#gu jest równy
A.
12
B.
1
2
C.
1
2
D.
12
Próbny egzamin maturalny z matematyki
Poziom podstawowy
5
BRUDNOPIS
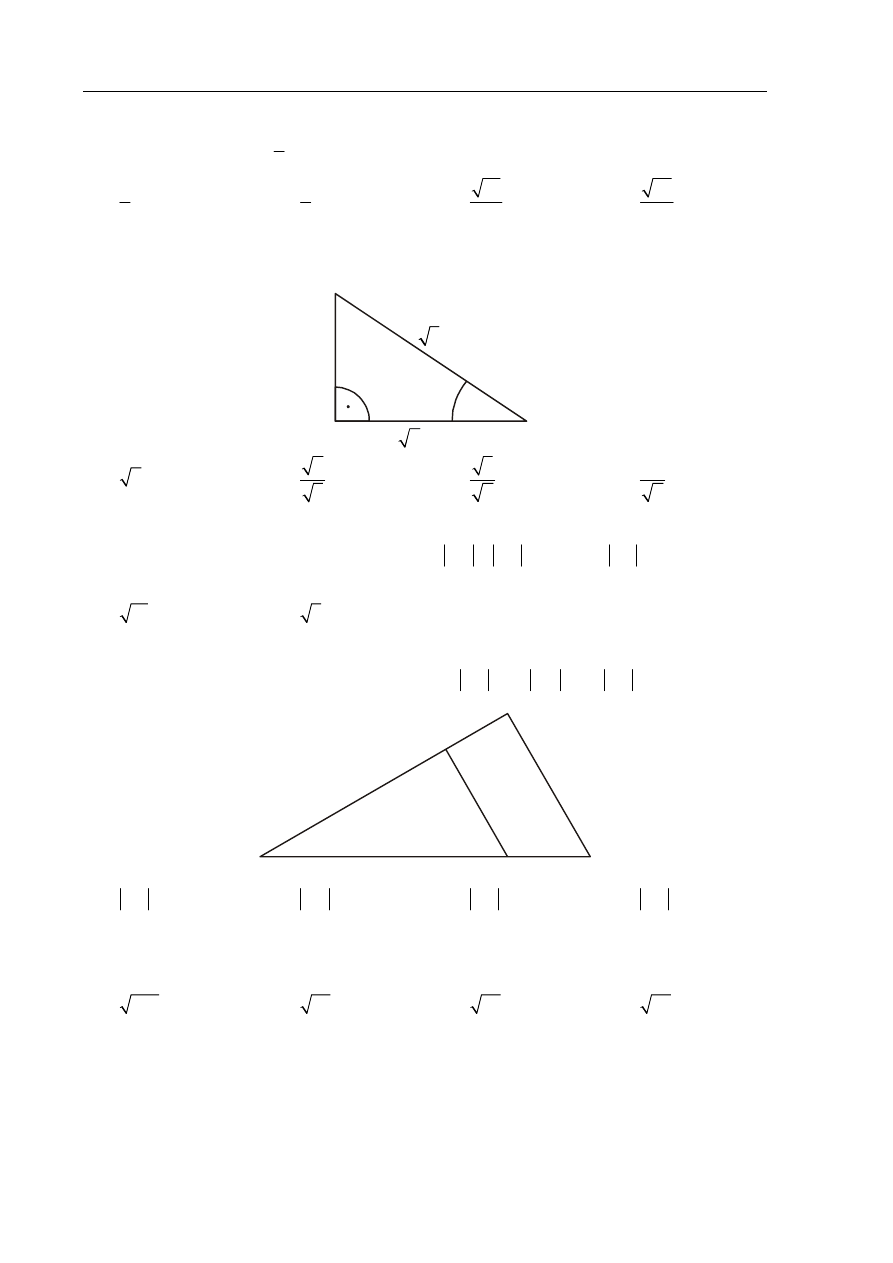
Próbny egzamin maturalny z matematyki
Poziom podstawowy
6
Zadanie 15. (1 pkt)
K#t
. jest ostry i
8
sin
9
.
# . Wtedy
cos
. jest równy
A.
1
9
B.
8
9
C.
17
9
D.
65
9
Zadanie 16. (1 pkt)
Dany jest trójk#t prostok#tny (patrz rysunek). Wtedy tg
.
jest równy
1
2
3
A.
2
B.
2
3
C.
3
2
D.
1
2
Zadanie 17. (1 pkt)
W trójk#cie równoramiennym
ABC
dane s#
7
AC
BC
#
# oraz
12
AB #
. Wysoko!%
opuszczona z wierzcho ka
C
jest równa
A.
13
B.
5
C. 1
D. 5
Zadanie 18. (1 pkt)
Oblicz d ugo!% odcinka
AE
wiedz#c, 'e
AB CD
i
6
AB # ,
4
AC #
,
8
CD # .
E
C
D
A
B
6
8
4
A.
2
AE #
B.
4
AE #
C.
6
AE #
D.
12
AE #
Zadanie 19. (1 pkt)
Dane s# punkty
+
,
2, 3
A #
oraz
+ ,
4, 6
B #
. D ugo!% odcinka
AB
jest równa
A.
208
B.
52
C.
45
D.
40
Zadanie 20. (1 pkt)
Promie$ okr&gu o równaniu
+
,
2
2
1
16
x
y
*
#
jest równy
A. 1
B. 2
C. 3
D. 4
Próbny egzamin maturalny z matematyki
Poziom podstawowy
7
BRUDNOPIS
Próbny egzamin maturalny z matematyki
Poziom podstawowy
8
Zadanie 21. (1 pkt)
Wykres funkcji liniowej okre!lonej wzorem
+ ,
3
2
f x
x
#
* jest prost# prostopad # do prostej
o równaniu:
A.
1
1
3
y
x
#
B.
1
1
3
y
x
#
*
C.
3
1
y
x
#
*
D.
3
1
y
x
#
Zadanie 22. (1 pkt)
Prosta o równaniu
+
,
4
2
7
y
x
m
#
*
przechodzi przez punkt
+
,
2, 1
A #
. Wtedy
A.
7
m #
B.
1
2
2
m #
C.
1
2
m #
D.
17
m #
Zadanie 23. (1 pkt)
Pole powierzchni ca kowitej sze!cianu jest równe 150 cm
2
. D ugo!% kraw&dzi tego sze!cianu
jest równa
A. 3,5 cm
B. 4 cm
C. 4,5 cm
D. 5 cm
Zadanie 24. (1 pkt)
(rednia arytmetyczna pi&ciu liczb: 5,
x
, 1, 3, 1 jest równa 3. Wtedy
A.
2
x #
B.
3
x #
C.
4
x #
D.
5
x #
Zadanie 25. (1 pkt)
Wybieramy liczb&
a
ze zbioru
/
0
2, 3, 4, 5
A #
oraz liczb&
b
ze zbioru
/ 0
1, 4
B #
. Ile jest takich par
+
,
,
a b , 'e iloczyn a b
- jest liczb# nieparzyst#?
A. 2
B. 3
C. 5
D. 20
Próbny egzamin maturalny z matematyki
Poziom podstawowy
9
BRUDNOPIS
Próbny egzamin maturalny z matematyki
Poziom podstawowy
10
ZADANIA OTWARTE
Rozwi"zania zada$ o numerach od 26. do 34. nale%y zapisa& w wyznaczonych miejscach
pod tre'ci" zadania.
Zadanie 26. (2 pkt)
Rozwi#' nierówno!%
2
3
2
0
x
x
* 1
.
Odpowied": …………………………………………………………………………………. .
Zadanie 27. (2 pkt)
Rozwi#' równanie
3
2
7
2
14
0
x
x
x
*
#
.
Odpowied": …………………………………………………………………………………. .
Próbny egzamin maturalny z matematyki
Poziom podstawowy
11
Zadanie 28. (2 pkt)
W uk adzie wspó rz&dnych na p aszczy"nie punkty
+
,
2, 5
A #
i
+
,
C
6, 7
#
s# przeciwleg ymi
wierzcho kami kwadratu
ABCD
. Wyznacz równanie prostej
BD
.
Odpowied": …………………………………………………………………………………. .
Zadanie 29. (2 pkt)
K#t
jest ostry i
4
tg
3
.
#
. Oblicz
.
.
cos
sin
*
.
Odpowied": ……………………………………………………………………………..….. .
Próbny egzamin maturalny z matematyki
Poziom podstawowy
12
Zadanie 30. (2 pkt)
Wyka', 'e dla ka'dego
m
ci#g
'
)
%
&
(
$
*
*
*
12
9
,
6
3
,
4
1
m
m
m
jest arytmetyczny.
Próbny egzamin maturalny z matematyki
Poziom podstawowy
13
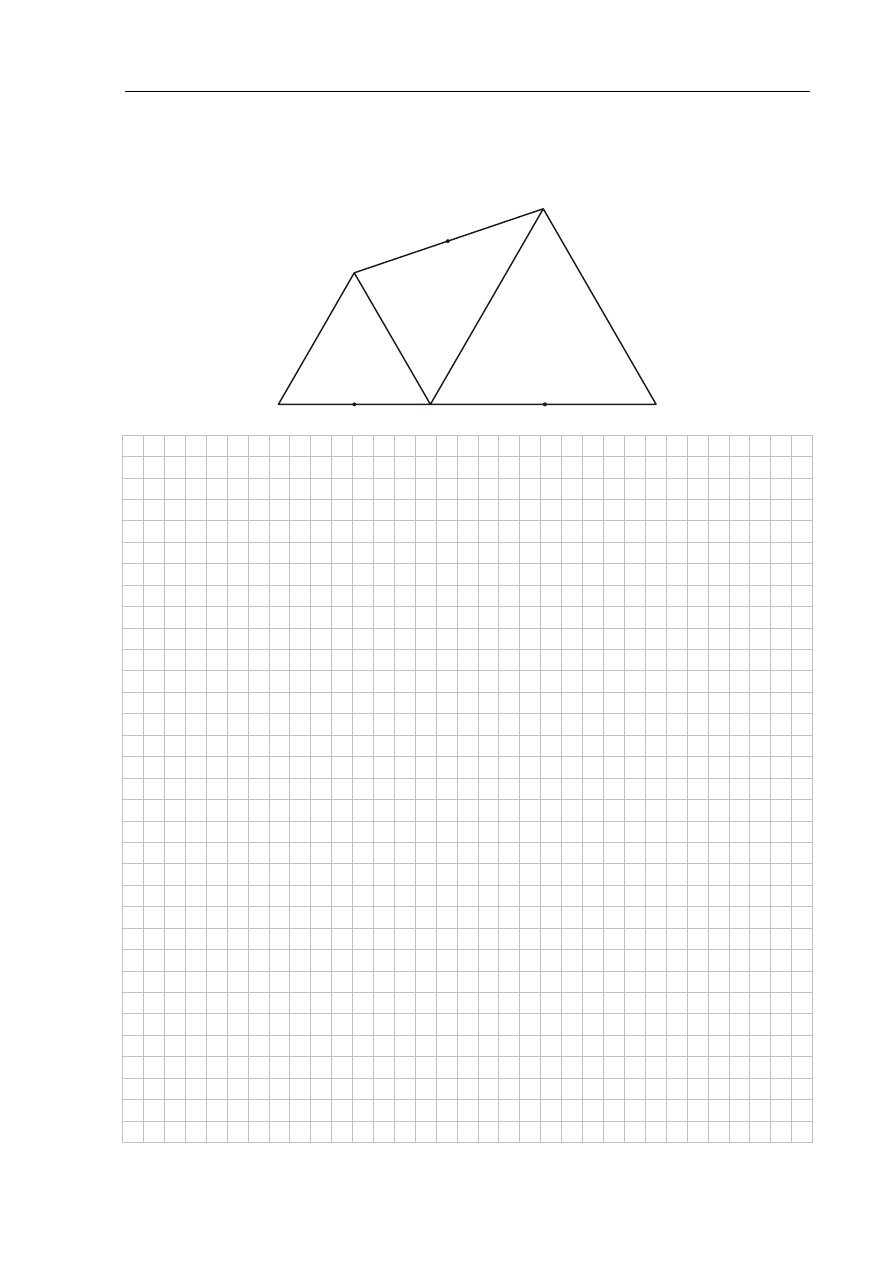
Zadanie 31. (2 pkt)
Trójk#ty ABC i CDE s# równoboczne. Punkty A, C i E le'# na jednej prostej. Punkty K, L i M
s# !rodkami odcinków AC, CE i BD (zobacz rysunek). Wyka', 'e punkty K, L i M
s# wierzcho kami trójk#ta równobocznego.
A
B
C
D
E
K
L
M
Próbny egzamin maturalny z matematyki
Poziom podstawowy
14
Zadanie 32. (5 pkt)
Ucze$ przeczyta ksi#'k& licz#c# 480 stron, przy czym ka'dego dnia czyta jednakow# liczb&
stron. Gdyby czyta ka'dego dnia o 8 stron wi&cej, to przeczyta by t& ksi#'k& o 3 dni
wcze!niej. Oblicz, ile dni ucze$ czyta t& ksi#'k&.
Odpowied": …………………………………………………………………………………. .
Próbny egzamin maturalny z matematyki
Poziom podstawowy
15
Zadanie 33. (4 pkt)
Punkty
+ ,
2, 0
A #
i
+
,
12, 0
B #
s# wierzcho kami trójk#ta prostok#tnego ABC
o przeciwprostok#tnej AB. Wierzcho ek C le'y na prostej o równaniu y
x
# . Oblicz
wspó rz&dne punktu C.
Odpowied": …………………………………………………………………………………. .
Próbny egzamin maturalny z matematyki
Poziom podstawowy
16
Zadanie 34. (4 pkt)
Pole trójk#ta prostok#tnego jest równe
2
60 cm . Jedna przyprostok#tna jest o 7 cm d u'sza
od drugiej. Oblicz d ugo!% przeciwprostok#tnej tego trójk#ta.
Odpowied": …………………………………………………………………………………. .
Próbny egzamin maturalny z matematyki
Poziom podstawowy
17
BRUDNOPIS