Arkusz 04: Stan naprężenia. Arkusz przeznaczony do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.
Notatki do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów”
Notatki do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów”
Arkusz 0
Arkusz 0
4: Stan naprężenia
4: Stan naprężenia
1. Stan naprężenia – pojęcia i definicje
Podstawy teoretyczne do zagadnienia stanu naprężenia należy opanować na podstawie wykładu i książek:
[1], [2].
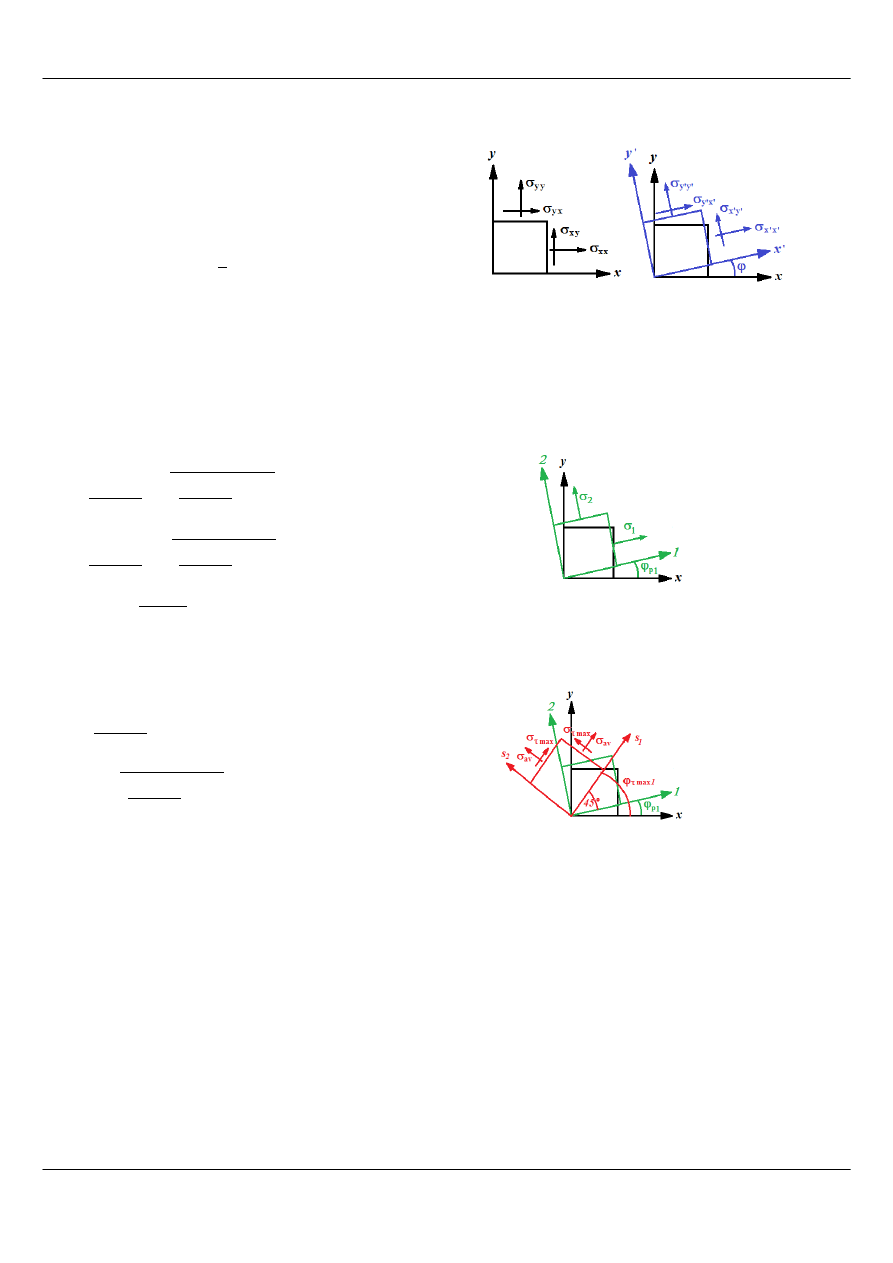
• Definicja naprężenia.
• Tensor naprężenia i kostka naprężenia. Naprężenia styczne i normalne.
• Przestrzenny stan naprężenia: zagadnienie postaci własnej tensora naprężenia, równanie wiekowe,
niezmienniki tensora naprężenia.
• Płaski stan naprężenia: wzory tansformacyjne dla orientacji obróconej o dowolny kąt, naprężenia główne,
orientacja maksymalnych naprężeń stycznych.
Zagadnienie postaci głównej (własnej) macierzy oraz wektorów głównych (własnych) macierzy jest w zasadzie
zagadnieniem algebraicznym. Dla macierzy reprezentującej wartości pewnej wielkości fizycznej (w naszym przypadku
długości składowych wektora naprężenia) postać główna ma swoją interpretację fizyczną. Jednak można, przygotowując
się do zajęć, po prostu przybliżyć sobie ten temat ćwicząc przykłady czysto algebraiczne.
2. Przestrzenny stan naprężenia
Należy rozwiązać zadania nr: 4.6.1, 4.6.2 z książki [2].
• Umiejętność narysowania kostki dla danego tensora naprężenia i odwrotnie: odczytanie tensora z kostki.
• Obliczenie wektora naprężenia przy przecięciu zadaną płaszczyzną.
3. Płaski stan naprężenia
Obowiązujące wzory transformacyjne:
© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.
1
Arkusz 04: Stan naprężenia. Arkusz przeznaczony do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.
a) Obrót do orientacji odwróconej o kąt dowolny
φ
T
σ
=
[
σ
xx
σ
xy
σ
yx
σ
yy
]
→
obrót o kąt
φ
T
σ '
=
[
σ
x ' x'
σ
x ' y'
σ
y ' x '
σ
y ' y '
]
σ
x ' x '
= σ
xx
⋅cos
2
φ+ σ
yy
⋅sin
2
φ+ σ
xy
⋅sin (2φ )
σ
y' y'
= σ
xx
⋅sin
2
φ + σ
yy
⋅cos
2
φ σ
xy
⋅sin(2φ )
σ
x ' y '
= σ
y ' x '
= (σ
yy
σ
xx
)⋅
1
2
⋅sin (2 φ )+ σ
xy
⋅(cos
2
φ sin
2
φ )
Istnieją inne zestawy wzorów, równoważne powyższemu zestawowi. Można znaleźć je w literaturze. Na zajęcia
obowiązuje znajomość jednego zestawu, ja polecam ten.
b) Obrót do orientacji głównej
T
σ
=
[
σ
xx
σ
xy
σ
yx
σ
yy
]
→
obrót o kąt
φ
p1
T
σ , p
=
[
σ
1
0
0
σ
2
]
σ
1
=
σ
xx
+ σ
yy
2
+
√
(
σ
xx
σ
yy
2
)
2
+ σ
xy
2
σ
2
=
σ
xx
+ σ
yy
2
√
(
σ
xx
σ
yy
2
)
2
+ σ
xy
2
φ
p1
= arctan
(
σ
1
σ
xx
σ
12
)
oraz
φ
p2
= φ
p1
+ 90 deg
c) Obrót do orientacji maksymalnych naprężeń stycznych
T
σ
=
[
σ
xx
σ
xy
σ
yx
σ
yy
]
→
obrót o kąt
φ
τ max 1
T
σ , s
=
[
σ
av
σ
τ max
σ
τ max
σ
av
]
σ
av
=
σ
xx
+ σ
yy
2
∣
σ
τ max
∣
=
√
(
σ
xx
σ
yy
2
)
2
+ σ
xy
2
φ
τ max1
= φ
p1
+ 45 deg
oraz
φ
τ max2
= φ
τ max1
+ 90 deg
Jak widać, powyższy wzór nie uwzględnia znaku naprężeń stycznych. Znak ten można obliczyć korzystając ze wzorów
transformacyjnych wypisanych w podpunkcie a). Wówczas przyjmujemy
φ = φ
τmax 1
i obliczamy
σ
x ' y '
. Przy okazji
jest to dobra kontrola obliczenia wartości naprężeń.
d) Jako sprawdzenie można zastosować niezmiennik tensora płaskiego stanu naprężenia
σ
xx
+ σ
yy
= σ
x ' x '
+ σ
y ' y '
= σ
p1
+ σ
p2
= σ
av
+ σ
av
© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.
2
Arkusz 04: Stan naprężenia. Arkusz przeznaczony do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.
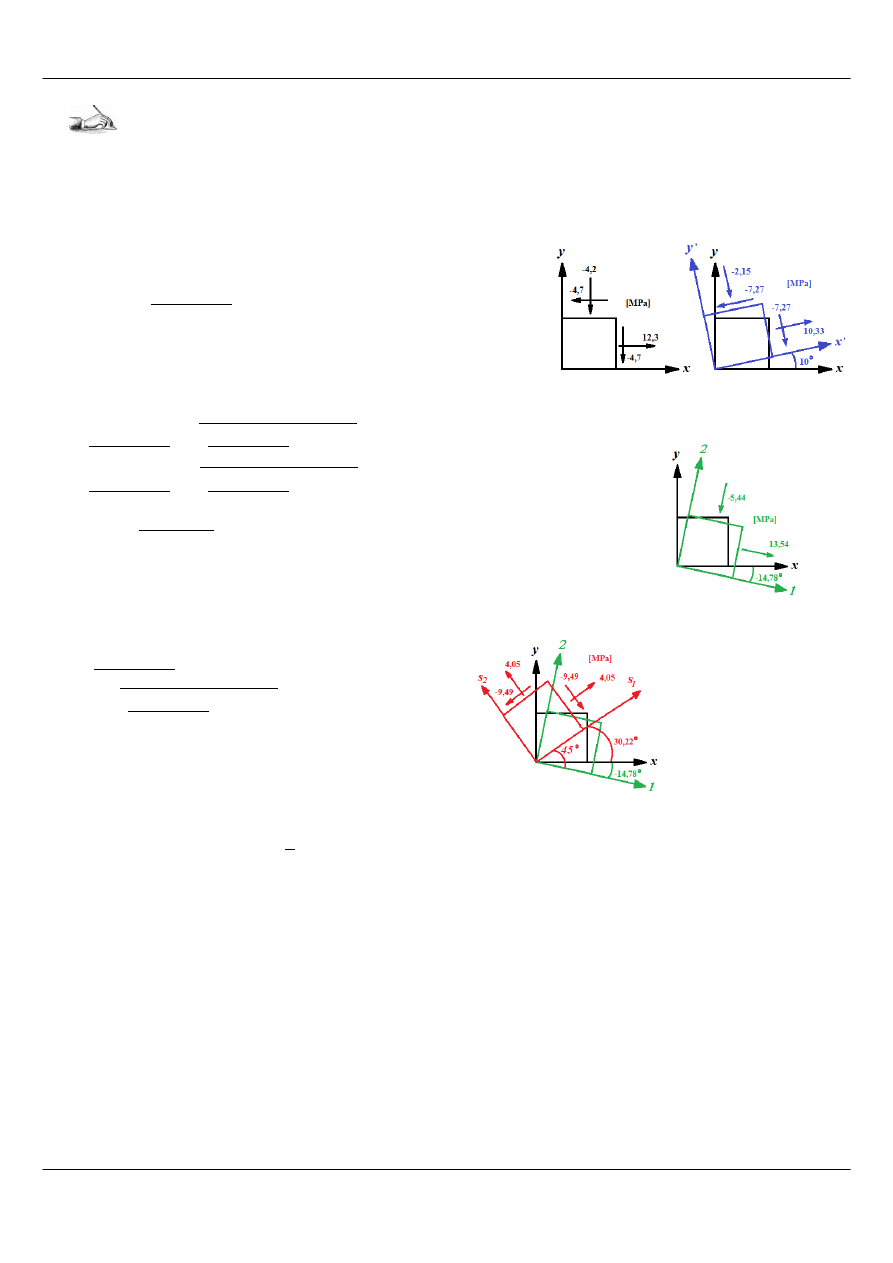
Zadanie 1
Dla zadanego tensora naprężenia T
σ
znaleźć postać przy obrocie o kąt
φ =10 deg
, przy obrocie do
orientacji głównej i do orientacji maksymalnych naprężeń stycznych. Zrobić odpowiednie rysunki.
T
σ
=
[
12,3
4,7
4,7
4,2
]
MPa
a) Obrót do orientacji odwróconej o kąt
φ =10 deg
σ
x ' x '
= 12,3⋅cos
2
10
+ ( 4,2 )⋅sin
2
10
+ ( 4,7)⋅sin(2⋅10) = 10,33 MPa
σ
y' y'
= 12,3⋅sin
2
10
+ ( 4,2)⋅cos
2
10
( 4,7)⋅sin( 2⋅10) = 2,15 MPa
σ
x ' y '
= σ
y ' x '
=
( 4,2 12,3)
2
⋅sin( 20)+ ( 4,7)⋅(cos
2
10 sin
2
10
) = 7,27 MPa
T
σ
=
[
12,3
4,7
4,7
4,2
]
MPa
→
obrót o kąt
φ
T
σ '
=
[
10,33
7,27
7,27
2,15
]
MPa
b) Obrót do orientacji głównej
σ
1
=
12,3
+ ( 4,2)
2
+
√
(
12,3
( 4,2)
2
)
2
+ ( 4,7)
2
= 13,54 MPa
σ
2
=
12,3
+ ( 4,2)
2
√
(
12,3
( 4,2)
2
)
2
+ ( 4,7)
2
= 5,44 MPa
φ
p1
= arctan
(
13,54 12,4
( 4,7)
)
= 14,78 deg
oraz
φ
p2
= 14,78deg + 90 deg = 75,22 deg
T
σ
=
[
12,3
4,7
4,7
4,2
]
MPa
→
obrót o kąt
φ
p1
T
σ , p
=
[
13,54
0
0
5,44
]
MPa
c) Obrót do orientacji maksymalnych naprężeń stycznych
σ
av
=
12,3
+ ( 4,2)
2
= 4,05 MPa
∣
σ
τ max
∣
=
√
(
12,3
( 4,2)
2
)
2
+ ( 4,7)
2
= 9,49 MPa
φ
τ max1
= 14,78 deg + 45 deg = 30,22 deg
φ
τ max2
= 30,22deg + 90 deg = 120,22 deg
Znak naprężenia stycznego obliczamy korzystając ze wzorów transformacyjnych; przyjmujemy
φ = φ
τmax 1
:
σ
x ' y '
= σ
y ' x '
= σ
τ max
= ( 4,2 12,3)⋅
1
2
⋅sin( 2⋅30,22)+ ( 4,7)⋅( cos
2
30,22
sin
2
30,22
) = 9,52 MPa
(Uwaga! Powstała tutaj mała różnica pomiędzy wartościami wynika z przyjętego w obliczeniach zaokrąglenia cos i sin do
dwóch miejsc po przecinku.)
T
σ
=
[
12,3
4,7
4,7
4,2
]
MPa
→
obrót o kąt
φ
τ max 1
T
σ , s
=
[
4,05
9,49
9,49
4,05
]
MPa
d) Sprawdzenie wg niezmienników
σ
xx
+ σ
yy
= σ
x ' x '
+ σ
y ' y '
= σ
p1
+ σ
p2
= σ
av
+ σ
av
12,4
+ ( 4,2 ) ≃ 10,33+ ( 2,15) ≃ 13,54+ ( 5,44) ≃ 4,05⋅2 ≃ 8,1 MPa
(Uwaga! Powstała tutaj mała różnica pomiędzy wartościami wynika z przyjętego w obliczeniach zaokrąglenia cos i sin do
dwóch miejsc po przecinku.)
© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.
3
Arkusz 04: Stan naprężenia. Arkusz przeznaczony do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.
Należy rozwiązać wybrane zadania z książki [3] dotyczące zagadnienia płaskiego stanu. Można także
rozwiązać zadania 5.4.1, 5.4.2 z książki [2].
• Umiejętność znalezienia postaci macierzy naprężeń dla stanu płaskiego w orientacji obróconej o dowolny
kąt, orientacji głównej, orientacji maksymalnych naprężeń stycznych.
• Ilustracja graficzna (bez koła Mohra).
4. Literatura
[1] Piechnik S. "Mechanika techniczna ciała stałego", Wydawnictwo PK, Kraków 2007
[2] Bodnar A. „Wytrzymałość materiałów. Podręcznik dla studentów wyższych szkół technicznych”, wydanie drugie
poszerzone i poprawione, Kraków 2004
[3] Niezgodziński M., Niezgodziński T. "Zadania z wytrzymałości materiałów", Wydawnictwo WNT, Warszawa 2012
[4] Programy komputerowe do obliczeń – zagadnienie postaci własnej macierzy, wektorów wlasnych.
© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.
4