1

0

d

d

2

d

d

2

0

2

2

=

+

+

x

t

x

t

x

ω

β

)

+

t

(

Ae

=

x

t

ϕ

ω

β

cos

−

)

+

t

(

e

A

)

+

t

(

e

A

=

t

x

t

t

ϕ

ω

ω

ϕ

ω

β

β

β

sin

cos

d

d

−

−

−

−

)

+

t

(

e

A

)

+

t

(

e

A

=

t

x

t

t

ϕ

ω

βω

ϕ

ω

ω

β

β

β

sin

2

cos

)

(

d

d

2

2

2

2

−

−

+

−

[

]

0

cos

sin

cos

2

sin

2

cos

)

(

2

0

2

2

=

+

−

−

+

+

+

−

−

−

−

−

−

)

+

t

(

Ae

)

+

t

(

e

A

)

+

t

(

e

A

)

+

t

(

e

A

)

+

t

(

e

A

t

t

t

t

t

ϕ

ω

ω

ϕ

ω

ω

ϕ

ω

β

β

ϕ

ω

βω

ϕ

ω

ω

β

β

β

β

β

β

0

cos

)

2

(

2

0

2

2

2

=

+

−

−

−

)

+

t

(

e

A

t

ϕ

ω

ω

β

ω

β

β

2

2

0

2

β

ω

ω

−

=

2

2

0

β

ω

ω

−

=

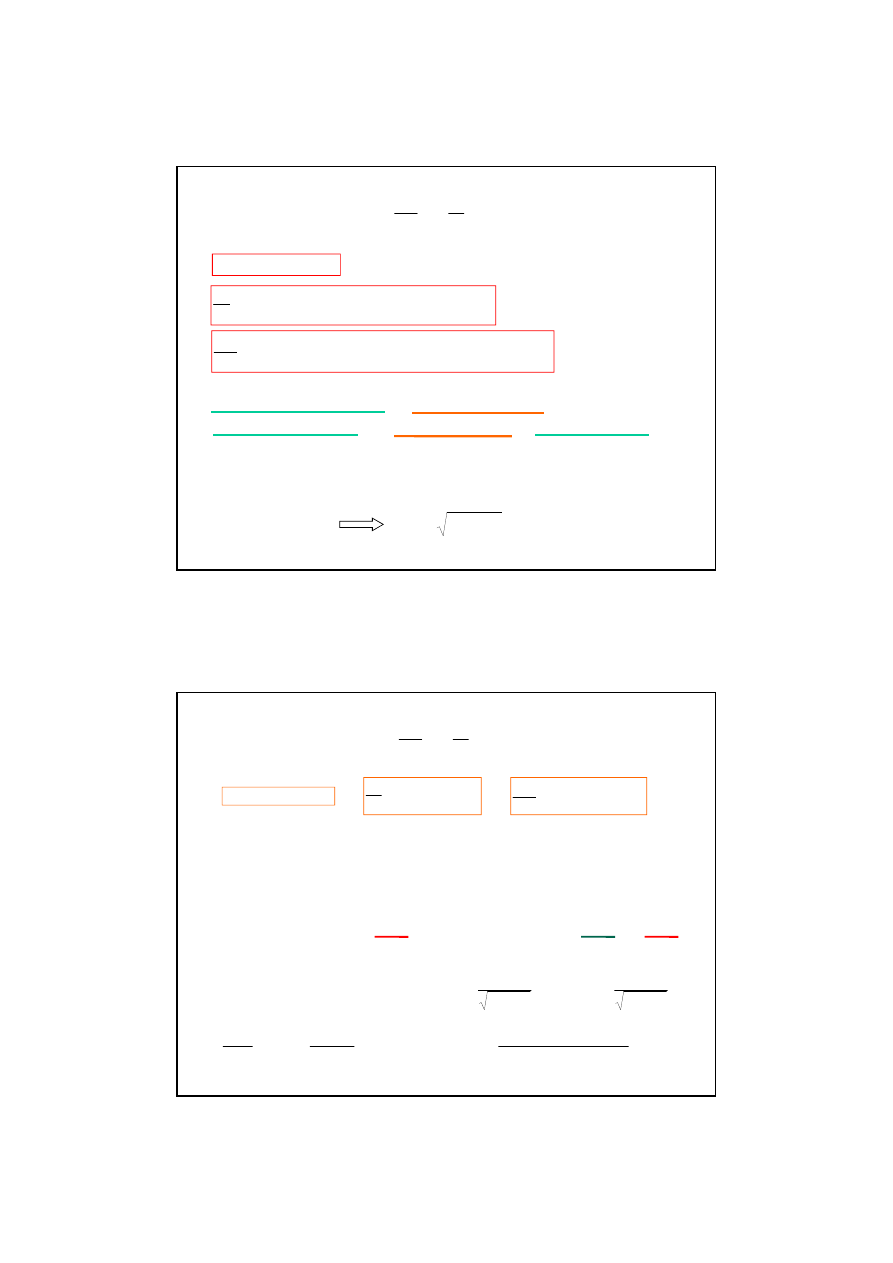
Rozwi

ą

zanie równania:

Dodatek 1:

Rozwi

ą

zanie równania:

Dodatek 2:

t

x

t

x

t

x

ω

α

ω

β

sin

d

d

2

d

d

0

2

0

2

2

=

+

+

)

sin(

)

(

ϕ

ω

+

=

t

A

t

x

)

cos(

d

d

ϕ

ω

ω

+

=

t

A

t

x

)

sin(

d

d

2

2

2

ϕ

ω

ω

+

−

=

t

A

t

x

(

)

t

t

A

t

A

ω

α

ϕ

ω

βω

ϕ

ω

ω

ω

sin

)

cos(

2

)

sin(

0

2

2

0

=

+

+

+

−

ϕ

ω

ϕ

ω

ϕ

ω

ϕ

ω

ϕ

ω

ϕ

ω

sin

sin

cos

cos

)

cos(

sin

cos

cos

sin

)

sin(

t

t

t

t

t

t

−

=

+

+

=

+

(

)

[

]

(

)

[

]

t

t

A

t

A

ω

α

ω

ϕ

βω

ϕ

ω

ω

ω

ϕ

βω

ϕ

ω

ω

sin

cos

cos

2

sin

sin

sin

2

cos

0

2

2

0

2

2

0

=

+

−

+

−

−

2

2

0

2

cos

sin

ω

ω

βω

ϕ

ϕ

ϕ

−

−

=

=

tg

2

/

1

2

2

2

2

2

0

0

]

4

)

[(

ω

β

ω

ω

α

+

−

=

A

ϕ

ϕ

ϕ

ϕ

ϕ

2

2

1

1

cos

1

sin

tg

tg

tg

+

=

+

=