K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

XI.

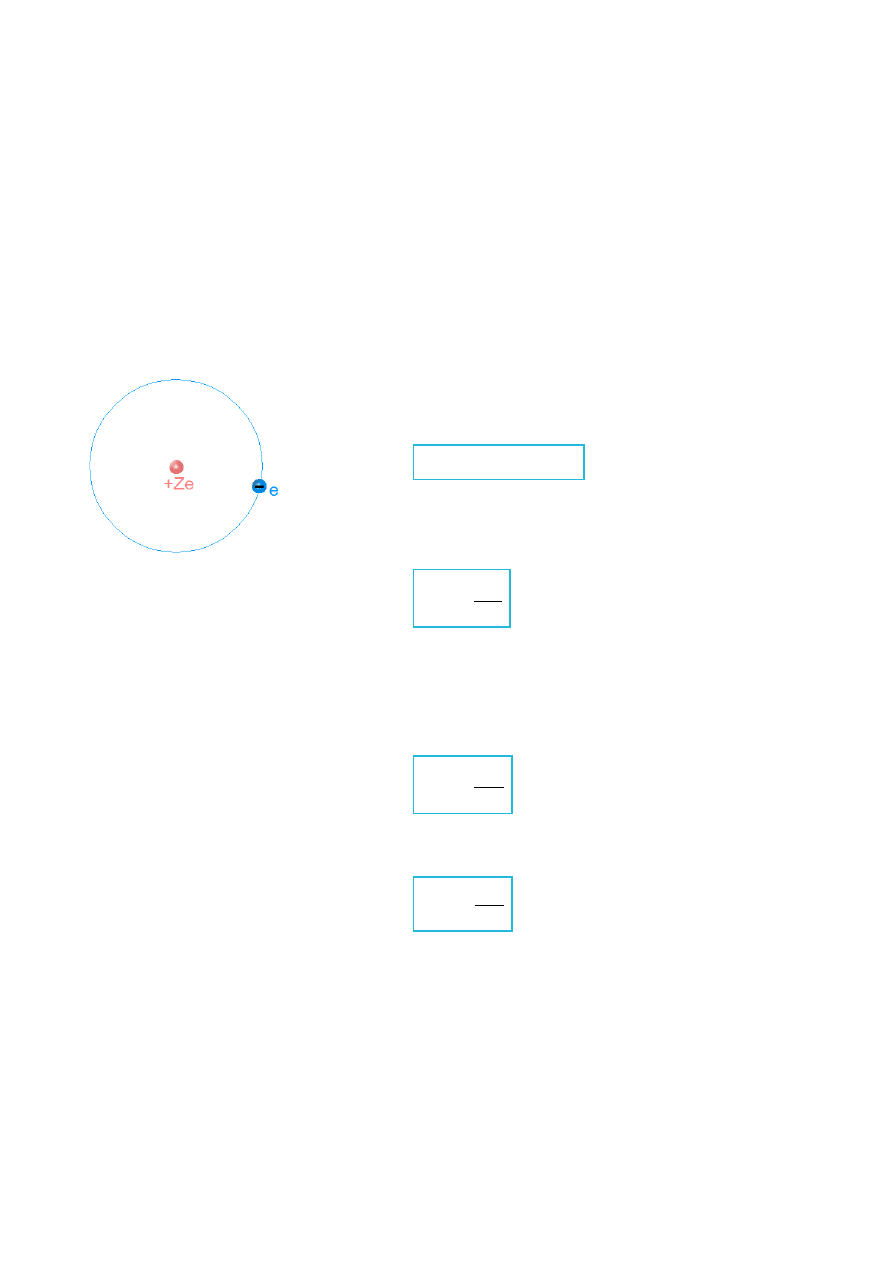
XI.1. ATOM WODOROPODOBNY

Atomy wodoropodobne, to pierwiastki posiadające tylko jeden elektron, np. He

+

, Na

++

, itd.

Energię możemy wyrazić z pomocą wzoru:

E

'

= E

K

1

+ E

K

2

+ V

(XI.1)

gdzie

E

K

1

– energia kinetyczna elektronu

E

K

1

=

p

1

2

2m

(XI.1.2a)

m – masa elektronu

p – pęd elektronu

E

K

2

– energia kinetyczna jadra atomowego

E

K

2

=

p

2

2

2M

(XI.1.2b)

V – energia potencjalna (potencjał)

V

= −

Ze

2

r

(XI.1.2c)

Masa jądra atomowego M jest znacznie większa od masy elektronu m.

– 1 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

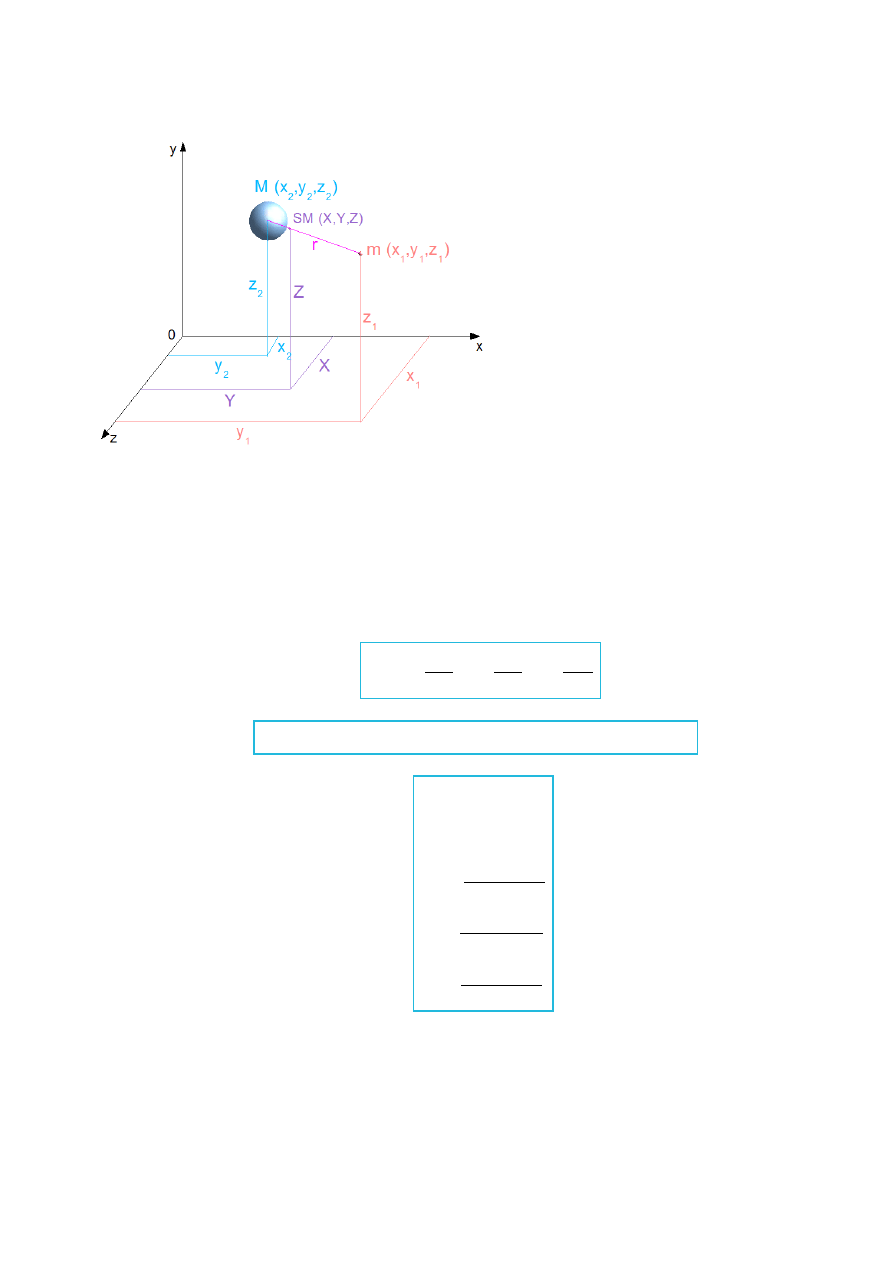
Rys.XI.1. Schematyczna ilustracja atomu wodoropodobnego umieszczonego w kartezjańskim układzie
współrzędnych.

Równanie Schrődingera dla atomu wodoropodobnego znajdujemy posługując się regułami
Jordana:

E

'

 H

p

1

 p

1

, p

2

 p

2

, p

3

 p

3

H =− ℏ

2

2m



1

−

ℏ

2

2m



2

−

Ze

2

r

(XI.1.3)

H x

1

, y

1

, z

1

; x

2

, y

2

, z

2

 = E

'

 x

1

, y

1

, z

1

; x

2

, y

2

, z

2



(XI.1.4)

x

= x

2

− x

1

y

= y

2

− y

1

z

= z

2

−z

1

X

=

m

x

1

 M

x

2

m

 M

Y

=

m

y

1

 M

y

2

m

 M

Z

=

m

z

1

 M

z

2

m

 M

(XI.1.5)

We wzorze (XI.1.5) współrzędne x, y, z to współrzędne względne (położenie elektronu
względem jądra lub odwrotnie).

– 2 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

separujemy zmienne:

 x , y , z , X ,Y , Z  =  x , y , z⋅  X ,Y ,Z 

(XI.1.6)

Ze wzorów (XI.1.3) oraz (XI.1.6) otrzymujemy:

−ℏ

2

m

 M

 X ,Y , Z  = E

'

− E  X ,Y , Z 

(XI.1.7a)

−ℏ

2

2



[

−

Ze

2

r

]

 x , y , z = E  x , y , z

(XI.1.7b)

Równanie (XI.1.7a) opisuje ruch atomu jako całości, z energią kinetyczną równą (E' – E).

Uwaga:

XI.1.7a  = ∂

2

∂ X

2

+ ∂

2

∂Y

2

+ ∂

2

∂ Z

2

 XI.1.7b = ∂

2

∂ x

2

+ ∂

2

∂ y

2

+ ∂

2

∂ z

2

 =  X ,Y , Z  = exp

[

i

k

x

x

 k

y

y

 k

z

z



]

(XI.1.8)

Wyrażenie (XI.1.8a) opisuje falę płaską.

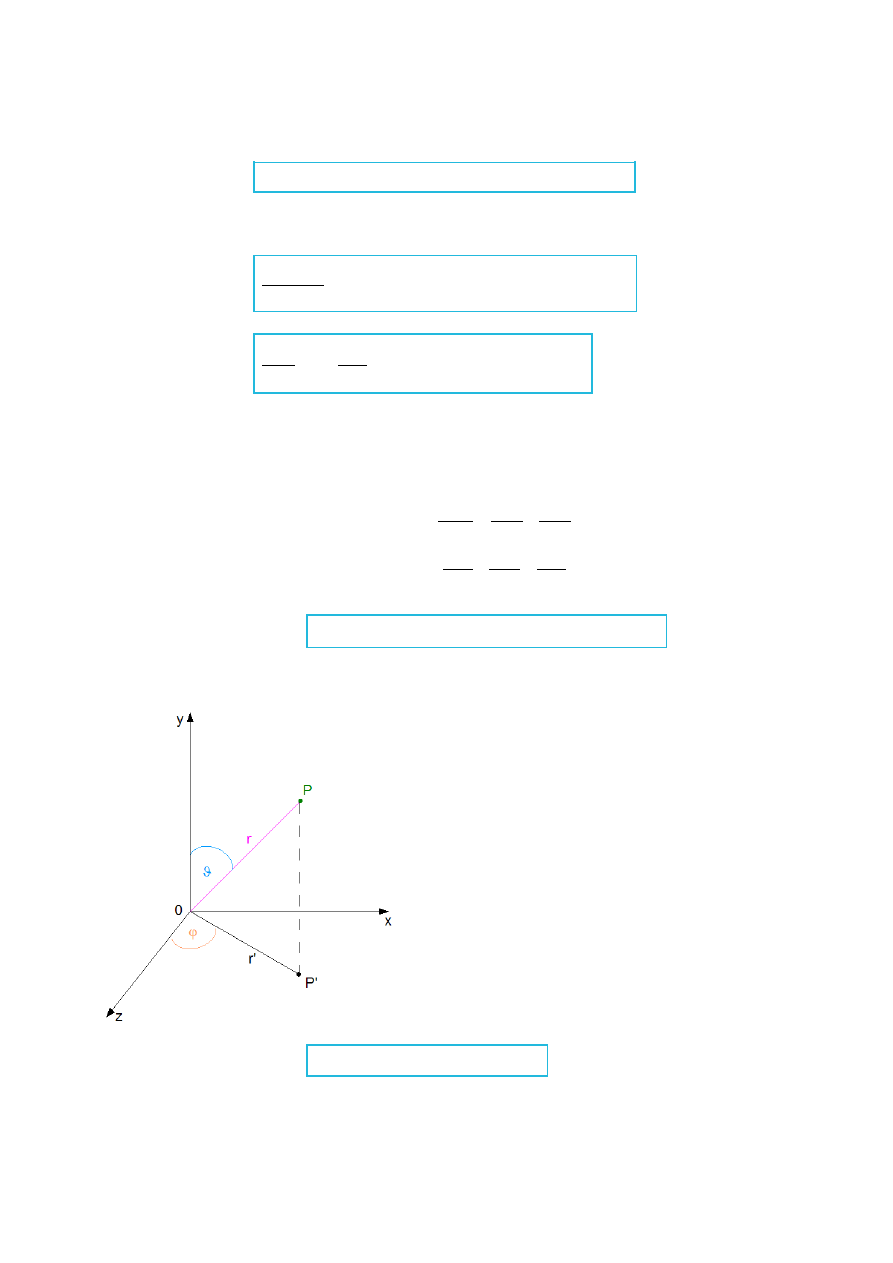
ϕ

– kąt azymutalny

ϑ

– kąt biegunowy

H r , , = Er , ,

(XI.1.9)

– 3 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

H =− ℏ

2

2



[

1

r

2

∂

∂ r



r

2

∂

∂r





1

r

2

sin

2



∂

2

∂ 

2



1

r

2

sin



∂

∂ 



sin

 ∂

∂ 



]

−

Ze

2

r

(XI.1.10)

µ

jest to tzw. masa zredukowana i jest ona równa:

 =

df

mM

m

 M

Równanie (XI.1.9) rozwiązuje się metodą separacji zmiennych czyli zakładamy, że:

r , , = Rr

(XI.1.11)

R – funkcja radialna

Wykorzystujemy znajomość funkcji własnej

L

2

(patrz rozdział X.5.)



L

2

~ℏ

2

l

l1



Z równania (XI.1.10) oraz wykorzystując funkcję własną

L

2

otrzymujemy:

H = ℏ

2

2



[

−1

r

2

∂

∂ r



r

2

∂

∂r





1

r

2

L

2

]

−

Ze

2

r

(XI.1.12)

Po podstawieniu do równania (XI.1.12) wartości własnej operatora

L

2

{

ℏ

2

2



[

−1

r

2

∂

∂r



r

2

∂

∂ r





l

l 1ℏ

2

r

2

]

−

Ze

2

r

}

r , , = E r , ,

(XI.1.13)

Szukamy rozwiązań postaci:

r , , = RrY  ,

(XI.1.14)

R

 r – część radialna

Y

 , – część kątowa

Z równań (XI.1.13) oraz (XI.1.14) otrzymujemy:

{

ℏ

2

2



[

−1

r

2

d

d r



r

2

d

d r





l

l1ℏ

2

r

2

]

−

Ze

2

r

}

R

r = ERr 

(XI.1.15)

– 4 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

Równanie (XI.1.15) to równanie Laguerra

a) E ≥ 0, E jest ciągła
b) E < 0 – elektron związany – tworzy razem z jądrem atom.

{E

n

}: E

n

= −

nZ

2

e

4

2

ℏ

2

n

r

l 1

2

= −

nZ

2

e

4

2

ℏ

2

n

2

(XI.1.16)

Równanie (XI.1.16) to zbiór rozwiązań równania (XI.1.15) przy warunku b).

Z teorii Bohra – Sommerfelda:

E

~

1

n

2

n – główna liczba kwantowa

l = 0,1,....,n-1 – orbitalna liczba kwantowa

R

ln

r = Cx

l +1

e

−x

2

L

n + 1

2l +1

 x

(XI.1.17)

gdzie

L

n + 1

2l +1

 x

jest wielomianem Lagguera.

x

=

2rZ

na

H

; a

H

=

ℏ

2

ne

2

Elektron

n

l

L

n +1

2l +1

 x

1s

1

0

L

2

1

 x =−1 !

na 1 orbicie

2s

2p

2
2

0
1

L

3

1

= 2x−4

L

3

3

= −3!

3s

3p
3d

3
3
3

0
1
2

L

4

1

= −3x

2

+ 18x

−18

24x

−96

−5 !

Tabela 1. Przykłady postaci wielomianu Laguerra dla kilku wartości n i l.



nlm

r , , = Y

lm

 , R

nl

r  = 

m



lm

 R

nl

r

(XI.1.18)

– 5 –

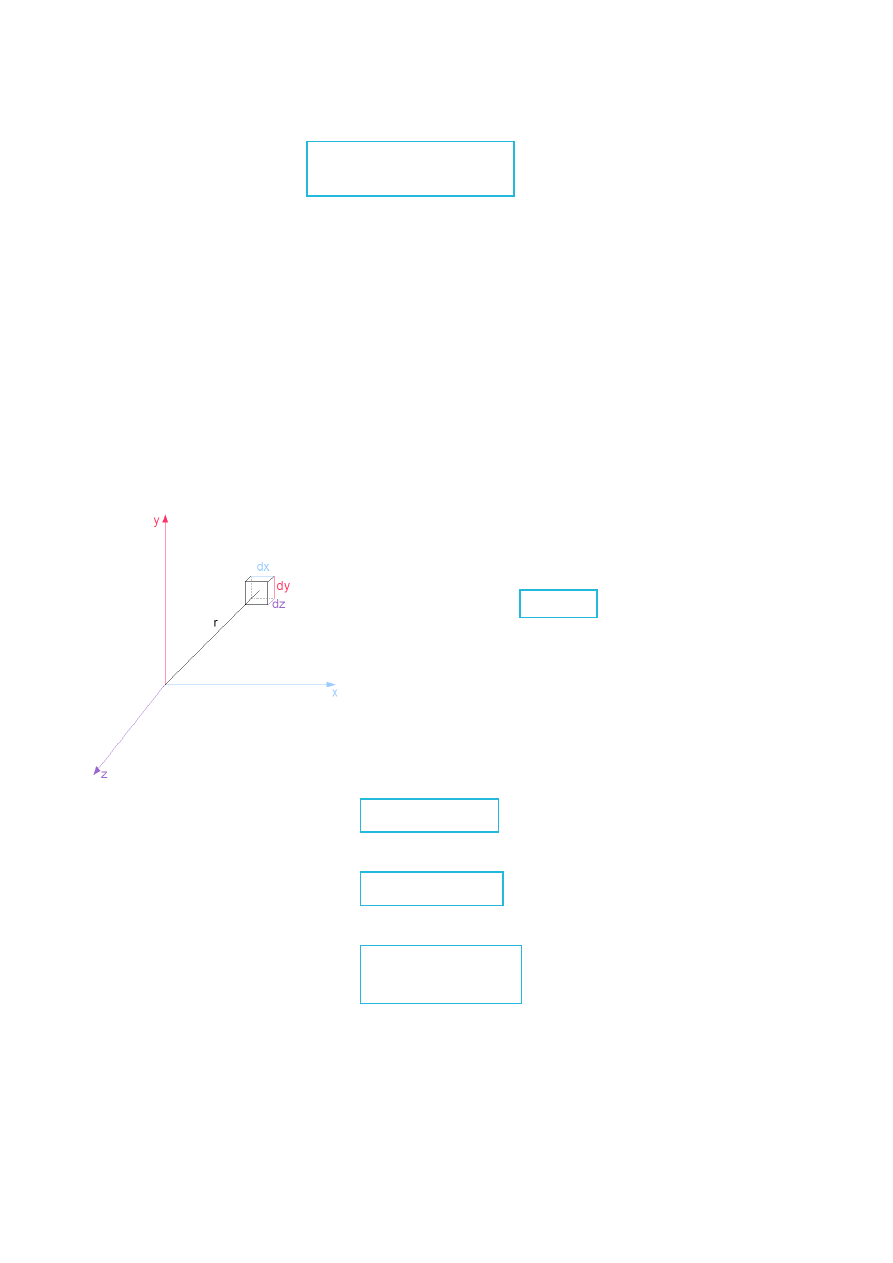
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

∀

n

 E

n

 ∃

∑

l / 0

n

−1

2l +1 = n

2

funkcji własnych

(XI.1.19)

–

istnieje degeneracja stopnia n

2

.

Tylko elektronowi w stanie podstawowym (n = 1) odpowiada jedna funkcja własna – stan
elektronu jest niezdegenerowany. Na następnych orbitach stopień degeneracji rośnie.
Każdy stan atomu wodoropodobnego określony jest przez 3 wartości liczb całkowitych: n,
l, m.

XI.2. KWANTOWO – MECHANICZNY OBRAZ ATOMU (WG BORNA)

Prawdopodobieństwo znalezienia elektronu w objętości

dV:

* dV

(XI.2.1)

Przy czym funkcja

ψ

dana jest równaniem

(XI.1.18)



m

 = Ae

i m



(XI.2.2)



m'

*

= Ae

- i m '



(XI.2.2a)

∫

0

2





m



m '

*

d

 = 

mm'

(XI.2.2b)

Z wyrażeń (XI.2.2b), (XI.2.2a) oraz (XI.2.2) otrzymujemy:

– 6 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

A

2

∫

0

2



e

i

m - m '

d

 = A

2

Z warunku normalizacji:

A

=

1



2



(XI.2.3)



m

 =

1



2



e

i m



(XI.2.3a)



lm

 =



2l + 1l−|m |!

2

l + |m |!

sin

m

 P

l

| m|

cos

(XI.2.4)

R

nl

r  =



n−l−1!

[2n + 1!]

3

a

H

x

2+1

e

−x

2

L

n+ 1

2l+ 1

 x

(XI.2.5)

Znormalizowana funkcja falowa atomu wodoropodobnego wyraża się wzorem:

r ,  ,  =

1



2



e

i m



⋅



2l + 1l−|m |!

2

l + |m|!

sin

m

 P

l

| m|

cos ⋅



n−l−1!

[2 n +1!]

3

a

H

x

2 + 1

e

− x

2

L

n + 1

2l +1

 x

Prawdopodobieństwo znalezienia elektronu w objętości dV:

* dV = 

m



m

*

d



lm



lm

*

sin

d  R

nl

R

nl

*

r

2

dr

(XI.2.6)

Gęstość prawdopodobieństwa:

* = 

m



m

*



lm



lm

*

R

nl

R

nl

*

(XI.2.7)

A) Zależność

* od





m



m

*

=

1

2



=const

Prawdopodobieństwo wszędzie jest stałe – ma charakter izotropowy.

– 7 –

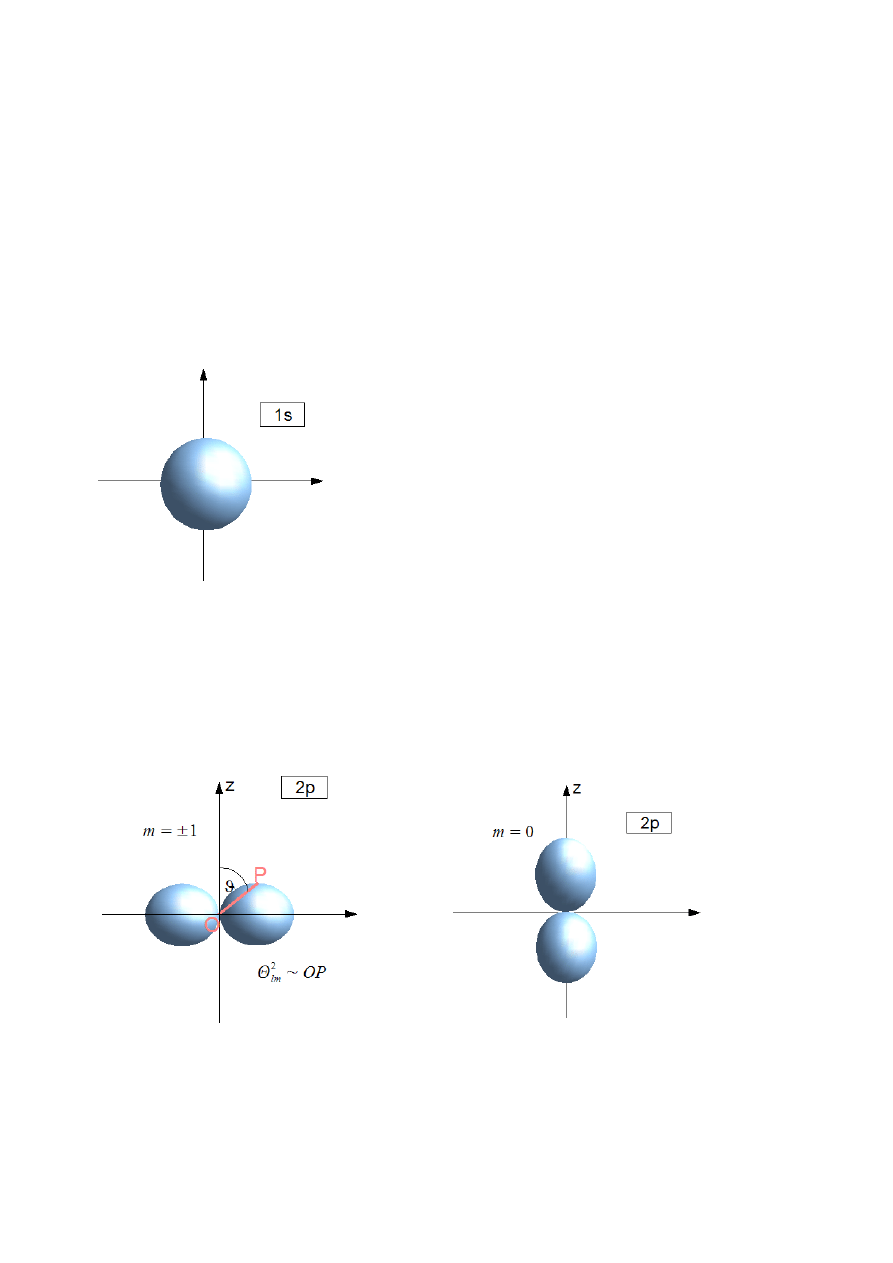
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

B) Zależność

* od 



lm



lm

*

=

lm

*

Stan kwantowy dla danej trójki liczb kwantowych nazywa się orbitalem.

n

= 0  l = 0, m = 0  

00

2

Rys.XI.2. Orbital typu s.

Orbital 1s – dla tych stanów rozkład gęstości jest sferycznie symetryczny.

n

= 1  l = 0, 1, m = −1, 0, 1

l = 1 – stan “p”

Rys.XI.2. Orbitale typu p.

OP – odcinek łączący początek układu z punktem P pod kątem

ϑ.

Rozkład gęstości jest typowo anizotropowy.

– 8 –

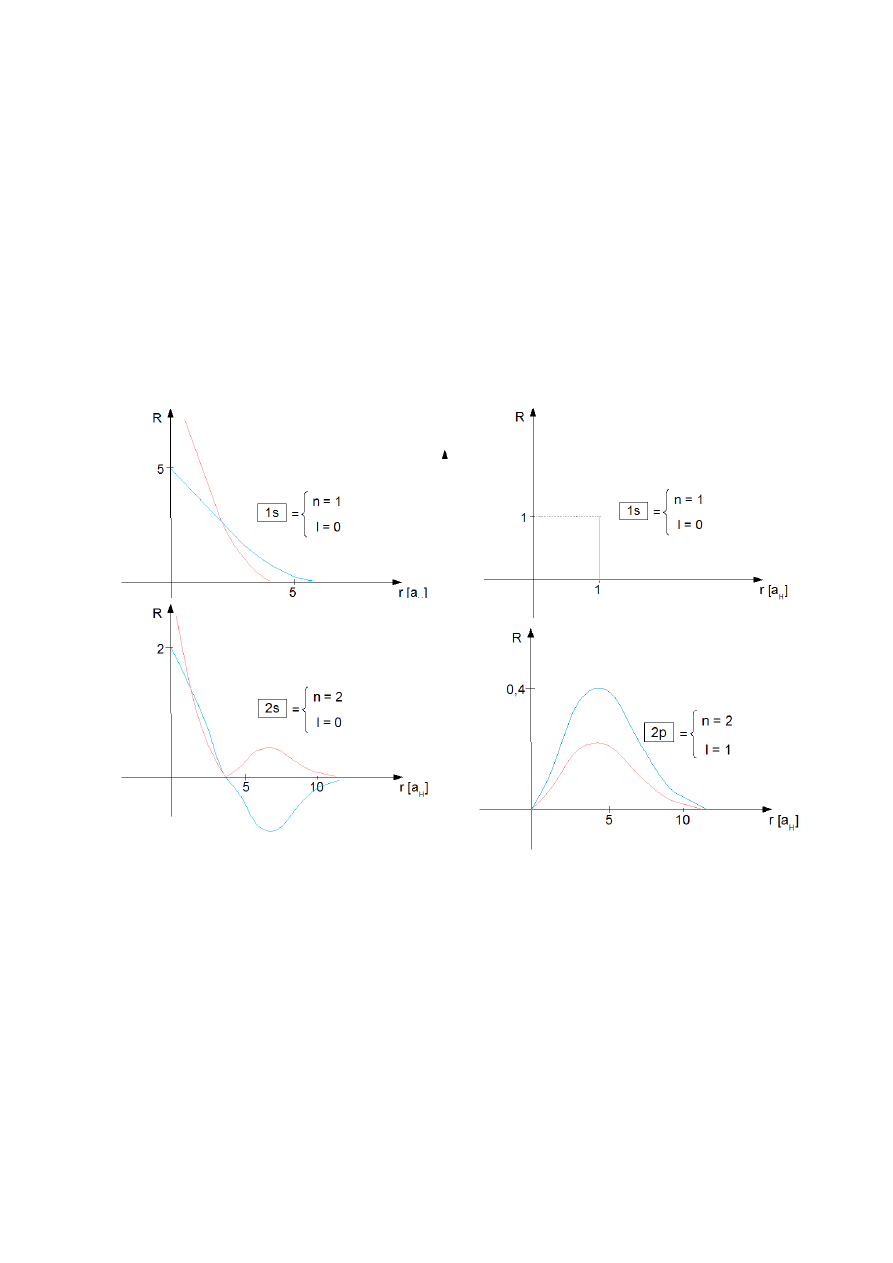
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.

C) Zależność

 r

:

 r* r = R

nl

R *

nl

= R

nl

2

R

nl

– zależność samej funkcji falowej od r

R

nl

2

– gęstość prawdopodobieństwa

a)

b)

c)

d)

Rys.3. Zależność funkcji R od r. Czerwona linia – wykres gęstości prawdopodobieństwa, niebieska –
zależność funkcji falowej od r.

Mechanika kwantowa przewiduje możliwość penetracji jądra atomowego przez elektron –
pewne prawdopodobieństwo, że elektron znajduje się wewnątrz jądra.
Tylko elektrony typu s mają gęstość prawdopodobieństwa różną od zera w obszarze jądra
atomowego.

Funkcja falowa radialna stanu podstawowego (n = 1, l = 0, m = 0).

– 9 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej.



100

r  = −

1







z

a

H



2
3

e

-

z

a

H

⋅r

(XI.2.8)

Indeks 100 oznacza trzy liczby kwantowe (n = 1, l = 0, m = 0)



100



100

*

=

100

2

r e

− Z

a

H

2r

(XI.2.9)

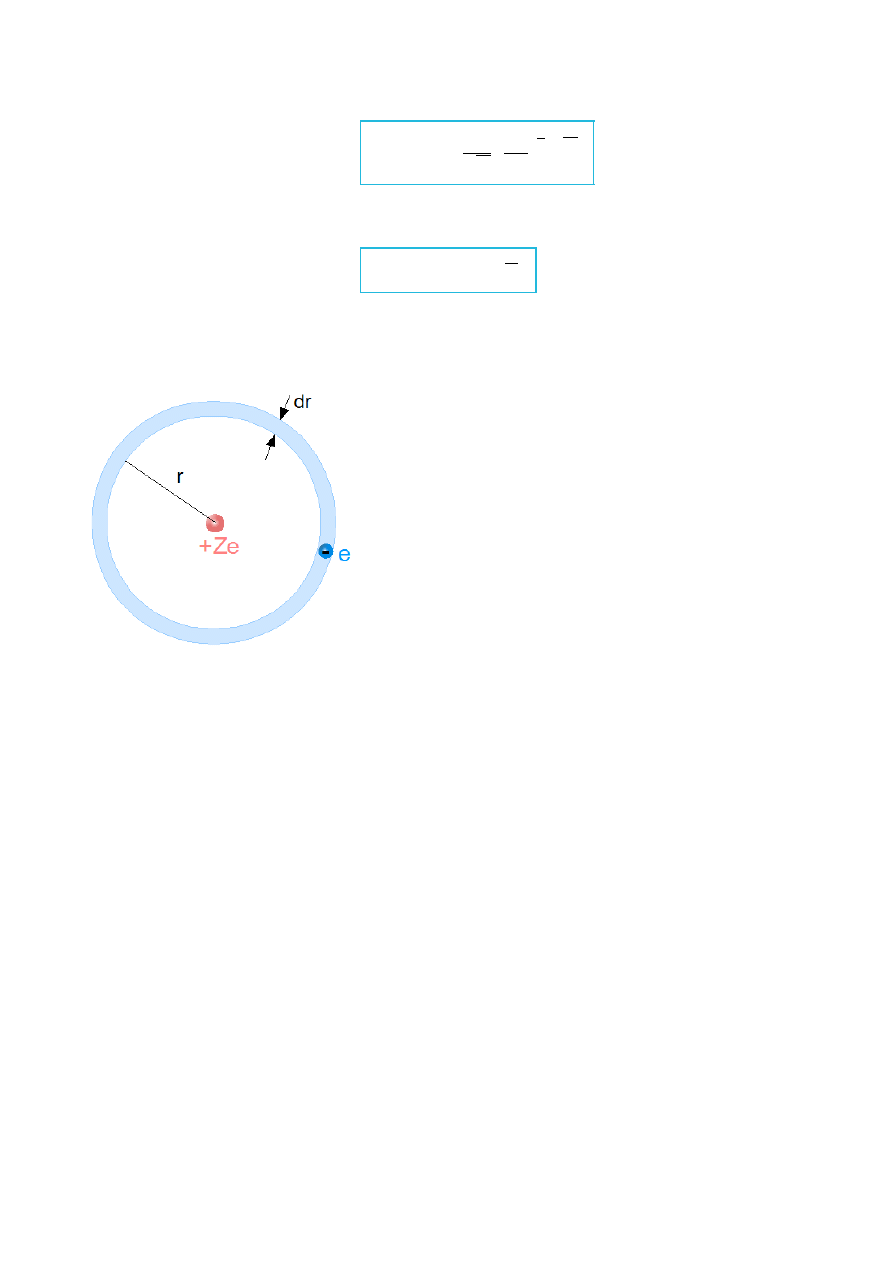
Inną wielkością, którą obrazuje się położenie elektronu w atomie jest częstość
przebywania elektronu w powłoce sferycznej o promieniu r i grubości dr (rys.XI.4):

 = 4  r

2

dr R

2

rys.XI.4. Elektron w powłoce sferycznej.

Model orbitalny wprowadzony przez Bohra i Sommerfelda nie znajduje potwierdzenia w
fizyce kwantowej (kształty orbitali).

– 10 –