
Ćwiczenia 1
Struktura modelu ekonometrycznego
Zadanie 1.1
W poniższych modelach wskaż zmienne objaśniane, zmienne objaśniające, zmienne
endogeniczne, zmienne egzogeniczne, parametry strukturalne i składniki losowe:
a)
t
t
t
t
x
x
y
ξ
β
β
β
+
+
+
=
2
2
1
1
0
,
b)
t
t
t
t
z
y
p
ξ
γ
β
α
+
+
+
=
,
c)
t
t
t
t
t
y
y
y
y
ε
δ
δ
δ
δ
+
+
+
+
=
−
−
−
3
3
2
2
1
1
0
,
d)
t
t
t
t
t
x
x
x
w
µ
α
α
β
β
+
+
+
+
=
−
−
2
2
1
1
1
0
,
e)
2
1
0
β
β
β
t
t
t
Z
M
Q
=
,
f)
{
}
t
t
t
e
u
ξ
α
α
+
+
=
1
0
.
Zadanie 1.2
Odpowiedz na poniższe pytania.
a) Jaka jest część wspólna zbioru zmiennych objaśnianych i zmiennych endogenicznych?
b) Jaka jest część wspólna zbioru zmiennych egzogenicznych i zmiennych objaśniających?
c) Jaka jest rola składnika losowego
t
ξ
w modelu ekonometrycznym?
d) O czym informują nas parametry strukturalne występujące w modelu ekonometrycznym?
Zadanie 1.3
Zaproponuj i naszkicuj wykres modelu wykładniczego dla dowolnej zmiennej objaśnianej. Niech
w modelu występuje jedna zmienna objaśniająca. Jak nazywa się taki model? Jak przebiega
wykres tej funkcji w zależności od wartości parametrów strukturalnych? Do opisu jakich zjawisk
wykorzystywana jest ta funkcja?
Zadanie 1.4
Który z poniższych modeli jest dynamiczny i dlaczego?
a)
t
t
t
t
x
x
y
ξ
α
α
α
+
+
+
=
2
2
1
1
0
,
b)
t
t
t
t
t
y
y
y
y
ξ
α
α
α
α
+
+
+
+
=
−
−
−
3
3
2
2
1
1
0
,

c)
t
t
t
t
x
x
y
ξ
γ
α
α
+
+
+
=
−1
1
1
0
,
d)
t
t
t
t
y
ξ
β
β
β
+
+
+
=
2
2
1
0
.
Zadanie 1.5
Dokonaj klasyfikacji poniższych modeli, nazwij wszystkie zmienne występujące w tych
modelach i zapisz te modele w postaci macierzy.
a)
10
,...,
2
,
1
,
1
0
=
+
+
=
t
x
y
t
t
t
ξ
β
β
gdzie: y
t
– miesięczne zużycie paliwa przez autobusy ZKM (w litrach), x
t
– liczba kilometrów
przejechanych przez autobusy w ciągu miesiąca;
b)
25
,...
2
,
1
,
=
+
+
+
=
t
z
y
p
t
t
t
t
ξ
γ
β
α
;
gdzie: p
t
–
c)
24
,....,
2
,
1
,
,
2
2
1
1
0
=
+
+
+
=
−
−
t
y
y
y
t
t
t
t
ε
δ
δ
δ
,
gdzie: y
t
– miesięczne wynagrodzenie netto w sektorze prywatnym (w złotych),
d)
1,2,...,18
t
,
1
2
1
0
=
+
+
=
t
t
w
t
λ
λ
λ
;
gdzie: w
t
– wielkość zapasów
e)
32
,...,
2
,
1
,
2
1
0
=
=
t
Z
M
Q
t
t
t
β
β
β
;
gdzie:
Q
t
– wielkość produkcji stoczni Gdynia (w mln zł),
M
t
– wartość majątku trwałego stoczni
w cenach stałych (w mln zł),
Z
t
– liczba osób zatrudnionych w stoczni (w osobach).
f)
{
}
20
,...,
2
,
1
,
1
0
=
=
+
+
t
e
u
t
t
t
ξ
α
α
,

Ćwiczenia 2
Interpretacja parametrów przeciętnych, krańcowych i elastyczności.
Zadanie 2.1
Dana jest funkcja popytu konsumpcyjnego postaci:
t
t
t
x
y
ξ
β
β
+
+
=
1
0
, gdzie:
y
t
- wydatki
gospodarstw domowych na pewne dobro,
x
t
- przeciętna wielkość dochodu na gospodarstwo
domowe. Wyznacz i zinterpretuj elastyczność dochodową wydatków.
Zadanie 2.2
Dla danych z okresu 1989-1999 oszacowano funkcję produkcji i otrzymano następującą postać:
t
t
t
Z
M
Q
ln
ˆ
ln
ˆ
ˆ
ˆ
ln
2
1
0
α
α
α
+
+
=
gdzie Q
t
- produkcja (w mln zł), M
t
- nakłady majątku trwałego (w mln zł), Z
t
- nakłady siły
roboczej (w tysiącach osób).
a) Zapisz model w postaci pierwotnej i sklasyfikuj go.
b) Sklasyfikuj zmienne występujące w modelu.
c) Zinterpretuj oceny parametrów strukturalnych.
d) Wyznacz elastyczność produkcji względem nakładów majątku trwałego.
Zadanie 2.3
Oszacowano parametry strukturalne liniowego modelu popytu na pieczywo i otrzymano
następujące wyniki:
t
t
c
p
45
,
0
250
ˆ
−
=
gdzie p
t
- tygodniowe spożycie pieczywa w gospodarstwie domowym, c
t
- średnia cena pieczywa
za dekagram.
a) Czy jest to regresja szeregu czasowego czy regresja szeregu przekrojowego?
b) Sporządź wykres linii regresji.
c) Zinterpretuj wyraz wolny. Określ, czy ta interpretacja ma sens ekonomiczny?
d) Zinterpretuj współczynnik nachylenia. Jaki jest związek tego współczynnika z parametrem
określanym jako krańcowy?
e) Oblicz i zinterpretuj elastyczność cenową dla dowolnego poziomu ceny pieczywa c
0
=10.
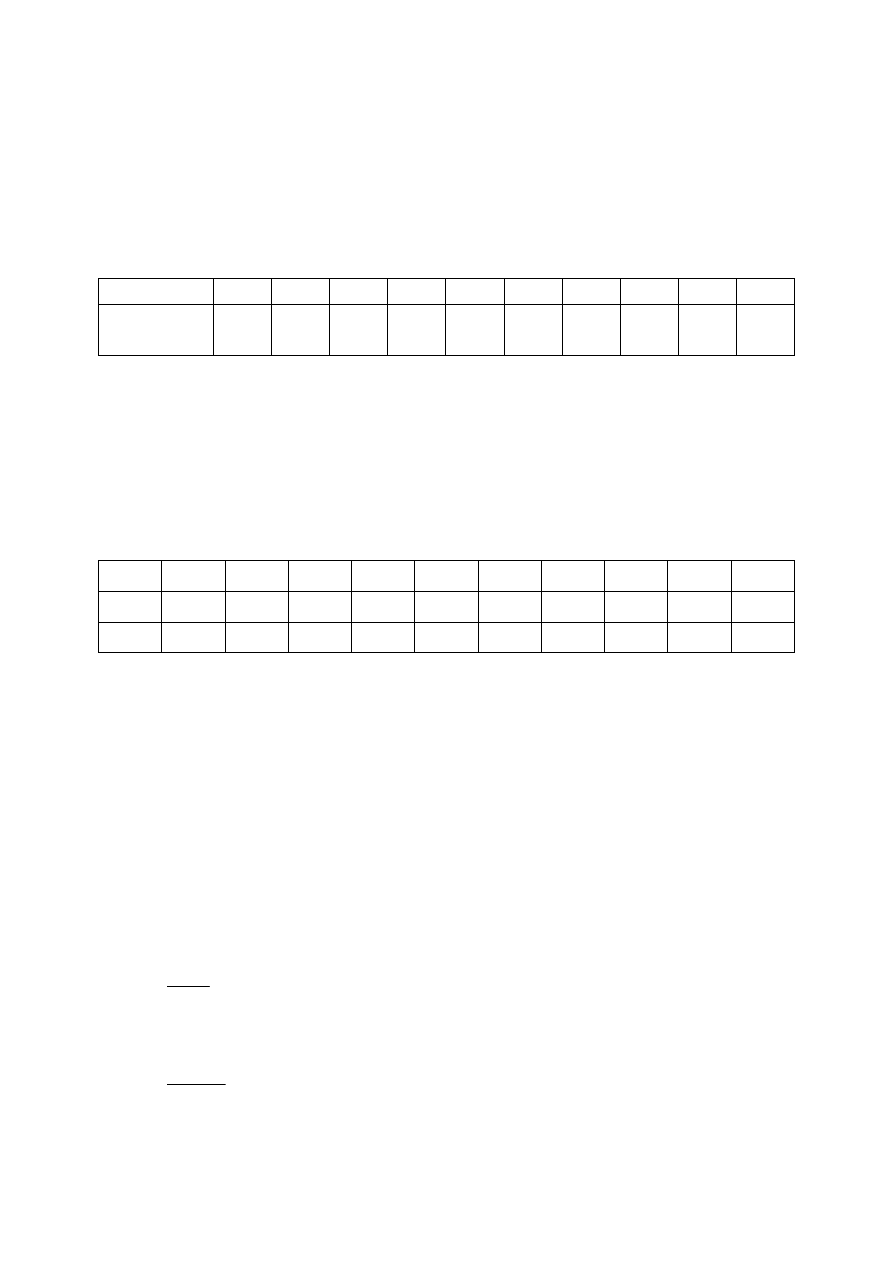
Zadanie 2.4
Na podstawie danych zamieszczonych w tablicy dobierz postać analityczną modelu tendencji
rozwojowej, wyznacz średnią roczną stopę wzrostu liczby absolwentów.
Tablica 2.1: Liczba absolwentów szkół wyższych w Polsce w latach
Rok
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
Absolwenci
(w tys. osób)
61,4
64,2
70,3
89
115,9
150,3
192
229,1
304
342,1
Źródło: Rocznik Statystyczny GUS 2002.
Zadanie 2.5
W tablicy zamieszczono dane dotyczące wielkości dochodów d
t
i wydatków w
t
przypadających
na osobę w przeciętnym gospodarstwie domowym (w zł).
Tablica 2.2
00Q1
00Q2
00Q3
00Q4
01Q1
01Q2
01Q3
01Q4
02Q1
02Q2
d
t
430
444
484
500
510
522
515
528
545
560
w
t
67
69
82
82
87
89
91
90
96
100
Źródło: dane umowne.
Czy
w
przypadku
tych
szeregów
można
zastosować
krzywą
Engla
postaci:
t
t
t
d
w
ξ
β
β
+
+
=
ln
1
0
?
Jakie są zalety i wady tej relacji? Jaką interpretację ekonomiczną mają parametry strukturalne?
Zadanie 2.6
Omów właściwości następujących funkcji i sporządź ich wykresy. W jaki sposób można
doprowadzić je do postaci funkcji liniowej?
a)
1
0
α
α
t
t
x
y
=
,
b)
b
x
ax
y
t
t
t
+
=
,
c)
t
x
t
e
y
1
0
β
β +
=
,
d)
ct
t
be
a
y
−
+
=
1
.
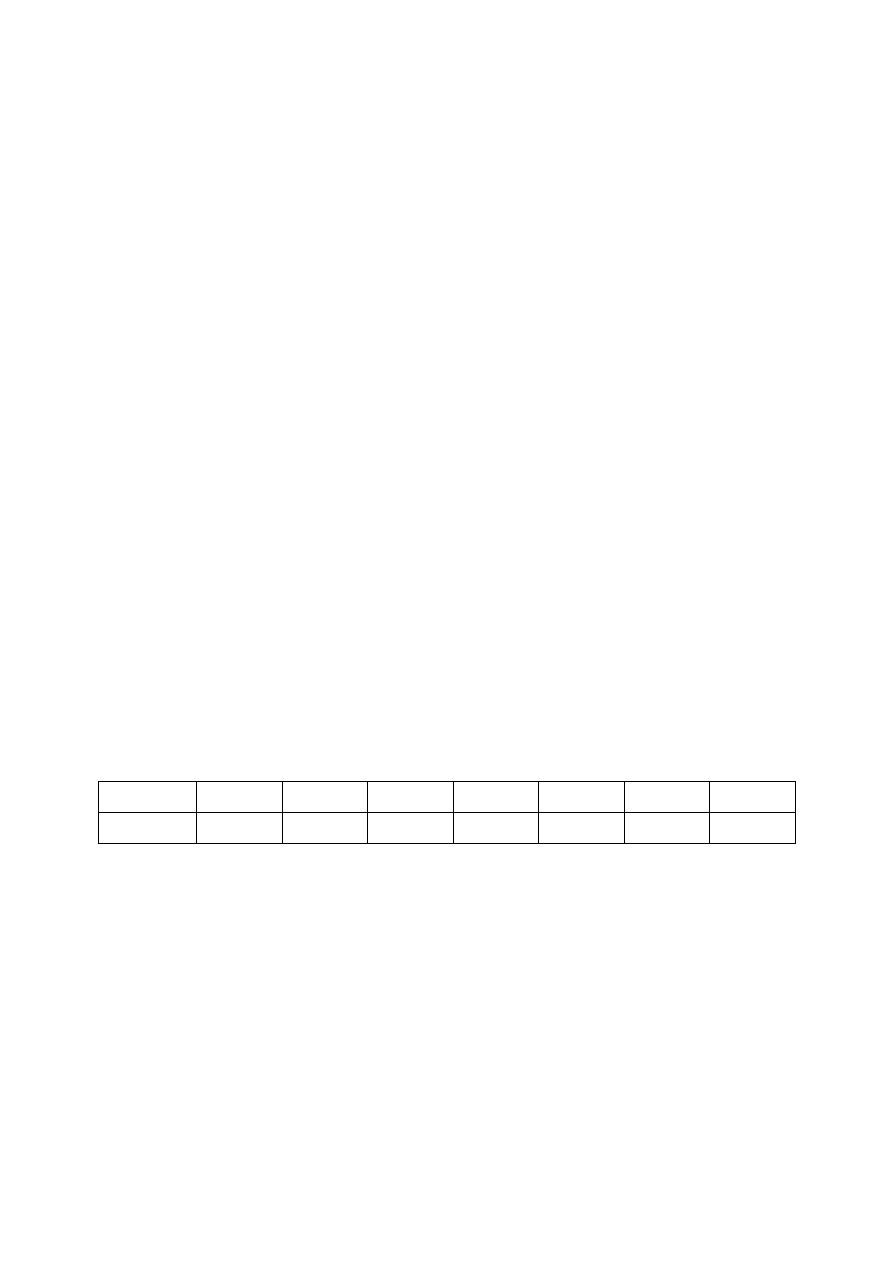
Ćwiczenia 3
Estymacja parametrów strukturalnych modelu za pomocą MNK.
Zadanie 3.1
Dany jest model ekonometryczny postaci:
t
t
t
t
x
x
y
ξ
β
β
β
+
+
+
=
2
2
1
1
0
. W oparciu o założenia
numeryczne MNK, zaproponuj najmniejszą możliwą liczbę obserwacji.
Zadanie 3.2
Czy można zastosować estymator MNK do wyznaczenia ocen parametrów strukturalnych
modelu
t
t
t
t
x
x
y
ξ
β
β
β
+
+
+
=
2
2
1
1
0
mając dane następujące macierzy obserwacji:
=
=
15
11
8
9
3
1
6
2
1
3
1
1
y
X
.
Zadanie 3.3
Za pomocą estymatora MNK oszacuj parametry strukturalne modelu
t
t
t
x
y
ξ
β
β
+
+
=
1
0
, gdzie y
t
– wartość lokat zdeponowanych w pewnym banku w tys.zł, x
t
– wysokość stopy oprocentowania
depozytów w %, wiedząc że:
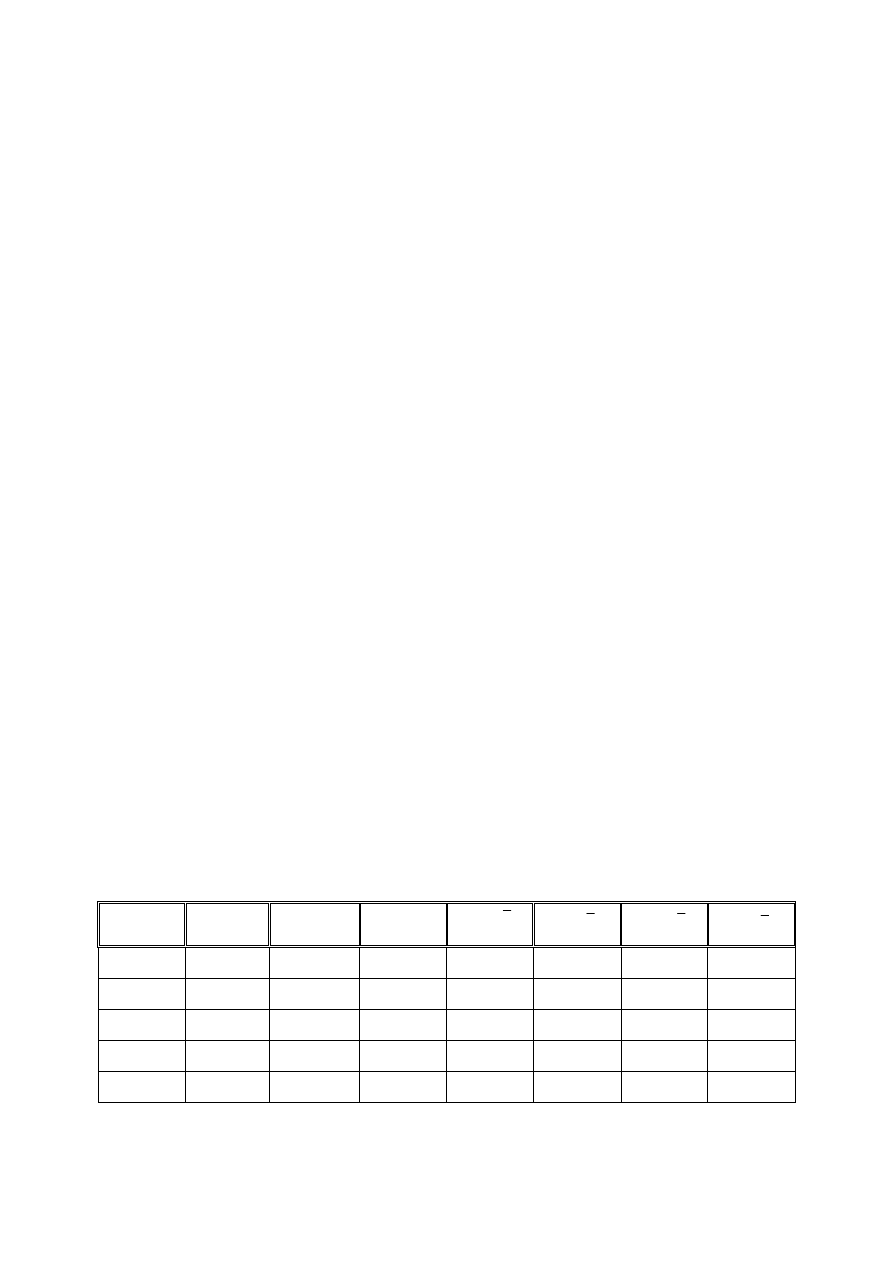
Tablica 3.1
y
t
(w tys.zł)
10
10
8
7
5
3
3
x
t
(w %)
5
5
4
4
3
3
2
Źródło: dane umowne.
Zadanie 3.4
Mając dane macierze:
=
=
0
64
30
10
10
14
y
X
X
T
a) oszacuj parametry strukturalne modelu postaci:
t
t
t
x
y
ξ
β
β
+
+
=
1
0
,
b) oblicz i zinterpretuj parametr krańcowy,
c) oblicz i zinterpretuj elastyczność cząstkową.
Zadanie 3.5
Mając dane macierze:
=
−
−
−
=
−
210
120
100
30
5
25
,
0
?
20
53
,
13
?
?
781
,
16
)
(
1
y
X
X
T
a) oszacuj parametry strukturalne modelu postaci:
t
t
t
t
x
x
y
ξ
β
β
β
+
+
+
=
2
2
1
1
0
,
b) oblicz i zinterpretuj parametry krańcowe,
c) oblicz i zinterpretuj elastyczności cząstkowe.
Zadanie 3.7
Oszacuj za pomocą metody najmniejszych kwadratów parametry strukturalne modelu postaci:
t
t
t
x
y
ξ
β
β
+
+
=
1
0
, wiedząc, że :
25
10
31
4
10
1
10
1
10
1
2
10
1
=
=
=
=
∑
∑
∑
∑
=
=
=
=
t
t
t
t
t
t
t
t
t
y
x
y
x
x
Ćwiczenia 4
Weryfikacja modelu ekonometrycznego – syntetyczne miary dopasowania
Zadanie 4.1
Uzupełnij poniższą tabelę, wykorzystując wyniki estymacji modelu postaci:
t
t
t
x
y
ξ
β
β
+
+
=
1
0
.
Tablica 4.1
t
y
t
x
t
yˆ
t
ξ
ˆ
(
)
y
y
t
−
(
)
2
y
y
t
−
(
)
y
y
t
ˆ
ˆ
−
(
)
2
ˆ
ˆ
y
y
t
−
12
1
10
2
9
3
9
4
7
5
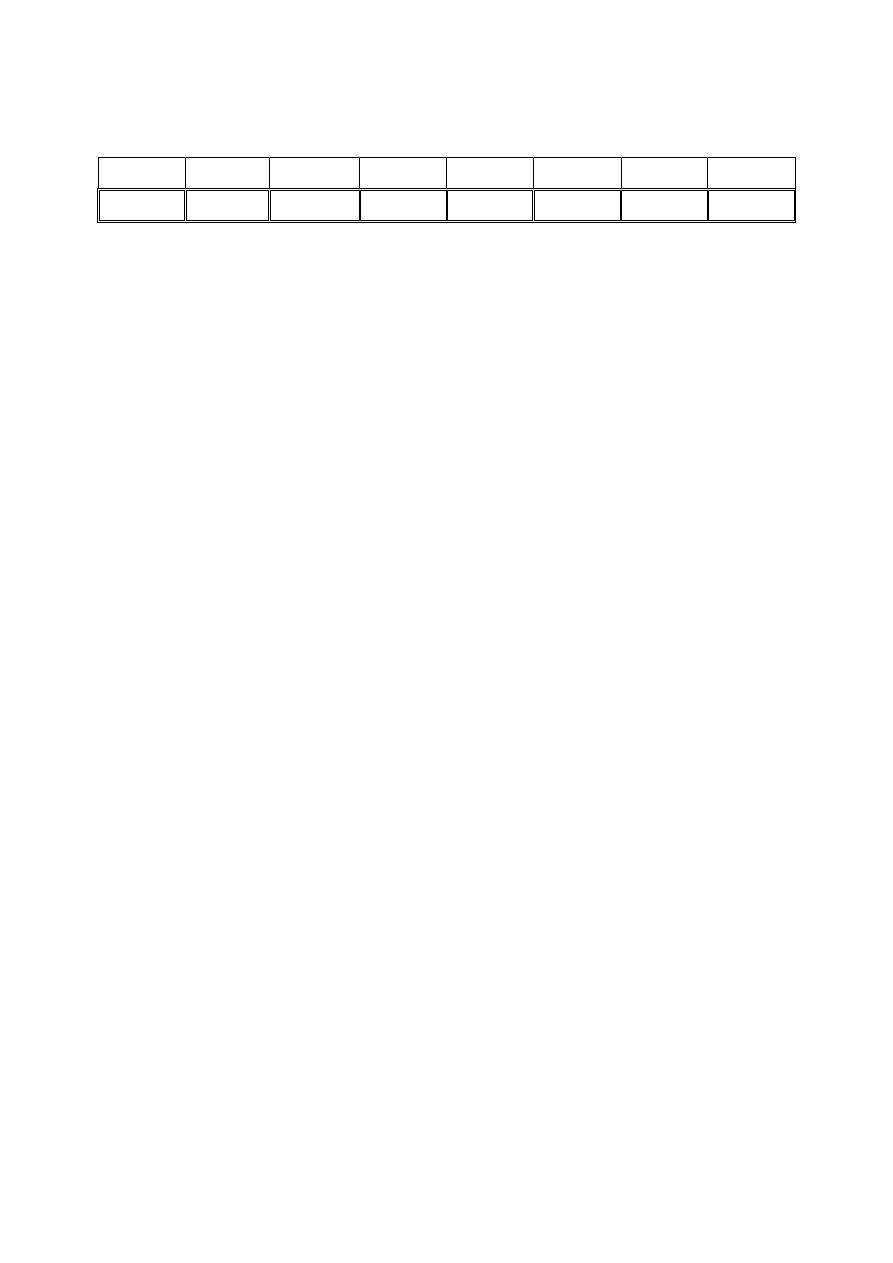
8
6
a) Zapisz oszacowaną postać modelu.
b) Oblicz i zinterpretuj odchylenie standardowe składnika resztowego.
c) Oblicz średnie błędy szacunku parametrów strukturalnych.
d) Oblicz i zinterpretuj współczynnik zmienności losowej.
e) Oblicz i zinterpretuj współczynniki: determinacji i zbieżności.
Zadanie 4.2
Zmienne endogeniczne
1
t
y i
2
t
y przybierały w analizowanym okresie następujące wartości:
1
t
y -
4, 6, 8, 11, 11, 10 oraz
2
t
y - 22, 25, 24, 21, 26,30. Dla obu zmiennych oszacowano modele i
otrzymano w obu przypadkach identyczny ciąg reszt:
t
ξ
ˆ - 2, 1, 0, -1, -3, 1. Który z modeli jest
lepiej dopasowany?
Zadanie 4.3
Mając dane wyniki obserwacji
t
y : 4, 3, 0, 1, 2, współczynnik determinacji
715
,
0
2
=
R
oraz
wariancję resztową
95
,
0
ˆ
2
=
ξ
σ
, wskazać który z poniższych modeli w wyniku estymacji MNK
dał takie rezultaty.
a)
t
t
t
x
y
ξ
β
β
+
+
=
1
1
0
b)
t
t
t
t
x
x
y
ξ
β
β
β
+
+
+
=
2
2
1
1
0
c)
t
t
t
t
t
x
x
x
y
ξ
β
β
β
β
+
+
+
+
=
3
3
2
2
1
1
0
d)
t
t
t
t
t
t
x
x
x
x
y
ξ
β
β
β
β
β
+
+
+
+
+
=
4
4
3
3
2
2
1
1
0
Zadanie 4.4
Oszacowano liniowy model ekonometryczny postaci
t
t
t
t
t
x
x
x
y
ξ
β
β
β
β
+
+
+
+
=
3
3
2
2
1
1
0
i
otrzymano następujące wartości szeregu reszt:
Tablica 4.2

t
y
2
4
4
3
5
9
10
8
12
14
11
t
ξ
ˆ
0
-1
-2
3
3
0
1
2
-3
2
1
Źródło: dane umowne.
a) Oblicz i zinterpretuj odchylenie standardowe składnika resztowego.
b) Oblicz i zinterpretuj współczynnik zmienności losowej.
c) Oblicz i zinterpretuj współczynniki: determinacji i zbieżności.
Zadanie 4.5
Mając dane:
∑
∑
∑
∑
∑
=
=
=
=
=
=
220
210
80
60
25
20
2
2
t
t
t
t
t
t
y
y
x
y
x
x
T
,
a) oszacuj parametry strukturalne modelu postaci
t
t
t
x
y
ξ
β
β
+
+
=
1
0
,
b) oblicz i zinterpretuj średnie błędy szacunku parametrów strukturalnych,
c) oblicz i zinterpretuj syntetyczne miary dopasowania.
Wyszukiwarka
Podobne podstrony:
ekonometria mat aa4 mat aa4
ekonometria, mat aa2 mat aa2
ekonometria mat aa2 mat aa2
ekonomia mat, sem 1, mikroekonomia
ekonometria, mat aa3 mat aa3
ekonometria mat aa1 mat aa1
ekonometria, mat aa1 mat aa1
konspekt6 v2 mat dla stud 2[1], EKONOMIA
ZARZ DZANIE PRZEDSIEBIORSTWEM - MAT. DODATK.. DODATK, Ekonomia i zarządzanie
wmagania stawiane mat. opakowaniom-ściąga, Ekonomia
konspekt6 v2 mat dla stud[1], EKONOMIA
konspekt 6 mat stud, EKONOMIA
ek mat ii funkcja produkcji cobba douglasa, ekonomia
wmagania stawiane mat. opakowaniom-ściąga, Ekonomia, ekonomia
Wyklad2 mat
Mat 10 Ceramika
więcej podobnych podstron