Ekonometria

Wykład 1

Chow (1995):

„Ekonometria jest nauką i sztuką stosowania metod

statystycznych do mierzenia relacji ekonomicznych.”

Pawłowski (1978):

„Ekonometria jest nauką o metodach badania ilościowych

prawidłowości występujących w zjawiskach ekonomicznych

za

pomocą

odpowiednio

wyspecjalizowanego

aparatu

matematyczno-statystycznego.”

Hellwig (1973):

„Metody ekonometryczne - metody statystyczne i

matematyczne.”

Zastosowanie metod ekonomicznych jest możliwe w

przypadku spełnienia poniższych warunków:

Ekonometria

Wykład 1

Rodzaje danych:

Podstawowe zadania ekonometrii można podzielić na:

Model ekonometryczny

Narzędziem ekonometrycznym, służącym do analizy

zależności zachodzących między różnymi zjawiskami jest

model ekonometryczny.

Załóżmy następującą postać modelu:

)

,

(

ξ

x

f

y

=

Zmienna endogeniczna

y

jest to zmienna wyjaśniana przez

model.

Zmienna objaśniana y jest to zmienna wyjaśniana w danym

równaniu.

Zmienne objaśniające

x

to zmienne, które opisują

kształtowanie się zmiennej endogenicznej.

Zmienne egzogeniczne to takie zmienne objaśniające, które

występują w modelu w celu opisania kształtowania się

zmiennej

y

ale same nie są przedmiotem analizy.

Symbol

ξ

jest to składnik losowy.

Ekonometria

Wykład 1

W modelu występują dwa rodzaje parametrów:

♦ parametry strukturalne modelu

♦ parametry struktury stochastycznej modelu czyli parametry

rozkładu

ξ

modelu.

Etapy budowy modelu ekonometrycznego

Zasady interpretacji parametrów w modelach statycznych

3.1 Model liniowy

t

tk

k

t

t

t

x

x

x

y

ξ

β

β

β

β

+

+

+

+

+

=

...

2

2

1

1

0

T

t

,...,

1

=

czyli:

t

k

i

ti

i

t

x

y

ξ

β

β

+

+

=

∑

=1

0

Ekonometria

Wykład 1

wektor obserwacji na zmiennej endogenicznej oraz macierz

obserwacji na zmiennych egzogenicznych przyjmuj¹ postacie

odpowiednio:

Y

y

y

y

T

=

























1

2

:

,

X

x

x

x

x

x

x

x

x

x

k

k

T

T

Tk

=

























1

1

1

11

12

1

21

22

2

1

2

...

...

:

:

:

:

...

Interpretacja parametru

i

β

:

Jeżeli zmienna

i

x

wzrośnie o jednostkę, a pozostałe

+zmienne objaśniające nie ulegną zmianie to zmienna

endogeniczna zmieni się średnio o

i

β

jednostek.

3.2 Modele sprowadzalne do liniowych

3.2.1 Model potęgowy

t

tk

t

t

t

k

x

x

x

y

ξ

β

β

β

β

⋅

⋅

=

...

2

1

2

1

0

T

t

,...,

1

=

lub

t

tk

k

t

t

t

x

x

x

y

ξ

β

β

β

β

ln

ln

...

ln

ln

ln

ln

2

2

1

1

0

+

+

+

+

+

=

Ekonometria

Wykład 1

Y

y

y

y

T

=

























ln

ln

:

ln

1

2

,

X

x

x

x

x

x

x

x

x

x

k

k

T

T

Tk

=

























1

1

1

11

12

1

21

22

2

1

2

ln

ln

...

ln

ln

ln

... ln

:

:

:

:

ln

ln

... ln

Interpretacja parametru

i

β

:

Jeżeli zmienna

i

x

wzrośnie o 1%, a pozostałe zmienne

objaśniające nie ulegną zmianie to zmienna endogeniczna

zmieni się średnio o

i

β %.

3.2.2 Model wykładniczy

t

tk

k

t

t

x

x

x

t

e

y

ξ

β

β

β

β

+

+

+

+

+

=

...

2

2

1

1

0

T

t

,...,

1

=

y

e

t

x

i i

t

i

k

=

∑

+

+

=

{

}

β

β

ξ

0

1

w postaci liniowej:

t

tk

k

t

t

t

x

x

x

y

ξ

β

β

β

β

+

+

+

+

+

=

...

ln

2

2

1

1

0

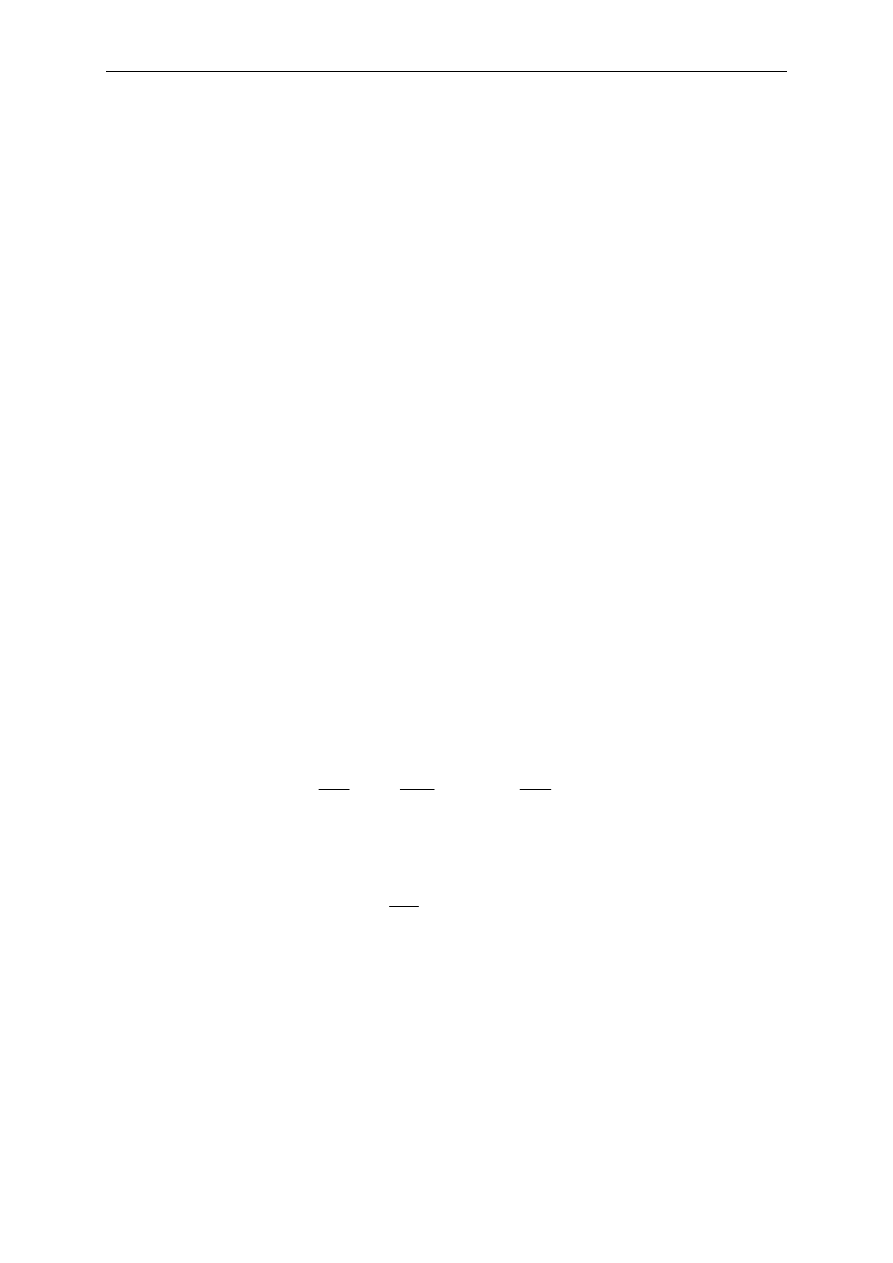
Ekonometria

Wykład 1

Y

y

y

y

T

=

























ln

ln

:

ln

1

2

,

X

x

x

x

x

x

x

x

x

x

k

k

T

T

Tk

=

























1

1

1

11

12

1

21

22

2

1

2

...

...

:

:

:

:

...

Interpretacja parametru

i

β :

Jeżeli zmienna

i

x

wzrośnie o jednostkę, a pozostałe

zmienne objaśniające nie ulegną zmianie to zmienna

endogeniczna zmieni się średnio o

(

)

e

i

β

− ∗

1 100%

czyli w

przybliżeniu

i

β

∗

100%

3.2.3 Model logistyczny

t

tk

x

k

t

x

t

x

x

t

e

y

ξ

β

β

β

β

+

+

+

+

+

=

1

2

1

2

1

1

1

0

...

T

t

,...,

1

=

y

e

t

x

i

ti

t

i

k

=

∑

+

+

=

{

}

β

β

ξ

0

1

1

w postaci liniowej:

Ekonometria

Wykład 1

t

tk

k

t

t

t

x

x

x

y

ξ

β

β

β

β

+

+

+

+

+

=

1

...

1

1

ln

2

2

1

1

0

Y

y

y

y

T

=

























ln

ln

:

ln

1

2

,

X

x

x

x

x

x

x

x

x

x

k

k

T

T

Tk

=









































1

1

1

1

1

1

1

1

1

1

1

1

11

12

1

21

22

2

1

2

...

...

:

:

:

:

...

Interpretacja parametru

i

β

:

Brak interpretacji bezpośredniej. W takim przypadku liczy

się i interpretuje elastyczność.

Miary przeciętne i krańcowe

Załóżmy, że obserwujemy zmienne

t

y

oraz

tk

t

t

x

x

x

,...,

,

2

1

♦ Miary przeciętne

Parametr przeciętny:

ti

t

ti

t

x

y

)

x

,

y

(

*

PP

=

=

=

=

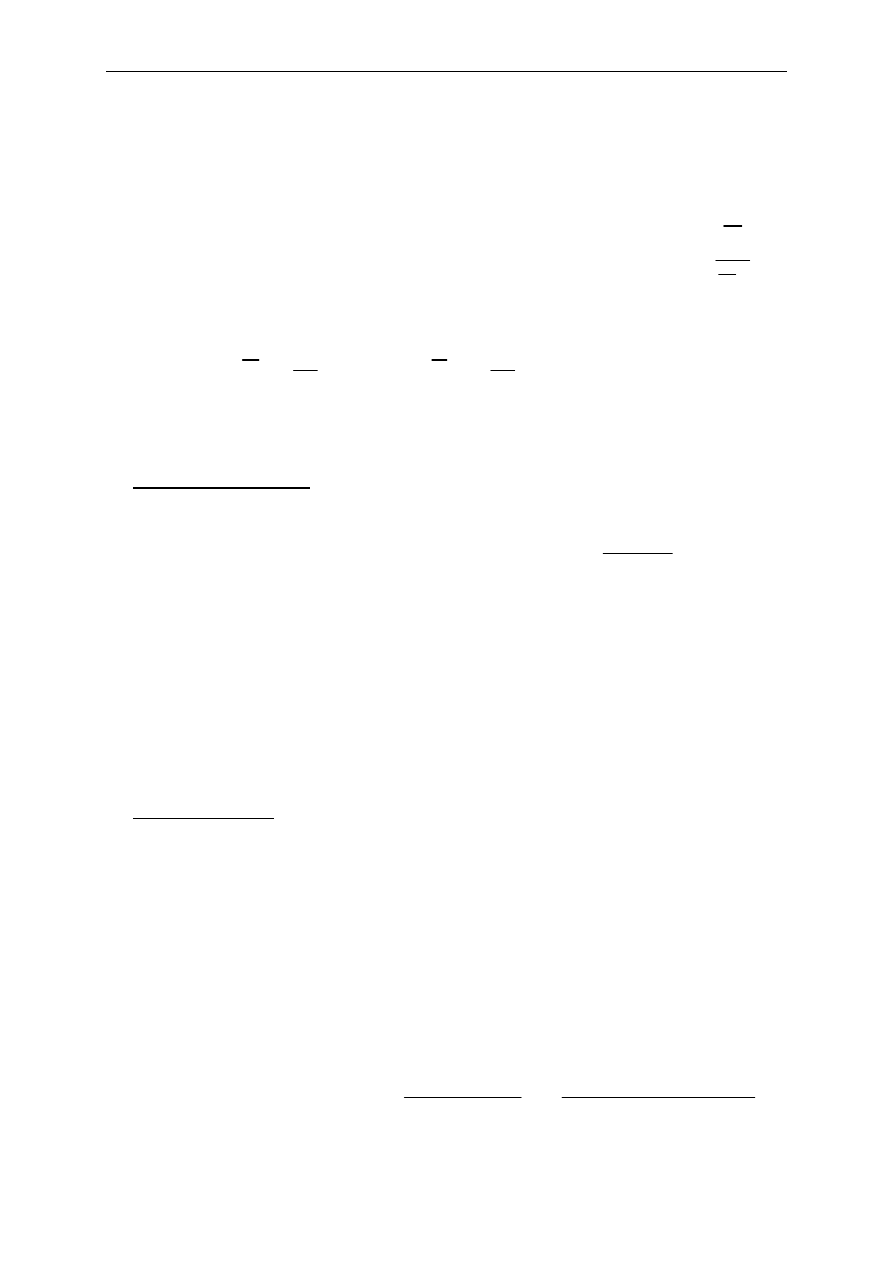
Ekonometria

Wykład 1

Określa ile jednostek jednej zmiennej przypada na jednostkę

drugiej zmiennej (w danym okresie).

Parametr przeciętny dla średnich

:

Gdzie:

♦ Miary krańcowe

Parametr krańcowy:

Gdzie:

Określa ile jednostek w okresie

t

wzrośnie (spadnie) zmienna

t

y

gdy zmienna

ti

x

wzrośnie o jednostkę.

♦ Elastyczność

Elastyczność różnicowa to stosunek relatywnego przyrostu

zmiennej

t

y

do relatywnego przyrostu zmiennej

ti

x

.

i

ti

t

x

y

)

x

,

y

(

*

PP

=

=

=

=

∑

∑

∑

∑

∑

∑

∑

∑

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

T

1

t

ti

i

T

1

t

t

x

T

1

x

,

y

T

1

y

ti

∆x

t

∆y

)

ti

x

,

t

(y

PK*

=

=

=

=

i

,

1

t

ti

ti

1

t

t

t

x

x

x

,

y

y

y

−

−

−

−

−

−

−

−

−

−

−

−

=

=

=

=

∆

∆

∆

∆

−

−

−

−

=

=

=

=

∆

∆

∆

∆

)

,

(

*

)

,

(

*

/

/

)

,

(

ti

t

ti

t

ti

ti

t

t

ti

t

x

y

PP

x

y

PK

x

x

y

y

x

y

E

=

∆

∆

=

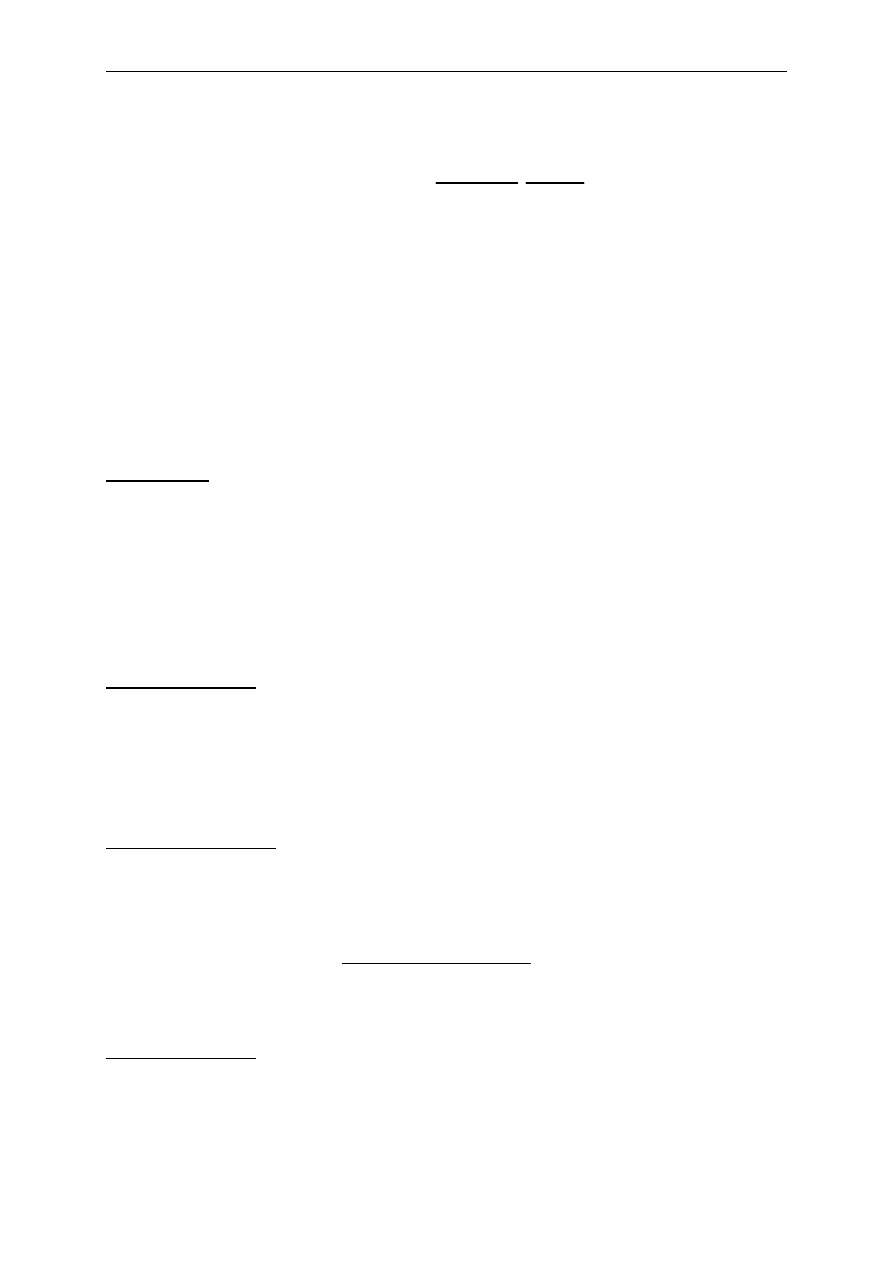
Ekonometria

Wykład 1

4. Prędkość i tempo zmian

4.1 Zmiany skokowe

- łańcuchowe

Szybkość (prędkość) - to różnica między wartością zmiennej y

w okresie t, a jej wartością w okresie t-1 . Służy do

obserwowania przyrostów bezwzględnych.:

S = y(t) - y(t-1)

interpretacja:

średnio z okresu t-1 do okresu t y wzrosło (spadło) średnio o S

jednostek.

Tempo zmian - służy do obserwowania przyrostów

względnych zmiennej

( )

(

)

(

)

T

y t

y t

y t

t

=

−

−

−

1

1

100%

interpretacja:

tempo zmian zmiennej y w okresie t w stosunku do okresu

poprzedniego wynosi T

t

%.

t

ti

ti

t

ti

t

y

x

x

y

)

x

,

y

(

E

∂

∂∂

∂

∂

∂∂

∂

=

=

=

=

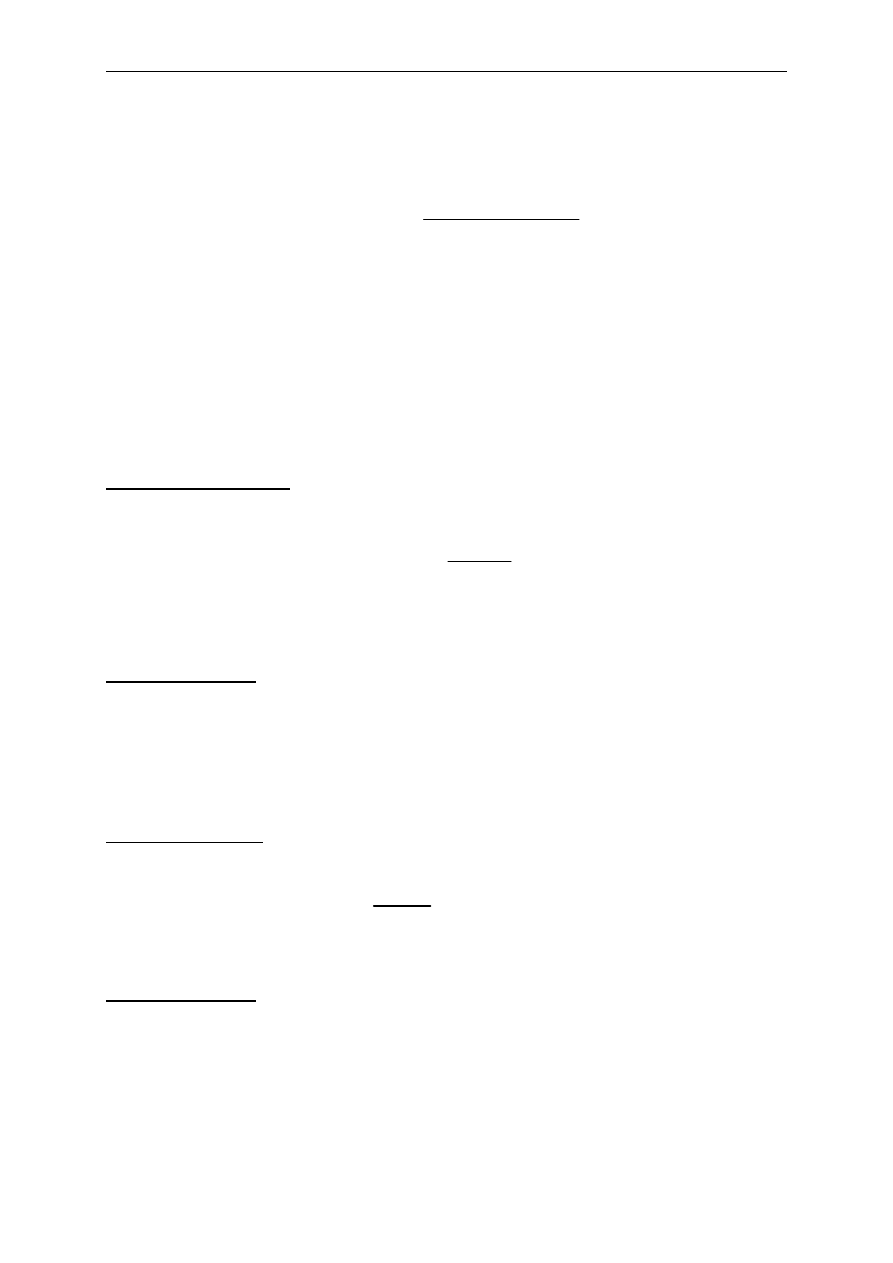
Ekonometria

Wykład 1

- jednopodstawowe

( )

( )

( )

( )

( )

S

y t

y t

T

y t

y t

y t

t

=

−

=

−

0

0

0

100%

;

,

gdzie t

0

oznacza okres przyjęty jako bazowy.

4.2 Zmiany ciągłe

Szybkość zmian:

S

y

x

t

ti

=

∂

∂

(

interpretacja:

średnio z okresu t-1 do okresu t y wzrosło (spadło) średnio o S

jednostek.

Tempo zmian:

%

100

y

/

x

y

T

t

ti

t

t

⋅⋅⋅⋅

∂

∂∂

∂

∂

∂∂

∂

=

=

=

=

interpretacja:

tempo zmian zmiennej y w okresie t w stosunku do okresu

poprzedniego wynosi T

t

%.