Mechanika teoretyczna

w 1

dr hab. inż. Włodzimierz Idczak,

konsultacje: ……………….

• wykłady - 30 godzin lekcyjnych

• ćwiczenia – 16 godzin lekcyjnych

• sylabus -e-dziekanat

• karta informacyjna przedmiotu - USOS

1

MT_SS - w 1

MT_SS - w 1

2

Literatura

Podstawowa

1. Jerzy Leyko – Mechanika ogólna, Statyka i kinematyka, tom 1,

PWN, Warszawa 2011

2. Ryszard Marian Janka – Podstawy mechaniki, Teoria i zagadnienia

metodyczne statyki, Uniwersytet Opolski, Opole 2007

3. Józef Giergiel, Mariusz Giergiel – Mechanika ogólna, Przykłady,

pytania i zadania, OW Politechniki Rzeszowskiej, Rzeszów 2009

4. Ludwik Janicki, Zdzisław Sawaniewicz – Poradnik, rozwiązywanie

zadań z mechaniki, cz. 1 – statyka, Wydawnictwo REA s.j.,
Warszawa 2006

MT_SS - w 1

3

Uzupełniająca

1. Edmund Wittbrodt, Stefan Saniak – Mechanika ogólna, teoria i

zadania, Wydawnictwo Politechniki Gdańskiej, Gdańsk 2010

2. Z. Dżygadło, S. Kaliski, L. Solarz, E. Włodarczyk – Drgania i Fale,

Część I, Drgania układów dyskretnych, skrypt WAT

3. Marian Klasztorny, Tadeusz Niezgoda – Mechanika Ogólna,

Podstawy teoretyczne, zadania z rozwiązaniami, Oficyna
Wydawnicza Politechniki Warszawskiej, Warszawa 2006

Rygory

• Egzamin pisemny –

możliwość egzaminu ustnego

• Dopuszczenie do egzaminu pisemnego

:

– zaliczenie ćwiczeń rachunkowych:

• zaliczenie 2 zadań domowych
• zaliczenie kolokwium

• Pytania egzaminacyjne –

będą opublikowane w CPP

4

MT_SS - w 1

Spis wykładów

Nr

wykładu

Treść wykładu

1.

Wprowadzenie; Klasyfikacja i definicje podstawowe;
Zasady statyki.

2.

Pojęcia podstawowe statyki: siła, rzut siły na oś i na
płaszczyznę, moment siły względem punktu i
względem osi, para sił.

3.

Twierdzenia statyki: wypadkowa układu sił w
metodzie analitycznej.

4.

Redukcja układu sił działających na ciało sztywne.

5

MT_SS - w 1

Nr

wykładu

Treść wykładu

5.

Warunki równowagi; Podpory.

6.

Metodyka rozwiązywania zagadnień technicznych.

7.

Zjawisko tarcia.

8.

Środki ciężkości; Momenty bezwładności.

9.

Metodyka rozwiązywania zagadnień statycznie
niewyznaczalnych

10. Kratownice; Metody rozwiązywania kratownic.

6

MT_SS - w 1

Nr

wykładu

Treść wykładu

11.

Kinematyka: ruch punktu materialnego i bryły
sztywnej.

12. Dynamika punktu materialnego i bryły sztywnej.

13.

Energia kinetyczna i energia potencjalna; Zasada
zachowania energii mechanicznej.

14. Drgania.

15. Współczynnik dynamiczności obciążenia.

7

MT_SS - w 1

Mechanika klasyczna

w-1

• Definicja
• Modele ciał materialnych
• „Klasyfikacja”
• Prawa mechaniki klasycznej
• Zasady statyki
• Treść zadania domowego nr 1.

8

MT_SS - w 1

MT_SS - w 1

9

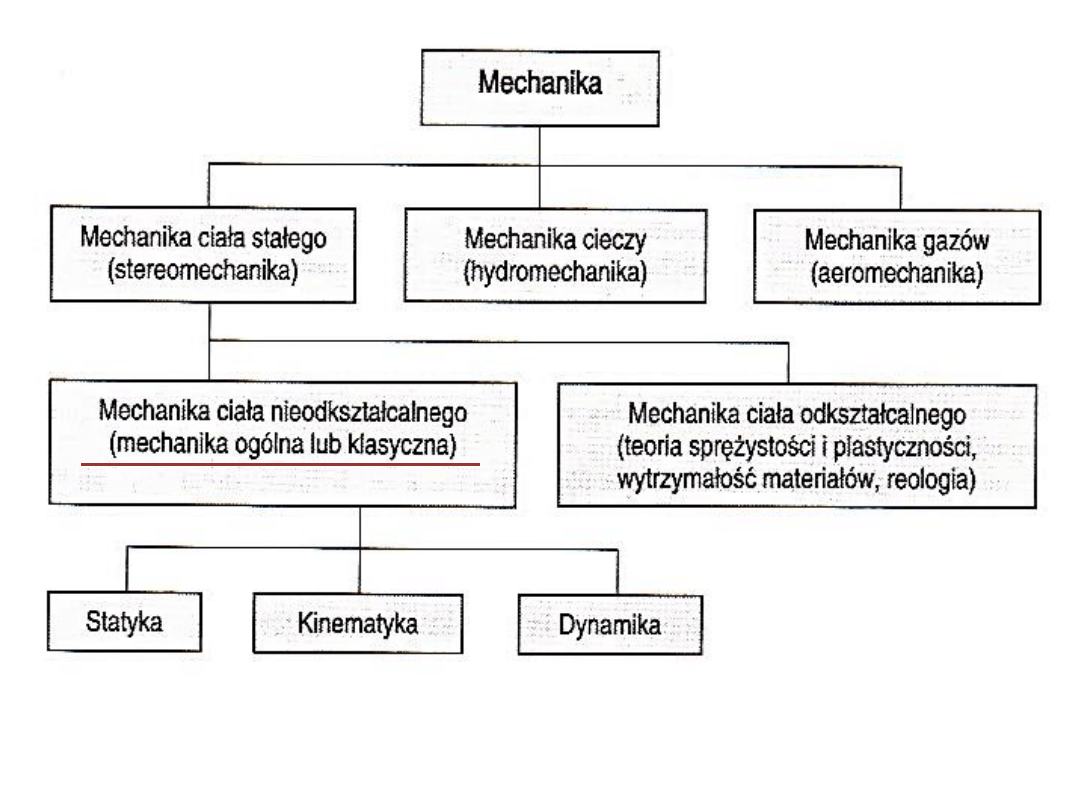
Mechanika ogólna (klasyczna):

• nauka o ruchu ciał materialnych

• zajmuje się:

– ustalaniem ogólnych praw ruchu ciał materialnych

– zastosowaniem tych praw do opisu pewnych

wyidealizowanych schematów ciał rzeczywistych

MT_SS - w 1

10

Schematy ciał materialnych:

• Punkt materialny

• Ciało doskonale sztywne

Punkt materialny

• Jest to model ciał o tak małych wymiarach w

porównaniu z wymiarami obszaru, w którym
ciało się porusza,

że

• można pominąć zmiany położenia tego ciała

wywołane przez obrót

i

• traktować to ciało jako punkt geometryczny,

któremu

• przypisujemy pewną skończoną ilość materii.

MT_SS - w 1

11

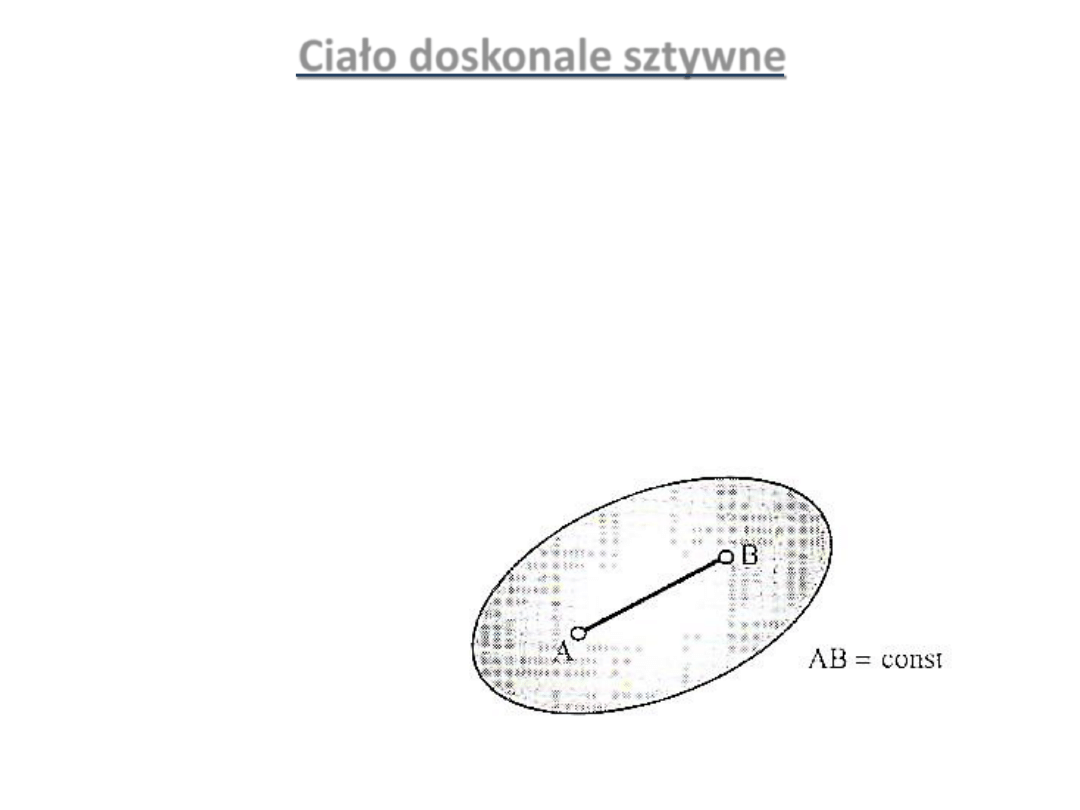
Ciało doskonale sztywne

• Jest to takie wyidealizowane ciało stałe,

którego

• punkty nie zmieniają wzajemnych odległości

• bez względu na oddziaływanie czynników

zewnętrznych

MT_SS - w 1

12

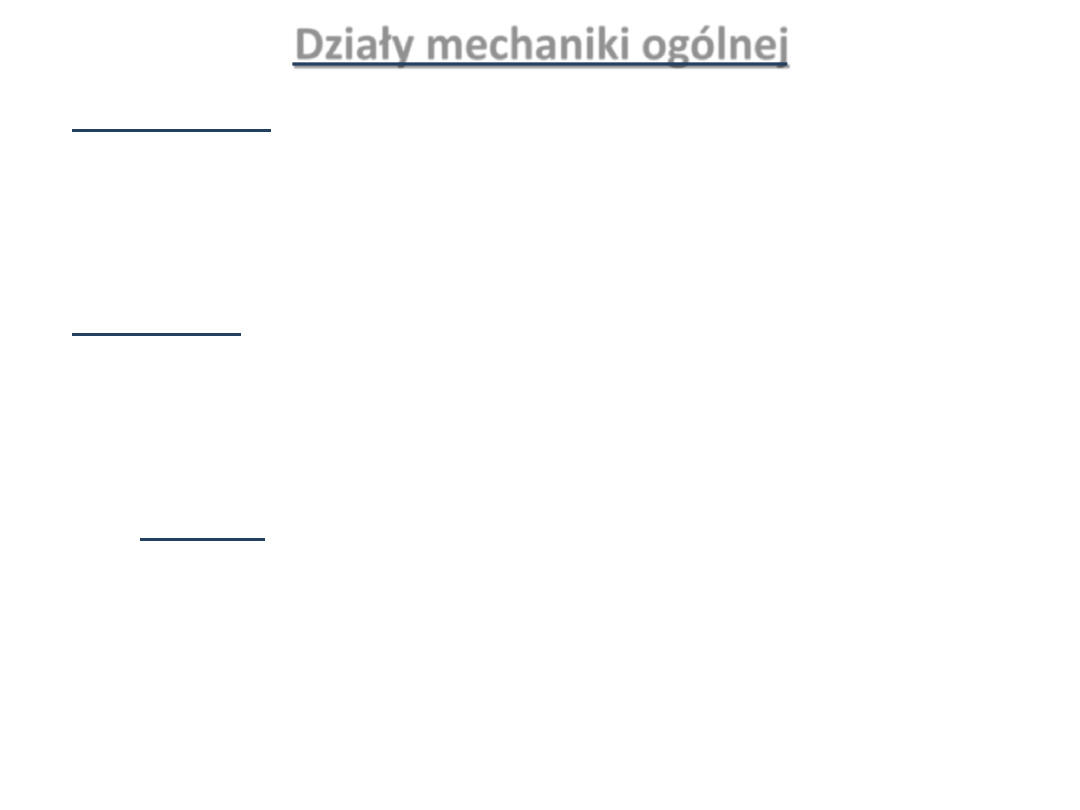
Działy mechaniki ogólnej

• Kinematyka

zajmuje się badaniem ilościowym ruchu ciał

niezależnie od czynników fizycznych

wywołujących ruch

• Dynamika

zajmuje się warunkami istnienia ruchu,

a więc rozpatruje ruch ciał materialnych

w zależności od sił działających na te ciała

Statyka

Jest częścią dynamiki dotyczącą tych

przypadków, w których działania wywierane

przez siły na ciało materialne znoszą się

wzajemnie, są więc w równowadze

MT_SS - w 1

13

Prawa mechaniki klasycznej

(Newton)

Dotyczą punktu materialnego poruszającego się pod

działaniem siły

PRAWO PIERWSZE

Punkt materialny, na który nie działa żadna siła, pozostaje w
spoczynku lub porusza się ruchem jednostajnym po linii
prostej

PRAWO DRUGIE

Przyśpieszenie

a punktu materialnego jest proporcjonalne

do siły P działającej na ten punkt i ma kierunek siły

m · a = P

m

– współczynnik proporcjonalności zwany masą

MT_SS - w 1

14

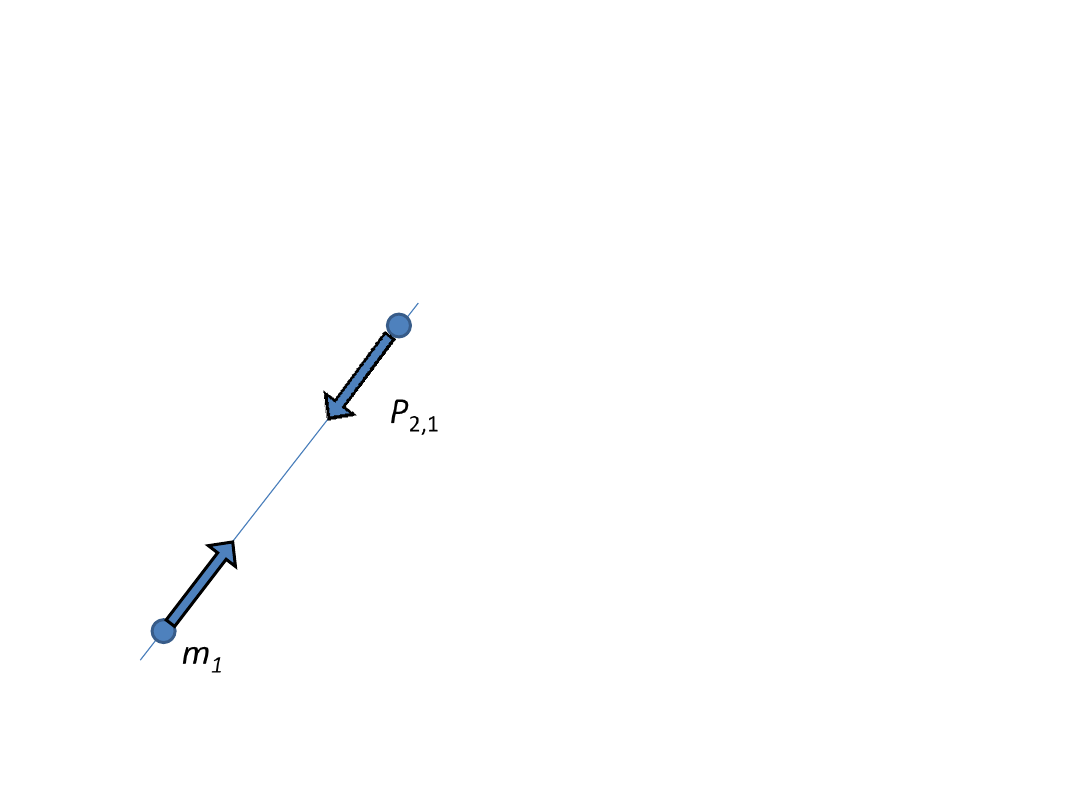
PRAWO TRZECIE

Siły wzajemnego oddziaływania dwóch punktów

materialnych są równe co do wartości i są przeciwnie

skierowane wzdłuż prostej łączącej oba punkty

MT_SS - w 1

15

m

2

P

1,2

P

1,2

= - P

2,1

P

1,2

= P

2,1

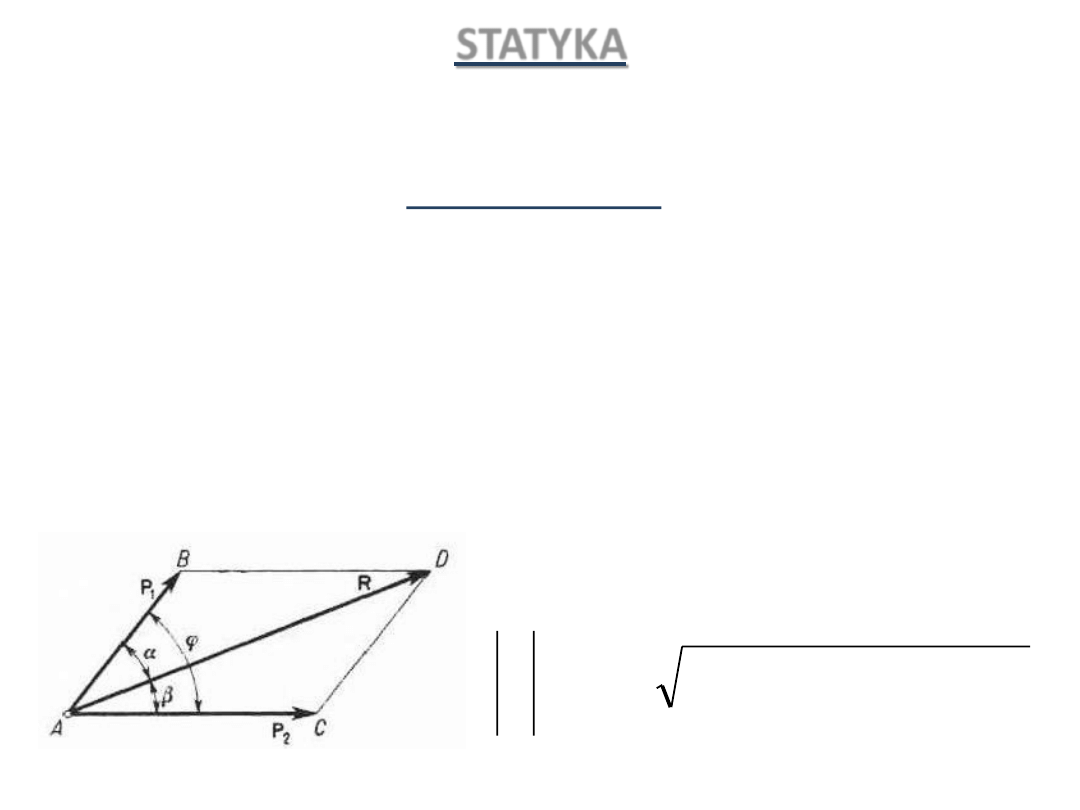
STATYKA

Równowaga ciał materialnych poddanych działaniom sił

Zasady statyki:

(6)

ZASADA RÓWNOLEGŁOBOKU SIŁ

Dowolne dwie siły P

1

i P

2

przyłożone do jednego punktu zastąpić możemy

siłą wypadkową R przyłożoną do tego punktu i przedstawioną jako wektor
będący przekątną równoległoboku ABCD zbudowanego na wektorach sił
danych.

MT_SS - w 1

16



cos

2

1

2

2

2

1

2

1

P

P

P

P

R

R

P

P

R





















MT_SS - w 1

17

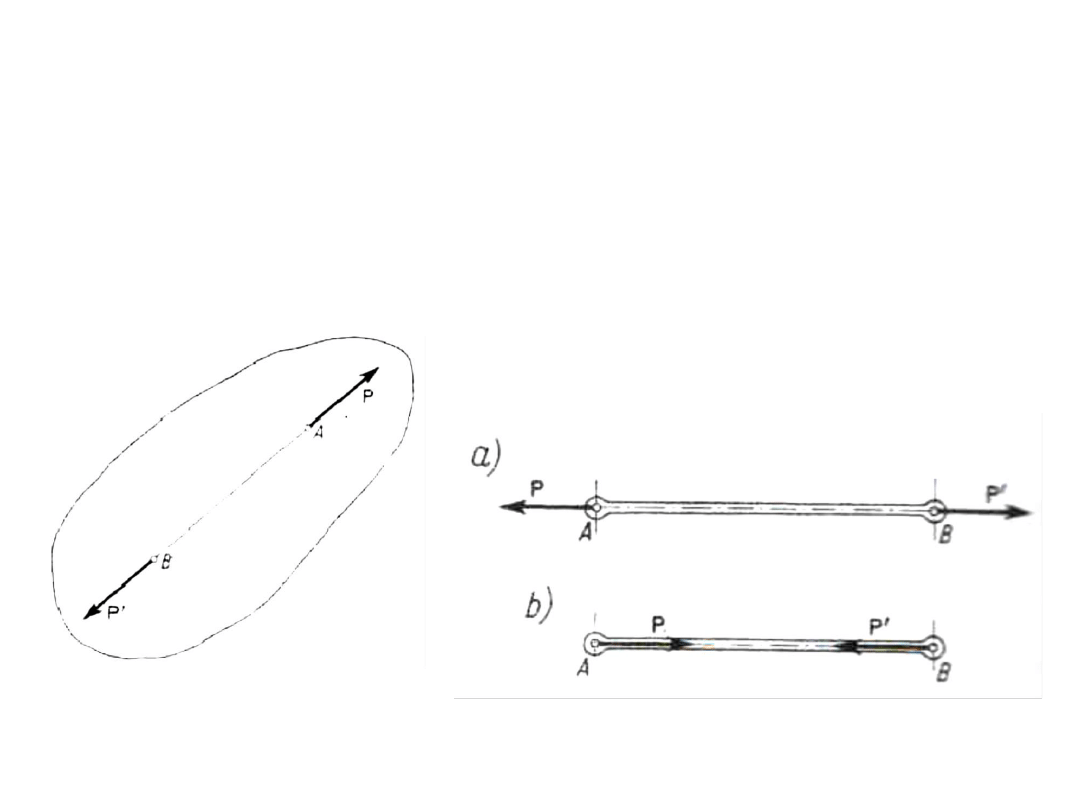
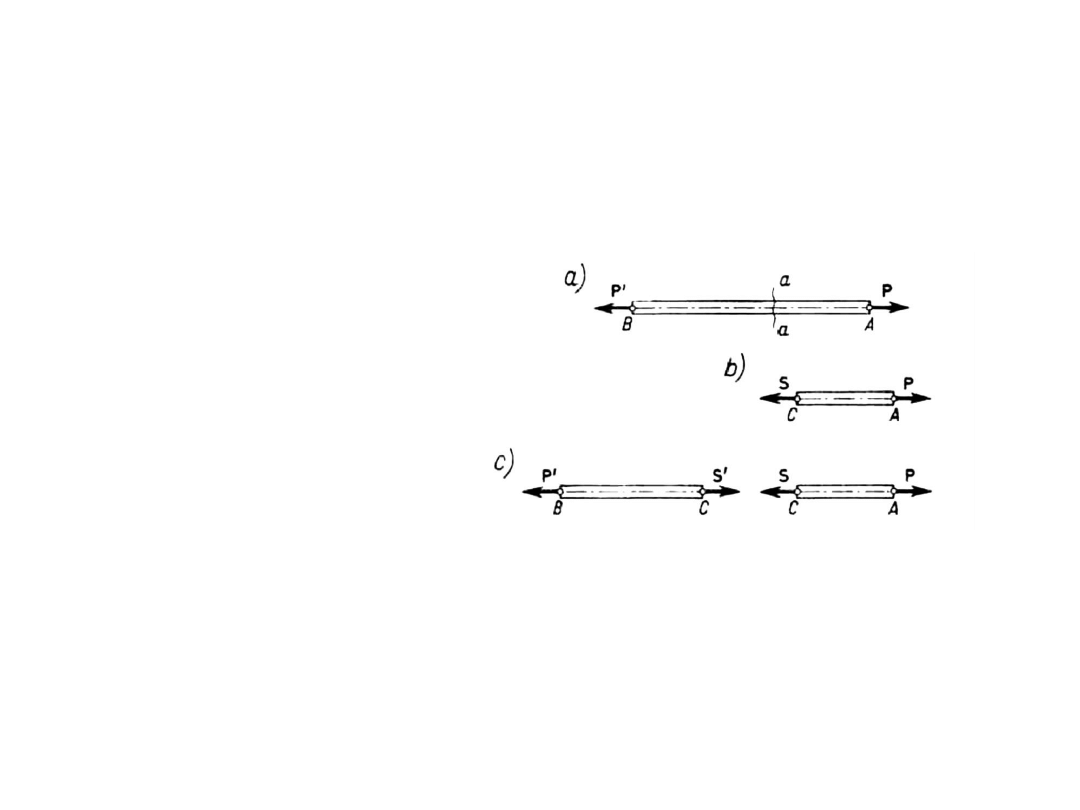
ZASADA RÓWNOWAGI DWÓCH SIŁ

Dwie siły przyłożone do ciała sztywnego równoważą się tylko wtedy,
gdy działają wzdłuż jednej prostej, są przeciwnie skierowane i mają te
same wartości liczbowe.

MT_SS - w 1

18

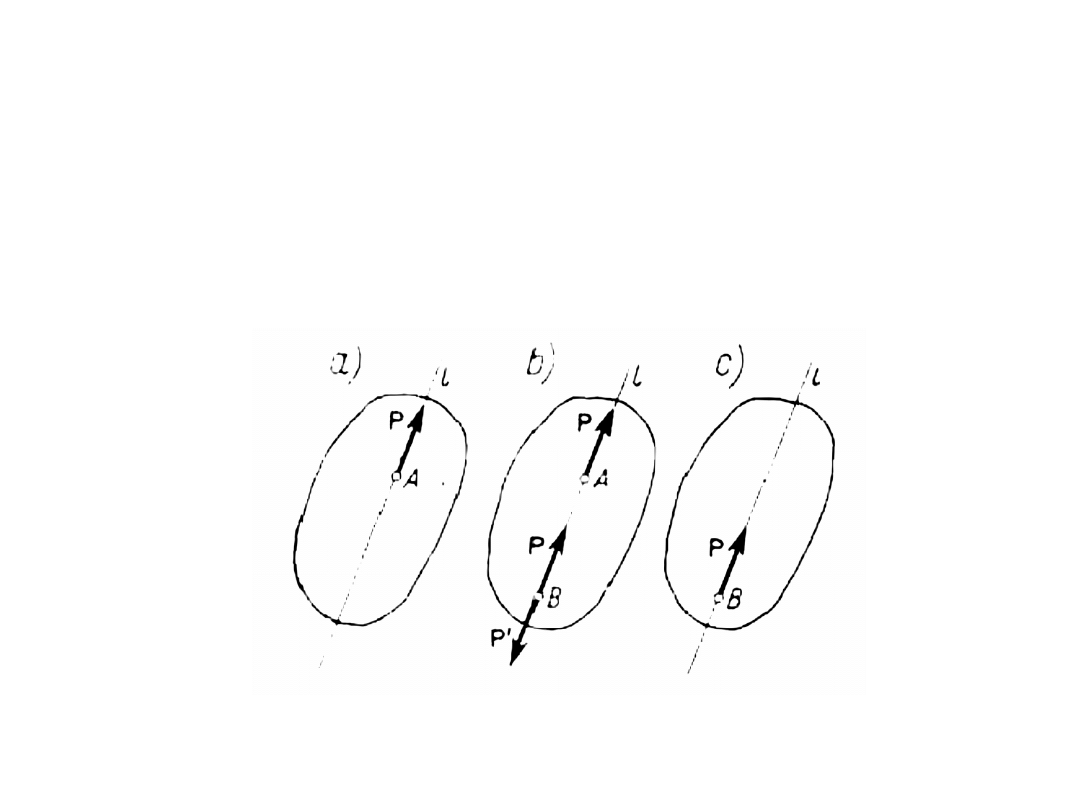
ZASADA NIEZALEŻNOŚCI DZIAŁANIA SIŁ

Działanie układu sił przyłożonych do ciała sztywnego nie ulegnie
zmianie, gdy do układu tego dodamy lub odejmiemy dowolny układ
równoważących się sił, czyli tzw. układ zerowy.

MT_SS - w 1

19

ZASADA ZESZTYWNIENIA

Równowaga sił działających na ciało odkształcalne nie zostanie
naruszona przez zesztywnienie tego ciała.

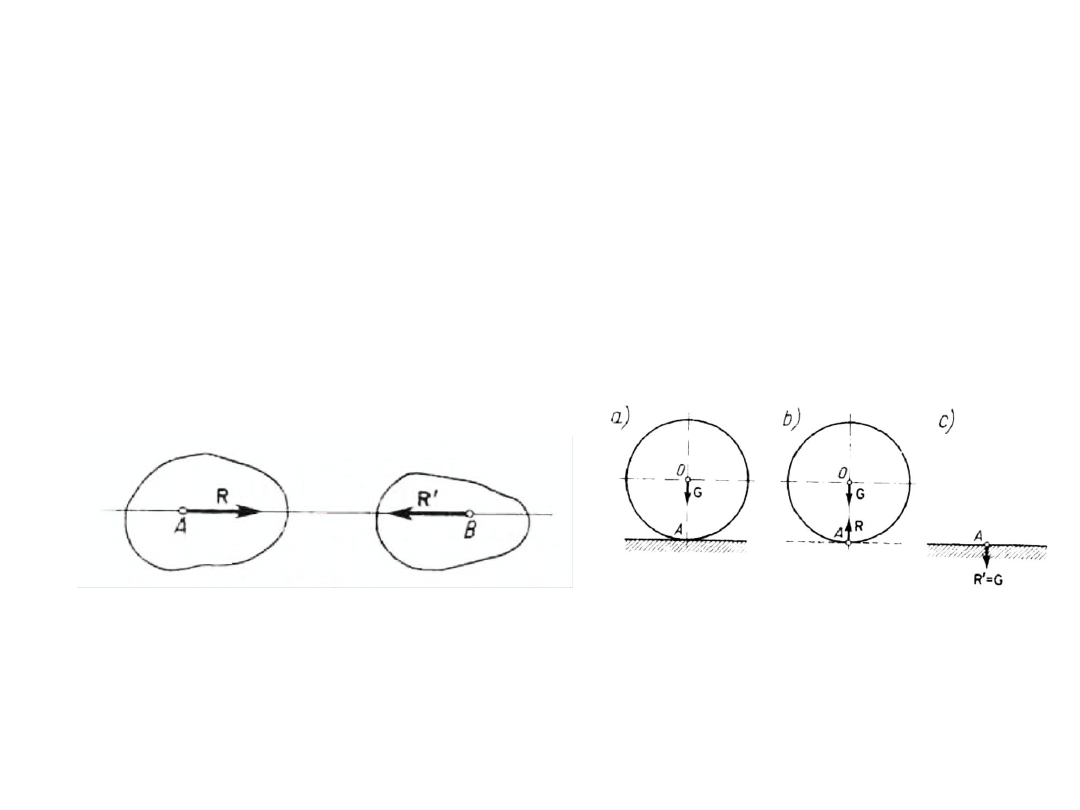
ZASADA AKCJI i REAKCJI

Każdemu działaniu towarzyszy równe co do wartości i przeciwnie
skierowane wzdłuż tej samej prostej przeciwdziałanie.

Siła z jaką ciało B działa na ciało A oznaczono przez R, a siłę z jaką
działa ciało A na ciało B oznaczono przez R’.

R = - R’ , R = R’

MT_SS - w 1

20

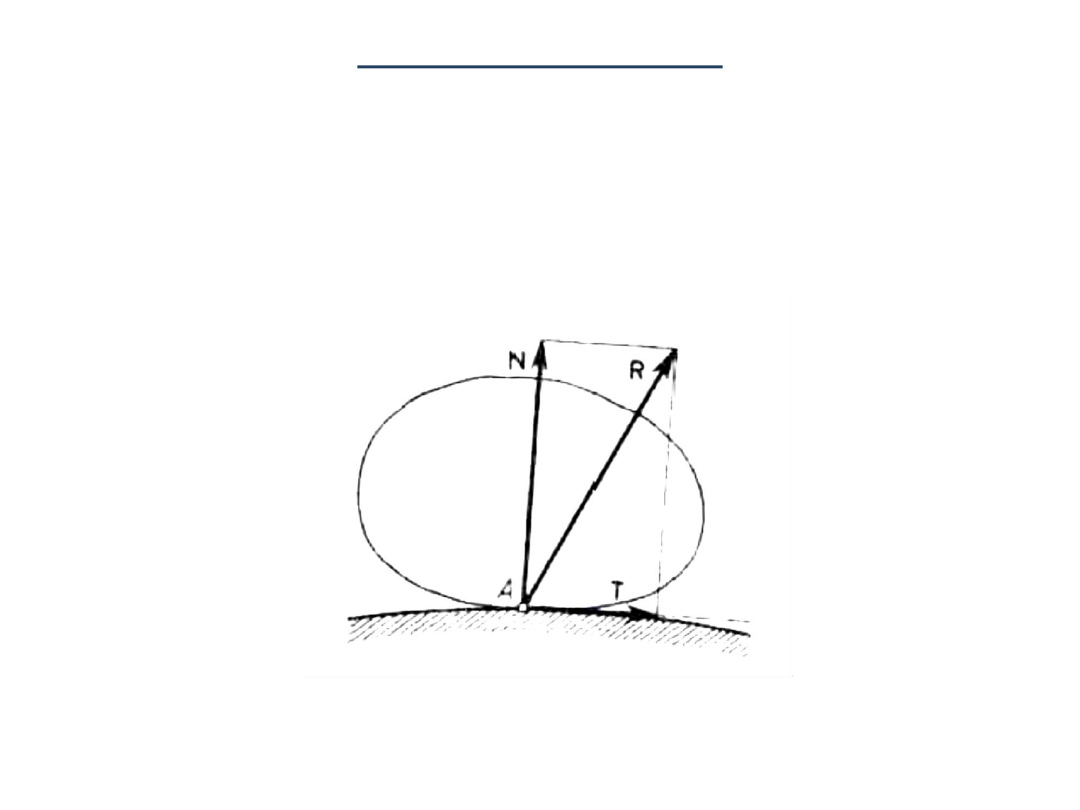
ZASADA OSWOBODZENIA OD WIĘZÓW

Każde ciało nieswobodne można

myślowo oswobodzić od więzów

zastępując przy tym ich działanie odpowiednimi reakcjami. Dalej
rozpatrywać można ciało tak, jak ciało swobodne podlegające
działaniu sił czynnych i sił reakcji

Więzami

nazywamy

ograniczenia ruchu ciała

przez stykanie się z

innymi ciałami. Takimi więzami są podpory tzn. elementy, za
pośrednictwem

których

element

konstrukcji

(

belka

,

rama

,

kratownica

,

łuk

, itp.) opiera się na fundamencie lub na innej

konstrukcji.

MT_SS - w 1

21

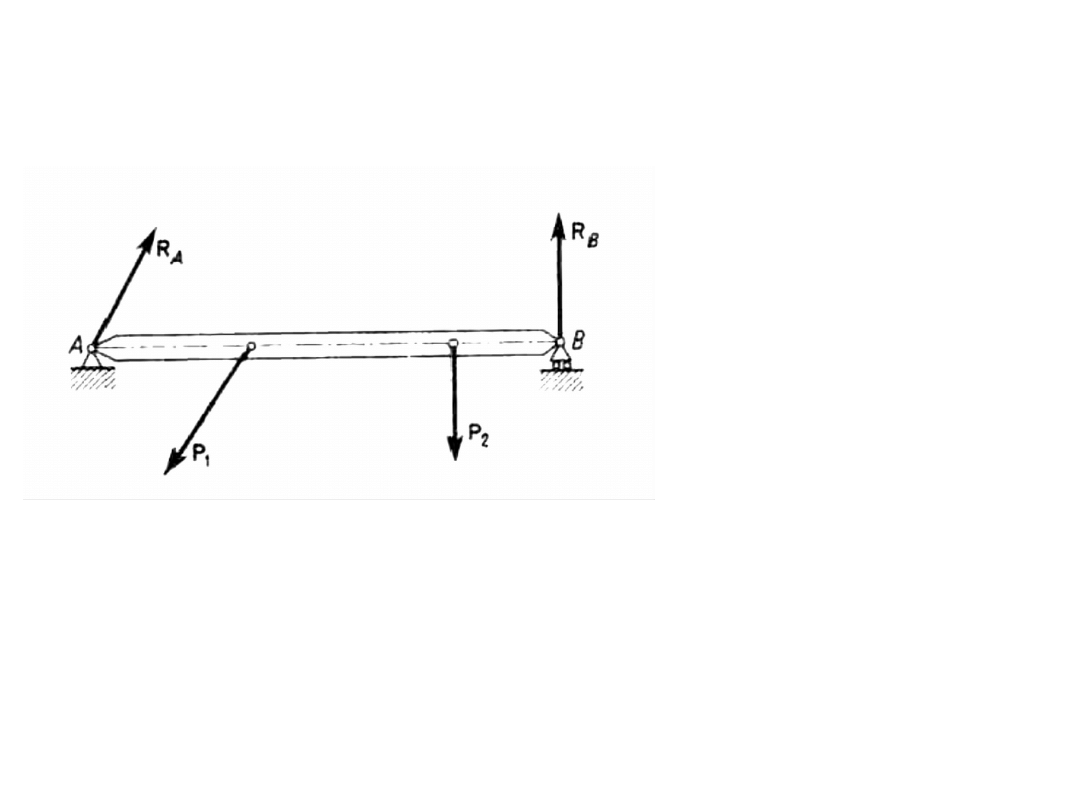
Więzy i ich reakcje

• Więzy idealne – więzy bez tarcia – T = 0

MT_SS - w 1

22

• Podpora przesuwna

(rolkowa)

• Podpora stała

(przegubowa)

B

– reakcja bez siły tarcia

(opór toczenia rolek pomijalnie mały)

A

- reakcja z dwoma składowymi

Wektor R

B

prostopadły do AB

MT_SS - w 1

23

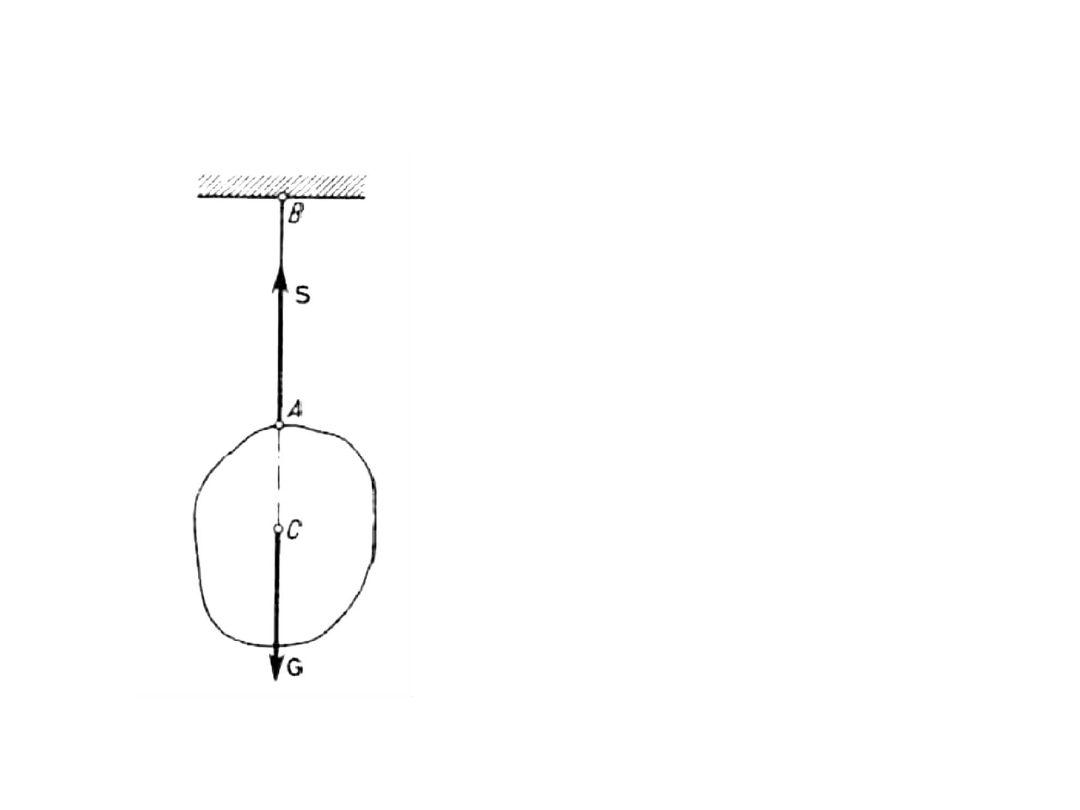
• Reakcja cięgna

Ciało zawieszone jest na cięgnie:
• nieważkim
• doskonale wiotkim

Cięgno nie stawia zatem oporu zginania

Reakcja „S” cięgna na ciało skierowana

wzdłuż cięgna

Cięgna są rozciągane

MT_SS - w 1

24

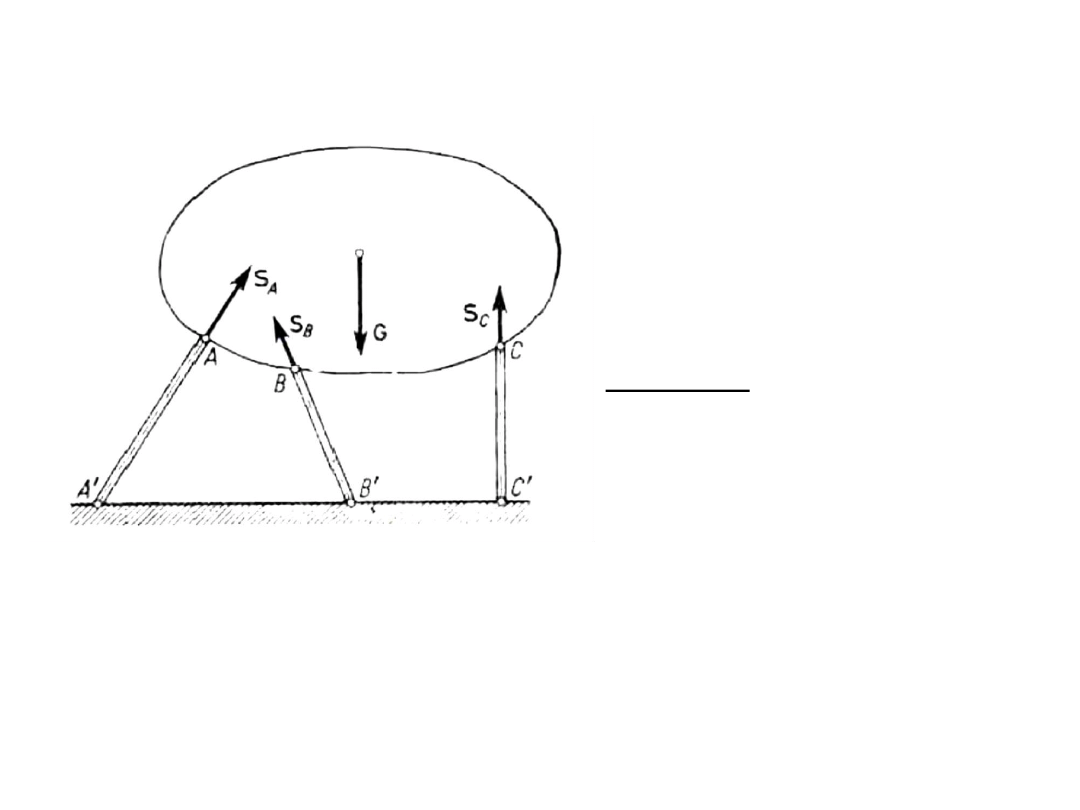
• Reakcja prętów przegubowych

Ciało unieruchomione za
pomocą prętów przegubowych

Pomijamy:
• ciężary własne prętów
• Tarcie w przegubach

Reakcje na ciało skierowane wzdłuż osi prętów

Pręty mogą być ściskane i rozciągane

MT_SS - w 1

25

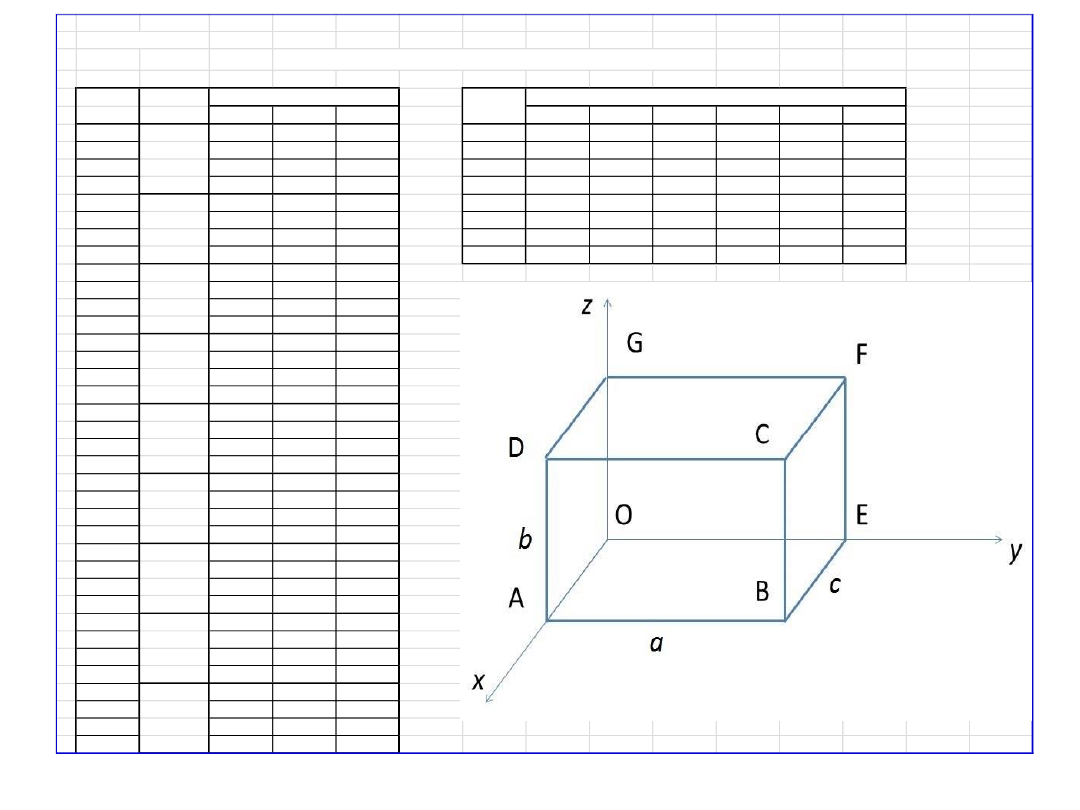
zadanie domowe nr 1.

Zredukuj układ sił do początku układu współrzędnych "O"

Numer

Punkty

zadania przyłożenia

F1

F2

F3

1

2

3

4

5

6

1 F1 - A

1

2

4

A

AB

AD

AO

AC

AG

AE

2 F2 - B

1

3

5

B

BE

BC

BA

BF

BD

BO

3 F3 - C

2

3

6

C

CD

CB

CF

CG

CA

CE

4

3

4

5

D

DG

DA

DC

DF

DO

DB

5 F1 - A

1

2

4

O

OA

OE

OG

OD

OB.

OF

6 F2 - B

1

3

5

E

EF

EB

EO

EG

EA

EC

7 F3 - D

2

3

6

F

FG

FC

FE

FD

FO

FB

8

3

4

5

G

GD

GO

GF

GE

GA

GC

9 F1 - A

1

2

4

10 F2 - B

1

3

5

11 F3 - O

2

3

6

12

3

4

5

13 F1 - A

1

2

4

14 F2 - B

1

3

5

15 F3 - E

2

3

6

16

3

4

5

17 F1 - A

1

2

4

18 F2 - B

1

3

5

19 F3 - F

2

3

6

20

3

4

5

21 F1 - A

1

2

4

22 F2 - B

1

3

5

23 F3 - G

2

3

6

24

3

4

5

25 F1 - A

1

2

4

26 F2 - C

1

3

5

27 F3 - D

2

3

6

28

3

4

5

29 F1 - A

1

2

4

30 F2 - C

1

3

5

31 F3 = O

2

3

6

32

3

4

5

33 F1 - A

1

2

4

34 F2 - C

1

3

5

35 F3 = O

2

3

6

36

3

4

5

Kierunek siły

Siła

Kierunek i zwrot

MT_SS - w 1

26

Never ever give up !