
MT SS - w 11
Kinematyka
Kinematyka
–
–
ruch punktu materialnego
ruch punktu materialnego
i bry
i bry
ł
ł
y sztywnej.
y sztywnej.
w-11
1
•
Kinematyka jest dzia
ł
em mechaniki zajmuj
ącym się
opisem ruchu cia
ł
, bez wnikania w zwi
ązek między
ruchem badanego cia
ł
a, a si
ł
ami, które na to cia
ł
o
dzia
ł
aj
ą.
•
Kinematyka jest pewnego rodzaju geometrią ruchu,
gdy
ż operujemy w niej tylko dwoma podstawowymi
poj
ęciami:
•
przestrzeni
ą i
•
czasem.
MT SS - w 11
2
Pojęcia podstawowe
:
Def 1.
Ruch
em
cia
ł
a
nazywamy zjawisko polegaj
ące
na zmianie w czasie po
ł
o
żenia tego cia
ł
a
wzgl
ędem pewnego innego cia
ł
a, które
umownie przyjmujemy jako nieruchome.
Def 2.
Cia
ł
em odniesienia
nazywamy cia
ł
o, które przy
badaniu ruchu przyjmujemy umownie jako
nieruchome.
Def 3.
Uk
ł
ad
em
odniesienia
nazywamy uk
ł
ad
wspó
ł
rz
ędnych, sztywno związany z cia
ł
em
odniesienia pozwalaj
ący określić po
ł
o
żenie
innych cia
ł
w stosunku do obranego cia
ł
a
odniesienia.

MT SS - w 11
3
Uk
ł
ad odniesienia b
ędzie
prostokątnym kartezjańskim
uk
ł
adem odniesienia.
Do ilo
ściowego opisu związków przestrzennych między
badanymi wielko
ściami kinematycznymi będzie stosowany
kartezja
ński uk
ł
ad wspó
ł
rz
ędnych
.
Wszystkie zjawiska opisywane w mechanice dziej
ą się w
czasoprzestrzeni
Ω, której elementami są:
•
przedzia
ł
czasowy,
•
trójwymiarowej przestrzeń Euklidesa.
Uk
ł
ad wspó
ł
rzędnych kartezjańskich s
ł
u
ży do
sparametryzowania tej przestrzeni
MT SS - w 11
4
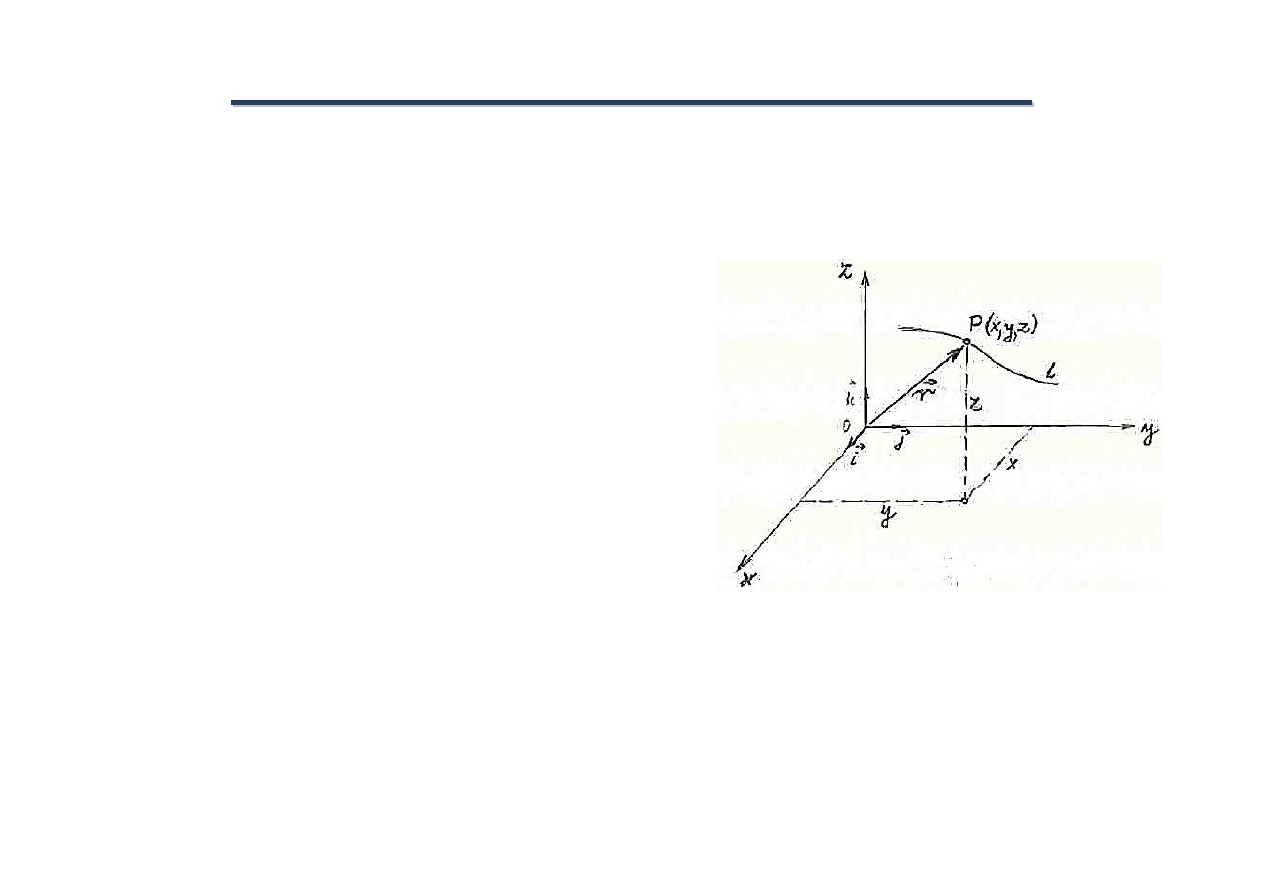
Po
ł
o
żenie punktu w tej przestrzeni Euklidesa można opisać
za pomoc
ą:
•
jego trzech wspó
ł
rz
ędnych (x, y, z) lub
•
wektora wodz
ącego r
z
k
y
j
x
i
r
⋅
+
⋅
+
⋅
=
→
→
→
→
Punkt P, poruszaj
ąc się, zajmuje kolejne po
ł
o
żenia w
obranym uk
ł
adzie wspó
ł
rz
ędnych
(x, y, z), okre
ś
lone
jednoznacznie za pomoc
ą
wektora wodz
ą
cego
r
.
Kinematyka
Kinematyka
–
–
ruch
ruch
punktu materialnego
punktu materialnego

MT SS - w 11
5
zatem
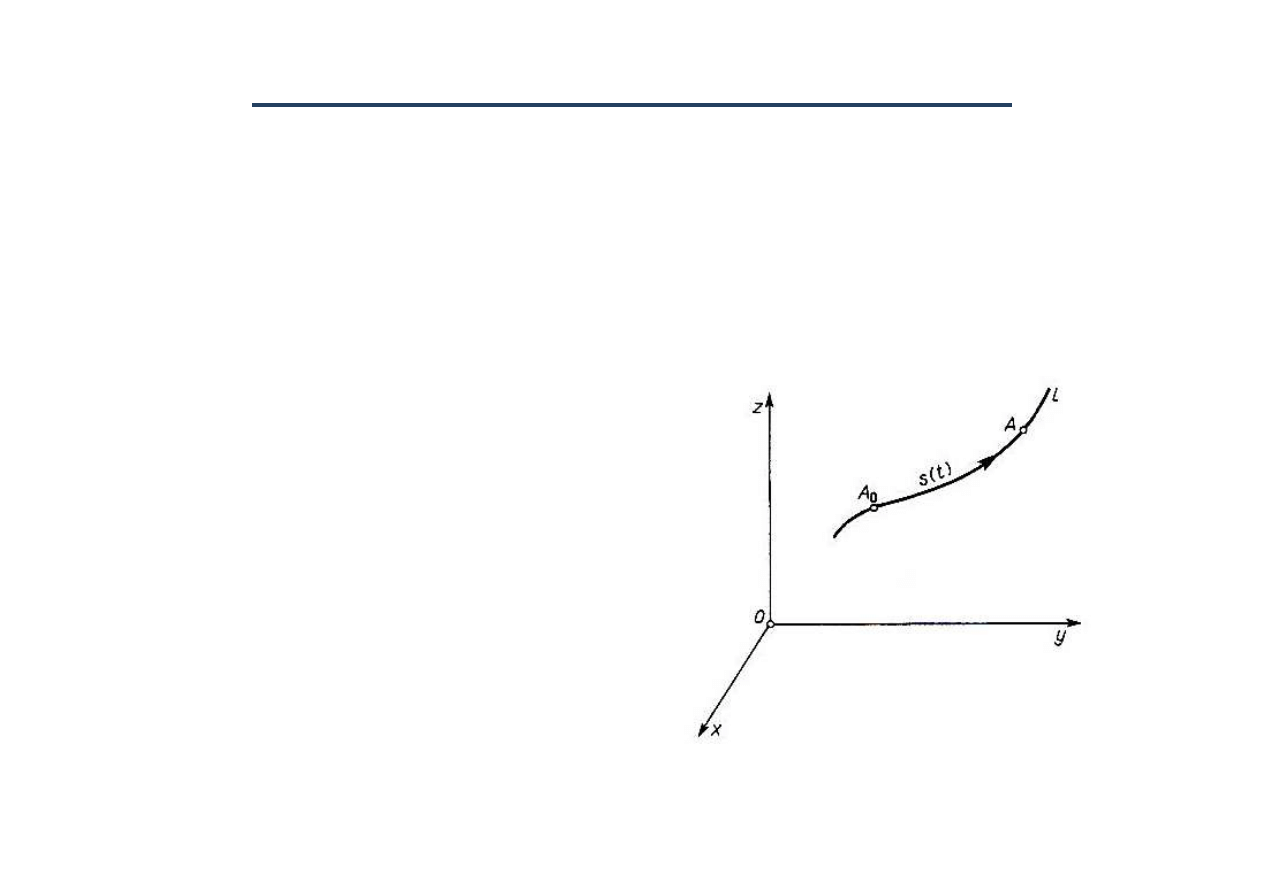
Def 4.
Torem punktu
nazywamy miejsce
geometryczne kolejnych po
ł
o
żeń punktu.
Ponadto przyjmujemy,
że:
•
czas jest niezale
żny od uk
ł
adu odniesienia,
•
czas jest taki sam dla wszystkich punktów przestrzeni.
Zatem b
ędziemy mówili o
czasie absolutnym
.
Jednostki stosowane w mechanice:
•
jednostka d
ł
ugo
ści – 1 m,
•
jednostka czasu – 1 s.

MT SS - w 11
6
Równania ruchu punktu materialnego uk
ł
adu
punktów materialnych i bry
ł
y sztywnej.
Wiadomo
Wiadomo
ś
ś
ci wst
ci wst
ę
ę
pne
pne
.
Ruch uk
ł
adu materialnego, tzn.:
•
uk
ł
adu punktów materialnych,
•
cia
ł
a sztywnego,
•
uk
ł
adu cia
ł
sztywnych
mo
żna opisać podając sk
ł
adowe tego ruchu, zwi
ązane z
poj
ęciem
STOPNI SWOBODY
tego uk
ł
adu materialnego.
Def 5.
Liczb
ę niezależnych parametrów uk
ł
ad,
koniecznych do okre
ślenia jego chwilowego
po
ł
o
żenia w przestrzeni, nazywamy
liczbą stopni swobody
tego uk
ł
adu.

MT SS - w 11
7
Punkt materialny
– 3 stopnie swobody:
•
przesunięcia w kierunkach wyznaczonych przez osie
uk
ł
adu kartezja
ńskiego.
Bry
ł
a sztywna
– 6 stopni swobody:
•
przemieszczenia w kierunkach wyznaczonych przez
osie uk
ł
adu kartezja
ńskiego oraz
•
obroty wokó
ł
tych osi.

MT SS - w 11
8
Ograniczenia ruchu
Je
żeli uk
ł
ad n punktów materialnych A
1
, A
2
, …, A
n
:
- posiadaj
ący 3n stopni swobody
- poddany jest pewnym ograniczeniom ruchu,
czyli gdy mamy do czynienia z uk
ł
adem nieswobodnym,
ograniczonym wi
ęzami
wówczas wspó
ł
rz
ędne prostokątne tych punktów nie są od
siebie niezale
żne i spe
ł
nia
ć muszą pewną liczbę równań,
zwanych
RÓWNANIAMI WIĘZÓW
(
)
k
i
z
y
x
z
y
x
f
n
n
n
i
...,
,
2
,
1
,
0
,
,
...,
,
,
,
1
1
1
=
=

MT SS - w 11
9
Je
żeli dla uk
ł
adu materialnego z
ł
o
żonego z n punktów
materialnych okre
ślimy:
n – liczba punktów materialnych uk
ł
adu,
s – liczba stopni swobody,
k – liczba równa
ń odpowiadająca liczbie ograniczeń
ruchu wi
ęzami
wówczas
s = 3·n - k
Dla uk
ł
adu materialnego z
ł
o
żonego z n cia
ł
sztywnych:
s = 6·n - k
Aby jednoznacznie okre
ślić ruch uk
ł
adu materialnego
posiadaj
ącego s stopni swobody należy sformu
ł
owa
ć s
równa
ń ruchu.

MT SS - w 11
10
Ruch uk
ł
adu materialnego z
ł
o
żonego
z n punktów materialnych
nale
ży określić s równań określających zmianę w czasie
po
ł
o
żeń punktów q
i
mierzonych wzd
ł
u
ż osi obranego
uk
ł
adu wspó
ł
rz
ędnych
Ruch uk
ł
adu materialnego z
ł
o
żonego
z n cia
ł
sztywnych
nale
ży określić zmiany w czasie:
( )
s
i
t
q
q
i
i
...,
,
2
,
1
=
=
( )
( )
s
m
m
i
t
m
i
t
q
q
i
i
i
i
...,
,
2
,
1
...,
,
2
,
1
+
+
=
=
=
=
ϕ
ϕ
po
ł
o
żeń
k
ątów obrotu:
MT SS - w 11
11
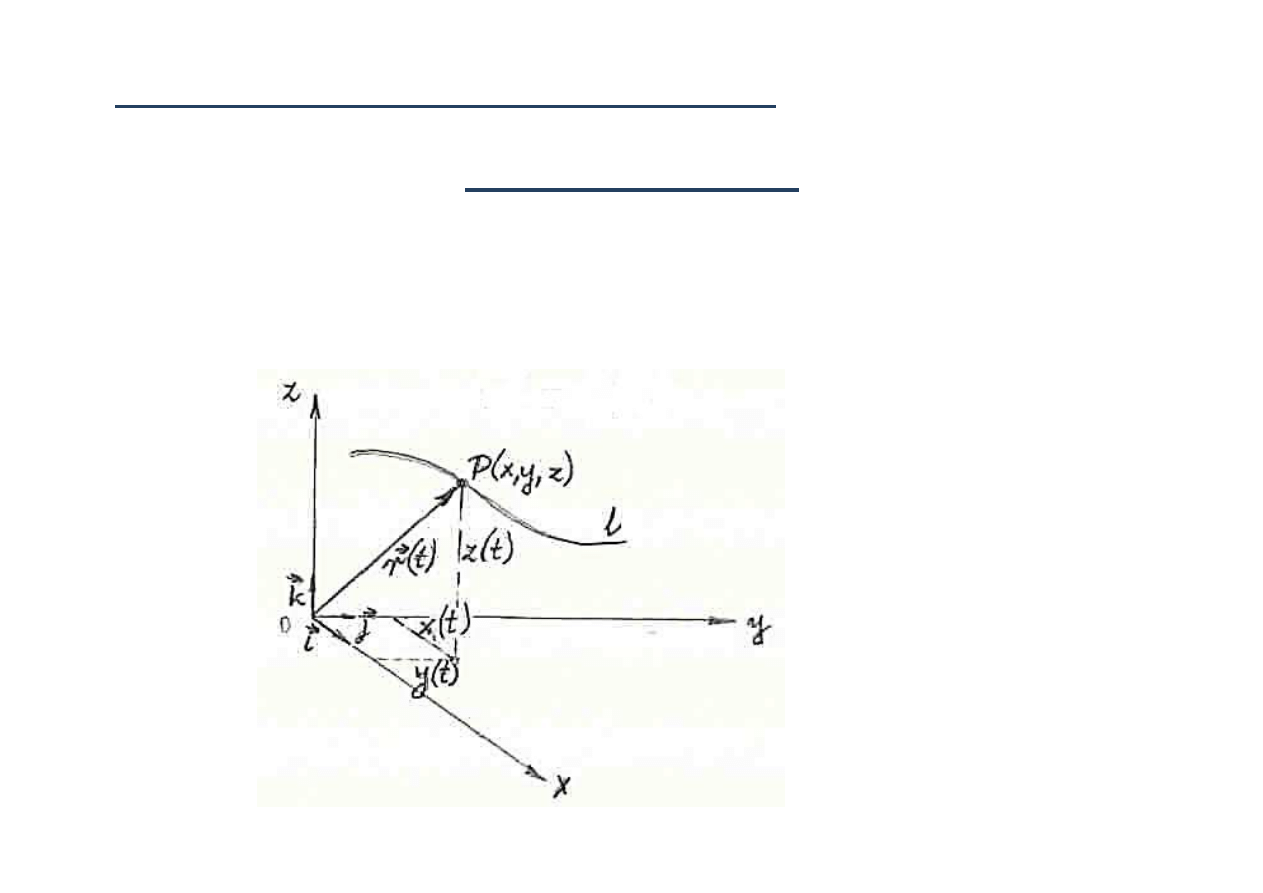
Równania ruchu punktu materialnego
OPIS WEKTOROWY
Okre
ślając początek uk
ł
adu wspó
ł
rz
ędnych oraz kierunek i
wielko
ść wektora r w kolejnych chwilach czasu otrzymamy
WEKTOROWE RÓWNANIE RUCHU.
( )
t
f
r
→
→
=

MT SS - w 11
12
OPIS we WSPÓ
Ł
RZĘDNYCH PROSTOKĄTNYCH
Podaj
ąc zmiany w czasie wszystkich wspó
ł
rz
ędnych punktu
P(x, y, z) otrzymujemy RÓWNANIA RUCHU tego punktu.
( )
( )
( )
.
,
,
3
2
1
t
f
z
t
f
y
t
f
x
=
=
=
z
k
y
j
x
i
r
⋅
+
⋅
+
⋅
=
→
→
→
→
Wektorowe równanie ruchu wyrazi si
ę zatem za pomocą
trzech równa
ń sk
ł
adowych
MT SS - w 11
13
OPIS we WSPÓ
Ł
RZĘDNYCH NATURALNYCH
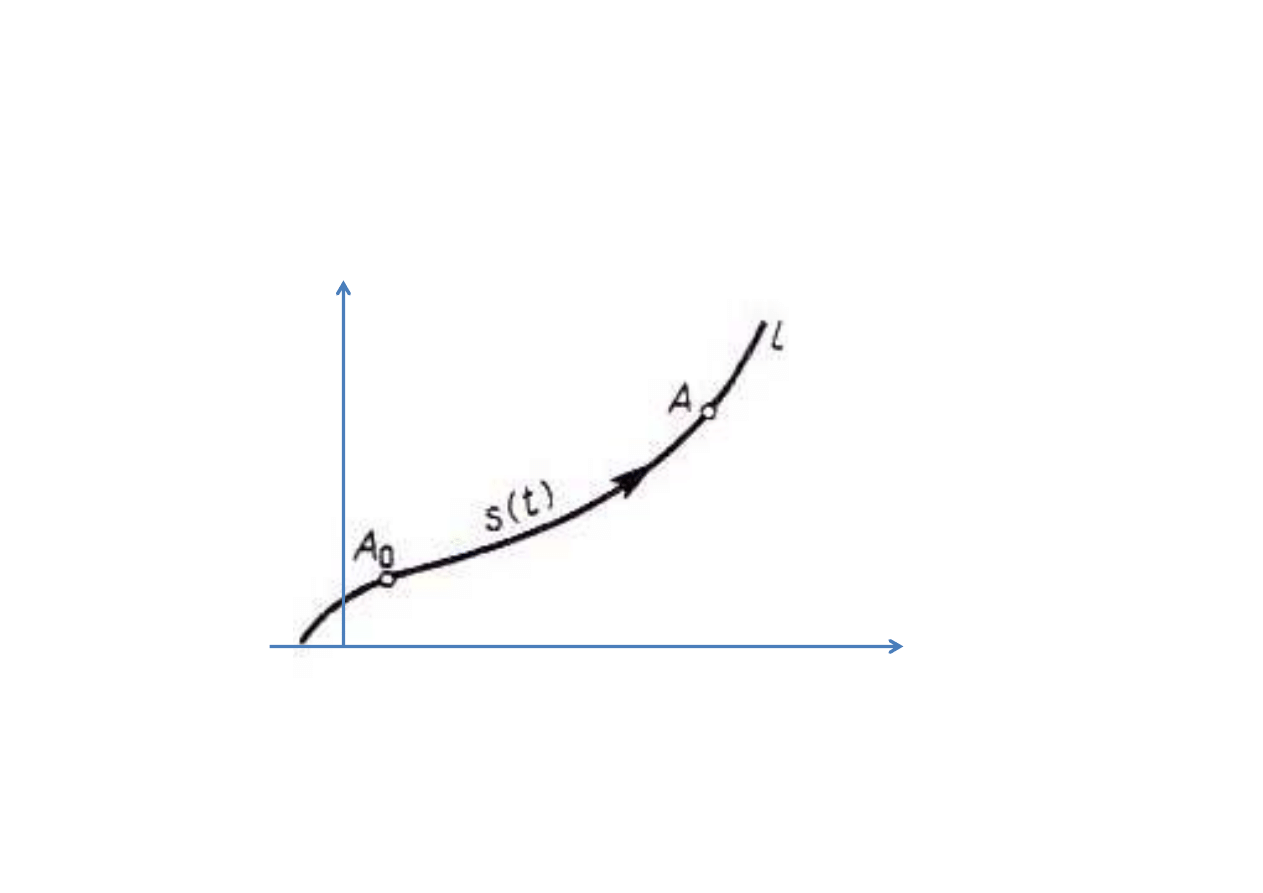
Gdy znany jest tor poruszaj
ącego się punktu A, wówczas
po
ł
o
żenie tego punktu w przestrzeni określić można
podaj
ąc wspó
ł
rz
ędną s mierzoną wzd
ł
u
ż tego toru od
pewnego nieruchomego punktu A
0
.
Równanie ruchu, zwane w tym
przypadku
SKALARNYM RÓWNANIEM
RUCHU
ma posta
ć
( )
t
f
s
=

MT SS - w 11
14
Funkcj
ę s = F(t) można wyrazić w następujący sposób:
a) analitycznie
np. dla ruchu jednostajnie przy
śpieszonego
2
0
0
2
1
t
a
t
s
s
⋅
+
⋅
+
=
υ
gdzie:
a – przy
śpieszenie punktu,
– pr
ędkość początkowa punktu,
s – droga przebyta przez punkt.
b) parametryczne
t
0
1
2
3
4
s
10
12
14
18
24
0
υ
MT SS - w 11
15
c) Wykreślnie
Zmiana w czasie drogi S punktu mo
że być poddana
wykre
ślnie
t
S
MT SS - w 11
16
Prędkość i przyśpieszenie punktu
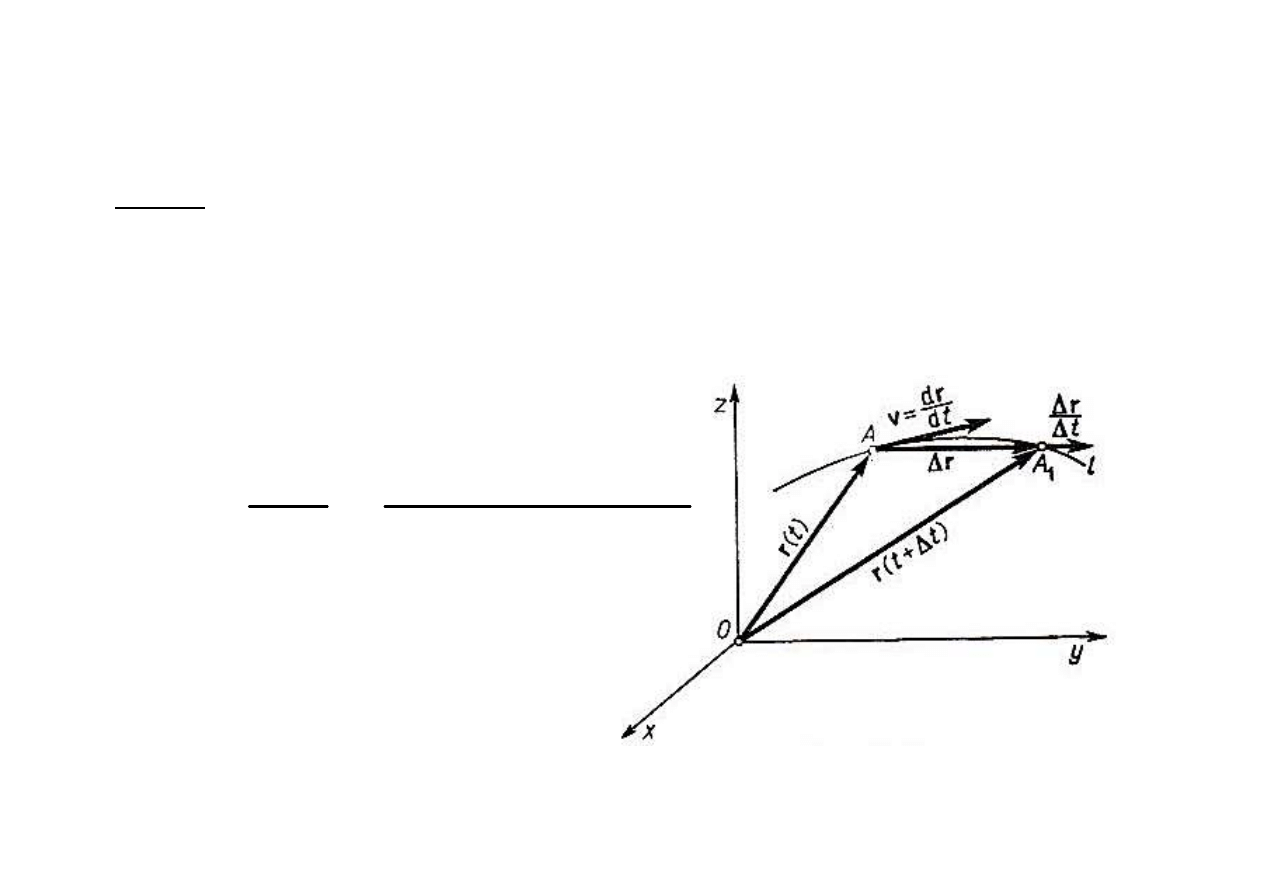
Def 6.
Prędkością średnią
v
śr
punktu nazywamy
stosunek przyrostu wektora wodz
ącego r do
przedzia
ł
u czasowego
∆t, w którym ten przyrost
nast
ąpi
ł
.
(
) ( )
t
t
r
t
t
r
t
r
ś
r
∆
−
∆
+
=
∆
∆
=
→
→
→
→
υ
MT SS - w 11
17
Def 7.
Prędkością chwilową
v
punktu nazywamy
granic
ę stosunku przyrostu wektora
wodz
ącego r do przedzia
ł
u czasowego
∆t, w
którym ten przyrost nast
ąpi
ł
, przy przedziale
∆t
d
ążącym do zera.
(
) ( )
•
→
→
→
∆
→
→
→
∆
→
=
∆
∆
=
∆
−
∆
+
=
r
t
r
t
t
r
t
t
r
t
t
0
0
lim
lim
υ
W uk
ł
adzie jednostek miar SI jednostk
ą prędkości jest
[m/s]
MT SS - w 11
18
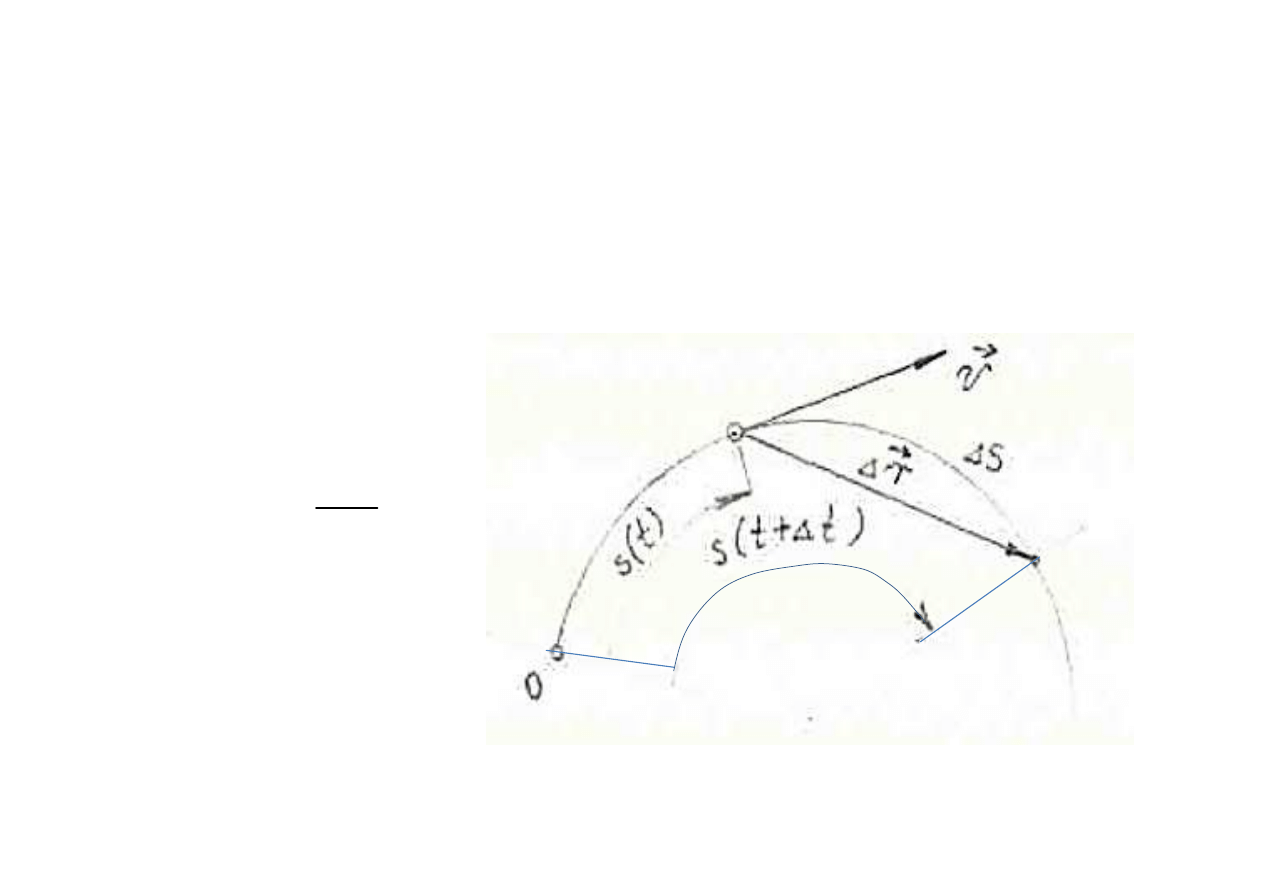
Prędkość w mierze
ł
ukowej
jest warto
ścią skalarną, równą granicy do jakiej dąży
stosunek przyrostu drogi
ł
ukowej punktu do
przedzia
ł
u czasowego, w którym ten przyrost nast
ąpi
ł
przy warto
ści przedzia
ł
u czasowego d
ążącej do zera.
•
→
∆
=
∆
∆
=
s
t
s
t
0
lim
υ
MT SS - w 11
19
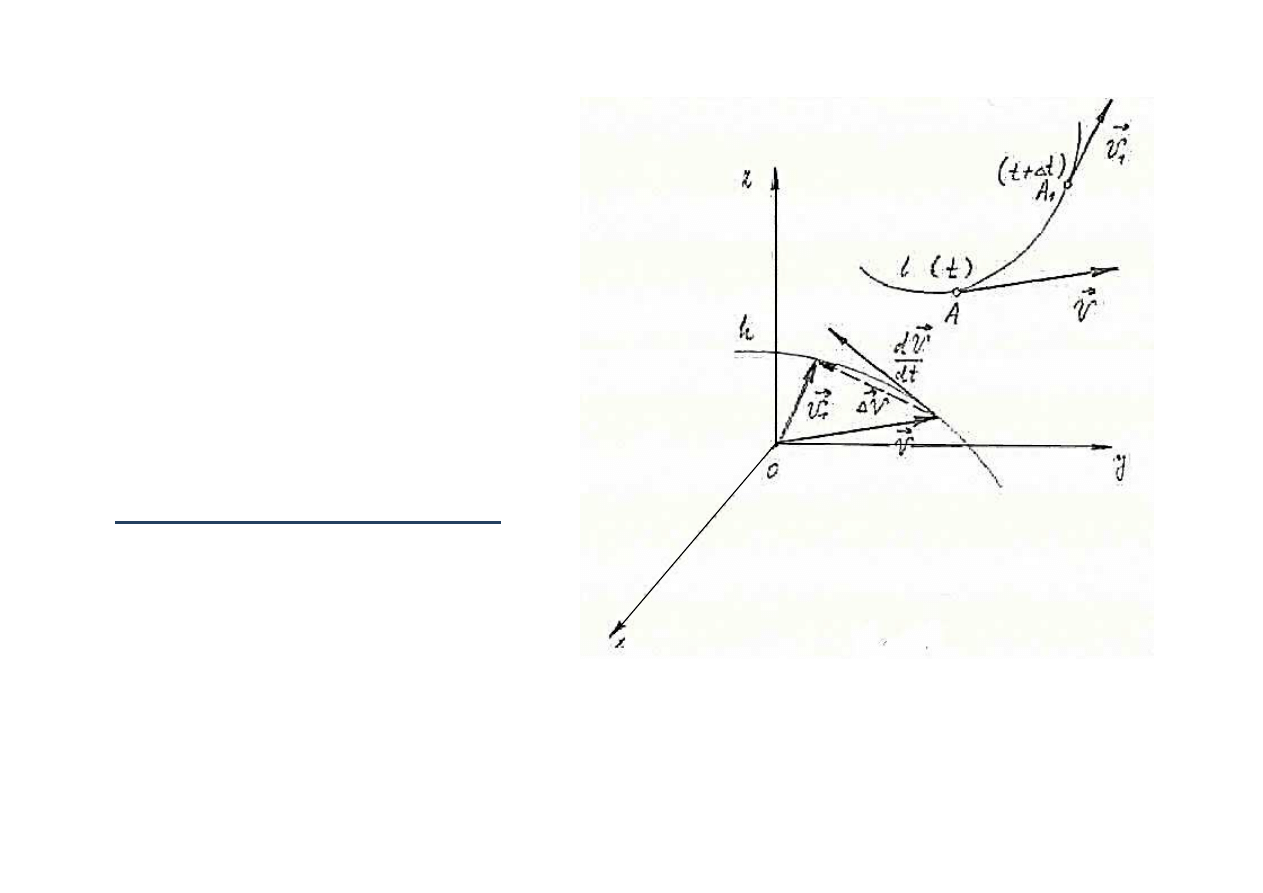
Przyśpieszenie punktu
Pr
ędkość
v
punktu A poruszaj
ącego
si
ę w przestrzeni może zmieniać
sw
ą wartość i swój kierunek, jest
zatem
wektorową funkcją czasu t.
Dwa po
ł
o
żenia punktu:
•
w chwili t – po
ł
o
żenie A,
pr
ędkość v
•
w chwili t + ∆t – po
ł
o
żenie A
1
,
pr
ędkość v
1
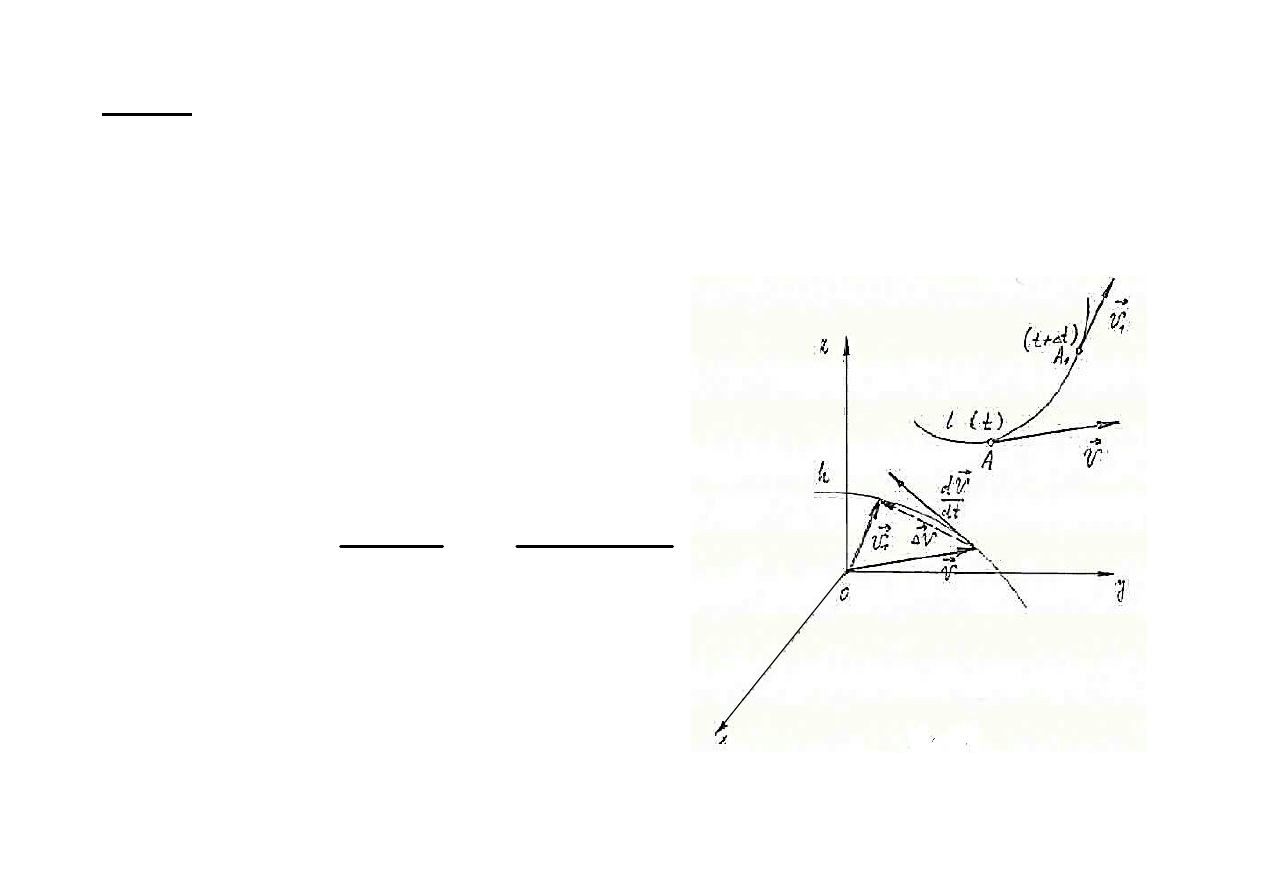
MT SS - w 11
20
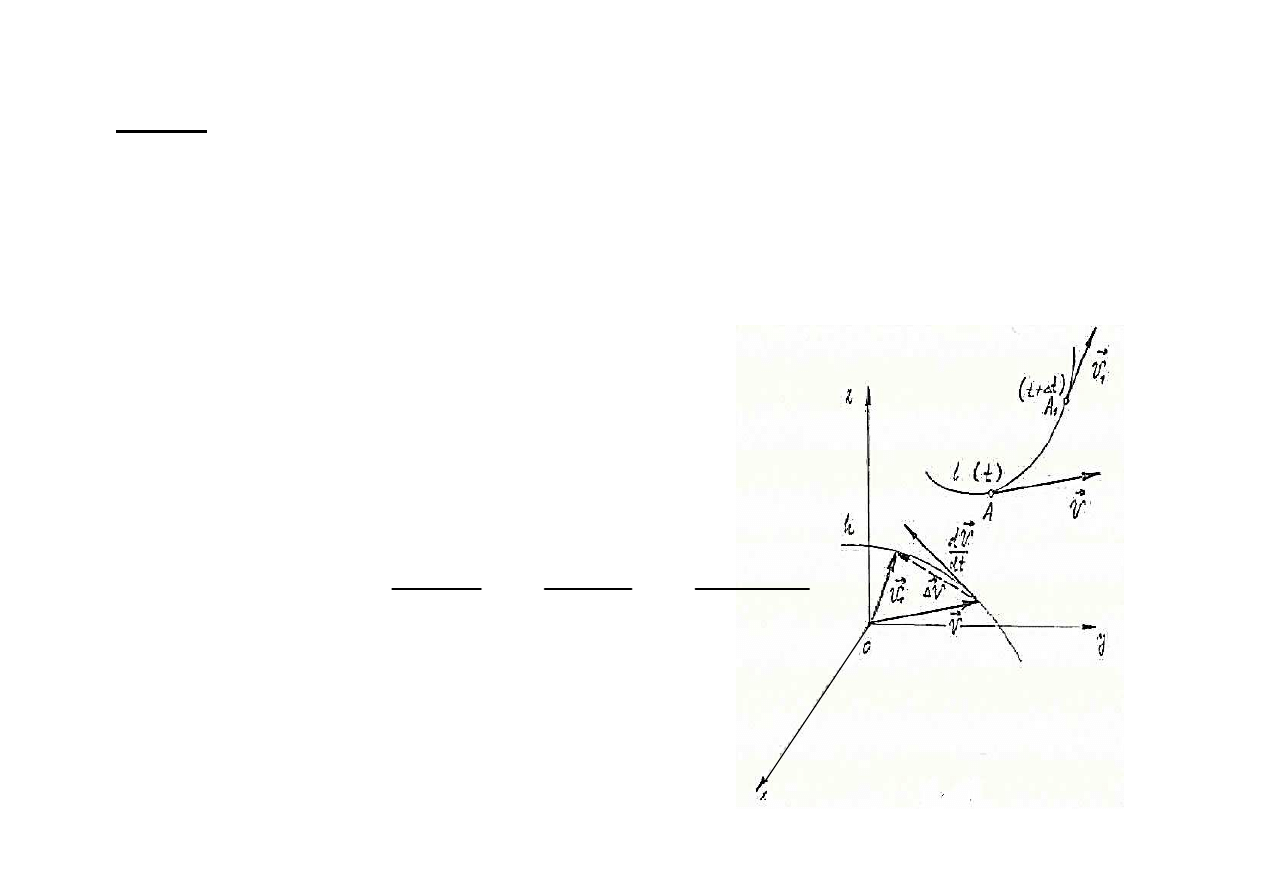
Def 8.
Przyśpieszeniem średnim a
śr
punktu
nazywamy stosunek przyrostu wektora
pr
ędkości v tego punktu do przedzia
ł
u
czasowego ∆t
,
w którym ten przyrost nast
ąpi
ł
.
t
t
a
ś
r
∆
−
=
∆
∆
=
→
→
→
→
υ
υ
υ
1
MT SS - w 11
21
Def 9.
Przyśpieszeniem chwilowym
punktu
a
nazywamy granic
ę, do której dąży stosunek
przyrostu geometrycznego pr
ędkości v tego
punktu do przedzia
ł
u czasowego ∆t
,
w którym
ten przyrost nast
ąpi
ł
, przy przedziale ∆t
d
ążącym do zera.
2
2
0
lim
dt
r
d
dt
d
t
a
t
→
→
→
→
∆
→
=
=
∆
∆
=
υ
υ

MT SS - w 11
22
Sk
ł
adowe prędkości i przyśpieszenia punktu określimy
różniczkując równania ruchu punktu.
( )
( )
( )
( )
( )
z
y
x
z
y
x
a
k
a
j
a
i
z
k
y
j
x
i
r
a
k
j
i
z
k
y
j
x
i
r
t
t
z
k
t
y
j
t
x
i
t
r
⋅
+
⋅
+
⋅
=
⋅
+
⋅
+
⋅
=
=
=
⋅
+
⋅
+
⋅
=
⋅
+
⋅
+
⋅
=
=
⋅
+
⋅
+
⋅
=
→
→
→
•
•
→
•
•
→
•
•
→
→
→
→
→
→
→
•
→
•
→
•
→
→
→
→
→
→
→
•
•
•
•
υ
υ
υ
υ
υ
gdzie:
x = x(t), y = y(t), z = z(t)
s
ą to znane równania
ruchu punktu
MT SS - w 11
23
Warto
ści liczbowe wektora prędkości i wektora
przy
śpieszenia wyznaczamy z następujących zależności:
2
2
2
2
2
2
2
2
2
2
2
2
+
+
=
+
+
=
+
+
=
+
+
=
•
•
•
•
•
•
•
•
•
z
y
x
a
a
a
a
z
y
x
z
y
x
z
y
x
υ
υ
υ
υ
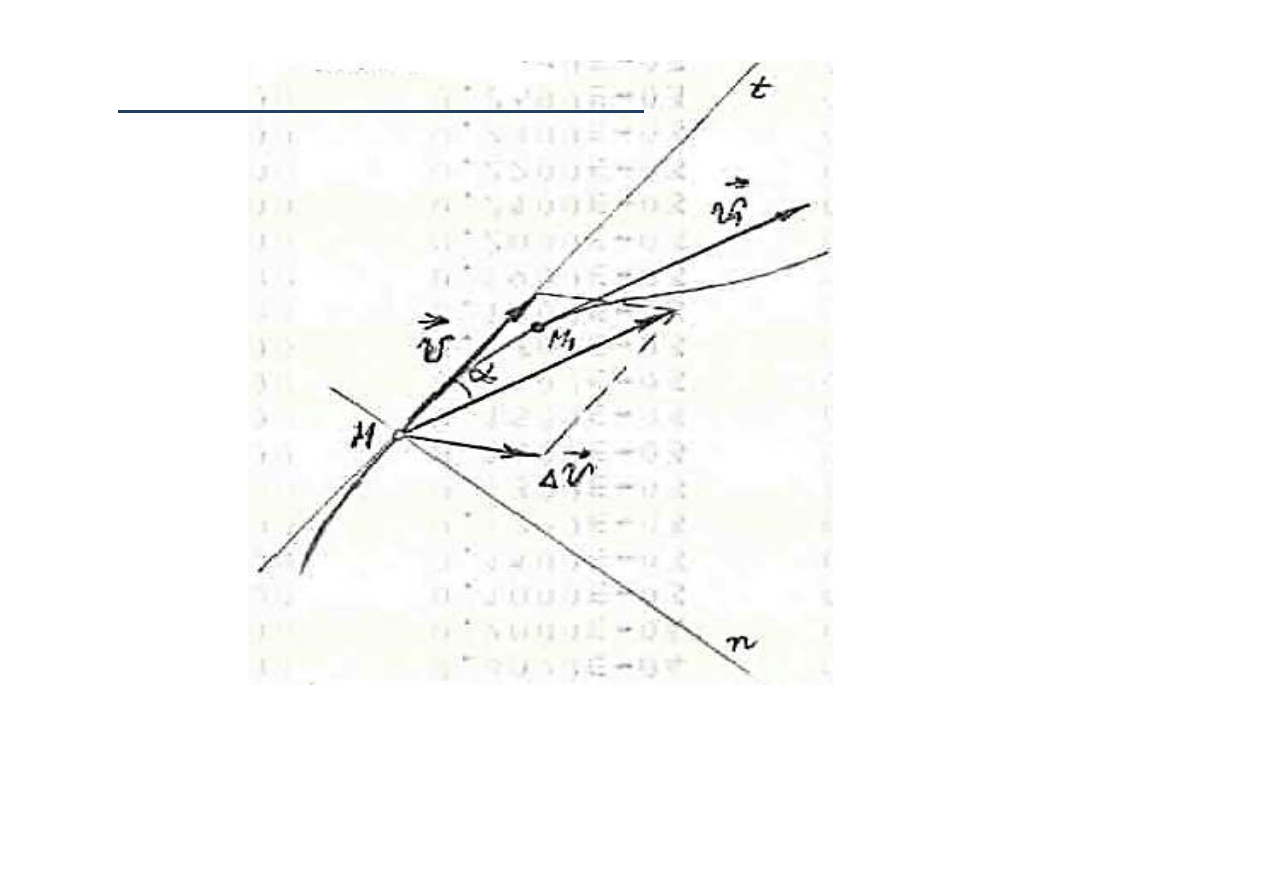
MT SS - w 11
24
trajektoria punktu
M – po
ł
ożenie punktu w chwili t,
M
1
– po
ł
ożenie punktu w chwili t+
∆
t
W sytuacji opisanej na rysunku
Przyśpieszenie chwilowe punktu posiada dwie sk
ł
adowe:
•
styczną i
•
normalną
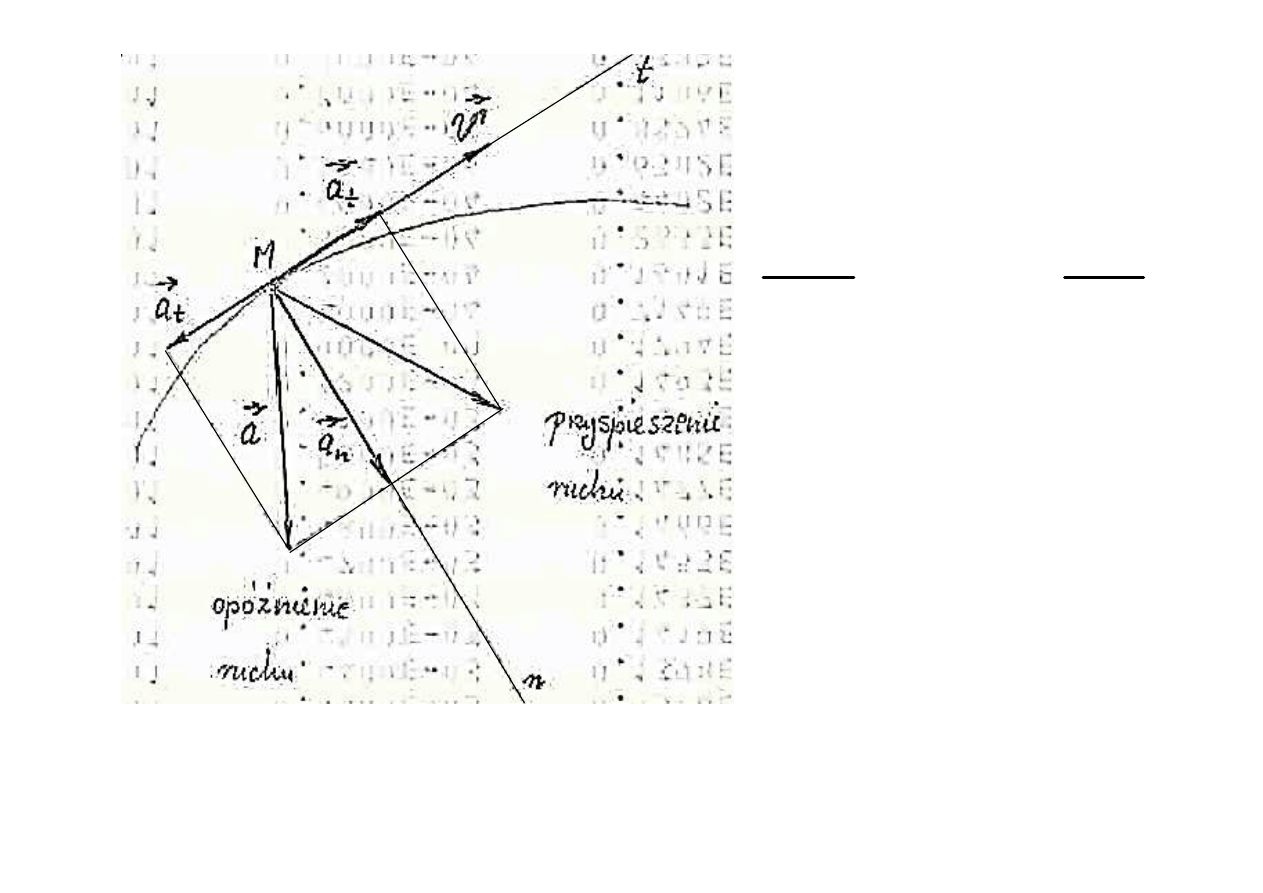
MT SS - w 11
25
ρ
υ
υ
2
=
=
n
t
a
dt
d
a
gdzie:
ρ – promie
ń krzywizny toru w punkcie M
MT SS - w 11
26
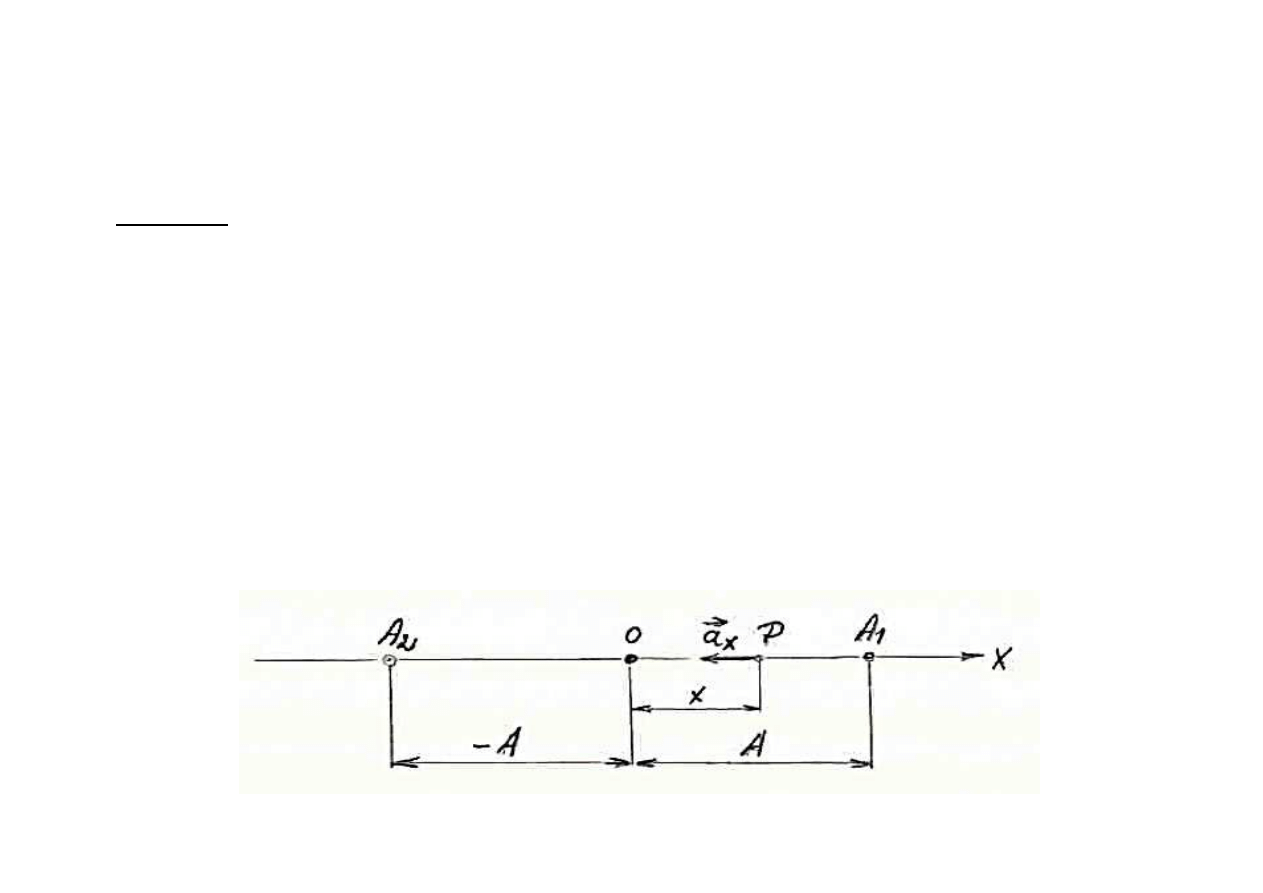
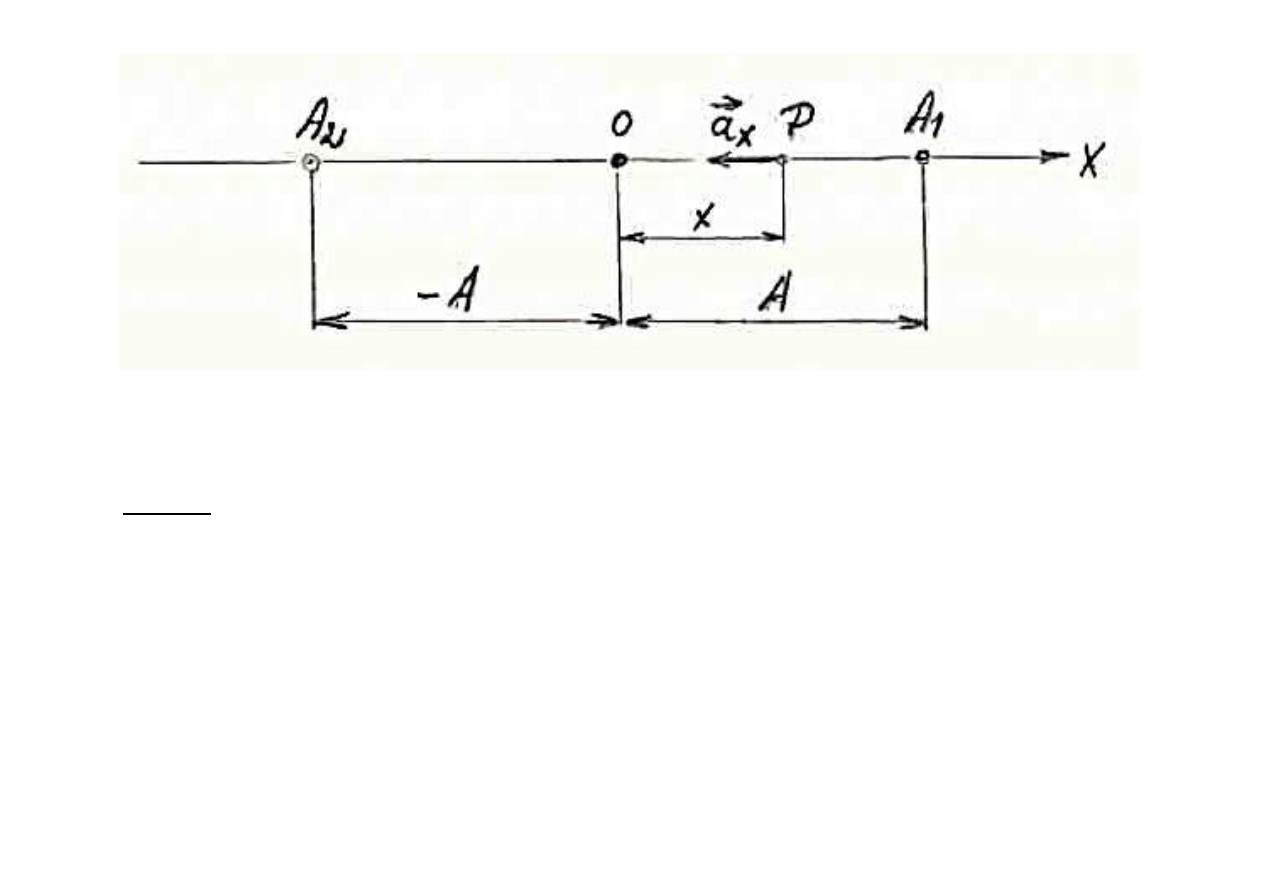
Def 10.
Ruch punktu P po prostej, odbywaj
ący się
zgodnie z równaniem harmonicznym nazywamy
ruchem harmonicznym prostym.
Szczególny ruch, cz
ęsto rozważany w mechanice budowli
Ruch harmoniczny
.
(
)
0
sin
ϕ
ω
+
⋅
=
t
A
x
Torem punktu P jest odcinek A
1
A
2
, którego
środek znajduje
si
ę w punkcie 0, od którego odmierzamy odciętą x. Punkt 0
nosi nazw
ę środka ruchu harmonicznego.
MT SS - w 11
27
gdzie:
A – amplituda ruchu harmonicznego, równa
maksymalnemu wychyleniu punktu A z
po
ł
o
żenia równowagi 0,
ω – cz
ęstość ko
ł
owa ruchu harmonicznego,
φ
0
–
faza pocz
ątkowa ruchu harmonicznego.
(
)
0
sin
ϕ
ω
+
⋅
=
t
A
x
MT SS - w 11
28
Ruch harmoniczny jest ruchem okresowym, cechuj
ącym się:
•
okresem
T
,
•
cz
ęstością
f
.
π
ω
ω
π
2
1
,
2
=
=
=
T
f
T
Cz
ęstość
f
ruchu jest to liczba okresów
przypadaj
ąca na jednostkę czasu
MT SS - w 11
29
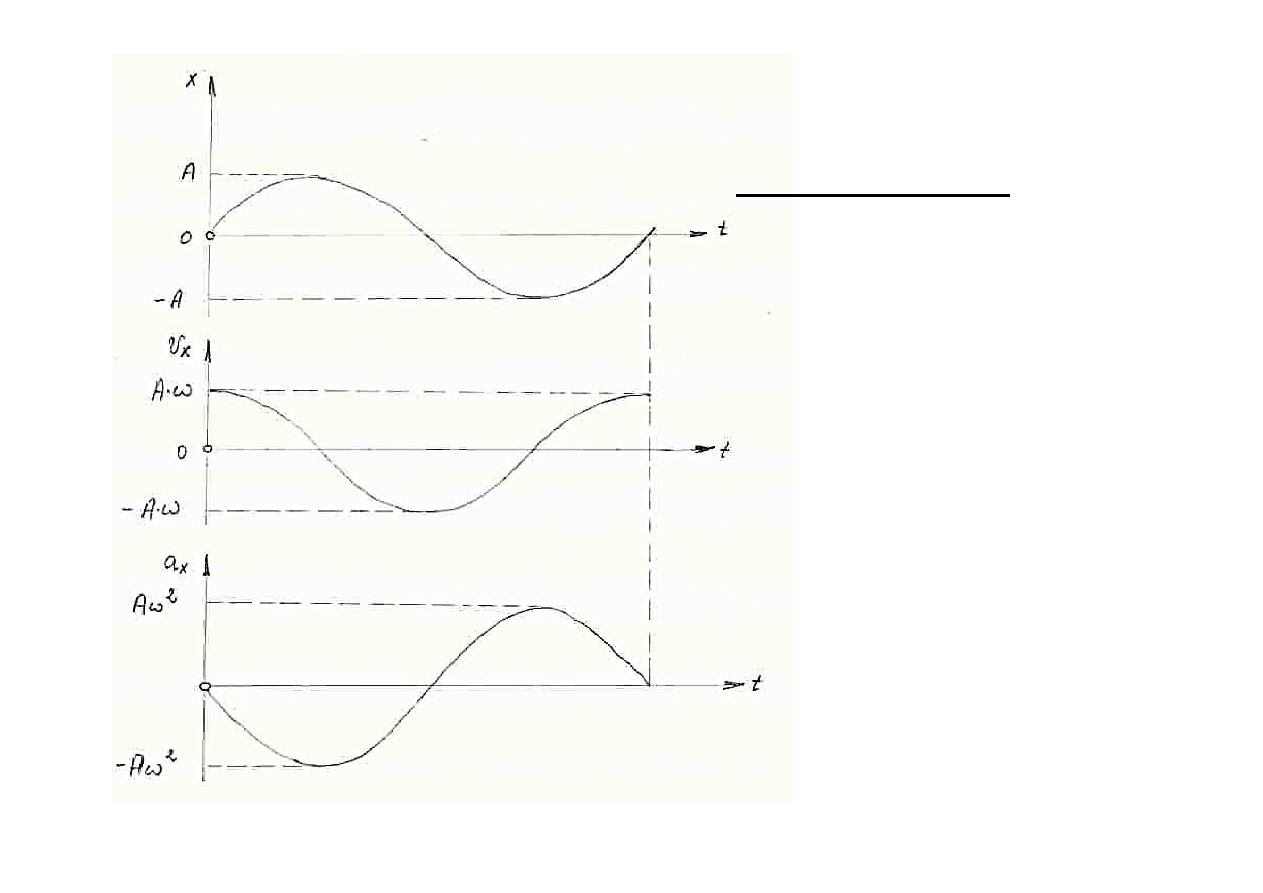
Przy fazie pocz
ątkowej ruchu harmonicznego ϕ
0
= 0.
Zmiany w czasie:
odci
ętej x
miary pr
ędkości v
x
miary przy
śpieszenia a
x
MT SS - w 11
30
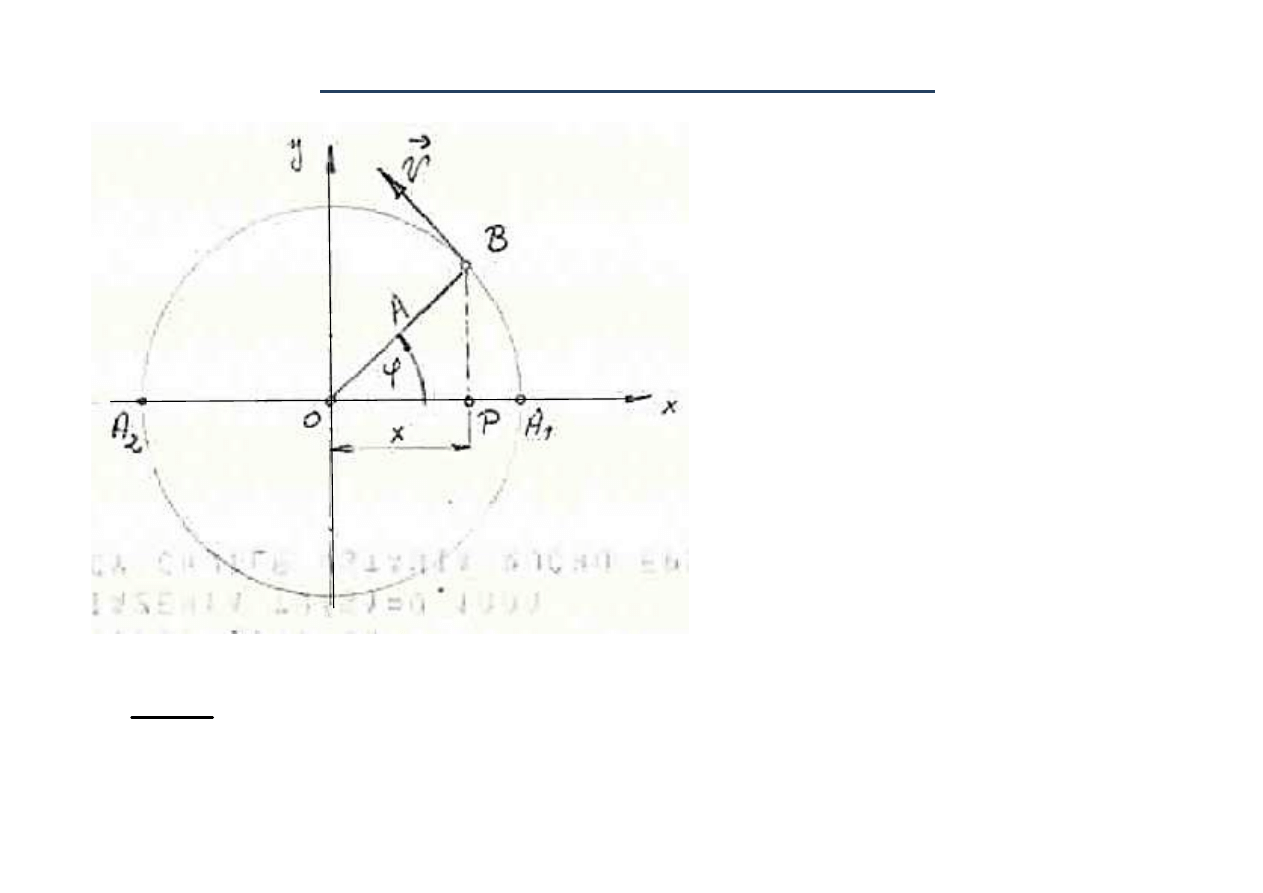
Interpretacja ruchu harmonicznego
•
rozwa
żamy ruch punktu B
•
po okr
ęgu ko
ł
a o promieniu A
•
ruch jednostajny ze sta
ł
ą
co do warto
ści prędkością v
v = A·ω = const
ω
–
pr
ędkość kątowa promienia
wodz
ącego 0B – sta
ł
a
ϕ – kąt, który promień 0B
tworzy z osi
ą 0x
const
dt
d
=
=
ω
ϕ
MT SS - w 11
31
Ca
ł
kuj
ąc, przy zerowych warunkach początkowych mamy:
t
⋅
=
ω
ϕ
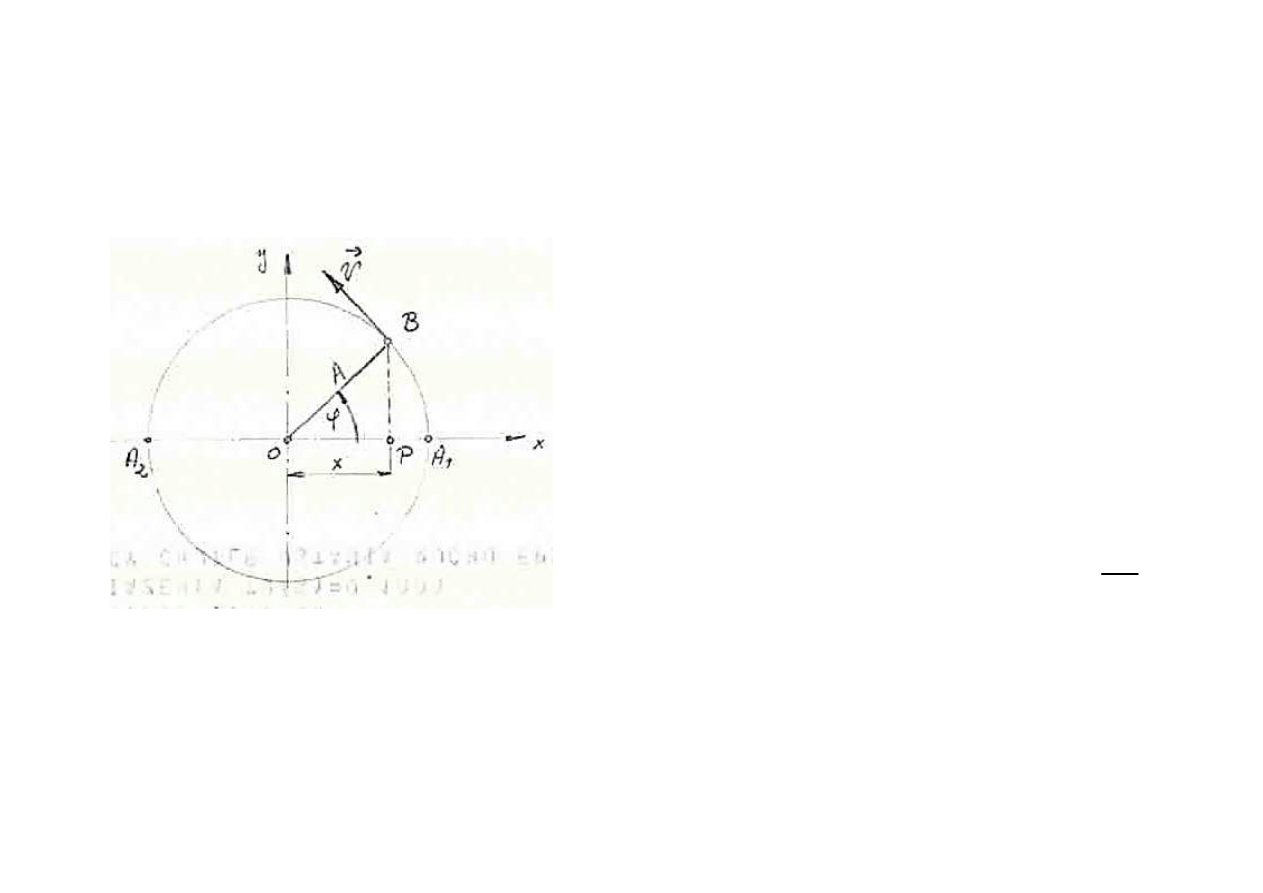
Je
śli punkt P jest rzutem punktu B na
średnicę A
1
A
2
, wzd
ł
u
ż której
skierowana jest o
ś 0x, wówczas
+
⋅
=
⋅
=
⋅
=
2
sin
cos
cos
π
ω
ω
ϕ
t
A
t
A
A
x
Tak wi
ęc punkt P porusza się ruchem harmonicznym o
cz
ęstości ko
ł
owej równej pr
ędkości kątowej ω promienia
wodz
ącego 0B i fazie początkowej φ
0
=
π/2.

MT SS - w 11
Kinematyka
Kinematyka
–
–
ruch cia
ruch cia
ł
ł
a sztywnego
a sztywnego
32
Klasyfikacja ruchów cia
ł
a sztywnego
Cia
ł
o sztywne, które nie jest ograniczone wi
ęzami
posiada 6 stopni swobody, tzn. mo
że:
- porusza
ć się wzd
ł
u
ż trzech osi uk
ł
adu wspó
ł
rz
ędnych,
- wykonywa
ć obroty wokó
ł
trzech osi.

MT SS - w 11
33
MT SS - w 11
34
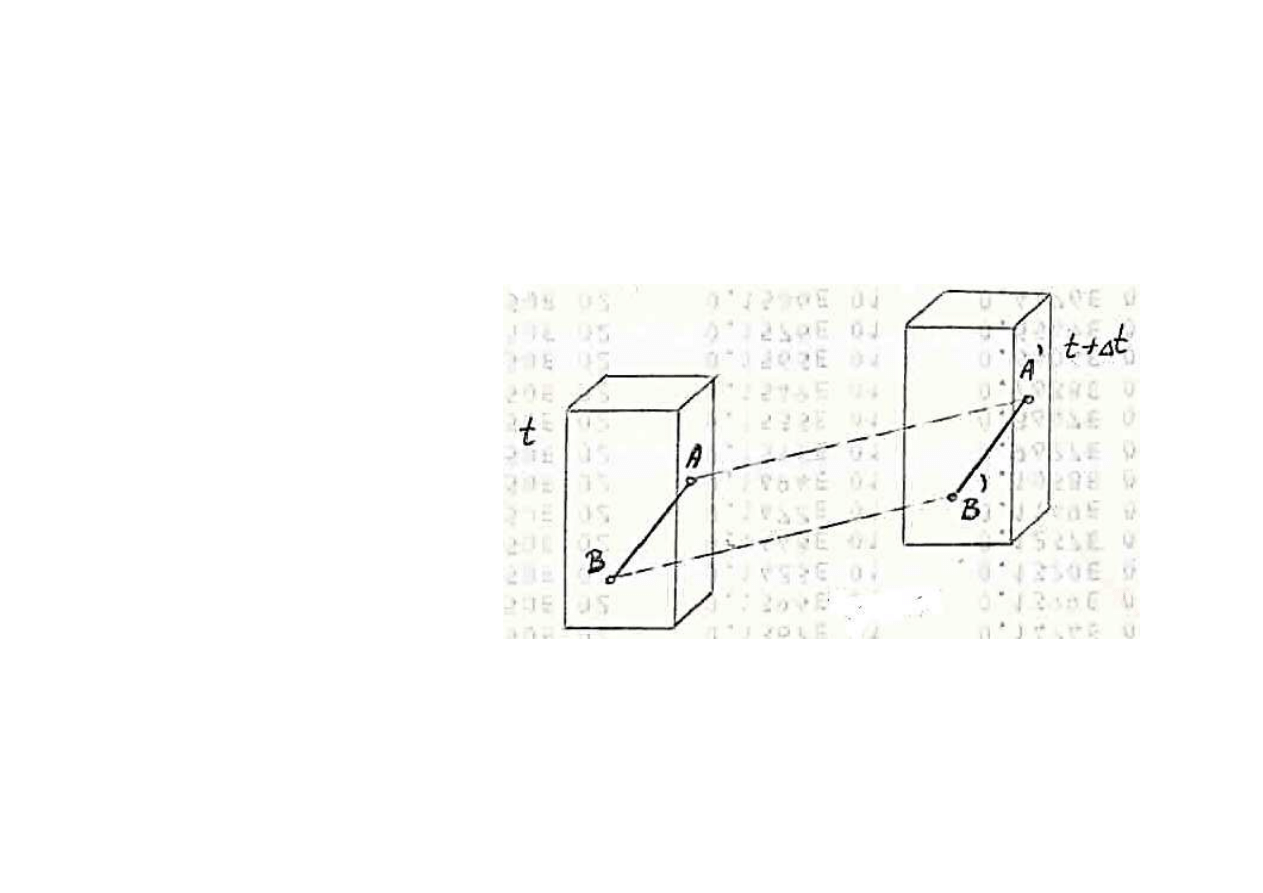
RUCH POSTĘPOWY CIA
Ł
A SZTYWNEGO
Def. 1. Ruchem post
ępowym cia
ł
a sztywnego nazywamy
taki ruch, w którym kolejne po
ł
o
żenie cia
ł
a s
ą
równoleg
ł
e.
Z przedstawionej definicji wynika,
że w ruchu postępowym
pr
ędkość i przyśpieszenie wszystkich punktów cia
ł
a s
ą
jednakowe.
MT SS - w 11
35
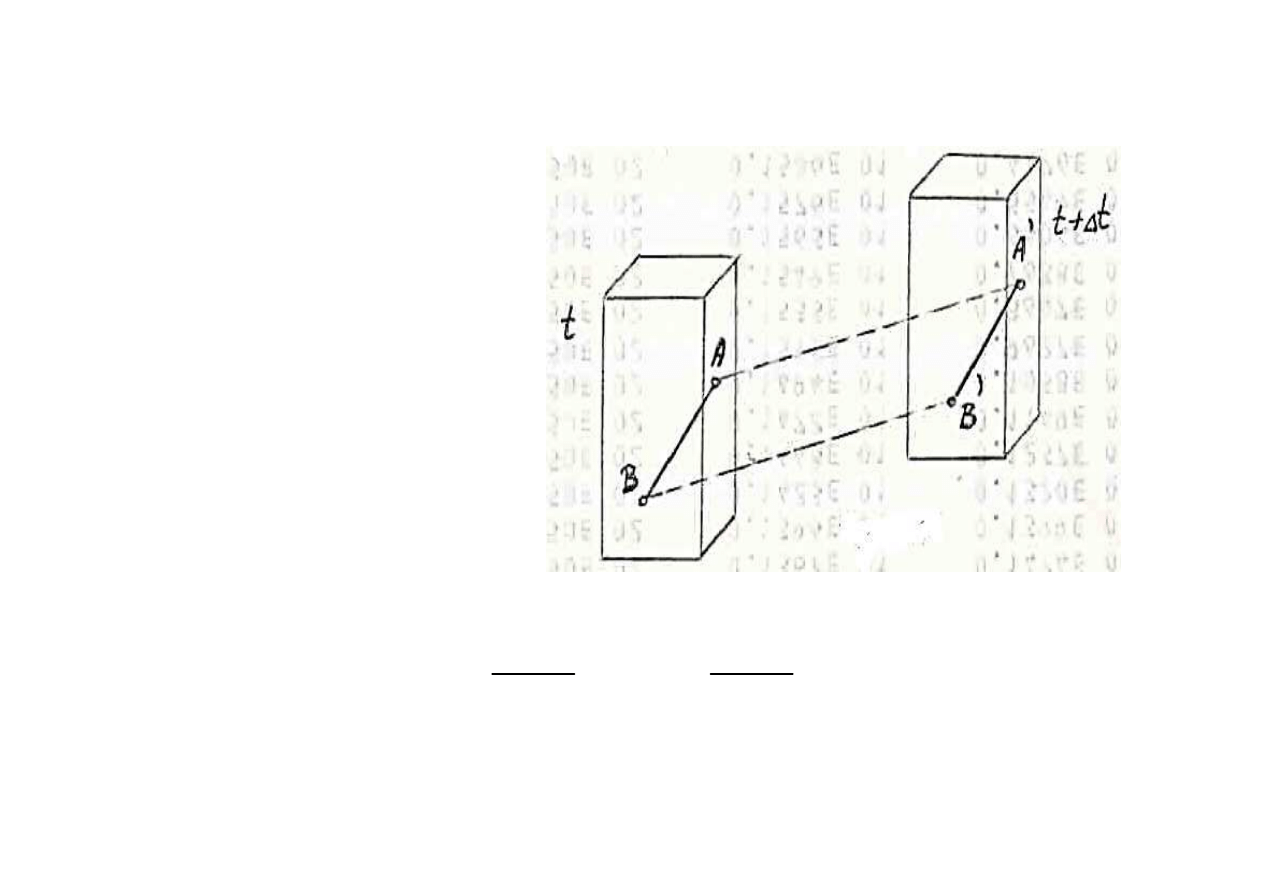
Poniewa
ż
AA’BB’ – równoleg
ł
obok
AA’ = BB’
st
ąd
t
B
B
t
A
A
t
t
∆
′
≡
∆
′
→
→
∆
→
→
∆
0
0
lim
lim
MT SS - w 11
36
W konsekwencji otrzymujemy zale
żność wyrażającą
równość prędkości i przyśpieszenia
dwóch dowolnie wybranych punktów cia
ł
a sztywnego.
→
→
→
→
≡
≡
B
A
B
A
a
a
,
υ
υ
Wnioski:
1) Opis ruchu post
ępowego cia
ł
a sztywnego jest
jednoznaczny z opisem ruchu jednego punktu cia
ł
a,
2) W ruchu post
ępowym możemy mówić o prędkości
cia
ł
a i przy
śpieszeniu cia
ł
a.

MT SS - w 11
37
RUCH OBROTOWY CIA
Ł
A SZTYWNEGO
Def. 2. Ruchem obrotowym cia
ł
a sztywnego nazywamy
taki ruch, w którym dwa punkty cia
ł
a s
ą nieruchome.
wnioski:
•
istnieje prosta
ł
ącząca punkty nieruchome, zwana osią obrotu
cia
ł
a sztywnego, przy czym o
ś ta może leżeć poza cia
ł
em,
•
torami punktów cia
ł
a w ruchu obrotowym s
ą okręgi po
ł
o
żone
w p
ł
aszczyznach prostopad
ł
ych do osi obrotu i
środkach
le
żących na tej osi,
•
promienie
ρ
wspomnianych kó
ł
równe s
ą odleg
ł
o
ściom
punktów cia
ł
a od osi obrotu,
•
drogi k
ątowe zakreślone przez różne punkty cia
ł
a s
ą dla
wszystkich punktów jednakowe i równe
KĄTOWI OBROTU
CIA
Ł
A
.

MT SS - w 11
38
Wobec powy
ższego
W ruchu obrotowym cia
ł
a sztywnego istnieje:
•
wspólny k
ąt obrotu ϕ,
•
wspólna pr
ędkość obrotowa (kątowa) ω i
•
wspólne przy
śpieszenie kątowe ɛ,
tzn.
dla dwóch dowolnych punktów A i B cia
ł
a sztywnego
zachodz
ą następujące zależności:
.
,
,
B
A
B
A
B
A
ε
ε
ω
ω
ϕ
ϕ
≡
≡
≡

MT SS - w 11
39
Wniosek
W ruchu obrotowym mo
żna mówić o:
•
k
ącie,
•
pr
ędkości kątowej i
•
przy
śpieszeniu kątowym cia
ł
a
przy czym
gdzie:
υ – prędkość liniowa punktu cia
ł
a,
a
t
– sk
ł
adowa styczna liniowego przy
śpieszenia punktu,
a
n
– sk
ł
adowa normalna liniowego przy
śpieszenia punktu.
ρ
ω
ρ
ε
ρ
ω
υ
⋅
=
⋅
=
⋅
=
2
,
,
n
t
a
a
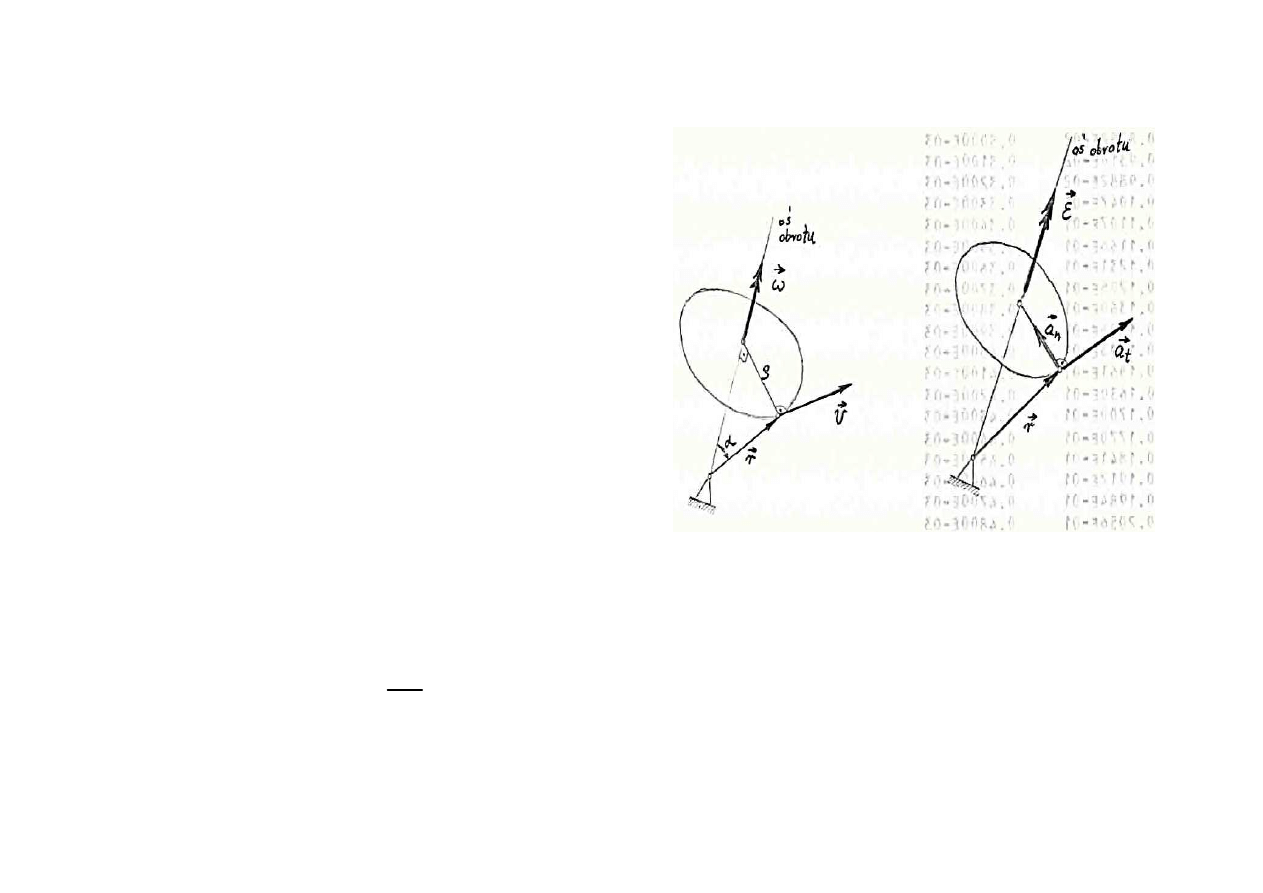
MT SS - w 11
40
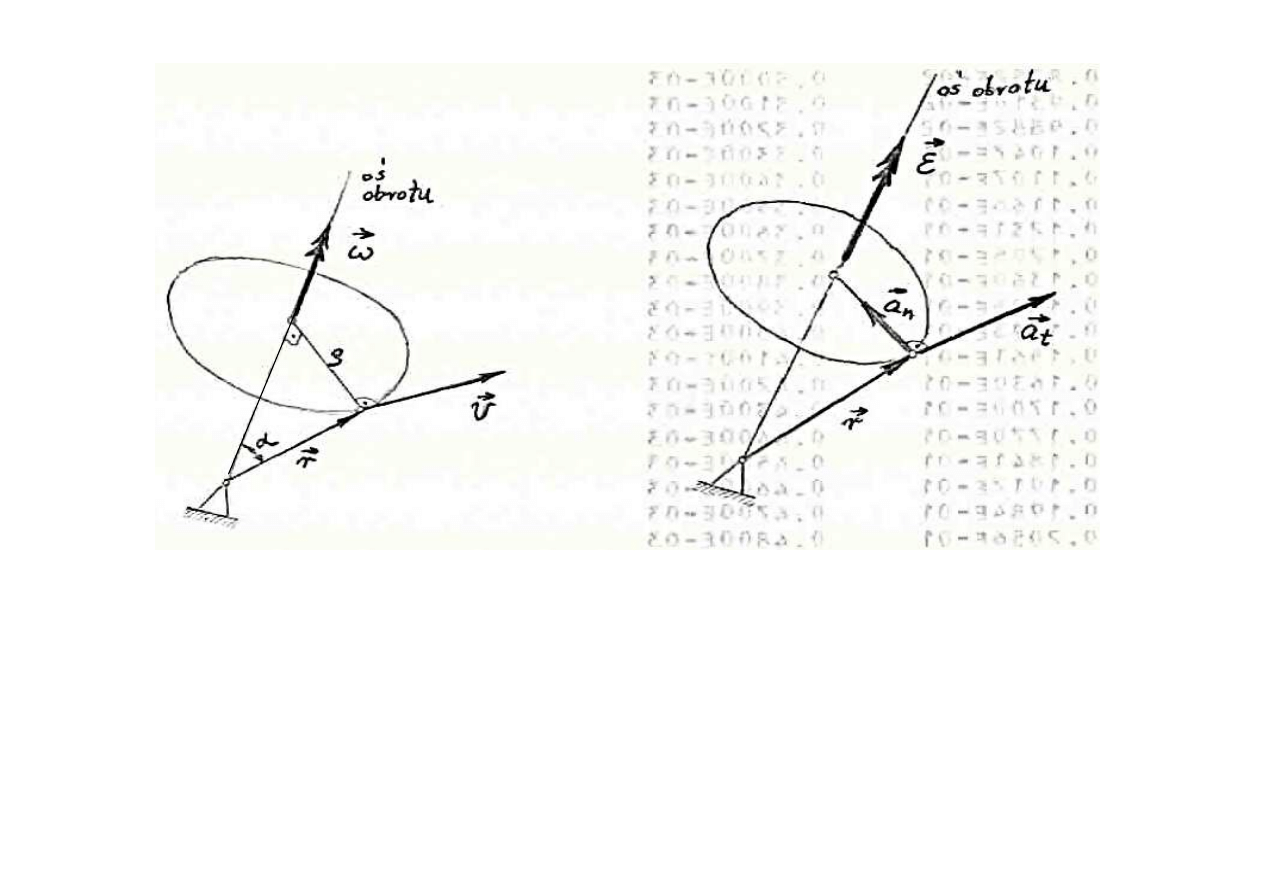
Wektor pr
ędkości kątowej
ω
ω
ω
ω:
•
le
ży na osi obrotu,
•
jest skierowany zgodnie z regu
ł
ą korkociągu,
•
jego d
ł
ugo
ść jest równa wartości prędkości kątowej.
Wektor r jest to promie
ń wektor określający po
ł
o
żenie punktu.
MT SS - w 11
41
Zależności:
→
→
→
•
→
→
→
→
→
+
=
=
⋅
=
⋅
⋅
=
×
=
n
t
a
a
a
r
r
,
,
sin
,
ω
ε
ρ
ω
α
ω
υ
ω
υ
→
→
→
→
→
→
×
=
×
=
υ
ω
ε
n
t
a
r
a
,
ρ
ω
ρ
ω
ω
υ
ω
π
υ
ω
ρ
ε
α
ε
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
=
2
2
sin
,
sin
n
t
a
r
a

MT SS - w 11
42
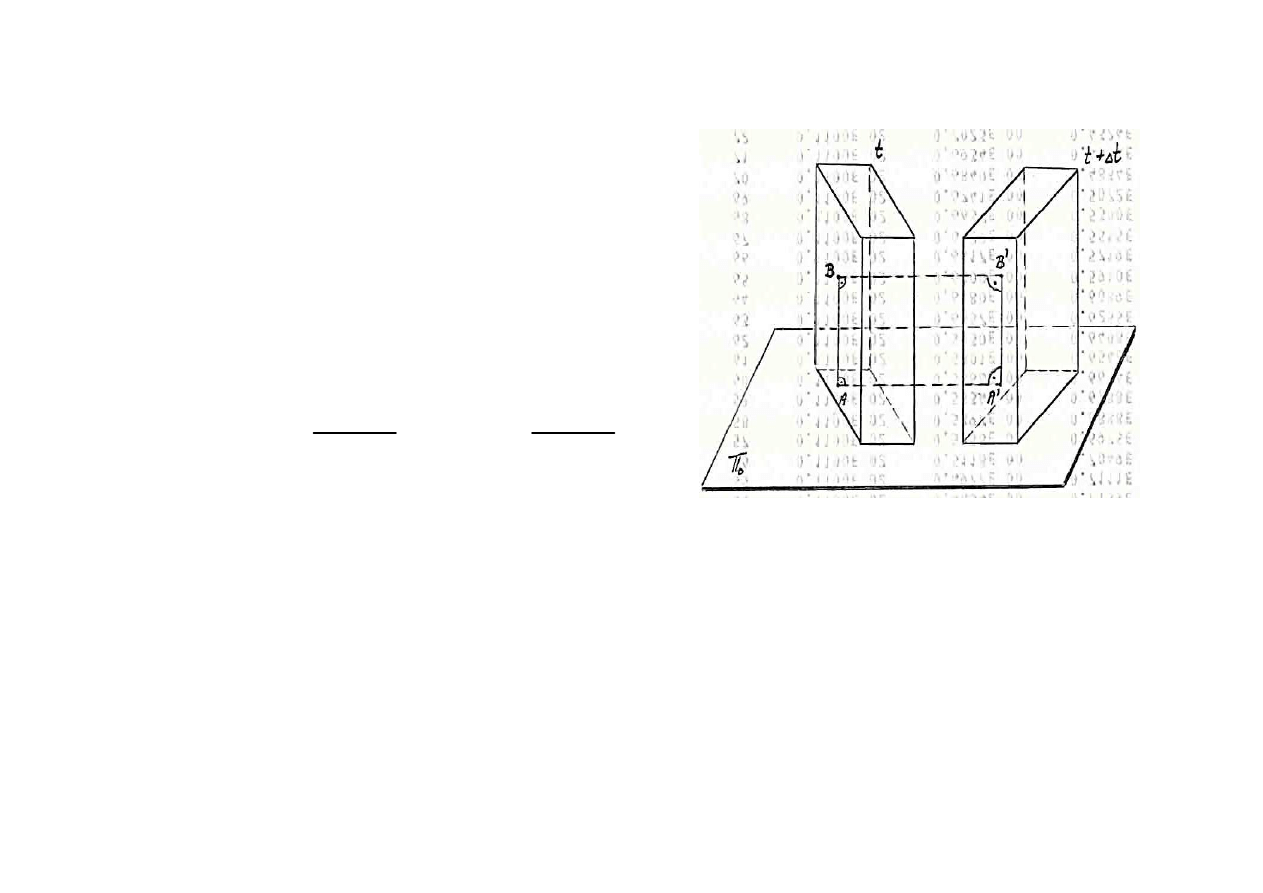
RUCH P
Ł
ASKI CIA
Ł
A SZTYWNEGO
Def. 3.
Ruchem p
ł
askim cia
ł
a sztywnego nazywamy
ruch, podczas którego wszystkie punkty cia
ł
a
poruszaj
ą się w p
ł
aszczyznach równoleg
ł
ych do
pewnej nieruchomej p
ł
aszczyzny zwanej
P
Ł
ASZCZYZNĄ KIERUJĄCĄ
.
Z powy
ższej definicji wynika,
że punkty leżące na prostych
prostopad
ł
ych do kierownicy
maj
ą jednakowe prędkości
i przy
śpieszenia.
MT SS - w 11
43
Zgodnie z definicj
ą i rysunkiem możemy napisać
nast
ępujące zależności:
st
ąd:
Tak wi
ęc, dla punktu B oraz dla punktu A, który jest rzutem
punktu B na kierownic
ę π
o
zachodzi nast
ępująca
zale
żność:
AA’ = BB’
.
lim
lim
0
0
t
B
B
t
A
A
t
t
∆
′
≡
∆
′
→
→
∆
→
→
∆
.
→
→
≡
B
A
υ
υ

MT SS - w 11
44
Wobec powy
ższego
Opis ruchu p
ł
askiego cia
ł
a sztywnego jest jednoznaczny
z opisem ruchu figury p
ł
askiej b
ędącej rzutem cia
ł
a
sztywnego na kierownic
ę.
Ponadto
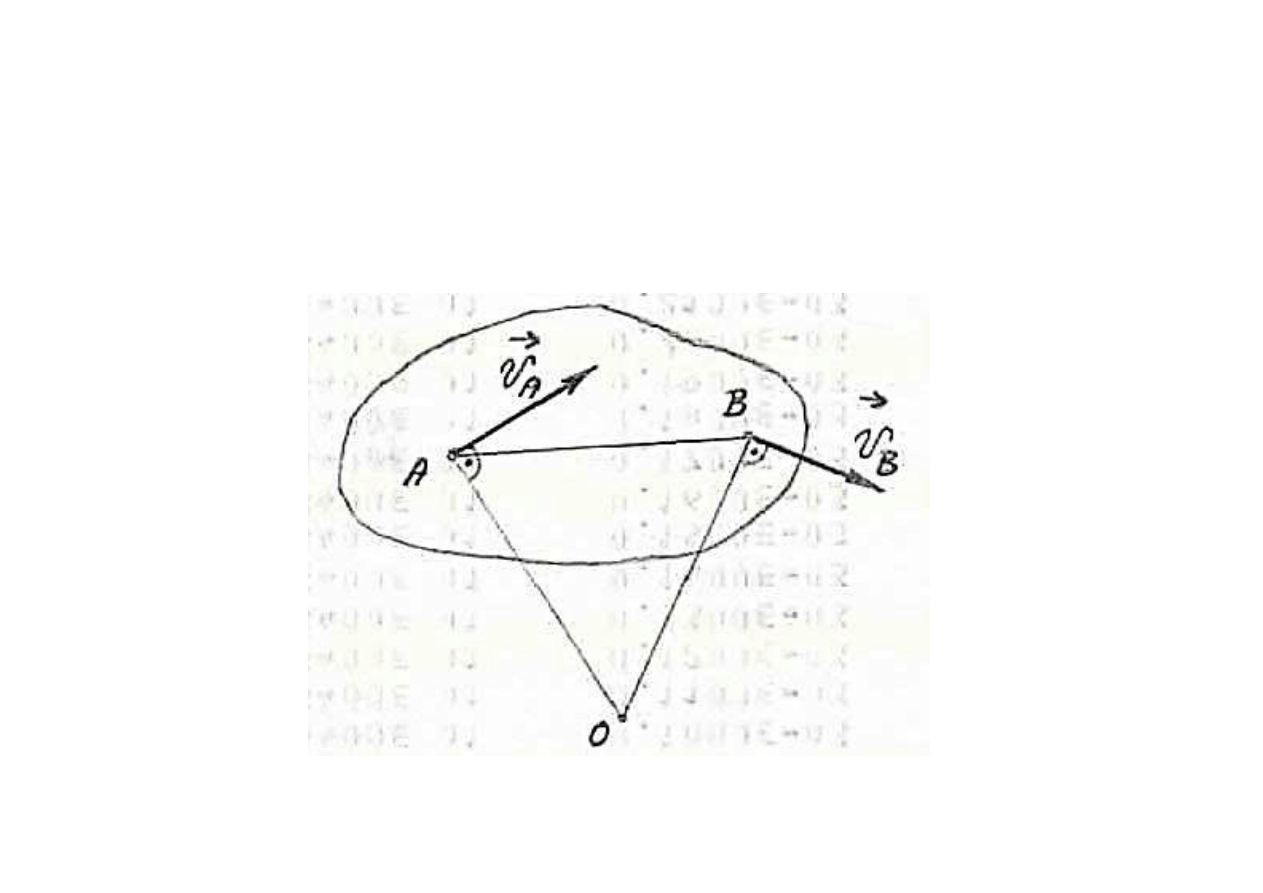
W ruchu p
ł
askim cia
ł
a sztywnego wyst
ępuje pewien
charakterystyczny punkt o pr
ędkości równej zero zwany
środkiem chwilowego obrotu.
Zatem
Def. A.
Środkiem chwilowego obrotu cia
ł
a sztywnego
nazywamy punkt sztywno zwi
ązany z cia
ł
em,
posiadaj
ący zerową prędkość ( ).
0
=
υ
MT SS - w 11
45
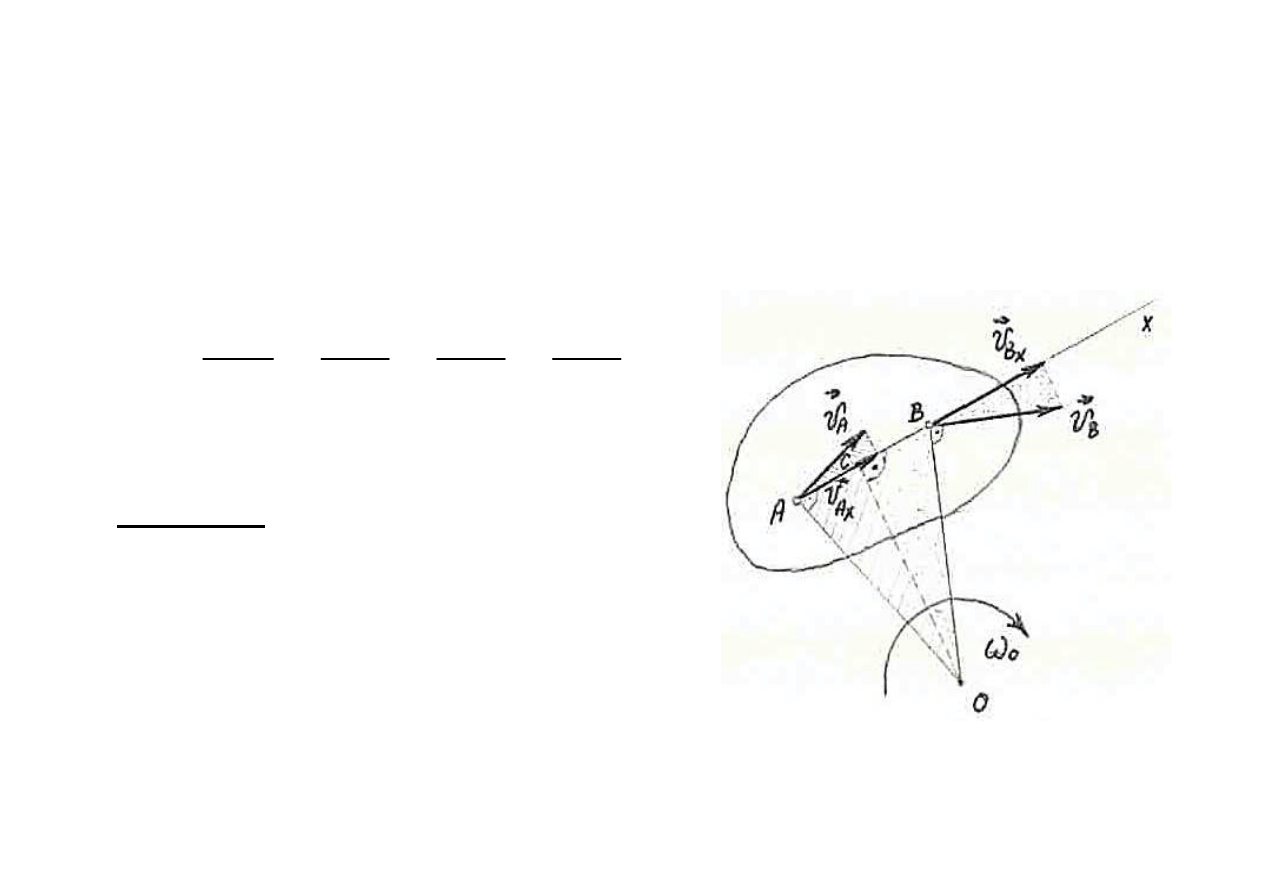
Środkiem chwilowego obrotu cia
ł
a le
ży na przecięciu
prostych prostopad
ł
ych do wektorów pr
ędkości punktów
cia
ł
a.
MT SS - w 11
46
W
ł
a
ściwością
ruchu p
ł
askiego jest to, i
ż stosunek
pr
ędkości do promienia wyprowadzonego ze środka
chwilowego obrotu jest jednakowy dla wszystkich punktów
i nazywamy go chwilow
ą prędkością kątową.
Wniosek:
Pr
ędkość w ruchu p
ł
askim cia
ł
a sztywnego
mo
żna obliczyć tak, jak w ruchu obrotowym
dooko
ł
a
środka chwilowego obrotu.
.
const
BO
CO
CO
AO
B
B
A
A
o
x
x
=
=
=
=
=
υ
υ
υ
υ
ω
MT SS - w 11
47
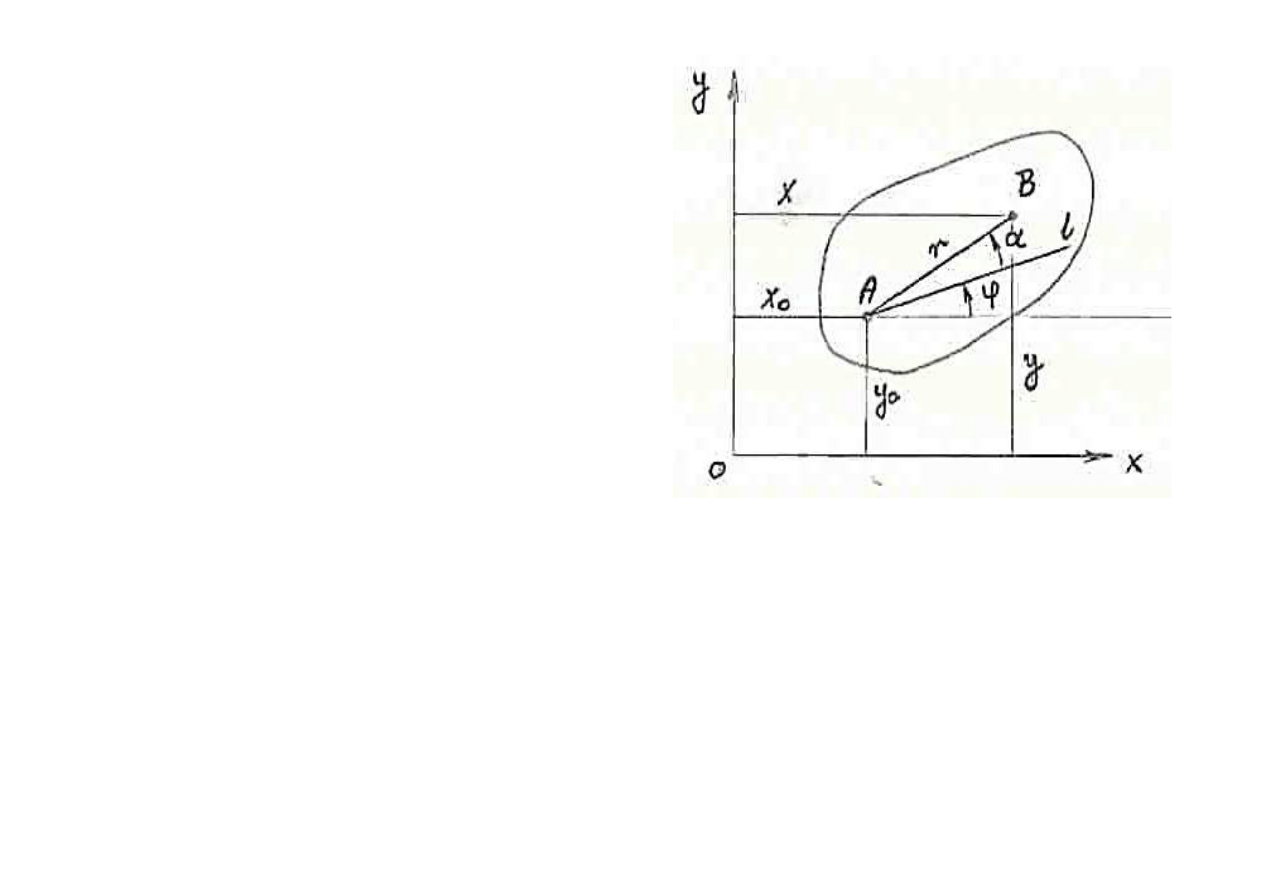
Analiza ruchu p
ł
askiego
Ruch figury p
ł
askiej w jej p
ł
aszczy
źnie może być
traktowany jako ruch z
ł
o
żony z:
•
ruchu postępowego
, którego pr
ędkość dowolnie
wybranego bieguna A oraz
•
ruchu obrotowego
figury wokó
ł
tego bieguna.
Pr
ędkość kątowa
ruchu obrotowego figury
nie zale
ży przy tym
od wyboru bieguna.
MT SS - w 11
48
A – biegun zwi
ązany z figurą p
ł
ask
ą,
l – prosta zwi
ązana z figurą p
ł
ask
ą,
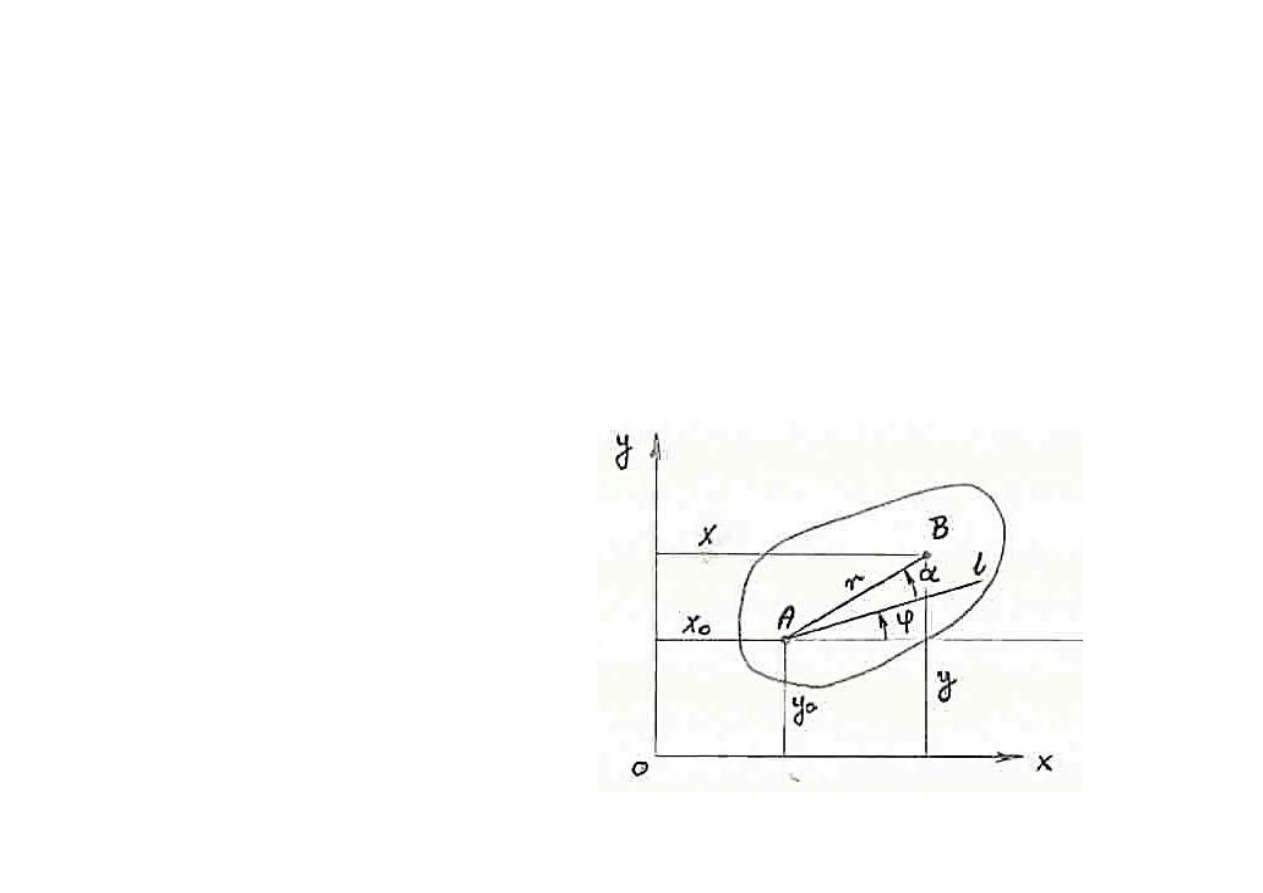
ϕ – kąt obrotu figury p
ł
askiej.
Ruch figury p
ł
askiej opisuj
ą w sposób jednoznaczny
nast
ępujące
równania ruchu p
ł
askiego
:
( )
( )
( )
t
f
t
f
y
t
f
x
A
A
3
2
1
,
,
=
=
=
ϕ
MT SS - w 11
49
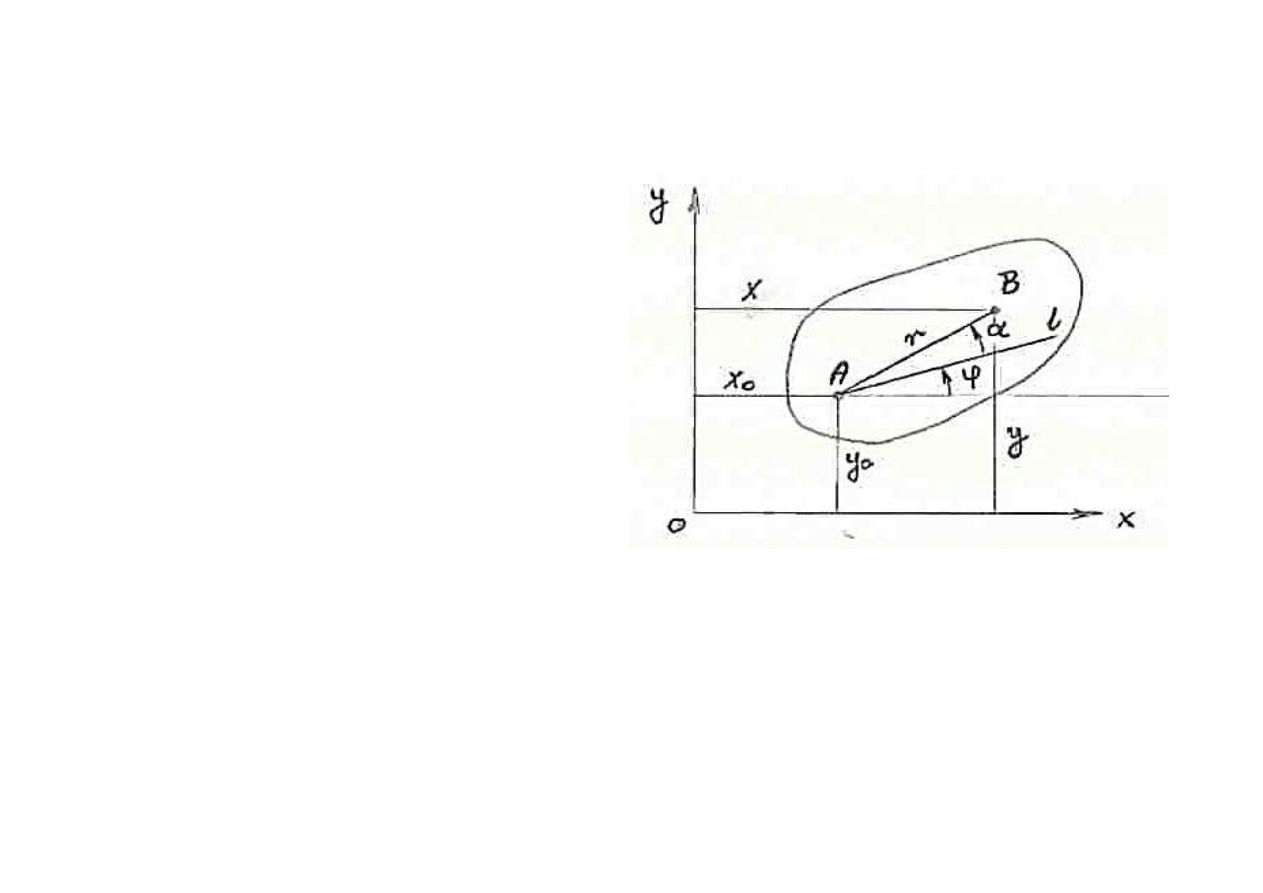
Znaj
ąc równania ruchu p
ł
askiego, cia
ł
a, mo
żemy wyznaczyć
równania ruchu dowolnego punktu okre
ślonego na tym
ciele.
Równania ruchu punktu B.
(
)
(
)
,
sin
,
cos
ϕ
α
ϕ
α
+
+
=
+
+
=
r
y
y
r
x
x
A
A
Ró
żniczkując w/w równania
wzgl
ędem czasu otrzymujemy
Zale
żności określające prędkość i przyśpieszenie punktu B.
(
)
(
)
,
cos
,
sin
ϕ
α
ϕ
υ
ϕ
α
ϕ
υ
+
+
=
=
+
−
=
=
•
•
•
•
•
•
r
y
y
r
x
x
A
y
A
x

MT SS - w 11
50
(
)
(
)
,
cos
,
sin
ϕ
α
ϕ
υ
ϕ
α
ϕ
υ
+
+
=
=
+
−
=
=
•
•
•
•
•
•
r
y
y
r
x
x
A
y
A
x
Ró
żniczkowanie wyrażenia określające prędkość
otrzymujemy wyra
żenia określające przyśpieszenie punktu B.
Jest to zatem ruch z
ł
o
żony.
(
)
(
)
(
)
(
)
.
sin
cos
,
cos
sin
2
2
ϕ
α
ϕ
ϕ
α
ϕ
υ
ϕ
α
ϕ
ϕ
α
ϕ
υ
+
−
+
+
=
=
=
+
−
+
−
=
=
=
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
r
r
y
y
a
r
r
x
x
a
A
y
y
A
x
x

MT SS - w 11
51
Sk
ł
adowe ruchu p
ł
askiego
Za
ł
o
żenie 1.
cia
ł
o porusza si
ę ruchem postępowym
wraz z biegunem, tzn.
ϕ = const.
W tym przypadku mamy:
•
•
=
=
A
y
A
x
y
x
post
post
υ
υ
,
A
y
A
post
x
y
a
x
a
post
•
•
•
•
=
=
,

MT SS - w 11
52
Za
ł
o
żenie 2.
istnieje tylko ruch cia
ł
a dooko
ł
a bieguna
A, ruch przy którym k
ąt obrotu zmienia
si
ę tak, jak w badanym ruchu p
ł
askim.
W tym przypadku mamy:
(
)
(
)
(
)
(
)
ϕ
α
ϕ
ϕ
α
ϕ
ϕ
α
ϕ
ϕ
α
ϕ
+
−
+
+
=
+
−
+
−
=
•
•
•
•
•
•
sin
cos
,
cos
sin
2
2
r
r
a
r
r
a
obr
obr
y
x
(
)
(
)
ϕ
α
ϕ
υ
ϕ
α
ϕ
υ
+
+
=
+
−
=
•
•
cos
,
sin
r
r
obr
obr
y
x
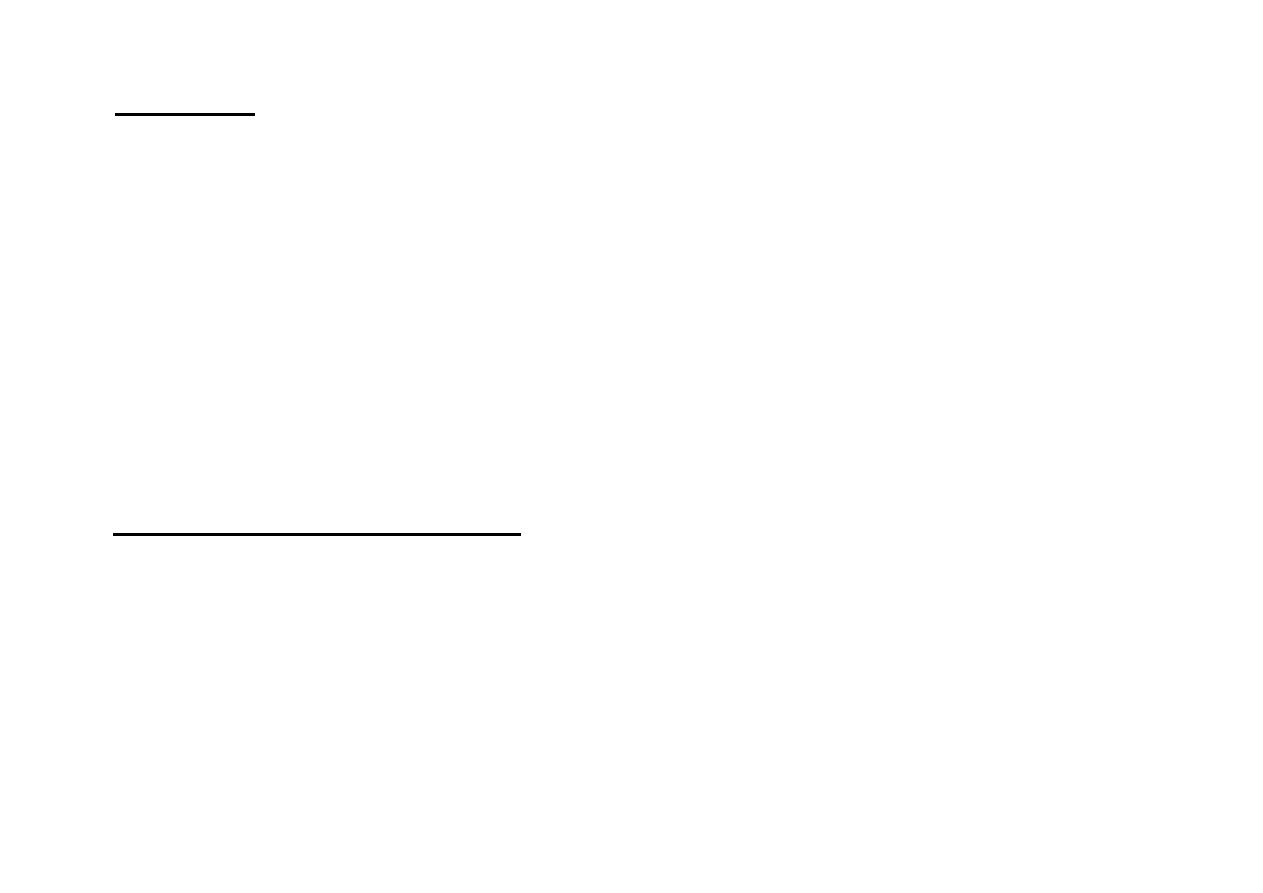
MT SS - w 11
53
wniosek.
Dowolny punkt B cia
ł
a sztywnego b
ędącego w
ruchu p
ł
askim posiada
dwie sk
ł
adowe ruchu
:
obr
post
obr
post
y
y
y
x
x
x
υ
υ
υ
υ
υ
υ
+
=
+
=
,
obr
post
obr
post
y
y
y
x
x
x
a
a
a
a
a
a
+
=
+
=
,
W zapisie wektorowym:
obr
post
obr
post
a
a
a
→
→
→
→
→
→
+
=
+
=
,
υ
υ
υ
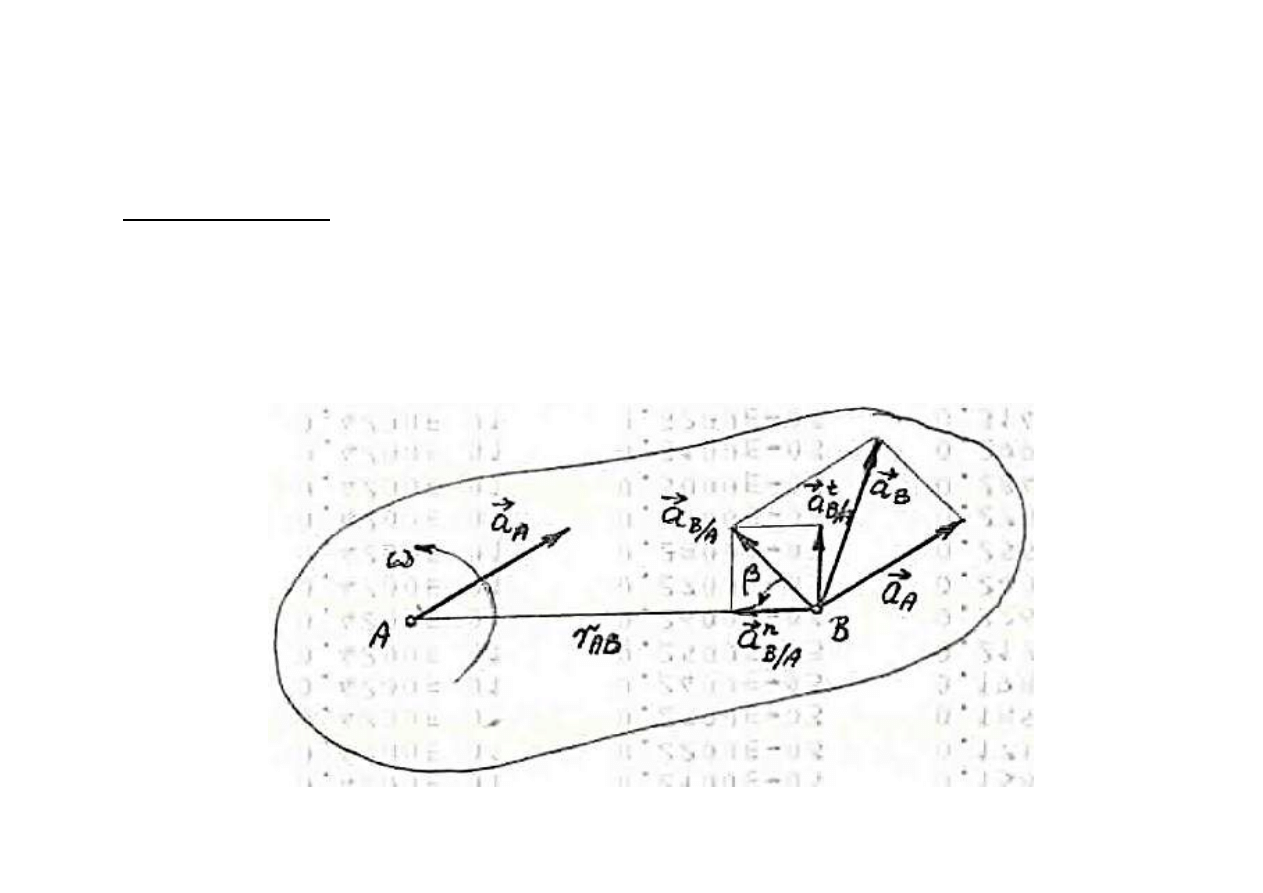
MT SS - w 11
54
Na podstawie zapisu wektorowego
mo
ż
na stwierdzi
ć
:
Przy
ś
pieszenie dowolnego punktu B figury płaskiej poruszaj
ą
cej si
ę
w swojej
płaszczy
ź
nie równe jest sumie geometrycznej przy
ś
pieszenia dowolnie
wybranego
bieguna
A
oraz
przy
ś
pieszenia
punktu
B
wzgl
ę
dem
bieguna A.
obr
post
obr
post
a
a
a
→
→
→
→
→
→
+
=
+
=
,
υ
υ
υ

MT SS - w 11
55
Mo
żemy zatem napisać następujące zależności:
n
t
A
B
A
B
A
B
A
B
A
B
a
a
a
a
a
a
/
/
/
/
,
→
→
→
→
→
→
+
=
+
=
→
→
→
→
→
×
=
AB
AB
t
r
r
a
A
B
ε
ε
,
/
→
→
→
→
→
→
×
×
=
AB
AB
n
r
r
a
A
B
ω
ω
ω
,
/
MT SS - w 11
56
Ze wzgl
ędu na to, że:
Zatem, warto
ści bezwzględne przyśpieszenia
stycznego i normalnego wyra
żą się zależnościami:
a
B/A
t
= ε · r
AB
, a
B/A
n
=
ω
2
· r
AB
,
,
,
→
→
→
→
AB
AB
r
r
ω
ε
( ) ( )
.
,
2
4
2
2
/
2
/
/
const
tg
r
a
a
a
AB
n
A
B
t
A
B
A
B
=
⇒
=
+
=
+
=
β
ω
ε
β
ω
ε
Warto
ść bezwzględna wektor a
B/A
jest proporcjonalna do odleg
ł
o
ści
punktu A od punktu B, natomiast k
ąt β jest wartością sta
ł
ą.

MT SS - w 11
57
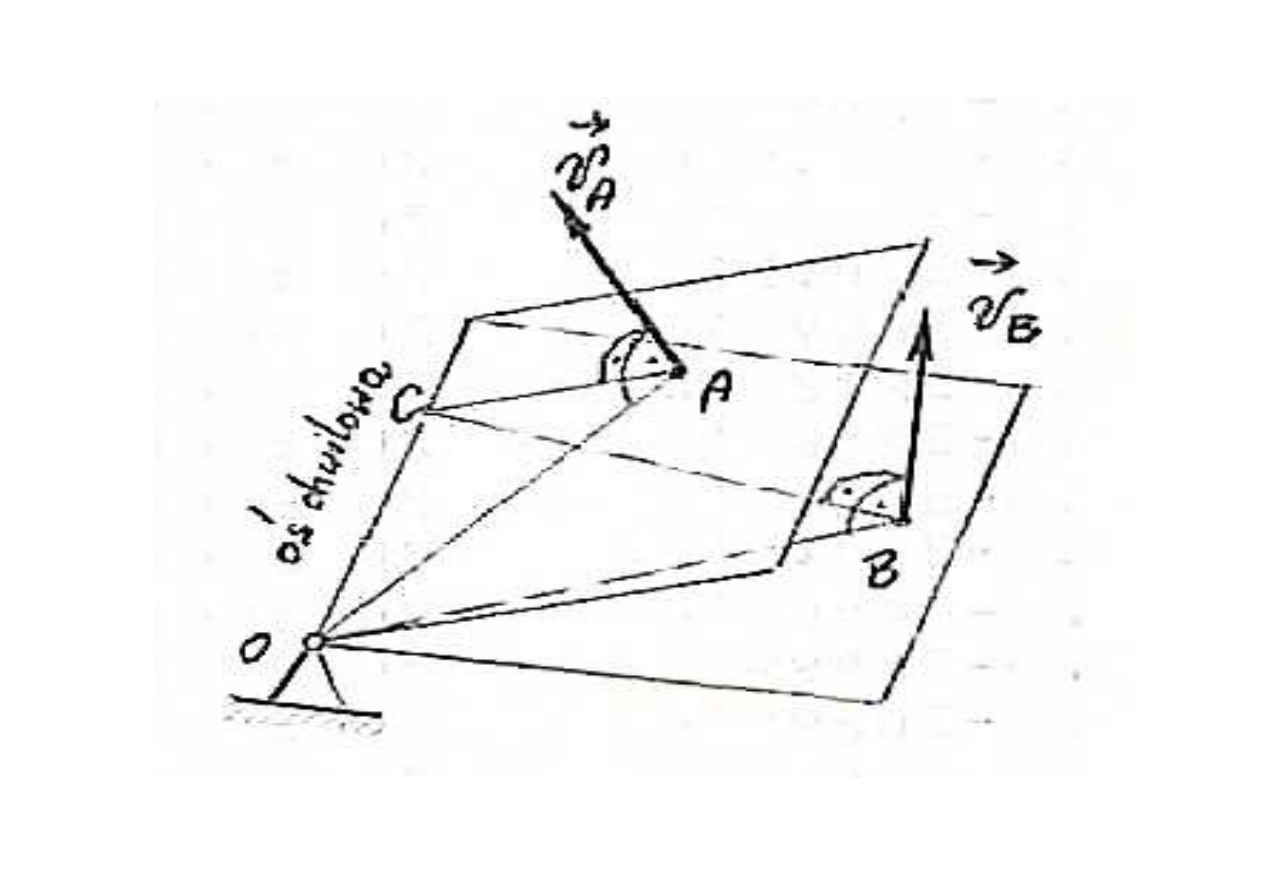
RUCH KULISTY CIA
Ł
A SZTYWNEGO
Def. 4.
Ruchem kulistym cia
ł
a sztywnego nazywamy
taki ruch, w którym jeden punkt cia
ł
a jest
nieruchomy.
W ruchu kulistym mo
żemy wyróżnić tzw.
OŚ CHWILOWEGO OBROTU CIA
Ł
A
.
Def. B.
Osi
ą chwilowego obrotu cia
ł
a doskonale
sztywnego nazywamy prost
ą, sztywno
zwi
ązaną z cia
ł
em, której pr
ędkość jest równa
zero.
O
ś chwilowego obrotu przechodzi przez środek ruchu kulistego i leży na
przeci
ęciu p
ł
aszczyzn prostopad
ł
ych do wektorów pr
ędkości.
MT SS - w 11
58
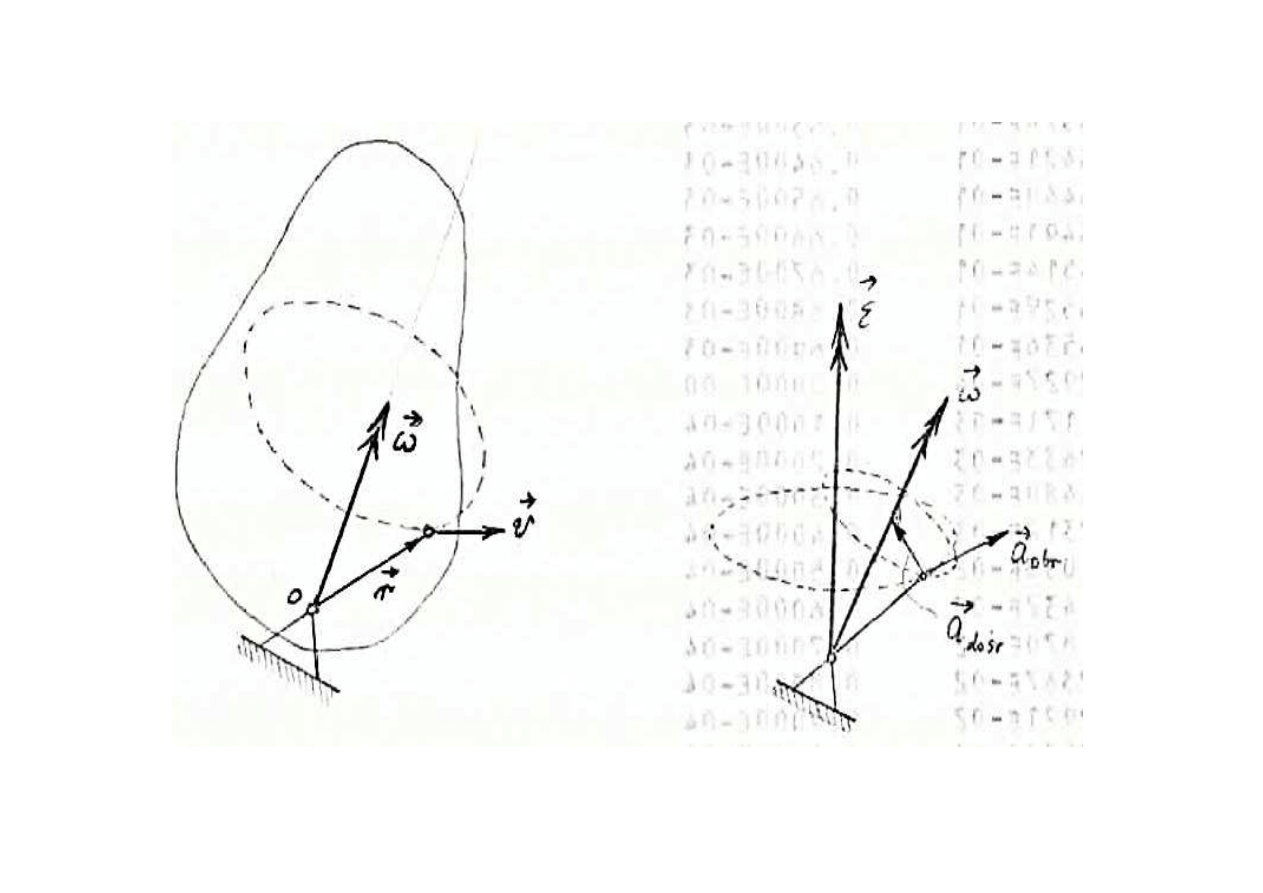
MT SS - w 11
59
W ruchu kulistym pr
ędkość dowolnego punktu
cia
ł
a okre
ślamy z zależności:
gdzie jest wektorem pr
ędkości kątowej.
Wektor pr
ędkości kątowej leży na osi chwilowego obrotu
lub jest do niej prostopad
ł
y.
Dw
.
st
ąd
→
→
•
→
→
×
=
=
r
r
ω
υ
→
ω
0
def
A
OA
=
×
=
→
→
ω
υ
OA
→
ω
MT SS - w 11
60
MT SS - w 11
61
Zale
żności analityczne spe
ł
niane w ruchu kulistym cia
ł
a
sztywnego
υ
ω
ε
ω
ω
υ
ω
υ
×
+
×
=
×
+
×
=
=
×
=
•
•
•
r
r
r
a
r ,
•
•
=
=
r
υ
ω
ε
,
Ale
zatem
,
doś
obr
a
a
r
=
×
=
×
υ
ω
ε
,
doś
obr
a
a
a
+
=

MT SS - w 11
62
gdzie:
a
obr
– przy
śpieszenie obrotowe obliczane tak, jak
przy
śpieszenie styczne przy obrocie dooko
ł
a
wektora ε z przy
śpieszeniem ε.
a
dośr
– przy
śpieszenie dośrodkowe obliczane tak, jak
przy
śpieszenie normalne w ruchu obrotowym
dooko
ł
a wektora ω z pr
ędkością ω.

MT SS - w 11
63
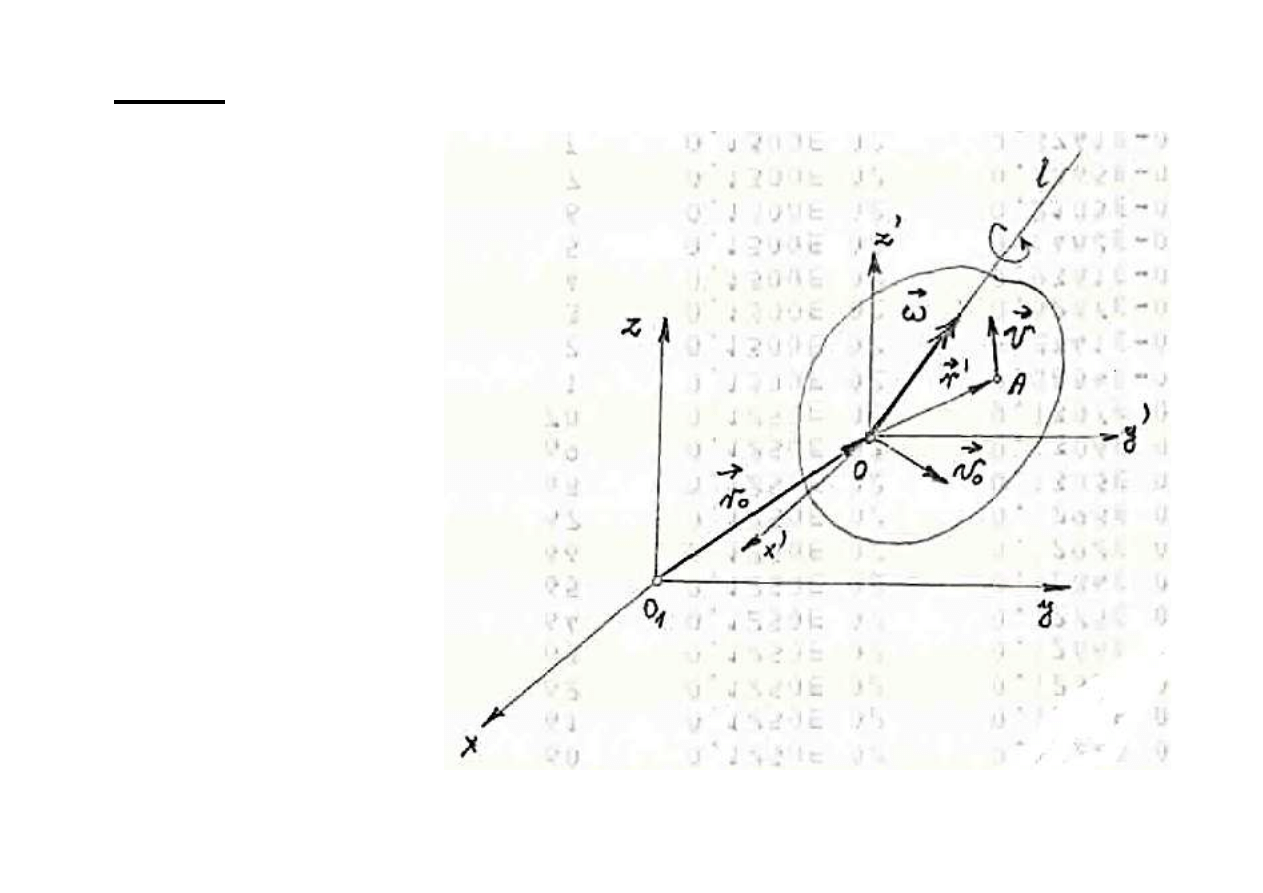
RUCH OGÓLNY CIA
Ł
A SZTYWNEGO
Def. 5.
Ruchem ogólnym cia
ł
a sztywnego nazywamy
ruch nie podlegaj
ący żadnym ograniczeniom.
Pr
ędkość dowolnego punktu A cia
ł
a sztywnego r uchu
ogólnym równa jest sumie geometrycznej:
pr
ędkości dowolnie obranego bieguna O należącego do
tego cia
ł
a oraz
pr
ędkości punktu A w chwilowym ruchu obrotowym
cia
ł
a wokó
ł
osi chwilowej przechodz
ącej przez punkt O
Pr
ędkość kątowa tego ostatniego ruchu nie zależy
od wyboru tego bieguna.
MT SS - w 11
64
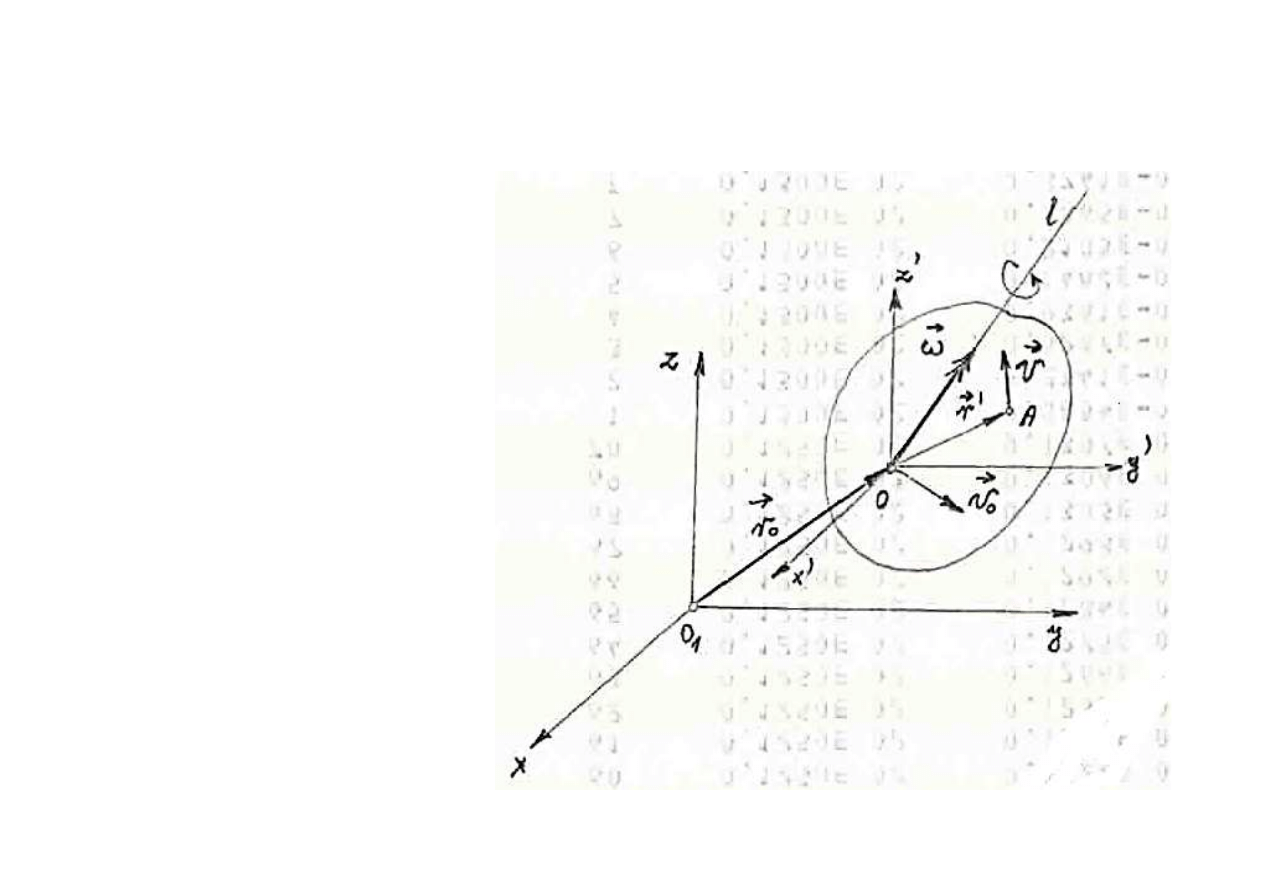
Zatem:
Ruch ogólny
cia
ł
a sztywnego mo
że być traktowany
jako
ruch z
ł
ożony
z:
•
ruchu post
ępowego i
•
chwilowego
ruchu obrotowego.
MT SS - w 11
65
•
Pr
ędkość ruchu postępowego zależy od wyboru
bieguna;
•
Pr
ędkość kątowa ruchu obrotowego nie zależy od
wyboru bieguna.
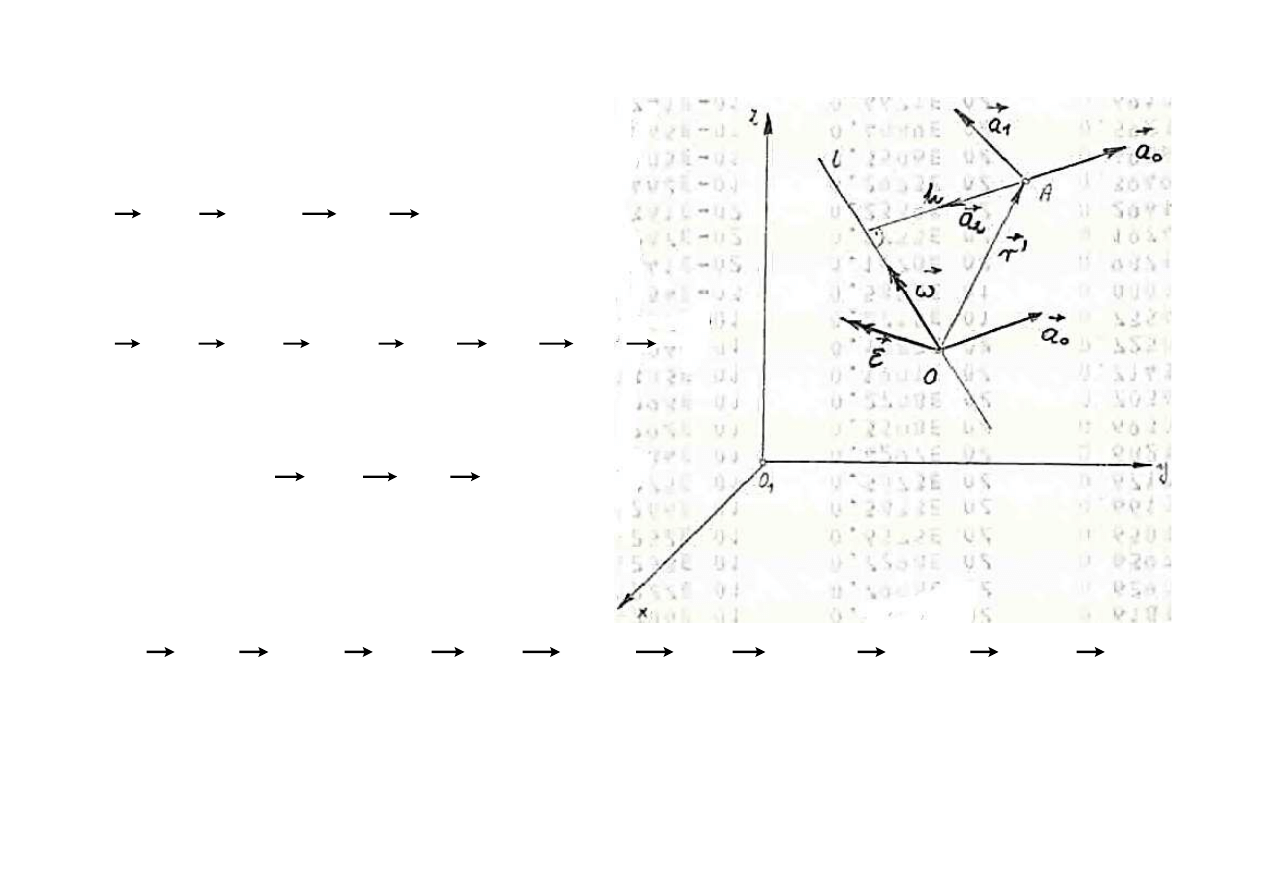
MT SS - w 11
66
Zależności analityczne
obowiązujące w ruchu ogólnym cia
ł
a
sztywnego
•
•
•
×
+
×
+
=
=
×
+
=
'
'
,
'
r
r
a
r
o
o
ω
ε
υ
υ
ω
υ
υ
ale
zatem
gdzie
'
'
r
r
×
=
•
ω
2
1
)
'
(
'
a
a
a
r
r
a
o
o
+
+
=
×
×
+
×
+
=
•
ω
ω
ε
υ
h
a
⋅
=
2
2
ω
Wyszukiwarka
Podobne podstrony:
mt ss w 15 2014 lato
mt ss w 12 2014 lato
fd ss w3 2014 lato
fd ss w2 2014 lato
fd ss w1 2014 lato
mt ss w 1 2014 lato
mt ss w 5 2014 lato
mt ss w 3 2014 lato
mt ss w 4 2014 lato
mt ss w 8 2014 lato
mt ss w 7 2014 lato
mt ss w 9 2014 lato
mt ss w 6 2014 lato
Rozwój form kancelaryjnych 09.11.2014 Sroka, Zarządzanie dokumentacją, archiwistyka i infobrokerstwo
EKONOMIA MIĘDZYNARODOWA 16.11.2014-uzupełnienie, V rok, Wykłady, Ekonomia międzynarodowa
projekt opb& 11 2014
więcej podobnych podstron