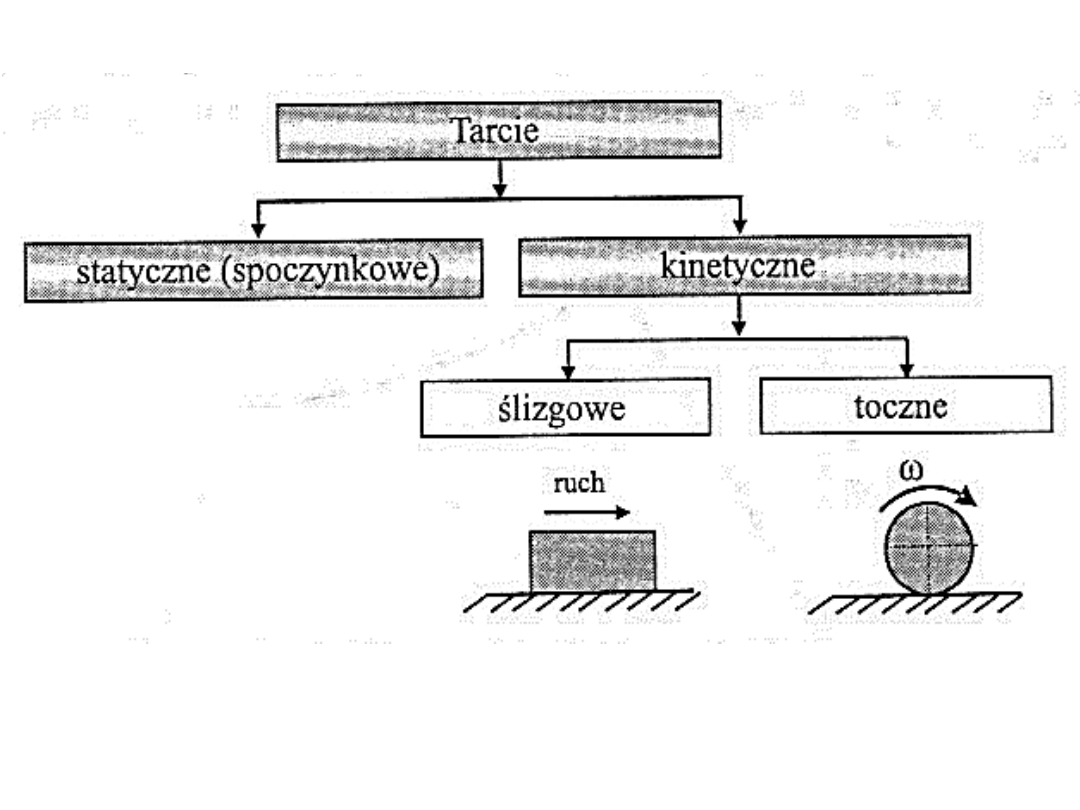
ZJAWISKO TARCIA
w-7
MT_SS - w 7
1
Bezpieczeństwo konstrukcji budowlanej jest zapewnione
wtedy, gdy spełnione są dwa zasadnicze warunki:
1. Konstrukcja musi być odpowiednio sztywna;
2. Konstrukcja musi być stateczna, tzn. nie może się ani
obrócić (przewrócić), ani przesunąć.
Przesunięcie się konstrukcji jest prawie zawsze
równoznaczne z katastrofą.
MT_SS - w 7
2
MT_SS - w 7
3
Przykłady
:
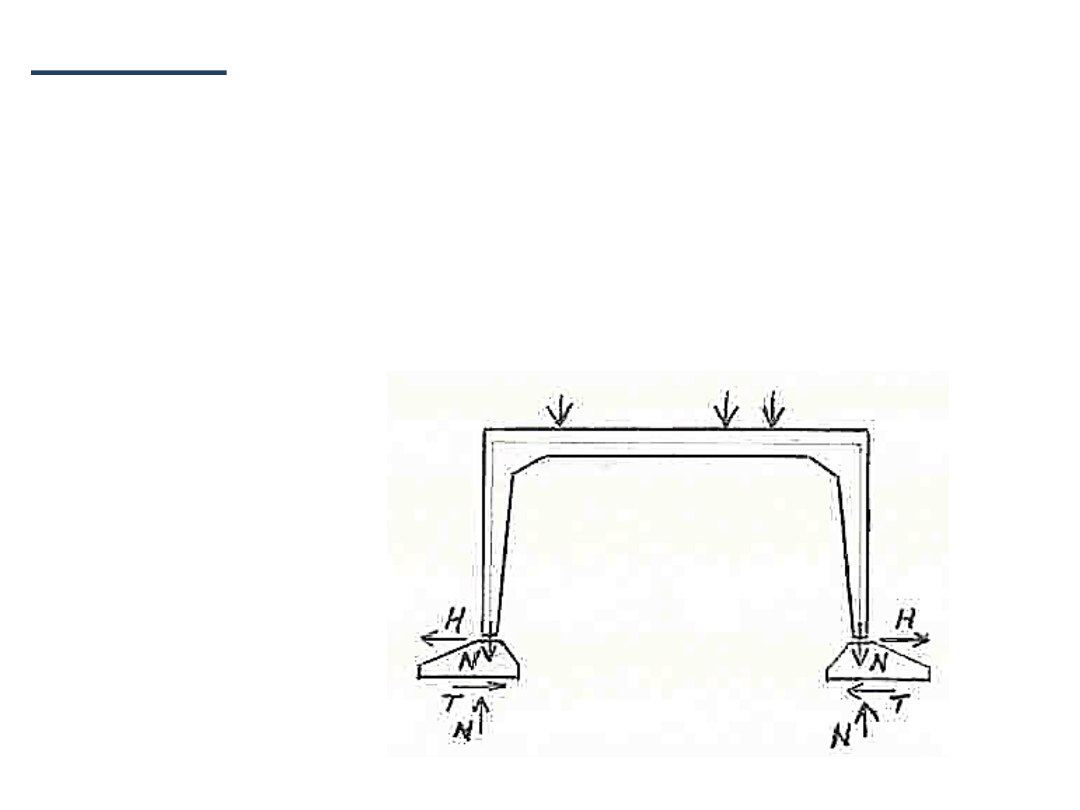
1. Obciążona rama
• Generowane są siły rozporu
H
, przekazywane na
fundament
• Siły
H
musi być zrównoważony siłą
T
występującą w
płaszczyźnie zetknięcia się stopy fundamentowej z
gruntem.
Siła
T
to sia tarcia.
MT_SS - w 7
4
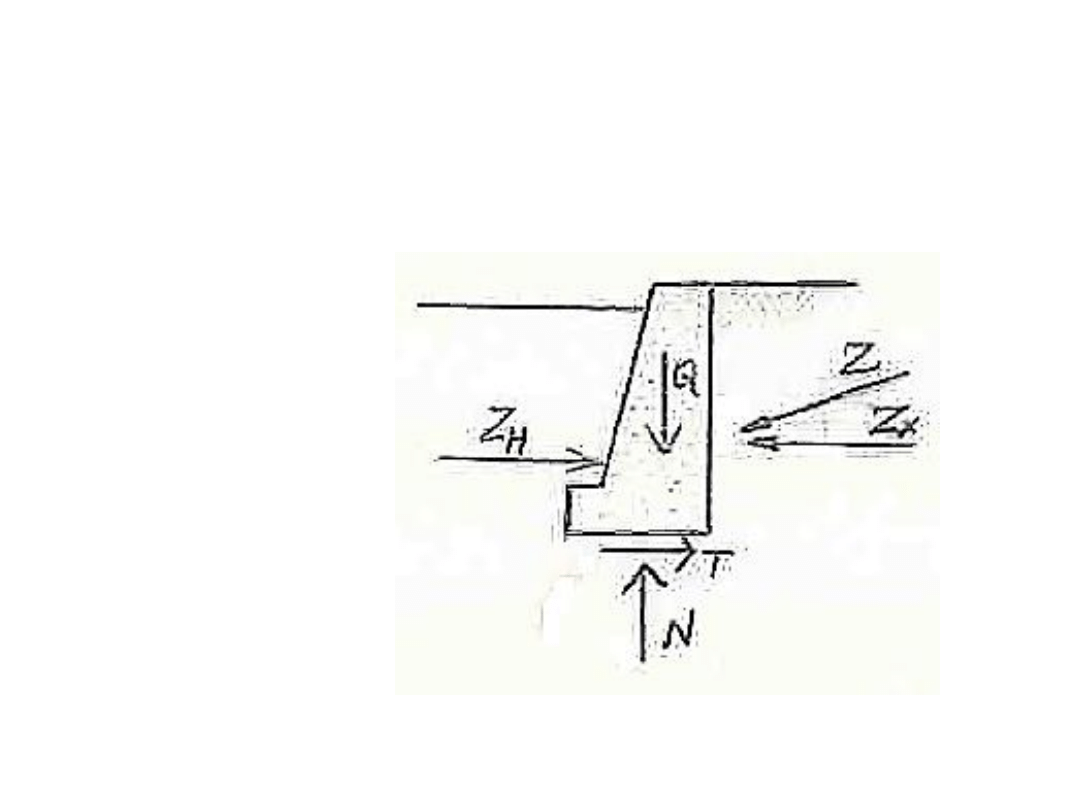
2. Mur oporowy
• Obciążony jest parciem wypadkowym
Z
w
• Przesunięciu muru przeciwstawia się siła tarcia
T
,
występująca w zetknięcia się muru z podłożem
gruntowym.
Z
w
= Z
x
– Z
H
Z
H
– parcie wody
Z
x
– składowa pozioma parcia ciała sypkiego
MT_SS - w 7
5
• Wartość siły tarcia zależy od
chropowatości
stykających
się powierzchni;
• W przypadku
idealnie gładkich powierzchni
, tarcie nie
występuje (
T
= 0 );
• Aby konstrukcje przedstawione w przykładach nie uległy
zniszczeniu,
siła
tarcia
powinna
co
najmniej
zrównoważyć siłę
H
i
Z
w
T ≥ H, T ≥ Z
w
;
• Jeśli powyższe warunki nie są spełnione, nastąpi poślizg
fundamentu i zniszczenie konstrukcji
.
MT_SS - w 7
6
Teoria
:
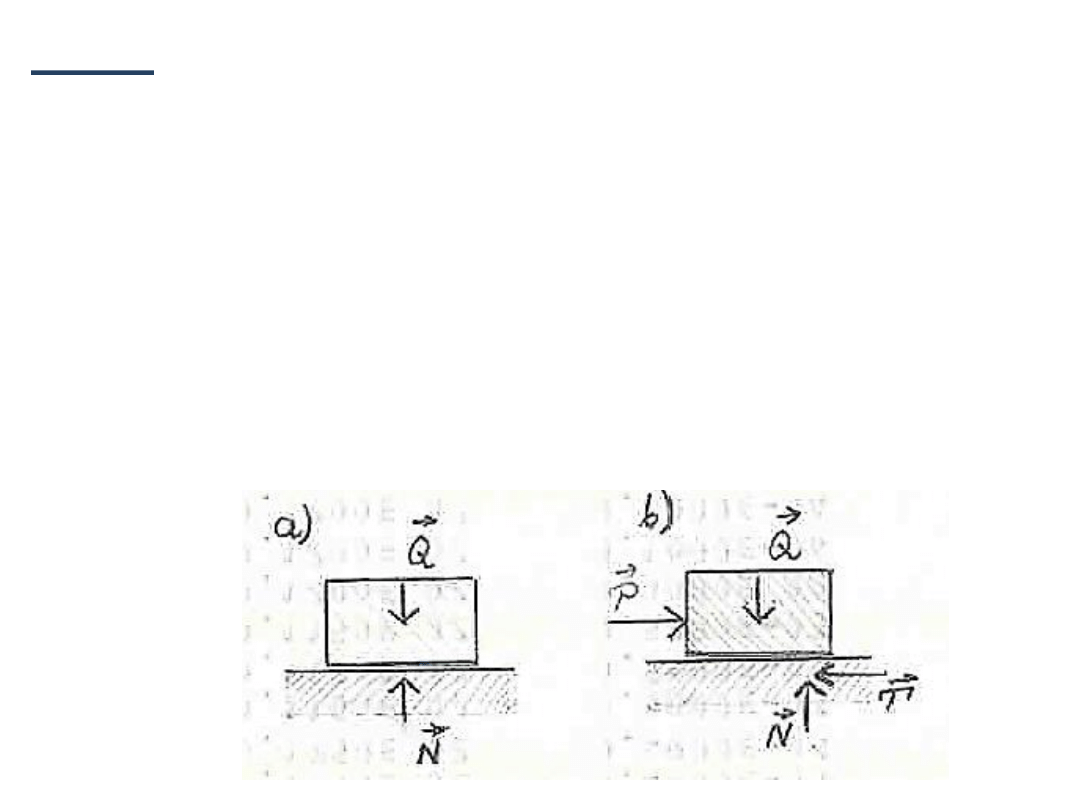
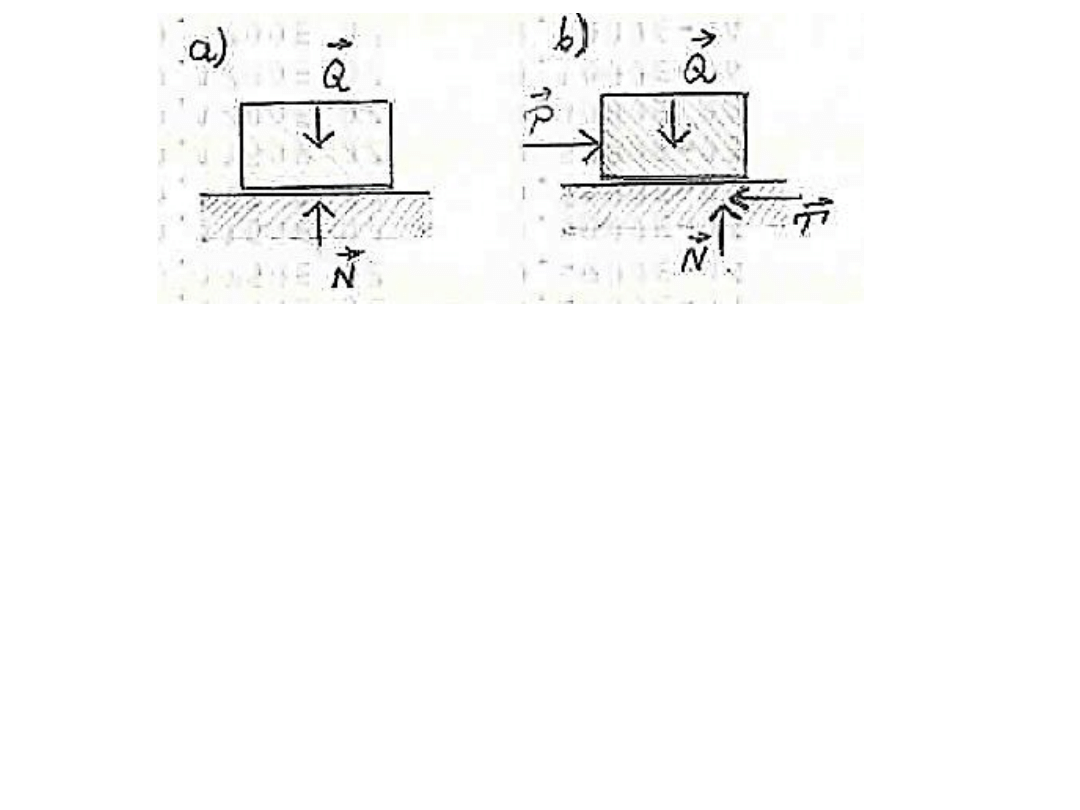
• Jeśli ciało o ciężarze Q spoczywa na podłożu poziomym,
to wywołuje ono reakcję
N = Q
skierowaną przeciwnie i prostopadle do płaszczyzny
styku
Q
N
Q
N
,
MT_SS - w 7
7
• Gdy do rozważanego ciała przyłożymy siłę P, to w
płaszczyźnie styku powstanie odpór w postaci siły tarcia
P
T
P
T
,
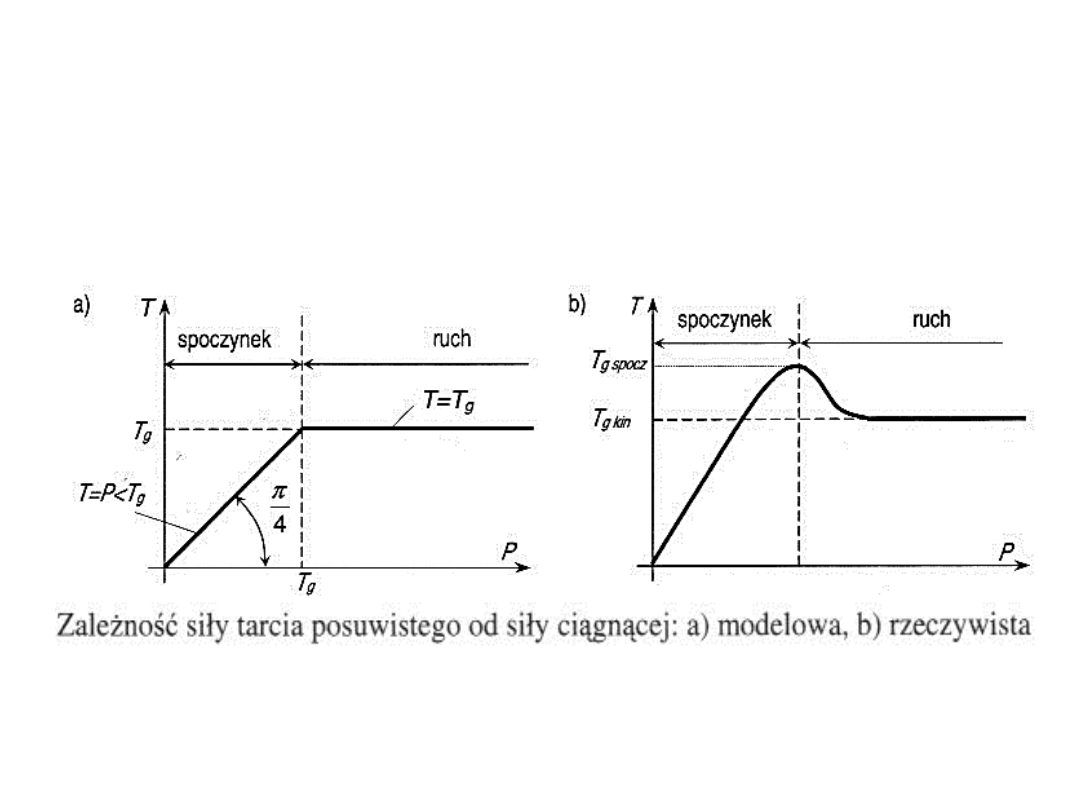
• Przy wzroście siły P wzrastać będzie proporcjonalnie siła
tarcia T, przy czym ciało pozostanie w spoczynku.
Tarcie występujące w stanie spoczynku ciała nazywamy
tarciem spoczynkowym
.
MT_SS - w 7
8
• Gdy siła P osiągnie pewną
graniczną wartość
, siła tarcia
osiągnie swoją wartość maksymalną, przy której ciało
będzie trwać jeszcze w równowadze, lecz po
przekroczeniu tej wartości nastąpi przesuwanie się ciała
w kierunku siły P.
Tarcie występujące podczas ruchu stykających się ciał
nazywamy
tarciem kinematycznym
.
MT_SS - w 7
9
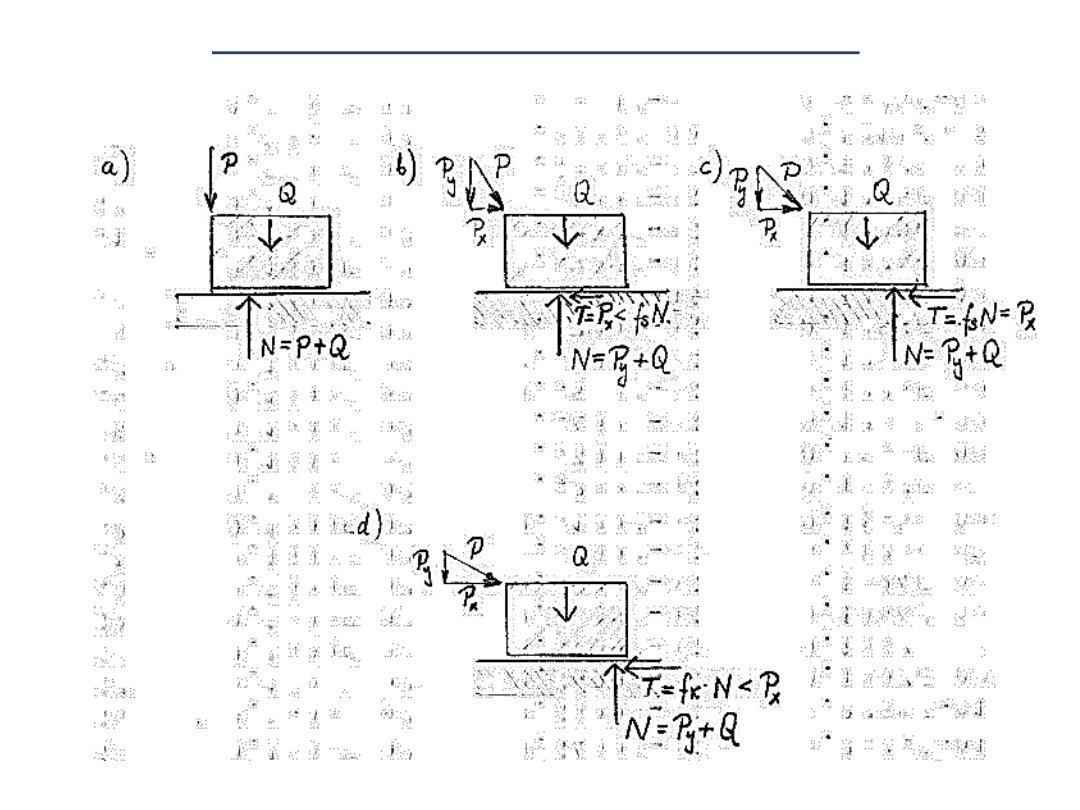
• Wartość siły tarcia zależy od:
• wartości nacisku normalnego na płaszczyznę styku,
• szorstkości stykających się ciał, charakteryzowanej
współczynnikiem tarcia.
oznaczenia:
f
s
– współczynnik tarcia statycznego,
f
k
– współczynnik tarcia kinetycznego.
W zagadnieniach budowlanych interesować nas będzie
tylko tarcie statyczne, którego wartość wyrażamy wzorem.
T = f
s
·N
MT_SS - w 7
10
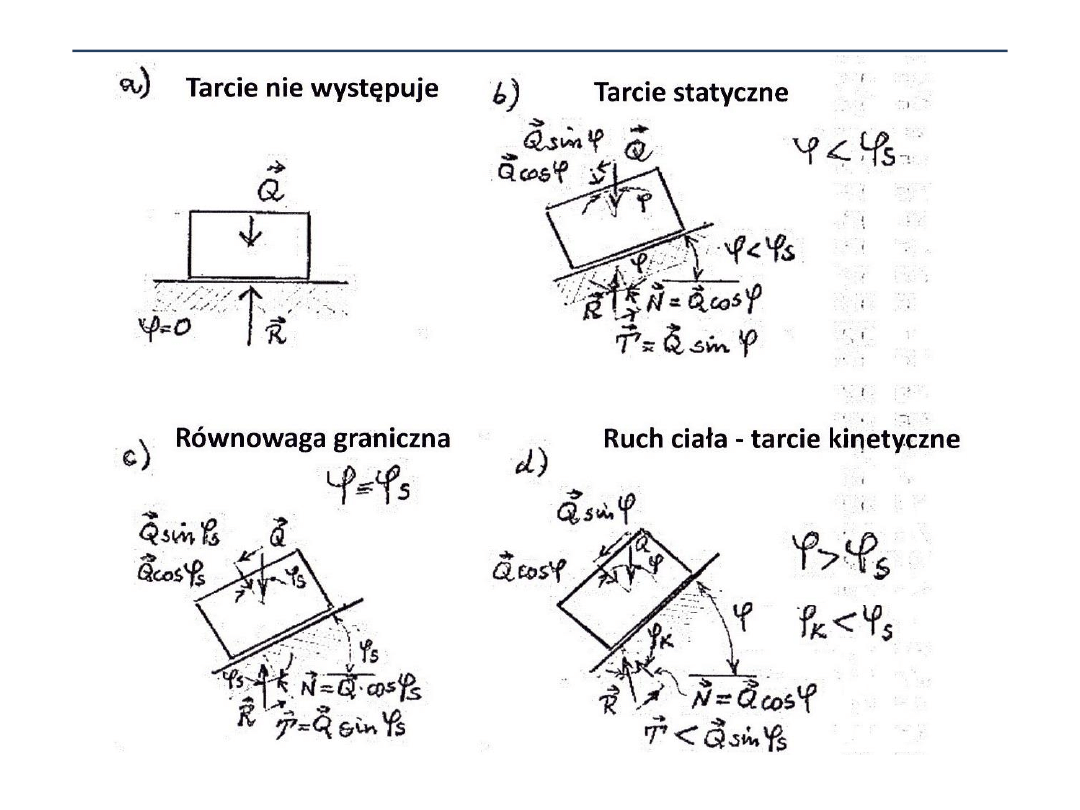
współczynnik tarcia – doświadczenie:
Tarcie nie występuje
Tarcie statyczne
Tarcie statyczne –
równowaga graniczna
Ruch ciała - tarcie kinetyczne
MT_SS - w 7
11
Wyznaczanie współczynników tarcia – doświadczenie:
MT_SS - w 7
12
1. Zwiększamy kąt nachylenia
płaszczyzny styku obu ciał,
2. W chwili równowagi granicznej kąt osiąga wartość
s
s
- kąt tarcia
3. Po zwiększeniu wartości kąta nastąpi poślizg ciał i
przesuwanie się jednego ciała po drugim,
4. W płaszczyźnie styku wystąpi wówczas tarcie kinetyczne.
MT_SS - w 7
13
Współczynnik tarcia statycznego jest równy tangensowi
kąta tarcia i jest wielkością niemianowaną.
s
s
s
s
s
tg
f
f
N
N
f
N
T
tg
czyli
•
Współczynnik tarcia zależy od chropowatości współpracujących
powierzchni.
•
Smarowanie tych powierzchni zmniejsza współczynnik tarcia.
MT_SS - w 7
14
Współczynniki tarcia posuwistego
dla materiałów stosowanych w budownictwie
podłoże
materiał
mur z cegły
beton o powierzchni
chropowatej gładkiej
miękkoplastyczny ił lub glina
0,20
0,25
0,10
plastyczny ił lub glina
0,23
0,35
0,20
glina zwarta, piasek gliniasty
0,30
0,40
0,25
piasek lub żwir
0,50
0,55
0,30
beton
0,75
0,75
----
mur na świeżej zaprawie
0,50-0,70
-----
----
izolacja papowa
0,20
0,7
----
MT_SS - w 7
15
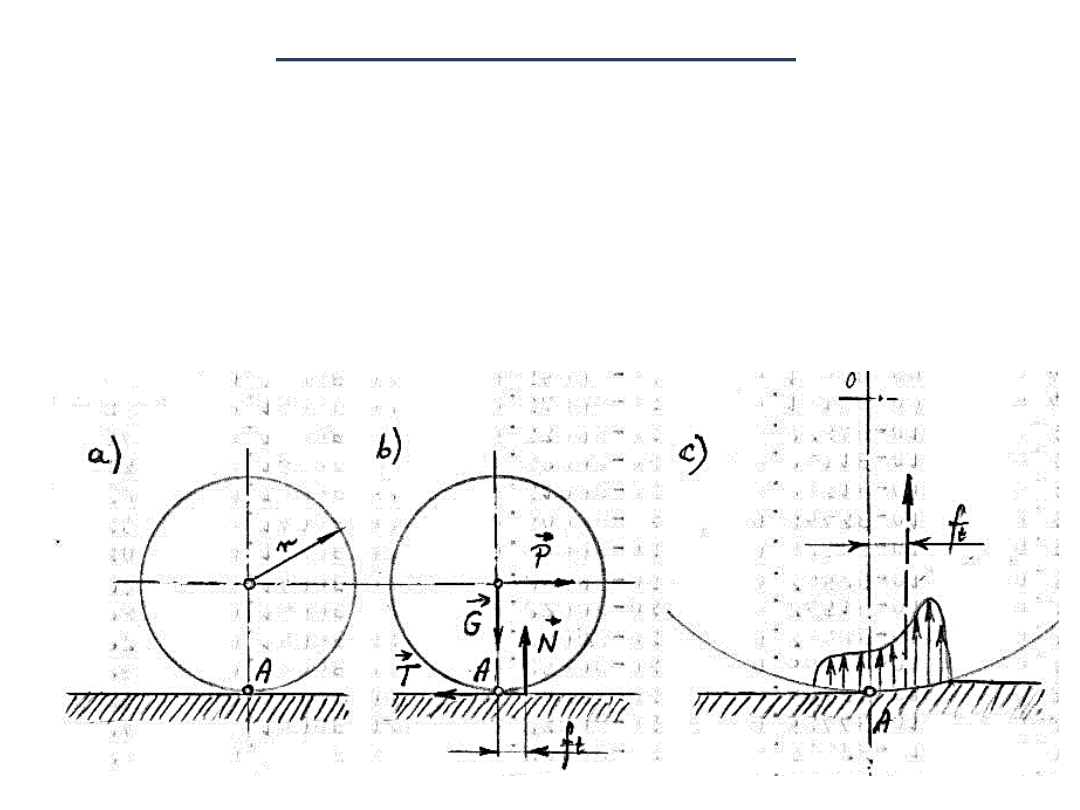
Opór przy toczeniu się ciał
1. Krążek o ciężarze G spoczywa na poziomej płaszczyźnie
2. Do środka krążka 0 przykładamy siłę P – krążek może się
toczyć
3. Dopóki wartość siły P będzie mniejsza od pewnej
wartości granicznej, dopóty krążek będzie pozostawał w
spoczynku
MT_SS - w 7
16
4. Po przekroczeniu przez siłę P wartości krytycznej krążek
zaczyna się:
• toczyć, lub
• ślizgać
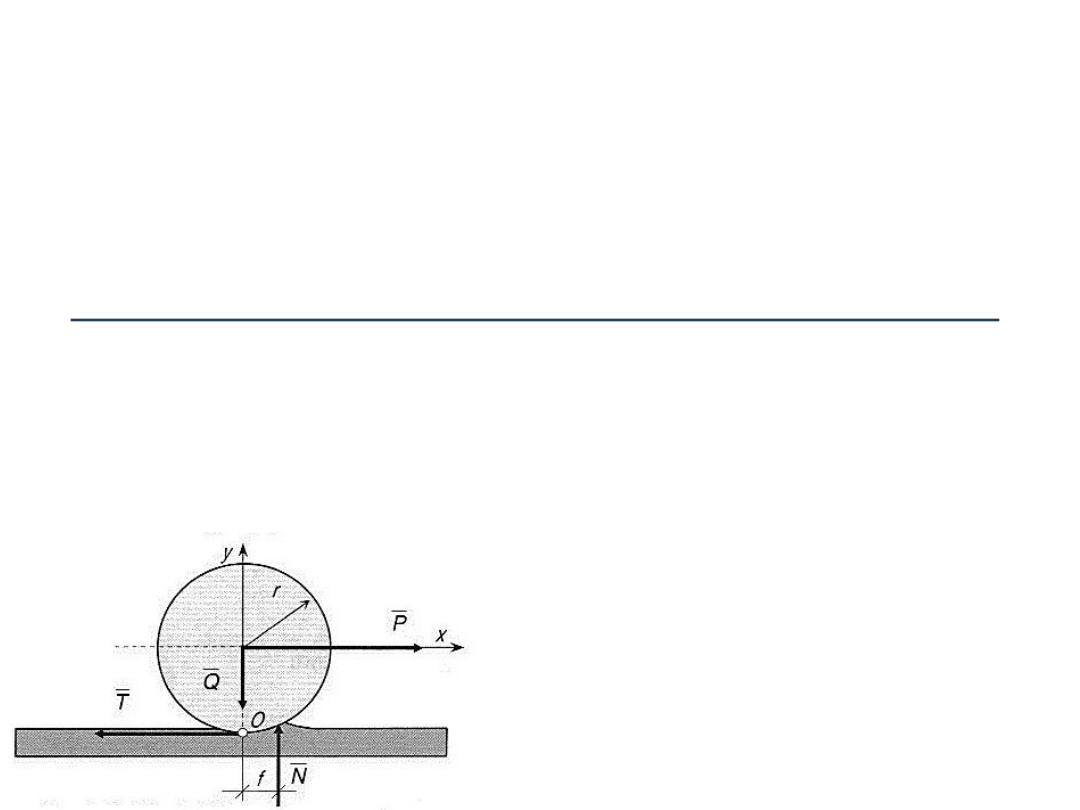
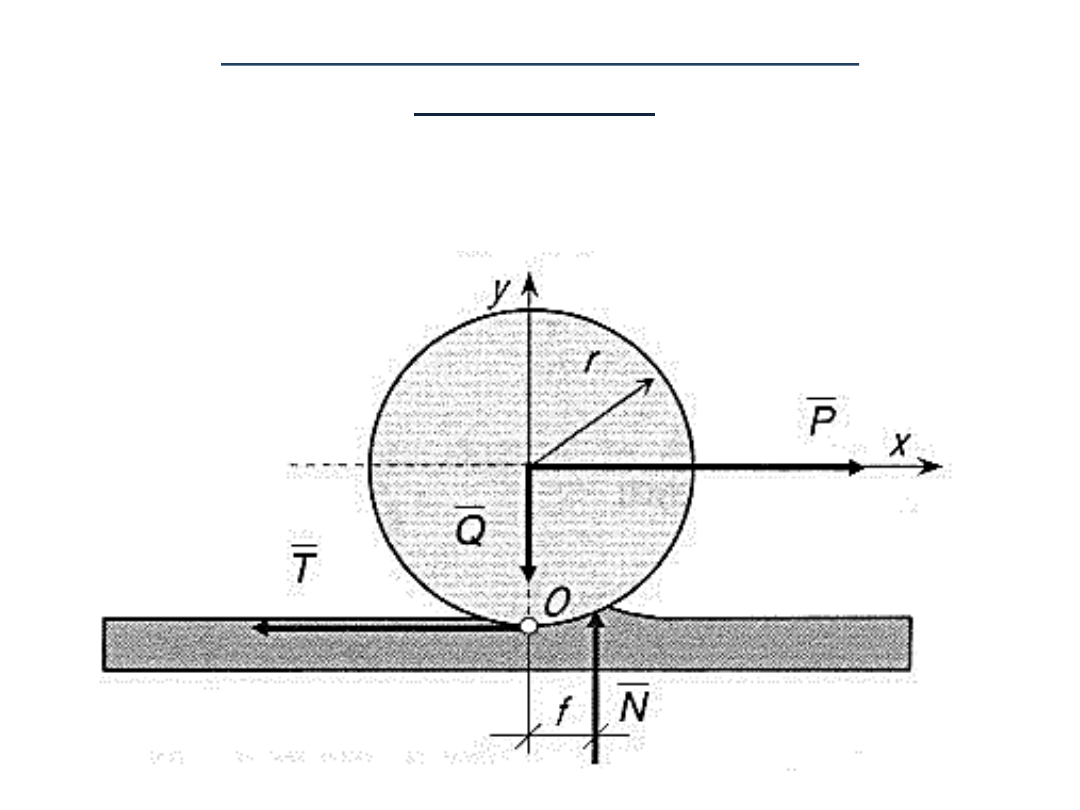
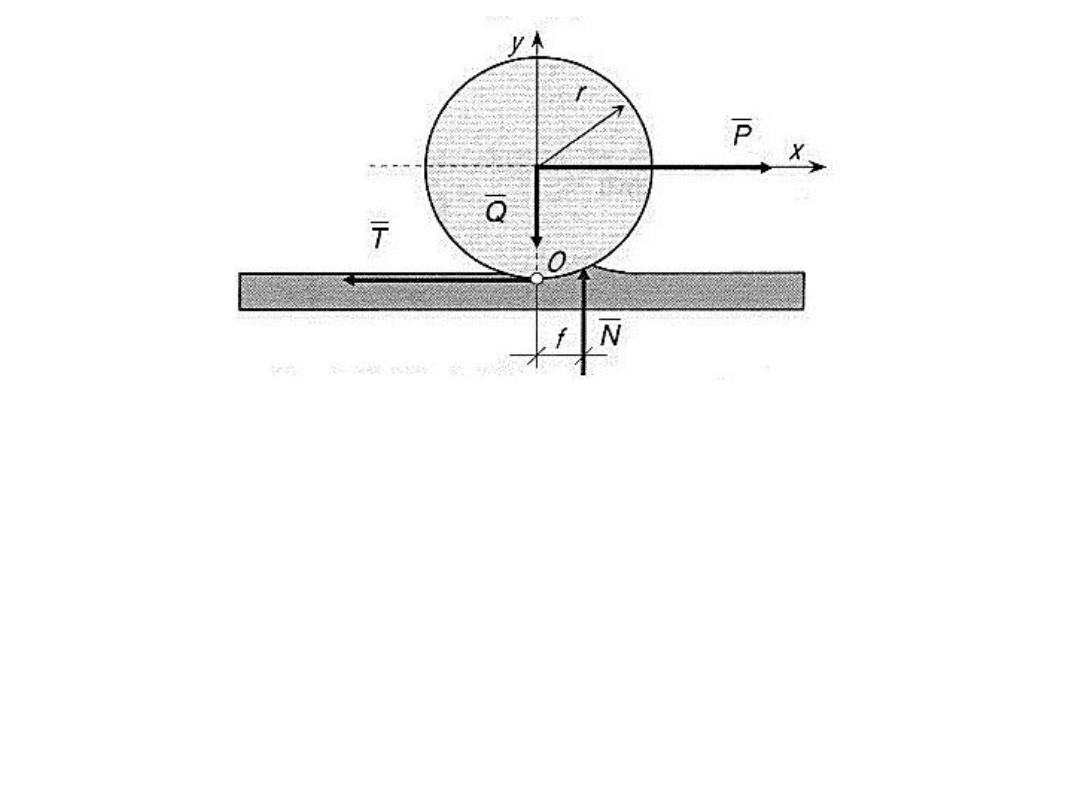
Na krążek pozostający jeszcze w spoczynku działają siły
:
1. siła ciężkości G (na poniższym rysunku to siła Q),
2. siła pozioma P,
3. reakcja płaszczyzny, na której krążek spoczywa o
składowych:
a) normalną N,
b) styczną, czyli siłę tarcia T.
MT_SS - w 7
17
Równowaga sił działających na krążek
poślizg krążka
:
N – G = 0, P – T = 0
stąd:
N = G, T = P
MT_SS - w 7
18
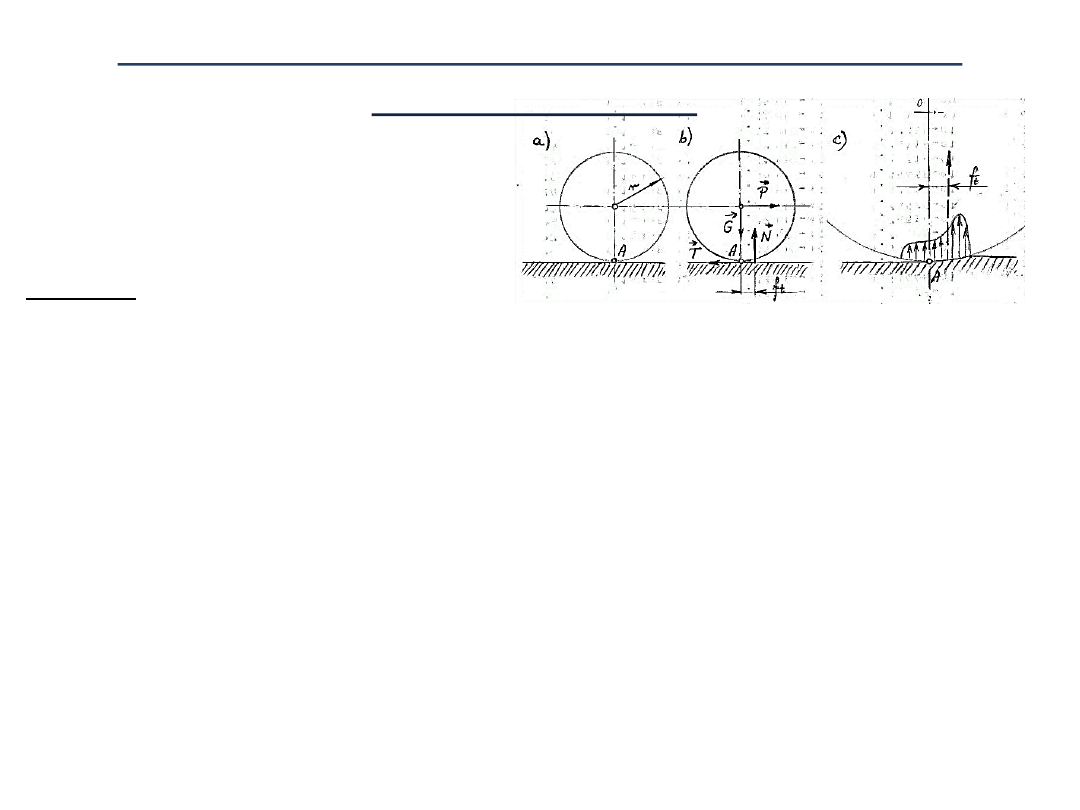
Aby krążek nie zaczął się
ślizgać
, musi być spełniony
warunek wynikający z praw tarcia.
G
f
N
f
P
s
s
gdzie: f
s
– współczynnik tarcia statycznego
MT_SS - w 7
19
Równowaga momentów sił działających na krążek
toczenie się krążka
:
uwaga:
• momenty sił G i T względem tego punktu = 0, zatem
• aby równanie momentów było spełnione, reakcja N musi
działać na pewnym ramieniu względem punktu A
• linia działania tej reakcji nie przechodzi więc przez
teoretyczny punkt styku A, lecz w pewnej od niego
odległości
• w rozpatrywanym przypadku linia działania reakcji musi
leżeć z prawej strony tego punktu, aby zrównoważyć
moment siły P.
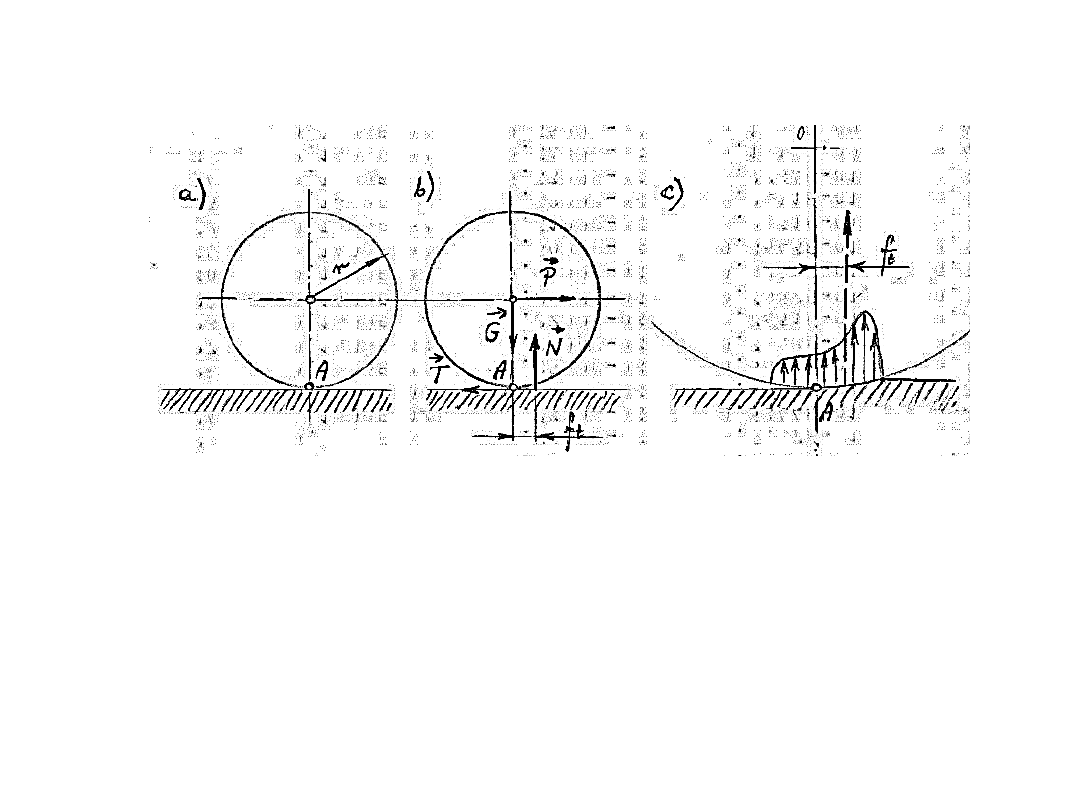
MT_SS - w 7
20
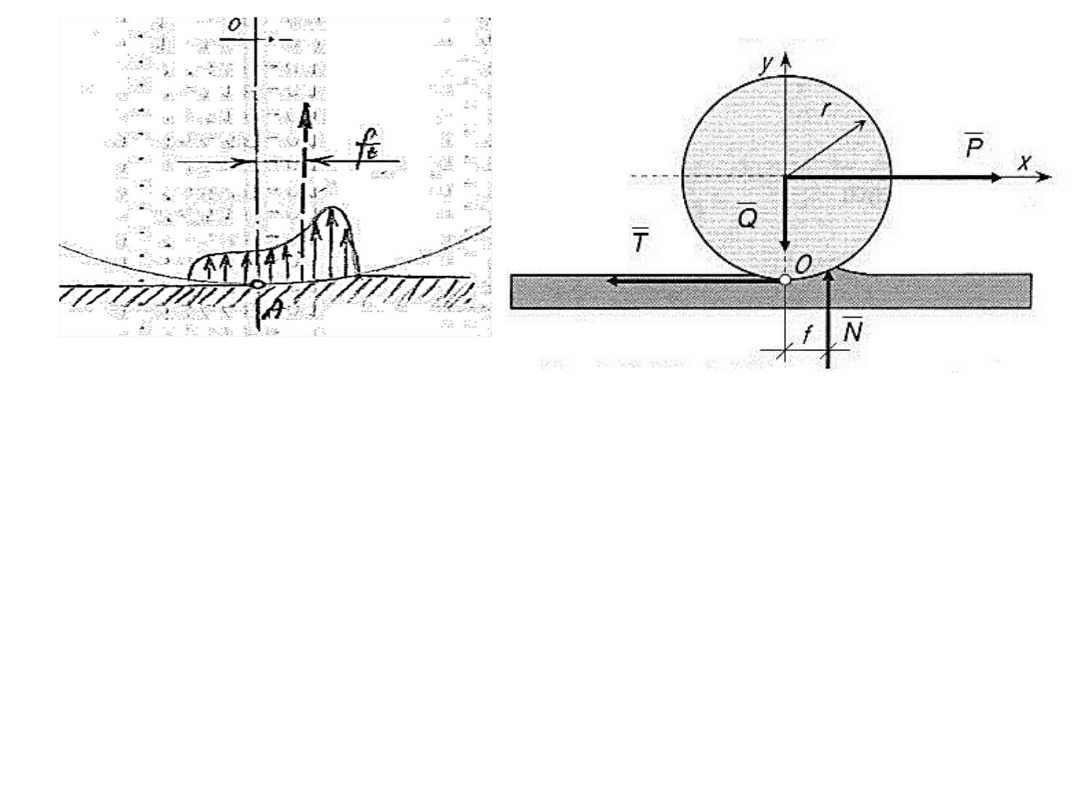
Równanie równowagi momentów względem punktu A, w
którym krążek styka się z podłożem.
r
P
N
M
r
P
N
M
A
A
0
gdzie:
M
A
(N) – moment reakcji normalnej względem punktu A
r – promień krążka
MT_SS - w 7
21
odkształcone powierzchnie
stykających się ciał
Zwiększając wartość
siły P osiągamy stan
równowagi granicznej:
t
A
f
N
N
M
max
gdzie: f
t
– ramię działania siły N względem punktu A zwane
współczynnikiem oporu przy toczeniu
MT_SS - w 7
22
Aby rozpatrywany krążek nie zaczął się toczyć, musi być
spełniony następujący warunek:
t
A
f
N
M
r
P
max
stąd:
r
f
G
P
t
MT_SS - w 7
23
Warunki pozostawania krążka w spoczynku
Aby krążek pozostał w spoczynku, wartość poziomej siły P
nie może przekroczyć mniejszej z wartości wynikających z
warunków:
Dwa sposoby utraty spoczynku:
1. gdy
(f
t
/r) < f
s
– krążek zacznie najpierw się
toczyć nim nastąpi poślizg,
2. gdy
(f
t
/r) > f
s
– krążek najpierw wpadnie w
poślizg nim zacznie się toczyć.
Zwykle
(f
t
/r) < f
s
MT_SS - w 7
24
Wartości współczynnika f
t
dla niektórych przypadków
Rodzaj stykających się powierzchni
współczynnik
oporu
f
t
[cm]
krążek drewniany po podłożu z drewna
0,05÷0,06
krążek z miękkiej stali po podłożu miękkiej stali
0,005
krążek drewniany po podłożu ze stali
0,03÷0,04
kulka z hartowanej stali po podłożu ze stali
0,001
MT_SS - w 7
25
Przykłady
Podręczniki wskazane w:
• Sylabusie – e-dziekanat,
• Karcie informacyjnej przedmiotu – USOS,
• Wykładzie 1.