MT SS - w 12

1

DYNAMIKA

Zasada zachowania energii mechanicznej

w - 12

Dynamika

Dział mechaniki poświęcony badaniu zależności między:

• ruchem ciał materialnych, a
• siłami działającymi na te ciała.

Dynamika opiera się na prawach ruchu Newtona, które
dotyczą punktu materialnego

(model ciała rzeczywistego)

.

Z kinematyki wiemy, że w ogólnym przypadku ruch ciała jest
ruchem złożonym z :

• ruchu postępowego i
• ruchu obrotowego.

MT SS - w 12

2

Gdy traktujemy ciało jako punkt materialny, wówczas
pomijamy ruch obrotowy i bierzemy pod uwagę jedynie
ruch postępowy.

Na podstawie drugiego prawa dynamiki Newtona, możemy
wyznaczyd przyśpieszenie punktu materialnego wywołane
działaniem określonej siły.

Gdy na punkt materialny działa kilka sił, wówczas jego

przyśpieszenie określimy z

ZASADY NIEZALEŻNOŚCI DZIAŁANIA SIŁ

.

2

MT SS - w 12

3

3

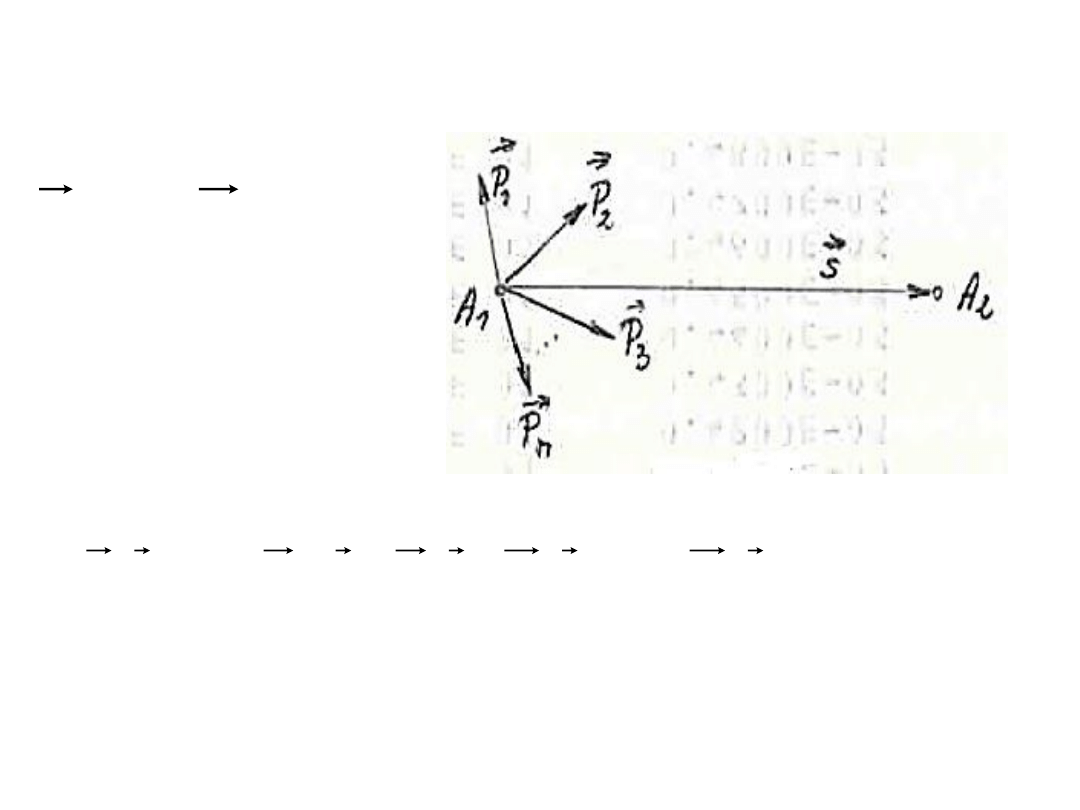
ZASADY NIEZALEŻNOŚCI DZIAŁANIA SIŁ

Przyśpieszenie punktu materialnego, na który działają siły
P

1

, P

2

, …, P

n

równe jest sumie geometrycznej przyśpieszeo,

które miałby ten punkt, gdyby każda z tych sił działała na
niego osobno.

gdzie:

p

1

, p

2

, …, p

n

– przyśpieszenia punktu materialnego

wywołane działaniem poszczególnych sił.

n

p

p

p

p













2

1

Z drugiego prawa mechaniki Newtona wynika, że:

n

n

P

p

m

P

p

m

P

p

m













,

...

,

,

2

2

1

1

MT SS - w 12

4

4

Mnożąc obie strony równania przez masę m





otrzymujemy:

m

p

p

p

p

n















/

2

1

n

P

P

P

p

m















2

1

Zatem, rozpatrywany punkt materialny ma takie samo
przyśpieszenie, jakie miałby wówczas, gdyby działała na
niego jedna tylko siła wypadkowa, równa sumie
geometrycznej sił

P

1

, P

2

, …, P

n

.

MT SS - w 12

5

5

Jeśli wypadkowa sił działających na punkt materialny jest
równa zeru,




wówczas przyśpieszenie tego punktu jest także równe zeru.

Oznacza to, że punkt materialny porusza się w tym

przypadku:

• ruchem jednostajnym po linii prostej lub
• pozostaje w spoczynku.

0





p

m

MT SS - w 12

6

6

• Drugie prawo dynamiki Newtona określa w jaki sposób

przyśpieszenie punktu materialnego zależy od siły,
działającej na ten punkt.

• Przyśpieszenie punktu materialnego zależy od wyboru

układu odniesienia, względem którego rozpatruje się
ruch.

• Należy zatem wskazad dla jakiego układu odniesienia

prawo to oraz pozostałe dwa prawa Newtona
obowiązują.

• Taki układ odniesienia, w którym ważne są prawa

Newtona nosi nazwę

UKŁADU BEZWŁADNOŚCIOWEGO,

albo układu Galileusza

.

MT SS - w 12

PRACA

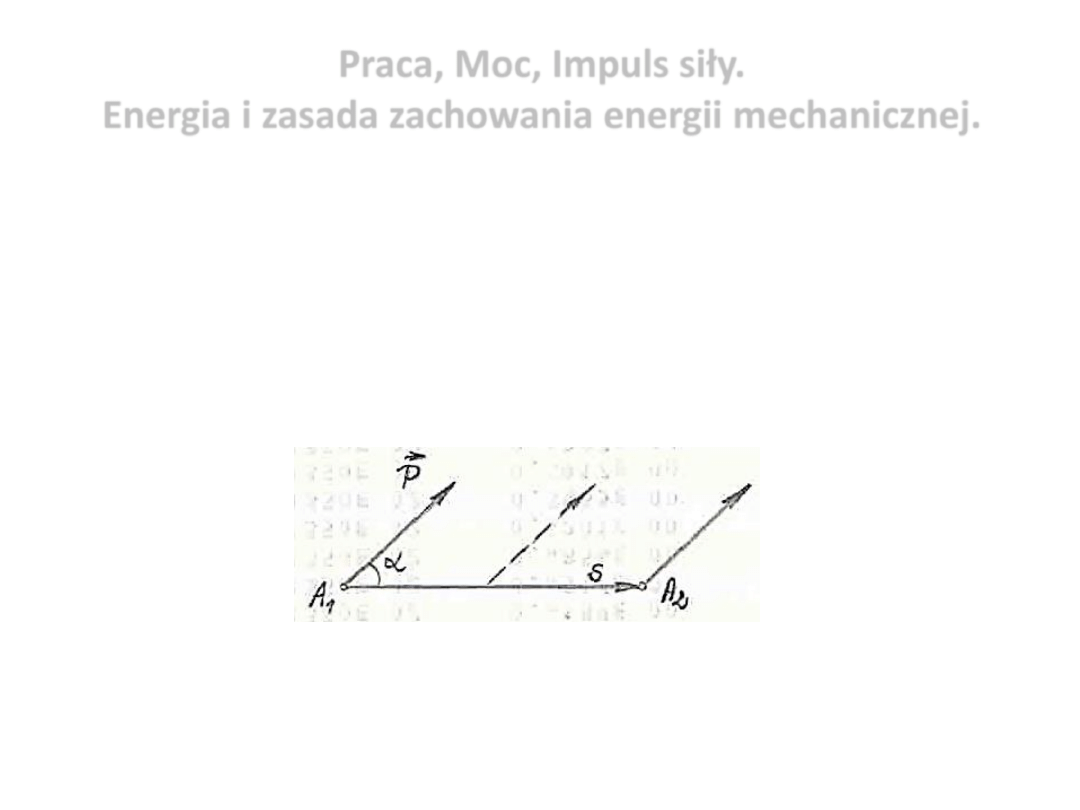
Def. 1. Pracą siły stałej na prostoliniowym przesunięciu

punktu przyłożenia tej siły nazywamy iloczyn

wartości bezwzględnej przesunięcia s i miary rzutu

siły na kierunek tego przesunięcia .

L = P·s·cosα

P·cosα – miara rzutu siły P na kierunek przesunięcia s

7

Praca, Moc, Impuls siły.

Energia i zasada zachowania energii mechanicznej.

MT SS - w 12

8

L = P·s·cosα

Mogą zaistnied następujące przypadki:

α < π/2

-

L > 0

α > π/2

-

L < 0

α = π/2

-

L = 0

P s

α = 0

-

L

= P·s

Tak więc możemy zapisad:

L = P·s

Na podstawie powyższego wzoru możemy wyznaczyd
wartośd pracy siły P w przypadku gdy dane są jej składowe
oraz składowe przesunięcia s w prostokątnym układzie
współrzędnych.

z

z

y

y

x

x

s

P

s

P

s

P

s

P

L

















MT SS - w 12

9

W przypadku, gdy siła P jest wypadkową n sił P

1

, P

2

, …,P

n

,

przyłożonych do jednego punktu, tzn.

wówczas można zapisad następujące zależności







n

i

i

P

P

1





















































n

i

i

n

n

n

i

i

L

L

L

L

L

s

P

s

P

s

P

s

P

s

P

L

1

2

1

2

1

1





MT SS - w 12

10

Tak więc:



gdzie:

L

i

= P

i

·s

jest pracą siły P na przesunięciu s.

Tw. Praca wypadkowej sił przyłożonych do jednego

punktu równa jest sumie prac poszczególnych sił.







n

i

i

L

L

1

MT SS - w 12

11

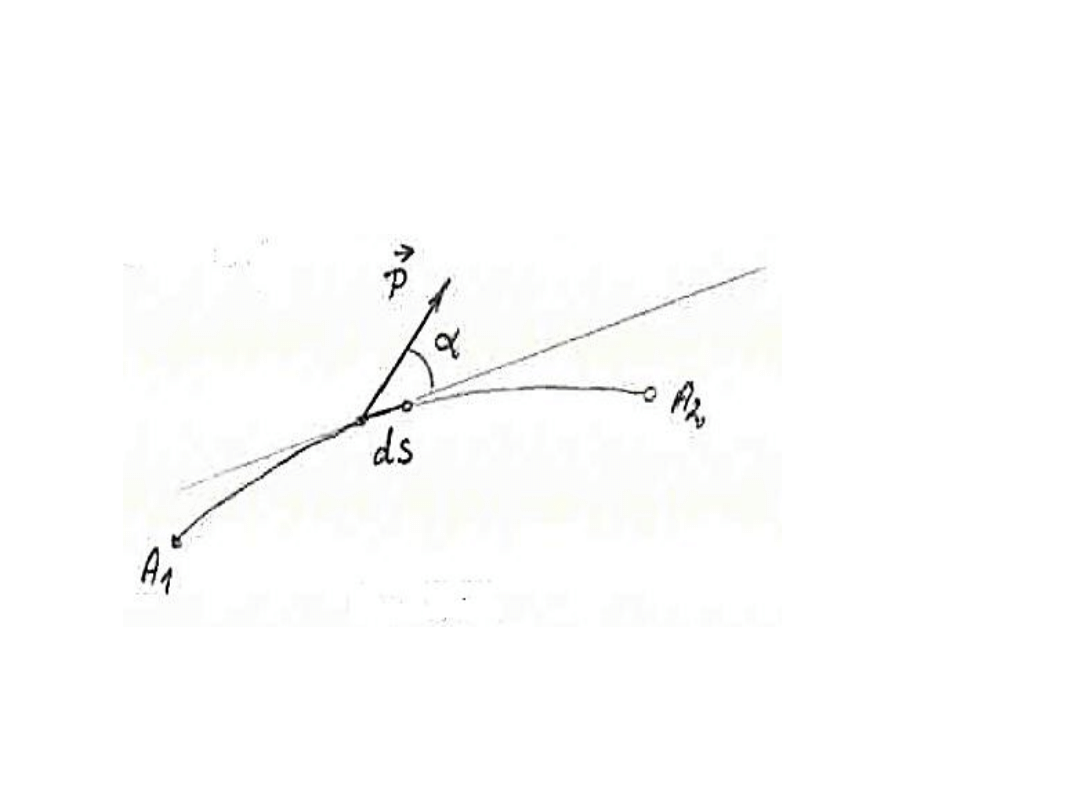
W przypadku, gdy punkt przyłożenia siły P doznaje dowolnego
krzywoliniowego przesunięcia należy w pierwszej kolejności
obliczyd tzw. PRACĘ ELEMENTARNĄ dL, tzn. pracę siły P na
elementarnym przesunięciu ds. punktu przyłożenia siły








gdzie: α jest kątem, który siła P tworzy ze styczną do toru
punktu przyłożenia siły.

ds

P

dL









cos

MT SS - w 12

12

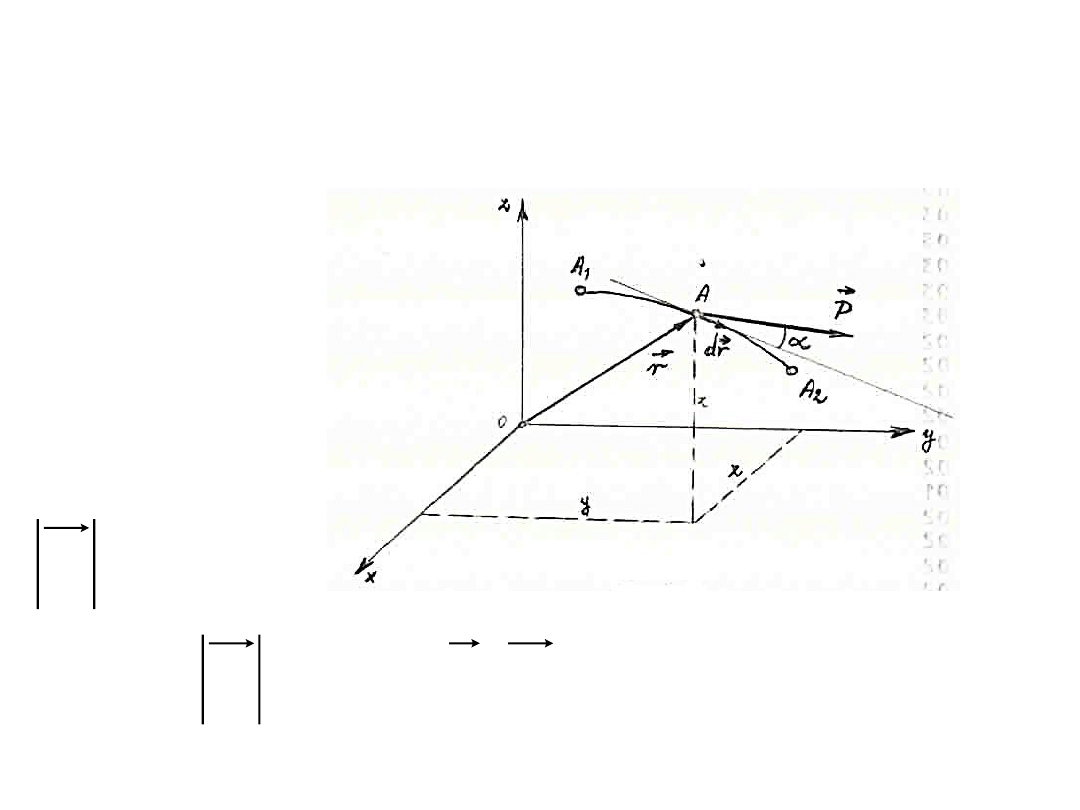
Jeśli położenie punktu materialnego określone jest w
prostokątnym

układzie

współrzędnych

za

pomocą

promienia-wektora r, wówczas

dz

P

dy

P

dx

P

dr

P

dr

P

dL

ds

dr

z

y

x



























cos

MT SS - w 12

13

Praca elementarna dL jest równa iloczynowi skalarnemu siły P
i różniczki geometrycznej dr promienia-wektora r.

dz

P

dy

P

dx

P

dr

P

dL

z

y

x

















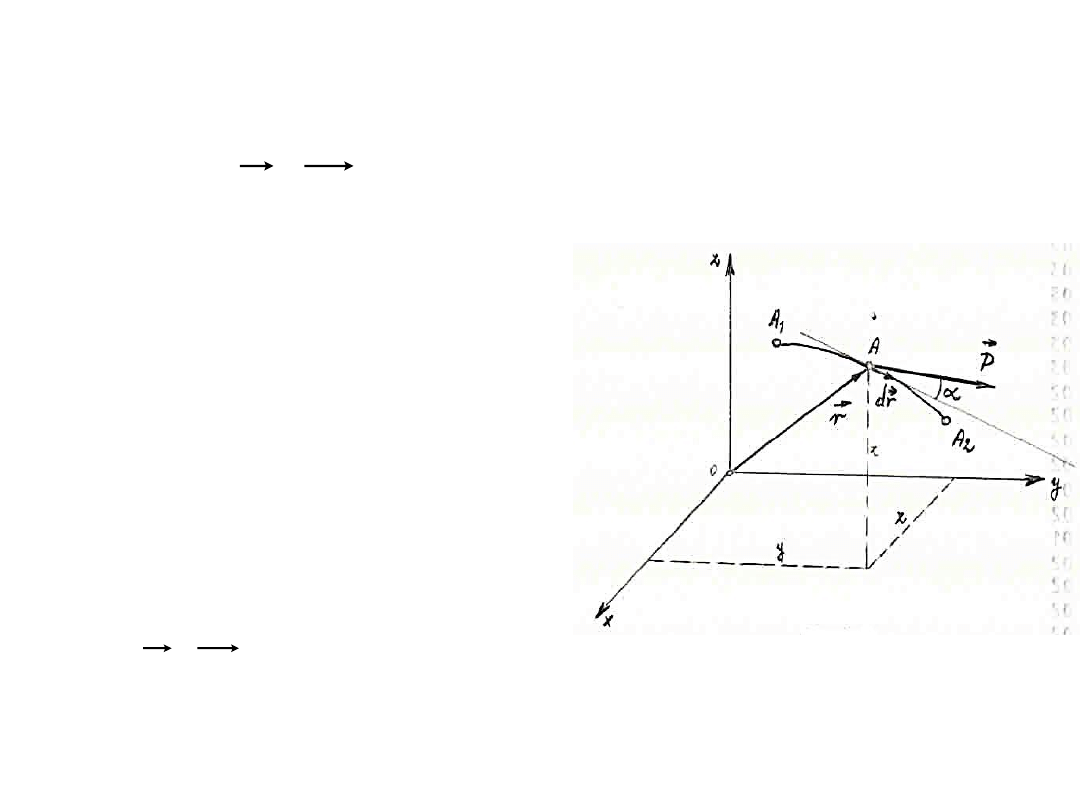
Aby obliczyd pracę siły P
w przypadku gdy jej punkt przyłożenia A
opisuje skooczony odcinek A

1

A

2

krzywoliniowego toru, należy scałkowad
wyrażenie określające pracę
elementarną wzdłuż łuku A

1

A

2

.































2

1

2

1

2

1

cos

A

A

z

y

x

A

A

A

A

dz

P

dy

P

dx

P

ds

P

dr

P

L



MT SS - w 12

14

W przypadku, gdy dane są równania ruchu punktu
przyłożenia siły P, tzn.:

x = x(t), y = y(t), z = z(t)

wówczas pod znakiem całki we wzorze

należy podstawid

otrzymując































2

1

2

1

2

1

cos

A

A

z

y

x

A

A

A

A

dz

P

dy

P

dx

P

ds

P

dr

P

L



,

,

,

dt

z

dz

dt

y

dy

dt

x

dx













dt

z

P

y

P

x

P

L

t

t

z

y

x



























2

1

MT SS - w 12

15

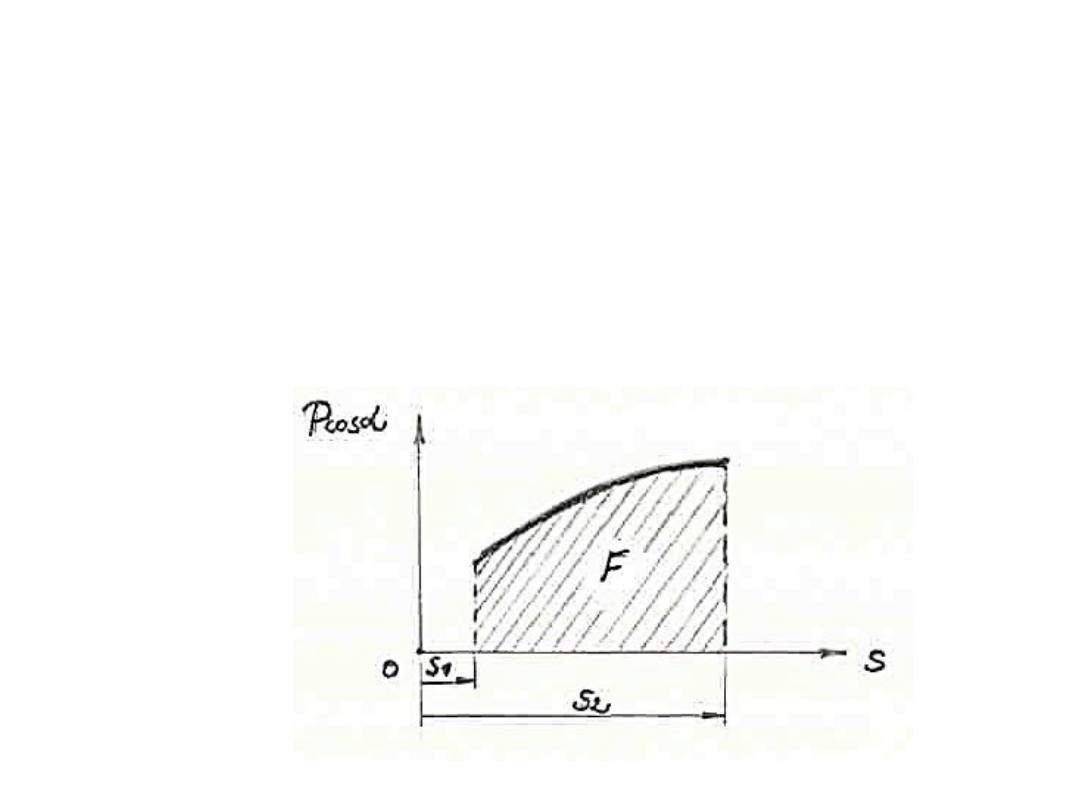
W szczególnym przypadku, gdy siła P, zależy od położenia
punktu A na torze, wówczas miarę rzutu siły na styczną do
toru, czyli P·cosα można wyrazid w zależności od
współrzędnej łukowej s odmierzonej wzdłuż toru punktu A.

W tym przypadku mamy





2

1

cos

s

s

ds

P

L



MT SS - w 12

16





2

1

cos

s

s

ds

P

L



Gdy zależnośd P·cosα od współrzędnej łukowej s dana jest w
postaci wykresu, wówczas całka występująca w powyższym
równaniu równa jest polu F powierzchni figury
zakreskowanej na rysunku.

MT SS - w 12

17

Praca siły wzdłuż skooczonego łuku A

1

A

2

toru punktu

materialnego poruszającego się w polu sił.

Założenie:

W pewnym obszarze na poruszający się punkt materialny
działa siła P zależna tylko od położenia tego punktu w
przestrzeni.

Ponieważ w tym przypadku każdemu punktowi

wspomnianego obszaru odpowiada określony wektor

przedstawiający siłę P, mamy do czynienia z niezależnym od

czasu polem wektorowym, które nazywamy

STACJONARNYM POLEM SIŁ

.

Jeżeli każdemu punktowi pola odpowiada taka sama siła, to
pole to nazywamy polem jednorodnym.

MT SS - w 12

18

W polu sił stacjonarnych składowe siły P są funkcjami
współrzędnych punktu przyłożenia, tzn.













.

,

,

,

,

,

,

,

,

z

y

x

P

P

z

y

x

P

P

z

y

x

P

P

z

z

y

y

x

x







Gdy punkt materialny porusza się w polu sił, wówczas praca
L sił tego pola określona jest za pomocą następującej całki
krzywoliniowej:































2

1

,

,

,

,

,

,

A

A

z

y

x

dz

z

y

x

P

dy

z

y

x

P

dx

z

y

x

P

L

Praca ta zależy na ogół od toru, po którym porusza się
rozpatrywany punkt przechodząc z położenia A

1

w

położenie A

2

.

MT SS - w 12

19

Istnieją takie pola sił, w których praca zależna jest tylko od
położenia początkowego i położenia koocowego i nie zależy
tym samym od postaci toru rozpatrywanego punktu.

Pola o takich właściwościach nazywamy

POLAMI ZACHOWAWCZYMI

.

W polu zachowawczym zdefiniowad można funkcję V(x, y, z),
której pochodne cząstkowe względem współrzędnych x, y, z
wzięte ze znakiem minus równe są składowym siły pola
wzdłuż odpowiednich osi układu współrzędnych, tzn.


V(x, y, z) –

POTENCJAŁ

zachowawczego pola sił,

Siła P –

GRADIENT POTENCJAŁU POLA

.

,

,

z

V

P

y

V

P

x

V

P

z

y

x

























MT SS - w 12

20

W przypadku istnienia potencjału pola V, praca
elementarna dL, występująca w równaniu



przyjmie postad






Wynika stąd, że praca elementarna równa jest różniczce
zupełnej potencjału V wziętej ze znakiem minus.































2

1

,

,

,

,

,

,

A

A

z

y

x

dz

z

y

x

P

dy

z

y

x

P

dx

z

y

x

P

L

.

dV

dz

z

V

dy

y

V

dx

x

V

dz

P

dy

P

dx

P

dL

z

y

x



















































MT SS - w 12

21

Praca siły wzdłuż skooczonego łuku A

1

A

2

toru punktu

materialnego poruszającego się w zachowawczym polu sił
jest określona następującym wzorem




gdzie V

1

i V

2

oznaczają wartości potencjału pola sił dla

położenia

początkowego

i

położenia

koocowego

rozpatrywanego punktu, czyli

x

1

, y

1

, z

1

- współrzędne punktu A

1

,

x

2

, y

2

, z

2

- współrzędne punktu A

2

.

2

1

2

1

2

1

V

V

dV

dz

z

V

dy

y

V

dx

x

V

L

A

A

A

A





















































.

,

,

,

,

,

2

2

2

2

1

1

1

1

z

y

x

V

V

z

y

x

V

V





MT SS - w 12

22

Z powyższego wynika następujące twierdzenie:

Tw. Praca w zachowawczym polu sił równa jest różnicy

potencjałów w położeniu początkowym i położeniu

koocowym punktu.

Praca w zachowawczym polu sił nie zależy zatem od tego,
po jakim torze poruszał się punkt materialny przechodząc z
położenia początkowego w położenie koocowe.

Interpretacja fizyczna potencjału pola sił

Potencjał V w określonym punkcie pola sił równy jest pracy,
którą wykonuje siła działająca na punkt materialny
poruszający się w tym polu z miejsca, w którym potencjał
równy jest V, do miejsca gdzie potencjał równy jest zeru.

MT SS - w 12

23

IMPULS SIŁY

Def. 2. Impulsem S siły P, działającej na punkt materialny

od chwili t

o

do chwili t nazywamy, wektor równy

iloczynowi tej siły i czasu (t – t

o

), w którym ta siła

działała.

Gdy t > t

o

, wówczas impuls S ma ten sam kierunek co

rozpatrywana siła, a jego składowe w prostokątnym układzie
współrzędnych są następujące





const

P

t

t

P

S

o









,













,

,

,

o

z

z

o

y

y

o

x

x

t

t

P

S

t

t

P

S

t

t

P

S



















MT SS - w 12

24

W przypadku, gdy siła działająca na punkt materialny,
zmienia z upływem czasu swoją wartośd i swój kierunek,
należy określid impuls elementarny siły, dS.

lub jego składowe

Impuls S siły P(t), działającej na punkt materialny w
skooczonym przedziale czasu od t

o

do t, równy jest

zaś jego składowe

dt

P

dS





.

,

,

dt

P

dS

dt

P

dS

dt

P

dS

z

z

y

y

x

x













 

,

dt

t

P

S

t

t

o





 

 

 

,

,

,

dt

t

P

S

dt

t

P

S

dt

t

P

S

t

t

z

z

t

t

y

y

t

t

x

x

o

o

o













MT SS - w 12

25

MOC SIŁY

Def. 3.

Mocą N siły P nazywamy pracę tej siły

wykonaną w ciągu jednostki czasu.

Ponieważ

gdzie υ jest prędkością punktu przyłożenia siły, zatem

α – kąt między wektorami P i υ, tzn. między siłą, a
styczną do toru punktu przyłożenia siły.

dt

r

d

P

dt

dL

N











dt

r

d







cos











P

P

N

MT SS - w 12

26

Jednostki w układzie SI

:

• Jednostka pracy

– DŻUL – 1 J

Tak więc,

1 J równy jest pracy siły 1N na przesunięciu 1m,

w przypadku gdy przesunięcie odbywa się w

kierunku działania siły.

• Jednostka mocy – WAT – 1W

• Jednostka impulsu siły – NIUTONOSEKUNDA

kg

s

m

m

s

kg

m

m

N

J



















2

2

2

1

1

1

1

1

1

kg

s

m

s

J

W











3

2

1

1

/

1

1

1

1

1

1

1













s

m

kg

s

N

Ns

MT SS - w 12

27

ENERGIA

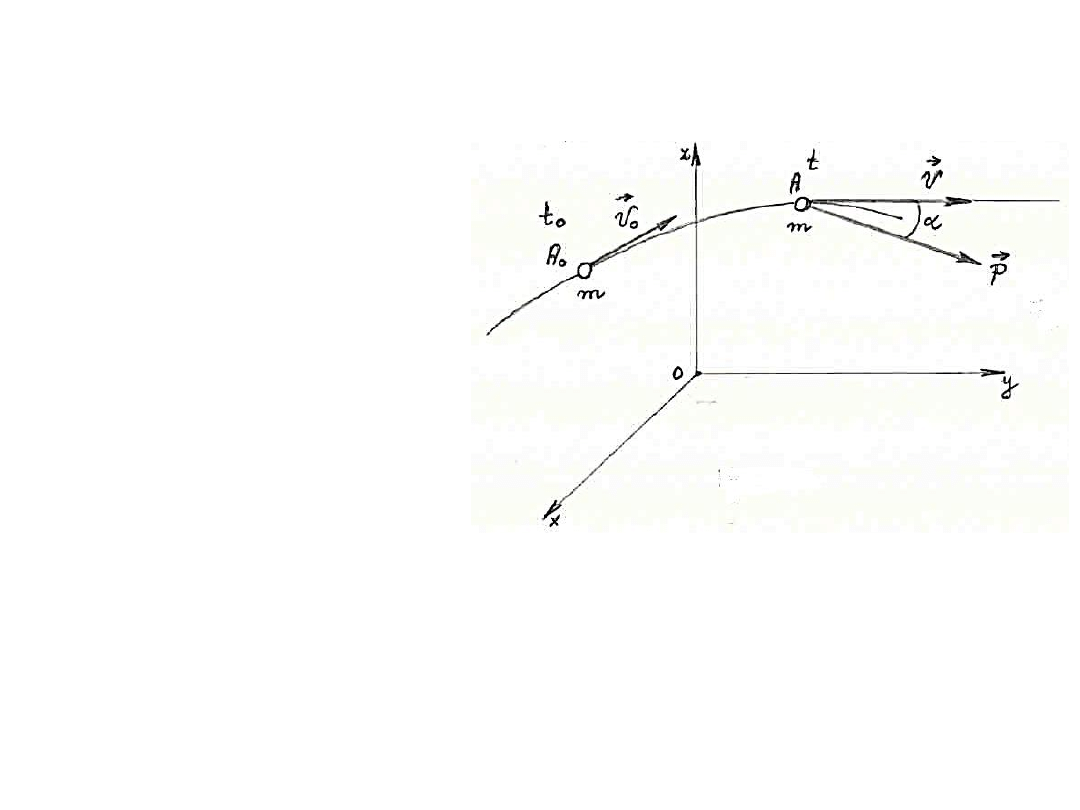
Niech punkt materialny o masie m porusza się po
krzywoliniowym torze l.

A

o

, A – położenia punktu

materialnego w

chwilach t

o

i t,

υ

o

, υ – prędkości tego punktu w

odpowiednich chwilach,

P – wypadkowa sił działających na punkt materialny,

α – kąt, który wypadkowa tworzy ze styczną do toru w

chwili t.

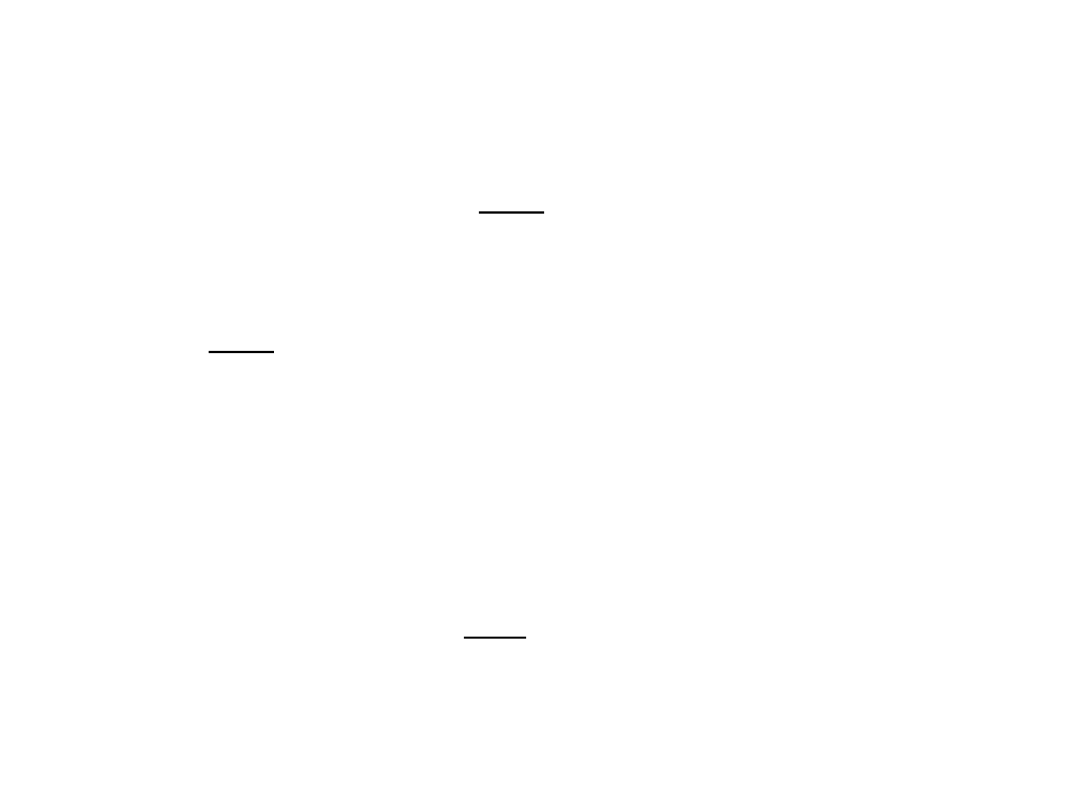
MT SS - w 12

28

Równanie dynamiczne ruchu wzdłuż stycznej do toru
rozpatrywanego punktu materialnego




gdzie


Mnożąc obie strony powyższego równania przez υ
otrzymamy

t

a

dt

d

P

dt

d

m















cos









cos











P

dt

d

m

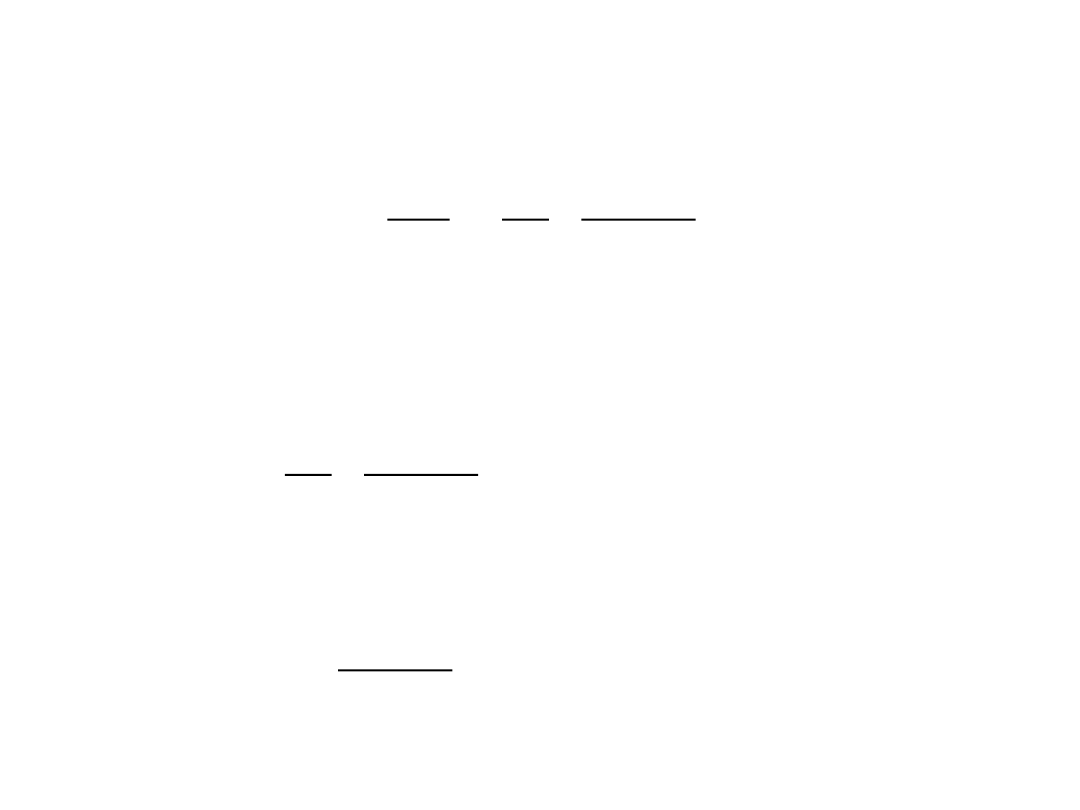
MT SS - w 12

29

Ponieważ masa m jest wielkością stałą, lewą stronę
powyższego równania można przedstawid jako




co po podstawieniu do równania z poprzedniej strony daje




lub

,

2

2











 













m

dt

d

dt

d

m







cos

2

2

















 

P

m

dt

d

dt

P

m

d



















 







cos

2

2

MT SS - w 12

30

We wzorze



Ale

υ ·dt = ds ,

gdzie ds oznacza elementarną drogę, którą rozpatrywany
punkt materialny przebywa w czasie dt.

Możemy zatem równanie powyższe zapisad jako

Energia kinetyczna punktu materialnego

dt

P

m

d



















 







cos

2

2

ds

P

m

d

















 





cos

2

2

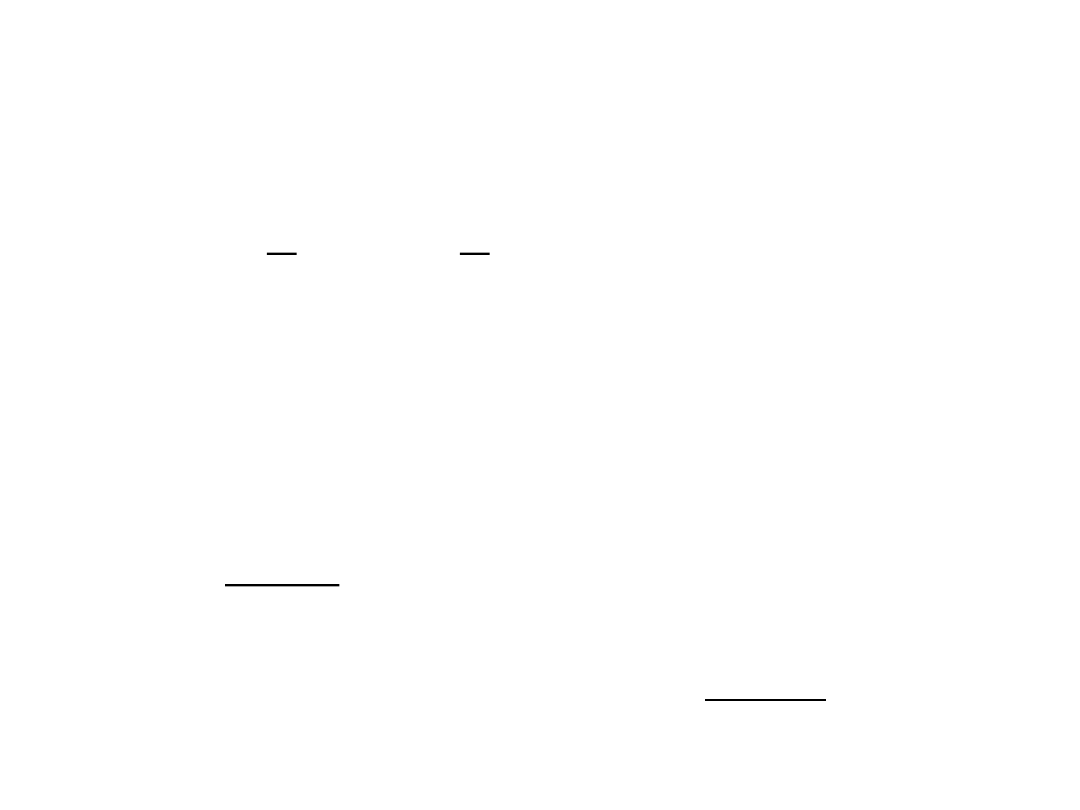
MT SS - w 12

31

Def. 4.

Energia kinetyczna T punktu materialnego jest

to wielkośd równa połowie iloczynu masy

punktu i kwadratu prędkości tego punktu.





2

2

2

2

2

1

2

1

z

y

x

m

m

T



















Ponieważ

gdzie dL oznacza elementarną pracę siły P, zatem równanie

możemy przedstawid jako

,

cos

dL

ds

P









ds

P

m

d

















 





cos

2

2

dL

m

d













 

2

2



MT SS - w 12

32

dL

m

d













 

2

2



Całkując równanie

w przedziale czasu t

o

do t otrzymujemy

Z powyższego równania wynika twierdzenie o energii

kinetycznej.

Tw. Przyrost energii kinetycznej punktu materialnego w

skooczonym przedziale czasu równy jest sumie prac,

które wykonały w tym samym czasie wszystkie siły

działające na ten punkt.

.

L

T

T

o





MT SS - w 12

33

W przypadku gdy punkt materialny porusza się w
zachowawczym polu sił, wówczas praca sił pola równa jest
różnicy potencjałów w położeniu początkowym i koocowym.

Można zatem sformułowad następującą definicję.

Def. 5.

Energia potencjalna punktu materialnego jest

to wielkośd równa pracy, którą wykonałaby siła

pola działająca na rozpatrywany punkt przy

przejściu punktu z danego położenia, w

położenie, w którym potencjał równy jest zeru.

V

V

L

o





MT SS - w 12

34

L

T

T

o





Podstawiając

do

otrzymujemy


czyli


Możemy zatem zapisad:

energia mechaniczna

V

V

L

o





V

V

T

T

o

o







.

o

o

V

T

V

T







const

V

T





MT SS - w 12

35

Def. 6.

Energią mechaniczną punktu materialnego

nazywamy sumę jego energii kinetycznej i

potencjalnej.

Z zależności


wynika następujące twierdzenie noszące nazwę:

ZASADA ZACHOWANIA ENERGII MECHANICZNEJ

const

V

T





Tw. Gdy punkt materialny porusza się w zachowawczym

polu sił, suma jego energii kinetycznej i energii

potencjalnej, zwane energią mechaniczną, jest

wielkością stałą.

MT SS - w 12

36

W przypadku, gdy na poruszający się punkt materialny,
oprócz sił o potencjale V(x, y, z), działają inne siły, wówczas
w równaniu


określającym przyrost energii kinetycznej, należy uwzględnid
również pracę tych ostatnich sił.

Oznaczając przez L pracę sił nie mających potencjału
otrzymujemy:


a stąd

V

V

T

T

o

o







,

L

V

V

T

T

o

o









L

V

T

V

T

o

o









MT SS - w 12

37

• Jeżeli siłami nie mającymi potencjału są siły oporów ruchu,

jak np. opór powietrza lub siły tarcia, to praca tych sił jest
ujemna, gdyż siły te mają kierunek przeciwny do kierunku
prędkości punktu materialnego.

• W przypadku, gdy L < 0 , z równania
wynika, że suma energii potencjalnej i kinetycznej w
położeniu koocowym jest mniejsza niż w położeniu
początkowym.

• Mamy wtedy do czynienia ze

stratą energii mechanicznej,

której częśd, zgodnie z ogólnym prawem zachowania
energii, zamienia się w inną formę energii, np. w energię
cieplną.

L

V

T

V

T

o

o









MT SS - w 12

38

Układ punktów materialnych

Energia kinetyczna układu n punktów materialnych opisana
jest wzorem,




w którym prędkośd punktu „i” określona jest względem
pewnego, nieruchomego układu odniesienia Oxyz, w
stosunku do którego badamy ruch układu punktów
materialnych.









n

i

i

i

m

T

1

2

2



MT SS - w 12

39

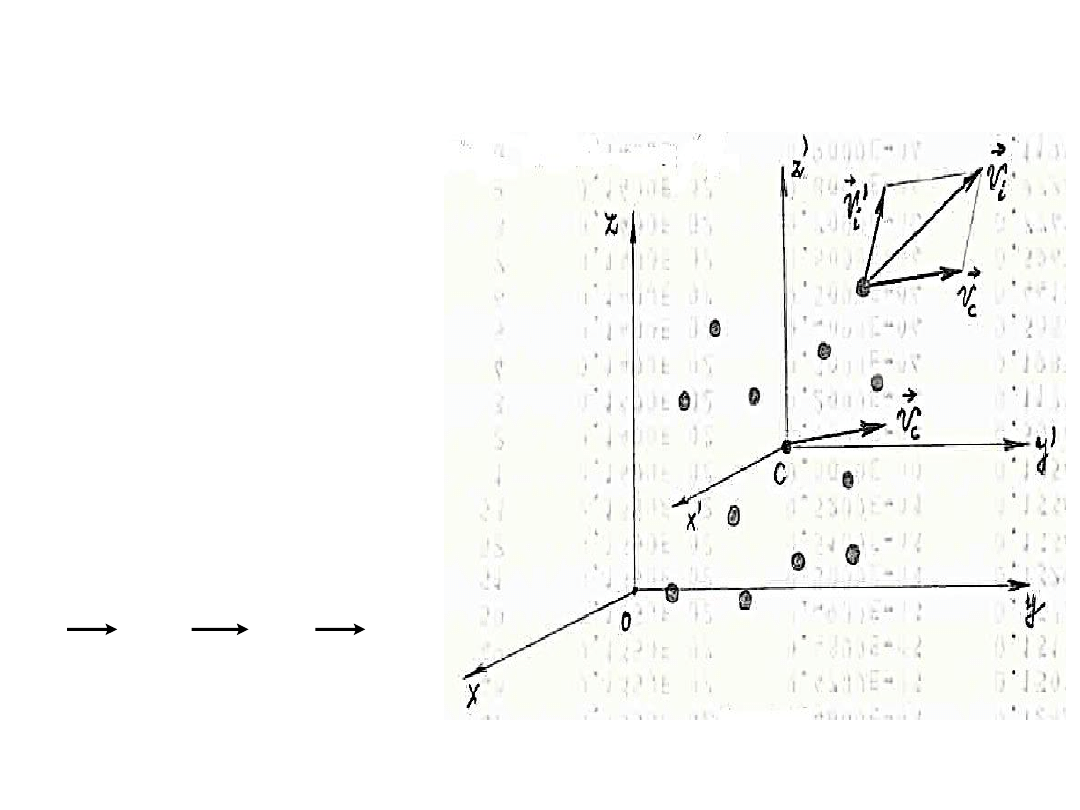
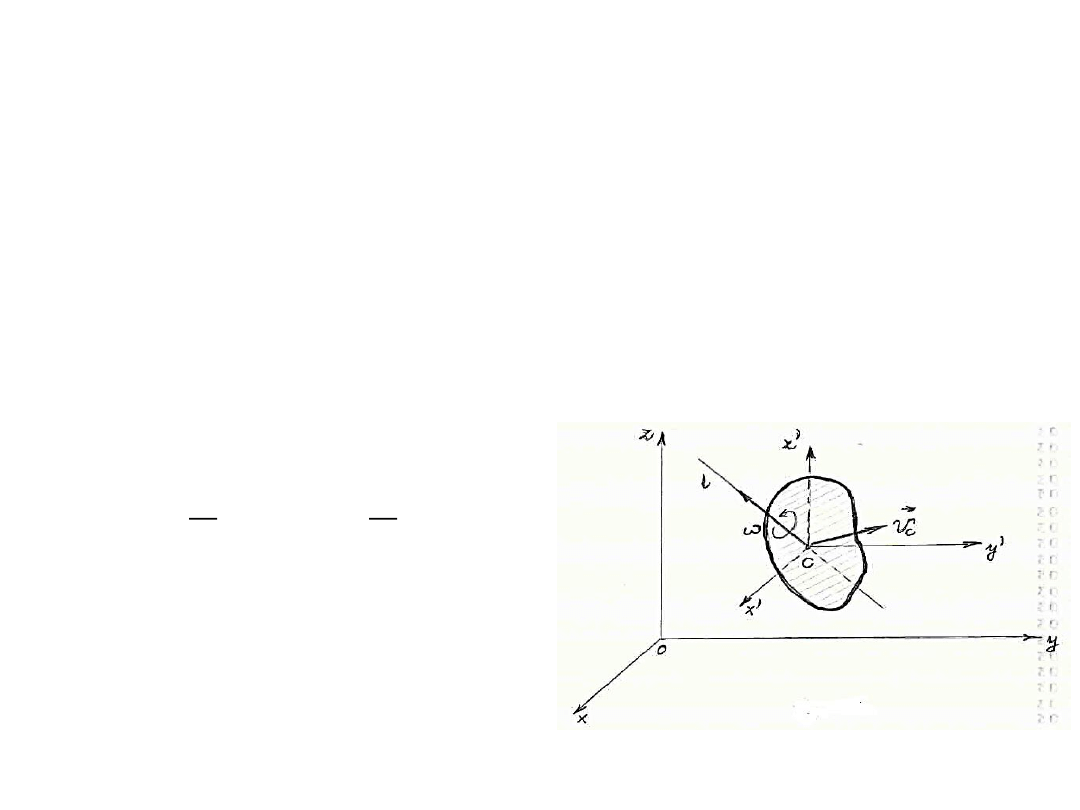
Wprowadźmy drugi układ odniesienia – Cx’y’z’ o początku w
środku masy układu C i poruszający się względem układu
Oxyz z prędkością środka masy υ

c

.

Prędkośd υ

i

punktu materialnego

rozważanego układu jest sumą
geometryczną prędkości υ

c

środka

masy i prędkości υ

i

’

punktu materialnego
względem ruchomego
układu odniesienia Cx’y’z’.

'

i

c

i











MT SS - w 12

40

Twierdzenie Koeniga

Energia kinetyczna układu punktów materialnych

równa jest sumie

energii kinetycznej, jaką miałby punkt materialny o masie

całego układu poruszający się z prędkością środka masy

oraz

energii kinetycznej tegoż układu w jego ruchu względem

środka masy.













n

i

i

i

c

m

m

T

1

2

2

2

'

2

1





MT SS - w 12

41

Dla układu punktów materialnych słuszne jest następujące
twierdzenie:

Przyrost energii kinetycznej układu punktów materialnych w
skooczonym przedziale czasu równy jest sumie prac, które
wykonały w tym samym czasie wszystkie siły zewnętrzne i
wszystkie siły wewnętrzne działające na rozpatrywany układ.

L

L

T

T

T

o













T – energia kinetyczna układu w czasie t,
T

o

– energia kinetyczna układu w czasie t

o

,

L – suma prac sił zewnętrznych,
L’ – suma prac sił wewnętrznych.

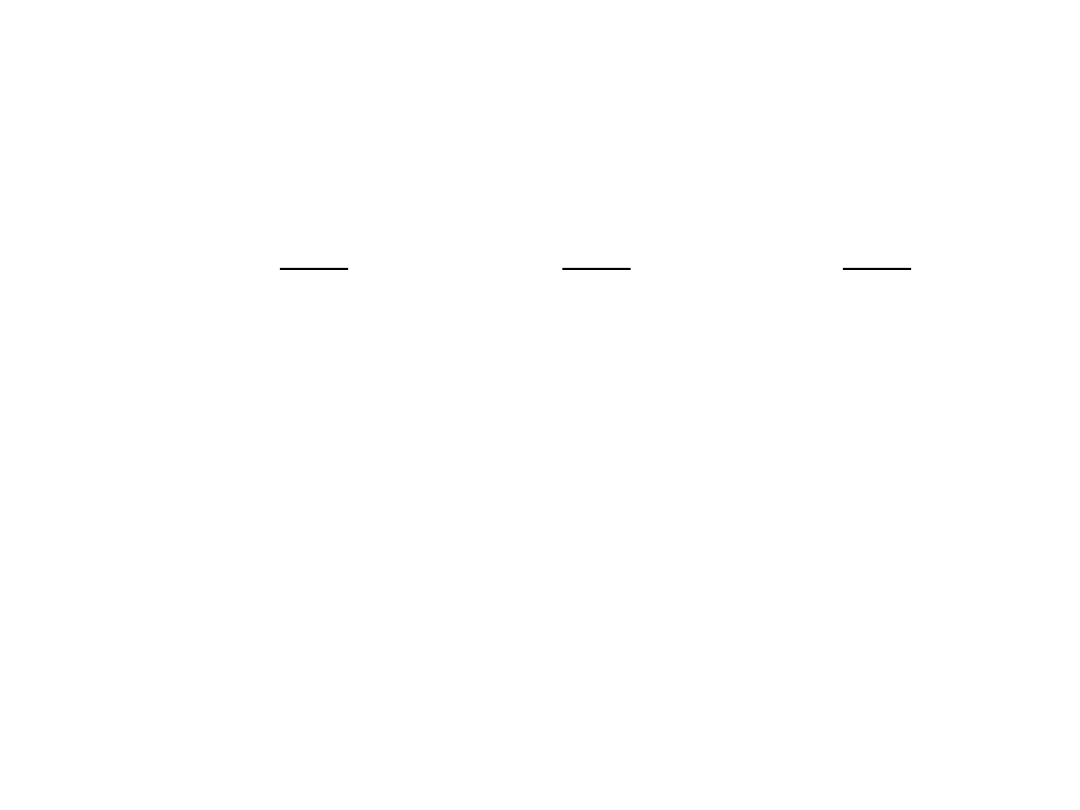
MT SS - w 12

42

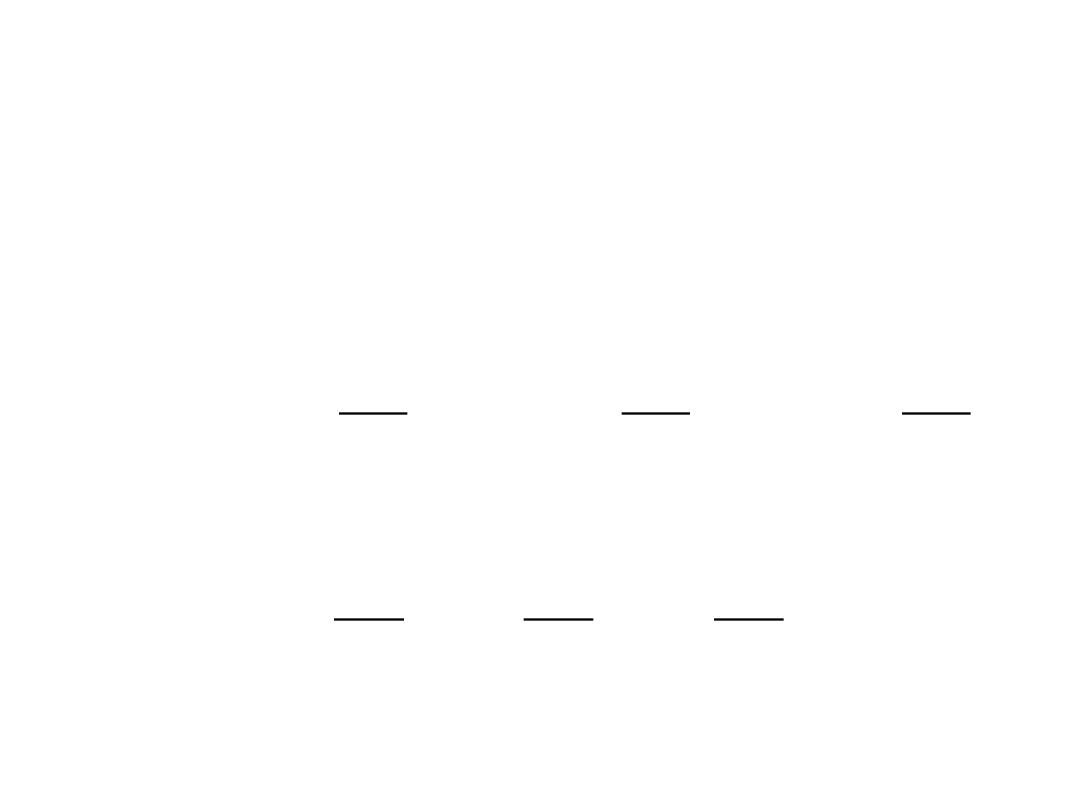
Jeśli układ punktów materialnych porusza się w
zachowawczym polu sił, wówczas składowe prostokątne siły
P

i

możemy wyrazid w następujący sposób:

x

i

, y

i

, z

i

– współrzędne punktu materialnego, na który działa

siła P

i

,

V – energia potencjalna sił zewnętrznych.

.

,

,

i

i

i

i

i

i

z

V

P

y

V

P

x

V

P

z

y

x





























n

n

n

z

y

x

z

y

x

z

y

x

V

V

,

,

,

,

,

,

,

,

,

2

2

2

1

1

1





MT SS - w 12

43

Suma prac elementarnych wszystkich sił określona jest
wzorem:



lub uwzględniając



otrzymujemy:





















n

i

i

i

i

i

i

i

n

i

i

dz

P

dy

P

dx

P

L

dL

z

y

x

1

1

.

,

,

i

i

i

i

i

i

z

V

P

y

V

P

x

V

P

z

y

x

























dV

dz

z

V

dy

y

V

dx

x

V

dL

n

i

i

i

i

i

i

i









































1

MT SS - w 12

44

Tak więc suma prac elementarnych sił zewnętrznych równa
jest różniczce zupełnej energii potencjalnej ze znakiem
minus.

Całkując powyższe równanie znajdujemy pracę sił w
skooczonym przedziale czasu:



przy czym:

V

o

–

energia potencjalna w położeniu początkowym układu

,

V –

energia potencjalna układu w położeniu koocowym układu

.

V

V

L

o





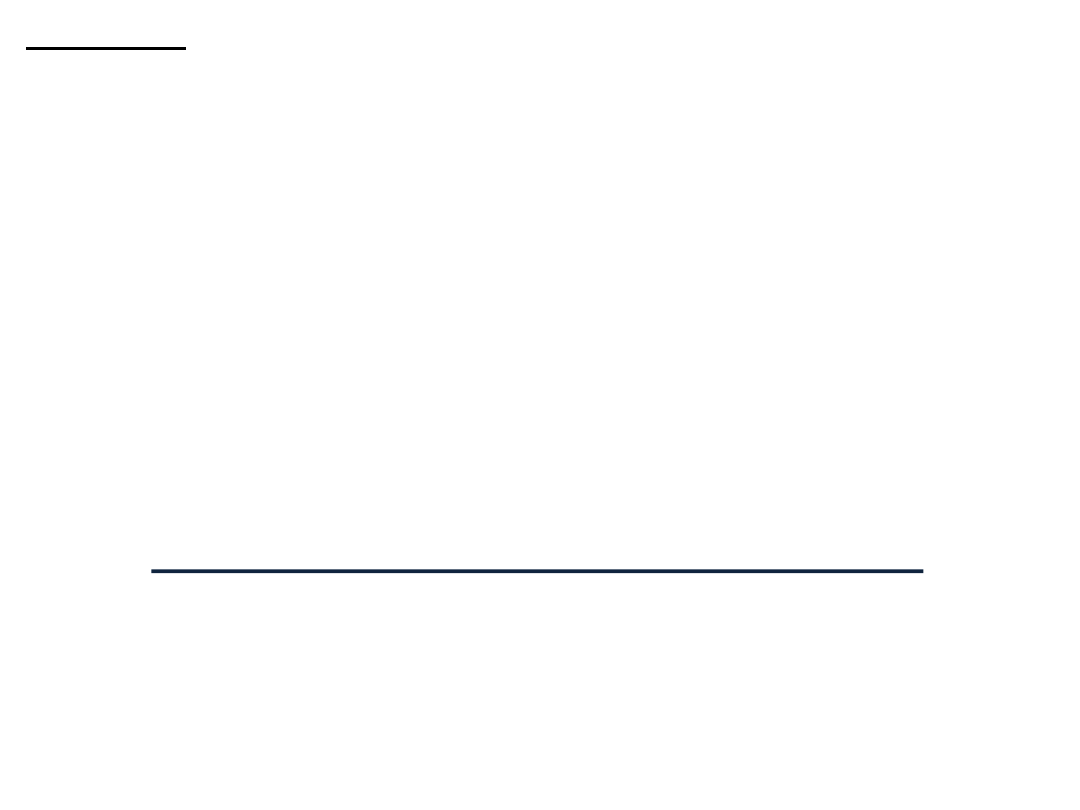
MT SS - w 12

45

Założenie:

Badamy ruch układu punktów materialnych działają jedynie
siły zachowawcze.

Po podstawieniu do równania

pracy sił zewnętrznych L

i pracy sił wewnętrznych

otrzymujemy:

czyli:

L

L

T

T

T

o













V

V

L

o





'

'

'

V

V

L

o





'

'

V

V

V

V

T

T

o

o

o











'

'

o

o

o

V

V

T

V

V

T











ZASADA ZACHOWANIA ENERGII MECHANICZNEJ

dla układu punktów materialnych

Gdy na układ punktów materialnych działają siły zachowawcze,

wówczas suma energii kinetycznej i energii potencjalnej (sił

wewnętrznych i zewnętrznych) tego układu jest wartością stałą.

MT SS - w 12

46

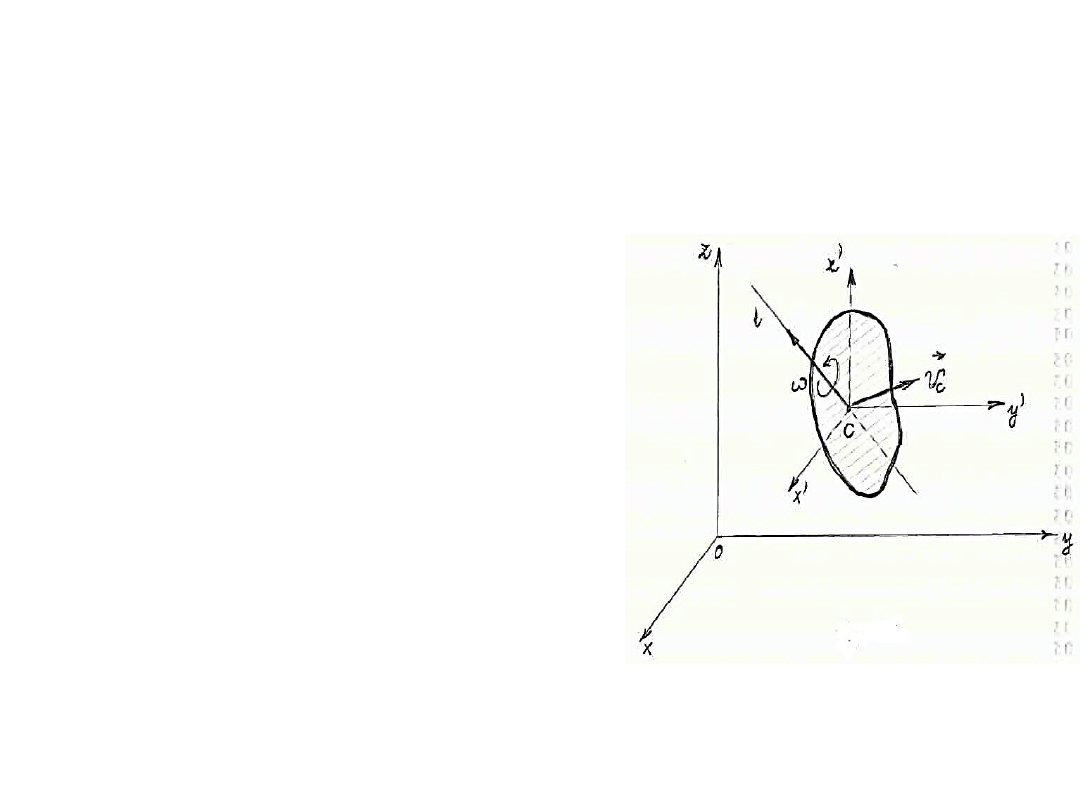
Ciało doskonale sztywne

Zgodnie z twierdzeniem Koeniga, energia kinetyczna takkiego
ciała określimy jako:

Energia kinetyczna ciała sztywnego w ogólnym przypadku
ruchu równa jest sumie energii kinetycznej ruchu
postępowego z prędkością równą prędkości środka masy i
energii kinetycznej w chwilowym ruchu obrotowym ciała
względem jego środka masy.

m –

masa całkowita ciała sztywnego

,

I

l

–

moment bezwładności ciała

względem osi chwilowej l

,

ω –

chwilowa prędkośd kątowa ciała

.

2

2

2

1

2

1













l

c

I

m

T

MT SS - w 12

47

Ponieważ w ciele doskonale sztywnym wzajemne odległości
punktów nie ulegają zmianie, dlatego też praca sił
wewnętrznych

w

ciele

sztywnym

przy

dowolnym

przemieszczeniu tego ciała jest równe zeru.

Tak więc, ponieważ L’ = 0,
zatem dla ciała sztywnego
mamy:

Tw.

Przyrost energii kinetycznej ciała

sztywnego w skooczonym przedziale
czasu równy jest sumie prac,
które wykonały w tym samym czasie siły zewnętrzne
działające na to ciało.

L

T

T

T

o









MT SS - w 12

48

Zasada zachowania energii mechanicznej

dla ciała sztywnego

Gdy na ciało sztywne działają siły zachowawcze, wówczas
suma energii kinetycznej i energii potencjalnej sił
zewnętrznych jest wielkością stałą.



lub

const

V

T

V

T

V

T

o

o









