Przekształcenia całkowe

Wykład 6

fragmenty

Zastosowania przekształceń Laplace’a

1. Równania różniczkowe liniowe
Dane jest równanie różniczkowe liniowe rzędu o stałych

współczynnikach:

Zakładamy, że oraz funkcja i szukane rozwiązanie

wraz ze wszystkimi pochodnymi są oryginałami.

n

( )

(

1)

0

1

1

( )

n

n

n

n

a y

a y

a

y

a y

f t

−

−

′

+

+

+

+

=

…

0

0

a

≠

( )

f t

( )

y t

Przekształcenie Laplace’a

Szukamy takiego rozwiązania równania, aby spełniało

one warunki początkowe (WP):

Przekształcenie Laplace’a

(

1)

0

1

2

1

(0)

,

(0)

,

(0)

,

,

(0)

.

n

n

y

b y

b y

b

y

b

−

−

′

′′

=

=

=

=

…

Przykład 1

Rozwiązać równanie

z warunkiem początkowym

2

( ) 3 ( )

5

2

4

y t

y t

t

t

′ +

=

+ +

(0) 1

y

=

Rozwiązanie:

Stosujemy transformatę Laplace’a do obu stron równania:

Odczytujemy z tablic uwzględniając WP:

[

]

(

)

[

]

[

]

( )

( )

( )

2

2

L

( ) 3 ( )

L 5

2

4

L

( ) +3L

( )

5L t

2L t

4L 1

y t

y t

t

t

y t

y t

′ +

=

+ +

′

=

+

+

Przekształcenie Laplace’a

[

]

[

]

[

]

L

( )

L

( )

(0)

L

( )

1

y t

s

y t

y

s

y t

′

=

−

=

−

( )

( )

( )

2

3

2

2

1

1

L t

=

L t =

L 1 =

s

s

s

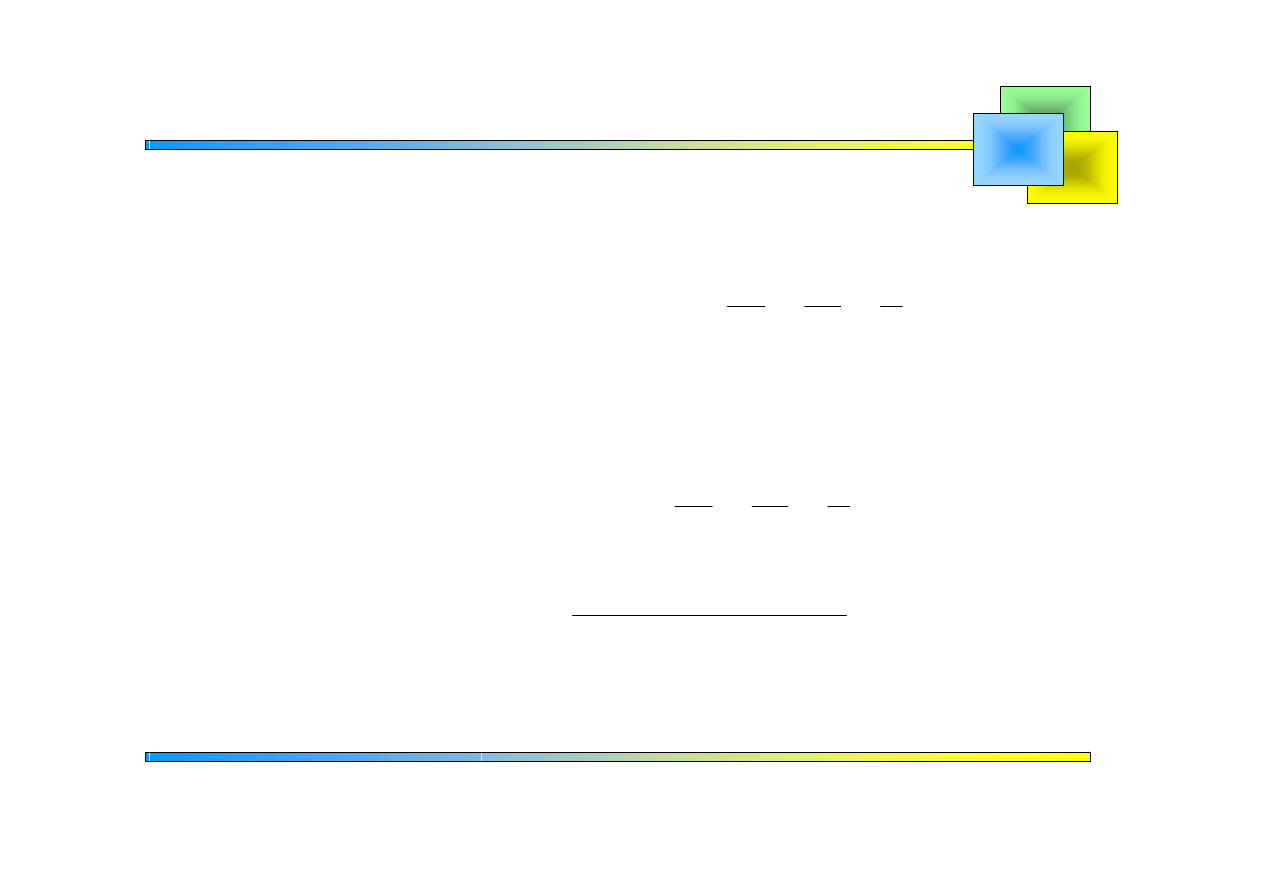
Wstawiamy do równania wyjściowego:

Rozwiązujemy równanie, w którym niewiadomą jest :

[

]

[

]

3

2

10

2

4

L

( )

3L

( )

1

s

y t

y t

s

s

s

+

− =

+

+

[

]

[

]

3

2

3

2

3

10

2

4

(

3)L

( )

1

4

2

10

L

( )

(

3)

s

y t

s

s

s

s

s

s

y t

s

s

+

= +

+

+

+

+

+

=

+

[

]

L

( )

y t

Przekształcenie Laplace’a

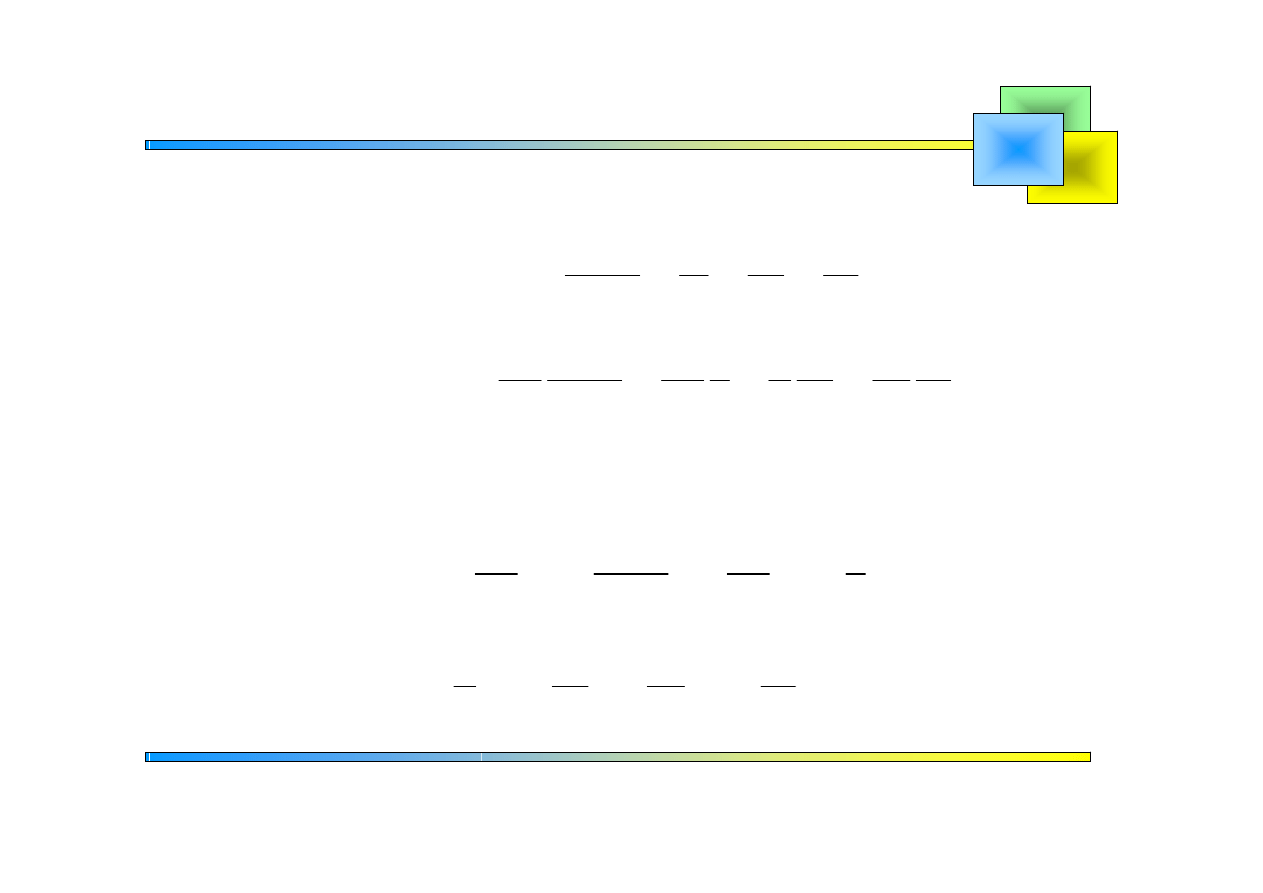
Rozkładamy prawą stronę równania na ułamki proste

Wykorzystujemy transformatę odwrotną

[

]

[

]

2

3

2

3

L

( )

3

13

1

40 1

4 1

10 1

L

( )

27

3

27

9

3

A

B

C

D

y t

s

s

s

s

y t

s

s

s

s

=

+ +

+

+

= −

+

−

+

+

1

1

1

1

2

3

13

1

40

1

( )

L

L

27

3

27

4

1

10

1

L

L

9

3

y t

s

s

s

s

−

−

−

−

⎛

⎞

⎛ ⎞

= −

+

−

⎜

⎟

⎜ ⎟

+

⎝

⎠

⎝ ⎠

⎛ ⎞

⎛ ⎞

−

+

⎜ ⎟

⎜ ⎟

⎝ ⎠

⎝ ⎠

Przekształcenie Laplace’a

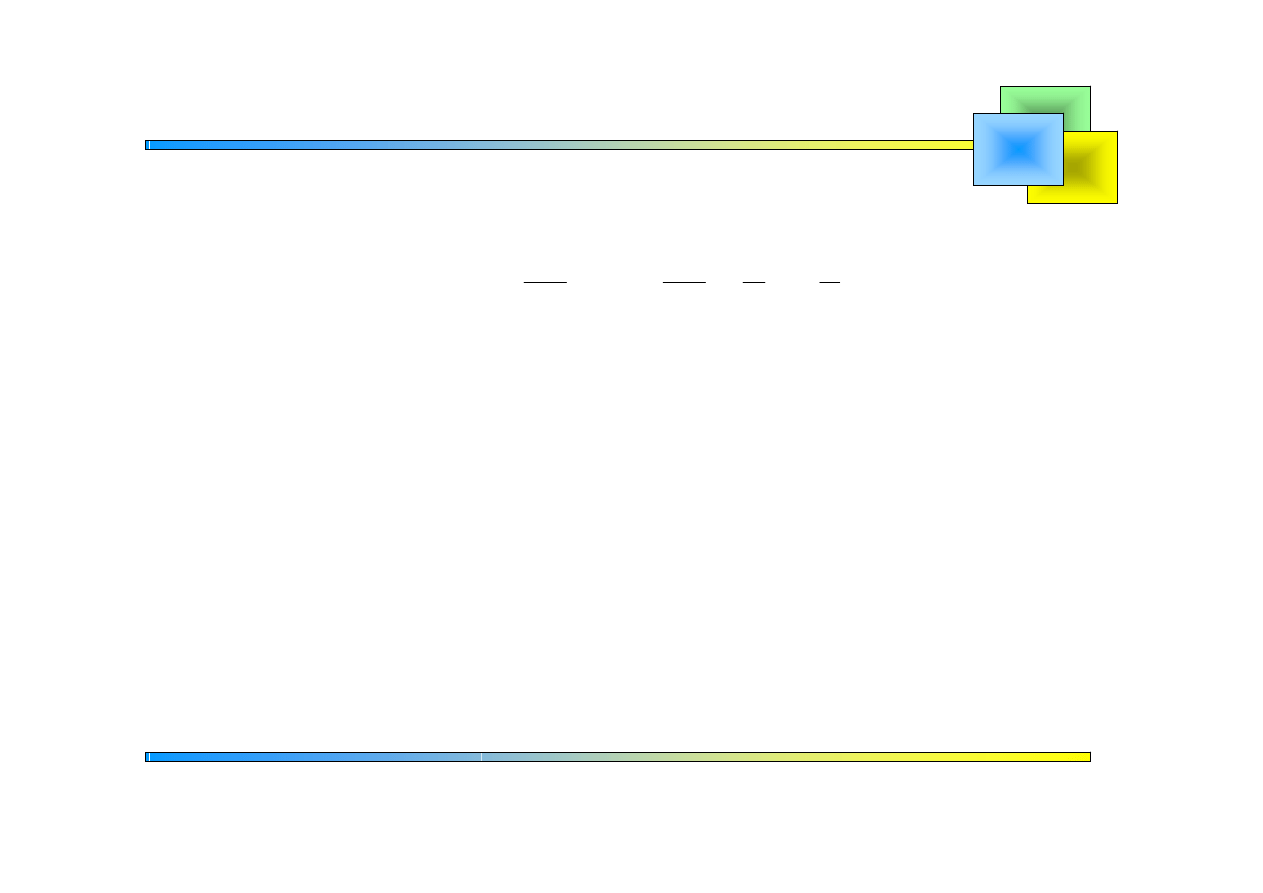
Czyli

3

2

13

40

4

5

( )

27

27

9

3

t

y t

e

t

t

−

= −

+

−

+

Przekształcenie Laplace’a

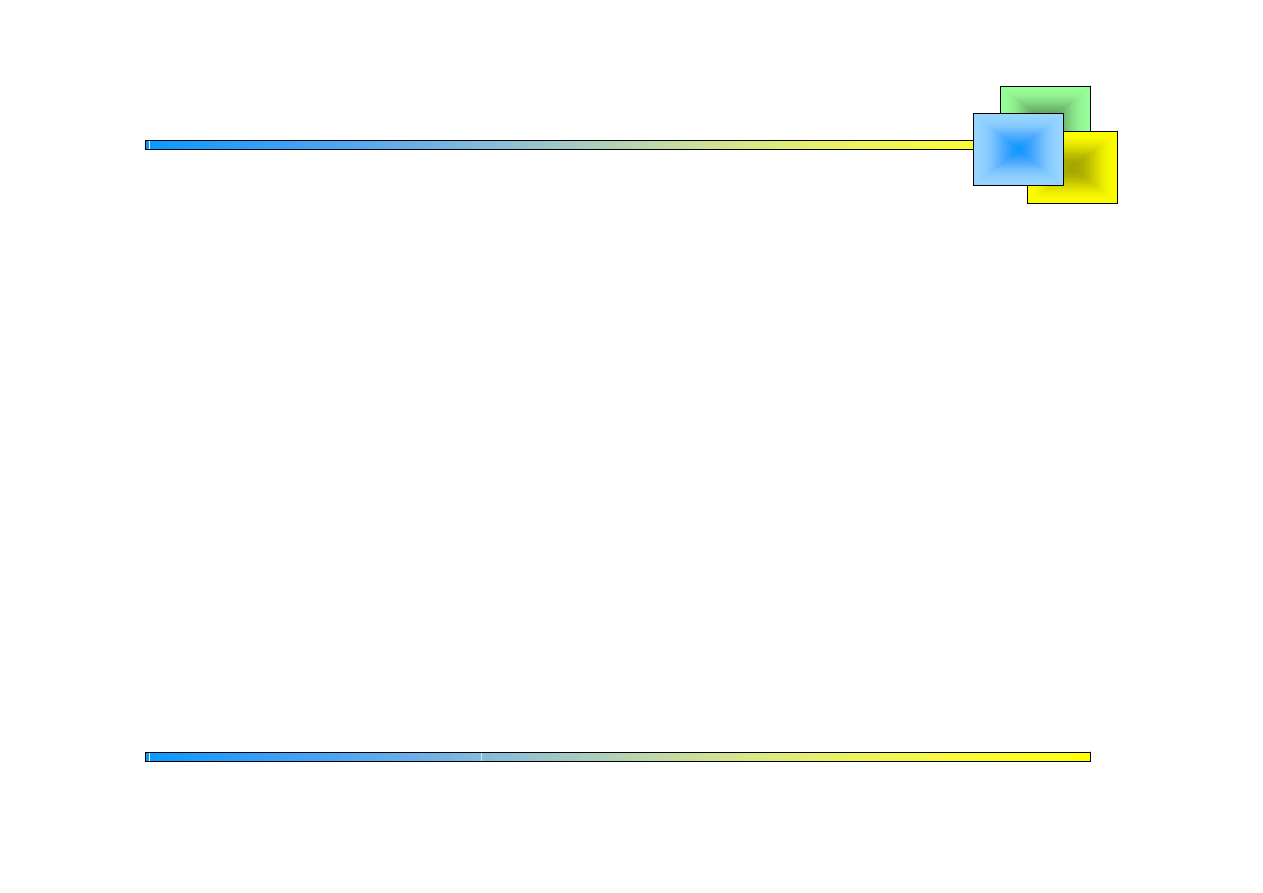
2. Układy równań różniczkowych liniowych

Przykład 1

Rozwiązać układ równań

z warunkami początkowymi

3

2

2

t

t

y

y

z

e

z

y

z

e

′

⎧ + − =

⎨

′ +

−

=

⎩

(0) 1,

(0) 1

y

z

=

=

Przekształcenie Laplace’a

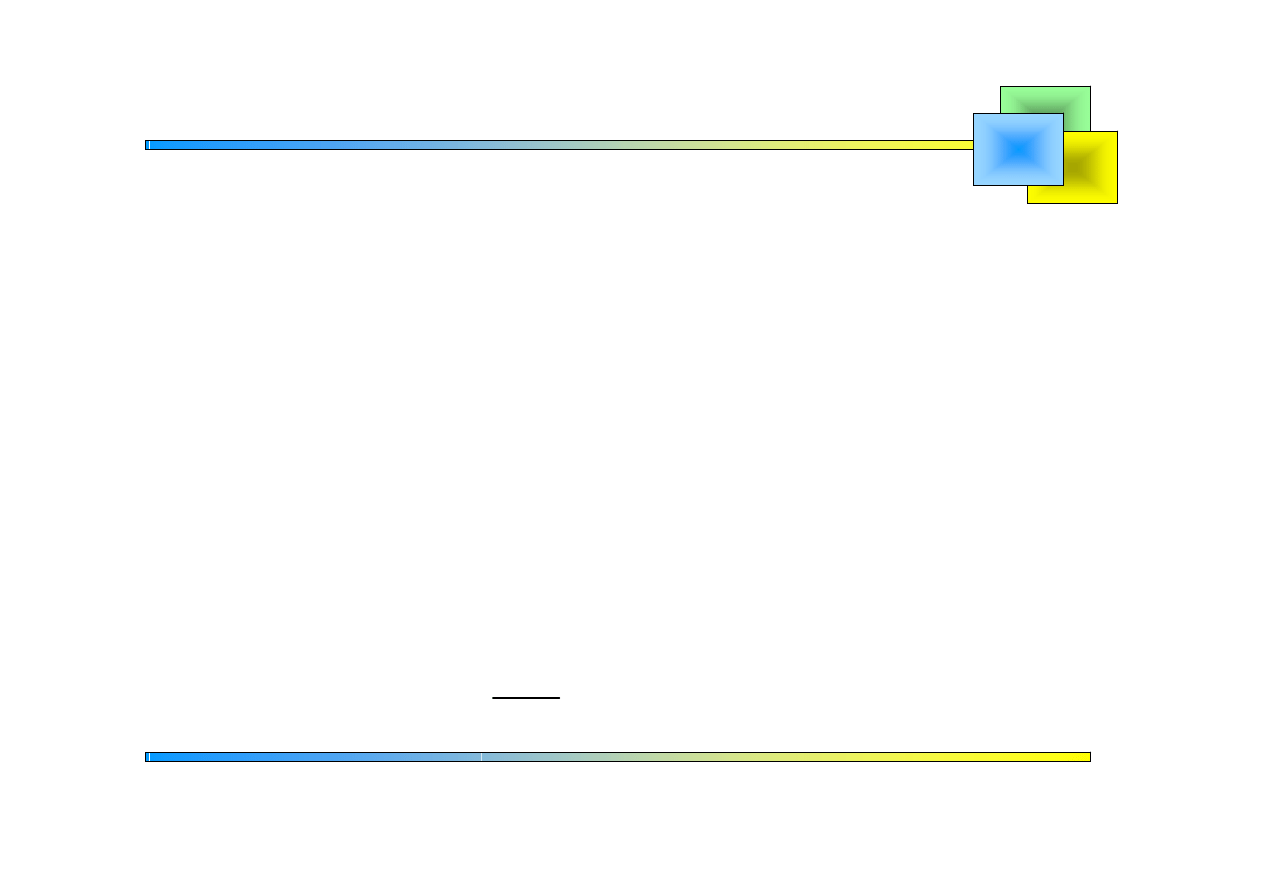
Rozwiązanie:

Stosujemy transformatę Laplace’a do obu stron równania:

Przekształcenie Laplace’a

Odczytujemy z tablic

[ ]
[ ]

( )

L

L( )

(0)

L( ) 1

L

L( )

(0)

L ( ) 1

1

L e

1

t

y

s

y

y

s

y

z

s

z

z

s

z

s

′ =

−

=

−

′ =

−

=

−

=

−

( )

( )

( )

( )

( )

( )

( )

( )

L

L

L

L

L

3L

2L

2L

t

t

y

y

z

e

z

y

z

e

⎧

′ +

−

=

⎪

⎨

′ +

−

=

⎪⎩

( )

( )

( )

( )

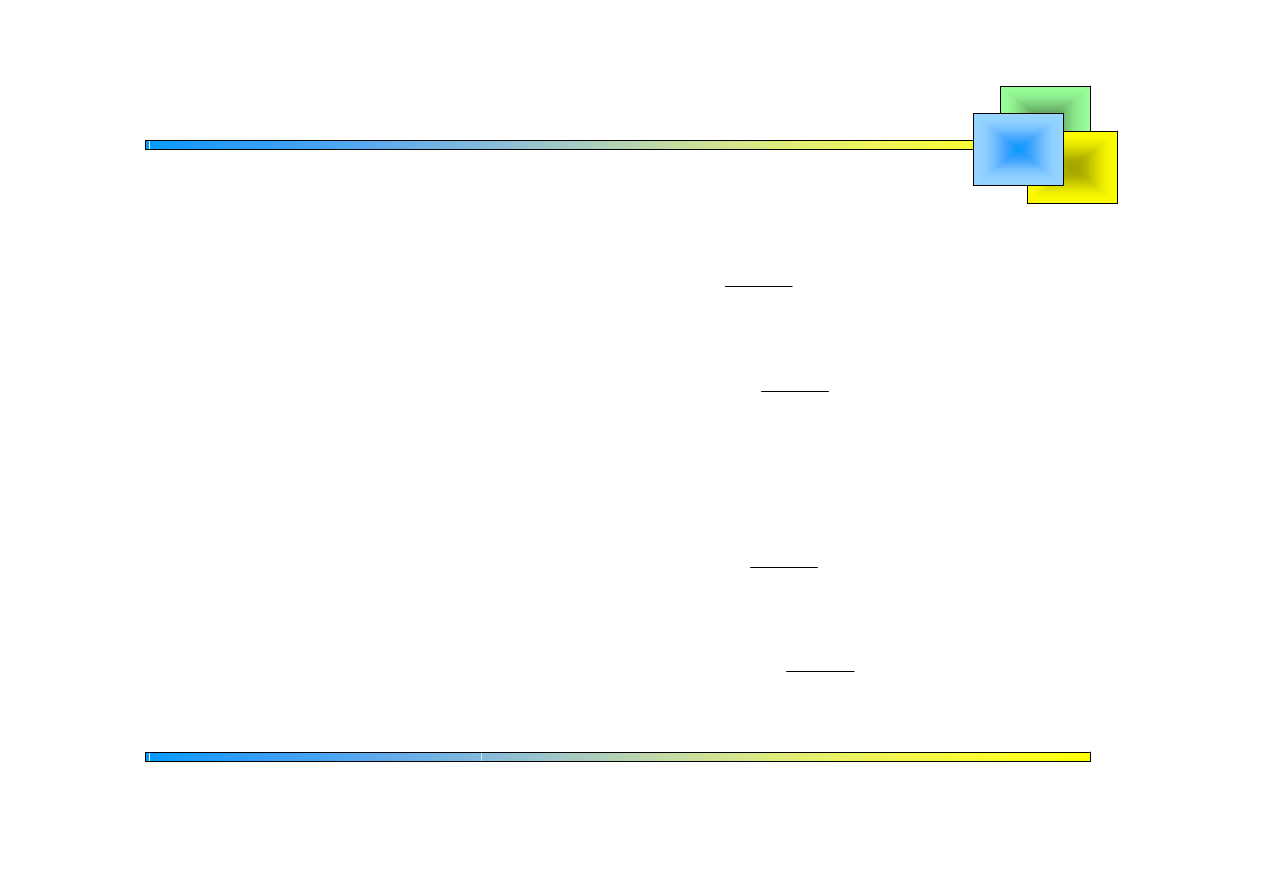
1

(s+1)L

L

1

1

2

3L

(

2)L

1

1

y

z

s

y

s

z

s

⎧

−

=

+

⎪⎪

−

⎨

⎪

+ −

=

+

⎪⎩

−

Wstawiamy do układu:

Rozwiązujemy ten układ względem niewiadomych i

L( )

y

L( )

z

Przekształcenie Laplace’a

( )

( )

( )

( )

(s+1)L

L

1

1

3L

(

2)L

1

s

y

z

s

s

y

s

z

s

⎧

−

=

⎪⎪

−

⎨

+

⎪

+ −

=

⎪⎩

−

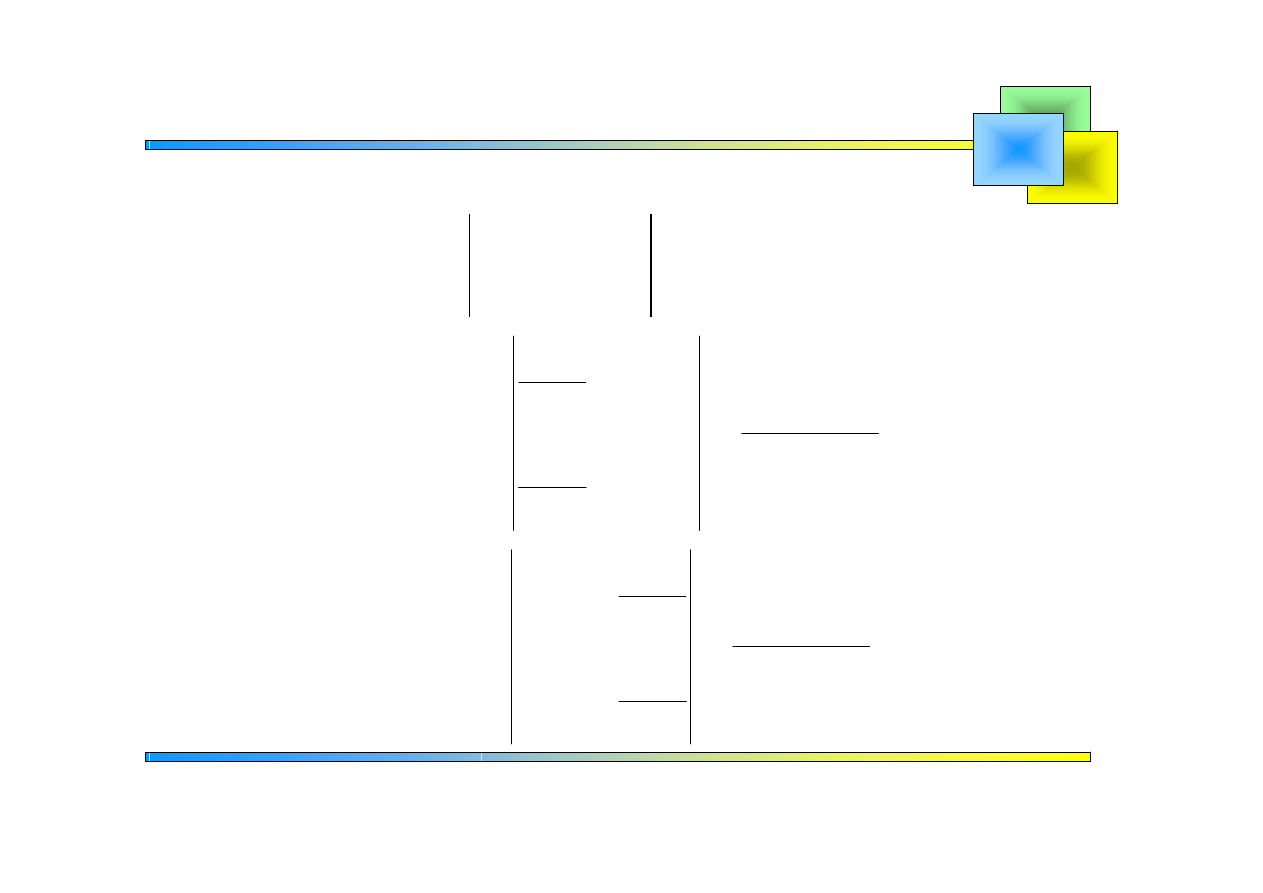
2

2

L( )

2

L( )

1

1

1

3

2

1

1

1
1

1

2

1

1

1

1
1

1

3

1

y

z

s

W

s

s

s

s

s

s

s

W

s

s

s

s

s

s

s

s

s

W

s

s

s

+

−

=

=

− +

−

−

− +

−

=

=

+

−

−

−

+

− +

−

=

=

+

−

−

Wyznaczamy niewiadome np. metodą wyznaczników:

Przekształcenie Laplace’a

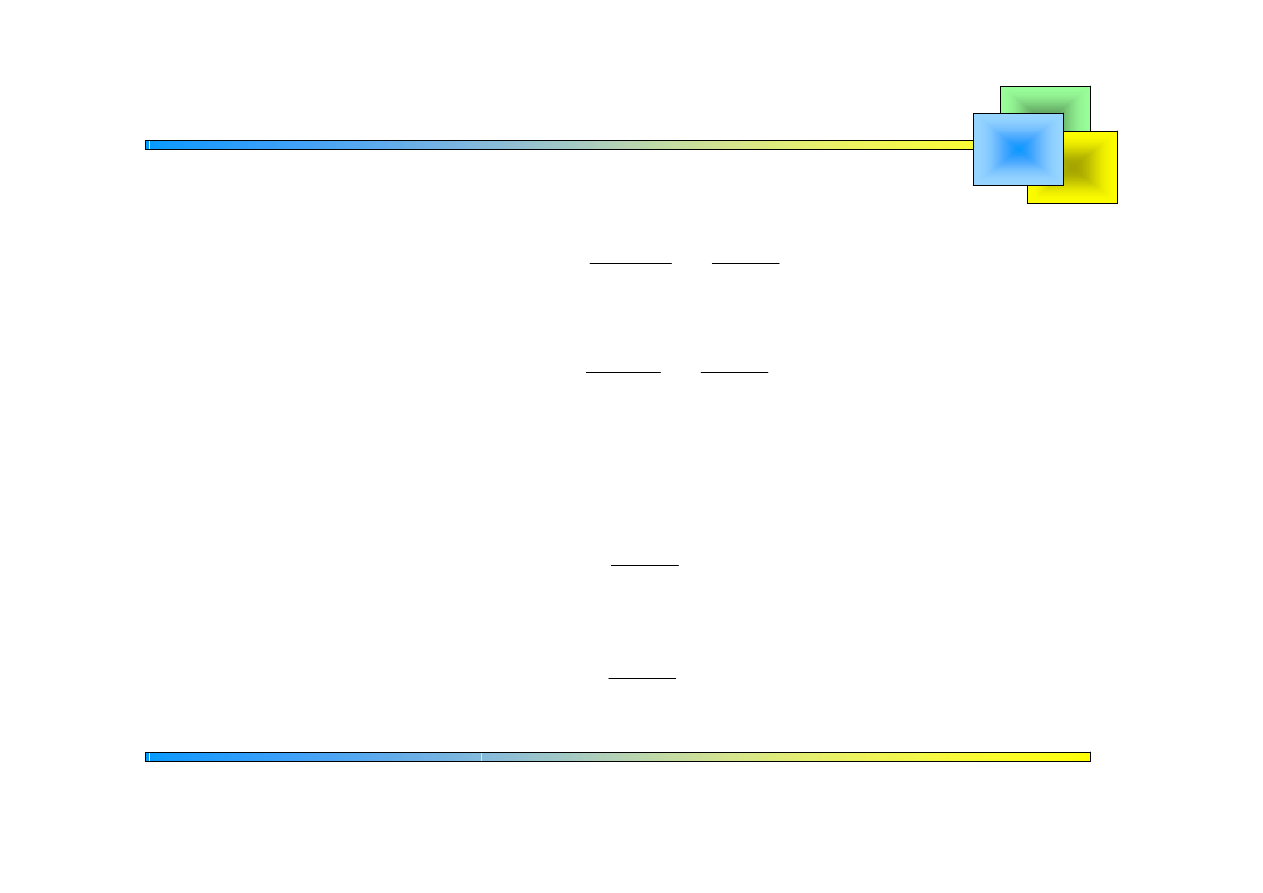
Otrzymujemy

Wykorzystujemy transformatę odwrotną

L( )

L( )

1

L( )

1

1

L( )

1

y

z

W

y

W

s

W

z

W

s

=

=

−

=

=

−

Przekształcenie Laplace’a

1

1

1

y=L

1

1

z=L

1

t

t

e

s

e

s

−

−

⎛

⎞ =

⎜

⎟

−

⎝

⎠

⎛

⎞ =

⎜

⎟

−

⎝

⎠