Przekształcenia całkowe
Wykład 7
Szeregi Fouriera
Definicja:
Mówimy, że ciąg funkcji całkowalnych z kwadratem
w przedziale jest ciągiem ortogonalnym, jeżeli
{
}
( )
n
X
x
[ , ]
a b
0
dla
,
( )
( ) d
0 dla
.
b
n
m
a
n
m
X
x X
x
x
A
n
m
≠
⎧
= ⎨
>
=
⎩
∫
Szeregi Fouriera
Zadanie
:
Sprawdzić, że ciąg funkcji
Jest ciągiem ortogonalnym w .
{
}
1, sin , cos , sin 2 , cos 2 ,
x
x
x
x …
[
, ]
−π π
Szeregi Fouriera
Rozwiązanie:
Należy sprawdzić (zakładając )
1)
2)
3)
4)
5)
6)
7)
8)
n
m
≠
sin
d
0
n x x
π
−π
=
∫
cos
d
0
n x x
π
−π
=
∫
sin
sin
d
0
n x
m x x
π
−π
=
∫
cos
cos
d
0
n x
m x x
π
−π
=
∫
sin
cos
d
0
n x
m x x
π
−π
=
∫
2
sin
d
0
n x x
A
π
−π
= >
∫
2
cos
d
0
n x x
A
π
−π
= >
∫
d
0
x
A
π
−π
= >
∫
Szeregi Fouriera
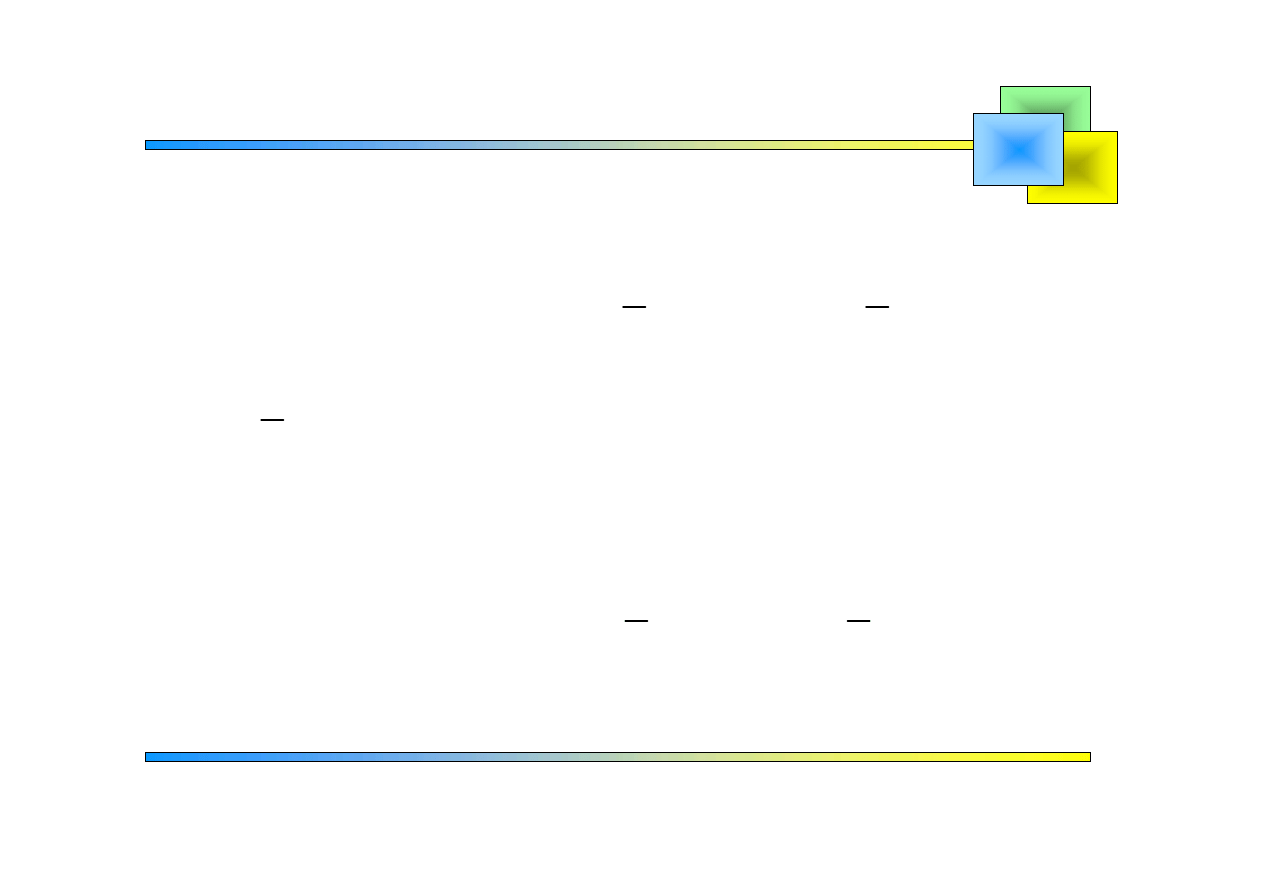
Zadanie 1
:
Szeregi Fouriera
[
]
[
]
1
1
sin
d
sin d
cos
d
d
1
cos
cos
0
n
n
n
n
u
n x
n x x
u u
u
u
n x
n
n
n
n
n
π
π
π
− π
−π
− π
⎫
=
⎧
=
=
= −
=
⎨
⎬
=
⎩
⎭
= −
π −
π =
∫
∫
Zadanie 2
:
[
]
1
1
cos
d
cos d
sin
0
d
d
n
n
n
n
u
n x
n x x
u u
u
u
n x
n
n
π
π
π
− π
−π
− π
⎫
=
⎧
=
=
=
=
⎨
⎬
=
⎩
⎭
∫
∫
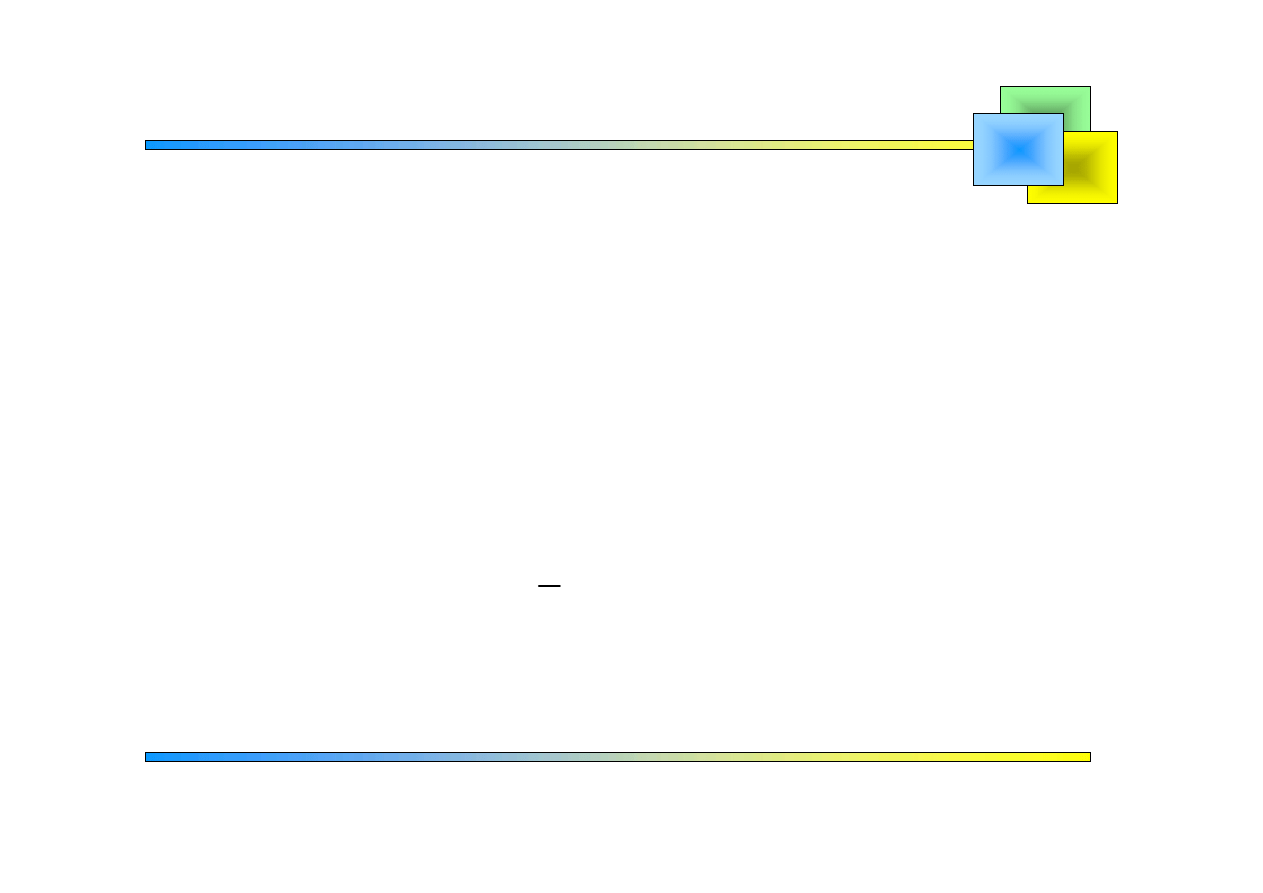
Wzory
Szeregi Fouriera
cos(
)
cos cos
sin sin
cos(
)
cos cos
sin sin
α + β =
α
β −
α
β
α − β =
α
β +
α
β
Po odjęciu stronami
[
]
cos(
)
cos(
)
2sin sin
1
sin sin
cos(
)
cos(
)
2
α − β −
α + β =
α
β
α
β =
α − β −
α + β
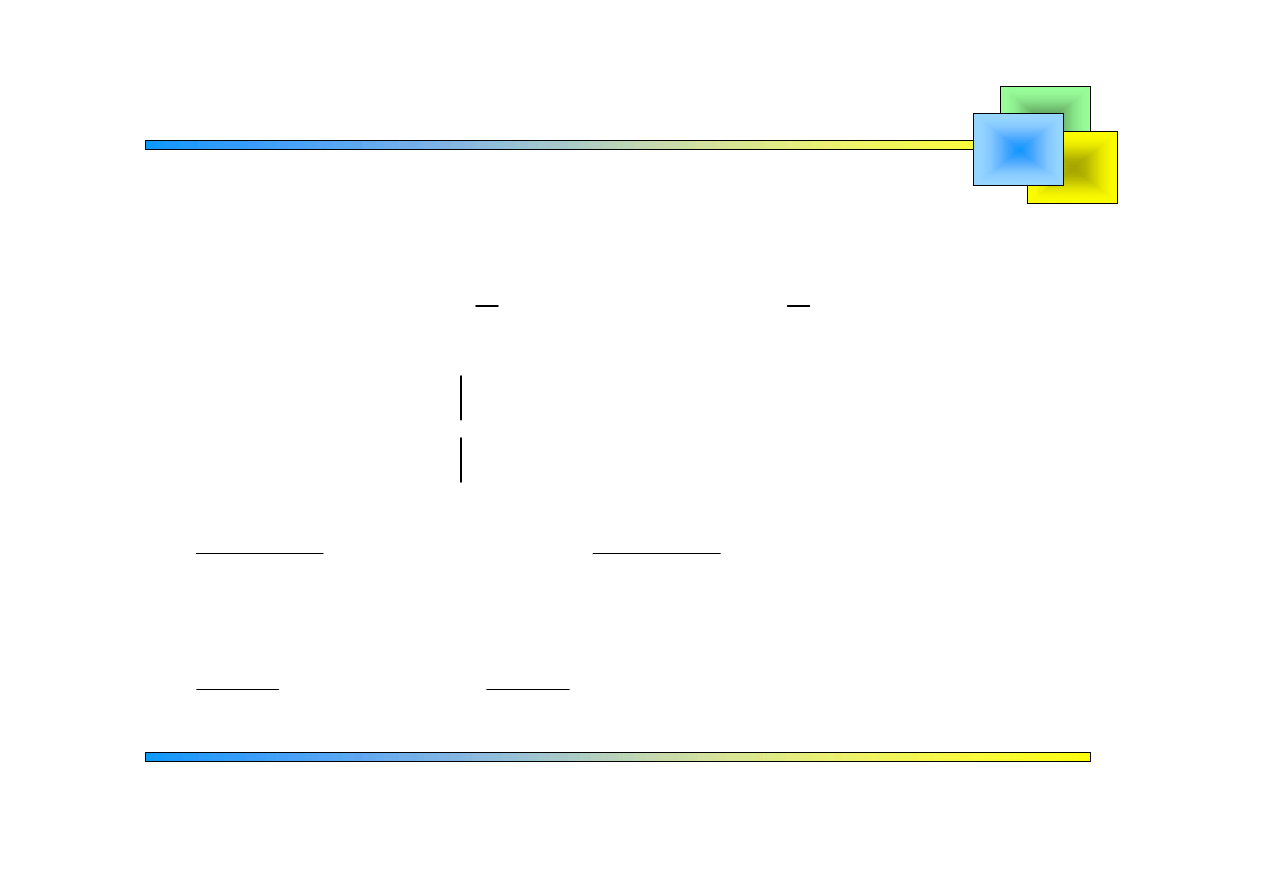
Zadanie 3
:
1
2
1
2
(
)
(
)
2
2
1
1
(
)
(
)
1
1
sin
sin
d
cos (
) d
cos (
) d
2
2
(
)
(
)
d
(
) d
d
(
) d
1
1
cos
d
cos
d
2(
)
2(
)
n m
n m
n m
n m
n x
m x x
n m x x
n
m x x
u
n
m x
u
n m x
u
n
m
x
u
n m
x
u
u
u
u
n m
n
m
π
π
π
−π
−π
−π
−
π
+
π
− −
π
− +
π
=
−
−
+
=
⎧
⎫
=
+
=
−
⎪
⎪
=
=
⎨
⎬
=
+
=
−
⎪
⎪
⎩
⎭
=
−
=
−
+
∫
∫
∫
∫
∫
Szeregi Fouriera
1
1
sin (
)
sin (
)
0
n m
n
m
n m
n
m
=
−
π −
+
π =
−
+
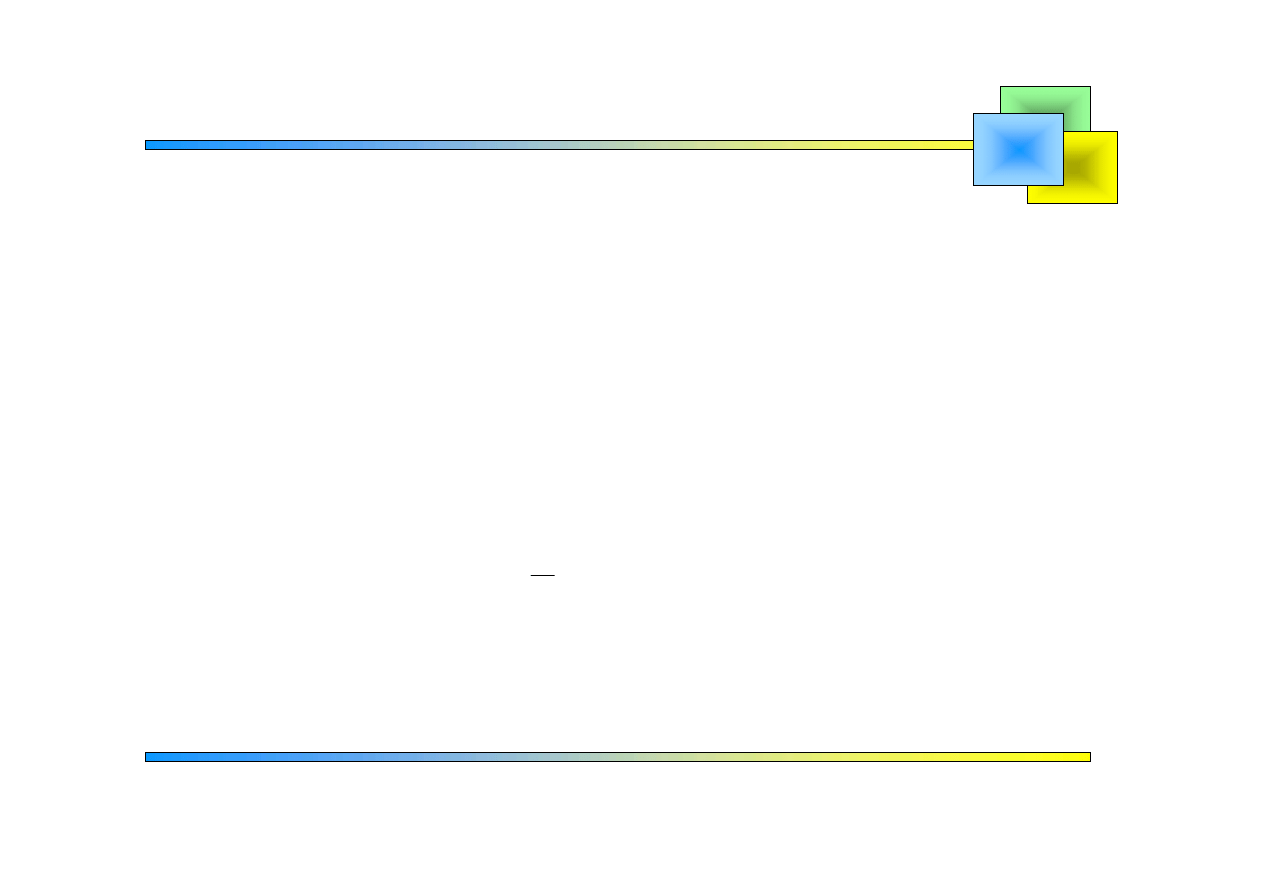
Wzory
Szeregi Fouriera
cos(
)
cos cos
sin sin
cos(
)
cos cos
sin sin
α + β =
α
β −
α
β
α − β =
α
β +
α
β
Po dodaniu stronami
[
]
cos(
) cos(
)
2cos cos
1
cos cos
cos(
) cos(
)
2
α + β +
α − β =
α
β
α
β =
α + β +
α − β
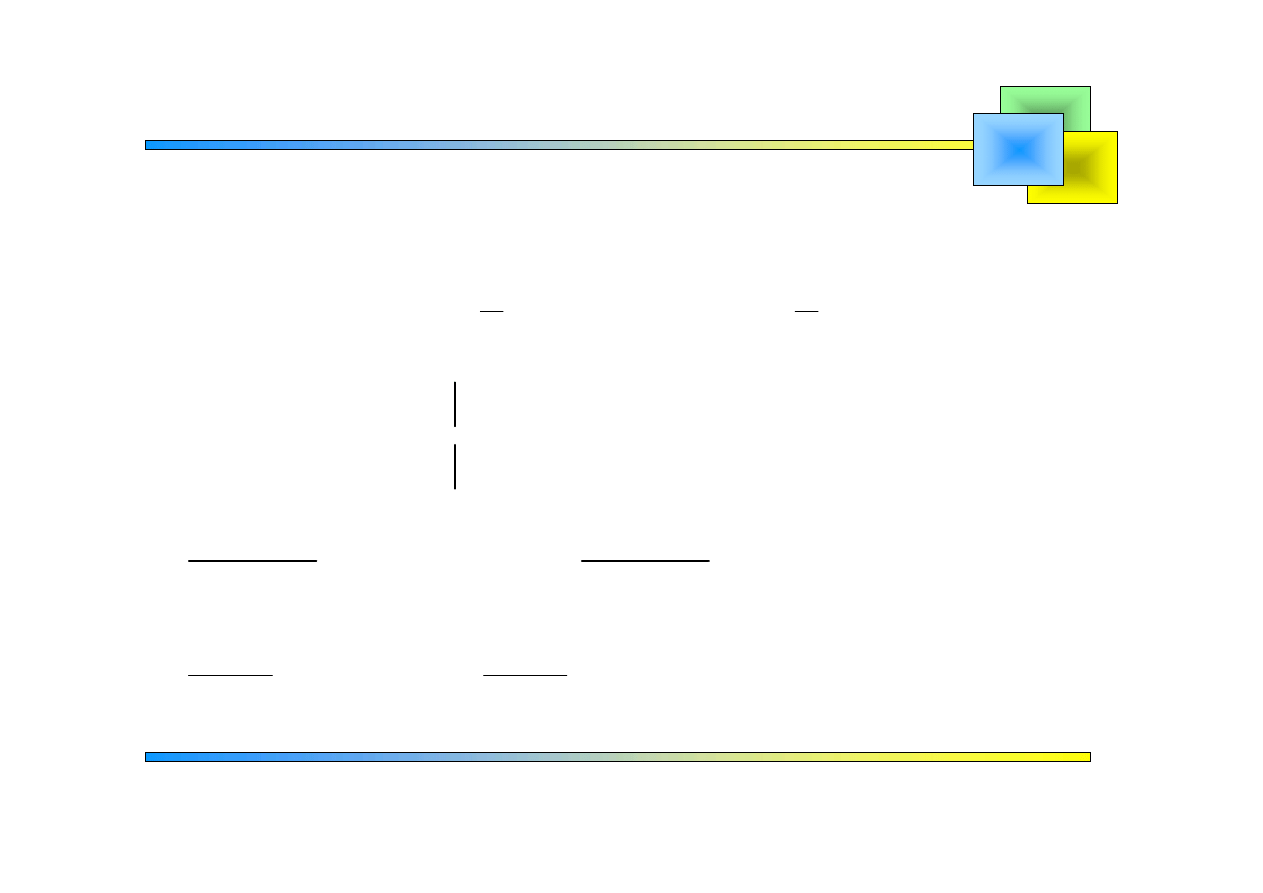
Zadanie 4
:
Szeregi Fouriera
1
2
1
2
(
)
(
)
1
1
2
2
(
)
(
)
1
1
cos
cos
d
cos (
) d
cos (
) d
2
2
(
)
(
)
d
(
) d
d
(
) d
1
1
cos
d
cos
d
2(
)
2(
)
1
1
sin (
)
sin (
)
0
n m
n m
n m
n m
n x
m x x
n
m x x
n m x x
u
n
m x
u
n m x
u
n
m
x
u
n m
x
u
u
u
u
n
m
n m
n
m
n m
n
m
n m
π
π
π
−π
−π
−π
+
π
−
π
− +
π
− −
π
=
+
+
−
=
⎧
⎫
=
+
=
−
⎪
⎪
=
=
⎨
⎬
=
+
=
−
⎪
⎪
⎩
⎭
=
+
=
+
−
=
+
π −
−
π =
+
−
∫
∫
∫
∫
∫
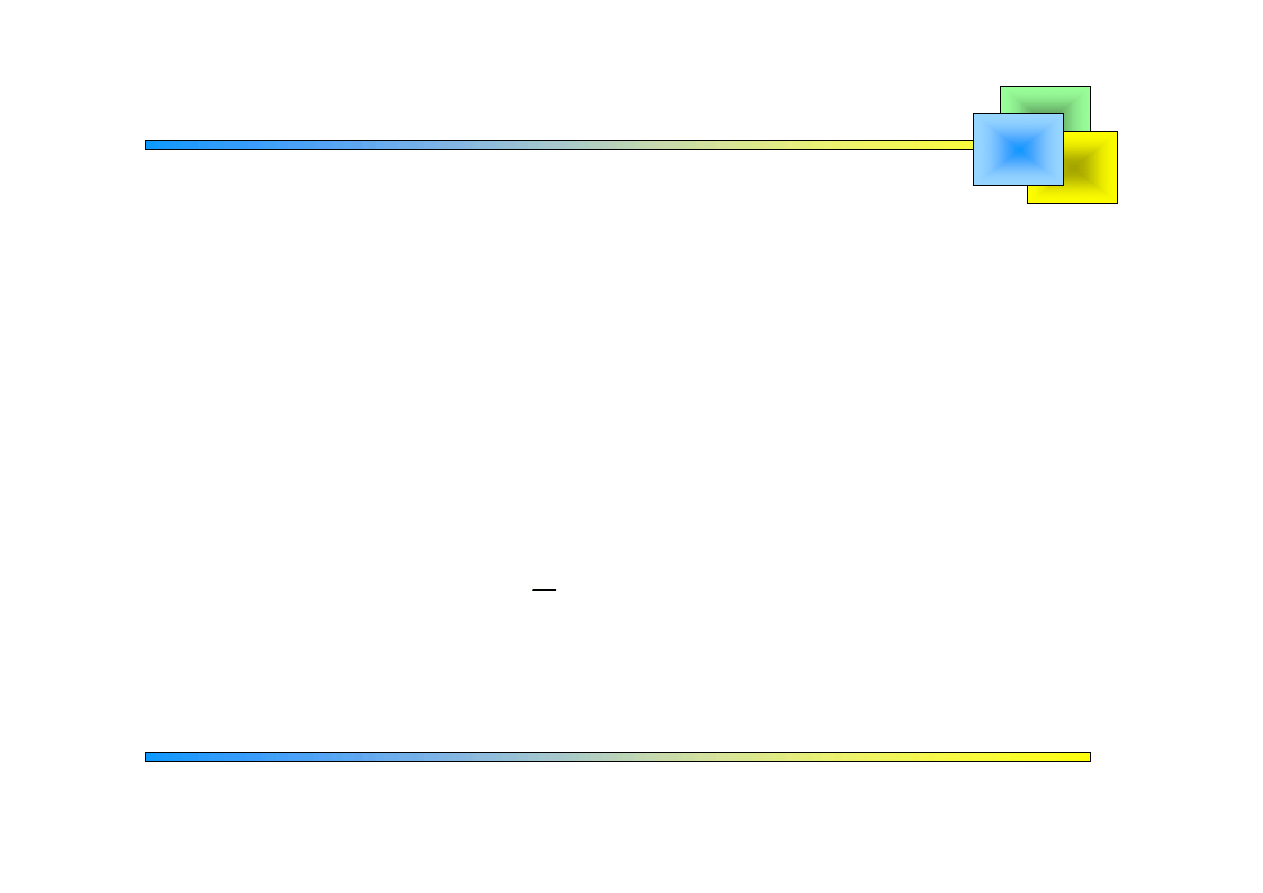
Wzory
Szeregi Fouriera
sin(
)
sin cos
cos sin
sin(
)
sin cos
cos sin
α + β =
α
β +
α
β
α − β =
α
β −
α
β
Po dodaniu stronami
[
]
sin(
)
sin(
)
2sin cos
1
sin cos
sin(
)
sin(
)
2
α + β +
α − β =
α
β
α
β =
α + β +
α − β
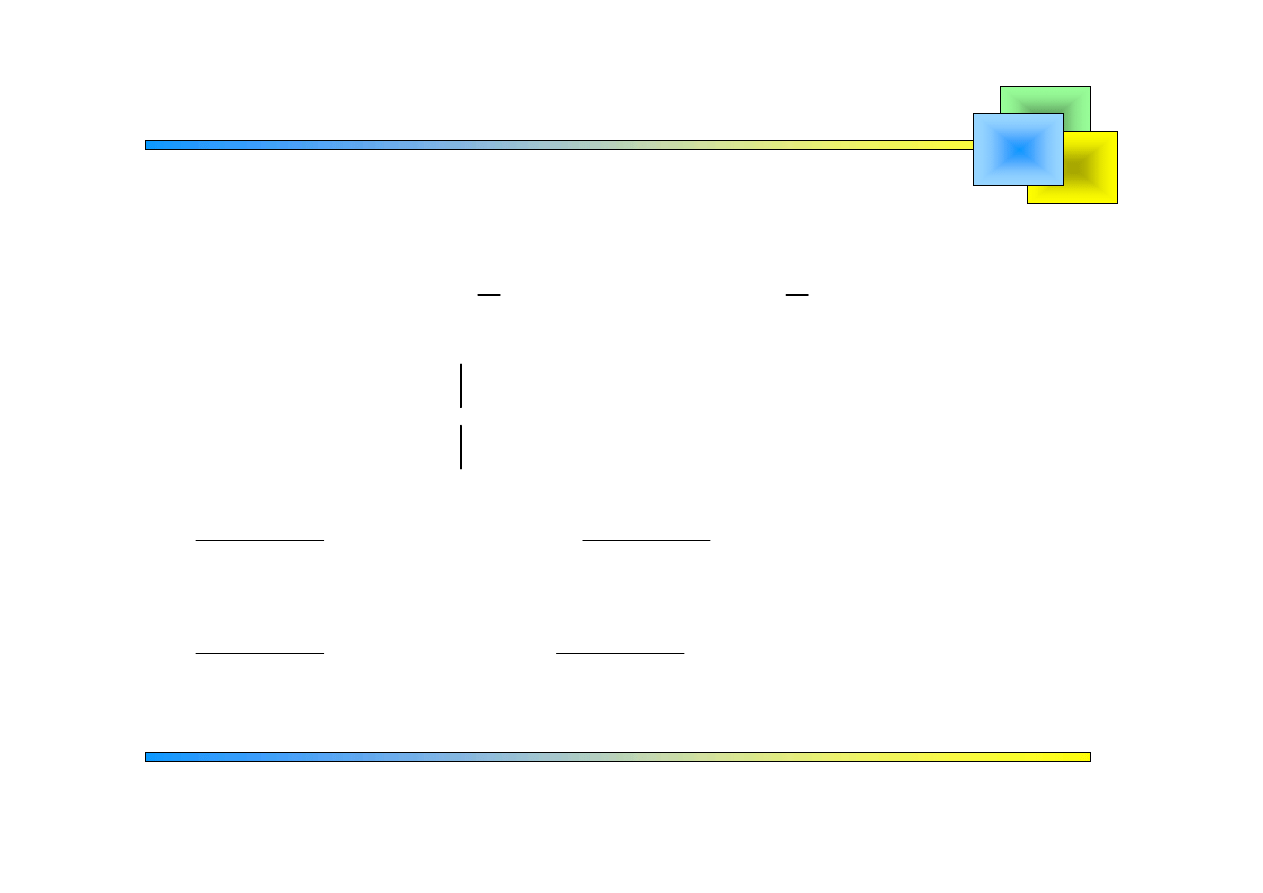
Zadanie 5
:
Szeregi Fouriera
[
]
1
2
1
2
(
)
(
)
1
1
2
2
(
)
(
)
(
)
1
(
)
1
1
sin
cos
d
sin (
) d
sin (
) d
2
2
(
)
(
)
d
(
) d
d
(
) d
1
1
sin
d
sin
d
2(
)
2(
)
1
1
cos
2(
)
2(
)
n m
n m
n m
n m
n m
n m
n x
m x x
n
m x x
n
m x x
u
n
m x
u
n
m x
u
n
m
x
u
n
m
x
u
u
u
u
n
m
n
m
u
n
m
n
m
π
π
π
−π
−π
−π
+
π
−
π
− +
π
− −
π
+
π
− +
π
=
+
+
−
=
⎧
⎫
=
+
=
−
⎪
⎪
=
=
⎨
⎬
=
+
=
−
⎪
⎪
⎩
⎭
=
+
=
+
−
=
+
+
−
∫
∫
∫
∫
∫
[
]
(
)
2
(
)
cos
0
n m
n m
u
+
π
− +
π
=
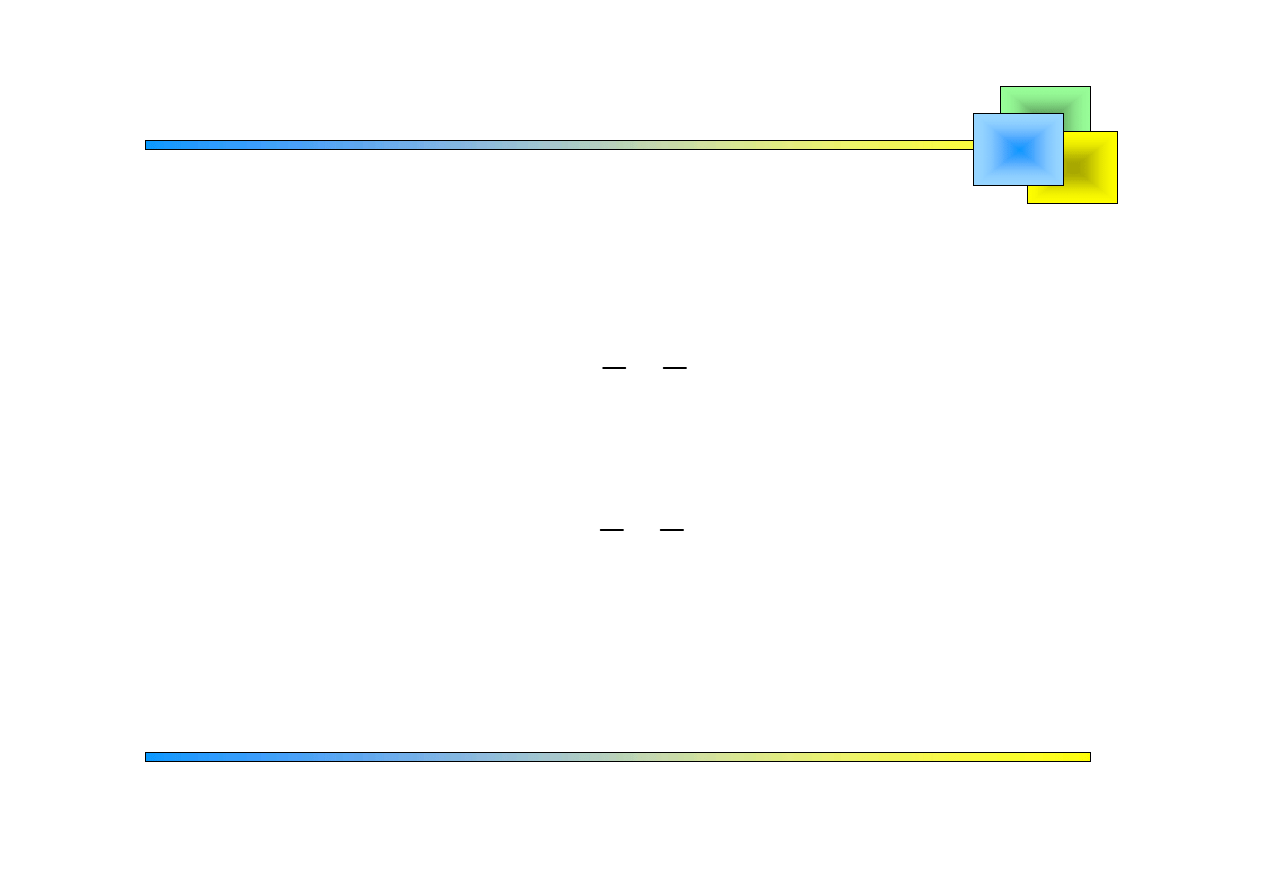
Wzory
Szeregi Fouriera
2
2
2
2
2
2
2
2
cos 2
cos
sin
2 cos
1
1
1
cos
cos 2
2
2
cos 2
cos
sin
1 2sin
1
1
sin
cos 2
2
2
α =
α −
α =
α −
α = +
α
α =
α −
α = −
α
α = −
α
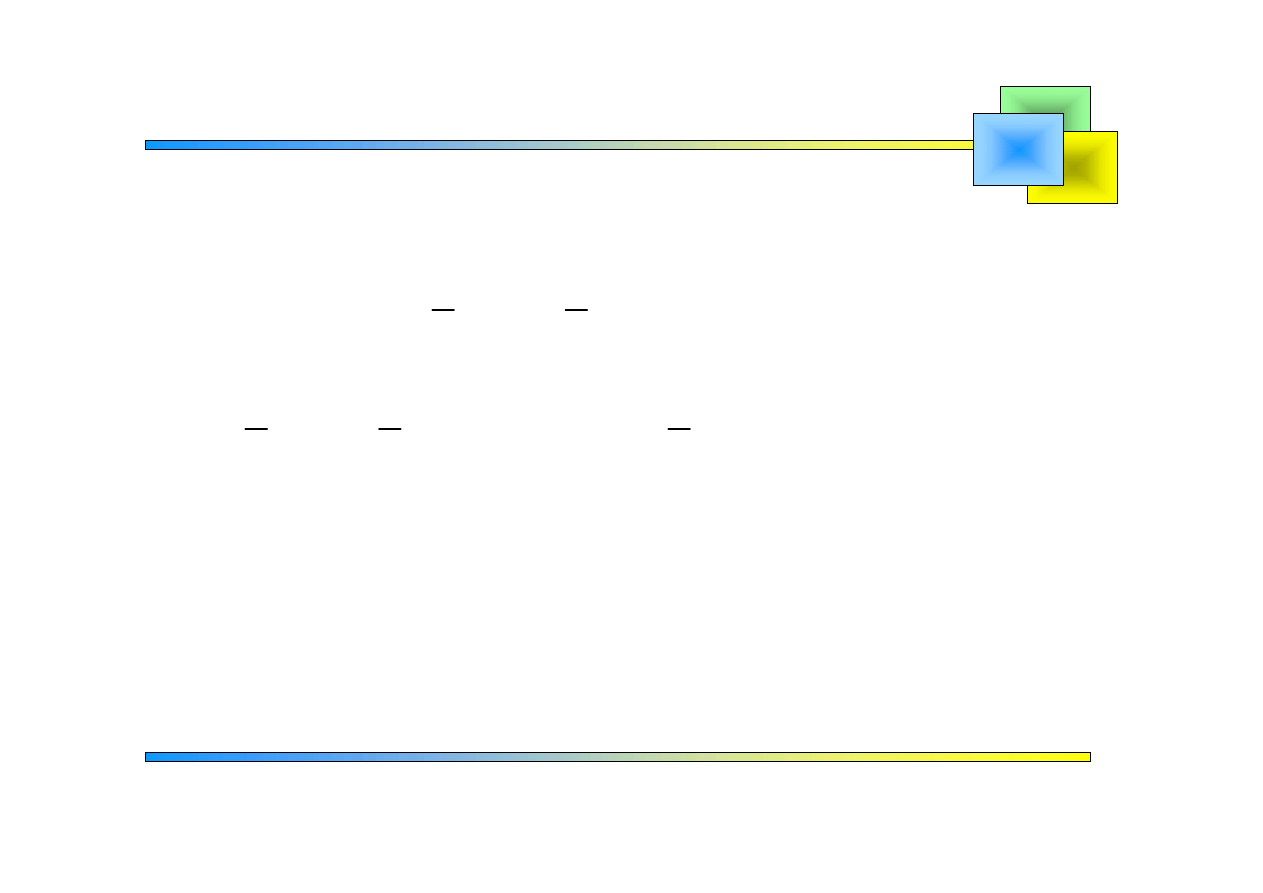
Zadanie 6
:
Szeregi Fouriera
[ ]
[
]
2
2
2
2
2
2
1
1
sin
d
d
cos 2
d
d
2 d
2
2
1
1
1
cos d
sin
0
2
2
2
n
n
n
n
u
n x
n x x
x
n x x
u
n x
x
u x
u
π
π
π
−π
−π
−π
π
π
π
−π
−
π
−
π
=
⎧
⎫
=
−
=
=
⎨
⎬
=
⎩
⎭
=
−
= π −
= π − = π
∫
∫
∫
∫
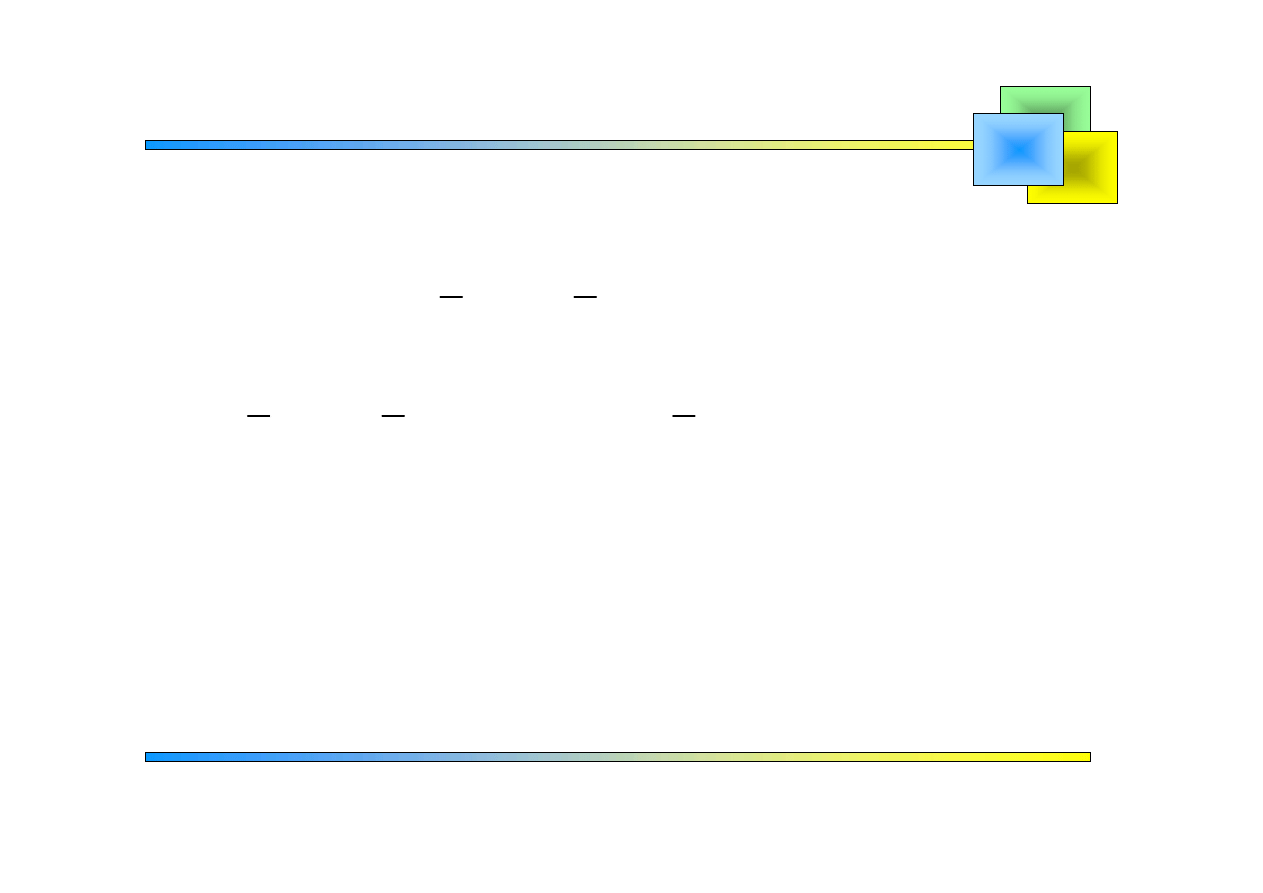
Zadanie 7
:
Szeregi Fouriera
[ ]
[
]
2
2
2
2
2
2
1
1
cos
d
d
cos 2
d
d
2 d
2
2
1
1
1
cos d
sin
0
2
2
2
n
n
n
n
u
n x
n x x
x
n x x
u
n x
x
u x
u
π
π
π
−π
−π
−π
π
π
π
−π
−
π
−
π
=
⎧
⎫
=
+
=
=
⎨
⎬
=
⎩
⎭
=
+
= π +
= π + = π
∫
∫
∫
∫
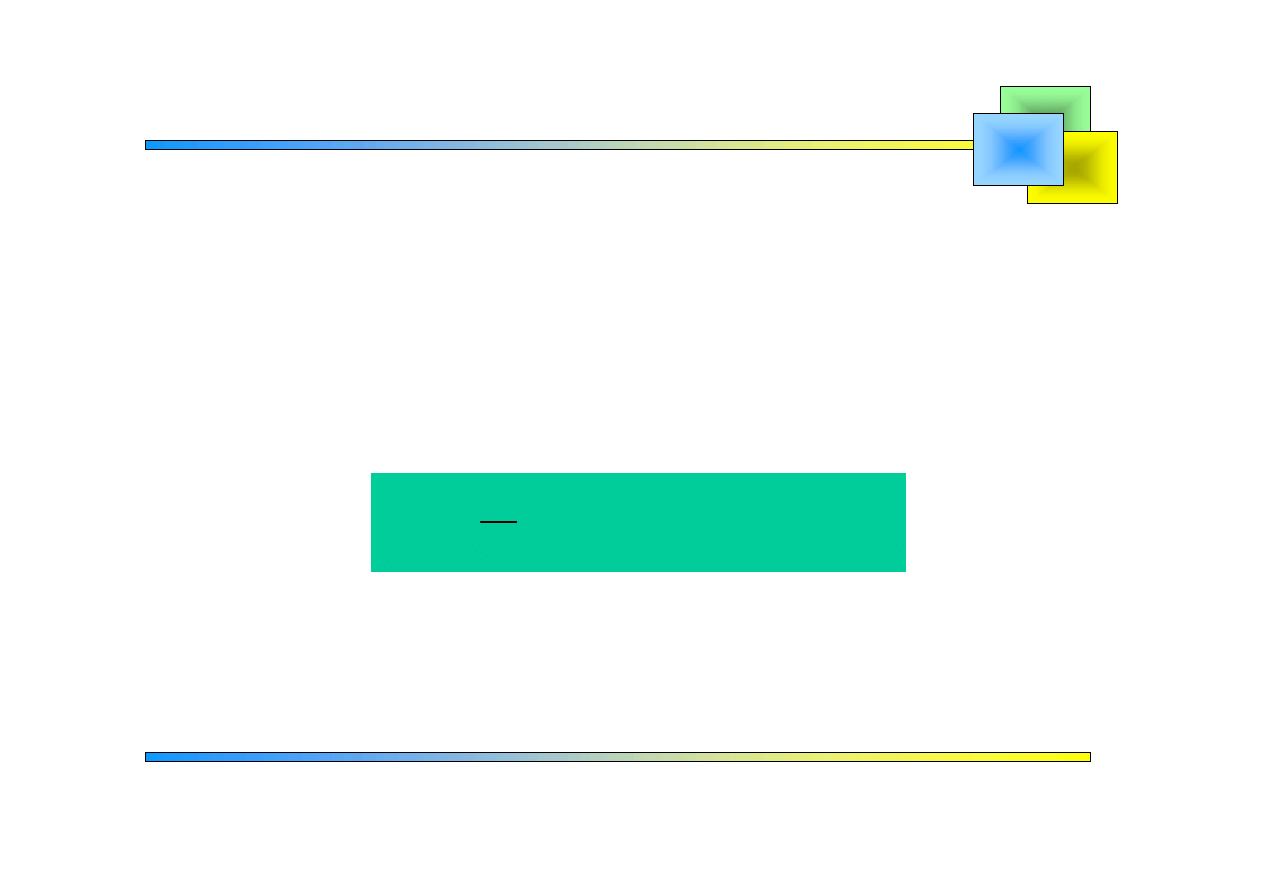
Sprawdziliśmy, że dany ciąg jest ortogonalny w przedziale
, przy czym
.
[
, ]
−π π
A
= π
Rozwinięcie funkcji w szereg Fouriera
Definicja:
Niech będzie funkcją o okresie mającą w przedziale
co najwyżej skończoną liczbę punktów nieciągłości
i całkowalną w tym przedziale.
Szeregiem Fouriera tej funkcji nazywamy szereg:
gdzie – współczynniki.
( )
f x
2
π
[
, ]
−π π
0
1
( )
(
cos
sin
),
2
n
n
n
a
f x
a
n x b
n x
∞
=
=
+
+
∑
0
,
,
n
n
a a b
Szeregi Fouriera
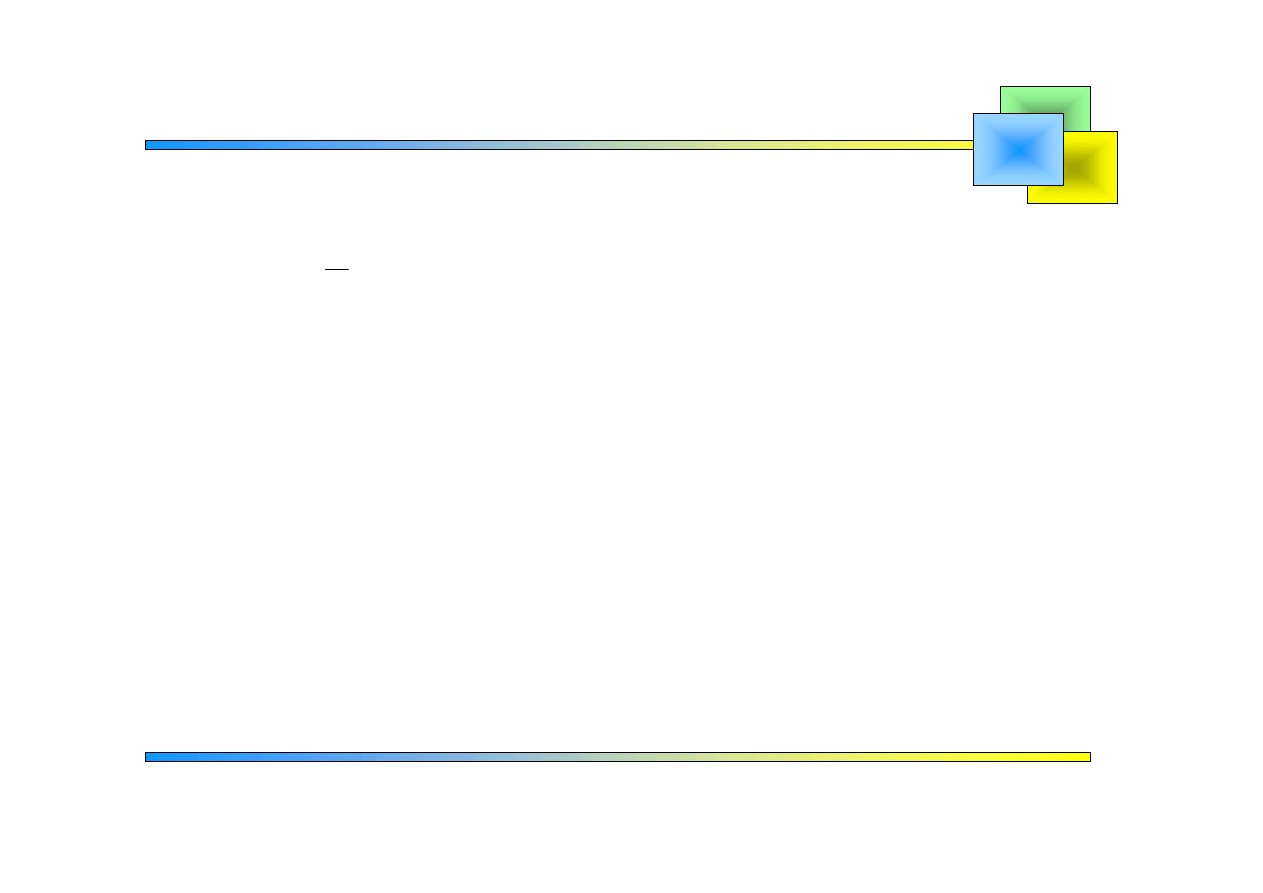
Czyli
Wyznaczanie współczynników
Wiemy, że ciąg
jest ciągiem ortogonalnym w przedziale . Obie strony
wzoru na szereg Fouriera całkujemy od do .
0
1
1
2
2
1
( )
cos
sin
cos 2
sin 2
2
f x
a
a
x
b
x
a
x
b
x
=
+
+
+
+
+…
{
}
1, sin , cos , sin 2 , cos 2 ,
x
x
x
x …
[
, ]
−π π
−π
π
Szeregi Fouriera
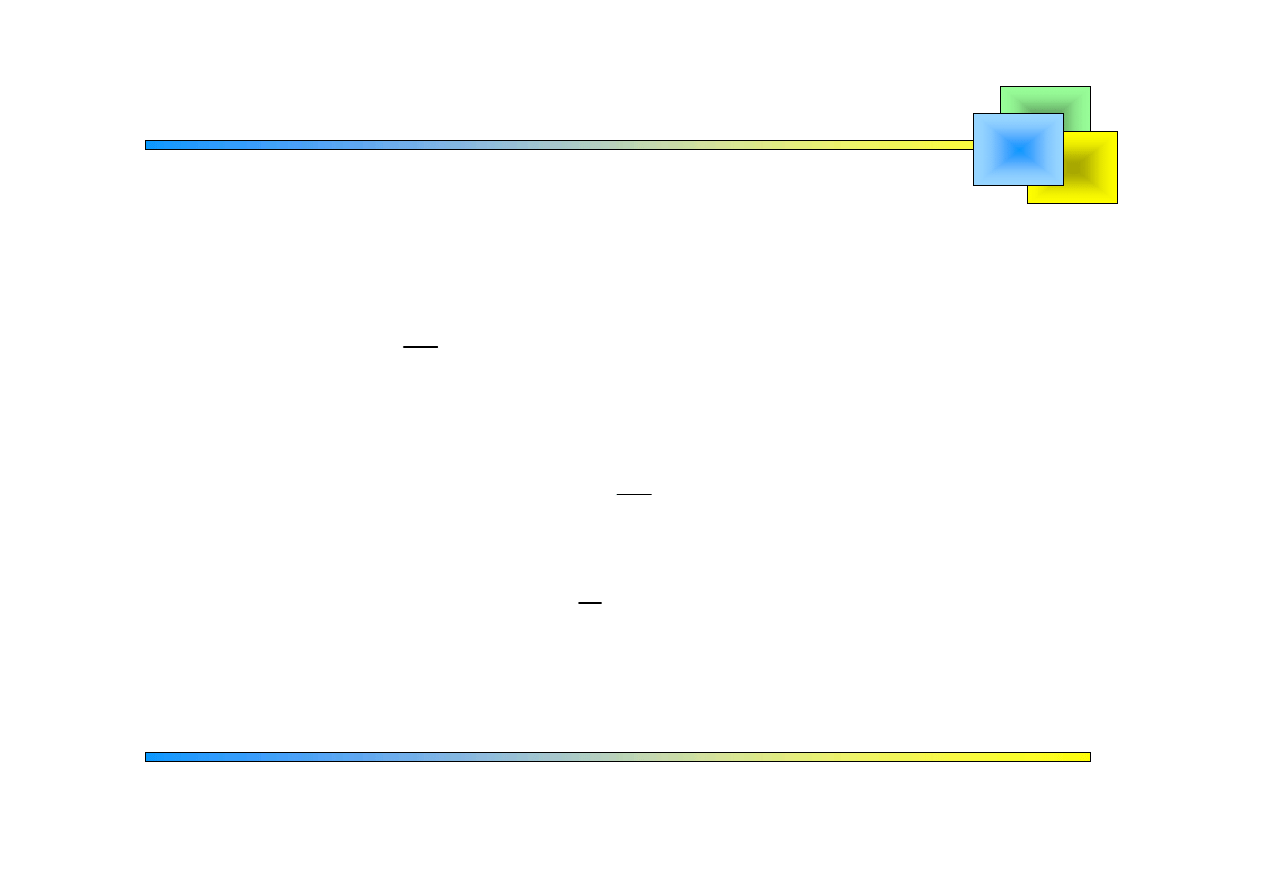
Otrzymujemy:
Szeregi Fouriera
[ ]
0
1
0
0
0
0
0
( ) d
d
cos
d
sin
d
2
( ) d
2
1
( ) d
n
n
n
a
f x
x
x
a
n x x b
n x x
a
f x
x
x
a
a
f x
x
π
π
π
π
∞
=
−π
−π
−π
−π
π
π
−π
−π
π
−π
⎛
⎞
⎜
⎟
=
+
+
⎜
⎟
⎜
⎟
⎜
⎟
⎝
⎠
=
=
π
=
π
∑
∫
∫
∫
∫
∫
∫
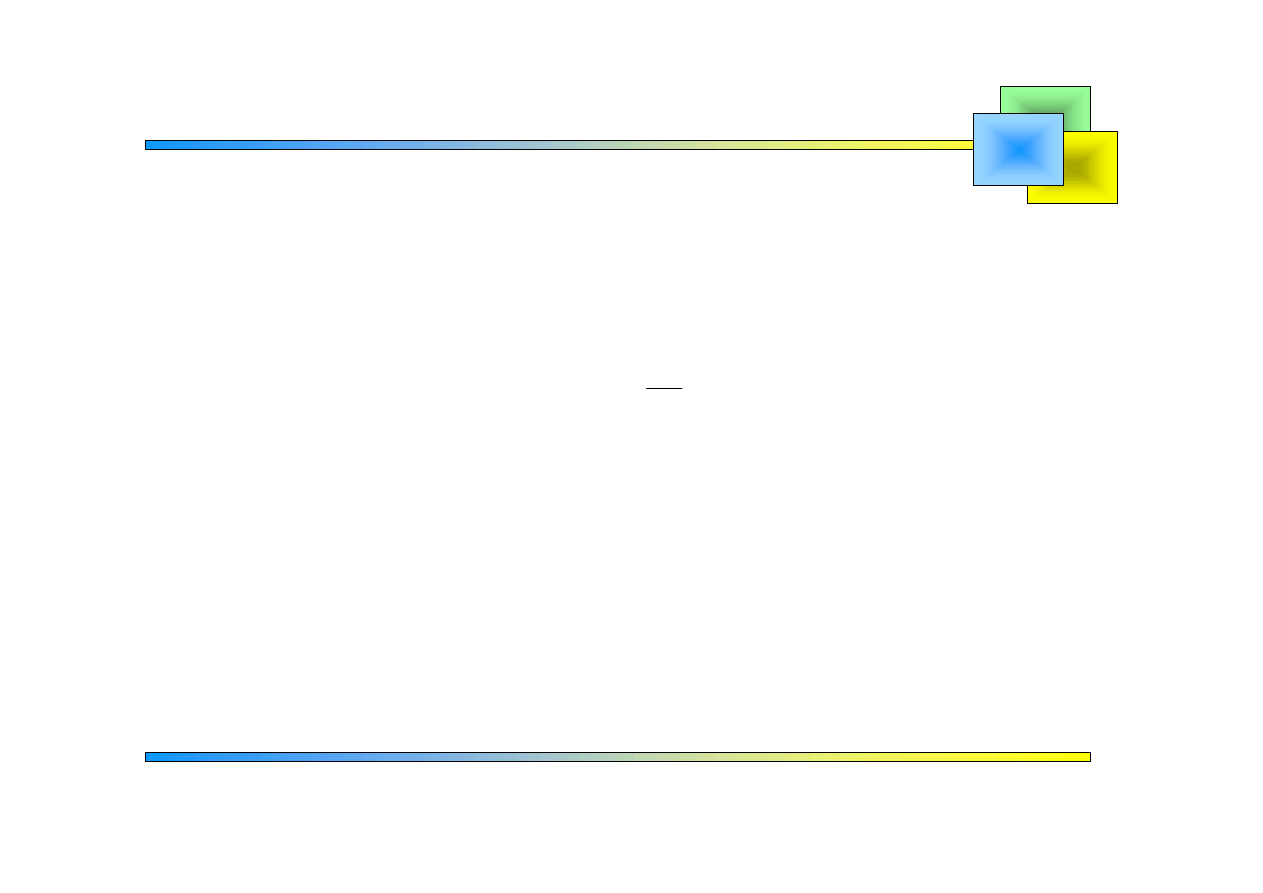
Obie strony równania wyjściowego mnożymy
przez i całkujemy od do .
Wówczas otrzymujemy:
cos m x
−π
π
Szeregi Fouriera
0
0
1
0
cos
( ) d
cos
d
2
cos
cos
d
sin
cos
d
n
n
n
dla n m
a
m x f x
x
m x x
a
n x
m x x b
n x
m x x
π
π
−π
−π
π
π
∞
=
−π
−π
π
=
=
+
⎛
⎞
⎜
⎟
⎜
+
+
⎟
⎜
⎟⎟
⎜
⎠
⎝
∫
∫
∑ ∫
∫
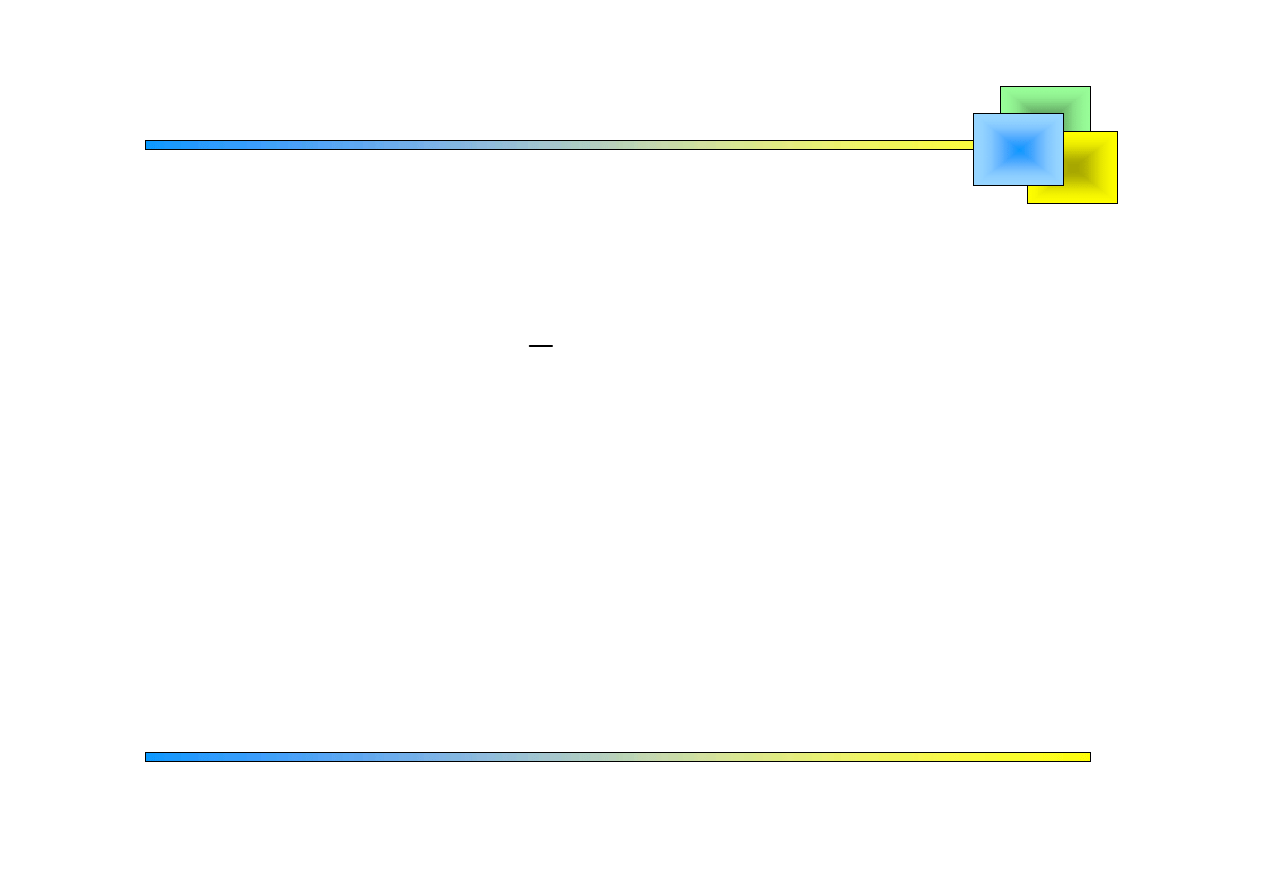
cos
( ) d
1
( ) cos
d
m
m
m x f x
x
a
a
f x
m x x
π
−π
π
−π
=
π
=
π
∫
∫
Szeregi Fouriera
Obie strony równania wyjściowego mnożymy przez
i całkujemy od do :
sin m x
−π
π
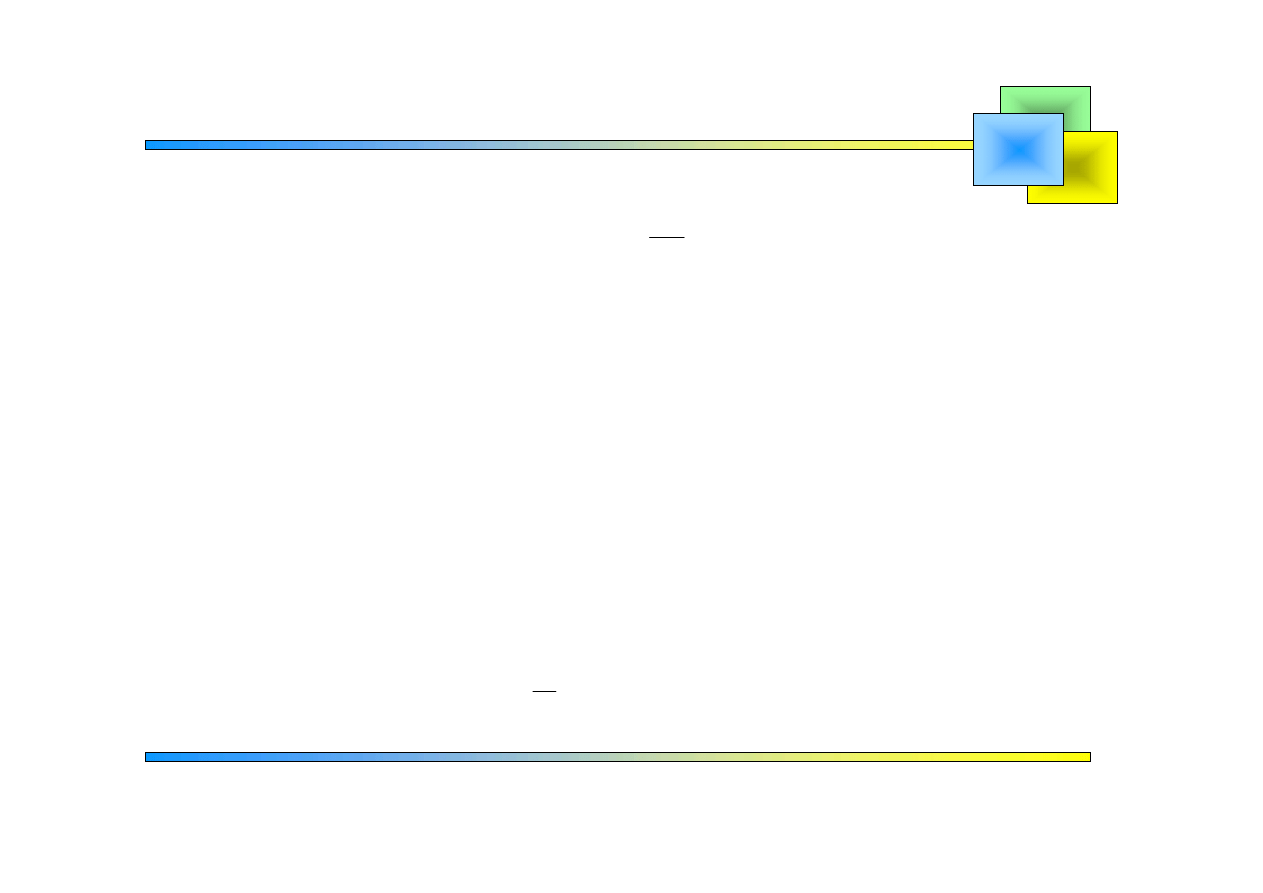
0
0
1
0
sin
( ) d
sin
d
2
cos
sin
d
sin
sin
d
sin
( ) d
1
( )sin
d
n
n
n
dla n m
m
m
a
m x f x
x
m x x
a
n x
m x x b
n x
m x x
m x f x
x
b
b
f x
m x x
π
π
−π
−π
π
π
∞
=
−π
−π
π
=
π
−π
π
−π
=
+
⎞
⎛
⎟
⎜
⎟
+
+
⎜
⎟
⎜⎜
⎟
⎝
⎠
=
π
=
π
∫
∫
∑ ∫
∫
∫
∫
Szeregi Fouriera
Szereg Fouriera
Szeregi Fouriera
0
1
0
( )
(
cos
sin
)
2
1
( ) d
1
( ) cos
d
1
( )sin
d
n
n
n
n
n
a
f x
a
n x b
n x
a
f x
x
a
f x
n x x
b
f x
n x x
∞
=
π
−π
π
−π
π
−π
=
+
+
=
π
=
π
=
π
∑
∫
∫
∫
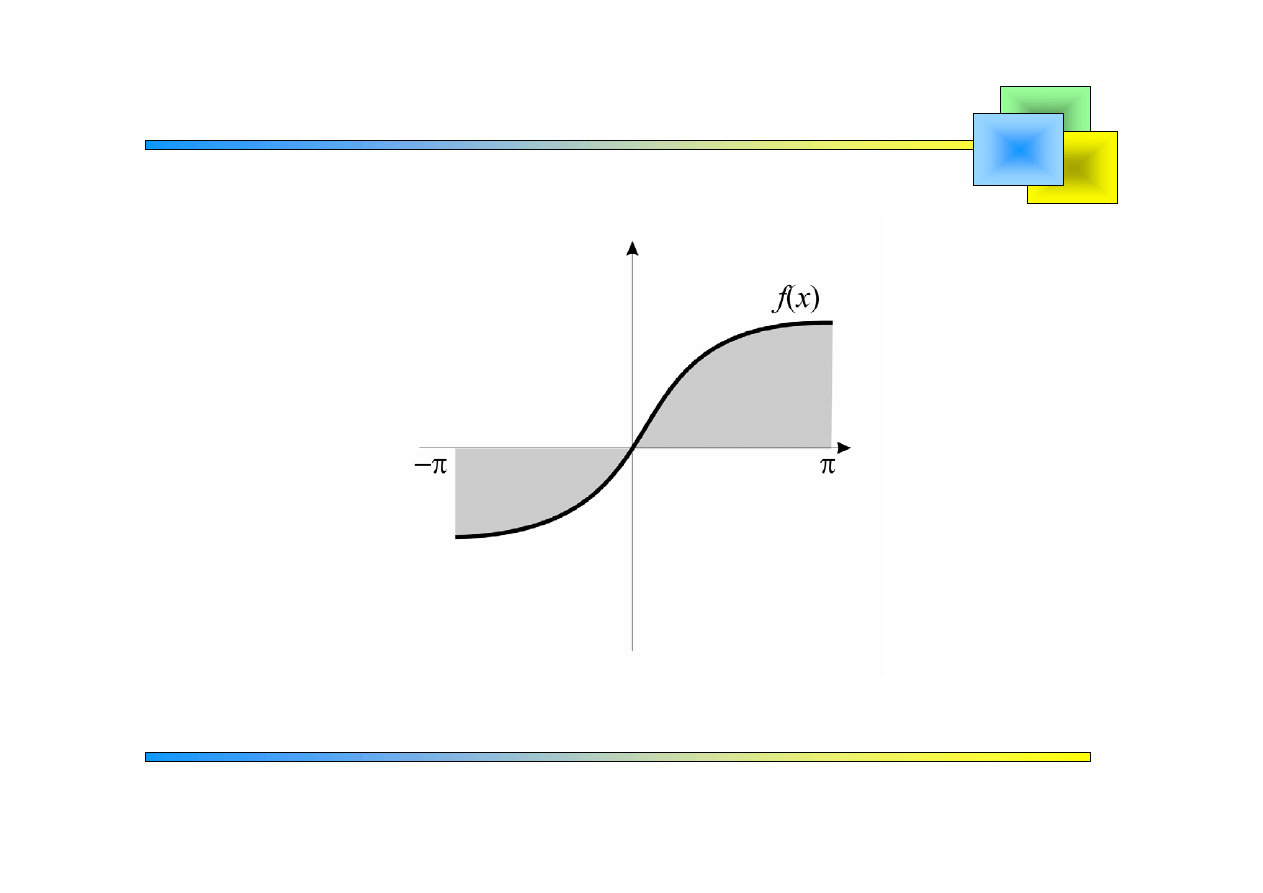
Jeżeli jest funkcją nieparzystą:
( )
f x
Szeregi Fouriera
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
=
=
⎥
⎦
⎤
⎢
⎣
⎡
+
=
=
=
⎥
⎦
⎤
⎢
⎣
⎡
+
=
=
=
⎥
⎦
⎤
⎢
⎣
⎡
+
=
=
−
−
−
−
−
−
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
0
0
0
0
0
0
0
0
sin
2
sin
sin
1
sin
1
0
cos
cos
1
cos
1
0
1
1
nxdx
x
f
nxdx
x
f
nxdx
x
f
nxdx
x
f
b
nxdx
x
f
nxdx
x
f
nxdx
x
f
a
dx
x
f
dx
x
f
dx
x
f
a
n
n
Szeregi Fouriera
Jeżeli jest funkcją parzystą:
( )
f x
Szeregi Fouriera
0
0
0
0
0
1
2
( ) d
( ) d
1
2
( ) cos
d
( ) cos
d
1
( )sin
d
1
( )sin
d
( )sin
d
0
n
n
a
f x
x
f x
x
a
f x
n x x
f x
n x x
b
f x
n x x
f x
n x x
f x
n x x
π
π
−π
π
π
−π
π
−π
π
−π
=
=
π
π
=
=
π
π
=
=
π
⎡
⎤
=
+
=
⎢
⎥
π ⎣
⎦
∫
∫
∫
∫
∫
∫
∫
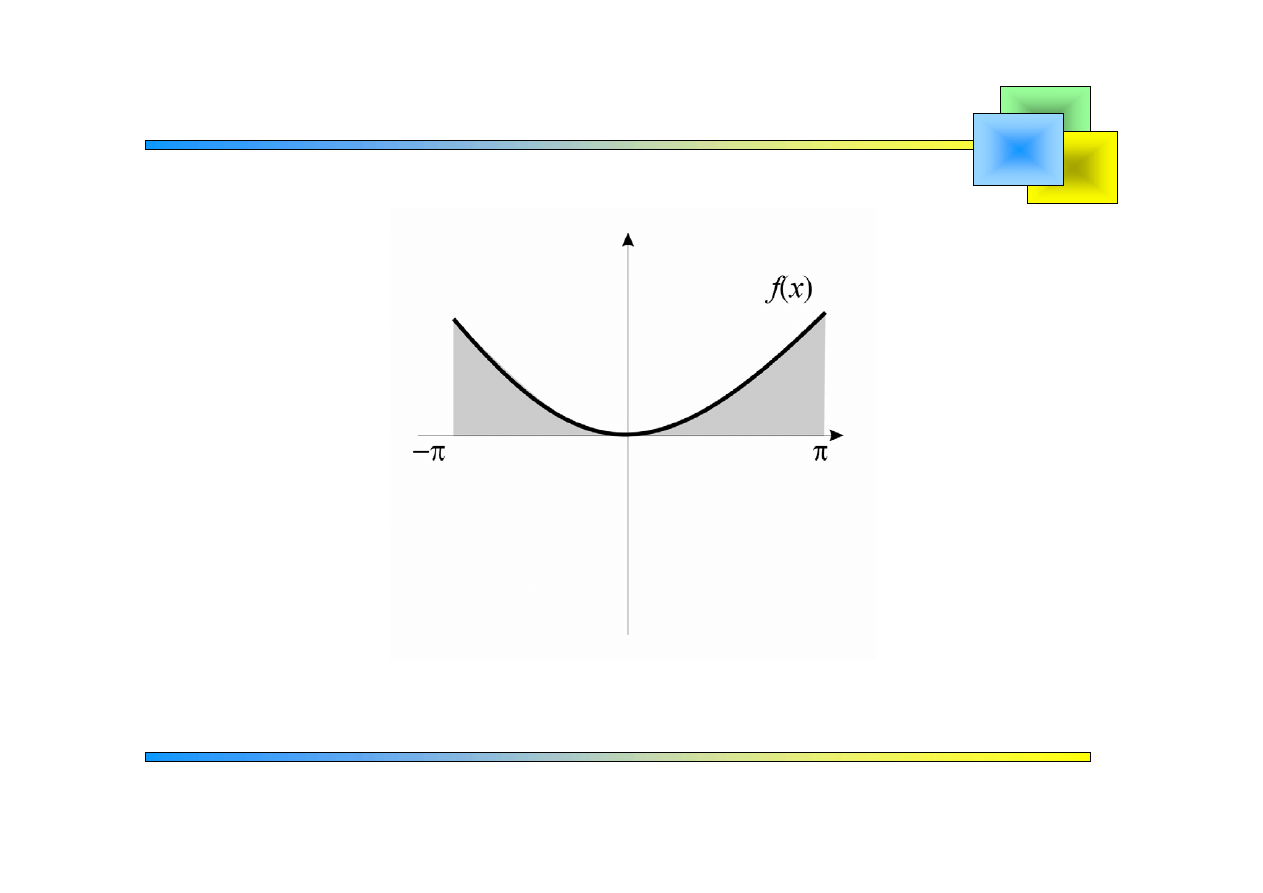
Szeregi Fouriera
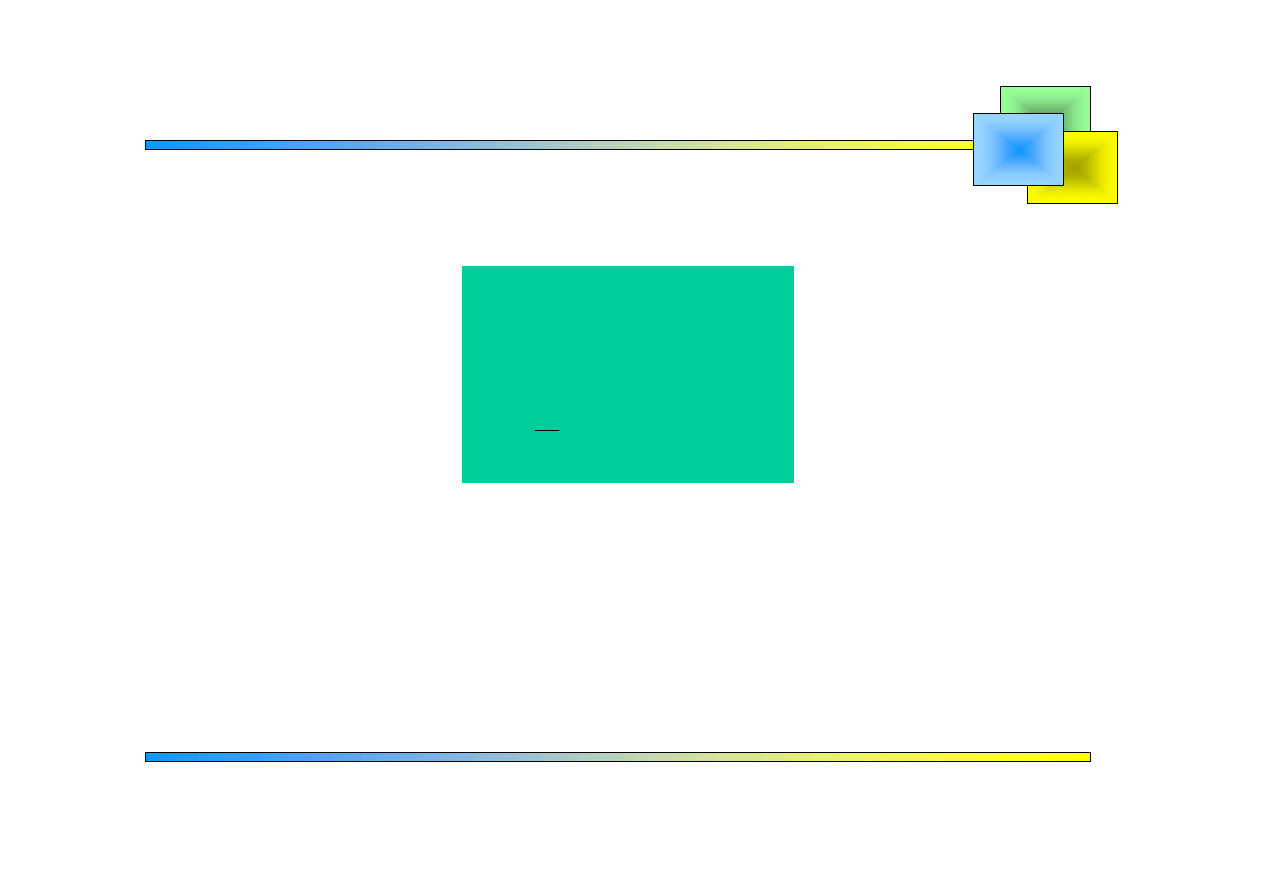
jest funkcją nieparzystą
( )
f x
Szeregi Fouriera
0
0
0
0
2
( )sin
d
n
n
a
a
b
f x
n x x
π
=
=
=
π
∫
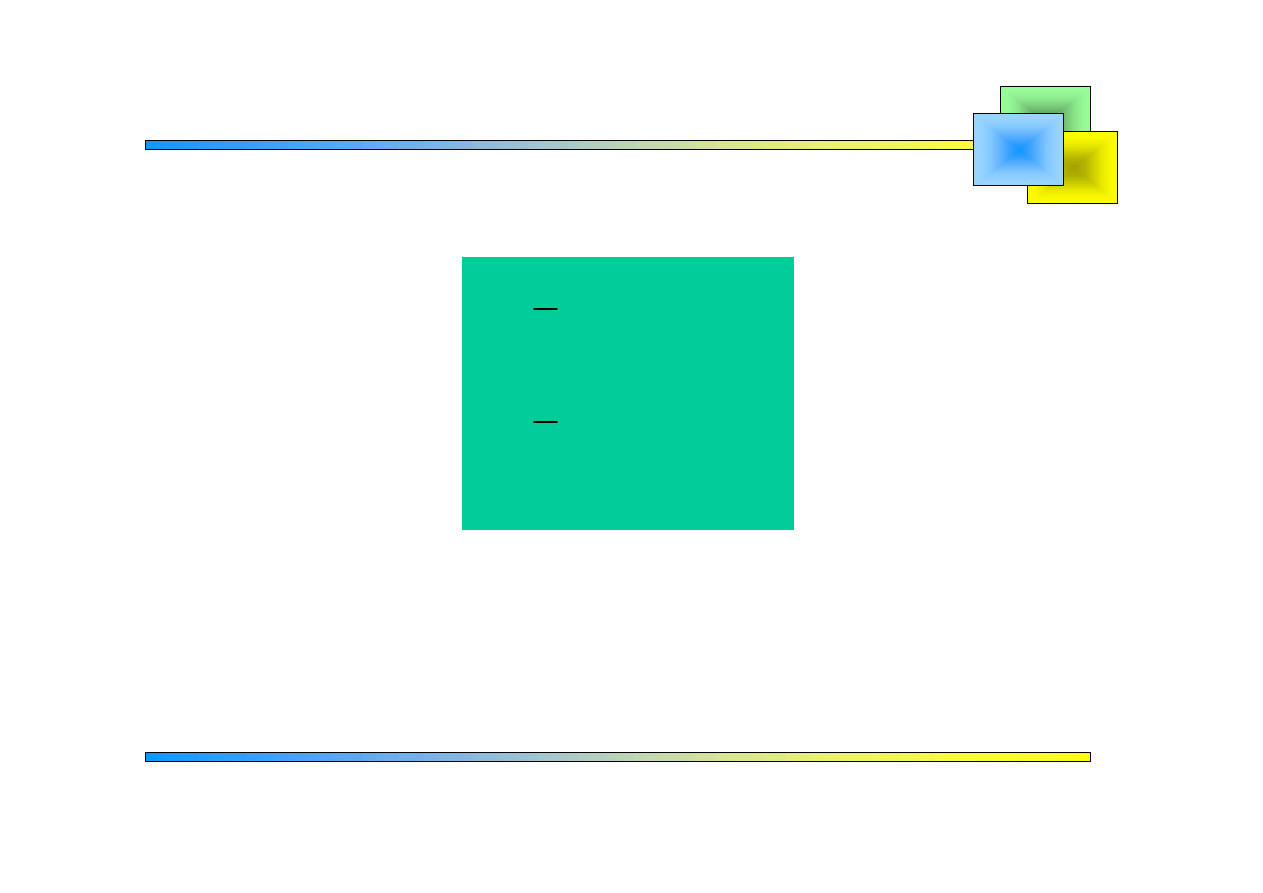
jest funkcją parzystą
( )
f x
Szeregi Fouriera
0
0
0
2
( ) d
2
( ) cos
d
0
n
n
a
f x
x
a
f x
n x x
b
π
π
=
π
=
π
=
∫
∫
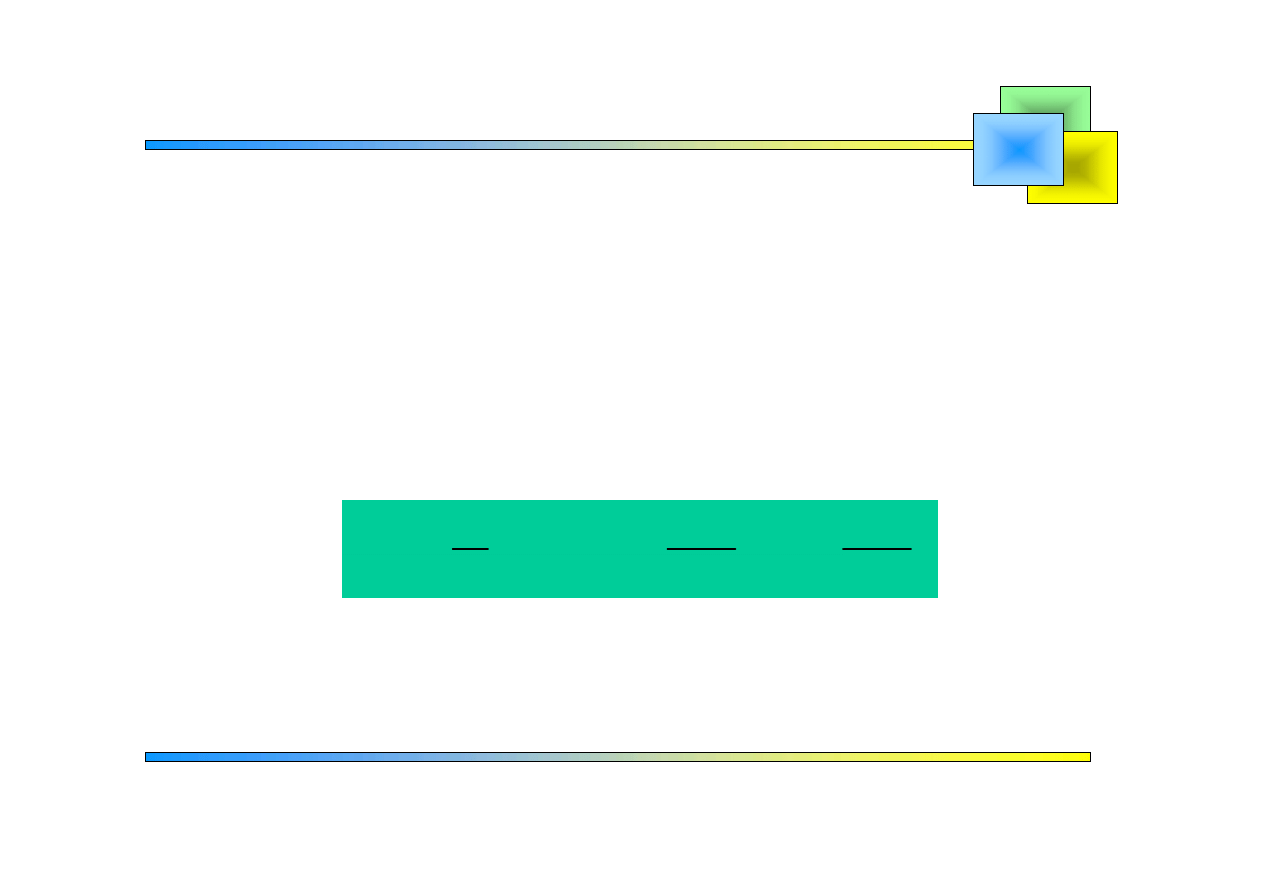
Rozwinięcie funkcji o okresie 2L w szereg Fouriera
Definicja:
Niech będzie funkcją o okresie mającą w przedziale
co najwyżej skończoną liczbę punktów nieciągłości i
całkowalną w tym przedziale.
( )
f x
[
, ]
L L
−
2L
Szeregi Fouriera
Szeregiem Fouriera tej funkcji nazywamy szereg:
gdzie – współczynniki.
0
1
( )
(
cos
sin
),
2
n
n
n
a
n x
n x
f x
a
b
L
L
∞
=
π
π
=
+
+
∑
0
,
,
n
n
a a b
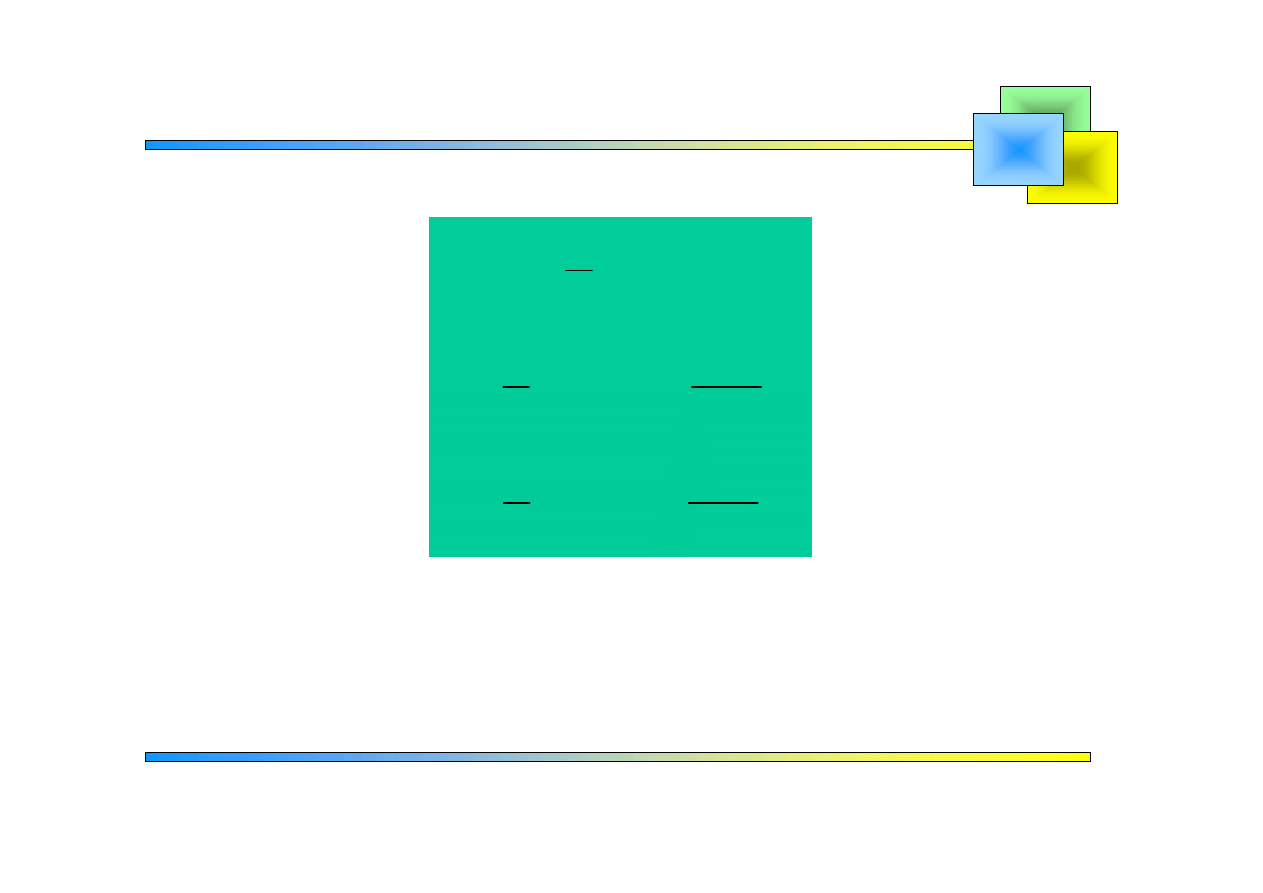
Szeregi Fouriera
0
1
( ) d
1
( ) cos
d
1
( )sin
d
L
L
n
L
n
L
a
f x
x
L
n x
a
f x
x
L
L
n x
b
f x
x
L
L
−
π
−π
−
=
π
=
π
=
∫
∫
∫
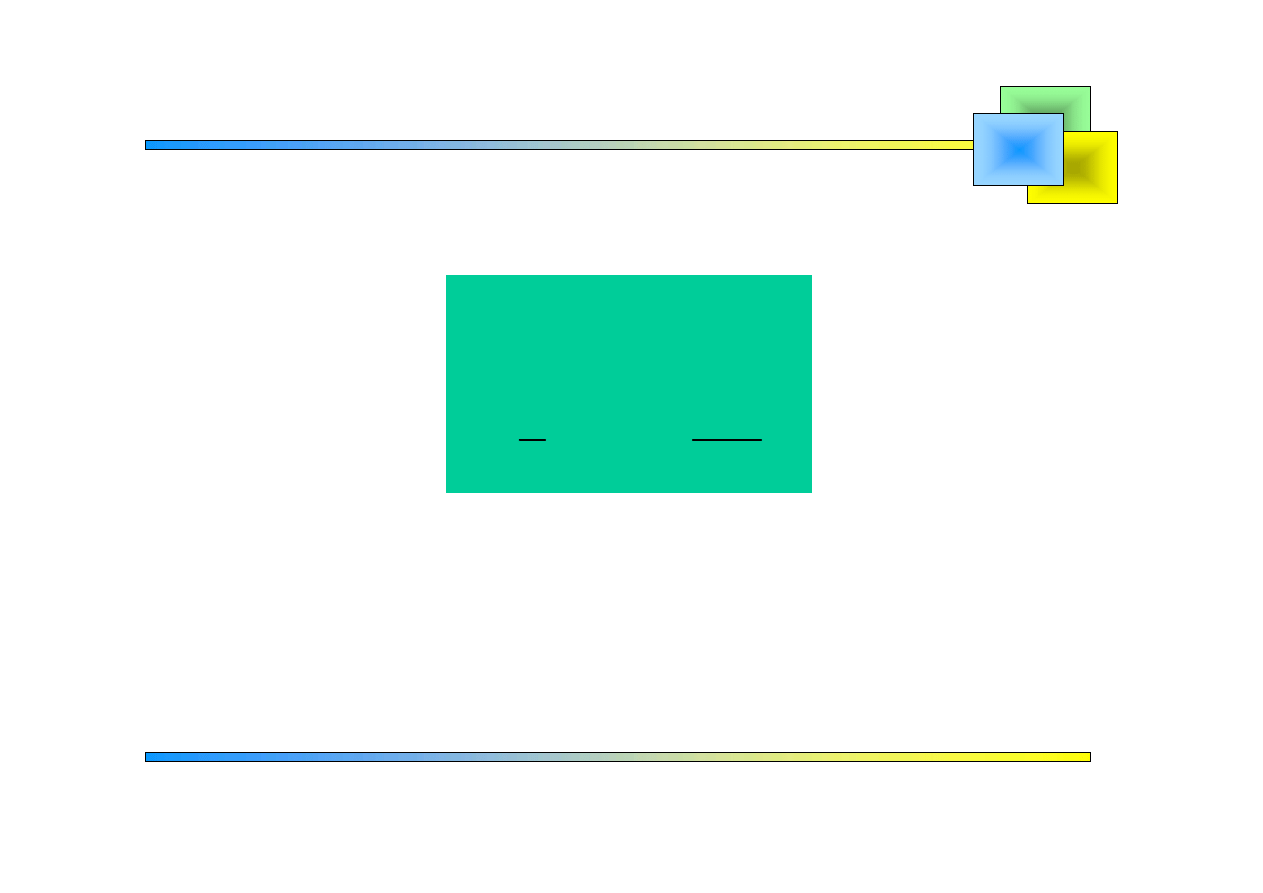
jest funkcją nieparzystą
( )
f x
Szeregi Fouriera
0
0
0
0
2
( )sin
d
n
L
n
a
a
n x
b
f x
x
L
L
=
=
π
=
∫
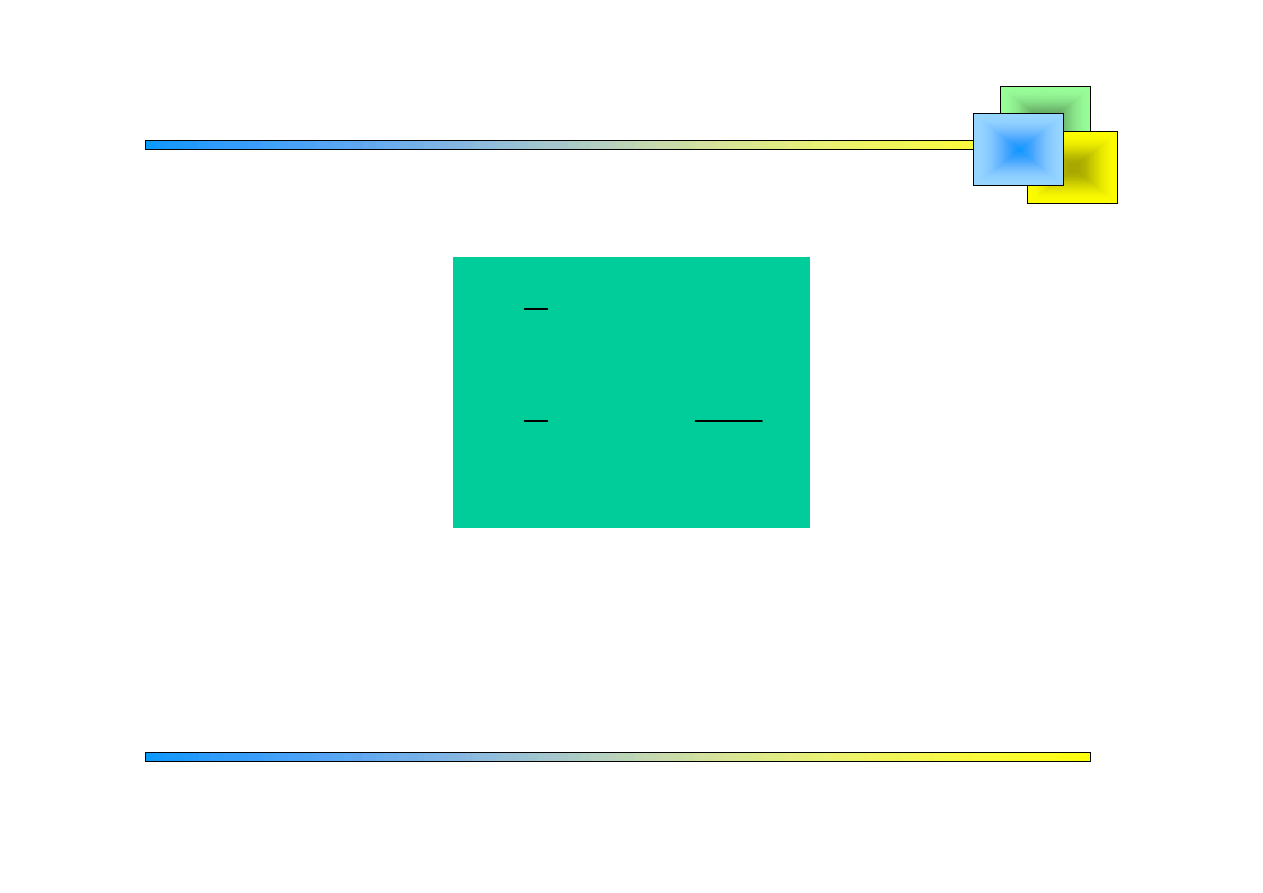
jest funkcją parzystą
( )
f x
Szeregi Fouriera
0
0
0
2
( ) d
2
( ) cos
d
0
L
L
n
n
a
f x
x
n x
a
f x
x
L
b
=
π
π
=
π
=
∫
∫
Wyszukiwarka
Podobne podstrony:
PPS 2011 W7 id 381592 Nieznany
PC w3 id 351840 Nieznany
PC w2 id 351839 Nieznany
IiP z w7 id 210535 Nieznany
ML1 W7 id 303805 Nieznany
4OS 2011 w7 id 39386 Nieznany
PC w6(1) id 351841 Nieznany
PPS 2011 W7 id 381592 Nieznany
PC w3 id 351840 Nieznany
PC E 5 id 351816 Nieznany
po w7 utf8 id 557615 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
więcej podobnych podstron