SCENARIUSZ LEKCJI MATEMATYKI 

NAUCZYCIEL: Adrian Weredycki 

KLASA: Ii (technikum) 

DATA: 15.03.2010 

TEMAT: Koła i okręgi. 

BAZA MERYTORYCZNA: 
Uczeń: 



 

Zna pojęcia: koło, okrąg,  promień, średnica. 

CELE: 
Uczeń : 



 

 Zna pojęcia: kąt wpisany, kąt środkowy, wycinek i odcinek koła. 



 

Zna i stosuje twierdzenie dotyczące kątów wpisanych i środkowych. 



 

Zna i stosuje wzory na obwód i pole koła. 



 

Potrafi obliczać długość łuku i pole wycinka koła. 

 
 

METODY: Praktyczna, poszukująca (pogadanka, dyskusja), ćwiczenia utrwalające. 
 
ZASADY NAUCZANIA: 



 

Zasada trwałości wiedzy 



 

Zasada poglądowości 

 
TOK LEKCJI: 

1.  Sprawy organizacyjne (powitanie, sprawdzenie obecności) 
2.  Sprawdzenie zadania domowego. 
3.  Wprowadzenie do lekcji 

N: Czym zajmowaliśmy się na ostatnich lekcjach? 
U: Wielokątami. 
N: Jakie znacie jeszcze figury, poza wielokątami? 
U: Okręgi. 
N: A inna figura związana z okręgiem? 
U: Koła 
N: Na dzisiejszej lekcji będziemy zajmowali się kołami i okręgami. 

4.  Lekcja właściwa: 

 N: Co to jest okrąg? 
U: To zbiór punktów płaszczyzny równoodległych od pewnego ustalonego 

punktu (środka okręgu). 

N:  A co to jest koło? 
U: To zbiór punktów płaszczyzny, których odległość od środka jest mniejsza 

bądź równa promieniowi tego koła. 

N: Dla wszystkich okręgów stosunek długości okręgu do długości jego 
średnicy jest taki sam: 

𝑑ł𝑢𝑔𝑜ść 𝑜𝑘𝑟ę𝑔𝑢

𝑑ł𝑢𝑔𝑜ść ś𝑟𝑒𝑑𝑛𝑖𝑐𝑦

= 𝜋 ≈ 3,14 

 

 

 

 

N: Jaki jest wzór na obwód i pole koła ? 
U: 

𝑂𝑏 = 2𝜋𝑟, 𝑃 = 𝜋𝑟

2

. 

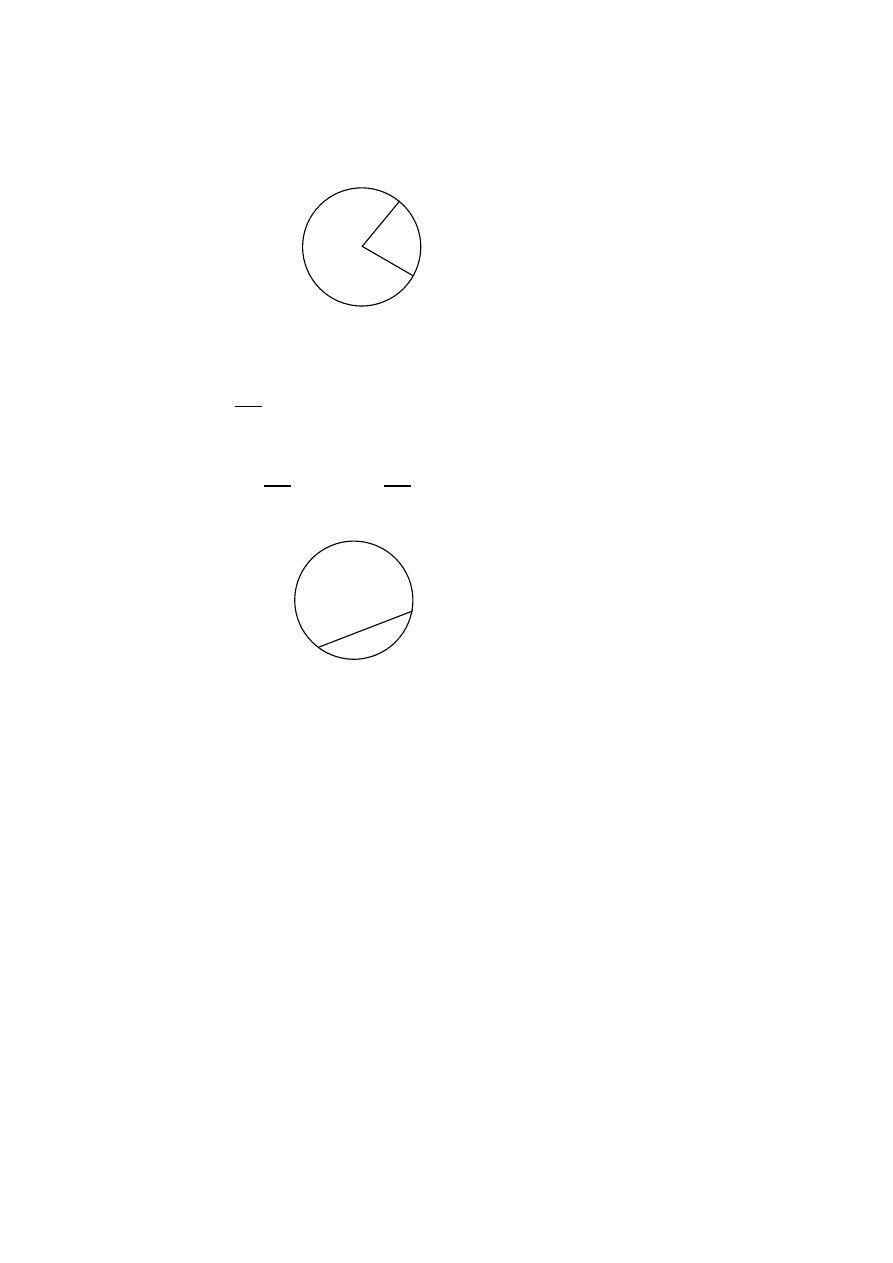
N: Rysuje na tablicy: 
 
 
 
 
 
 
Kąt α wyznacza pewien łuk na okręgu oraz wycina pewną część koła. 

Otrzymaną figurę nazywamy wycinkiem koła. Jaką częścią kąta pełnego jest 
kąt α? 

U: 

𝛼

360°

 

N:  To w takim razie jak policzyć długość łuku i pole wycinka wyznaczonego 

przez kąt α? 

U: 

𝑙 =

𝛼

360°

∙ 2𝜋𝑟,   𝑃 =

𝛼

360°

∙ 𝜋𝑟

2

 

N: A jak byście nazwali taką figurę? 
 
 
 
 
 
 
U: Odcinkiem koła. 
N: Jak policzyć pole odcinka? 
U: Od pola wycinka trzeba odjąć pole trójkąta. 
N: Wróćmy do naszego rysunku, jak można nazwać kąt α? 
U: Kątem środkowym. 
N: Co to jest kąt środkowy? 
U: To taki kąt, którego wierzchołek jest środkiem okręgu. 
N: Zauważmy, że na tym rysunku można wskazać jeszcze jeden kąt środkowy, 

którego miara wynosi 

360° − 𝛼. 

N: Rysuje kąt wpisany. A jak nazwiemy taki kąt? 
U: Kątem wpisanym. 
N: Co to jest kąt wpisany? 
U: To taki kąt, którego wierzchołek leży na okręgu a ramiona przecinają okrąg. 
N: Ile może być kątów środkowych opartych na danym łuku? 
U: Jeden. 
N:A kątów wpisanych? 
U: Nieskończenie wiele. 
N: Przypomnijmy trzy bardzo ważne twierdzenia: 

1.  Kąt wpisany ma dwa razy mniejszą miarę niż kąt środkowy oparty na 

tym samym łuku. 

α 

2.  Kąty wpisane oparte na tym samym łuku mają równe miary. 
3.  Kąt wpisany oparty na średnicy jest kątem prostym. 

Zadanie 1 str. 176 

a)  Oblicz pole koła o promieniu 7. (

49𝜋) 

b)  Jakie pole ma koło o średnicy 12? (

36𝜋) 

c)  Oblicz długość okręgu o średnicy 17. (

17𝜋) 

d)  Jaki promień ma koło o polu 10? (

10

 𝜋

) 

e)  Jaki promień ma okrąg o długości 5? (

5

2𝜋

) 

f)  Oblicz obwód koła o polu 4. (

4 𝜋 ) 

Zadanie 3 str.176 (po jednym przykładzie – reszta do domu) 
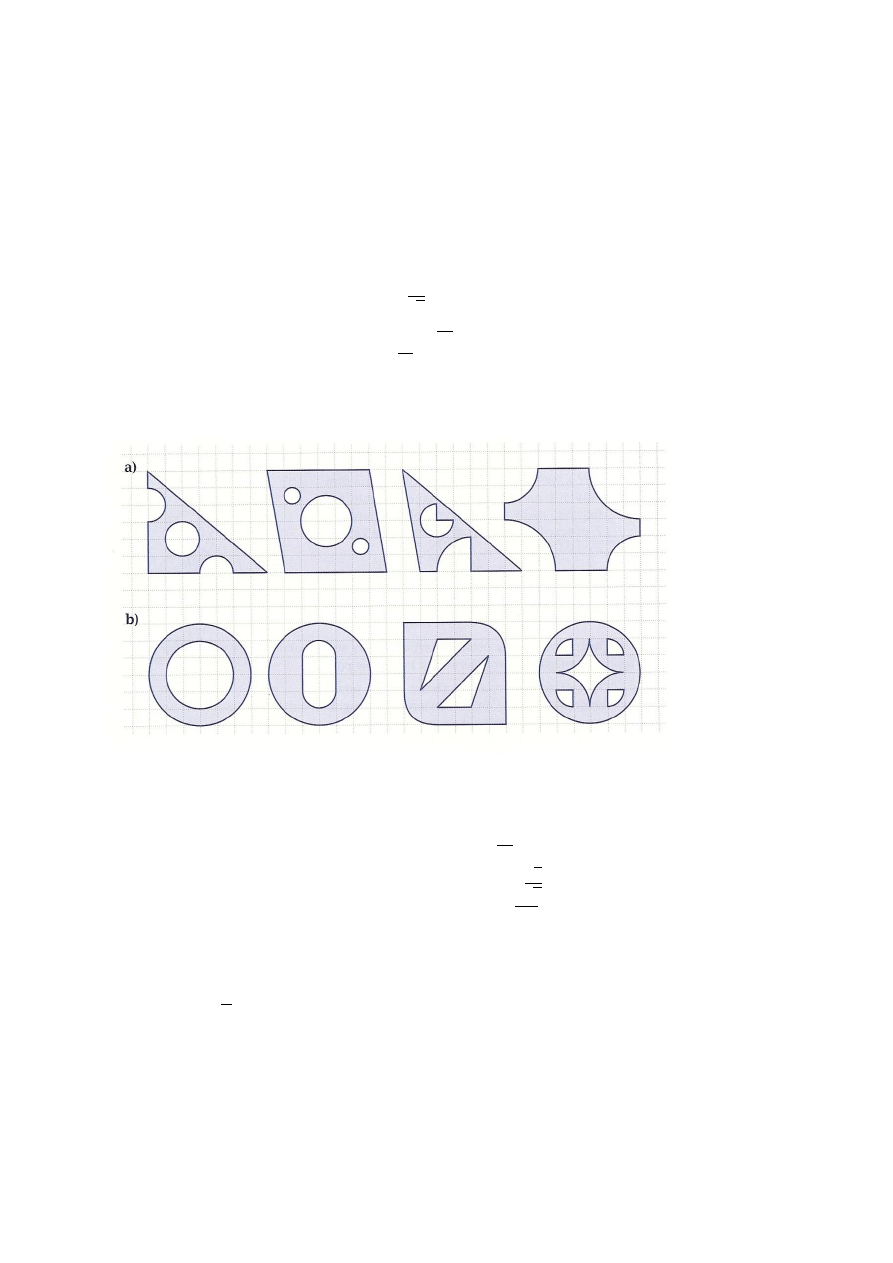
Oblicz pola zacieniowanych figur. Przyjmij, że bok kratki ma długość 1. 

 

Zadanie 4 str. 176 
Zapisz wzór, który pozwala obliczać: 

a)  Długość okręgu l, gdy dana jest jego średnica d. (

𝑙 = 𝜋𝑑) 

b)  Pole koła P, gdy dany jest jego obwód l. (

𝑃 =

𝑙

2

4𝜋

) 

c)  Średnicę koła d, gdy dane jest jego pole P. (

𝑑 = 2

 𝑃
 𝜋

) 

d)  Obwód koła l, gdy dane jest jego pole P. (

𝑙 = 2 𝑃𝜋) (zad. dom.) 

 

Zadanie 5 str. 177 

a)  Jaką długość ma bok kwadratu, który ma takie samo pole jak koło o promieniu r? 

(

𝑎 = 𝑟 𝜋) 

b)  Koło i kwadrat mają równe pola. Która figura ma większy obwód? Ile razy? (zad. 

dom.)