
Dopasowanie modelu do danych empirycznych
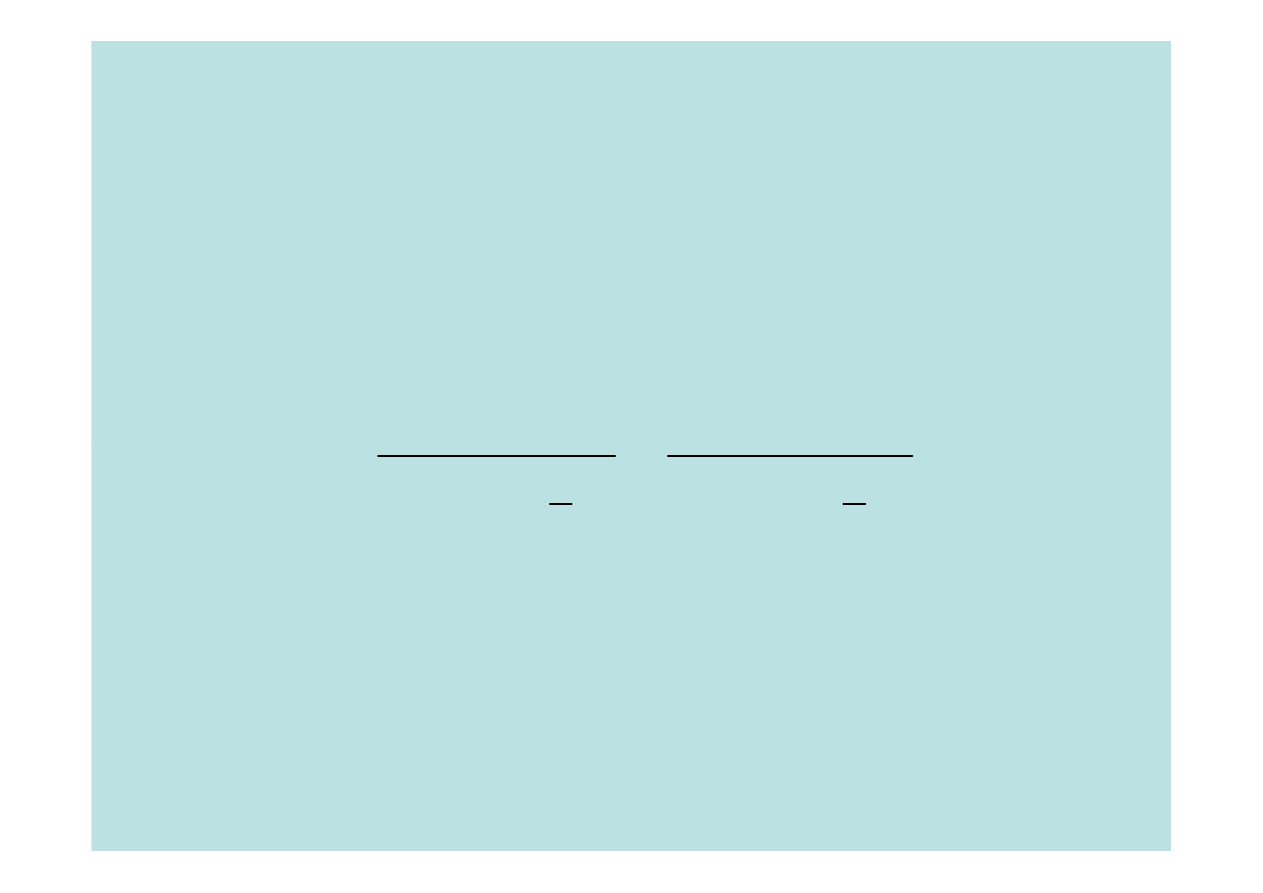
(
)
∑
∑
=
=
−
=
=
Φ
n
t
t
t
n
t
t
y
y
e
1
2
1
2
2
ˆ
Współczynnik zbie
ż
no
ś
ci
∑
∑
=
=
=
=
−
=
−
=
Φ
n
t
t
t
n
t
t
t
y
y
y
y
1
2
1
1
2
1
2
)
(
)
(

Współczynnik determinacji
2
2
1
Φ
−
=
R
1
Φ
−
=
R
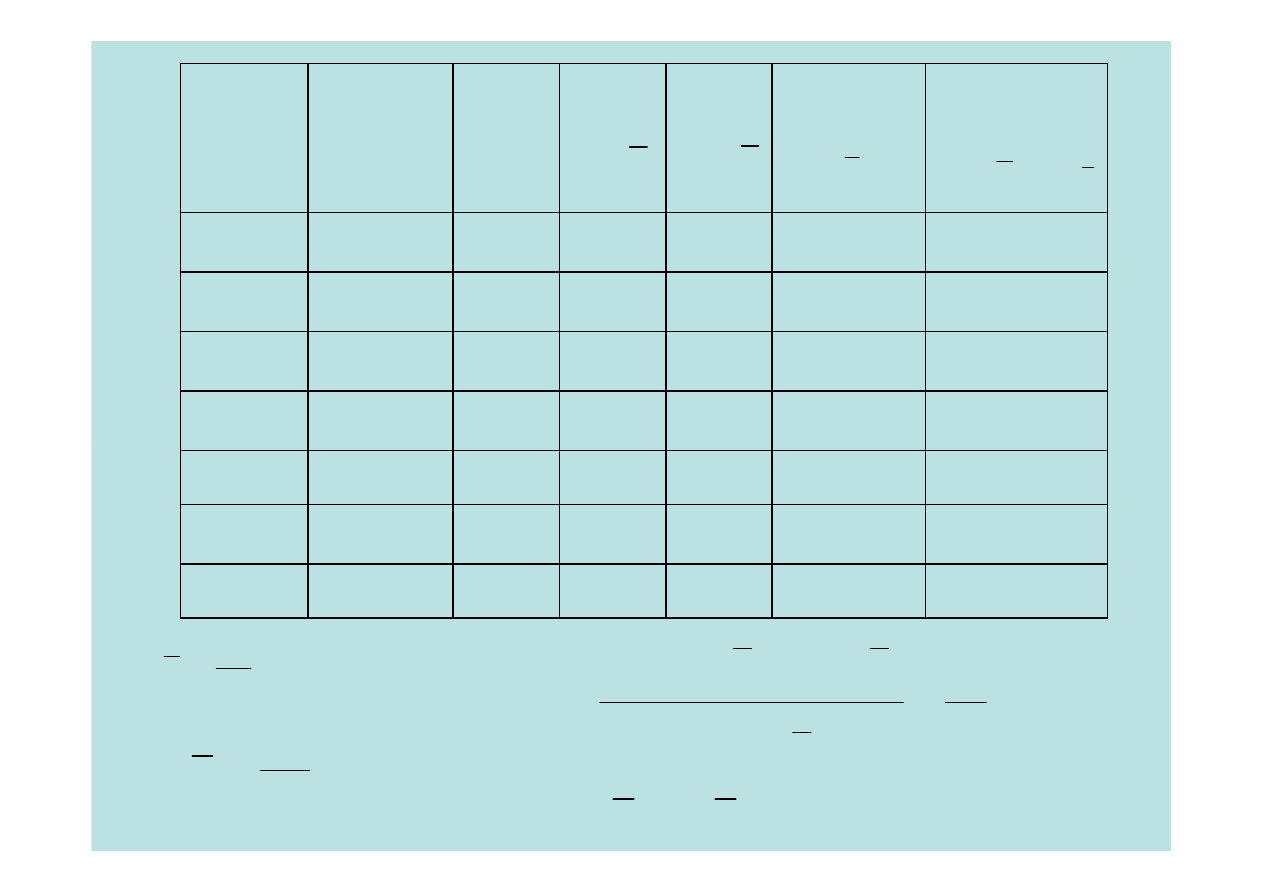
t
Produkcja Koszty
1
2
3
-1
-2
1
2
2
4
6
1
1
1
1
3
3
5
0
0
0
0
4
2
5
-1
0
1
0
(
)
y
y
t
−
(
)
x
x
t
−
(
)
2
x
x
t
−
x
x
t
−
y
y
t
−
t
y
t
x
5
6
8
3
3
9
9
6
1
3
-2
-2
4
4
SUMA
18
30
0
0
16
16
(
) (
)
(
)
1
16
16
18
1
2
18
1
1
=
=
−
−
⋅
−
=
∑
∑
=
=
t
t
t
t
t
x
x
y
y
x
x
a
2
3
*
1
-
5
1
0
=
=
−
=
x
a
y
a
3
6
18
=
=
x
5
6
30
=
=
y

x
y
+
=
2
ˆ
ε
+
+
=
x
y
2
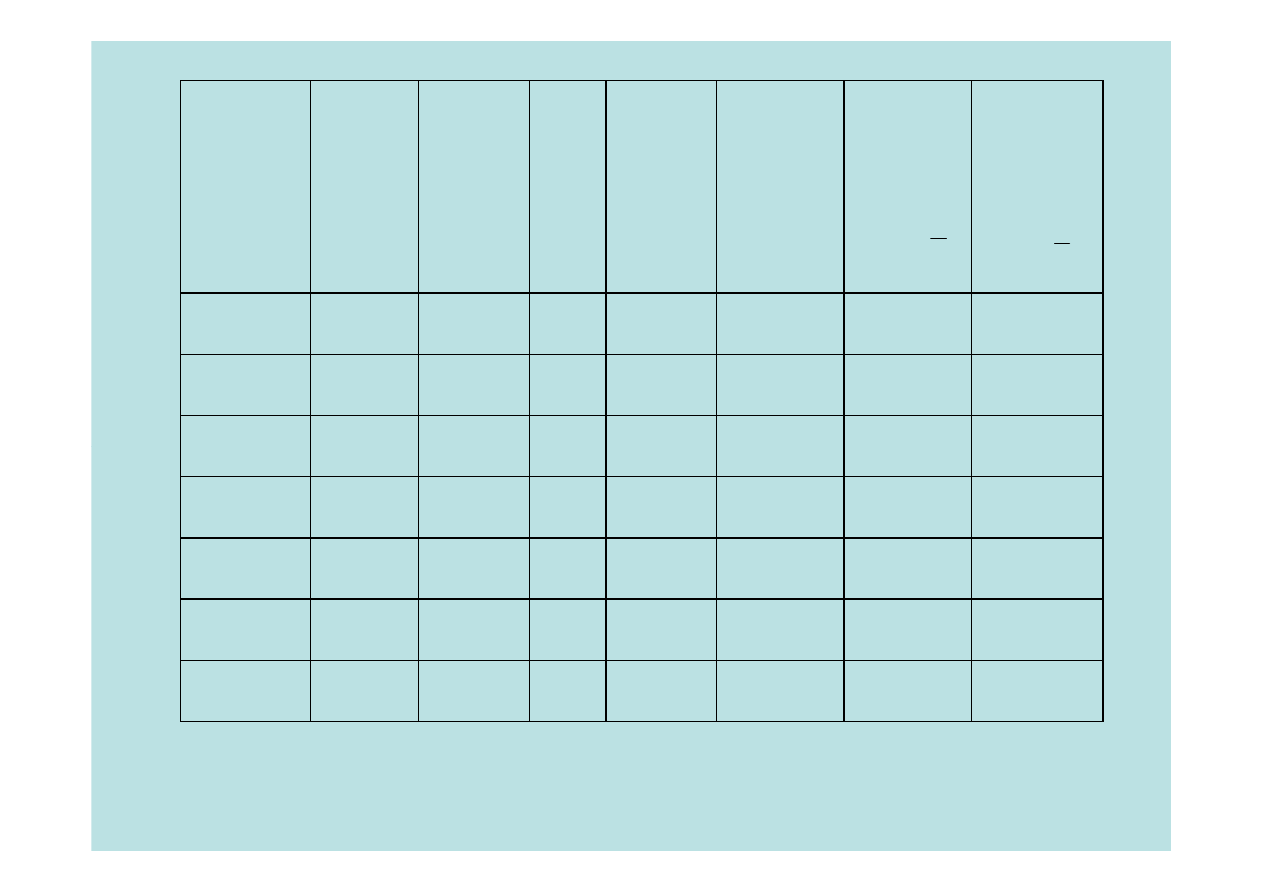
t
Produ
-kcja
Koszty
1
2
3
4
-1
1
-2
4
2
4
6
6
0
0
1
1
3
3
5
5
0
0
0
0
t
x
t
y
t
yˆ
t
t
y
y
ˆ
−
(
)
2
ˆ
t
t
y
y
−
(
)
2
y
y
t
−
y
y
t
−
3
3
5
5
0
0
0
0
4
2
5
4
1
1
0
0
5
6
8
8
0
0
3
9
6
1
3
3
0
0
-2
4
SUMA
18
30
0
0
2
0
18

(
)
11
,
0
18
2
)
(
ˆ
)
(
1
2
1
2
1
2
1
2
2
=
=
−
−
=
−
=
Φ
∑
∑
∑
∑
=
=
=
=
n
t
t
n
t
t
t
n
t
t
n
t
t
y
y
y
y
y
y
e
Współczynnik zbie
ż
no
ś
ci
89
,
0
11
,
0
1
1
2
2
=
−
=
Φ
−
=
R
Współczynnik determinacji
Estymator wariancji składnika losowego
(
)
ˆ
1
2
2
−
=
∑
=
y
y
S
n
t
t
t
1
1
2
−
−
=
=
k
n
S
t
ε
(
)
5
,
0
1
1
6
2
1
ˆ
1
2
2
=
−
−
=
−
−
−
=
∑
=
k
n
y
y
S
n
t
t
t
ε
71
,
0
5
,
0
=
=
ε
S

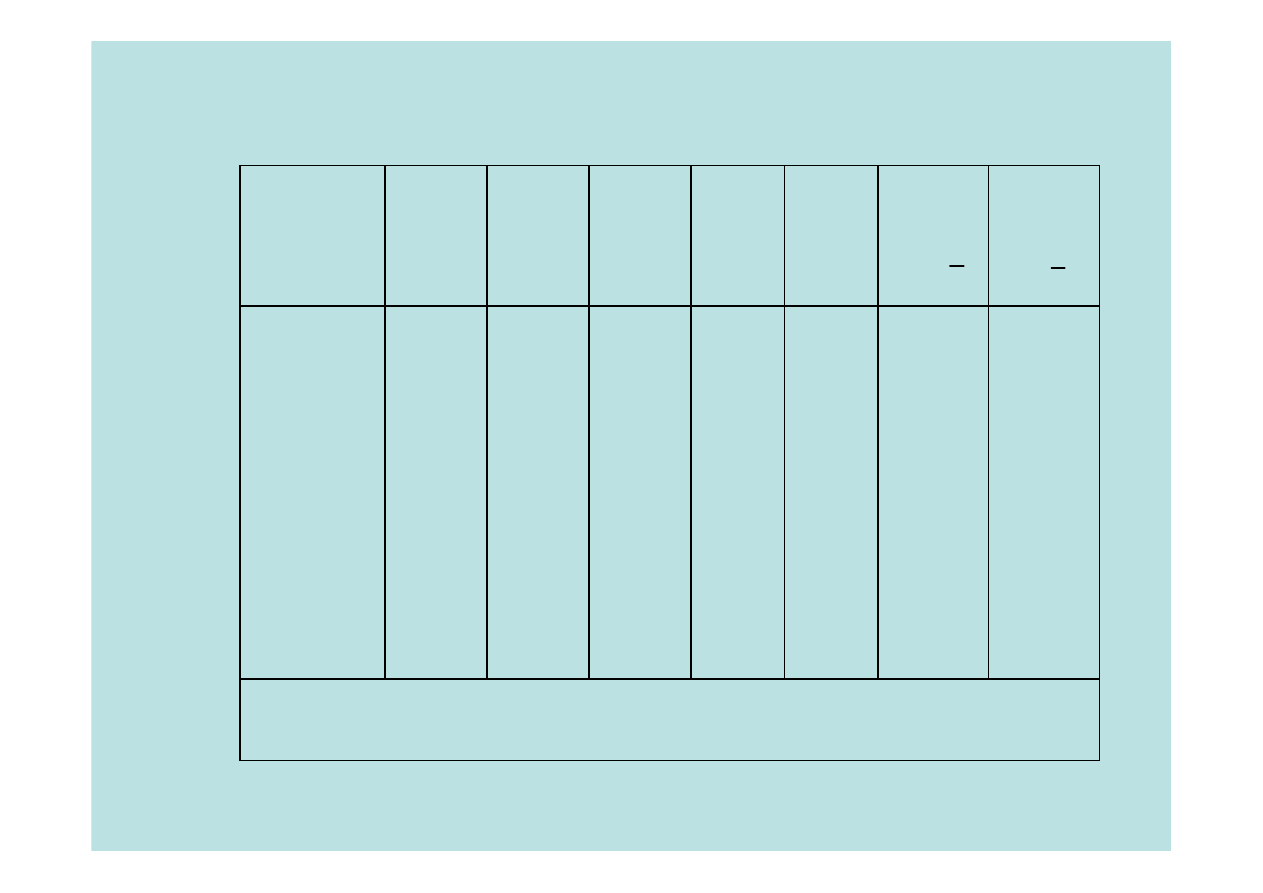
Estymatory wariancji i kowariancji
współczynników regresji
( )
(
)
=
⋅
=
−
1
2
2
X
X
S
S
T
ε
α
d
d
d
...
kk
k
k
k
k
d
d
d
d
d
d
d
d
d
...
...
...
...
...
...
...
1
0
1
11
10
0
01
00

( )
(
)
=
⋅
=
−
1
2
2
X
X
S
S
T
ε
α
=
=
−
=
∑
1
1
2
n
t
t
x
n
S
−
−
=
−
−
=
=
−
03
,
0
09
,
0
09
,
0
36
,
0
6
18
18
70
96
1
2
1
70
18
18
6
2
1
1
=
=
=
=
=
∑
∑
1
2
1
1
2
n
t
t
n
t
t
t
x
x
S
ε
Wytrzymało
ść
[kg/cm3]
Składnik
1
[%]
Składnik
2
[%]
5
0
0
4,60
0,40
0,16
0,80
0,64
1
0
1
1,53 -0,53
0,28
-3,20
10,24
y
1
x
2
x
y
y ˆ
−
(
)
2
ˆy
y
−
y
y
−
yˆ
(
)
2
y
y
−
6
1
0
6,40 -0,40
0,16
1,80
3,24
4
1
1
3,33
0,67
0,44
-0,20
0,04
5
2
1
5,13 -0,13
0,02
0,80
0,64
SUMA
1,07
14,80

(
)
07
,
0
8
,
14
07
,
1
)
(
ˆ
1
2
1
2
2
=
=
−
−
=
Φ
∑
∑
=
=
n
t
t
n
t
t
t
y
y
y
y
Współczynnik zbie
ż
no
ś
ci
Współczynnik determinacji
93
,
0
07
,
0
1
1
2
2
=
−
=
Φ
−
=
R
(
)
535
,
0
1
2
5
07
,
1
1
ˆ
1
2
2
=
−
−
=
−
−
∑
−
=
=
k
n
y
y
S
n
t
t
t
ε
Wariancja składnika losowego
Estymatory wariancji i kowariancji
współczynników regresji
( )
(
)
=
⋅
=
−
1
2
2
X
X
S
S
T
ε
α
−
−
−
−
−
−
=
−
−
−
−
−
−
⋅
=
50
,
0
11
,
0
21
,
0
11
,
0
21
,
0
11
,
0
21
,
0
11
,
0
32
,
0
14
3
6
3
6
3
6
3
9
15
1
535
,
0
Wyszukiwarka
Podobne podstrony:
2009 2010 STATYSTYKA WSKAZNIKI
2009 2010 STATYSTYKA ZALEZNOSC LINIOWA
2009 2010 STATYSTYKA ZMIENNE LOSOWE
2009 2010 STATYSTYKA NORMALNOSC
2009 2010 STATYSTYKA NORMALNOSCid 26680
2009 2010 STATYSTYKA TESTY PARA Nieznany
2009 2010 STATYSTYKA ZALEZNOSC LINIOWAid 26684
2009 2010 STATYSTYKA ANOVAid 26 Nieznany (2)
2009 2010 STATYSTYKA TESTY NIEPARAMETRYCZNEid 26681
2009 2010 STATYSTYKA ISTOTAid 2 Nieznany (2)
2009 2010 STATYSTYKA PARAMETRY Z PROBY
2009 2010 STATYSTYKA ISTOTA
więcej podobnych podstron