TESTY PARAMATRYCZNE

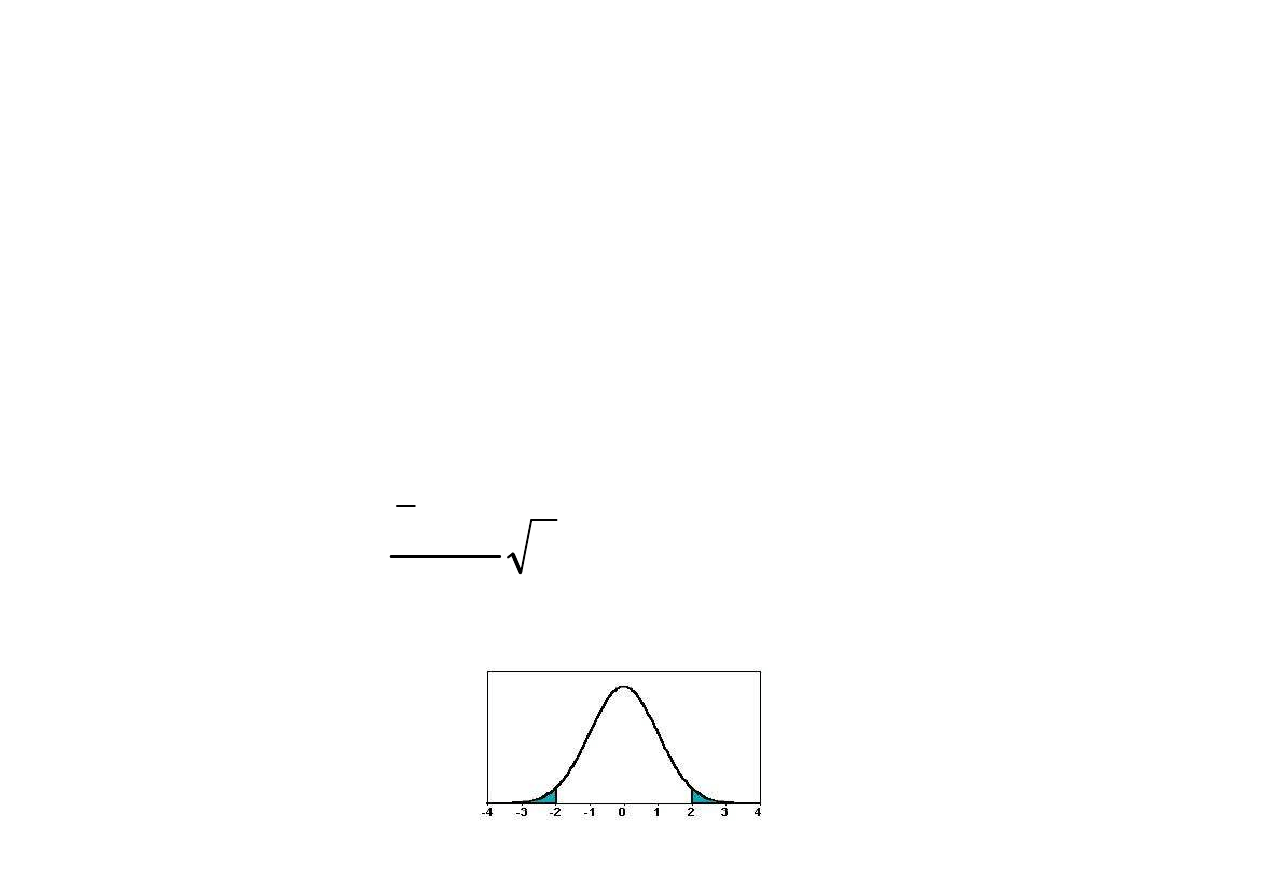
Test dla warto

ś

ci oczekiwanej

Zał.:

1. populacja ma rozkład normalny
2. dyspersja znana

0

0

:

m

m

H

=

0

1

:

m

m

H

≠

B. Gładysz 2007

rozkład normalny N(0,1)

Obszar krytyczny

n

m

x

u

σ

0

−

=

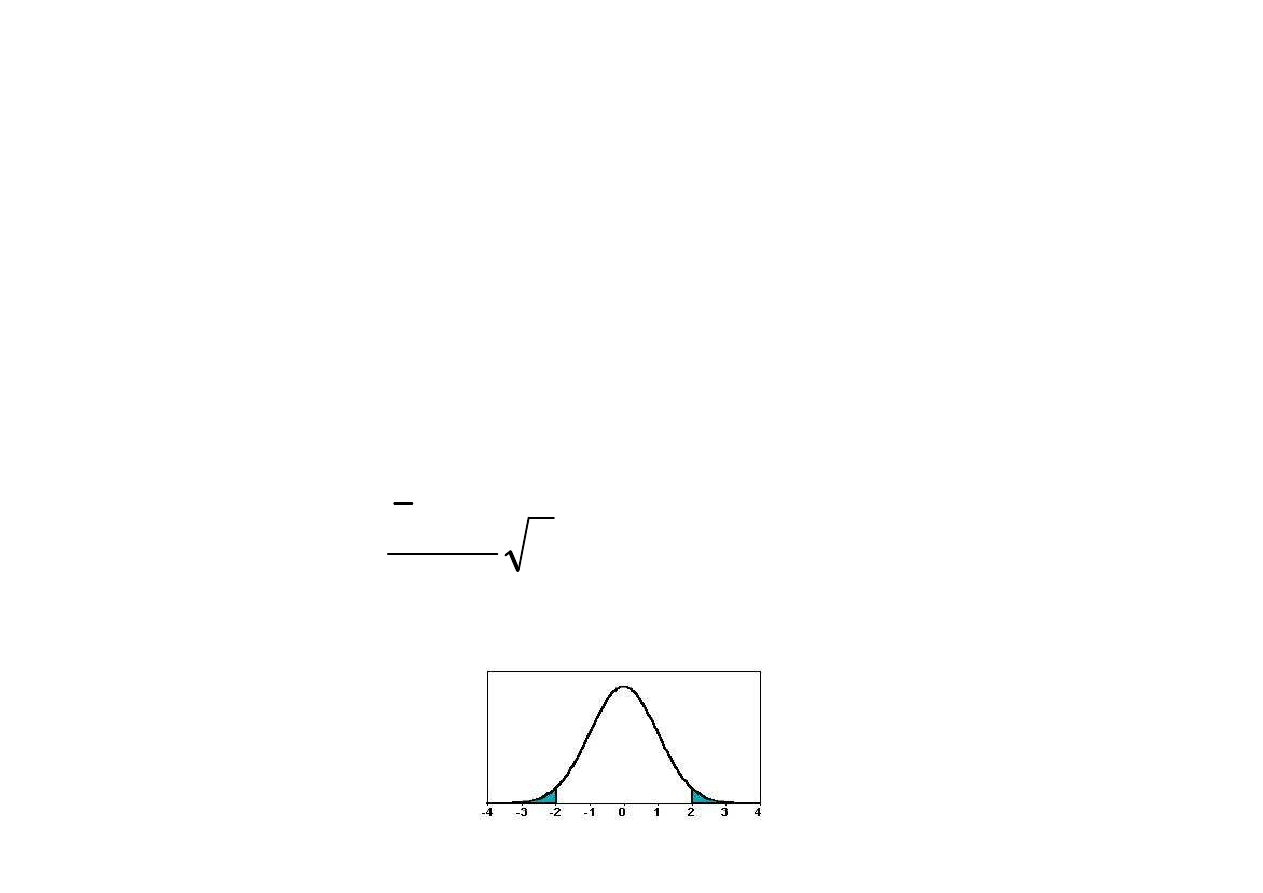
Test dla warto

ś

ci oczekiwanej

Zał.:

1. populacja ma rozkład normalny
2. mała próba
3. dyspersja nieznana

0

0

:

m

m

H

=

0

1

:

m

m

H

≠

B. Gładysz 2007

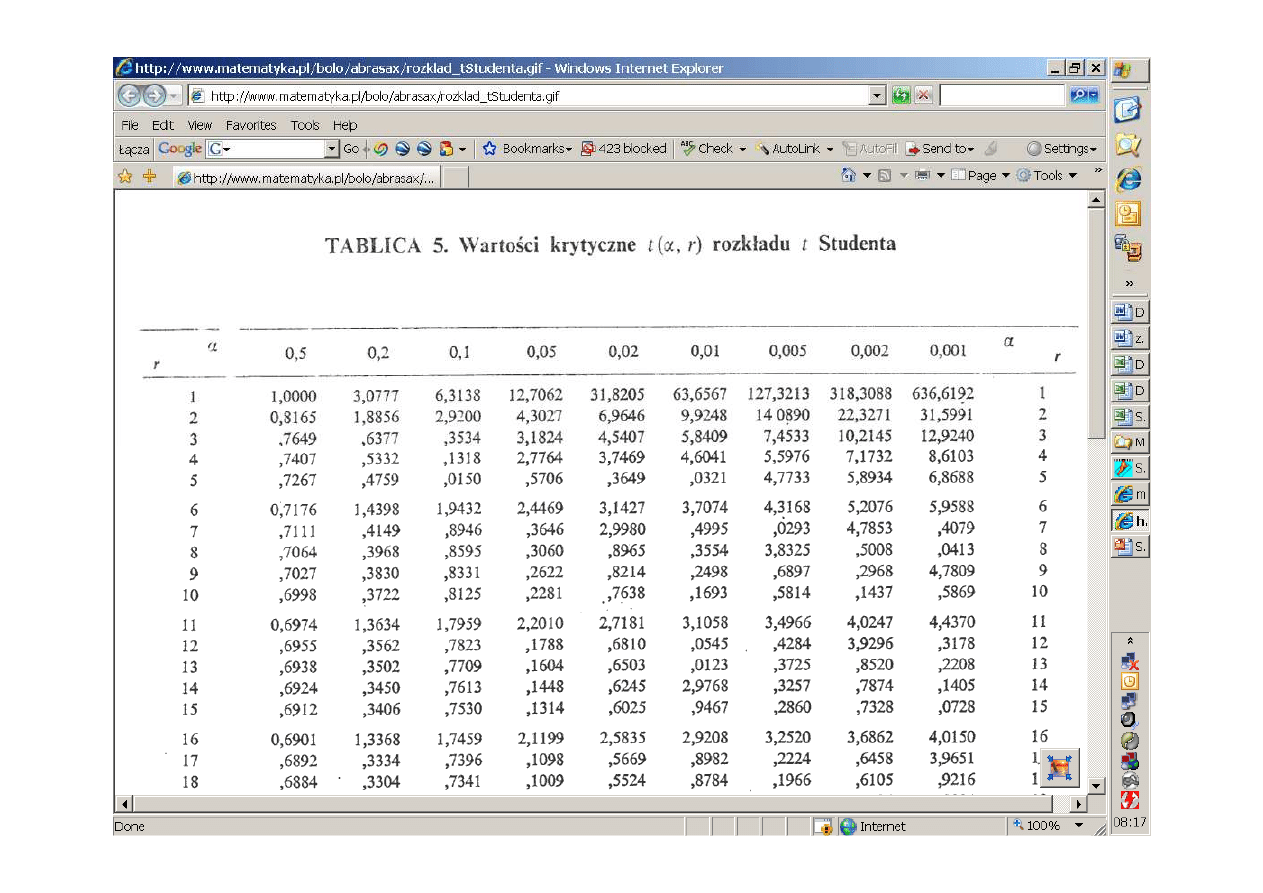
rozkład t-Studenta t(n-1)

Obszar krytyczny

n

S

m

x

t

ˆ

0

−

=

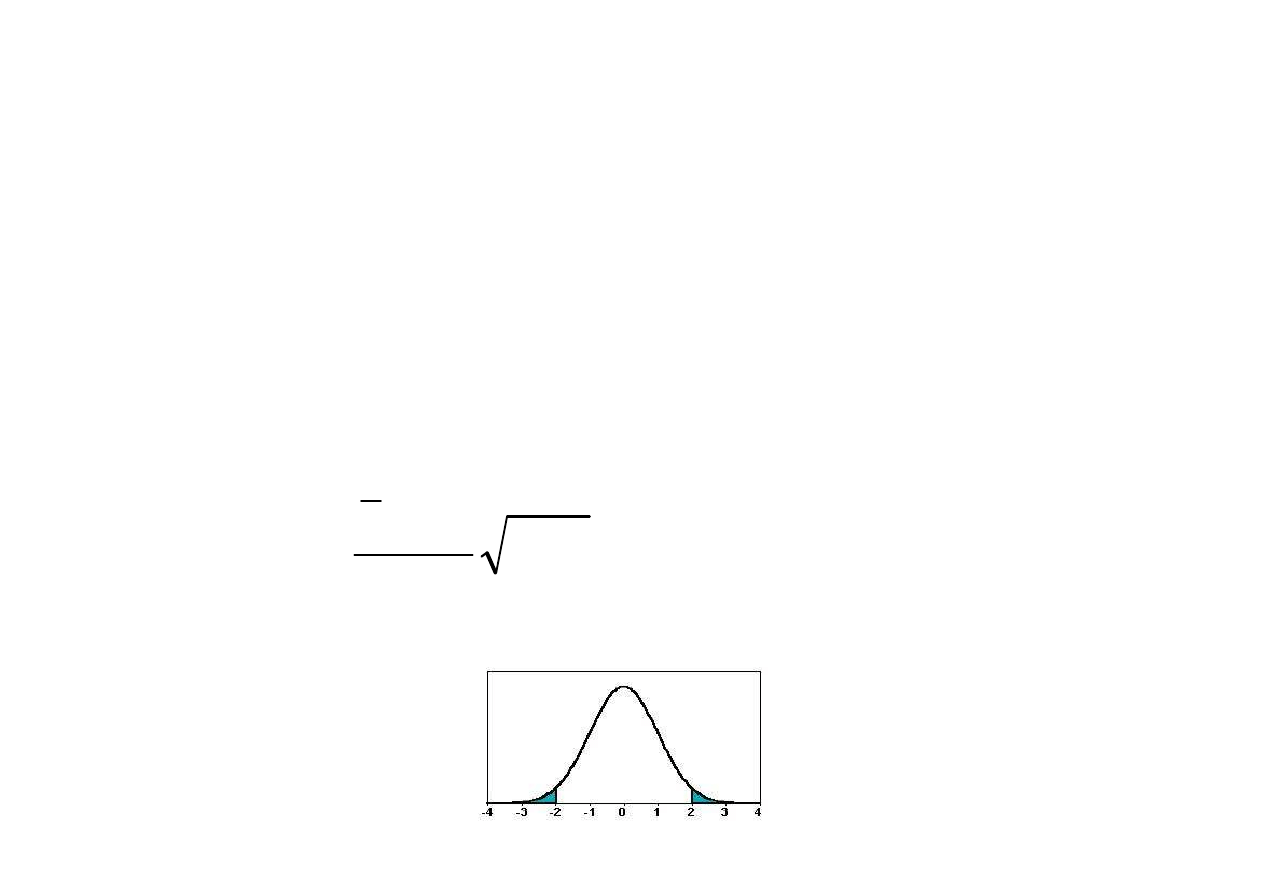
Test dla warto

ś

ci oczekiwanej

Zał.:

1. populacja ma rozkład normalny
2. mała próba
3. dyspersja nieznana

0

0

:

m

m

H

=

0

1

:

m

m

H

≠

B. Gładysz 2007

rozkład t-Studenta t(n-1)

Obszar krytyczny

1

0

−

−

=

n

S

m

x

t

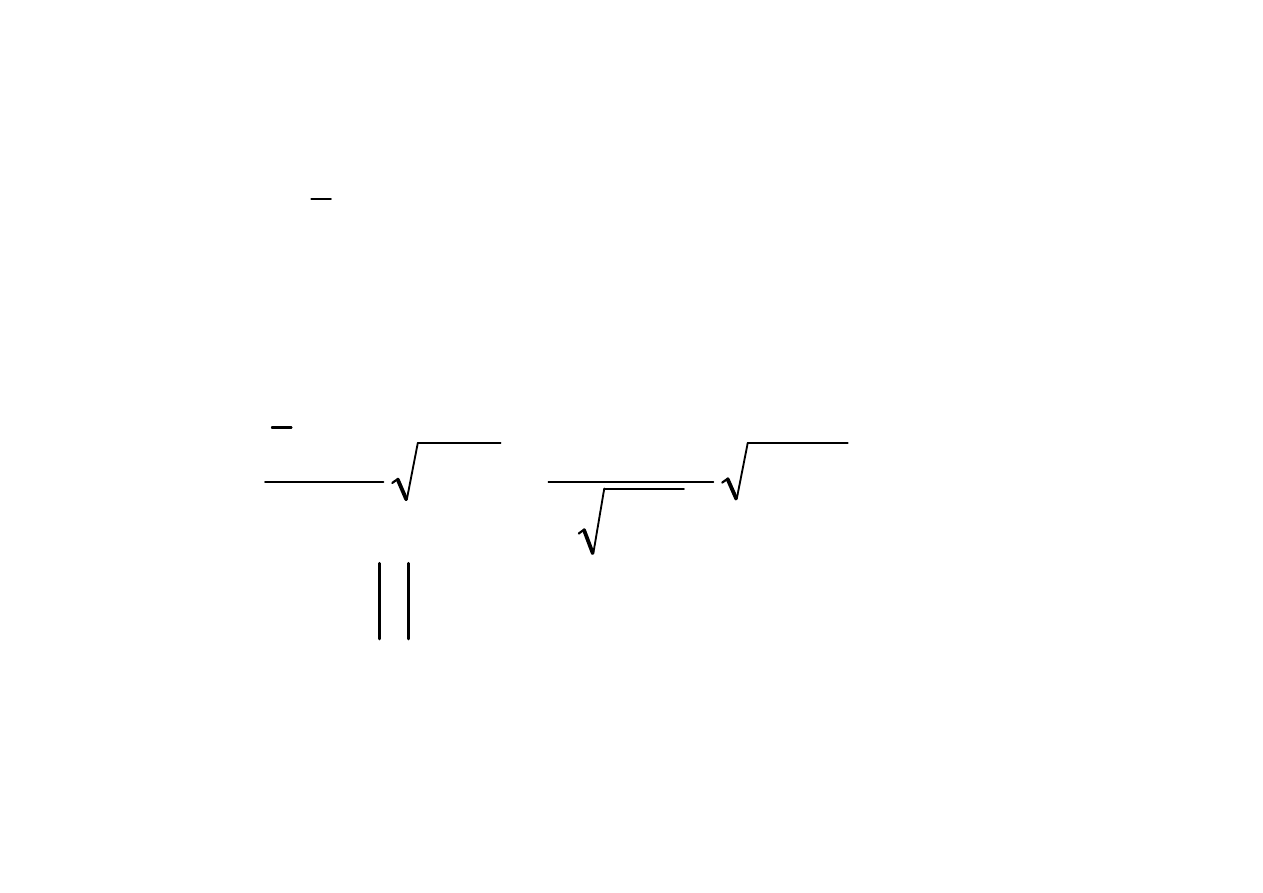
Test dla warto

ś

ci oczekiwanej wzrostu

165

:

0

=

m

H

165

:

1

≠

m

H

165

171

=

−

−

=

−

−

=

m

x

(160

160,

163,

165,

168,

170,

170,

173,

176,

178,

183, 186)

73

,

72

ˆ

7

,

66

171

2

2

=

=

=

S

S

x

B. Gładysz 2007

44

,

2

1

12

7

,

66

165

171

1

0

=

−

−

=

−

−

=

n

S

m

x

t

Obszar krytyczny

( )

2

,

2

11

44

,

2

05

,

0

=

>

=

t

t

Odrzucamy hipotez

ę

na korzy

ść

0

H

1

H

ś

redni wzrost jest ró

ż

ny od 165cm

B. Gładysz 2007

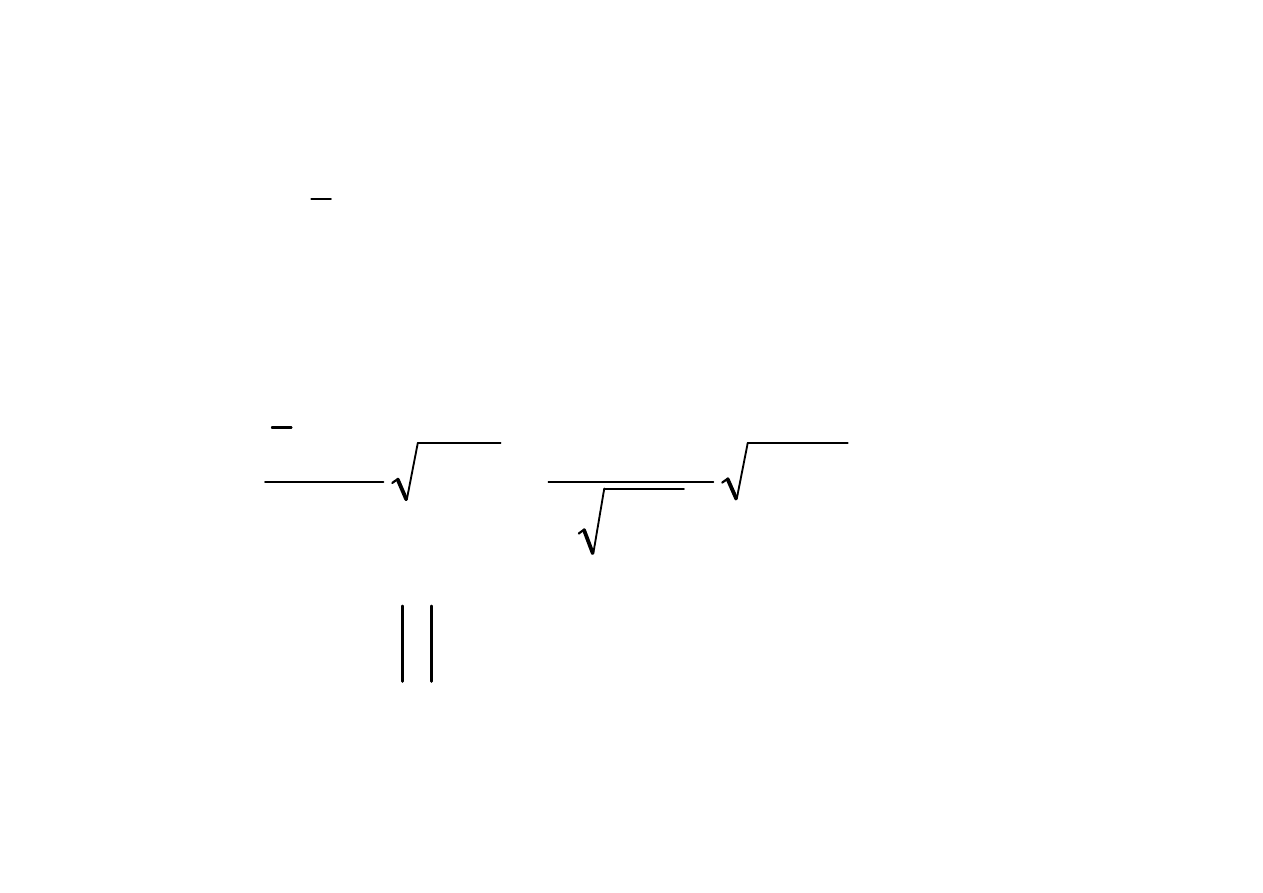
Test jednostronny dla warto

ś

ci oczekiwanej wzrostu

165

:

0

=

m

H

165

:

1

>

m

H

165

171

=

−

−

=

−

−

=

m

x

(160

160,

163,

165,

168,

170,

170,

173,

176,

178,

183, 186)

73

,

72

ˆ

7

,

66

171

2

2

=

=

=

S

S

x

B. Gładysz 2007

44

,

2

1

12

7

,

66

165

171

1

0

=

−

−

=

−

−

=

n

S

m

x

t

Obszar krytyczny

( )

8

,

1

11

44

,

2

05

,

0

=

>

=

t

t

Odrzucamy hipotez

ę

na korzy

ść

0

H

1

H

ś

redni wzrost jest wi

ę

kszy od 165cm

Test dla warto

ś

ci oczekiwanej

Zał.:

1. populacja ma rozkład normalny lub zbli

ż

ony do normalnego

2. du

ż

a próba

3. dyspersja nieznana

0

0

:

m

m

H

=

0

1

:

m

m

H

≠

B. Gładysz 2007

rozkład normalny N(0,1)

Obszar krytyczny

n

S

m

x

u

0

−

=

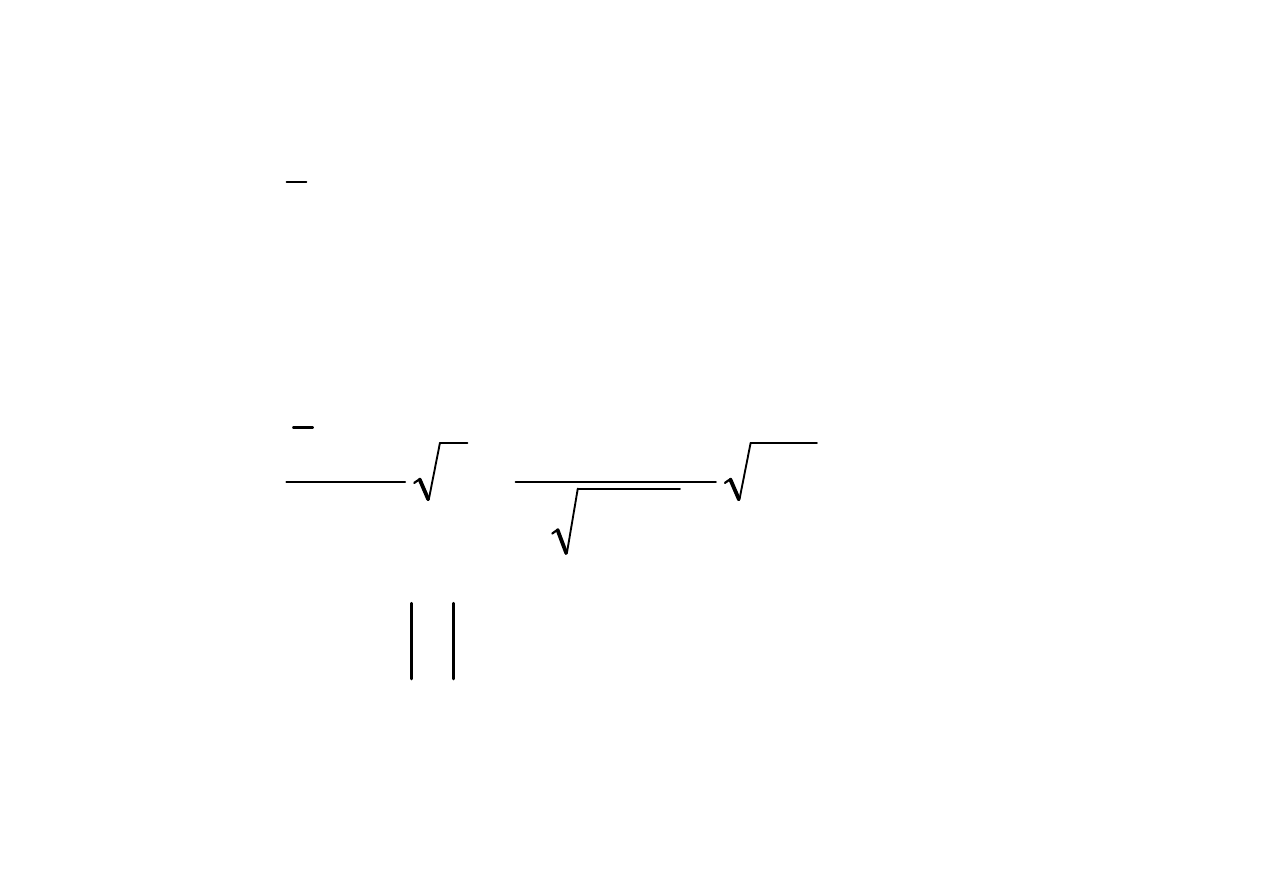
Test jednostronny dla warto

ś

ci oczekiwanej wzrostu

165

:

0

=

m

H

165

:

1

>

m

H

165

6

,

170

=

−

=

−

=

m

x

n=100

17

,

91

ˆ

26

,

90

6

,

170

2

2

=

=

=

S

S

x

B. Gładysz 2007

872

,

5

100

26

,

90

165

6

,

170

0

=

−

=

−

=

n

S

m

x

u

Obszar krytyczny

65

,

1

872

,

5

05

,

0

=

>

=

u

u

Odrzucamy hipotez

ę

na korzy

ść

0

H

1

H

ś

redni wzrost jest wi

ę

kszy od 165cm

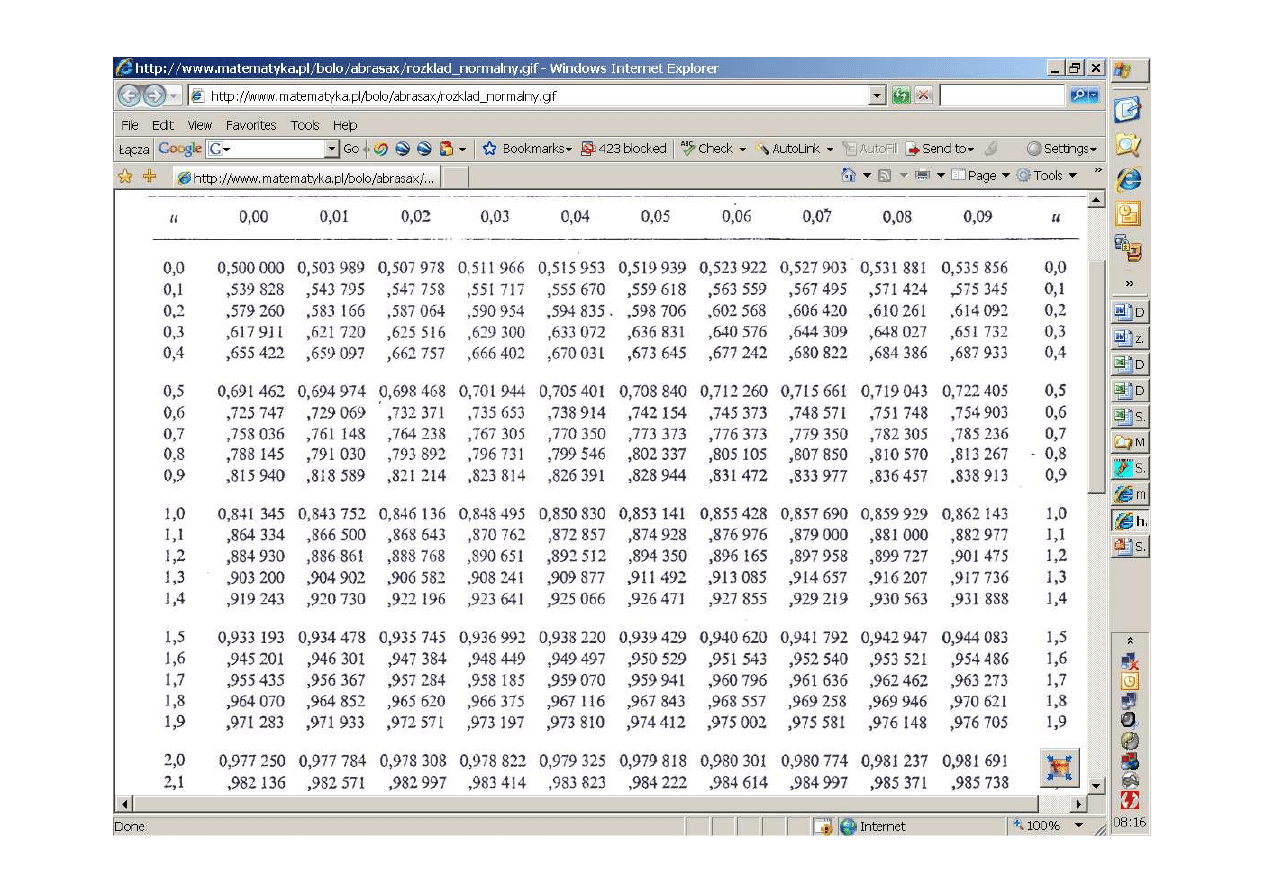
B. Gładysz 2007

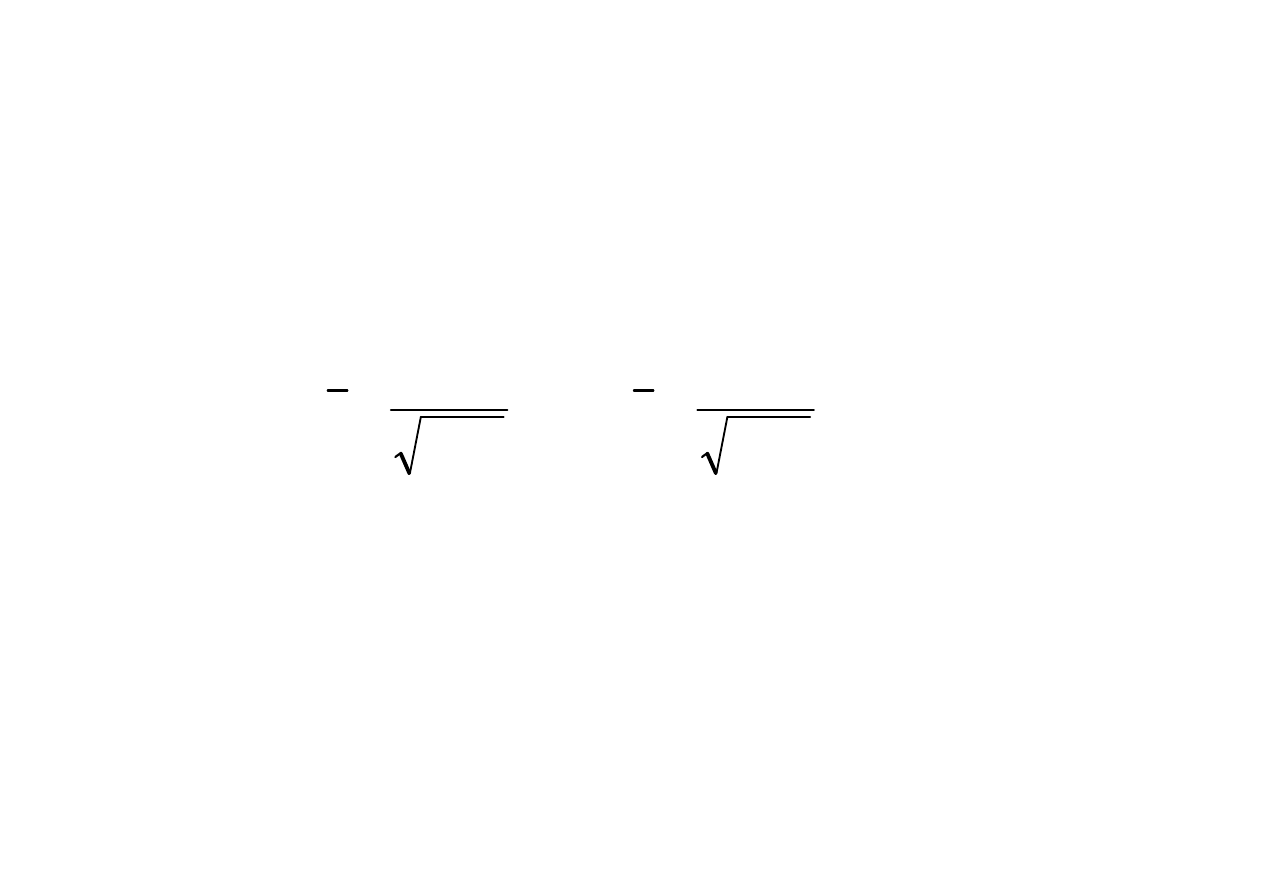
Przedział ufno

ś

ci dla warto

ś

ci oczekiwanej

Zał.:

1. populacja ma rozkład normalny
2. mała próba

α

α

α

−

=













−

⋅

+

<

<

−

⋅

−

1

1

1

n

s

t

x

m

n

s

t

x

P

B. Gładysz 2007

gdzie:
t

α

– warto

ść

krytyczna rozkładu t-Studenta t(n-1)





−

−

1

1

n

n

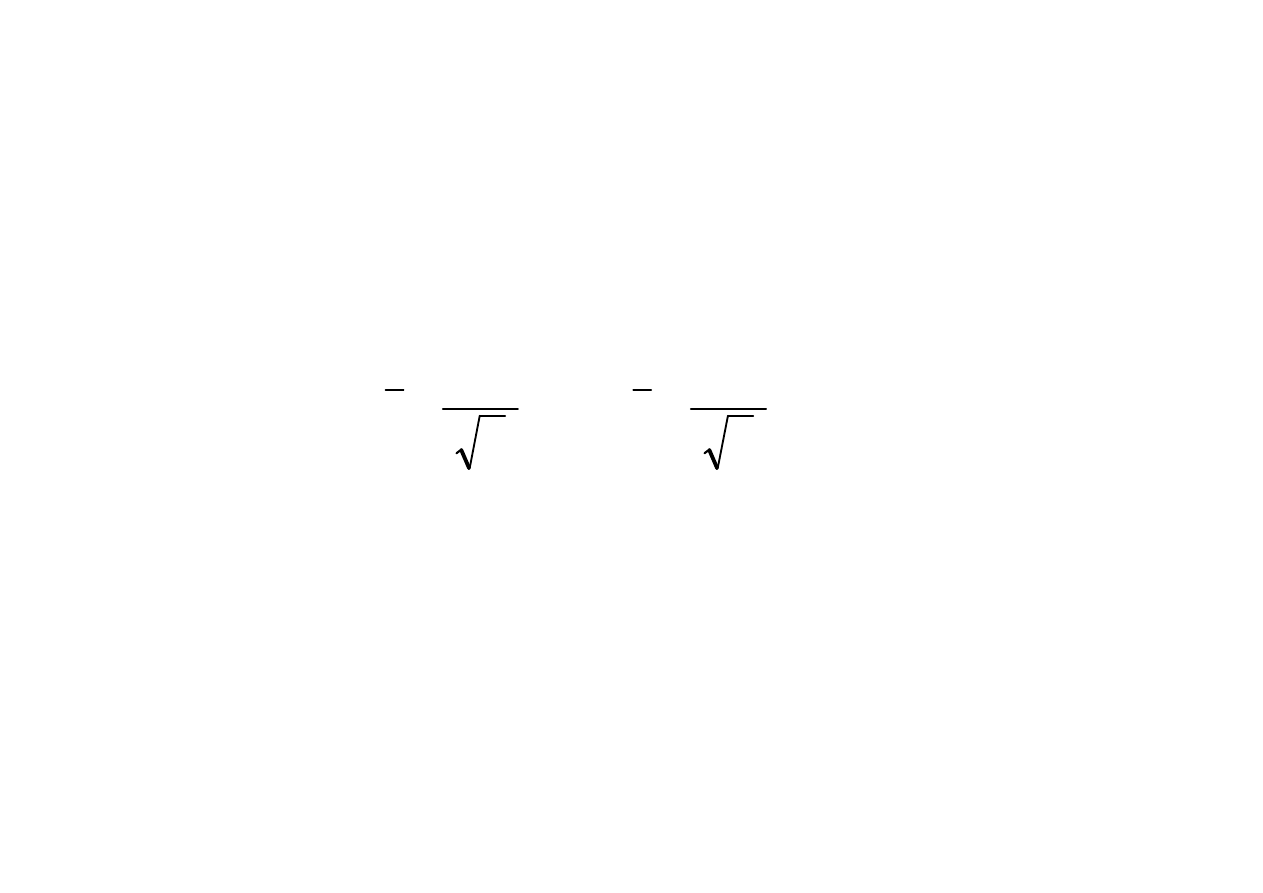
Przedział ufno

ś

ci dla warto

ś

ci oczekiwanej

Zał.:

1. populacja ma rozkład normalny
2. mała próba

α

α

α

−

=













⋅

+

<

<

⋅

−

1

ˆ

ˆ

n

s

t

x

m

n

s

t

x

P

B. Gładysz 2007

gdzie:
t

α

– warto

ść

krytyczna rozkładu t-Studenta t(n-1)





n

n

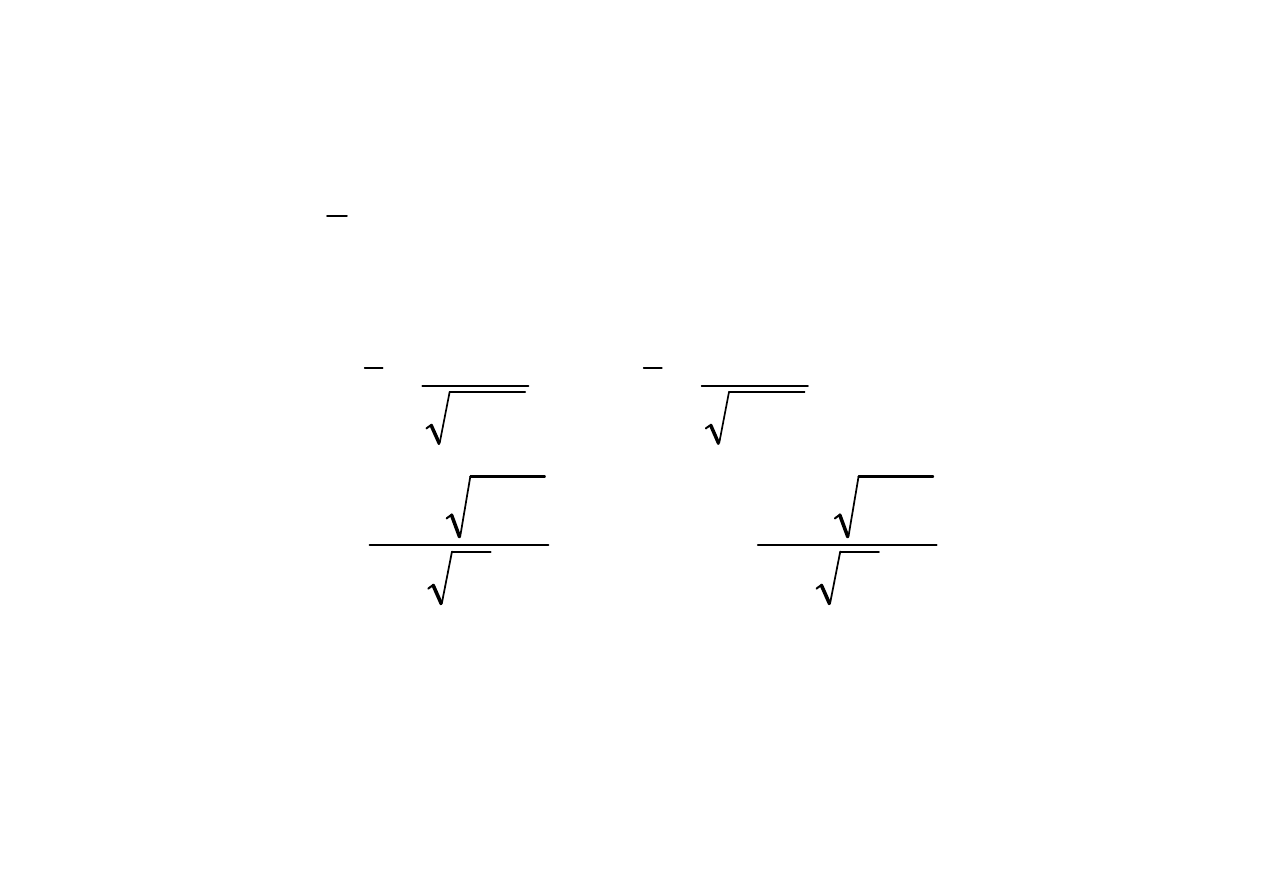
Przedział ufno

ś

ci dla warto

ś

ci oczekiwanej wzrostu

(160

160,

163,

165,

168,

170,

170,

173,

176,

178,

183, 186)

α

α

α

−

=













−

⋅

+

<

<

−

⋅

−

1

1

1

n

s

t

x

m

n

s

t

x

P

73

,

72

ˆ

7

,

66

171

2

2

=

=

=

S

S

x

B. Gładysz 2007

95

,

0

11

7

,

66

2

,

2

171

11

7

,

66

2

,

2

171

=















⋅

+

<

<

⋅

−

m

P





−

−

1

1

n

n

(

)

95

,

0

4

,

176

6

,

165

=

<

<

m

P

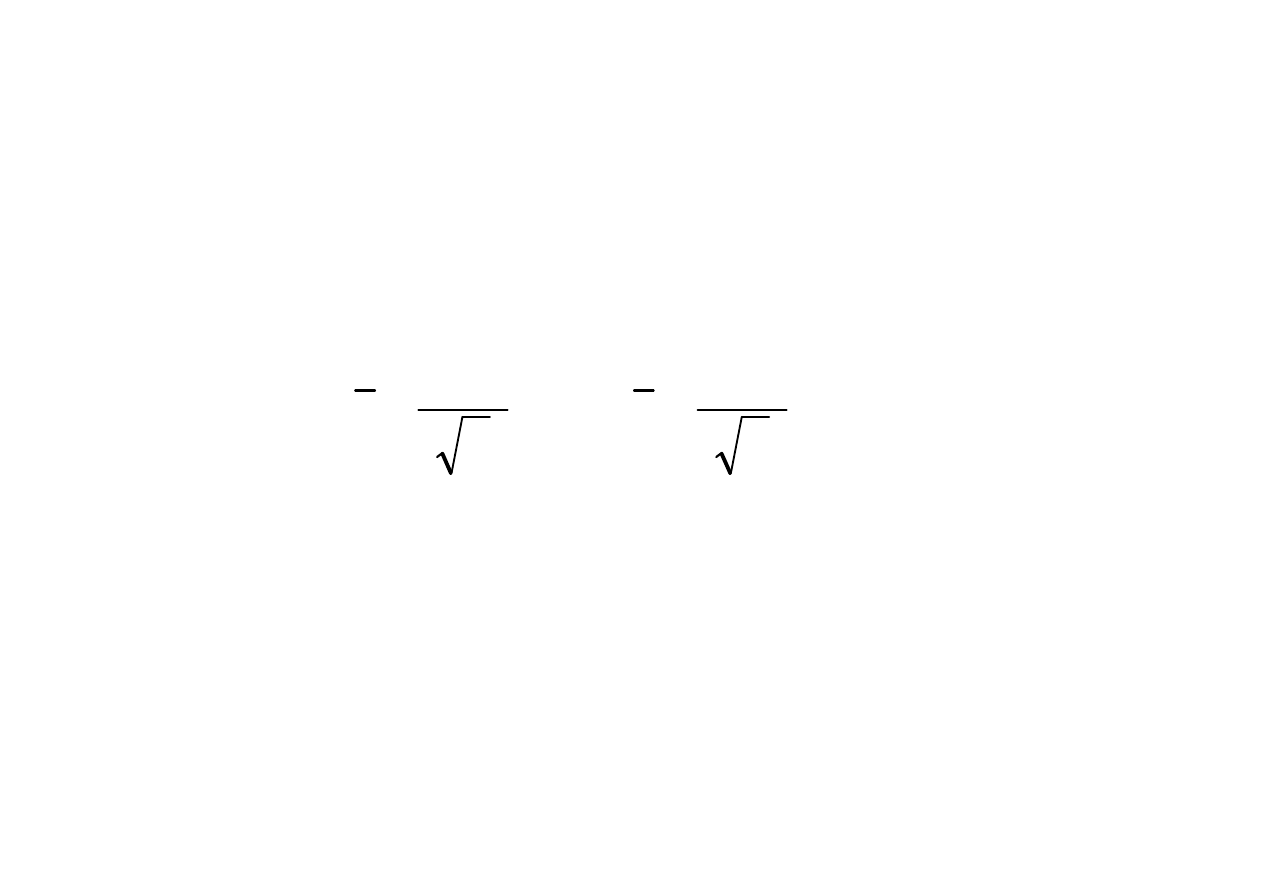
Przedział ufno

ś

ci dla warto

ś

ci oczekiwanej

Zał.:

1. populacja ma rozkład normalny lub zbli

ż

ony do normalnego

2. du

ż

a próba

α

α

α

−

=













⋅

+

<

<

⋅

−

1

n

s

u

x

m

n

s

u

x

P

B. Gładysz 2007

gdzie:
u

α

– warto

ść

krytyczna rozkładu normalnego N(0,1)





n

n

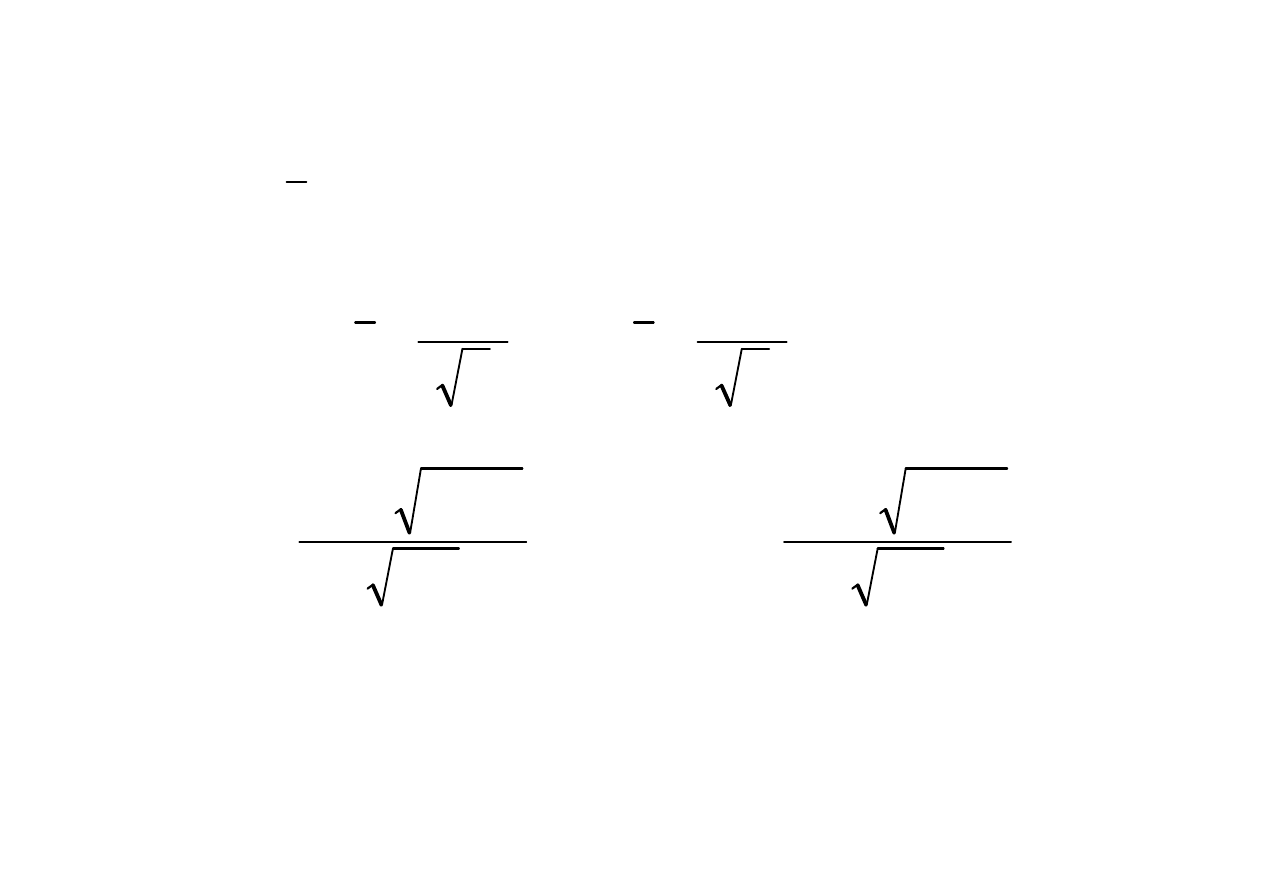
Przedział ufno

ś

ci dla warto

ś

ci oczekiwanej wzrostu

α

α

α

−

=













⋅

+

<

<

⋅

−

1

n

s

u

x

m

n

s

u

x

P

n=100

17

,

91

ˆ

26

,

90

6

,

170

2

2

=

=

=

S

S

x

B. Gładysz 2007

95

,

0

100

26

,

90

96

,

1

6

,

170

100

26

,

90

96

,

1

6

,

170

=















⋅

+

<

<

⋅

−

m

P

(

)

95

,

0

4

,

172

7

,

168

=

<

<

m

P

Test dla wariancji

Zał.:

1. populacja ma rozkład normalny

2

0

2

0

:

σ

σ

=

H

2

0

2

1

:

σ

σ

>

H

B. Gładysz 2007

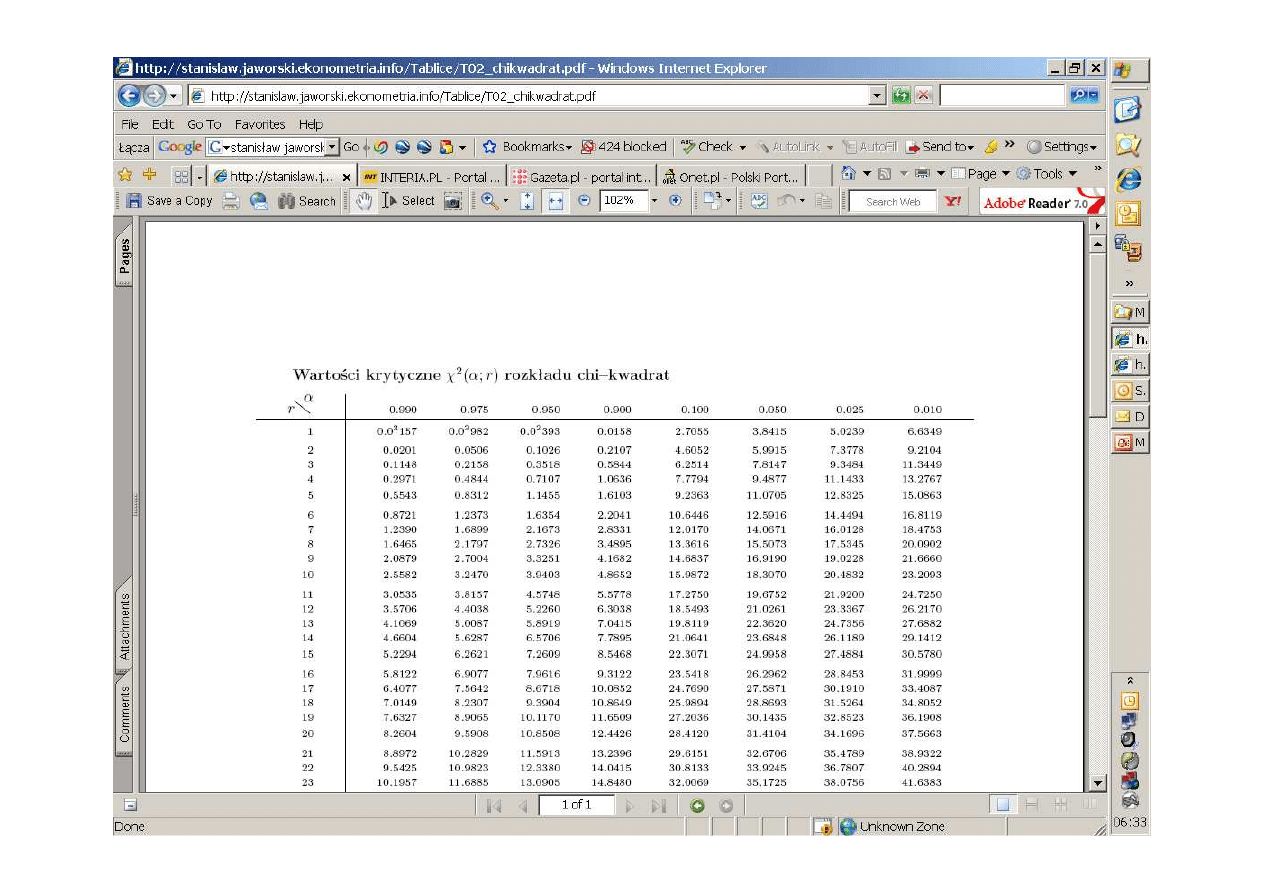
rozkład chi kwadrat

Χ

2

(n-1)

Obszar krytyczny

2

0

2

2

σ

χ

nS

=

Test dla wariancji

Zał.:

1. populacja ma rozkład normalny

2

0

2

0

:

σ

σ

=

H

2

0

2

1

:

σ

σ

>

H

B. Gładysz 2007

rozkład chi kwadrat

Χ

2

(n-1)

Obszar krytyczny

( )

2

0

2

2

ˆ

1

σ

χ

S

n

−

=

Test dla wariancji wzrostu

49

:

2

0

=

σ

H

49

:

2

1

>

σ

H

(160

160,

163,

165,

168,

170,

170,

173,

176,

178,

183, 186)

73

,

72

ˆ

7

,

66

6

,

170

2

2

=

=

=

S

S

x

B. Gładysz 2007

327

,

16

49

7

,

66

12

2

=

⋅

=

χ

( )

675

,

19

11

327

,

16

05

,

0

2

2

=

<

=

χ

χ

Nie ma podstaw do odrzucenia hipotezy
na korzy

ść

hipotezy

0

H

1

H

B. Gładysz 2007

Przedział ufno

ś

ci dla wariancji

Zał.:

1. populacja ma rozkład normalny
2. mała próba

α

σ

−

=









<

<

1

2

2

2

ns

ns

P

B. Gładysz 2007

– warto

ść

krytyczna rozkładu chi

2

dla

α

χ

σ

χ

−

=













<

<

1

2

1

2

2

2

ns

ns

P

(

) (

)

1

,

1

2

2

2

1

−

−

n

n

χ

χ

2

1

,

2

α

α

−

gdzie:

Przedział ufno

ś

ci dla wariancji wzrostu

α

χ

σ

χ

−

=













<

<

1

2

1

2

2

2

2

2

ns

ns

P

(160

160,

163,

165,

168,

170,

170,

173,

176,

178,

183, 186)

73

,

72

ˆ

7

,

66

6

,

170

2

2

=

=

=

S

S

x

B. Gładysz 2007





95

,

0

816

,

3

7

,

66

12

92

,

21

6

,

66

12

2

=













⋅

<

<

⋅

σ

P

(

)

95

,

0

7

,

209

5

,

36

2

=

<

<

σ

P

Przedział ufno

ś

ci dla wariancji

Zał.:

1. populacja ma rozkład normalny lub zbli

ż

ony do normalnego

2. du

ż

a próba

α

σ

−

=













<

<

1

s

s

P

B. Gładysz 2007

gdzie:
u

α

– warto

ść

krytyczna rozkładu normalnego N(0,1)

α

σ

α

α

−

=

















−

<

<

+

1

2

1

2

1

n

u

s

n

u

s

P

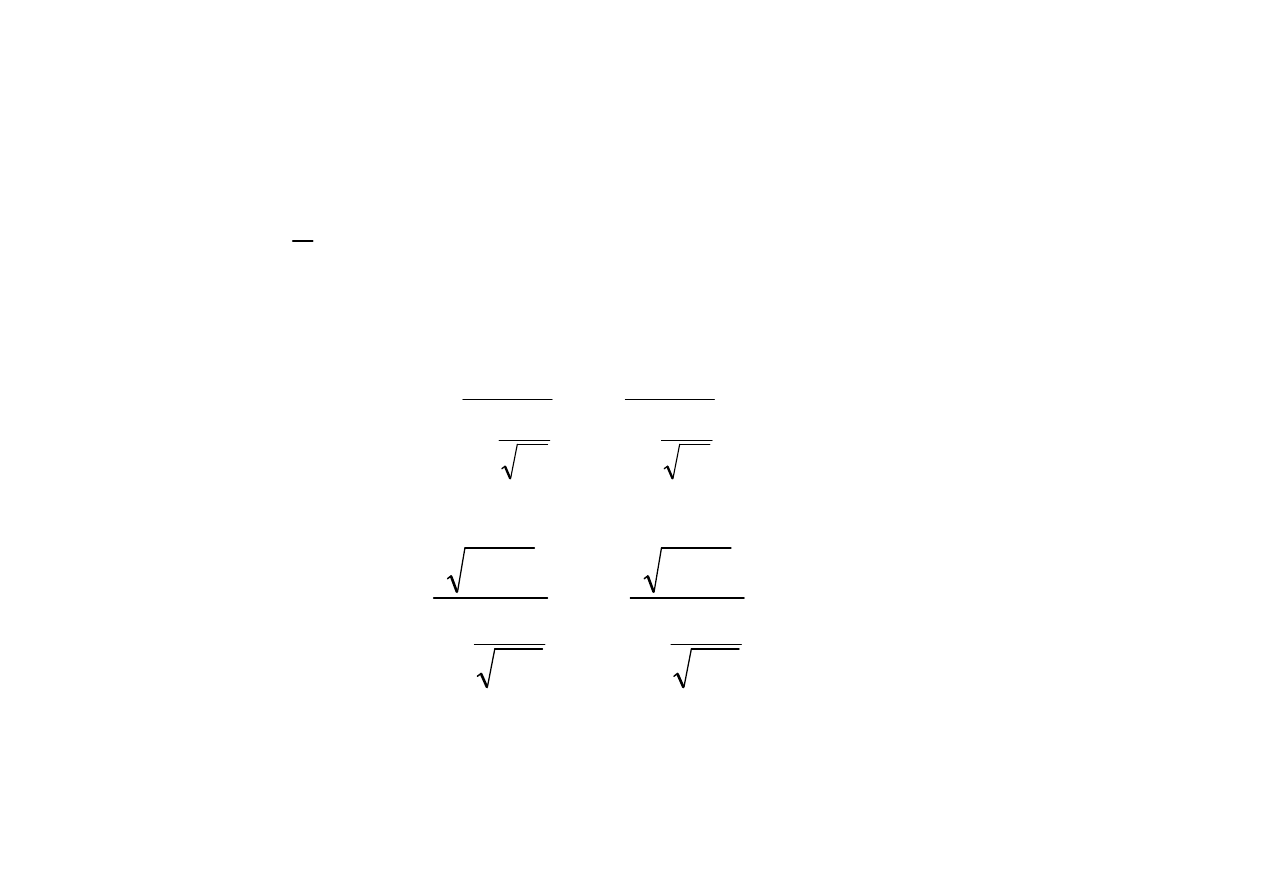
Przedział ufno

ś

ci dla wariancji wzrostu

n=100

17

,

91

ˆ

26

,

90

6

,

170

2

2

=

=

=

S

S

x

α

σ

α

α

−

=





















−

<

<

+

1

1

1

u

s

u

s

P

B. Gładysz 2007

95

,

0

200

96

,

1

1

26

,

90

200

96

,

1

1

26

,

90

=

























−

<

<

+

σ

P









−

+

2

1

2

1

n

n

(

)

95

,

0

03

,

11

34

,

8

=

<

<

σ

P

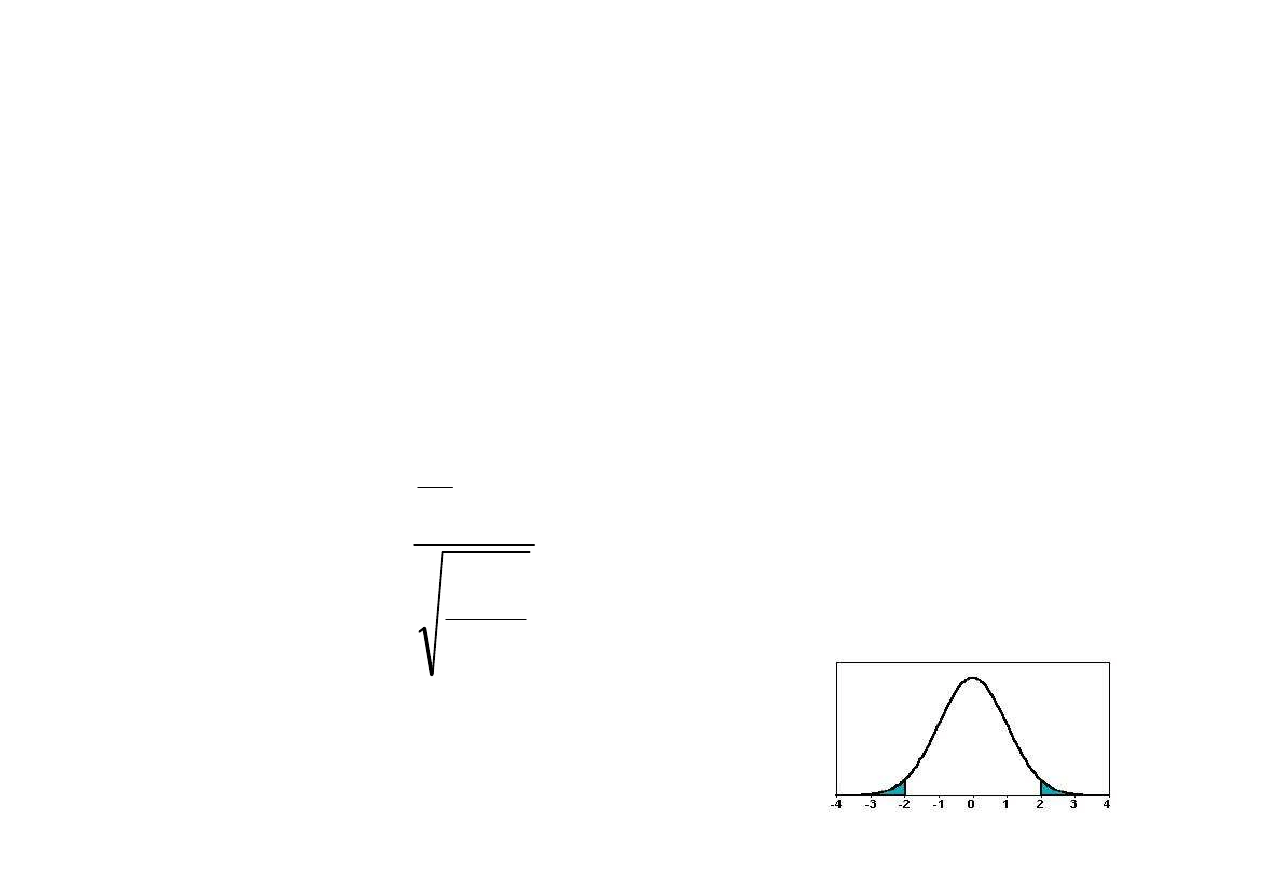
Test dla frakcji

Zał.:

1. populacja ma rozkład dwupunktowy
2. du

ż

a próba (n>100)

0

0

:

p

p

H

=

0

1

:

p

p

H

≠

m

B. Gładysz 2007

rozkład normalny N(0,1)

gdzie:

Obszar krytyczny

n

q

p

p

n

m

u

0

0

0

−

=

0

0

1

p

q

−

=

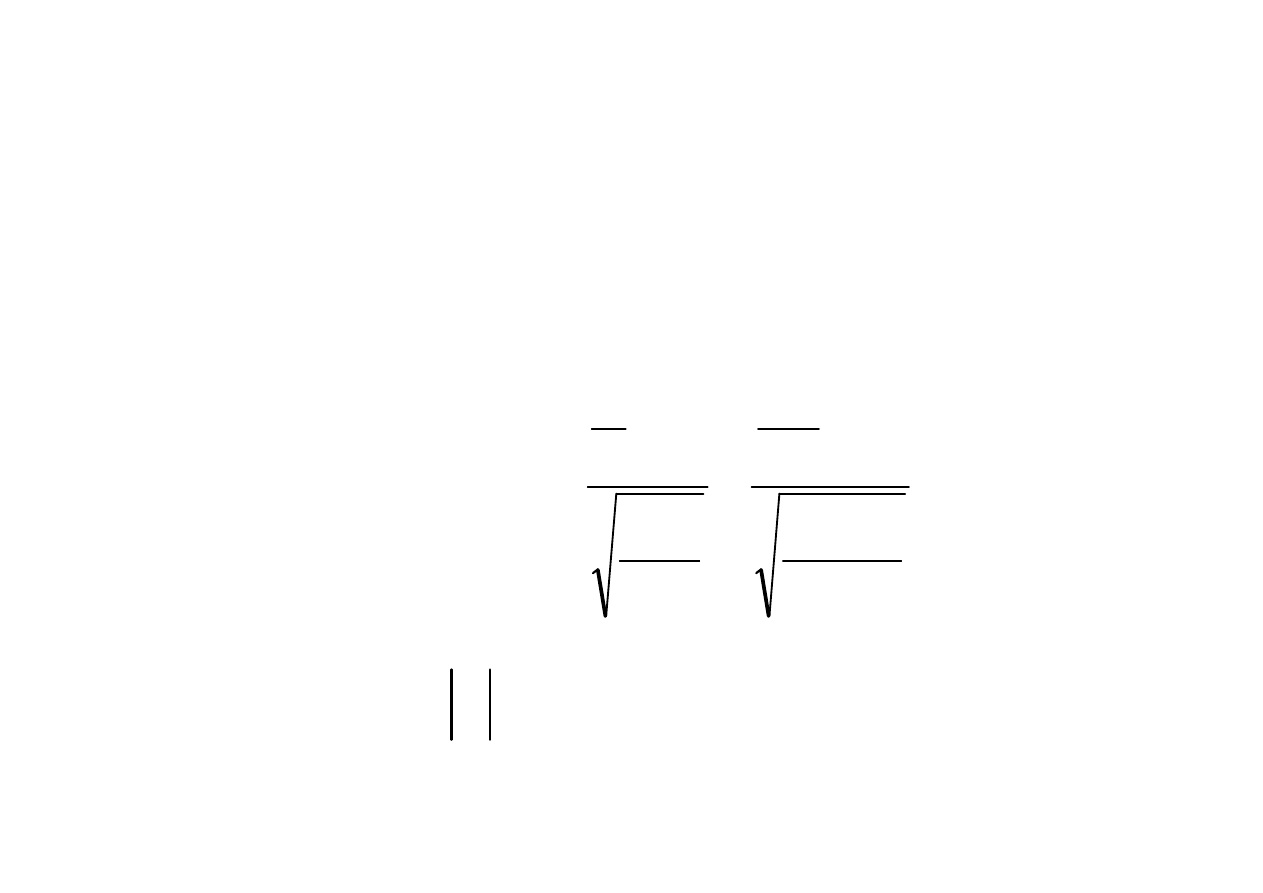
Test dla frakcji kobiet

5

,

0

:

0

=

p

H

5

,

0

:

0

1

≠

p

H

kobiet

m

n

45

100

=

=

5

,

0

100

45

0

−

−

p

n

m

B. Gładysz 2007

Obszar krytyczny

96

,

1

1

05

,

0

=

<

−

=

u

u

Nie ma podstaw do odrzucenia hipotezy

0

H

frakcja kobiet = 50%

1

100

5

,

0

5

,

0

5

,

0

100

0

0

0

−

=

⋅

−

=

−

=

n

q

p

p

n

u

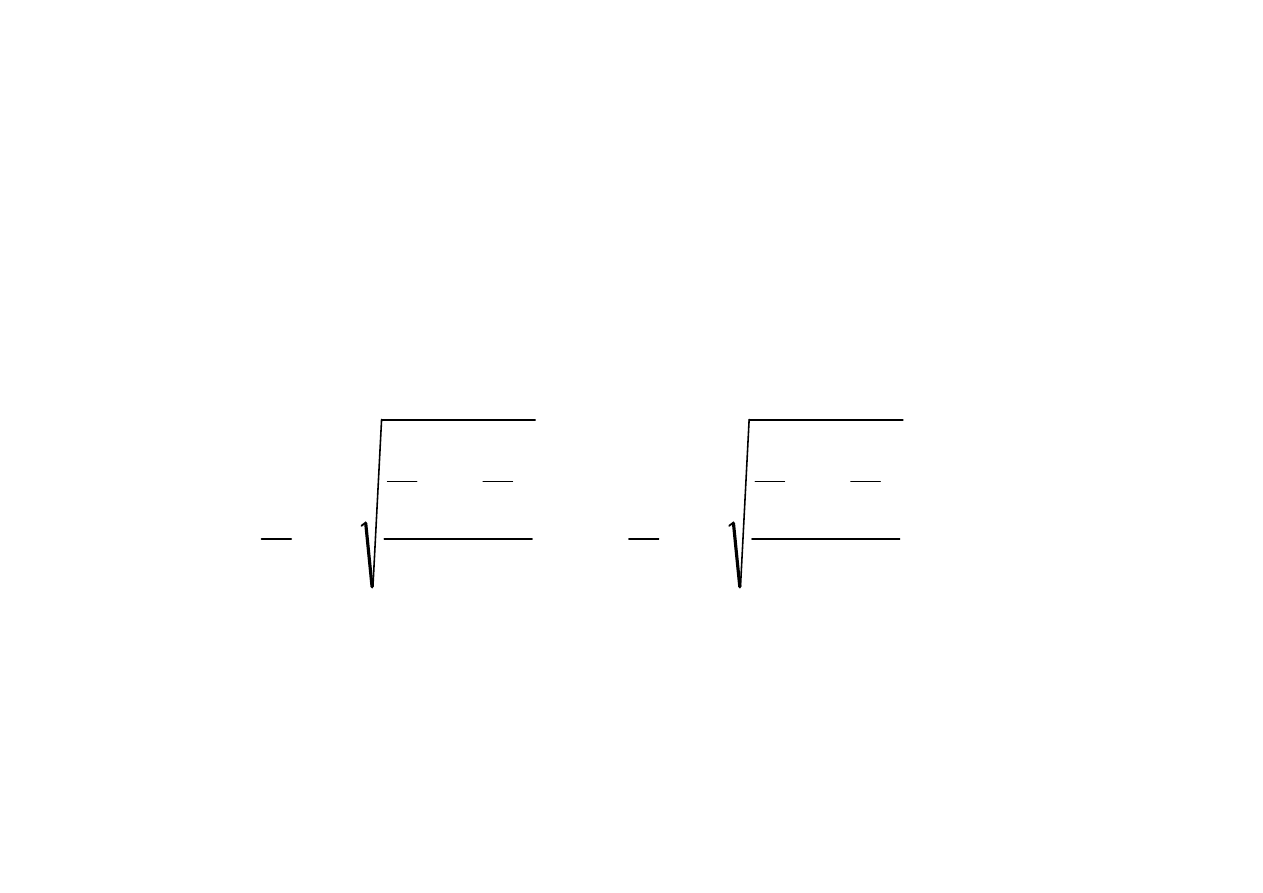
Przedział ufno

ś

ci dla frakcji

















m

m

m

m

Zał.:

1. populacja ma rozkład dwupunktowy
2. du

ż

a próba (n>100)

B. Gładysz 2007

α

α

α

−

≈









































−

+

<

<













−

−

1

1

1

n

n

m

n

m

u

n

m

p

n

n

m

n

m

u

n

m

P

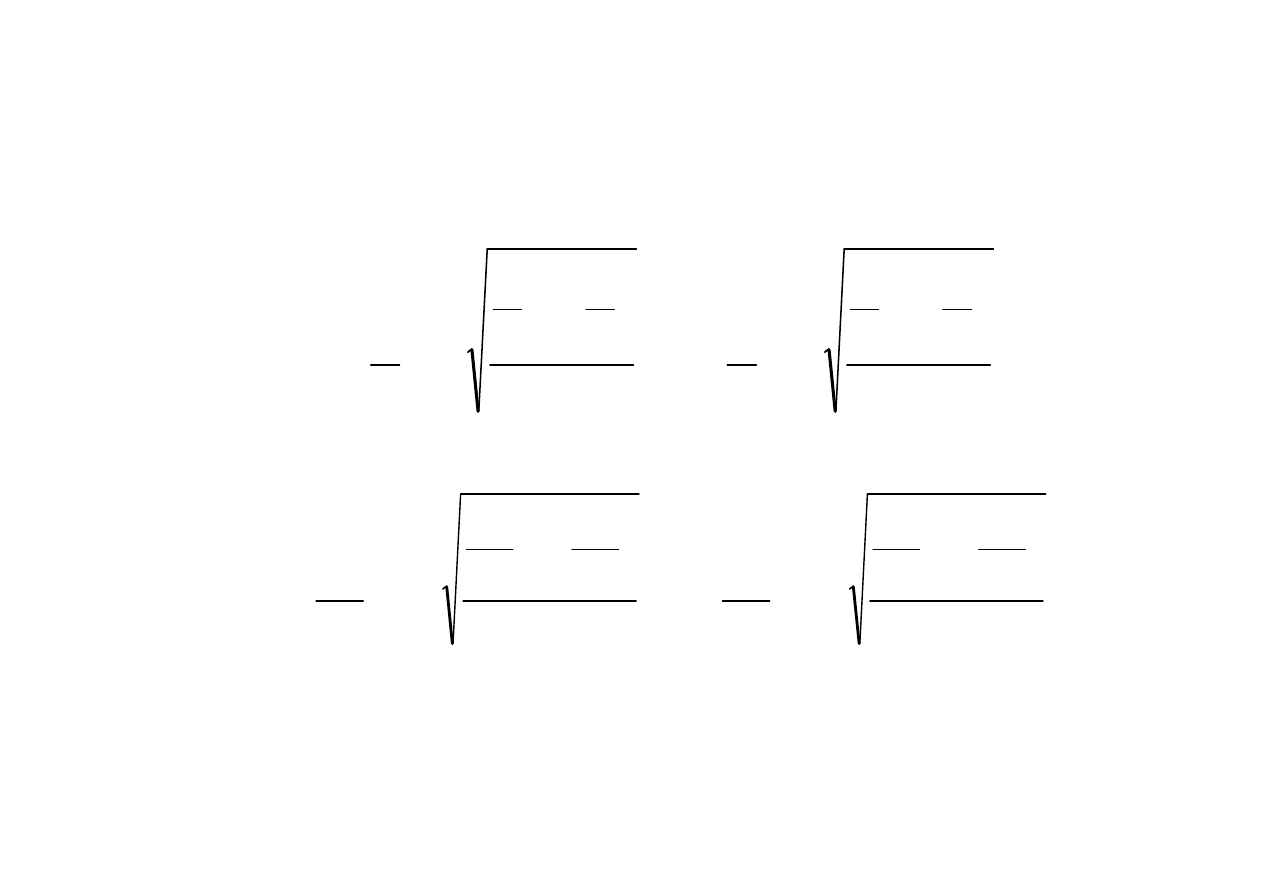
Przedział ufno

ś

ci dla frakcji kobiet

α

α

α

−

≈









































−

+

<

<













−

−

1

1

1

n

n

m

n

m

u

n

m

p

n

n

m

n

m

u

n

m

P

kobiet

m

n

45

100

=

=

B. Gładysz 2007

95

,

0

100

100

45

1

100

45

96

,

1

100

45

100

100

45

1

100

45

96

,

1

100

45

≈









































−

+

<

<













−

−

p

P









(

)

95

,

0

5475

,

0

3525

,

0

≅

<

<

p

P

Test równo

ś

ci dwóch wariancji

lub

2

2

2

1

:

δ

δ

=

o

H

2

1

2

2

1

:

δ

δ

>

H

2

2

2

1

1

:

δ

δ

>

H

Zał.:

1. populacje maj

ą

rozkłady normalne

B. Gładysz 2007

(

)

(

)

2

2

2

1

2

2

2

1

ˆ

,

ˆ

min

ˆ

,

ˆ

max

S

S

S

S

F

=

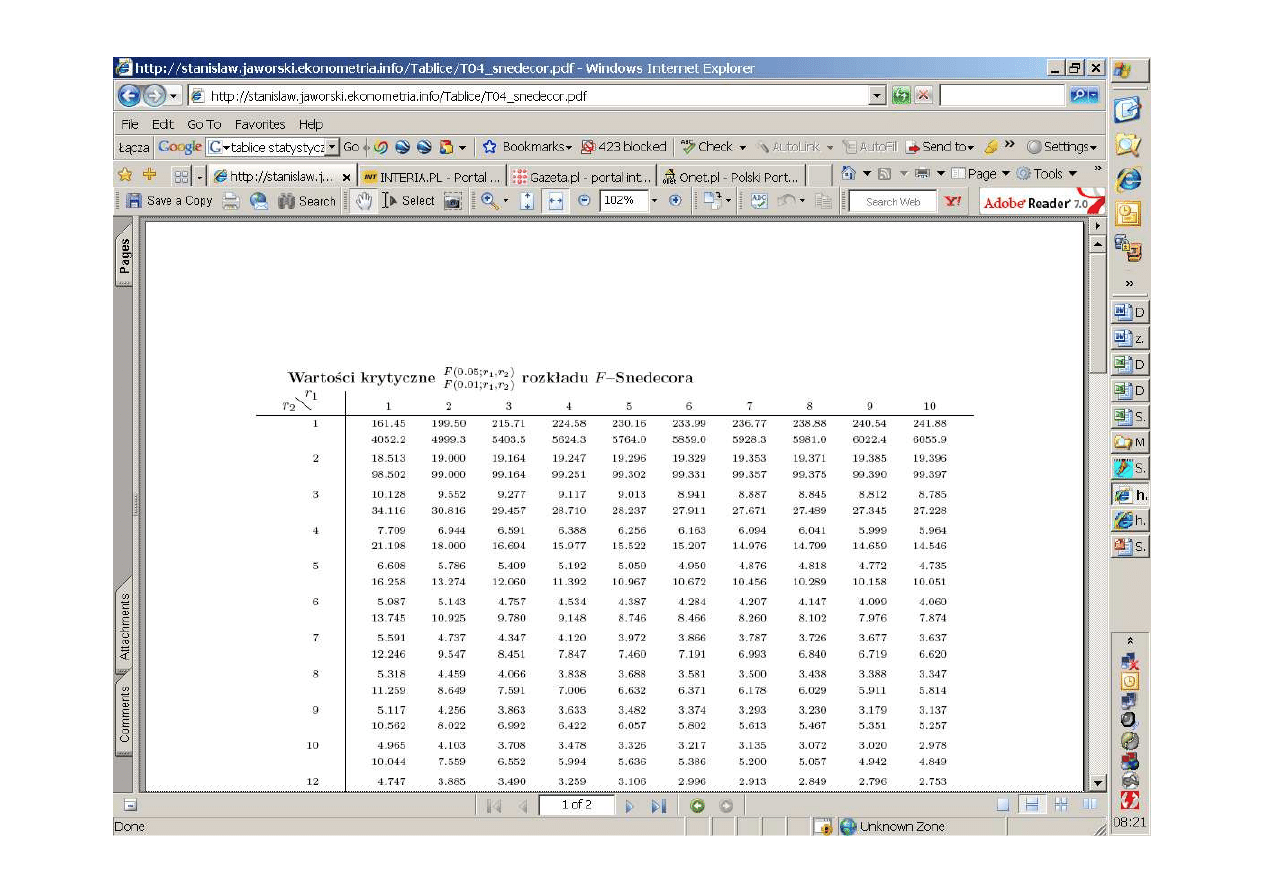
Rozkład F-Snedecora

(

)

1

,

1

2

1

−

−

n

n

F

Obszar krytyczny

Test równo

ś

ci dwóch wariancji

2

2

:

M

K

o

H

δ

δ

=

2

2

δ

δ

>

(160

160,

163,

165,

168,

170,

170,

173,

176,

178,

183, 186)

K K K K K K K M K M M M

86

,

30

ˆ

27

5

,

166

2

2

=

=

=

S

S

x

67

,

32

ˆ

5

,

24

180

2

2

=

=

=

S

S

x

Kobiety

M

ęż

czy

ź

ni

B. Gładysz 2007

05

,

1

86

,

30

67

,

32

=

=

F

2

2

1

:

K

M

H

δ

δ

>

( )

347

,

4

7

,

3

05

,

1

05

,

0

=

<

=

F

F

Nie ma podstaw do odrzucenia hipotezy
o jednakowym zró

ż

nicowaniu wzrostu m

ęż

czyzn i kobiet

0

H

B. Gładysz 2007

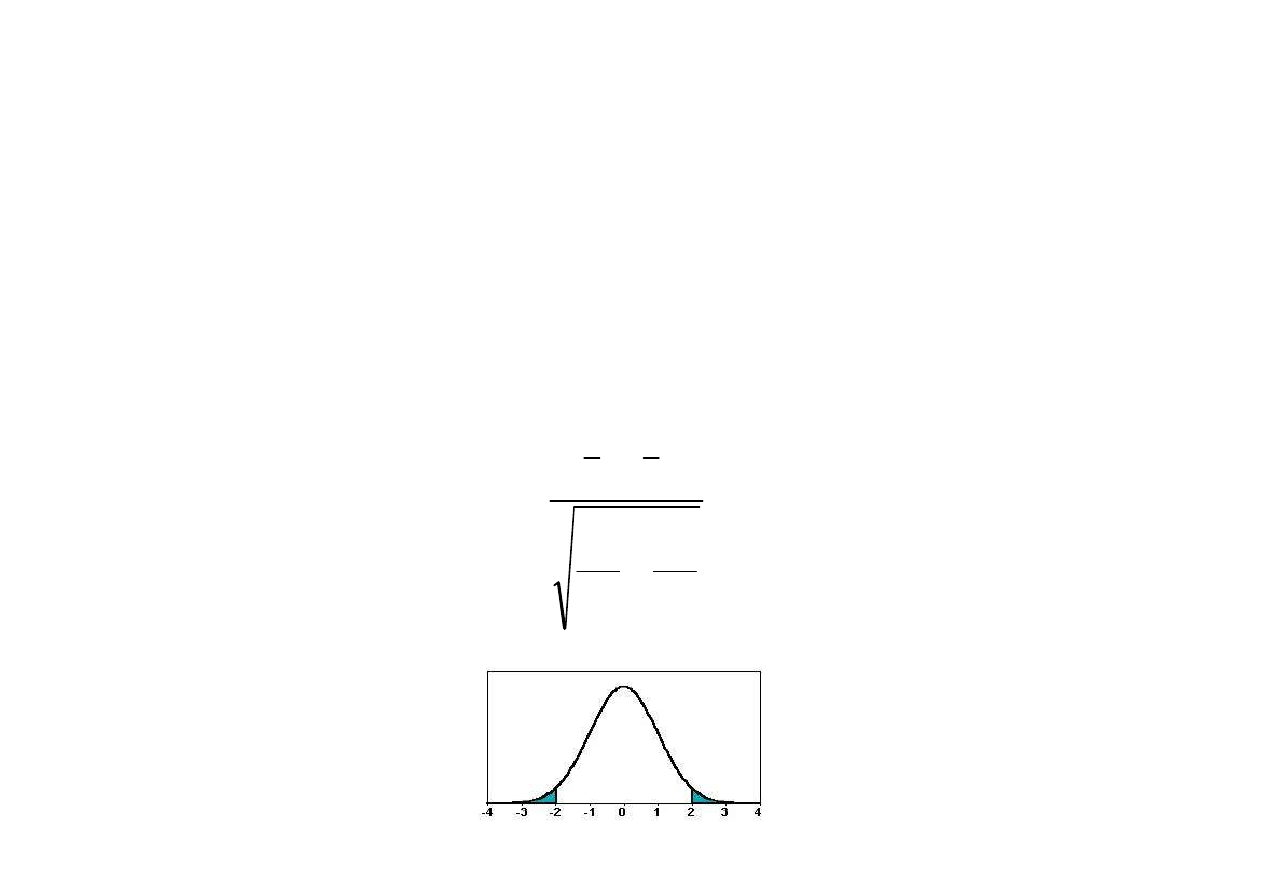
Test równo

ś

ci dwóch warto

ś

ci oczekiwanych

Zał.:

1. populacje maj

ą

rozkłady normalne

2. du

ż

e próby

2

1

0

:

m

m

H

=

2

1

1

:

m

m

H

≠

−

B. Gładysz 2007

rozkład normalny N(0,1)

Obszar krytyczny

2

2

2

1

2

1

2

1

n

n

x

x

u

σ

σ

+

−

=

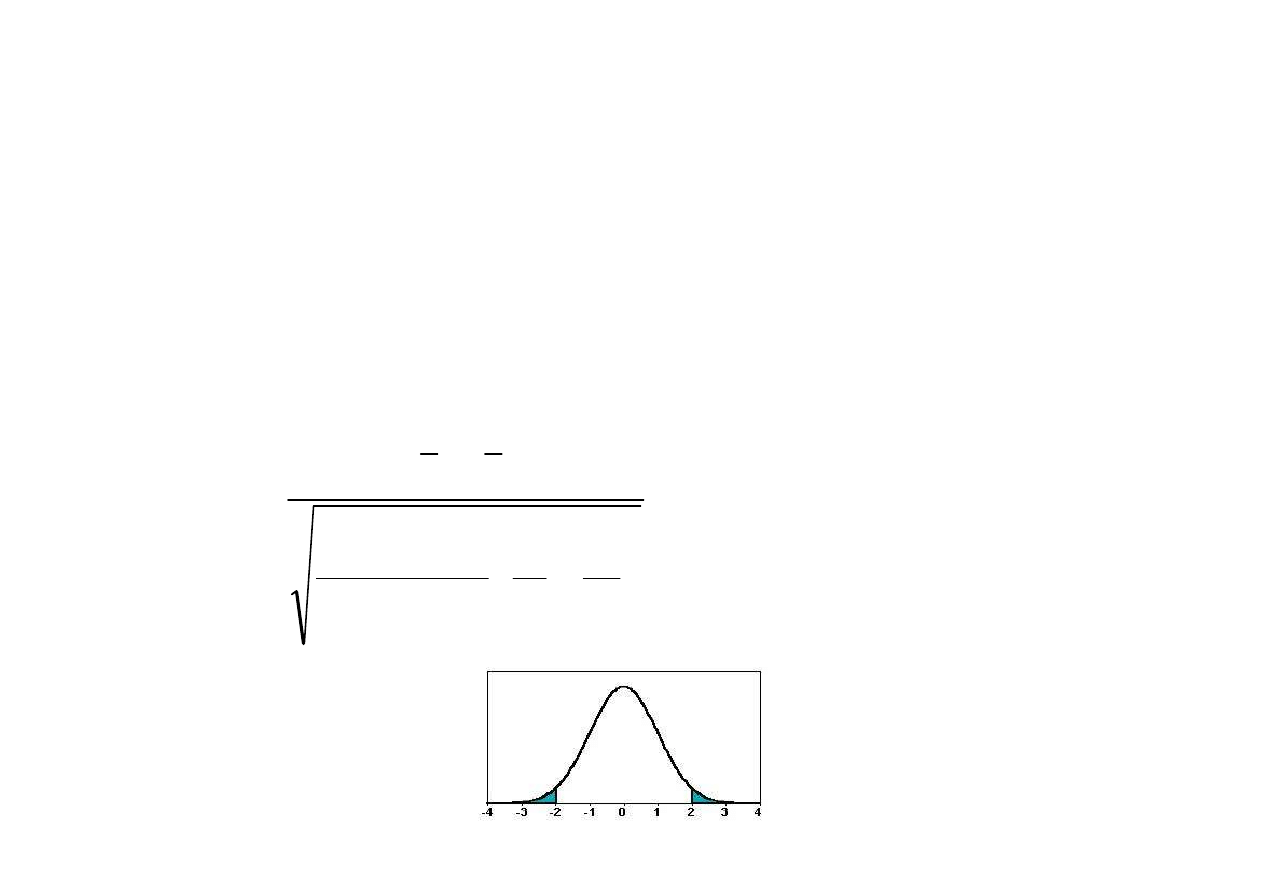
Test równo

ś

ci dwóch warto

ś

ci oczekiwanych

Zał.:

1. populacje maj

ą

rozkłady normalne

2. małe próby
3. jednakowe wariancje

2

1

0

:

m

m

H

=

2

1

1

:

m

m

H

≠

−

x

x

B. Gładysz 2007

rozkład t Studenta t(n

1

+n

2

-2)

Obszar krytyczny













+

−

+

+

−

=

2

1

2

1

2

2

2

2

1

1

2

1

1

1

2

n

n

n

n

S

n

S

n

x

x

t

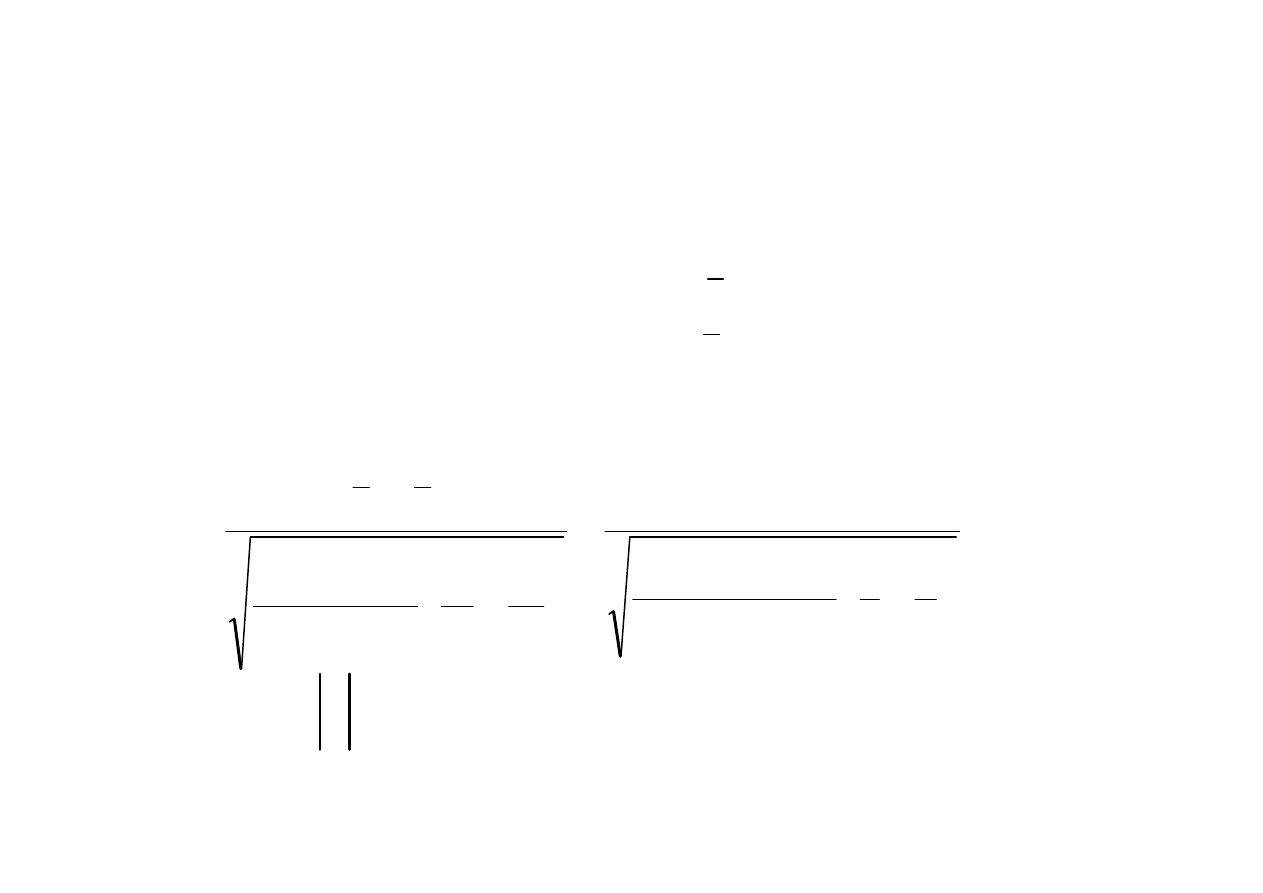
Test równo

ś

ci dwóch warto

ś

ci oczekiwanych

M

K

m

m

H

=

:

0

M

K

m

m

H

≠

:

1

(160

160,

163,

165,

168,

170,

170,

173,

176,

178,

183, 186)

K K K K K K K M K M M M

Kobiety

M

ęż

czy

ź

ni

86

,

30

ˆ

27

5

,

166

2

2

=

=

=

S

S

x

67

,

32

ˆ

5

,

24

180

2

2

=

=

=

S

S

x

B. Gładysz 2007

M

K

m

m

H

≠

:

1

93

,

3

4

1

8

1

2

4

8

5

,

24

4

27

8

180

5

,

166

1

1

2

2

1

2

1

2

2

2

2

1

1

2

1

−

=













+

−

+

⋅

+

⋅

−

=













+

−

+

+

−

=

n

n

n

n

S

n

S

n

x

x

t

( )

228

,

2

10

93

,

3

05

,

0

=

>

=

t

t

Odrzucamy hipotez

ę

o równo

ś

ci

ś

redniego wzrostu m

ęż

czyzn i kobiet

0

H

Test równo

ś

ci dwóch warto

ś

ci oczekiwanych

M

K

m

m

H

=

:

0

M

K

m

m

H

<

:

1

93

,

3

180

5

,

166

2

1

−

=

−

=

−

=

x

x

t

(160

160,

163,

165,

168,

170,

170,

173,

176,

178,

183, 186)

K K K K K K K M K M M M

B. Gładysz 2007

93

,

3

4

1

8

1

2

4

8

67

,

32

4

86

,

30

8

1

1

2

2

1

2

1

2

2

2

2

1

1

−

=













+

−

+

⋅

+

⋅

=













+

−

+

+

=

n

n

n

n

S

n

S

n

t

( )

812

,

1

10

93

,

3

05

,

0

−

=

<

−

=

t

t

Odrzucamy hipotez

ę

na korzy

ść

hipotezy

ś

redni wzrost kobiet jest mniejszy od

ś

redniego

wzrostu m

ęż

czyzn

1

H

0

H

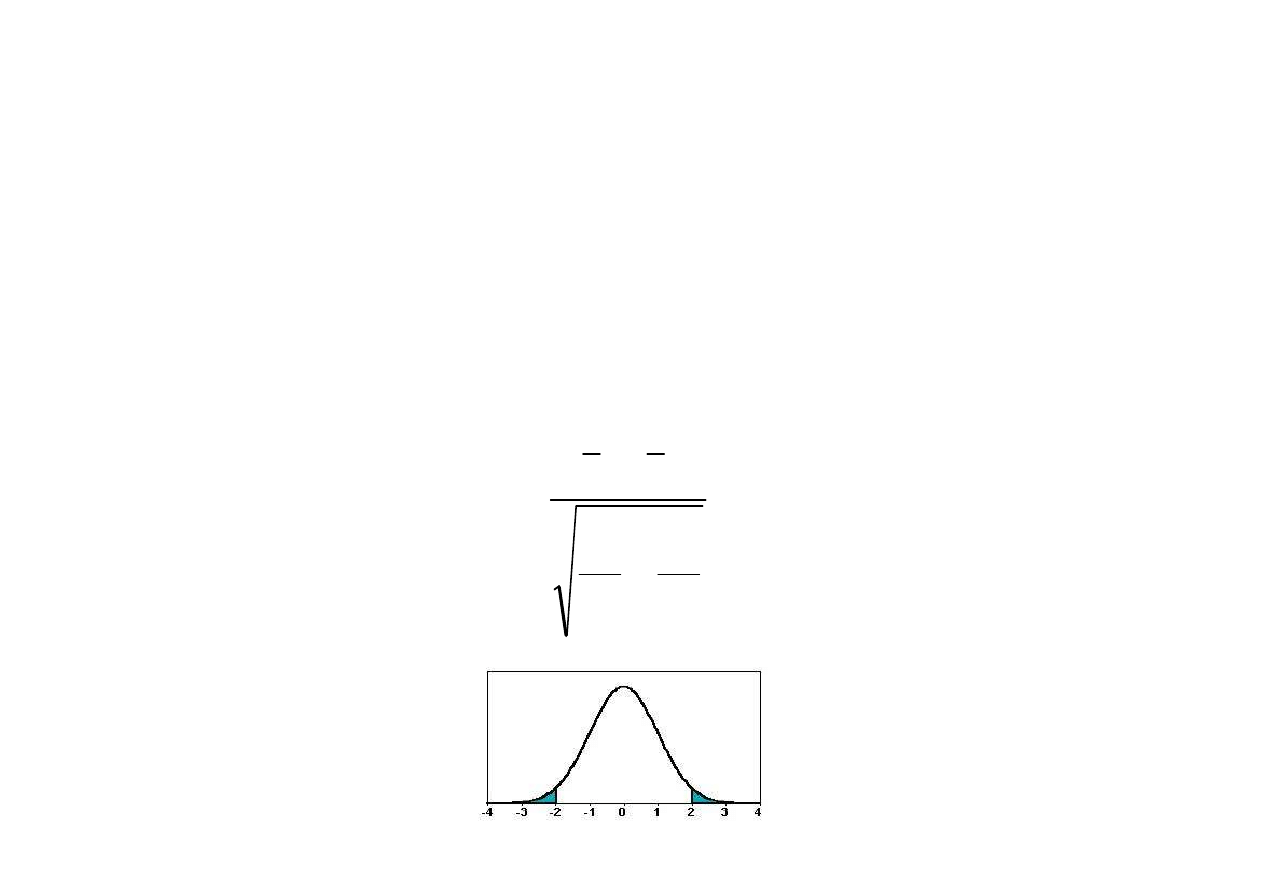
Test równo

ś

ci dwóch warto

ś

ci oczekiwanych

Zał.:

1. populacje maj

ą

rozkłady normalne lub zbli

ż

one do normalnego

2. du

ż

e próby

2

1

0

:

m

m

H

=

2

1

1

:

m

m

H

≠

x

x

−

B. Gładysz 2007

rozkład normalny N(0,1)

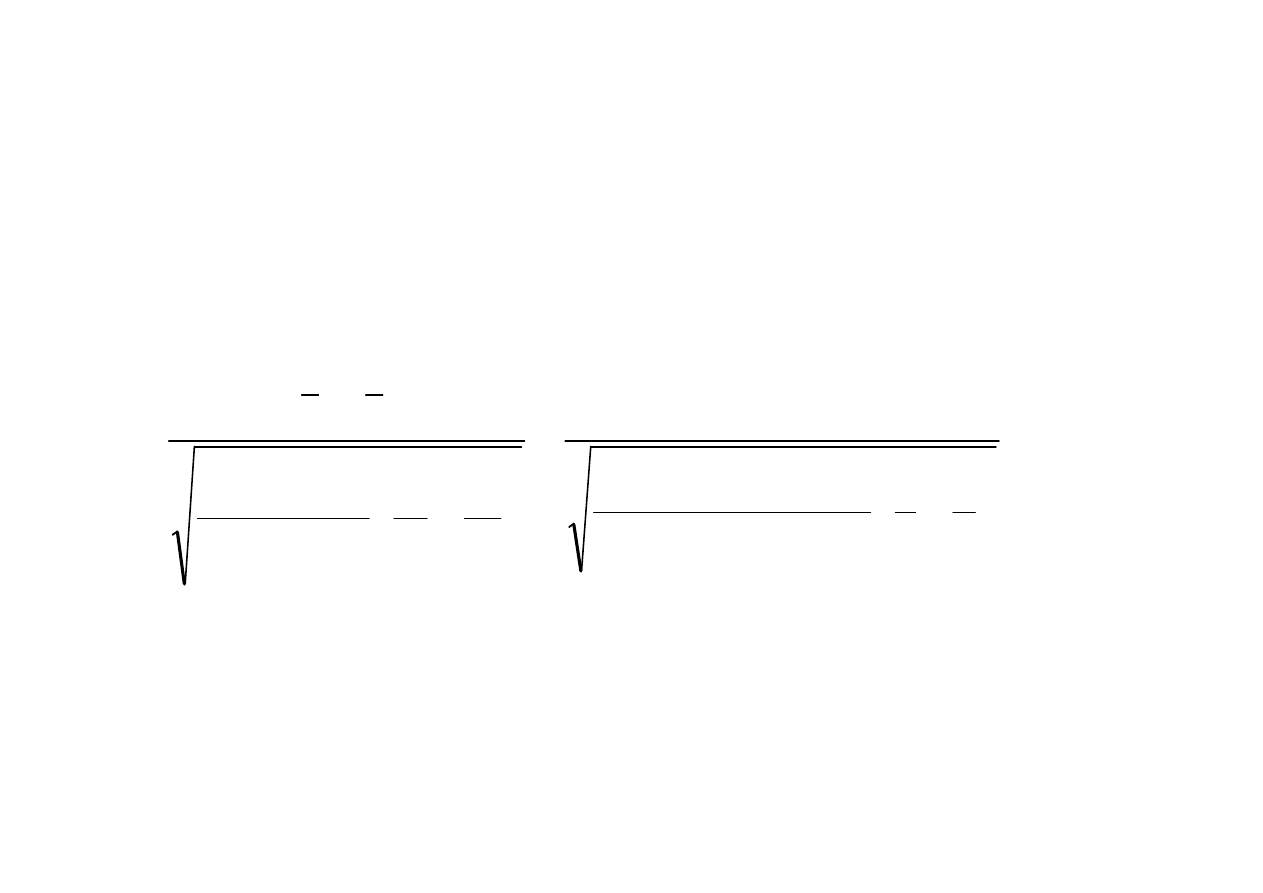
Obszar krytyczny

2

2

2

1

2

1

2

1

n

S

n

S

x

x

u

+

−

=

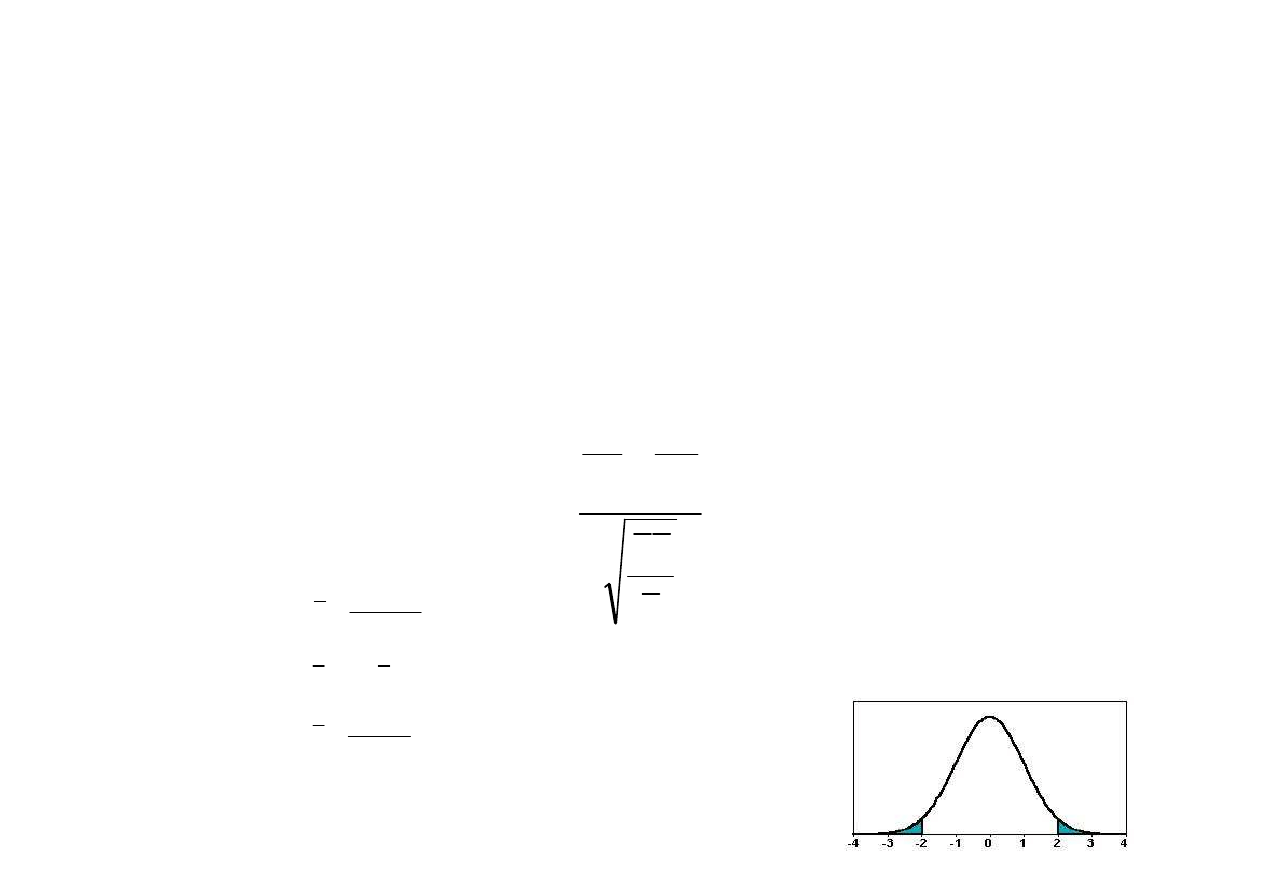
Test równo

ś

ci dwóch frakcji

Zał.:

1. populacje maj

ą

rozkłady dwupunktowe

2. du

ż

e próby (n

1

, n

2

>100

2

1

0

:

p

p

H

=

2

1

1

:

p

p

H

≠

m

m

2

1

−

B. Gładysz 2007

rozkład normalny N(0,1)

Obszar krytyczny

n

q

p

n

m

n

m

u

2

2

1

1

−

=

2

1

2

1

2

1

2

1

1

n

n

n

n

n

p

q

n

n

m

m

p

+

⋅

=

−

=

+

+

=

gdzie: