4/ 1

DYNAMIKA

„Phylosophiae naturalis principia mathematica”

(1687)

Pojęcia przestrzeni, czasu, układu odniesienia,
masy, siły, pędu, ...

Układ odosobniony to układ zamknięty, nie
mogący wymieniać materii z otoczeniem i nie
podlegający żadnym oddziaływaniom z zewnątrz.
Na układ taki nie może działać siła zewnętrzna,
która

powodowałaby

jego

przyciąganie

lub

odpychanie.

4/ 2

Zasady dynamiki Newtona

I zasada dynamiki Newtona:

Istnieje taki układ odniesienia, zwany układem
inercjalnym, w którym ciało lub układ odosobniony
porusza się ruchem jednostajnym prostoliniowym
lub pozostaje w spoczynku.

II zasada dynamiki Newtona:

Siła

F

r

działająca na ciało lub układ ciał jest

przyczyną zmiany jego pędu

/dt

p

d

F

r

r

=

Siła jest miarą oddziaływania, jest wielkością
fizyczną pochodną, którą definiujemy przy
pomocy jej skutków, posługując się wcześniej
zdefiniowanymi wielkościami.

a

m

F

r

r

=

[1N = 1 kg m s

–2

]

F

F

F

2

1

r

r

r

+

=

4/ 3

Zasada przyczynowości

Z II zasady dynamiki mamy:

/dt, t)

r

, d

r

(

F

dt

r

d

m

r

r

r

r

=

2

2

Zasada przyczynowości

Znajomość sił działających i warunków
początkowych umożliwia nam znalezienie
jednoznacznego opisu stanu ruchu cząstki
w dowolnej chwili.

Niezależność ruchów

z

y

x

F

F

F

F

r

r

r

r

+

+

=

to

z

y

x

z

y

x

z

y

x

r

r

r

r

v

v

v

v

a

a

a

a

r

r

r

r

r

r

r

r

r

r

r

r

+

+

=

+

+

=

+

+

=

w układach inercjalnych.

4/ 4

Trzecia zasada dynamiki Newtona

(zasada akcji i reakcji)

Gdy dwa ciała na siebie oddziaływają to siła F

12

wywierana przez ciało (1) na ciało (2) jest równa
sile F

21

wywieranej przez ciało (2) na ciało (1) lecz

jest przeciwnie skierowana.

21

12

F

-

F

r

r

=

Oddziaływania między cząstkami są przenoszone
przez pola fizyczne i nie rozchodzą się momentalnie

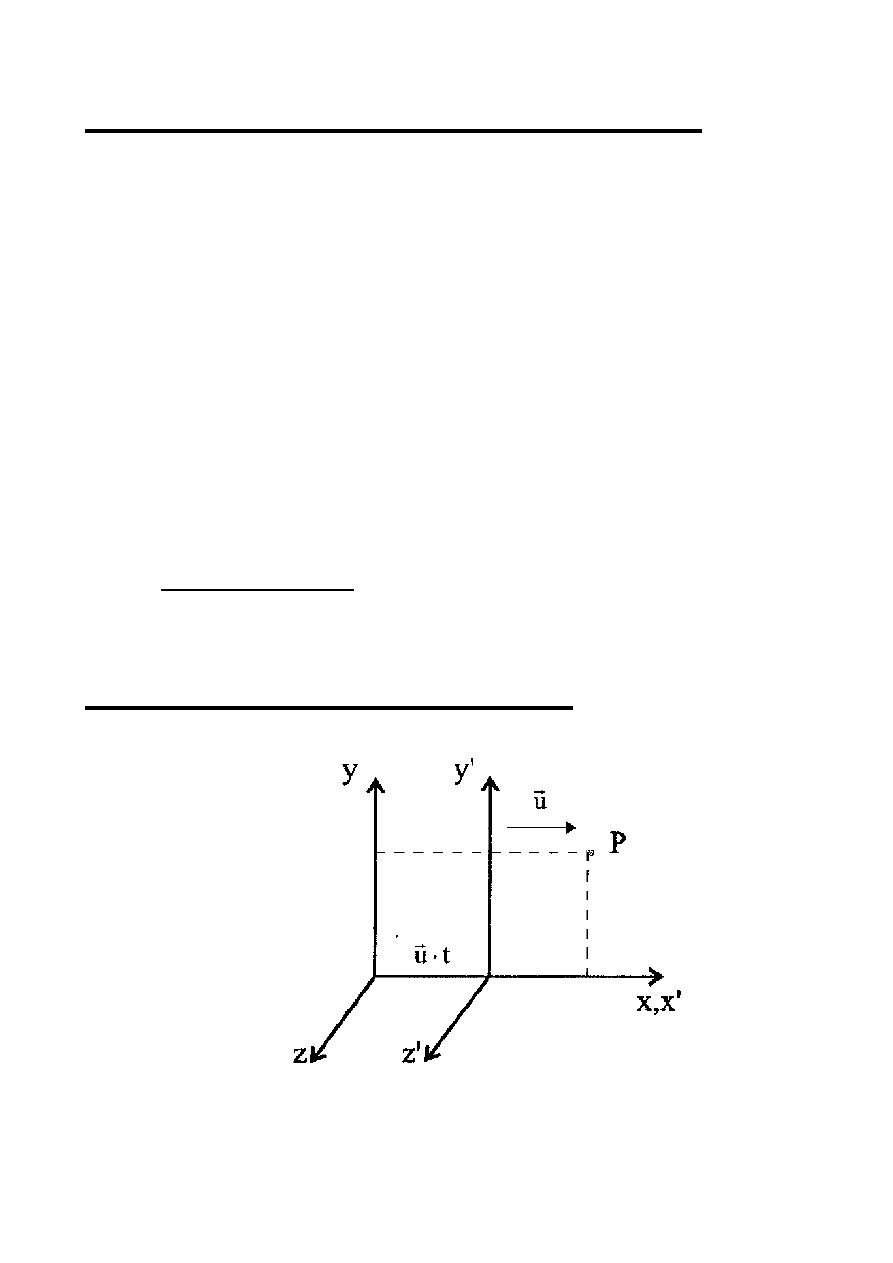
Transformacja

Galileusza

t

u

r

r

r

r

r

+

=

'

4/ 5

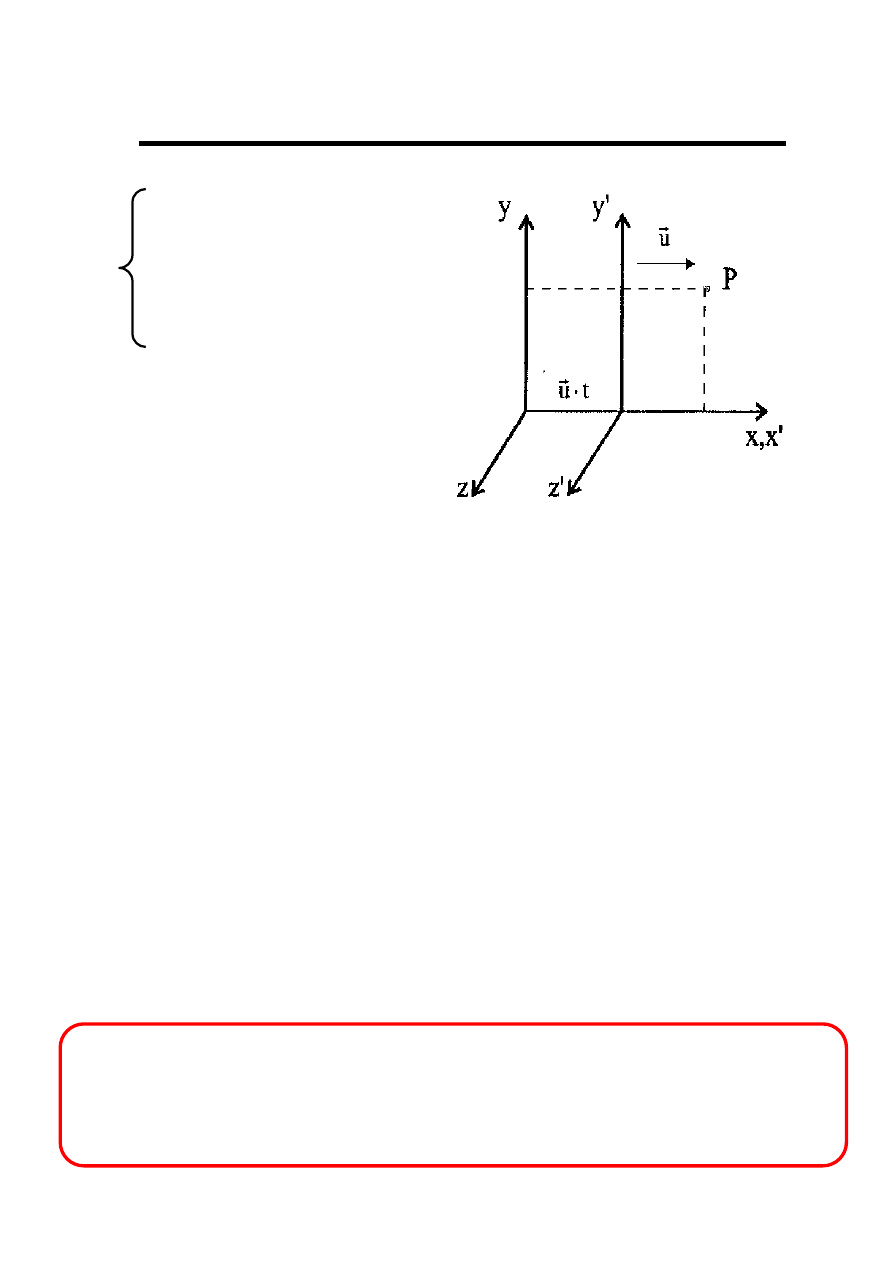
Niezmienniczość Galileusza

x’ = x – ut
y’ = y
z’ = z
t’ = t

v

x

’ = v

x

- u

v

y

’ = v

y

v

z

’ = v

z

a

x

’ = a

x

a

y

’ = a

y

a

z

’ = a

z

u

v

v

r

r

r

−

=

'

a

a

r

r

=

'

Odległość między dwoma punktami:

l = [(x

2

– x

1

)

2

+ (y

2

– y

1

)

2

+ (z

2

– z

1

)

2

]

1/2

l’ = [(x

2

’ – x

1

’)

2

+ (y

2

’ – y

1

’)

2

+ (z

2

‘ – z

1

’)

2

]

1/2

l = l’

Ponieważ

m’ = m

oraz

a

m

F

r

r

=

F

F

r

r

=

'

Zasady mechaniki newtonowskiej są takie
same w każdym inercjalnym układzie
odniesienia.