- 1 -

2. PODSTAWY TEORII OBWODÓW

ELEKTRYCZNYCH

2.1. PODSTAWOWE WIELKOŚCI ELEKTRYCZNE

NAPIĘCIE ELEKTRYCZNE

Różnicę potencjałów dwóch punktów A i B pola elektrycznego

nazywamy

napięciem elektrycznym u

między tymi punktami,

B

A

AB

V

V

u





(2.1)

Ponieważ napięcie elektryczne





BA

A

B

B

A

AB

u

V

V

V

V

u















(2.2)

jest wielkością skalarną opatrzoną znakiem, nazywamy je skalarem
zwrotnym. Jednostką napięcia elektrycznego jest wolt (V).

UWAGA:

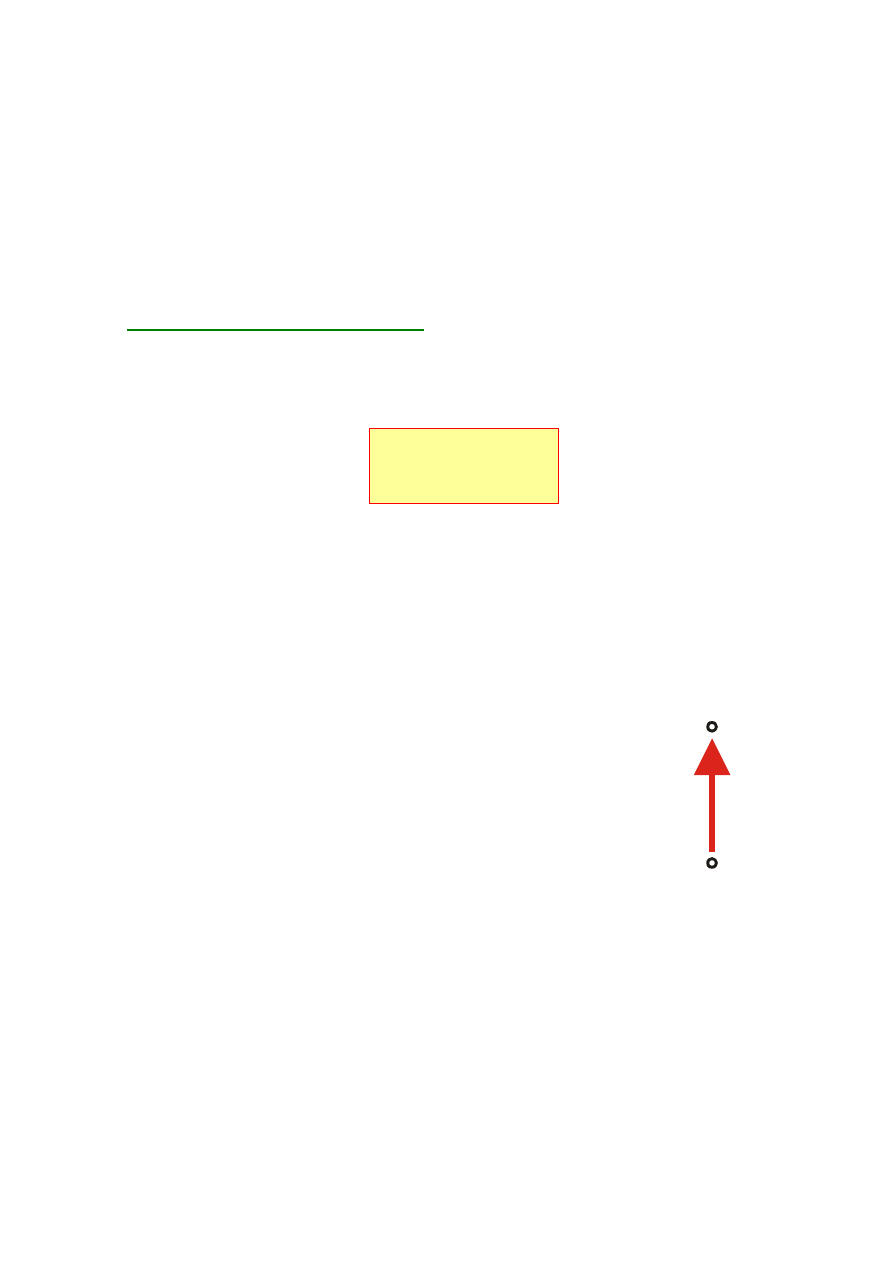
Przyjmuje się, że strzałka na-pięcia
związana

z

dwoma

punktami

środowiska, posiada grot skierowany
do punktu o wyższym potencjale. Jeśli
punkt, do którego skierowany jest grot
strzałki napięcia posiada potencjał
niższy to oznacza, że wartość tego
napięcia jest ujemna.

A

B

u

AB

V

A

V

B

V

A

> V

B

Strzałkowanie napięcia

- 2 -

PRĄD ELEKTRYCZNY

Pod pojęciem prąd elektryczny, rozumiemy:

 zjawisko uporządkowanego ruchu ładunków elektrycznych

przez badany przekrój poprzeczny środowiska występujące pod
wpływem działającego pola elektrycznego;

 wielkość skalarną stanowiącą skrót terminu natężenie prądu

elektrycznego.

Natężeniem prądu elektrycznego i

nazywamy granicę stosunku

ładunku elektrycznego



q przenoszonego przez cząstki naładowane

w ciągu pewnego czasu



t poprzez dany przekrój poprzeczny środowiska,

do rozpatrywanego czasu, gdy czas ten dąży do zera, tzn.

t

d

q

d

t

q

i

t









0

lim

(2.3)

Jednostką prądu elektrycznego jest amper (A), [i] = 1A = 1C/1s.

UWAGA:

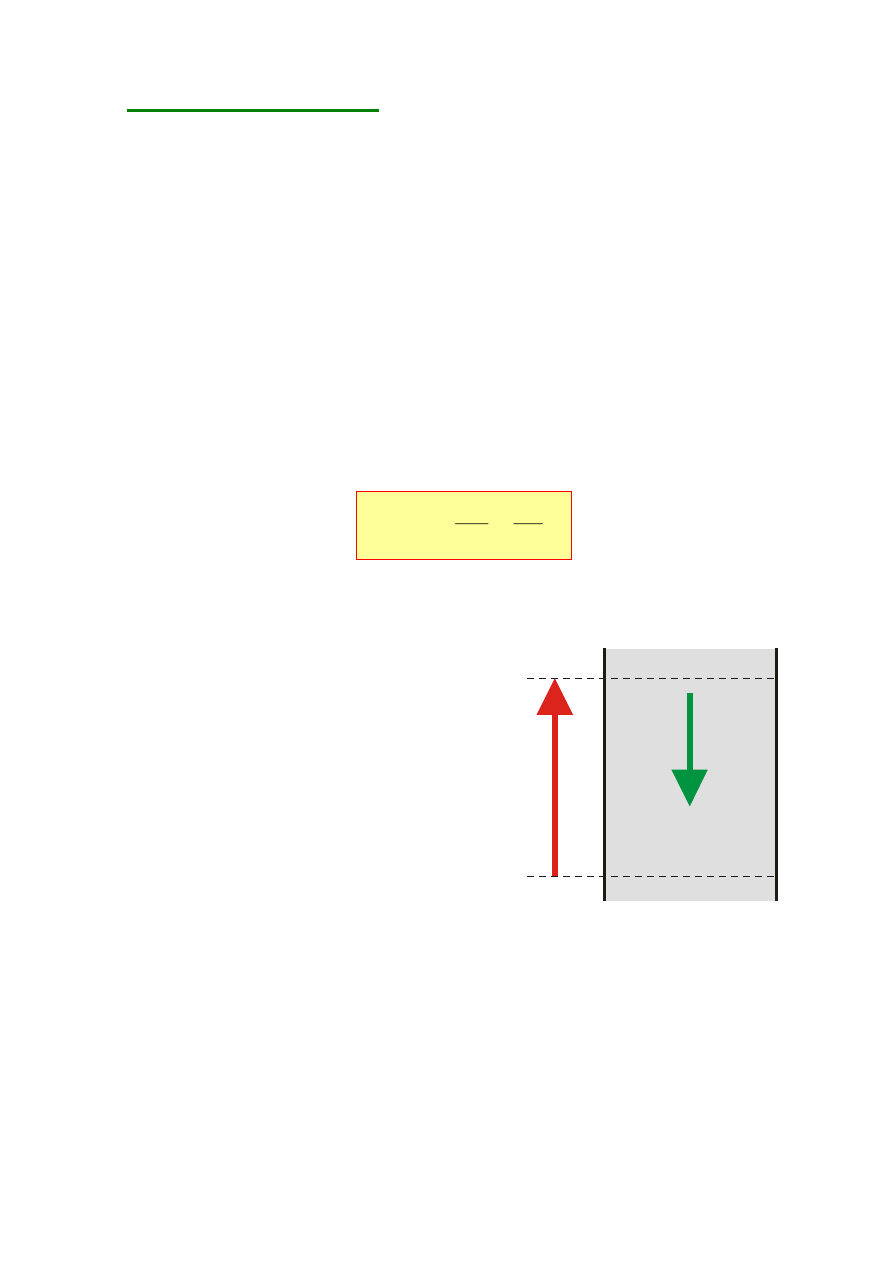
Prąd elektryczny jest skalarem
zwrotnym – oznacza się go za
pomocą

strzałki

o

grocie

skierowanym do obszaru o
niższym

potencjale

(strzałka

prądu wskazuje umowny kierunek
przepływu ładunku dodatniego), a
więc

prąd

strzałkuje

się

odwrotnie niż napięcie.

u

i

środowisko w którym

występuje prąd

Strzałkowanie prądu

- 3 -

MOC I ENERGIA ELEKTRYCZNA

Z każdym elementem przewodzącym, oprócz prądu i oraz napięcia u,

związana jest także moc p określona wzorem

i

u

p



(2.4)

Ponieważ u = u(t), i = i(t), zatem także p = p(t), co podkreśla się

często mówiąc

moc chwilowa

. Jednostką mocy jest wat (W).

Przy standardowym strzałkowaniu prądu oraz napięcia moc określona

zależnością (2.4) jest mocą pobieraną przez element z otoczenia.

Jeśli w chwili t

0

0

)

(

0



t

p

0

)

(

0



t

p

oznacza to, że moc jest faktycznie

pobierana

przez element z otoczenia

oddawana

przez element do otoczenia

Energia pobrana

przez element w przedziale czasu od t

1

do t

2

jest

całką z mocy pobieranej. Oznaczając ją symbolem W(t

1

, t

2

) piszemy:





 

dt

t

p

t

t

W

t

t





2

1

2

1

,

(2.5)

Jeśli

W(t

1

, t

2

) > 0

W(t

1

, t

2

) < 0

oznacza to, że w przedziale czasu < t

1

, t

2

> element faktycznie

pobrał

energię z otoczenia

oddał

energię do otoczenia

- 4 -

2.2. PARAMETRY PIERWOTNE I ELEMENTY IDEALNE

Parametry pierwotne opisują podstawowe zjawiska fizyczne

występujące w układzie elektrycznym

Parametry pierwotne (cechy fizyczne) są mierzalne.

Elementy idealne to takie elementy, w których zachodzi tylko jedno

zjawisko fizyczne. Każdy element idealny charakteryzowany jest

tylko jednym parametrem pierwotnym

REZYSTANCJA R

Jest to wielkość fizyczna charakteryzująca zdolność układu do

(jednokierunkowej) zamiany energii elektrycznej na energię cieplną
(DYSYPACJA - ROZPRASZANIE).

Rezystancję można definiować w oparciu o moc rozpraszaną p

R

(t):

 

 

t

i

t

p

R

R

df

2



(2.6)

Jednostką rezystancji jest om (

).

Często posługujemy się innym parametrem zwanym konduktancją G,

związaną z rezystancją relacją

R G = 1

(2.7)

jednostką konduktancji jest simens (S), [G] = 1S = 1



-1

.

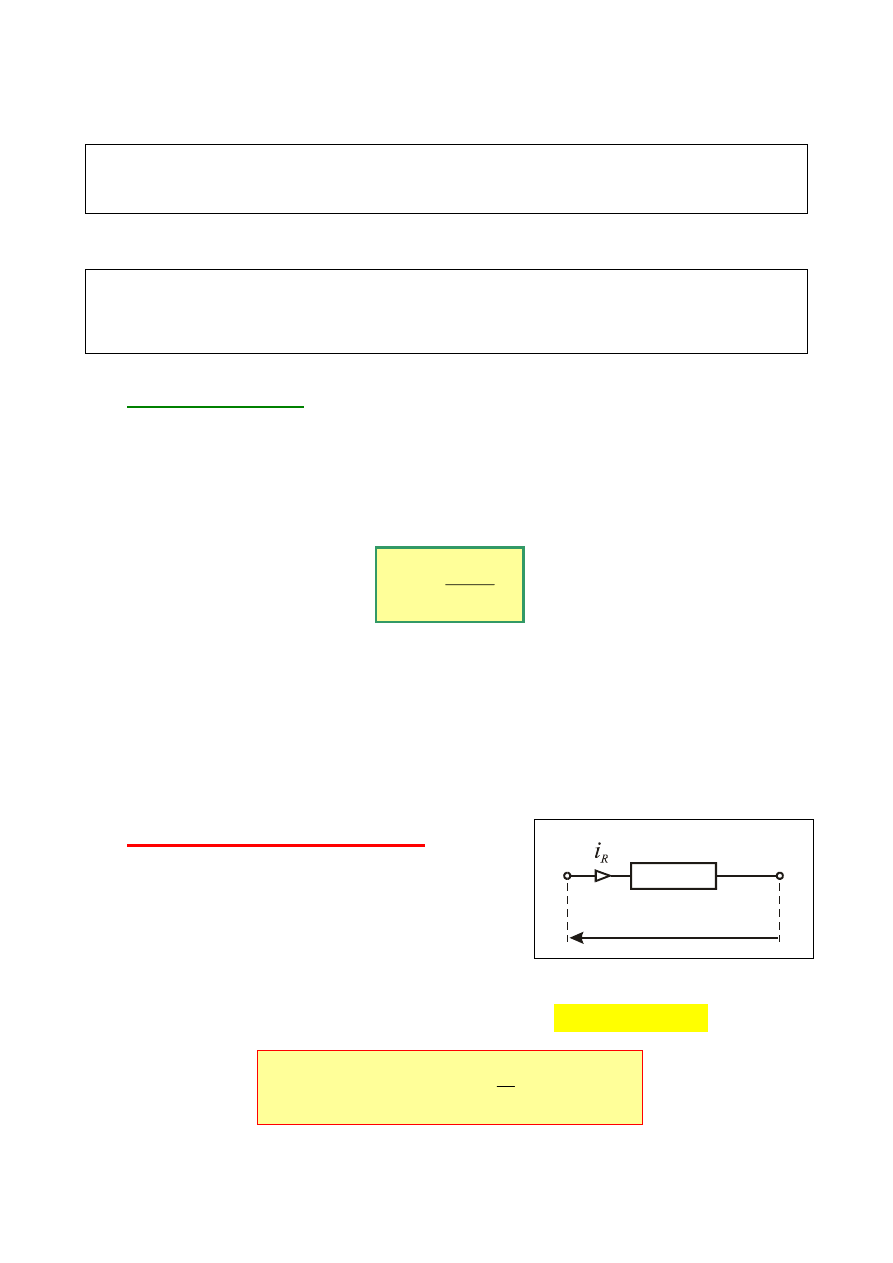
IDEALNY

REZYSTOR

jest

elementem o dwóch zaciskach, w którym
zachodzi jedynie proces dysypacji energii
elektrycznej.

Oznacza

to,

że

jest

charakteryzowany tylko rezystancją R.

u

R

R

Między prądem i napięciem (parą wielkości zaciskowych) idealnego

rezystora występuje proporcjonalność wyrażona

prawem Ohma

R

R

R

R

R

u

G

u

R

i

i

R

u







1

lub

(2.8)

- 5 -

INDUKCYJNOŚĆ L

Jest to wielkość fizyczna charakteryzująca zdolność układu do

wytwarzania pola magnetycznego (gromadzenia energii w polu
magnetycznym - AKUMULACJA).

.

const

i

L

df







(2.9)

Jednostką indukcyjności jest henr (H), [L]=1Wb/1A=1V

1s/1A=11s=1H

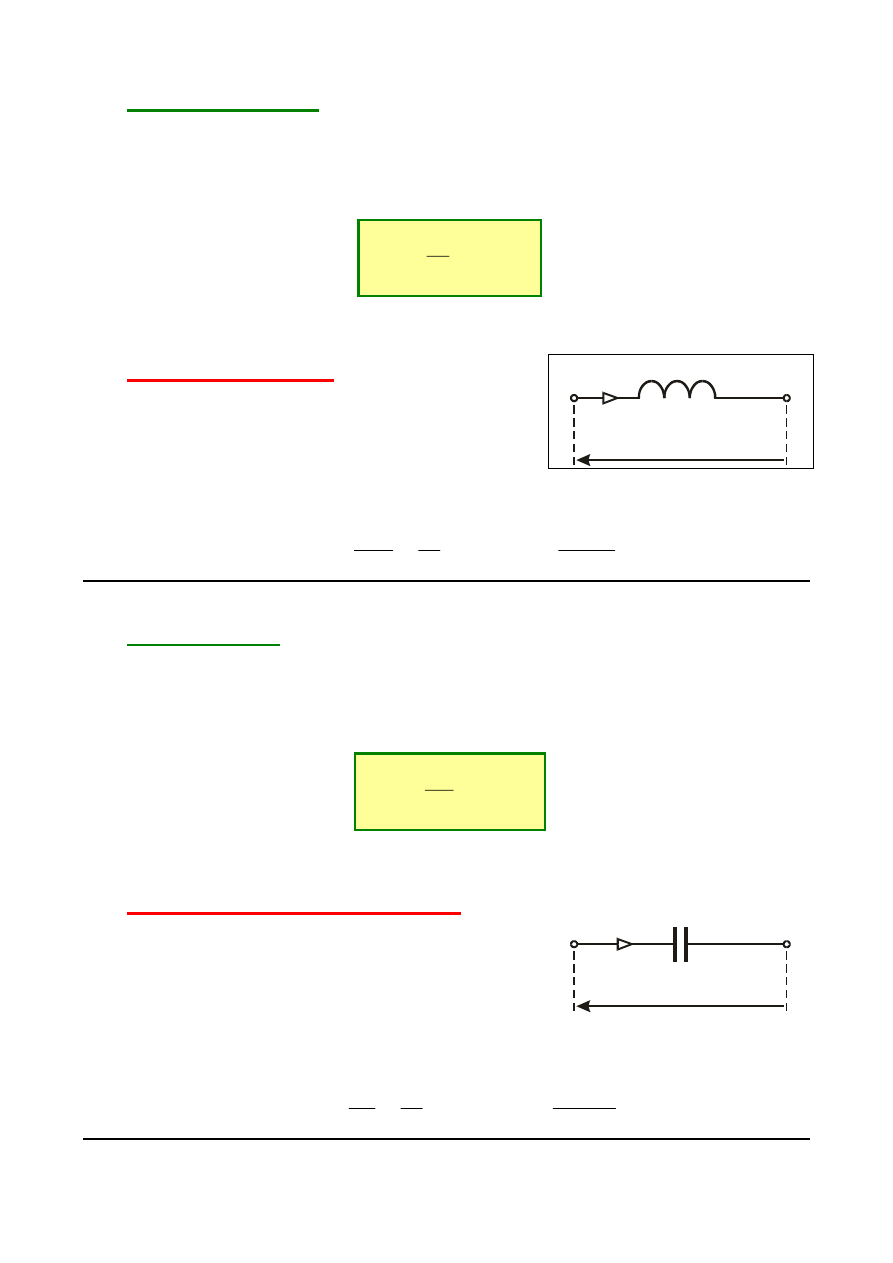
IDEALNA CEWKA

jest dwójnikiem, w

którym zachodzi jedynie proces akumulacji
energii w polu magnetycznym. Oznacza to, że
opisuje ją tylko indukcyjność L.

u t

L

( )

L

i t

L

( )

Napięcie na zaciskach cewki opisuje zależność:

 

 





 

dt

t

i

d

L

t

i

L

dt

d

dt

d

t

u

L

L

L









(2.10)

POJEMNOŚĆ C

Wielkość określająca zdolność układu do gromadzenia ładunku

elektrycznego pod wpływem przyłożonego napięcia - lub inaczej do
gromadzenia energii w polu elektrycznym (AKUMULACJA).

.

const

u

q

C

df





(2.11)

Jednostką pojemności jest farad (F), [C] = 1C/1V = 1A

1s/1V = 1F.

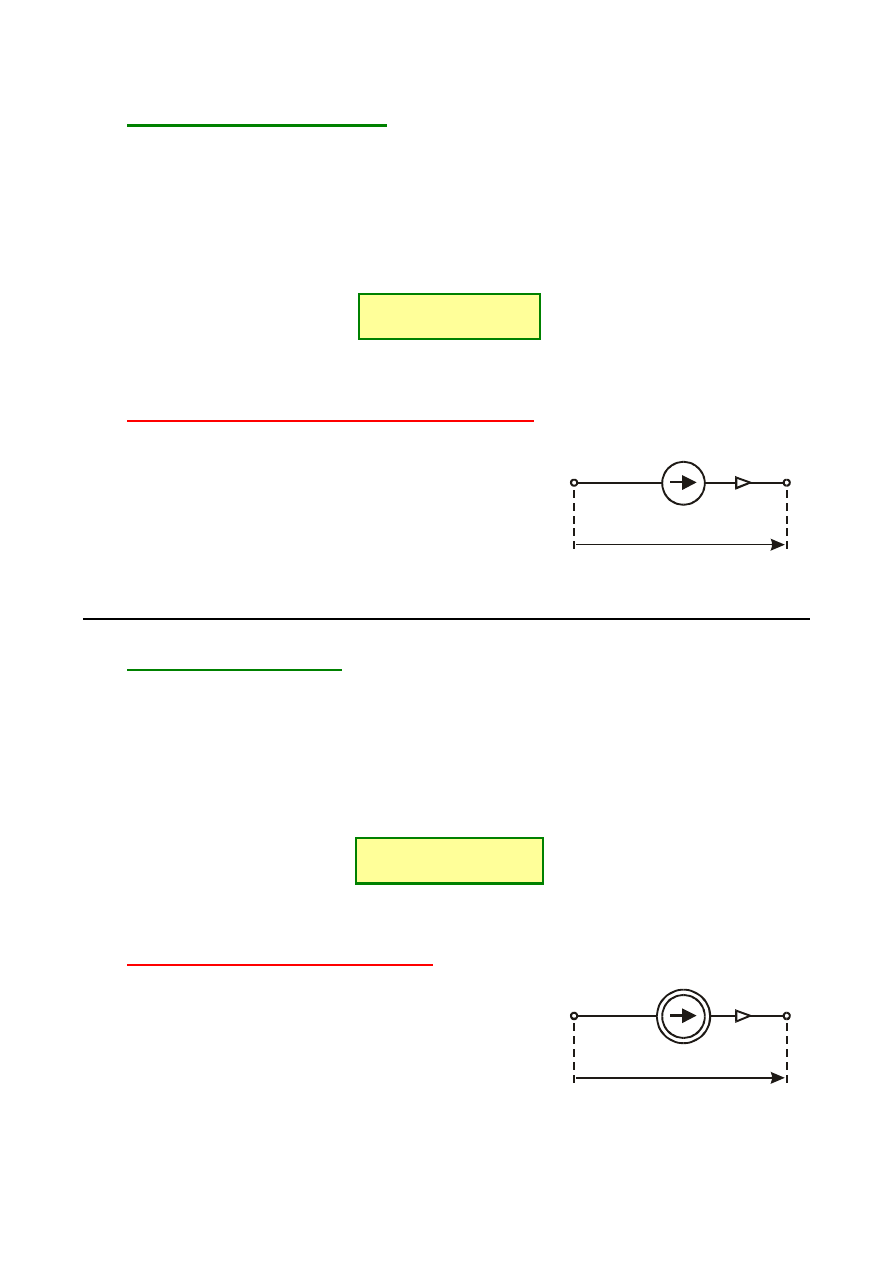
IDEALNY

KONDENSATOR

jest

dwójnikiem, w którym zachodzi jedynie
proces

akumulacji

energii

w

polu

elektrycznym. Oznacza to, że opisuje go tylko
pojemność C.

u t

C

( )

C

i t

C

( )

Prąd kondensatora opisuje zależność:

 

 





 

dt

t

du

C

t

u

C

dt

d

dt

dq

t

i

C

C

C







(2.12)

- 6 -

NAPIĘCIE ŹRÓDŁOWE

u

0

jest parametrem, występującego w układzie elektrycznym, procesu

przemiany innego rodzaju energii (mechanicznej, chemicznej, świetlnej
itp.) w energię elektryczną, a zatem jest parametrem opisującym własności
generacyjne występujące w układzie. Tę własność niezależną od innych
uwarunkowań układu opisuje zależność

 

 

t

u

t

u

i

0





(2.13)

Jednostką napięcia źródłowego jest wolt (V).

IDEALNE

ŹRÓDŁO

NAPIĘCIA

element o dwóch końcówkach (zaciskach), w
którym zachodzi wyłącznie generacja energii
uzewnętrzniająca się pod postacią napięcia
źródłowego u

0

(występującego pomiędzy

zaciskami

elementu),

niezależnego

od

obciążenia (prądu w układzie).

u t

( )

i t

( )

u t

0

( )

PRĄD ŹRÓDŁOWY

i

Z

Własności generacyjne układu elektrycznego mogą być również

charakteryzowane parametrem nazywanym natężeniem prądu źródłowego
lub krótko - prądem źródłowym.

Wartość parametru zwanego prądem źródłowym jest niezależna od

stanu pracy układu elektrycznego, co zapiszemy w postaci

 

 

Z

Z

u

t

i

t

i





(2.14)

Jednostką prądu źródłowego jest amper (A).

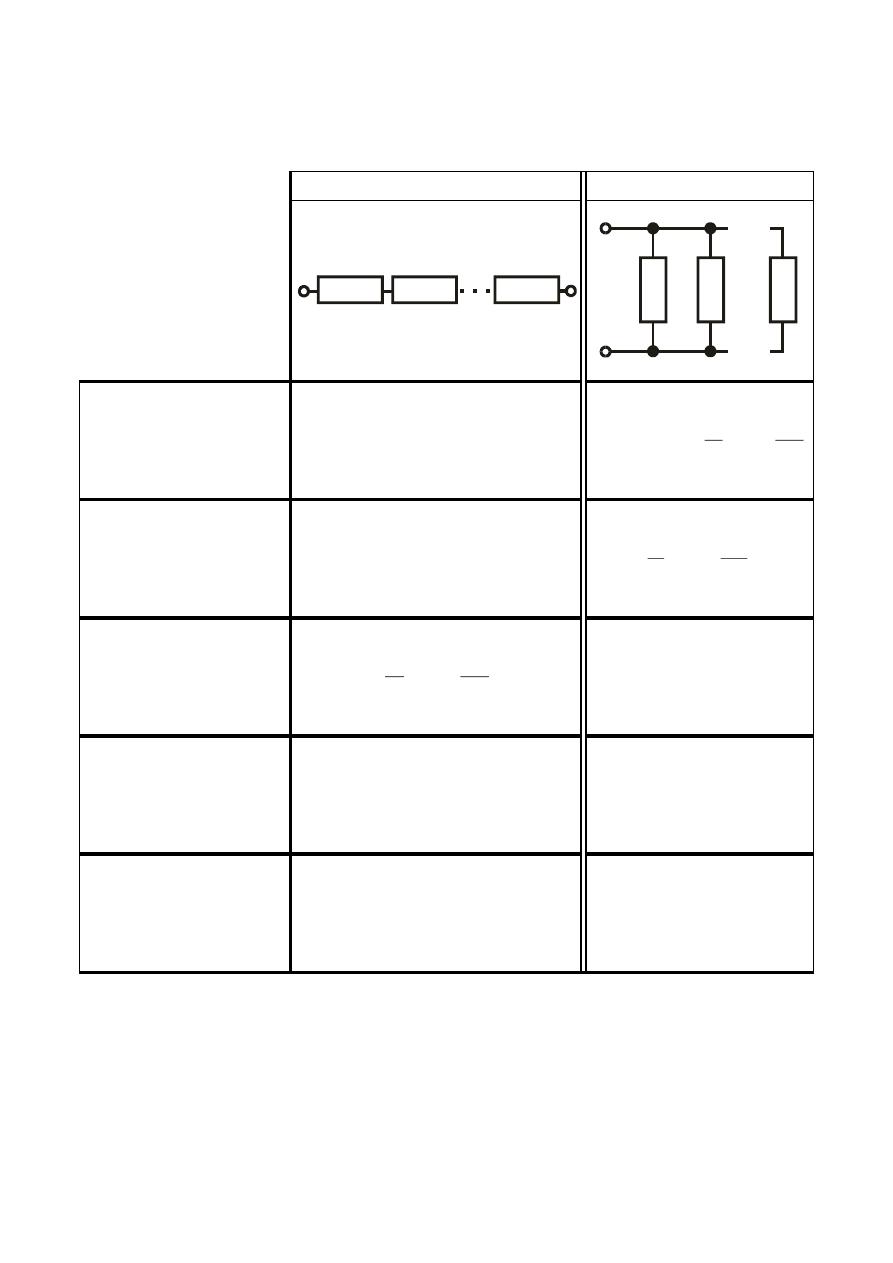
IDEALNE ŹRÓDŁO PRĄDU

element o

dwóch końcówkach (zaciskach), w którym
zachodzi

wyłącznie

generacja

energii

uzewnętrzniająca się pod postacią prądu
źródłowego i

Z

niezależnego od obciążenia

(napięcia na zaciskach).

u t

( )

i t

( )

i t

Z

( )

- 7 -

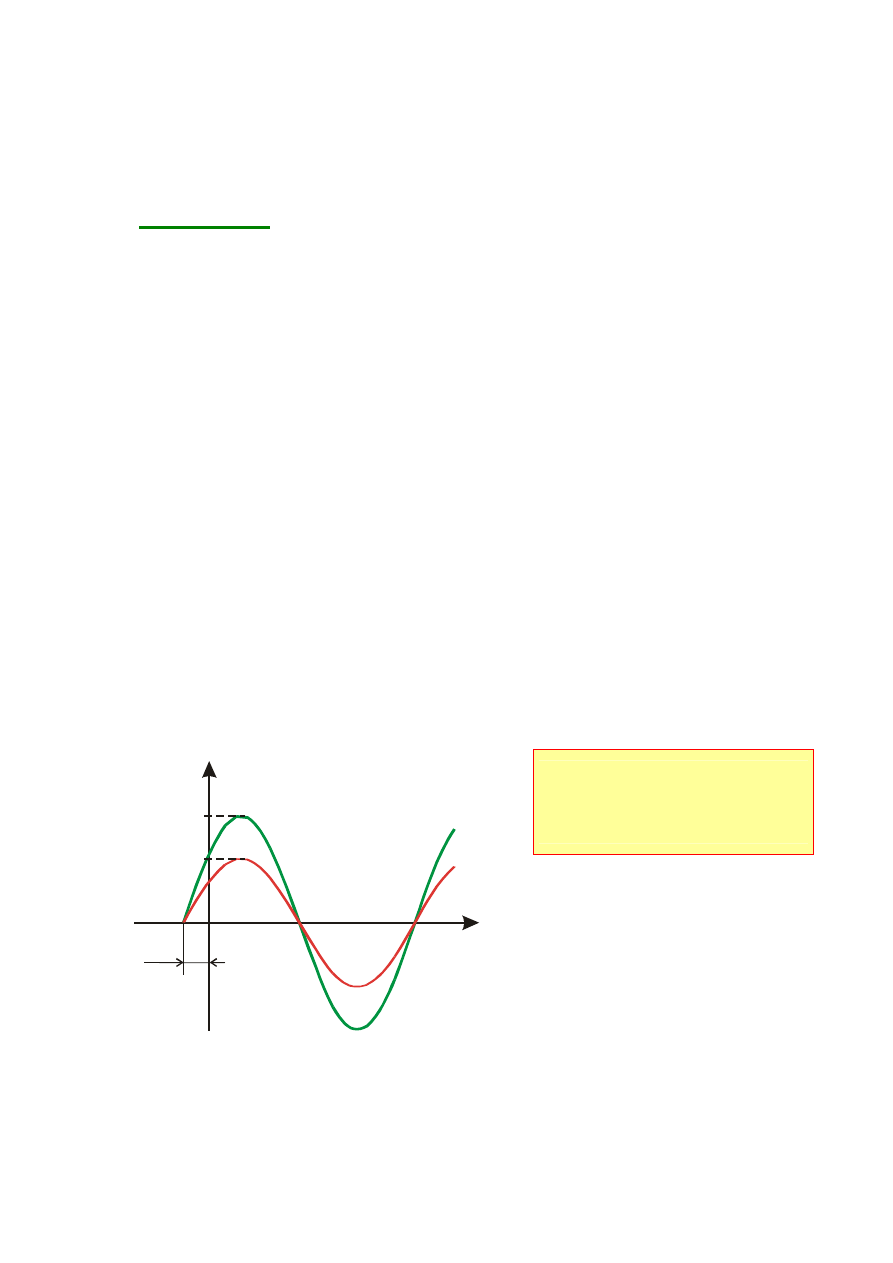
2.3.

ŁĄCZENIE ELEMENTÓW IDEALNYCH

SZEREGOWE

RÓWNOLEGŁE

1

2

n

...

...

1

2

n

REZYSTORÓW







n

k

k

R

R

1













n

k

k

n

k

k

R

R

G

G

1

1

1

1

;

CEWEK







n

k

k

L

L

1







n

k

k

L

L

1

1

1

KONDENSATORÓW







n

k

k

C

C

1

1

1







n

k

k

C

C

1

ŹRÓDEŁ

NAPIĘCIA







n

k

k

u

u

1

0

0

możliwe tylko w jednym

przypadku

ŹRÓDEŁ

PRĄDU

możliwe tylko w jednym

przypadku







n

k

k

Z

Z

i

i

1

- 8 -

2.4. ELEMENTY R, L, C W OBWODACH PRĄDU

HARMONICZNEGO



REZYSTOR

Przy występowaniu prądu harmonicznego

 





i

m

t

I

t

i









sin

(2.15)

w rezystorze o rezystancji R, na jego zaciskach pojawi się napięcie

 

 









u

m

i

m

t

U

t

I

R

t

i

R

t

u



















sin

sin

(2.16)

przy czym amplituda przebiegu napięcia

m

m

I

R

U



(2.17)

a faza początkowa

i

u







(2.18)

Czyli przesunięcie fazowe



między przebiegami u(t) i i(t) wynosi zero:

0







i

u







(2.19)

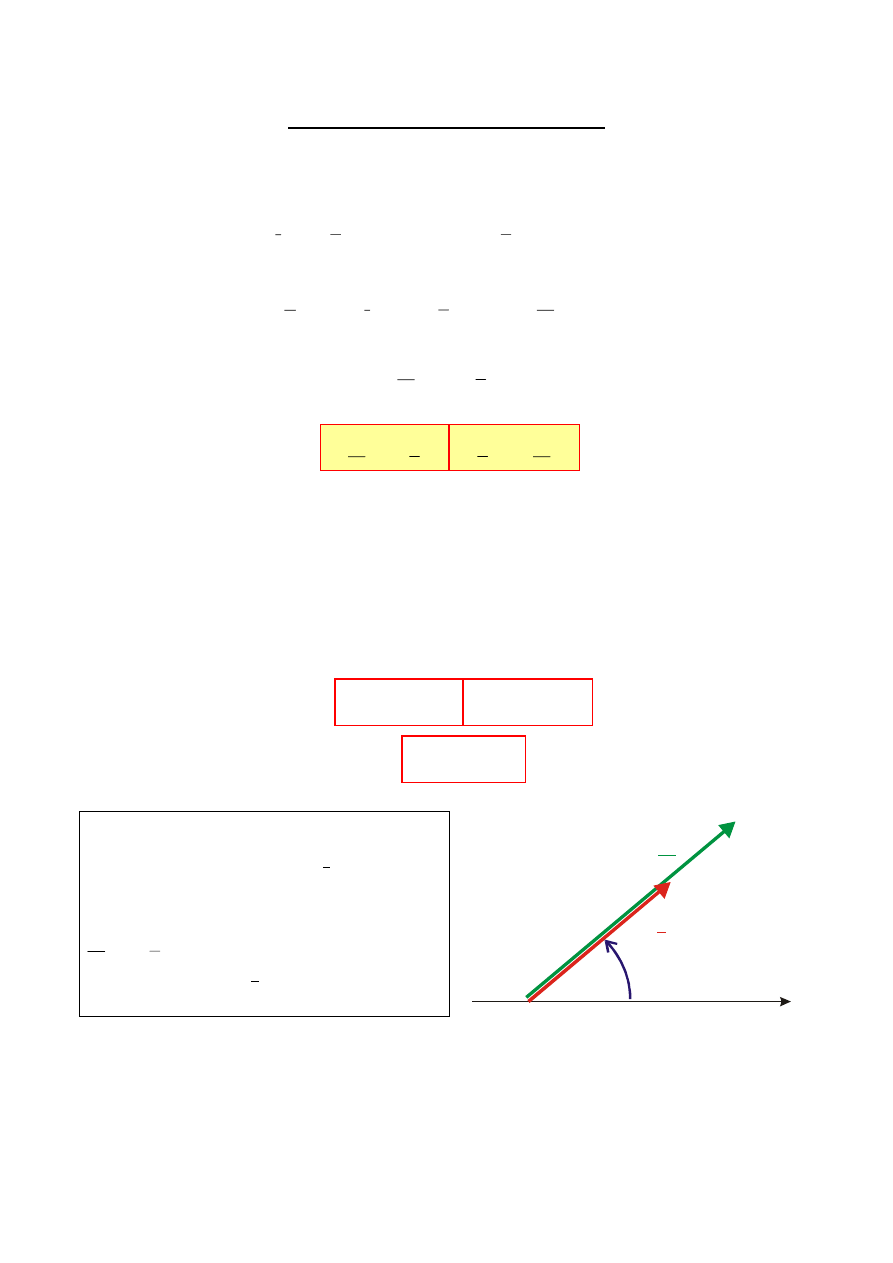
Napięcie na

idealnym rezystorze

jest w fazie z prądem

0

u t

( )

U

m

t

i t

( ),



u



i

I

m

- 9 -

W POSTACI SYMBOLICZNEJ

Symboliczna wartość chwilowa prądu

i

j

m

m

t

j

m

e

I

I

e

I

t

i









gdzie

)

(

(2.20)

napięcia

t

j

m

t

j

m

e

U

e

I

R

t

i

R

t

u











)

(

)

(

(2.21)

Zatem

m

m

I

R

U



(2.22)

co oznacza, że

I

R

U



U

G

I



(2.23)

Przedstawiając symboliczne wartości skuteczne w postaci

wykładniczej, otrzymujemy

i

u

j

j

e

I

R

e

U







(2.24)

Z przyrównania modułów w wyrażeniu (2.24) znajdujemy

I

R

U



U

G

I



(2.25)

a z przyrównania argumentów

i

u







(2.26)

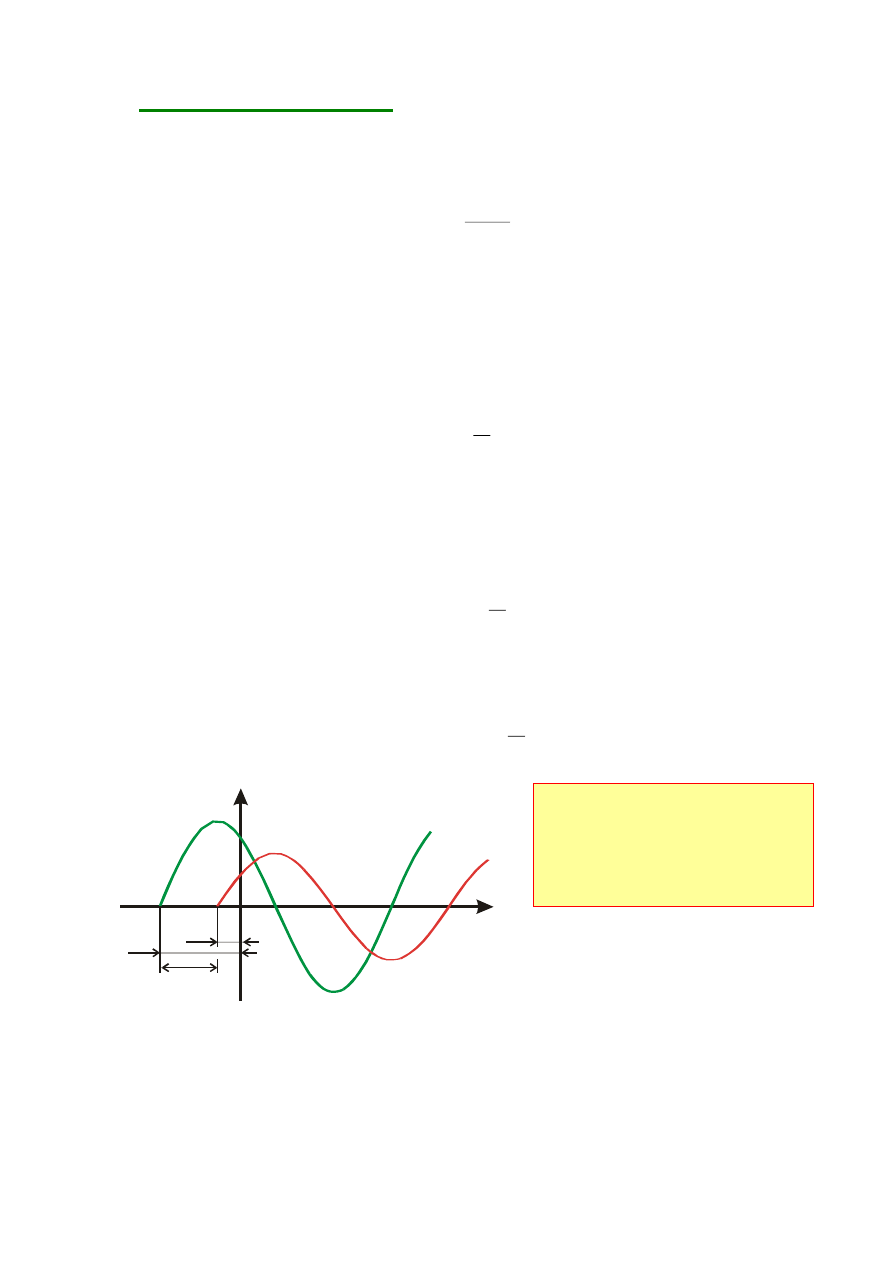
Pomnożenie wskazu I przez R
powoduje wydłużenie tego wskazu R
razy. Wobec tego wskaz napięcia

I

R

U



znajduje się na tej samej

prostej co wskaz I

U

I



u

=



i

- 10 -



CEWKA INDUKCYJNA

Przy przepływie prądu w cewce idealnej o indukcyjności L napięcie na

jej zaciskach wyraża zależność (2.10)

 

 

dt

t

i

d

L

t

u



Przyjmując, że w cewce występuje prąd harmoniczny

 





i

m

t

I

t

i









sin

(2.27)

napięcie na cewce wynosi

 





u

m

i

m

t

U

t

I

L

t

u



































sin

2

sin

(2.28)

Z powyższej zależności wynika, że amplituda przebiegu napięcia

m

m

I

L

U





(2.29)

natomiast faza początkowa

2











i

u

(2.30)

Czyli przesunięcie fazowe



między przebiegami u(t) i i(t) cewki

indukcyjnej wynosi:

2















i

u

(2.31)

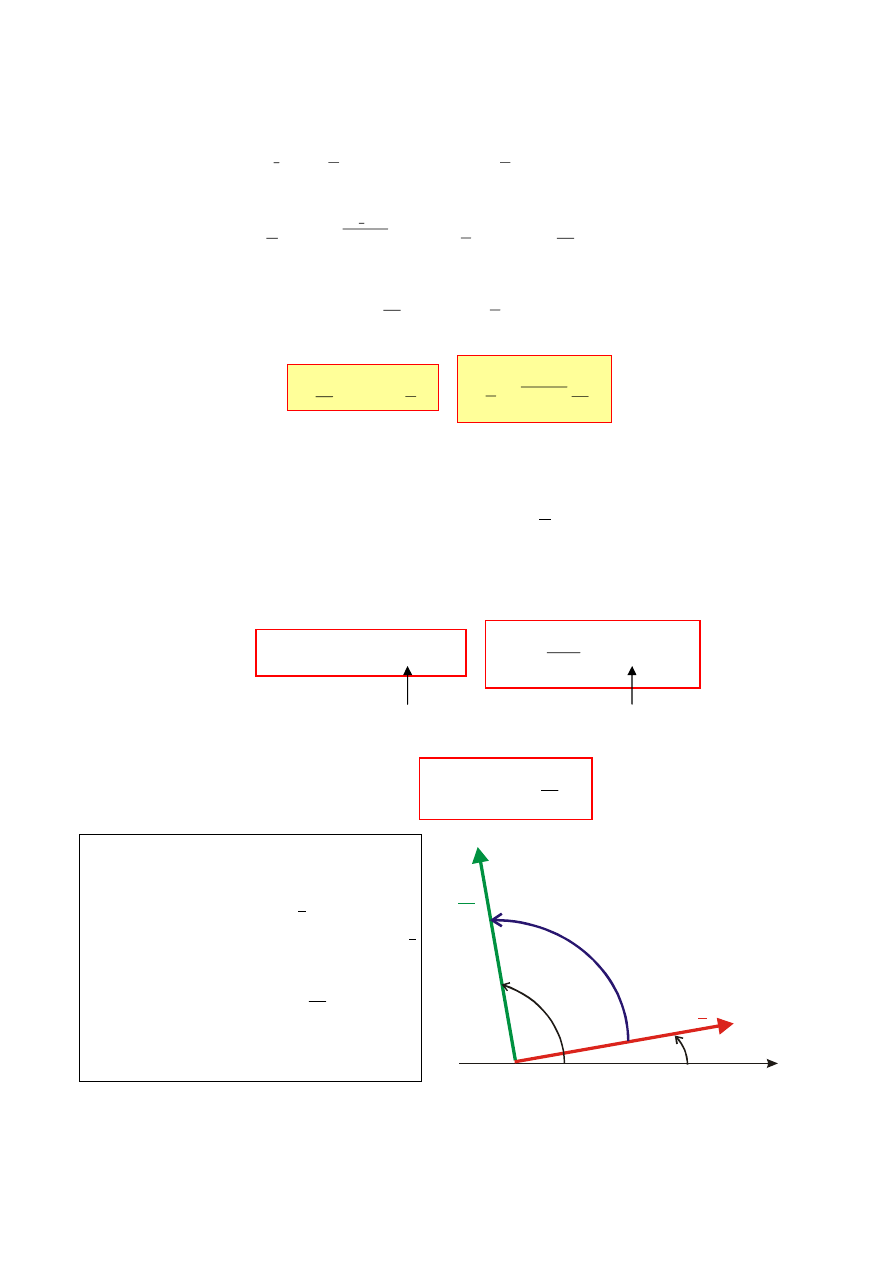
Napięcie na zaciskach

idealnej cewki

wyprzedza prąd

o 90

o

0

u t

( )

,

t

i t

( )



i



u

/2

- 11 -

Dla

cewki indukcyjnej - symboliczna wartość chwilowa prądu

i

j

m

m

t

j

m

e

I

I

e

I

t

i









gdzie

)

(

(2.32)

napięcia

 

 

t

j

m

t

j

m

e

U

e

I

L

j

dt

t

i

d

L

t

u













(2.33)

Zatem

m

m

I

L

j

U





(2.34)

co oznacza, że

I

L

j

U





U

L

j

I



1



(2.35)

Przedstawiając symboliczne wartości skuteczne w postaci

wykładniczej, otrzymujemy

















2









i

u

j

j

e

I

L

e

U

(2.36)

Z przyrównania modułów w wyrażeniu (3.36) znajdujemy

I

X

I

L

U

L







U

B

U

L

I

L







1

(2.37)

reaktancja indukcyjna

susceptancja indukcyjna

a z przyrównania argumentów

2











i

u

(2.38)

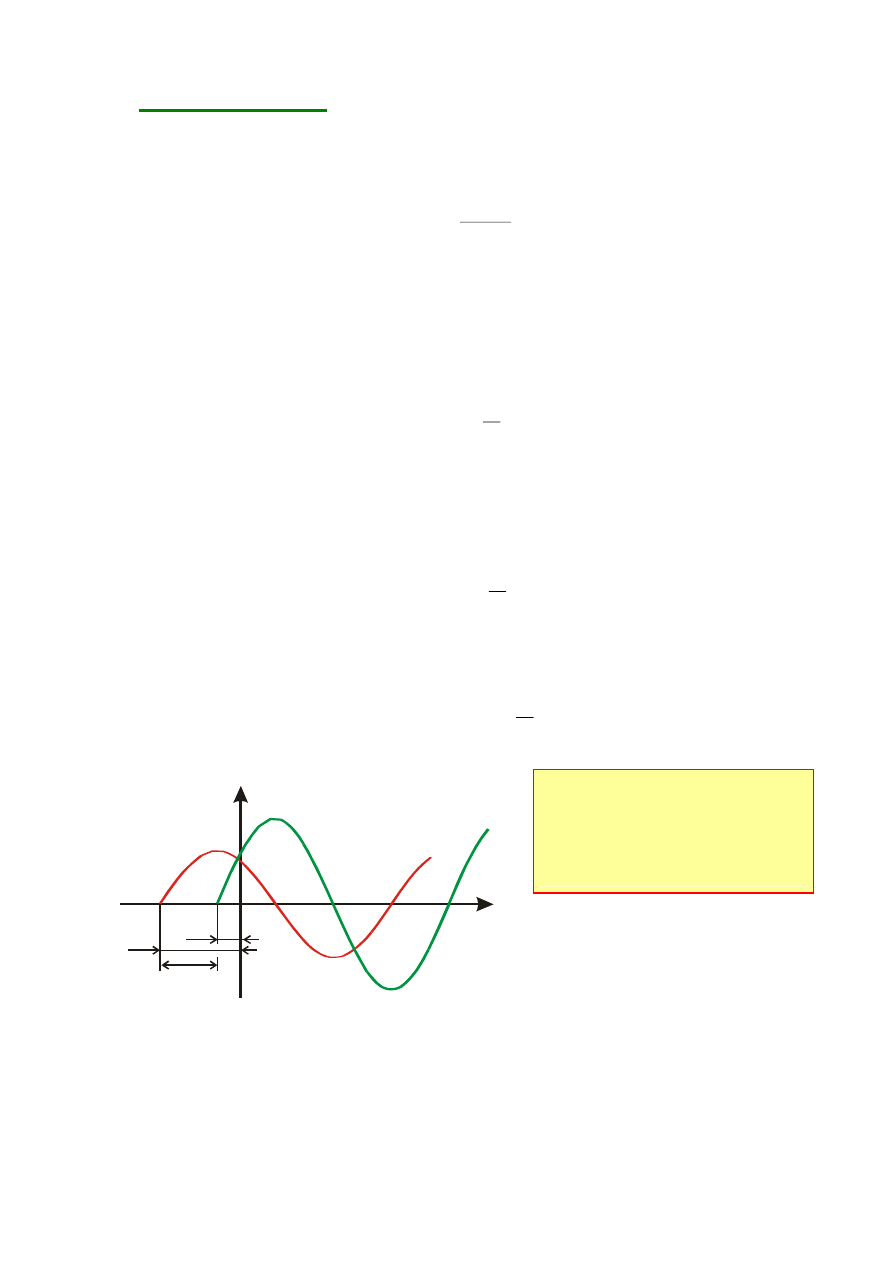
Pomnożenie wskazu I przez j



L

powoduje wydłużenie wskazu I
i jego obrót o 90

o

„w przód”

2















i

u

U

I



i



u

 

= /2

- 12 -



KONDENSATOR

Gdy istnieje napięcie u(t) na zaciskach idealnego kondensatora o

pojemności C, to prąd płynący przez kondensator opisuje zależność (2.12)

 

 

dt

t

u

d

C

t

i



Przyjmując, że na zaciskach kondensatora występuje napięcie

 





u

m

t

U

t

u









sin

(2.39)

prąd płynący przez kondensator wynosi

 





i

m

u

m

t

I

t

U

C

t

i



































sin

2

sin

(2.40)

Z powyższej zależności wynika, że amplituda przebiegu prądu

m

m

U

C

I





(2.41)

natomiast faza początkowa

2











u

i

(2.42)

Zatem przesunięcie fazowe



między przebiegami u(t) i i(t)

kondensatora wynosi:

2

















i

u

(2.43)

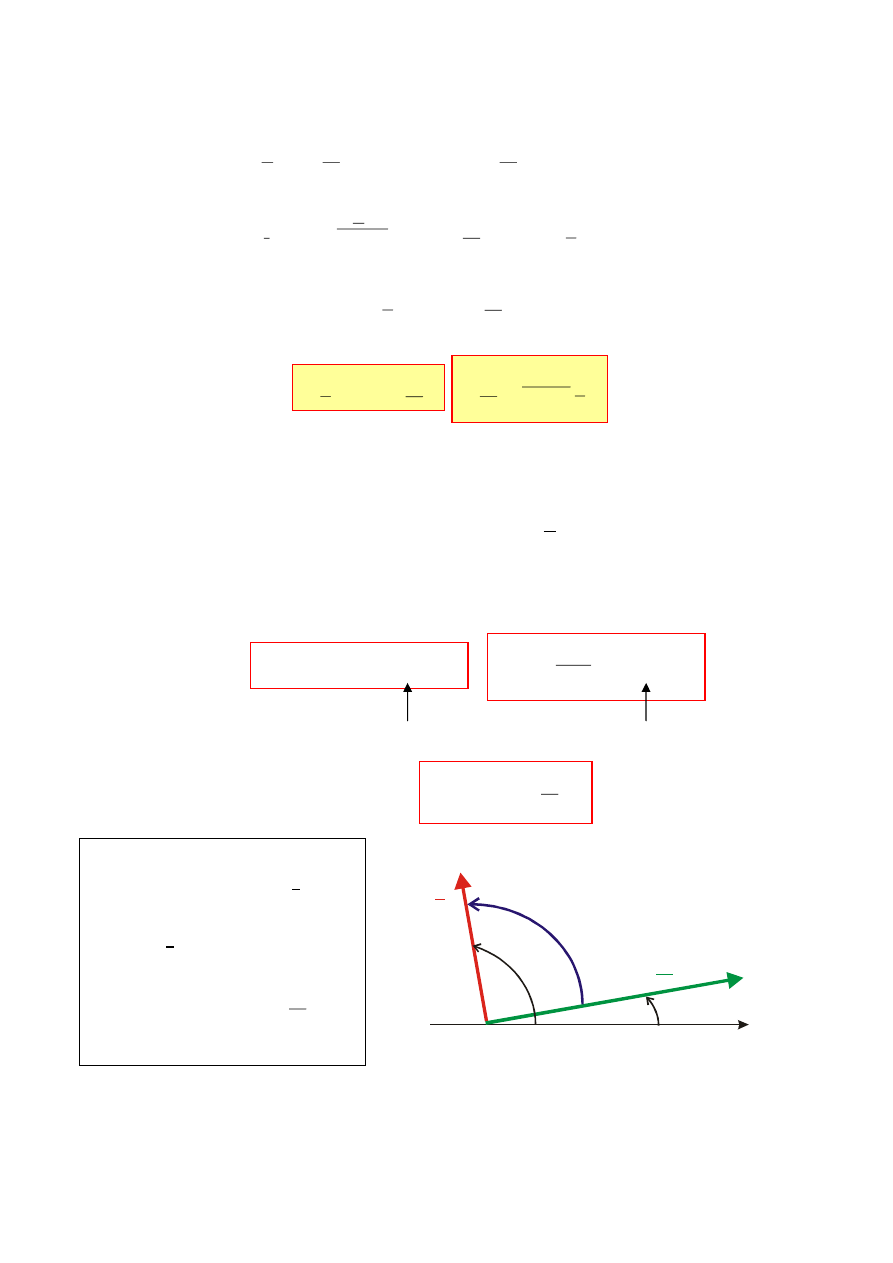
Prąd płynący przez

idealny kondensator

wyprzedza napięcie

o 90

o

0

u t

( )

,

t

i t

( )



i



u

/2

- 13 -

Dla kondensatora - symboliczna wartość chwilowa napięcia

i

j

m

m

t

j

m

e

U

U

e

U

t

u









gdzie

)

(

(2.44)

prądu

 

 

t

j

m

t

j

m

e

I

e

U

C

j

dt

t

u

d

C

t

i













(2.45)

Zatem

m

m

U

C

j

I





(2.46)

co oznacza, że

U

C

j

I





I

C

j

U



1



(2.47)

Przedstawiając symboliczne wartości skuteczne w postaci

wykładniczej, otrzymujemy

















2









u

i

j

j

e

U

C

e

I

(2.48)

Z przyrównania modułów, znajdujemy

U

B

U

C

I

C







I

X

I

C

U

C







1

(2.49)

susceptancja pojemnościowa

reaktancja pojemnościowa

a z przyrównania argumentów

2











u

i

(2.50)

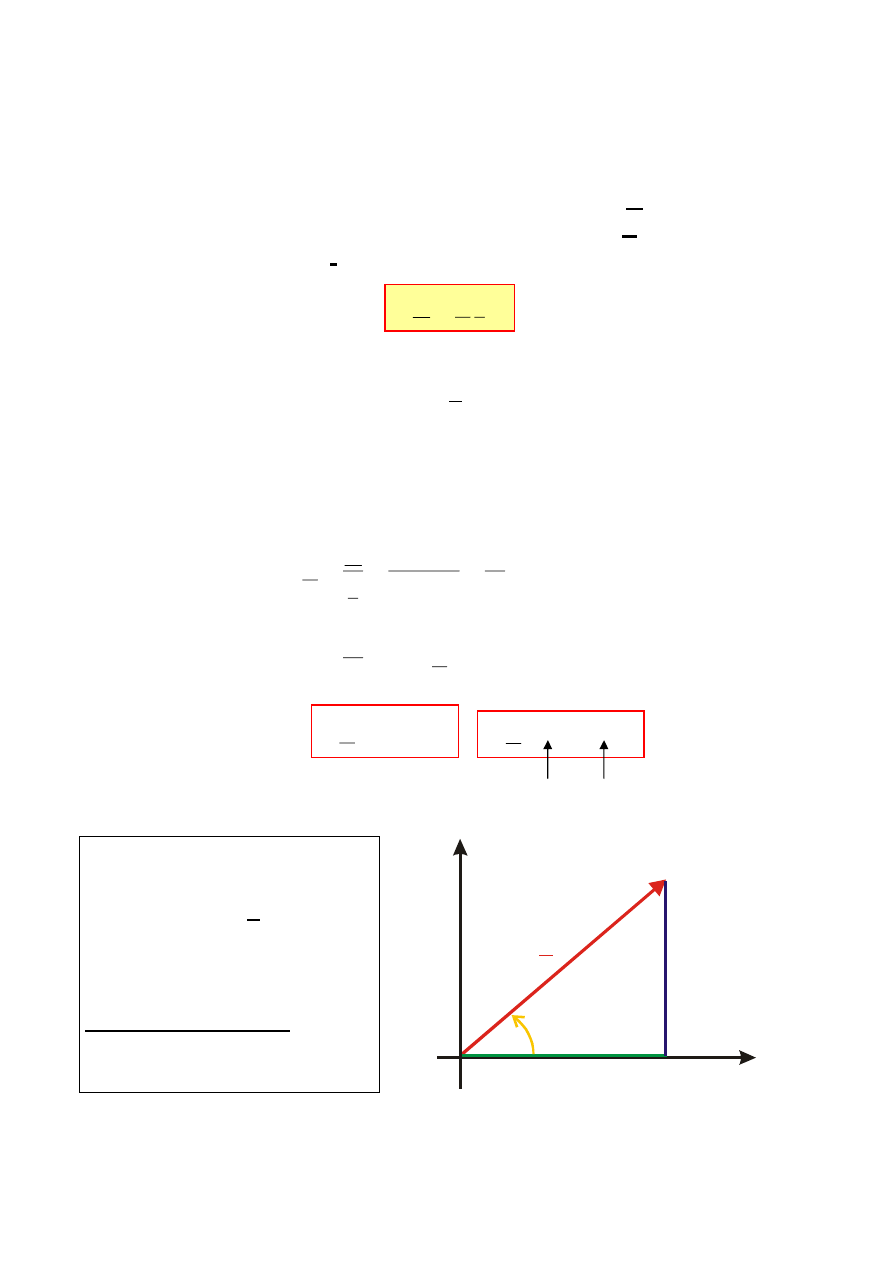
Pomnożenie wskazu I przez
1/j



C powoduje wydłużenie

wskazu I i jego obrót o 90

o

„wstecz”

2

















i

u

U

I



i



u

 

=- /2

- 14 -

2.5.

PODSTAWOWE PRAWA W POSTACI SYMBOLICZNEJ

Prawo Ohma

Symboliczna wartość skuteczna napięcia U dwójnika
równa się iloczynowi impedancji dwójnika Z i wartości
skutecznej prądu I w nim płynącego:

I

Z

U



(2.51)

Impedancja (opór zespolony) Z charakteryzuje przewodnictwo
elektryczne dwójnika przy przepływie prądu sinusoidalnego.

Podstawiając w (2.51) symboliczne wartości skuteczne w postaci

wykładniczej, otrzymujemy





i

u

i

u

j

j

j

e

I

U

e

I

e

U

I

U

Z

















(2.51)

czyli:



















i

u

Z

I

U

Z

arg

,

(2.52)

Zatem



j

e

Z

Z



X

j

R

Z





(2.53)

rezystancja

reaktancja

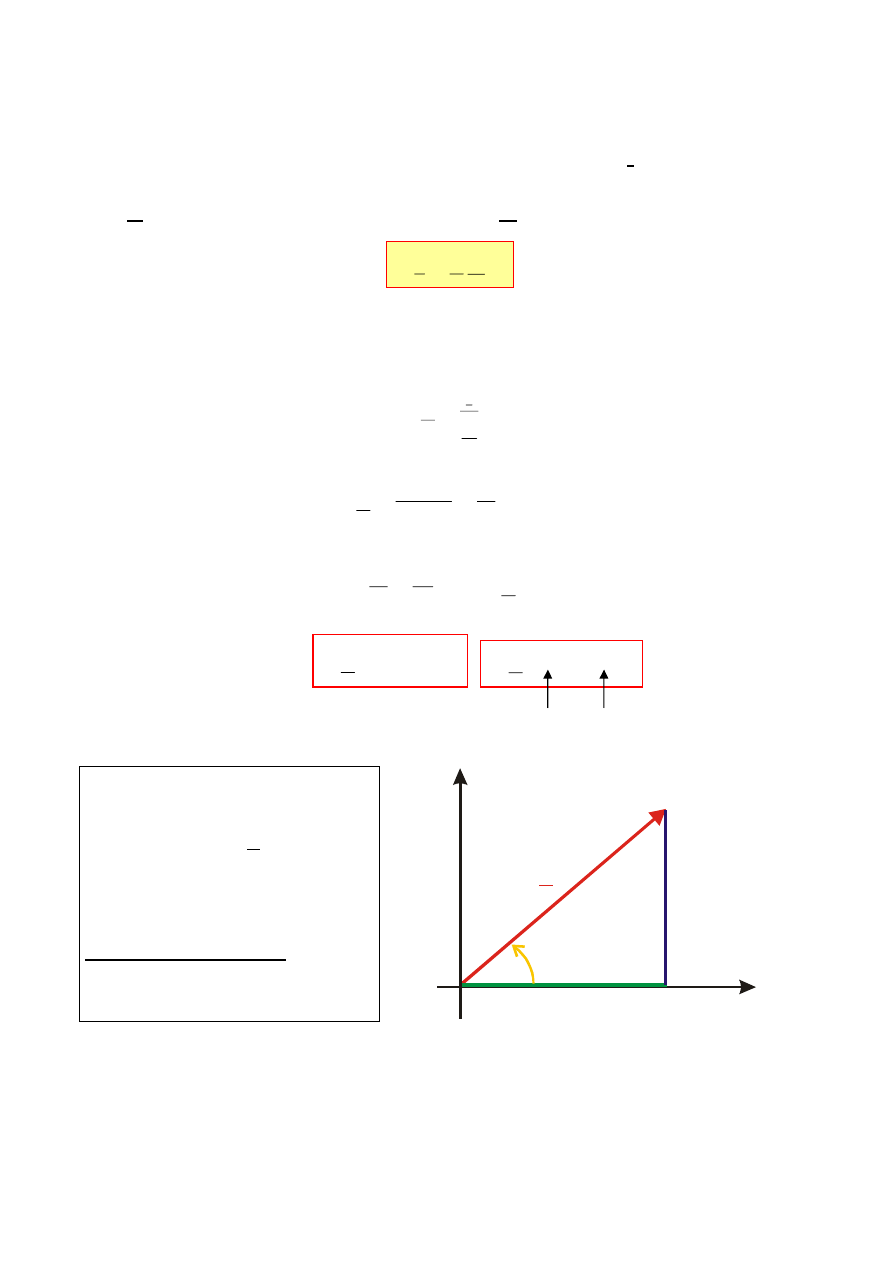
Impedancję

Z

można

przedstawić

geometrycznie

na płaszczyźnie zmiennej
zespolonej

za

pomocą

trójkąta impedancji.

Z



Im

Re

R

X

- 15 -

Prawo Ohma można także przedstawić następująco:

Symboliczna wartość skuteczna prądu I płynącego
przez dwójnik równa się iloczynowi admitancji dwójnika
Y i wartości skutecznej napięcia U na jego zaciskach:

U

Y

I



(2.54)

Admitancja (przewodność zespolona – jej jednostką jest simens S)
dwójnika równa się odwrotności jego impedancji:

Z

Y

1



(2.55)

co oznacza, że





j

j

e

Z

e

Z

Y







1

1

(2.56)

czyli:











Y

U

I

Z

Y

arg

,

1

(2.57)

Zatem



j

e

Y

Y





B

j

G

Y





(2.58)

konduktancja

susceptancja

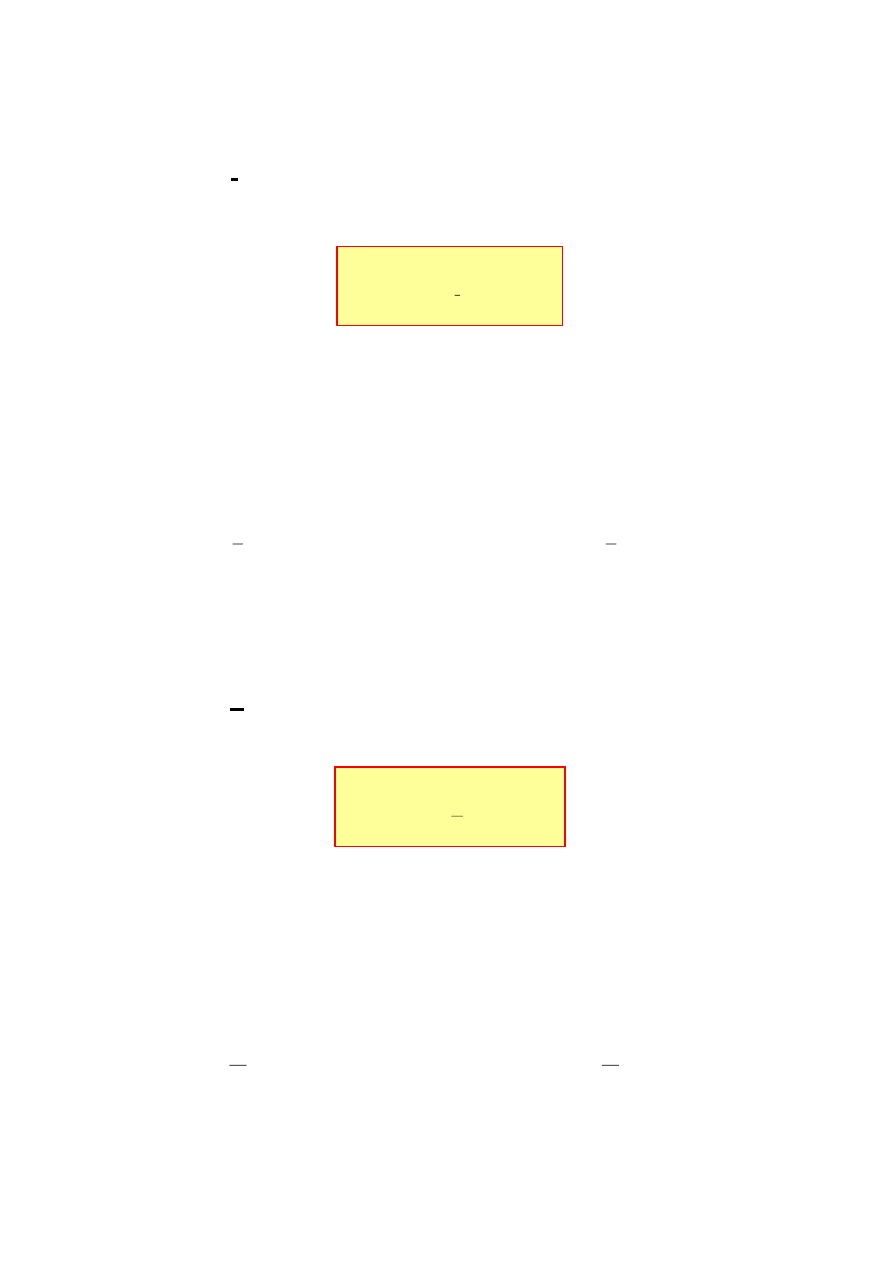
Admitancję

Y

można

przedstawić

geometrycznie

na płaszczyźnie zmiennej
zespolonej

za

pomocą

trójkąta admitancji.

Y

-



Im

Re

G

B

- 16 -

I prawo Kirchhoffa - prądowe prawo Kirchhoffa (PPK)

Algebraiczna suma symbolicznych wartości chwilowych
prądów i

n

(t) we wszystkich gałęziach dołączonych do

jednego, dowolnie wybranego węzła obwodu jest w każdej
chwili czasu równa zeru:







n

k

k

k

t

t

i

1

0

)

(





(2.59)

gdzie:



k

=

1 („+” jeśli prąd elektryczny ma zwrot do węzła; „-” jeśli zwrot

jest przeciwny, od węzła)

Jest ono także słuszne dla symbolicznych amplitud (2.59a) oraz

symbolicznych wartości skutecznych (2.59) odpowiednich prądów:







n

k

k

m

k

I

1

0



(2.59a)







n

k

k

k

I

1

0



(2.59b)

II prawo Kirchhoffa - napięciowe prawo Kirchhoffa (NPK)

Algebraiczna suma symbolicznych wartości chwilowych
napięć u

n

(t) na wszystkich elementach, tworzących

dowolnie wybrane oczko obwodu jest w każdej chwili
czasu równa zeru:







n

k

k

k

t

t

u

1

0

)

(





(2.60)

gdzie:



k

=

1 („+” jeśli zwrot napicia jest zgodny z przyjętym za dodatni

kierunkiem obiegu oczka; „-” jeśli jest przeciwny)

Jest ono także słuszne dla symbolicznych amplitud (2.60a) oraz

symbolicznych wartości skutecznych (2.60b) odpowiednich napięć







n

k

k

m

k

U

1

0



(2.60a)







n

k

k

k

U

1

0



(2.60b)

- 17 -

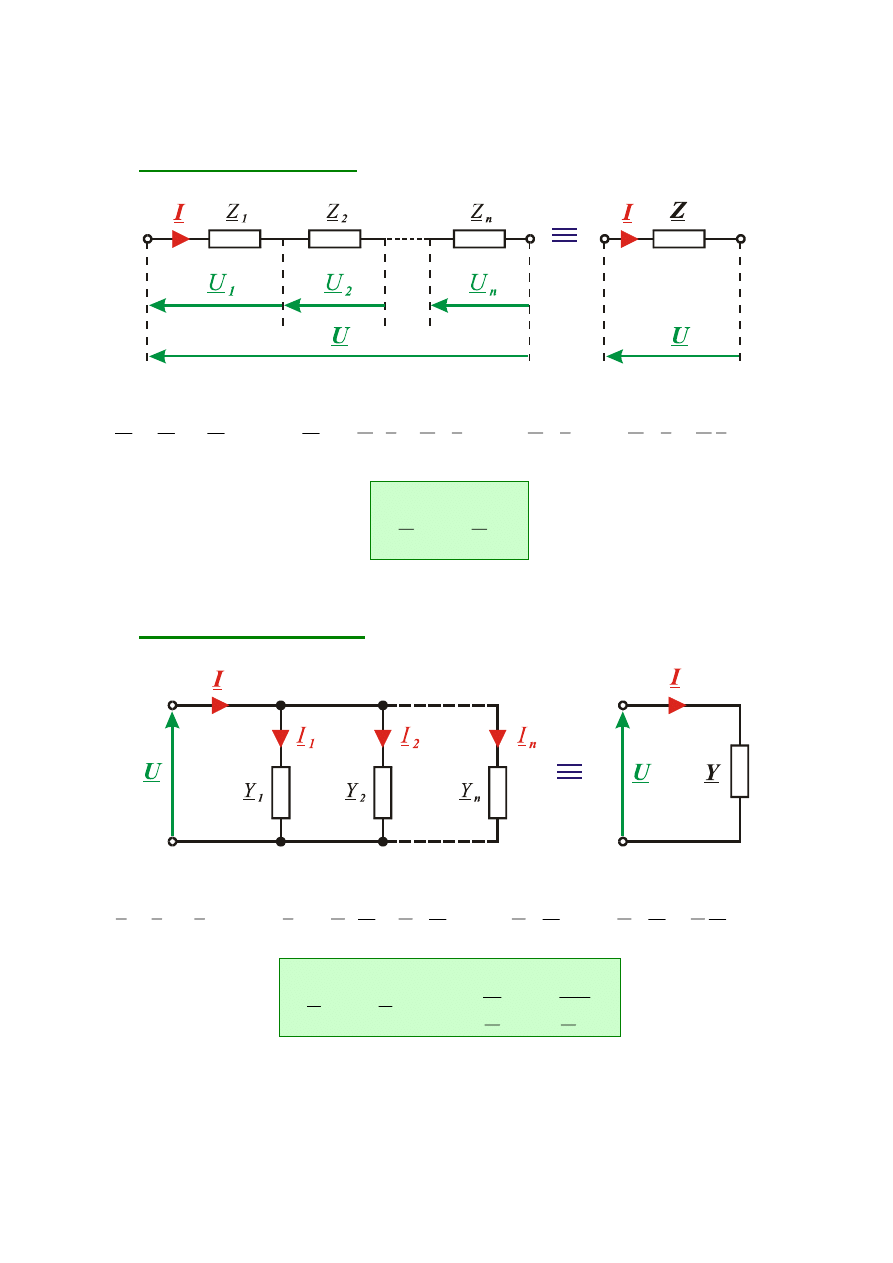
2.6. POŁĄCZENIA DWÓJNIKÓW



Połączenie szeregowe

n dwójników

I

Z

I

Z

I

Z

I

Z

I

Z

U

U

U

U

n

k

k

n

n























1

2

1

2

1





(2.61)







n

k

k

Z

Z

1

(2.62)



Połączenie równoległe

n dwójników

U

Y

U

Y

U

Y

U

Y

U

Y

I

I

I

I

n

k

k

n

n























1

2

1

2

1





(2.63)













n

k

k

n

k

k

Z

Z

Y

Y

1

1

1

1

lub

(2.64)

- 18 -

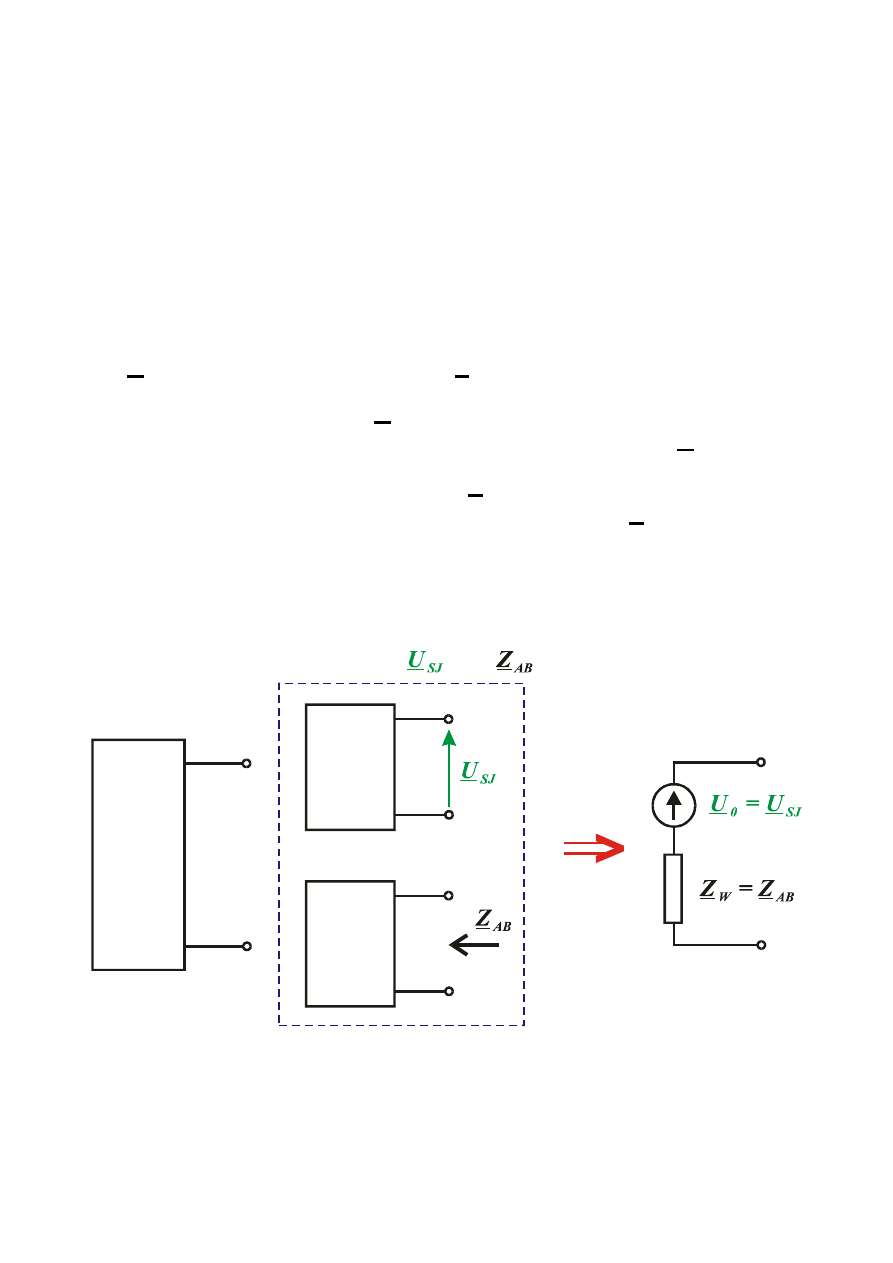
2.7. TWIERDZENIE THEVENINA I NORTONA W POSTACI

SYMBOLICZNEJ

TwierdzenieThevenina

(o zastępczym źródle/generatorze napięciowym)

Dowolny aktywny dwójnik klasy SLS można zastąpić
obwodem równoważnym, złożonym z szeregowego
połączenia idealnego źródła napięcia o napięciu źródłowym
U

0

i impedancji wewnętrznej Z

W

, przy czym:

- napięcie źródłowe U

0

jest równe napięciu na rozwartych

zaciskach dwójnika (napięciu stanu jałowego U

SJ

)

- impedancja wewnętrzna Z

W

, jest równa impedancji

zastępczej (impedancji wejściowej Z

AB

) dwójnika

pasywnego

(bezźródłowego)

otrzymanego

po

wyzerowaniu w wewnętrznej strukturze dwójnika
aktywnego wszystkich autonomicznych źródeł energii.

DA

A

B

A

B

A

B

DA

A

B

DP

Wyznaczenie: oraz

- 19 -

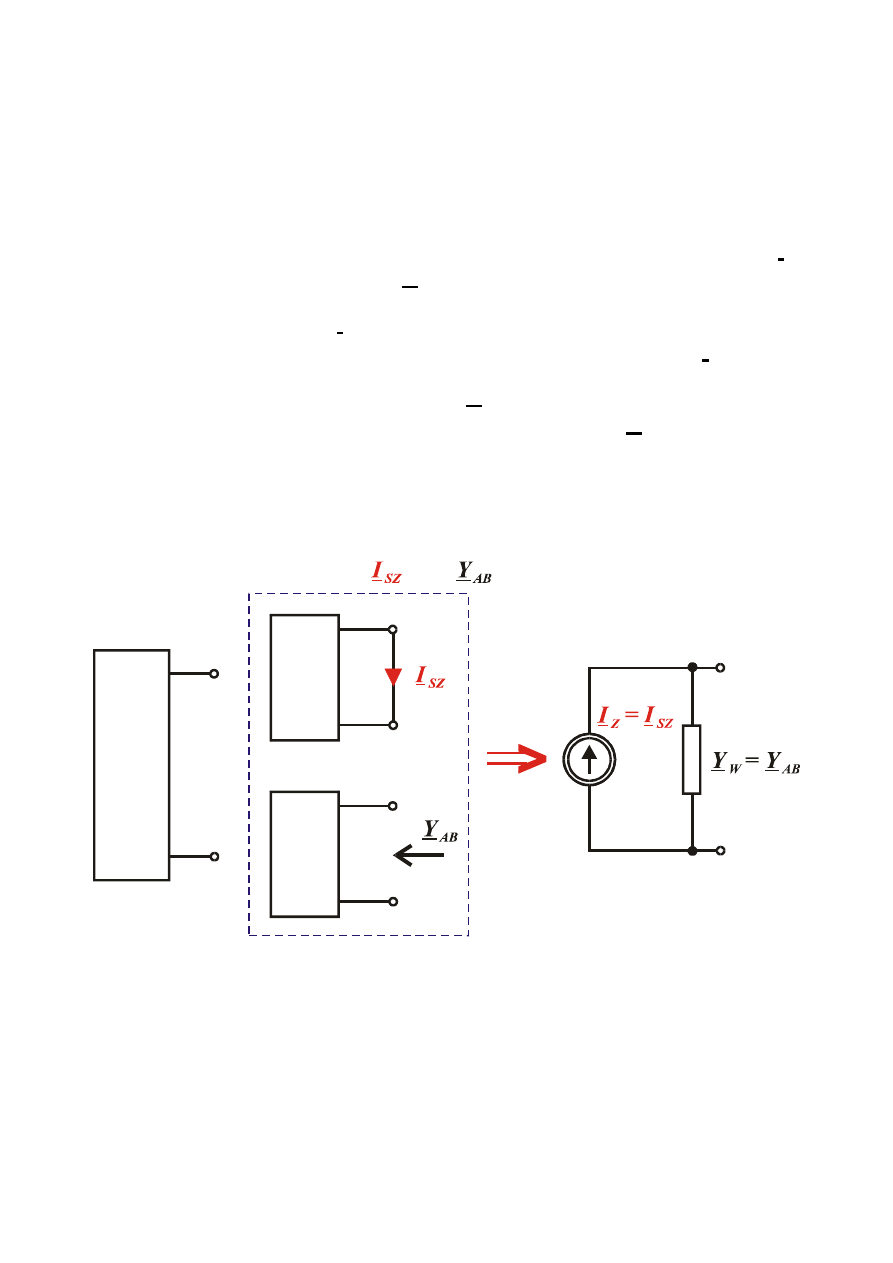
TwierdzenieNortona

(o zastępczym źródle/generatorze prądowym)

Dowolny aktywny dwójnik klasy SLS można zastąpić
obwodem równoważnym, złożonym z równoległego
połączenia idealnego źródła prądu o prądzie źródłowym I

Z

i

admitancji wewnętrznej Y

W

, przy czym:

- prąd źródłowy I

Z

jest równy prądowi płynącemu przez

zwarte zaciski dwójnika (prądowi stanu zwarcia I

SZ

)

- admitancja wewnętrzna Y

W

, jest równa admitancji

zastępczej (admitancji wejściowej Y

AB

) dwójnika

pasywnego

(bezźródłowego)

otrzymanego

po

wyzerowaniu w wewnętrznej strukturze dwójnika
aktywnego wszystkich autonomicznych źródeł energii.

DA

A

B

A

B

DA

A

B

DP

Wyznaczenie: oraz

A

B

- 20 -

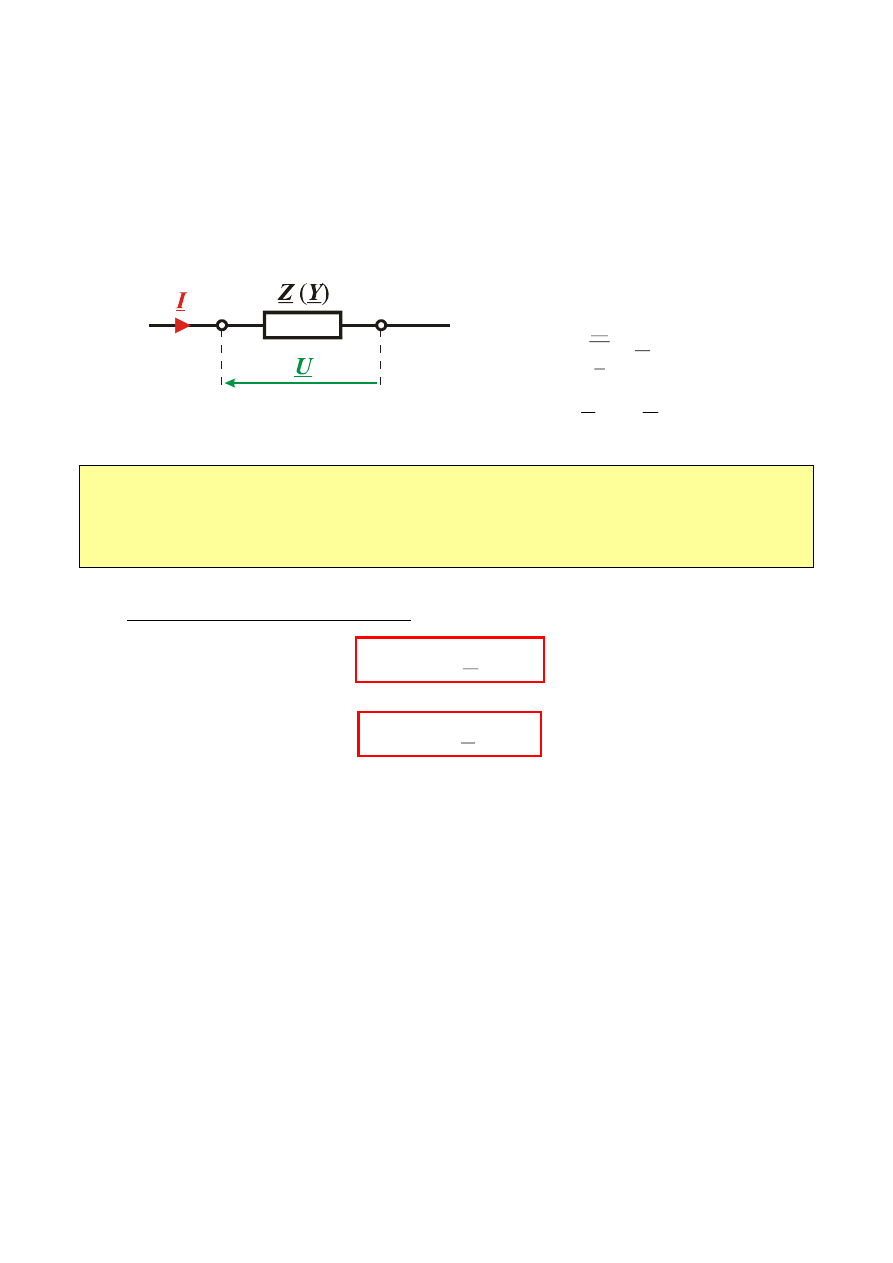
2.6. REZONANS ELEKTRYCZNY

Obwody elektryczne, w których występuje zjawisko rezonansu

nazywane są obwodami rezonansowymi lub drgającymi.

Rozpatrując bezźródłowy obwód elektryczny, przedstawiony

schematycznie na rys. jako dwójnik.

Rozpatrywany dwójnik

jX

R

Z

I

U







jB

G

Z

Y





 /

1

Zjawisko rezonansu przedstawia taki stan pracy obwodu
elektrycznego, przy którym reaktancja wypadkowa X lub
susceptancja wypadkowa B obwodu jest równa zeru

Warunkiem rezonansu jest

 

0

Im





Z

X

(2.65)

lub

 

0

Im





Y

B

(2.66)

Częstotliwość (pulsacja), przy której reaktancja wypadkowa lub

susceptancja wypadkowa obwodu jest równa zeru nazywana jest
częstotliwością (pulsacją) rezonansową.

Obwód elektryczny osiąga stan rezonansu, jeśli częstotliwość

doprowadzonego sygnału sinusoidalnego jest równa częstotliwości
rezonansowej obwodu.

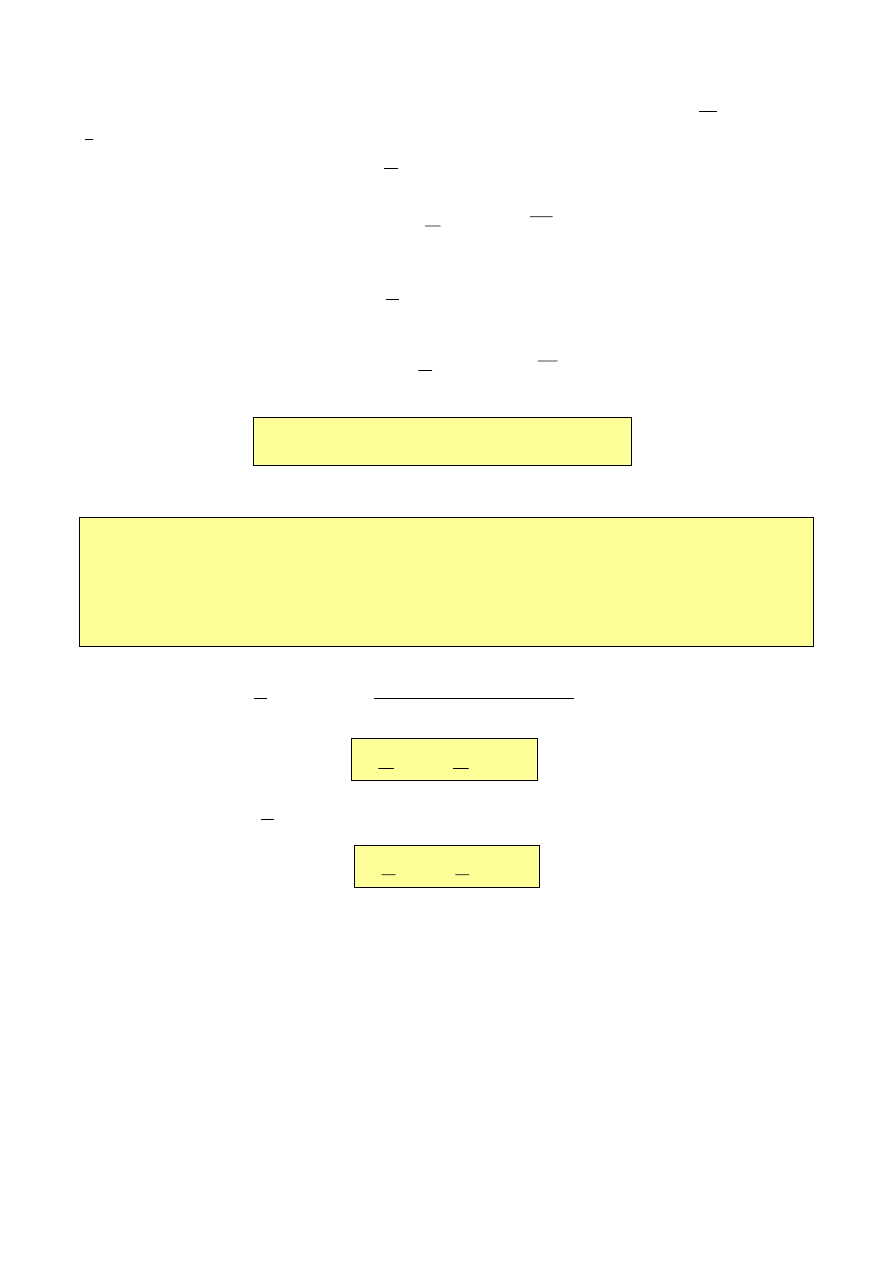
- 21 -

Ponieważ kąt



przesunięcia fazowego między napięciem U i prądem

I jest równy

 argumentowi impedancji Z, przy czym

 

R

X

arctg

Z



 arg



(2.67)

lub

 argumentowi admitancji Y wziętemu ze znakiem przeciwnym, przy

czym

 

G

B

arctg

Y







 arg



;

(2.68)

stąd



= 0 dla X = 0 lub B = 0

Oznacza to, że

zjawiskiem rezonansu nazywamy taki stan pracy obwodu
elektrycznego, przy którym prąd i napięcie na jego zaciskach są ze
sobą w fazie (a argument impedancji lub admitancji obwodu jest
równy zeru)

Impedancja Z obwodu w stanie rezonansu równa się rezystancji

obwodu

 

R

Z

Z



 Re

,

(2.69)

a jego admitancja Y , jest równa konduktancji G

 

G

Y

Y



 Re

.

(2.70)

Rezonans występujący w obwodzie, w którym elementy R, L, C

połączone są szeregowo, nazywamy

rezonansem napięć

lub rezonansem

szeregowym.

Rezonans występujący w obwodzie, w którym połączone są

równolegle gałęzie R, L oraz R, C lub gałęzie R, L, C nazywamy

rezonansem prądów

lub rezonansem równoległym.

- 22 -

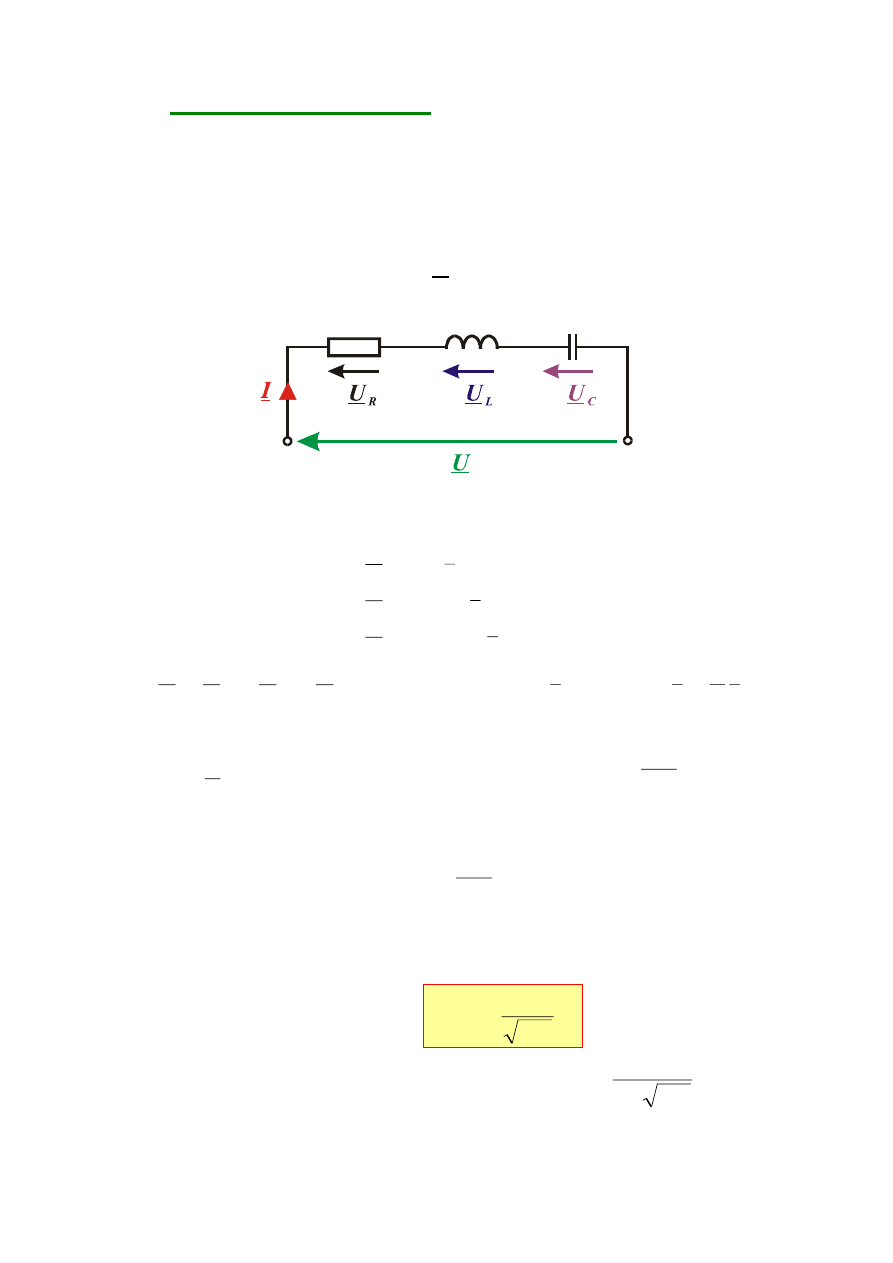
A) REZONANS NAPIĘĆ

PODSTAWOWE ZALEŻNOŚCI

Rozważając obwód składający się z elementów R, L i C połączonych

szeregowo - zakłada się, że przyłożone napięcie jest sinusoidalnie zmienne
o symbolicznej wartości skutecznej U i o pulsacji



= 2

f.

R

L

C

Dla rozpatrywanego obwodu słuszne są zależności



















I

jX

U

I

jX

U

I

R

U

C

C

L

L

R

(2.71)













I

Z

I

jX

R

I

X

X

j

R

U

U

U

U

C

L

C

L

R



















(2.72)

Impedancja obwodu wynosi

































C

L

j

R

X

X

j

R

jX

R

Z

C

L





1

.

(2.73)

Warunkiem rezonansu (2.65) jest to, aby X=0 lub X

L

=X

C

, czyli

C

L





1



.

(2.74)

Pulsację rezonansową



r

obwodu szeregowego RLC znajduje się z

powyższego równania, otrzymując

LC

r

1





,

(2.75)

stąd częstotliwość rezonansowa f

r

wynosi

LC

f

r



2

1



.

(2.76)

- 23 -

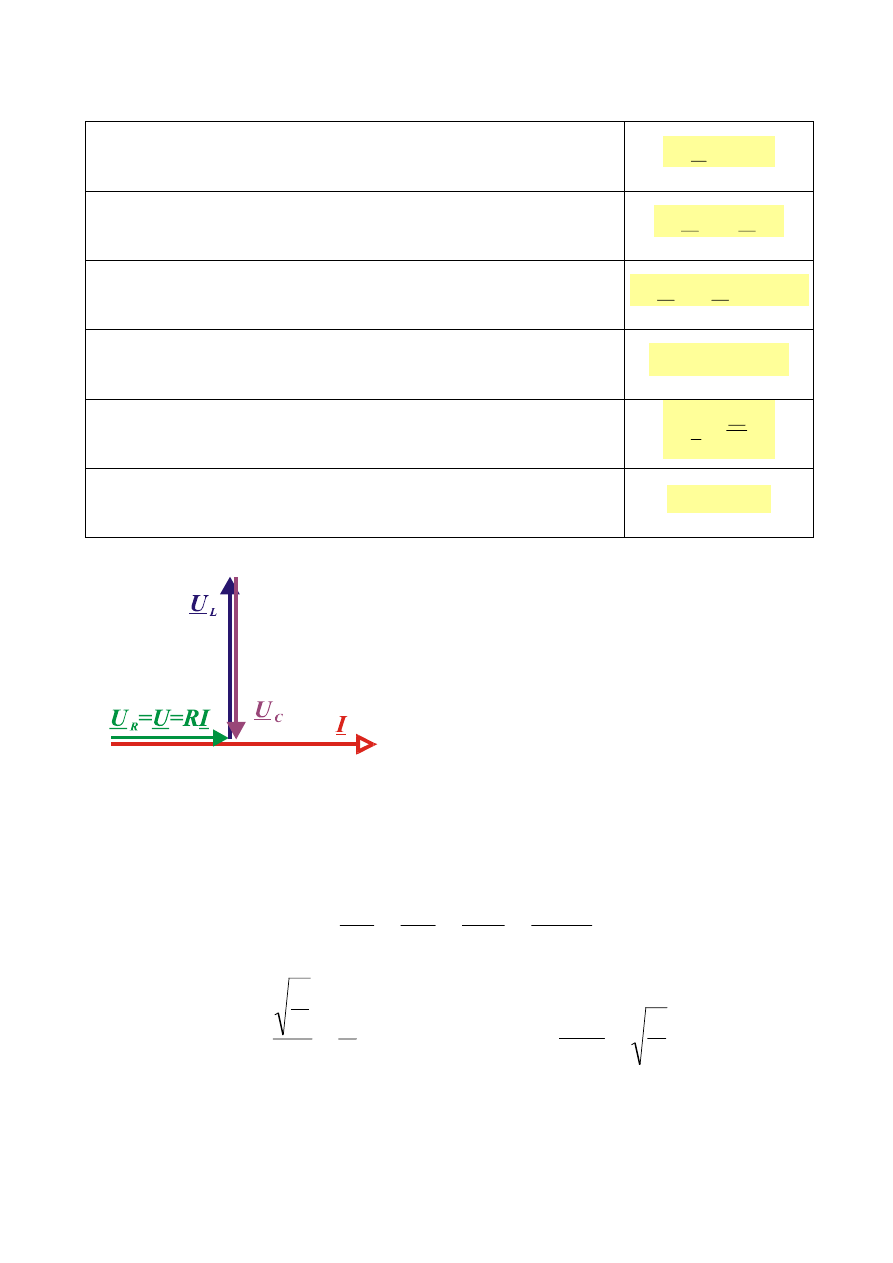
WŁASNOŚCI OBWODU W STANIE REZONANSU NAPIĘĆ

1. impedancja obwodu jest równa rezystancji

(impedancja osiąga wartość minimalną)

R

Z



2. napięcie na rezystancji obwodu jest równe

napięciu przyłożonemu do obwodu

U

U

R



3. suma geometryczna napięć na indukcyjności i

pojemności obwodu jest równa zeru

0





C

L

U

U

4. napięcie na indukcyjności jest co do modułu

równe napięciu na pojemności

C

L

U

U



5. wobec X=0, prąd w obwodzie osiąga wartość

maksymalną

R

U

I



6. kąt przesunięcia fazowego między przyłożonym

napięciem a prądem jest równy zeru

0





Wykres wskazowy

Ze względu na równość modułów
napięć na elementach reaktancyjnych i
fakt, że mogą być one wielokrotnie
większe

od

modułu

napięcia

przyłożonego

-

rezonans

w

rozpatrywanym obwodzie nazywamy
rezonansem napięć.

Parametrem, który wskazuje ile razy napięcie na indukcyjności lub

pojemności jest większe od napięcia na zaciskach obwodu w stanie
rezonansu jest dobroć Q.

RC

R

L

U

U

U

U

Q

r

r

R

C

R

L





1









.

(2.77)

R

R

C

L

Q







, gdzie

C

L

C

L

r

r













1

(2.78)



jest reaktancją charakterystyczną obwodu

- 24 -

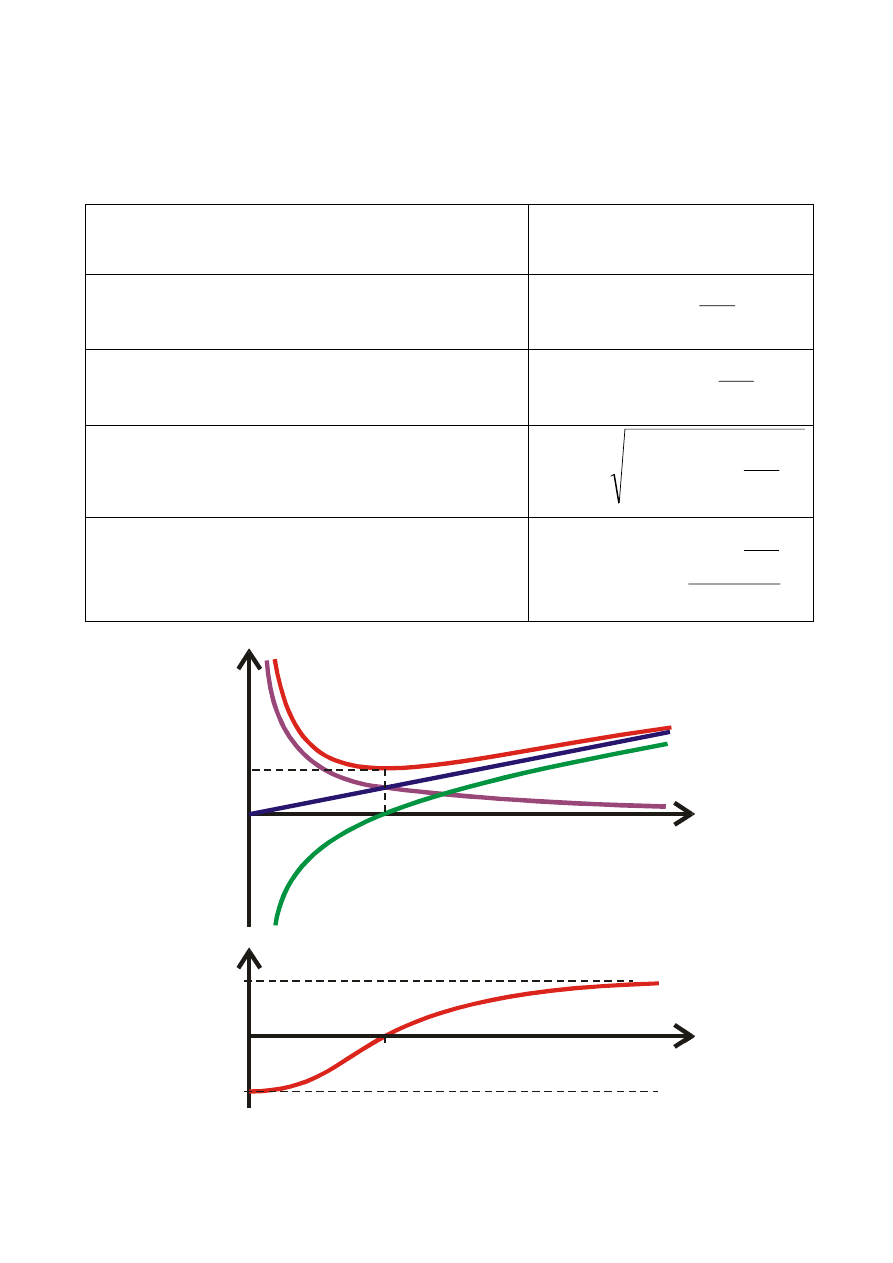
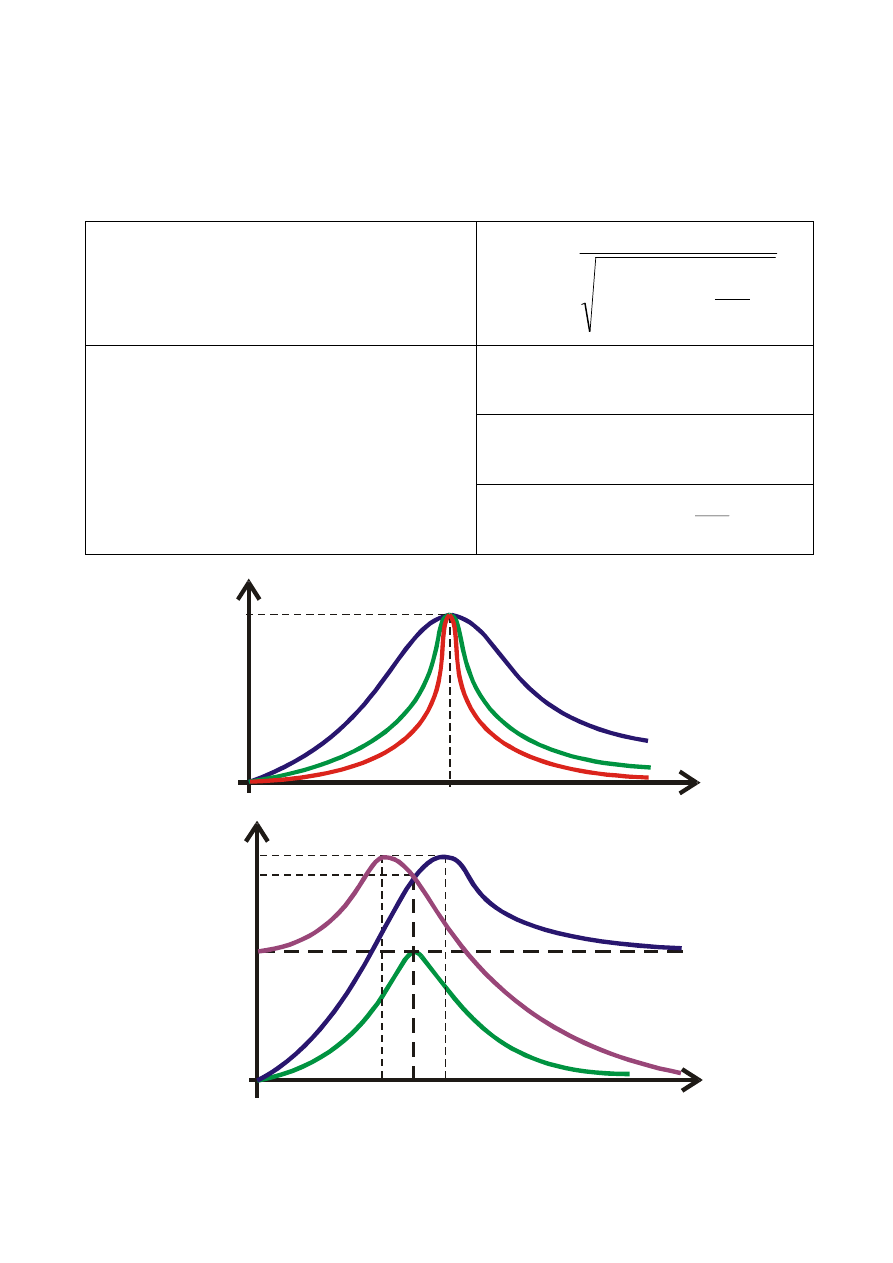
CHARAKTERYSTYKI CZĘSTOTLIWOSCIOWE

określają zależność parametrów wtórnych obwodów (impedancji,

reaktancji itd.) od częstotliwości (lub pulsacji).

 charakterystyka reaktancji indukcyjnej

obwodu

 

L

X

L







 charakterystyka reaktancji

pojemnościowej obwodu

 

C

X

C





1



 charakterystyka reaktancji wypadkowej

obwodu

 

C

L

X







1





 charakterystyka impedancji (modułu

impedancji) obwodu

 

2

2

1



















C

L

R

Z







 charakterystyka kąta przesunięcia

fazowego (argumentu impedancji)
obwodu

 

R

C

L

arctg









1





R



r

X( )



X ( )

L



X ( )

C





0



r





-



Z( )





- 25 -

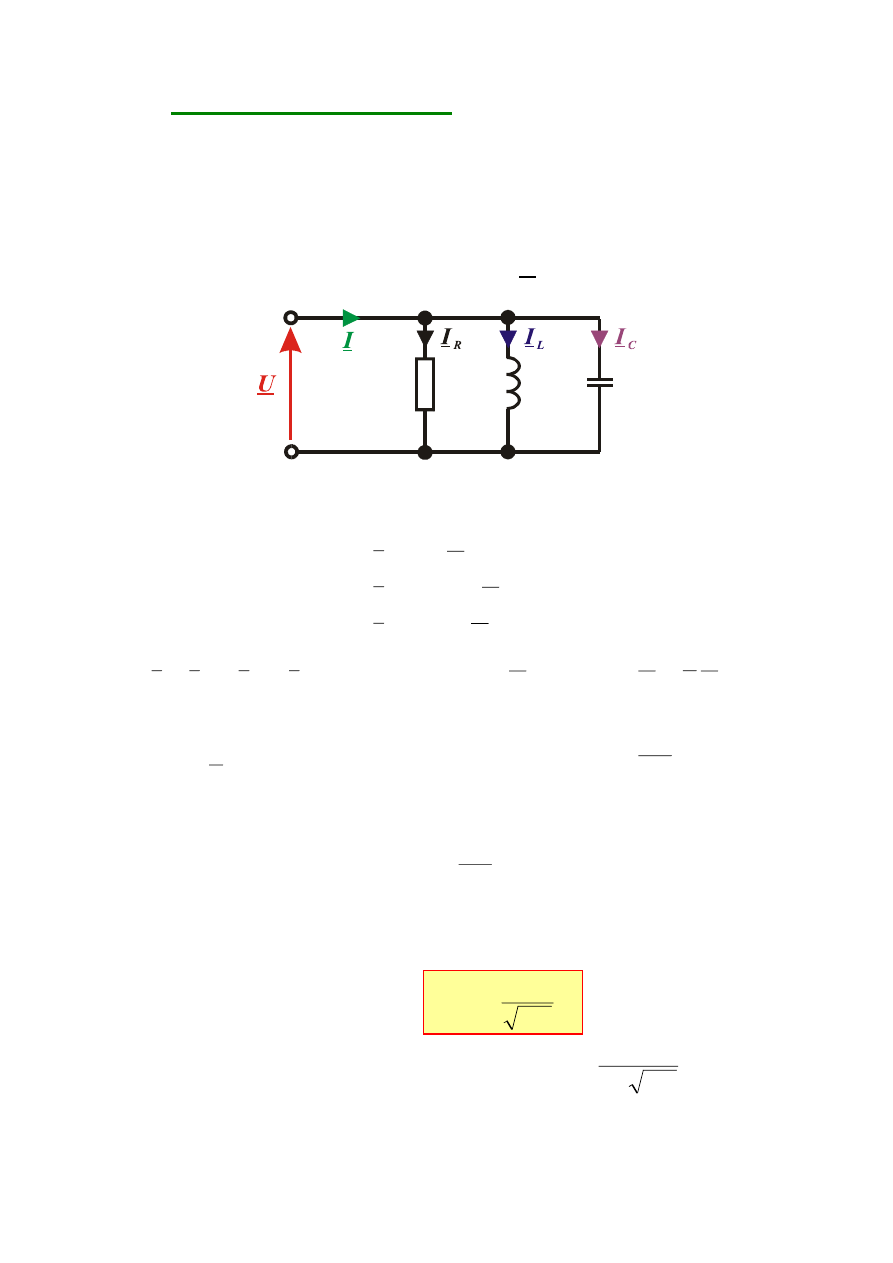
KRZYWE REZONANSOWE

Wykresy zależności wartości skutecznych napięć i prądów

obwodów rezonansowych od częstotliwości (lub pulsacji) noszą nazwę
krzywych rezonansowych

 krzywa rezonansowa prądu

 

2

2

1



















C

L

R

U

I







   

R

I

U

R







   

L

I

U

L









 krzywe rezonansowe napięć na

elementach obwodu

   

C

I

U

C







1



Q

1



Q

Q

Q

1

2

3

<

<

I

r

I



r

Q

2

Q

3

U



r



U ( )

R





Cmax

QU

U

=U

Lmax

Cmax

U ( )

C



U ( )

L





Lmax

- 26 -

B) REZONANS PRĄDÓW

PODSTAWOWE ZALEŻNOŚCI

Rozważając obwód składający się z elementów R, L i C połączonych

równolegle - zakłada się, że przyłożone napięcie jest sinusoidalnie
zmienne o symbolicznej wartości skutecznej U i o pulsacji



= 2

f.

R

L

C

Dla rozpatrywanego obwodu słuszne są zależności



















U

jB

I

U

jB

I

U

G

I

C

C

L

L

R

(2.79)













U

Y

U

jB

G

U

B

B

j

G

I

I

I

I

L

C

C

L

R



















(2.80)

Admitancja obwodu wynosi

































L

C

j

G

B

B

j

G

jB

G

Y

L

C





1

.

(2.81)

Warunkiem rezonansu (2.66) jest to, aby B=0 lub B

C

=B

L

, czyli

L

C





1



.

(2.82)

Pulsację rezonansową



r

obwodu równoległego RLC znajduje się z

powyższego równania, otrzymując

LC

r

1





,

(2.75/2.83)

stąd częstotliwość rezonansowa f

r

wynosi

LC

f

r



2

1



. (2.76/2.84)

- 27 -

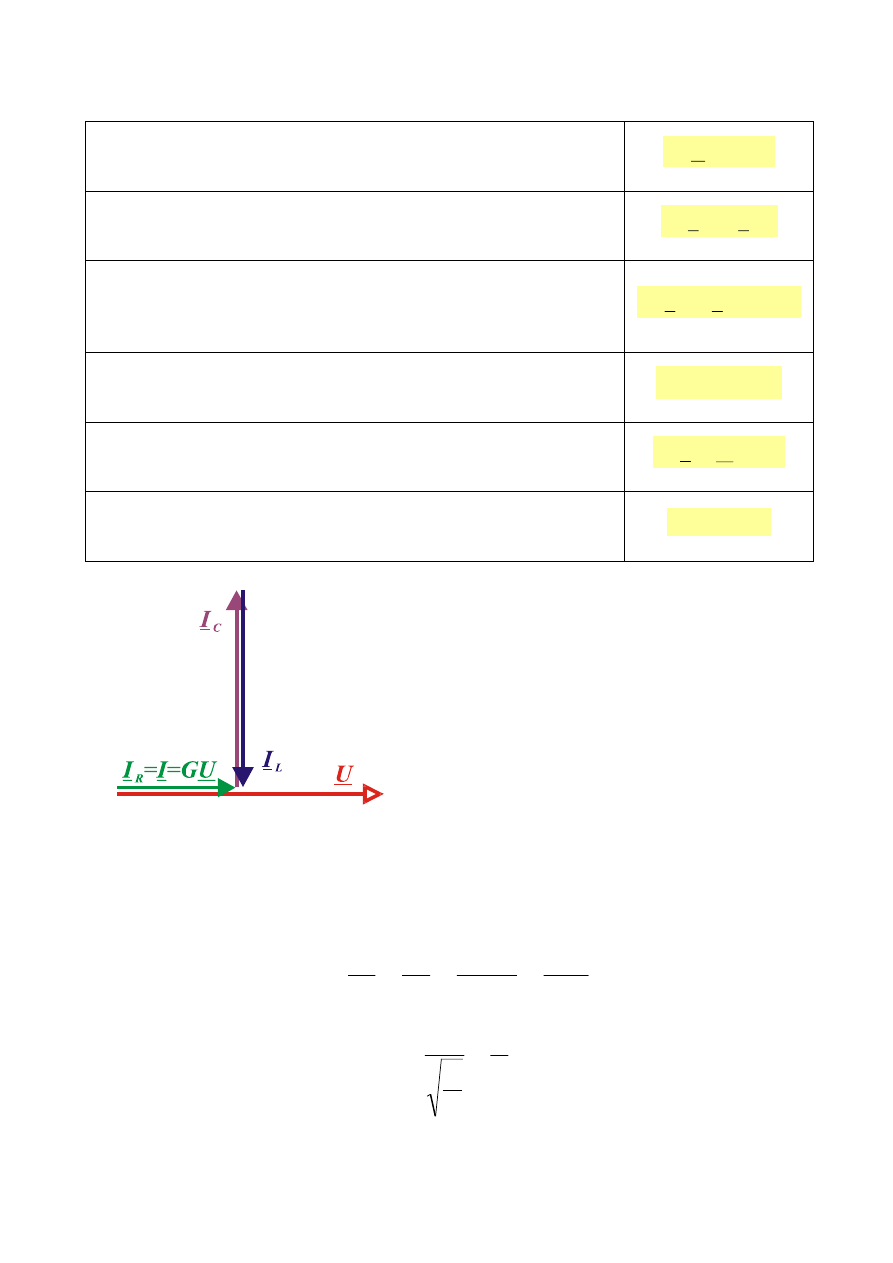
WŁASNOŚCI OBWODU W STANIE REZONANSU PRĄDÓW

1. admitancja obwodu jest równa konduktancji

(admitancja osiąga wartość minimalną)

G

Y



2. prąd w gałęzi rezystancyjnej jest równy

prądowi obwodu

I

I

R



3. suma

geometryczna

prądów

w

gałęzi

indukcyjności i pojemnościowej obwodu jest
równa zeru

0





C

L

I

I

4. prąd w gałęzi indukcyjnej jest co do modułu

równy prądowi w gałęzi pojemnościowej

C

L

I

I



5. wobec B=0, prąd w obwodzie osiąga wartość

minimalną

G

U

I



6. kąt przesunięcia fazowego między przyłożonym

napięciem a prądem jest równy zeru

0





Wykres wskazowy

Ze względu na równość modułów
prądów w gałęziach reaktancyjnych i
fakt, że mogą być one wielokrotnie
większe

od

modułu

prądu

dopływającego

do

obwodu

-

rezonans

w

rozpatrywanym

obwodzie nazywamy rezonansem
prądów

Parametrem, który wskazuje ile prąd w gałęzi z indukcyjnością lub

pojemnością jest większy od prądu dopływającego do obwodu w stanie
rezonansu jest dobroć Q.

G

C

LG

I

I

I

I

Q

r

r

R

C

R

L













1

.

(2.85)



R

C

L

R

Q





,

(2.86)

gdzie



jest reaktancją charakterystyczną obwodu

- 28 -

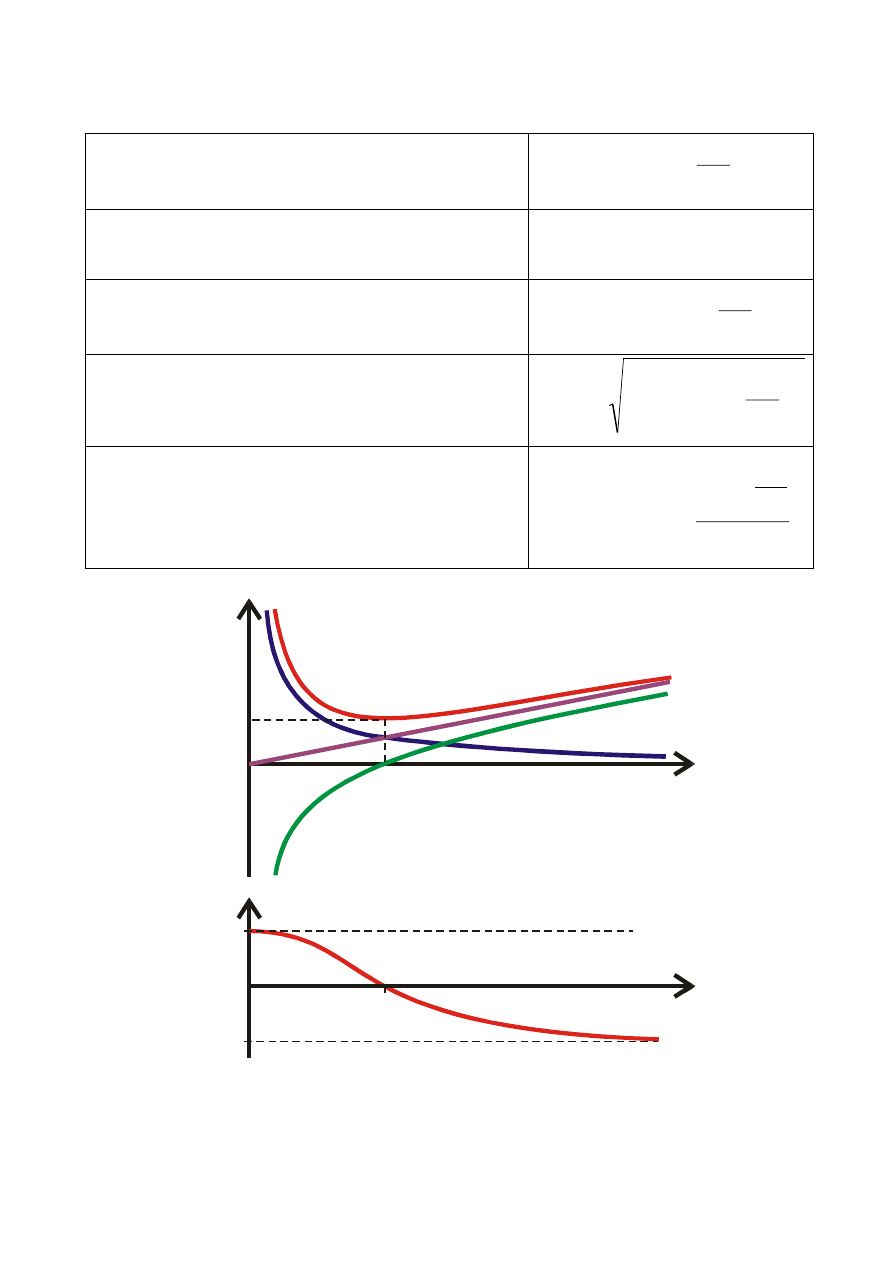
CHARAKTERYSTYKI CZĘSTOTLIWOSCIOWE

 charakterystyka susceptancji indukcyjnej

obwodu

 

L

B

L





1



 charakterystyka susceptancji

pojemnościowej obwodu

 

C

B

C







 charakterystyka susceptancji

wypadkowej obwodu

 

L

C

B







1





 charakterystyka admitancji (modułu

admitancji) obwodu

 

2

2

1



















L

C

G

Y







 charakterystyka kąta przesunięcia

fazowego (argumentu admitancji
wziętego ze znakiem przeciwnym)
obwodu

 

G

L

C

arctg









1







G



r

B( )



B ( )

L



B ( )

C





0



r





-



Y( )





- 29 -

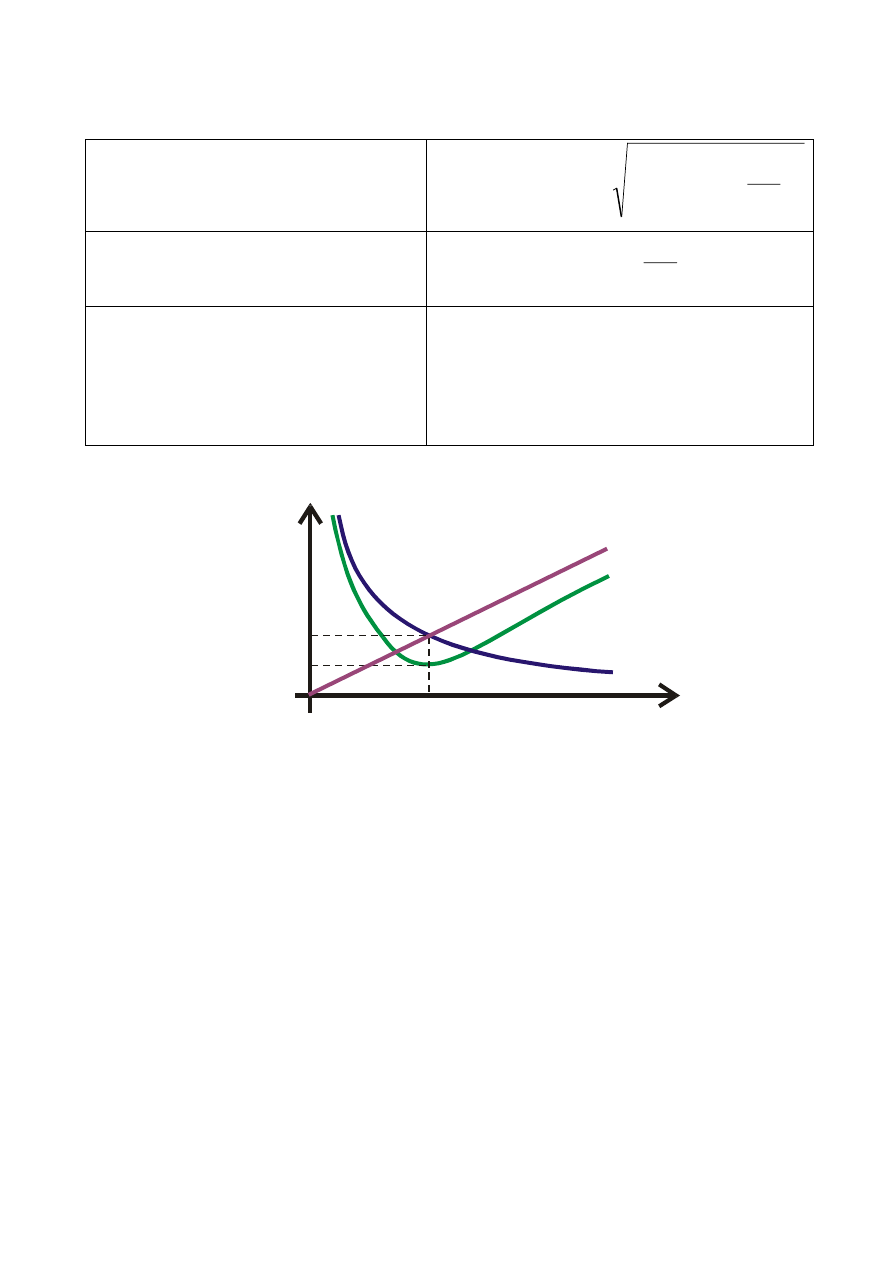
KRZYWE REZONANSOWE

 zależność prądu obwodu od

pulsacji

 

 

2

2

1





















L

C

G

U

Y

U

I









 zależność prądu w gałęzi

indukcyjnej od pulsacji

 

L

U

I

L







 zależność prądu w gałęzi

pojemnościowej od pulsacji

 

CU

I

C









r



I =GU

R

I ( )

C



I ( )

L



I( )



QI =QGU

R