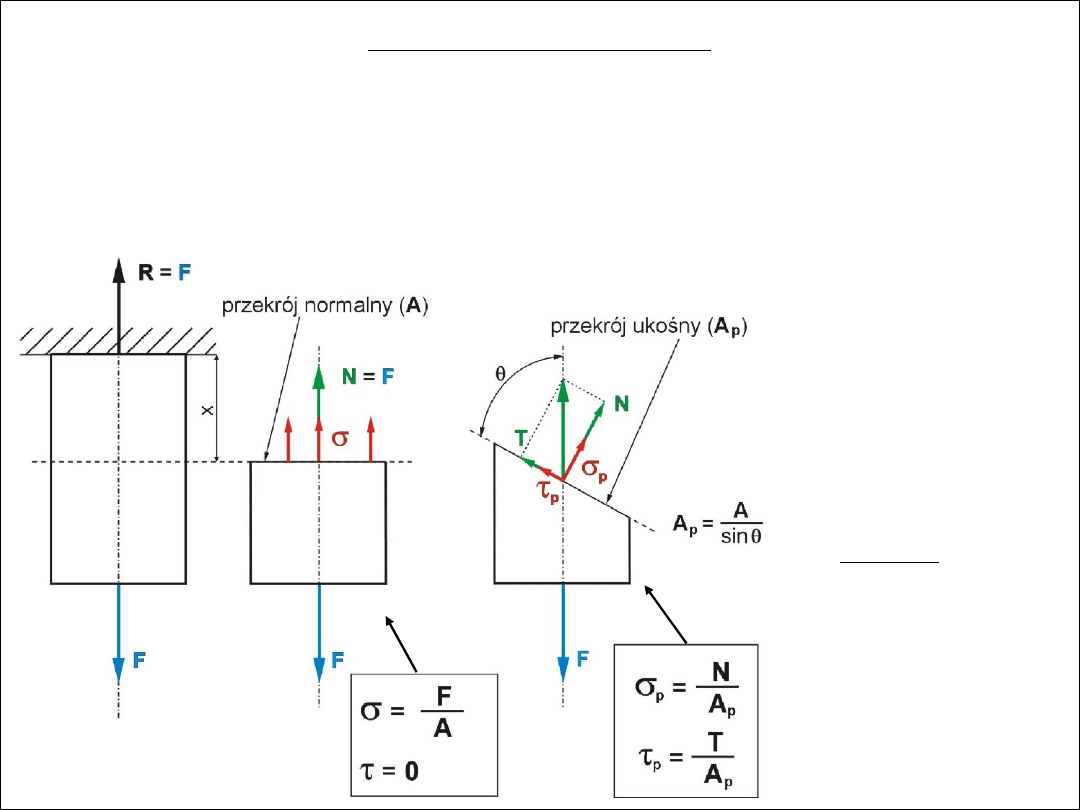
Naprężenie i odkształcenie
●
naprężenie
– siła przypadająca na jednostkę powierzchni przekroju,
●
naprężenie normalne
(rozciągające)
σ
– naprężenie normalne do przekroju pręta,
●
naprężenie styczne
(ścinające)
τ
– naprężenie styczne do przekroju pręta,
jednostki:
F, N, T [N]
A [m
2
]
τ
,
σ
[MPa] = [MN/m
2
]
zewnętrzna siła
obciążająca
reakcja
N
- składowa normalna siły wewnętrznej,
T
– składowa styczna siły wewnętrznej,
(megapaskal)
(niuton)
(+)
●
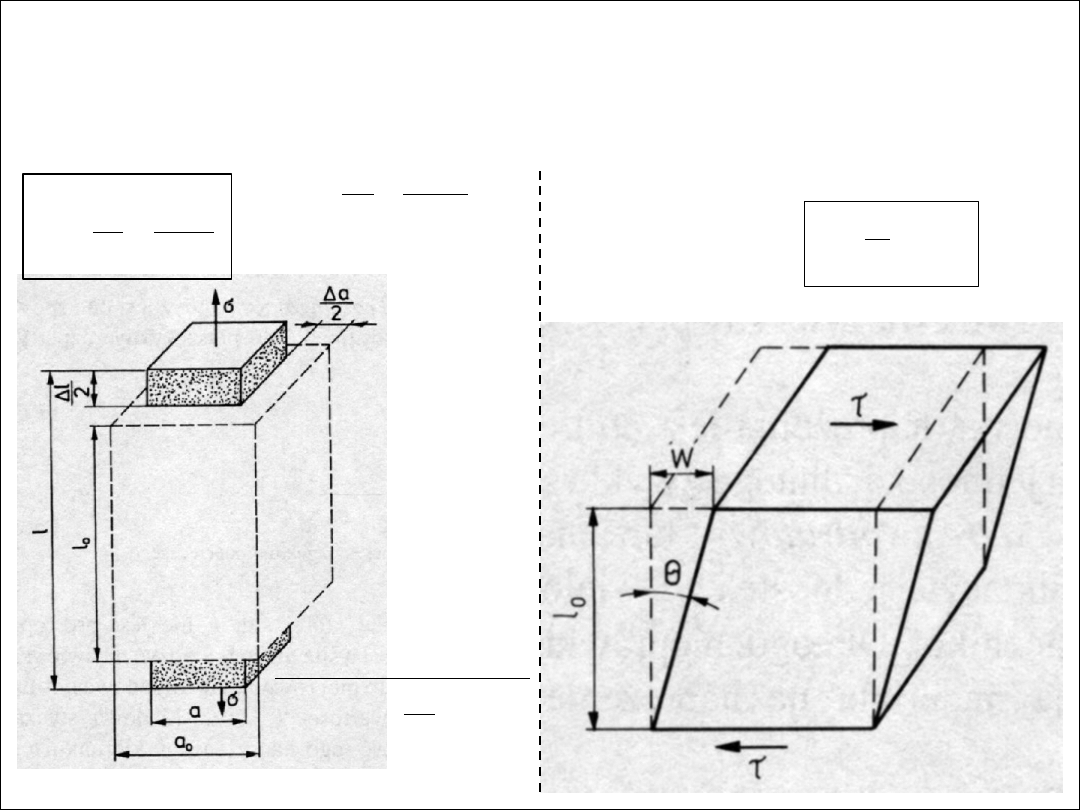
odkształcenie
-
jest wynikiem działania naprężenia w materiale,
●
odkształcenie liniowe
ε –
jest wynikiem działania naprężenia normalnego
σ
,
●
odkształcenie postaciowe
γ
- jest wywołane działaniem naprężenia stycznego
τ
,
0
0
0
//
l
l
l
l
l
−
=
∆
=
ε
0
0
0
a
a
a
a
a
−
=
∆
−
=
⊥
ε
//
ε
ε
υ
⊥
−
=
ν
-
współczynnik Poissona
(jedna ze stałych sprężystości)
⊥
ε
ε
,
//
θ
γ
tg
l
w
=
=
0
odkształcenie postaciowe
-
do kierunku
σ
przy jednoosiowym rozciąganiu:
(+)
●
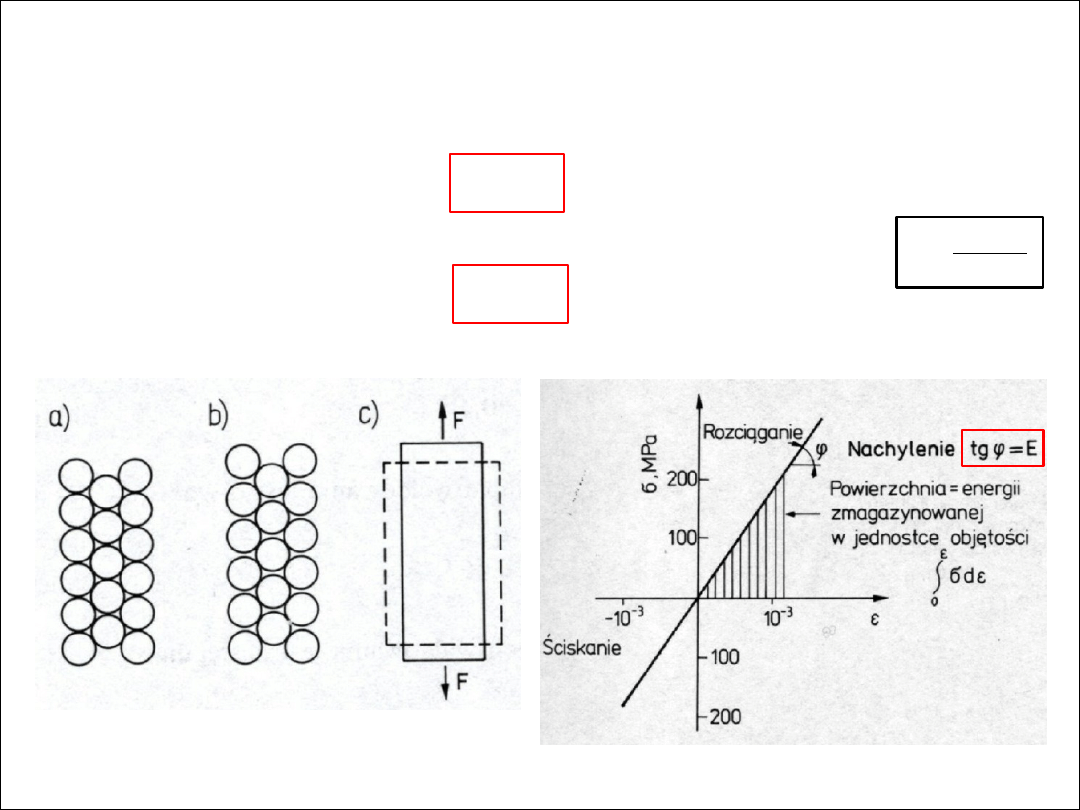
moduły sprężystości
–
zależności między naprężeniem a odkształceniem
,
● moduły sprężystości zdefiniowane są
prawem Hooke’a
:
(rozważania ograniczamy do jednoosiowego stanu naprężenia, małych wartości odkształceń oraz zakresu liniowo-sprężystego)
-
przy rozciąganiu i ściskaniu:
E – moduł Younga lub
współczynnik sprężystości wzdłużnej,
idea odkształcenia sprężystego rozciąganego kryształu
(jako wynik zmian odległości między atomami)
-
przy ścinaniu i skręcaniu:
G – moduł Kirchhooffa lub
współczynnik sprężystości poprzecznej,
)
1
(
2
ν
+
=
E
G
ε
σ
E
=
γ
τ
G
=
zależność naprężenia od odkształcenia w zakresie liniowo-sprężystym
przed
po
(+-)
●
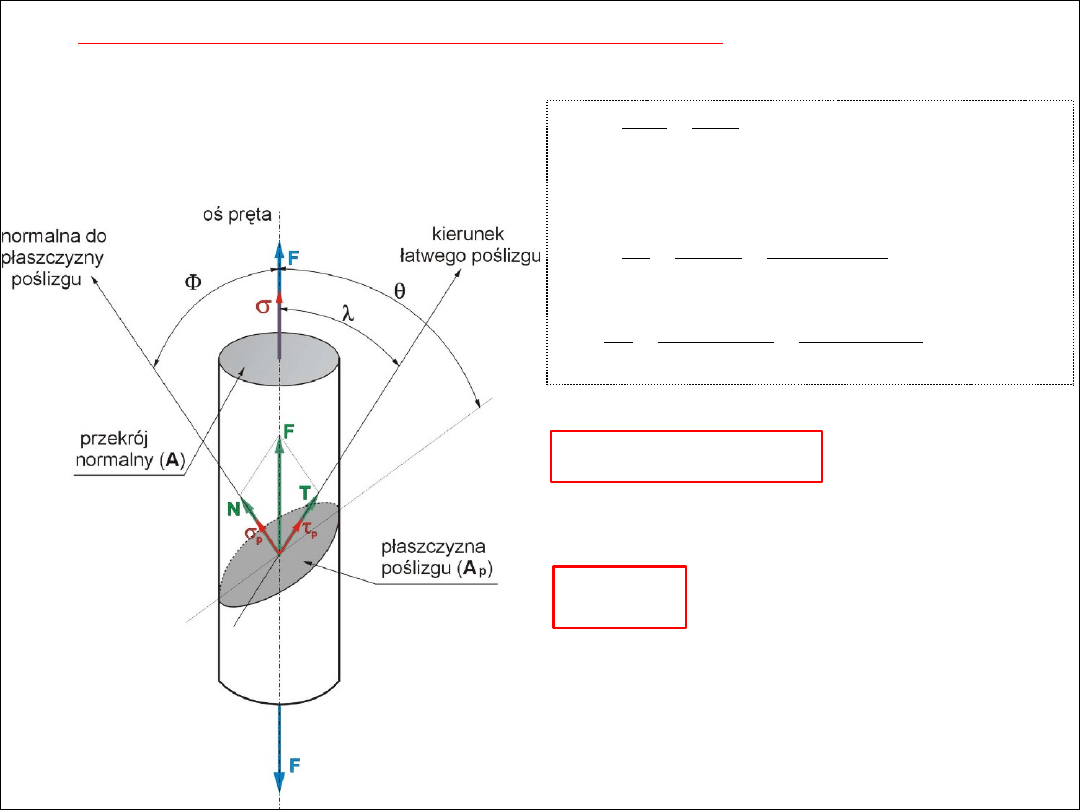
odkształcenie plastyczne metali – prawo Schmida-Boasa
● jednoosiowe rozciąganie monokryształu walcowego,
-
kąt nachylenia płaszczyzny poślizgu do osi pręta,
λ
-
kąt nachylenia kierunku poślizgu do osi pręta,
- przekrój pręta w płaszczyźnie poślizgu,
φ
θ
cos
sin
A
A
A
p
=
=
φ
sin
F
N
=
φ
cos
F
T
=
φ
θ
σ
φ
θ
σ
φ
σ
sin
sin
sin
sin
sin
=
=
=
=
A
A
A
F
A
N
p
p
p
φ
λ
σ
φ
λ
σ
φ
λ
τ
cos
cos
cos
cos
cos
cos
=
=
=
=
A
A
A
F
A
T
p
p
σ
φ
λ
τ
m
p
=
=
cos
cos
kr
p
τ
τ ≥
θ
-- warunek poślizgu
m
max
= 0,5 (gdy oba kąty wynoszą po 45
0
)
τ
kr
-
minimalne naprężenie styczne potrzebne do
pokonania oporów ruchu dyslokacji,
- dla danego metalu zależy od czystości, temperatury,
prędkości odkształcania, gęstości dyslokacji,
- wartości niewielkie, ok.
1
÷
10 kPa
(dla czystych metali),
- składowe siły w przekroju,
prawo Schmida-Boasa
(+-)
σ
=
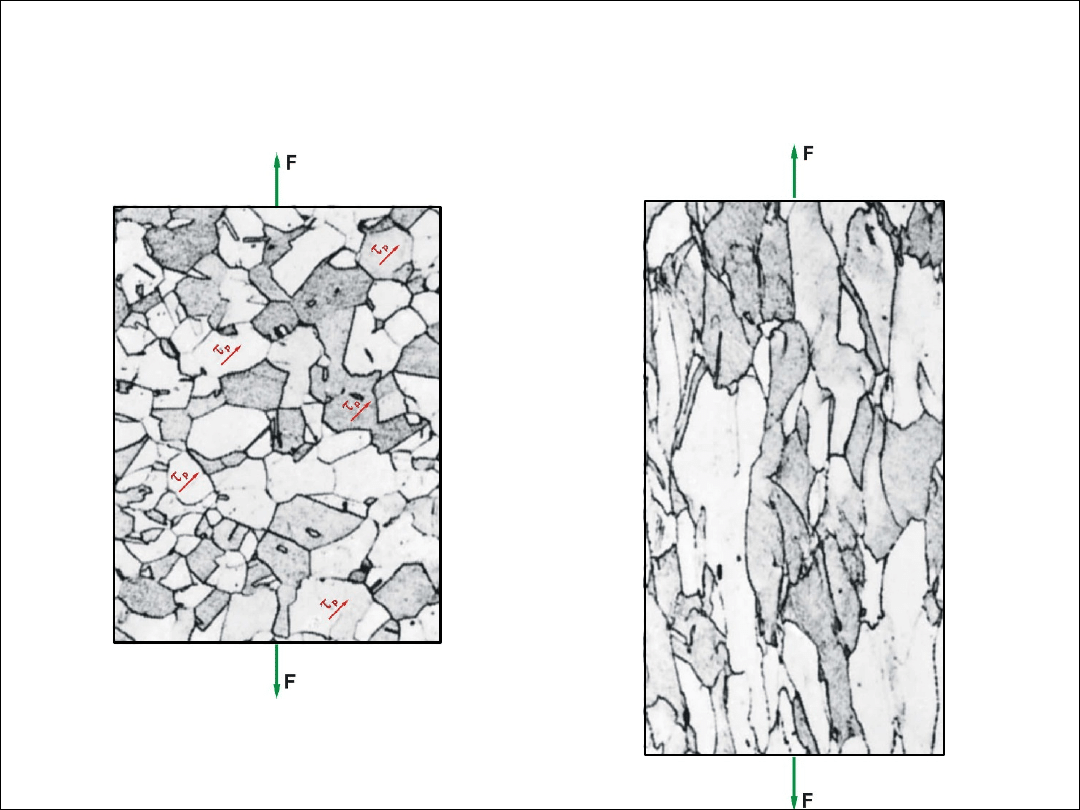
● odkształcenie plastyczne w rozciąganym polikrysztale metalu,
- początkowo odkształcenie (poślizg) ma charakter lokalny (w nielicznych ziarnach),
- po przekroczeniu granicy plastyczności poślizg zachodzi we wszystkich ziarnach (plastyczne płynięcie),
odkształcają się ziarna o odpowiedniej orientacji,
w których:
kr
p
τ
τ
≥
(+-)
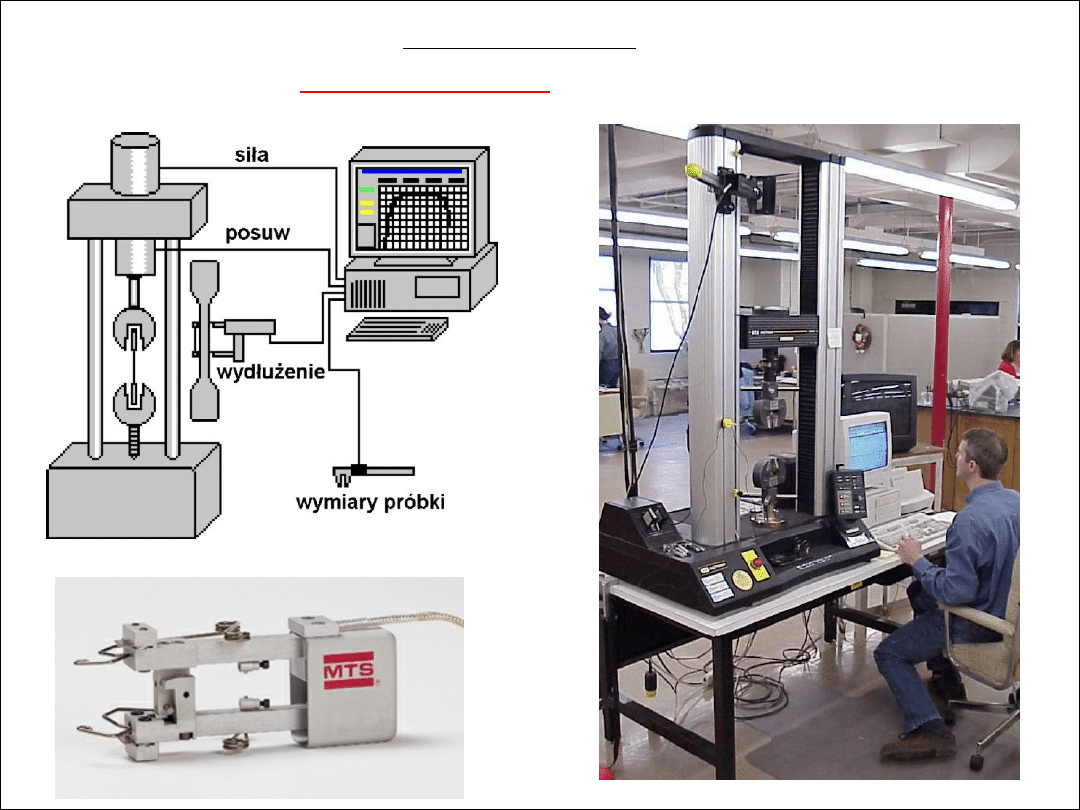
www.ptli.com/testlopedia/ subs/tensile.asp
www.mts.com
Próba rozciągania (1)
ekstensometr do pomiaru wydłużenia
● założeniem próby jest
stała prędkość rozciągania
[mm/min] – siła jest odpowiedzią materiału próbki,
(-+)
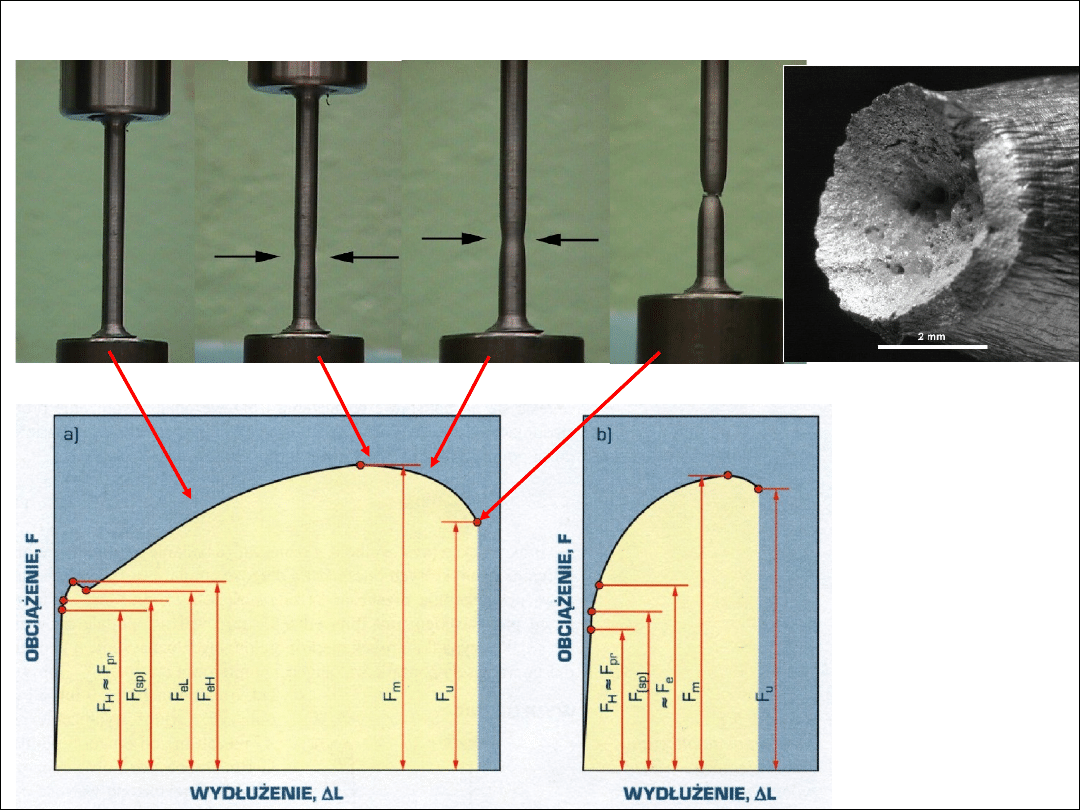
● kolejne fazy rozciągania próbki z ciągliwego metalu
powstawanie szyjki
przełom w szyjce
● wykresy rozciągania:
a) z wyraźną granicą
plastyczności,
b) bez wyraźnej granicy
plastyczności,
[mm]
[mm]
[N
]
(L.A. Dobrzański)
www.seas.upenn.edu
www.doitpoms.ac.uk
(+-)
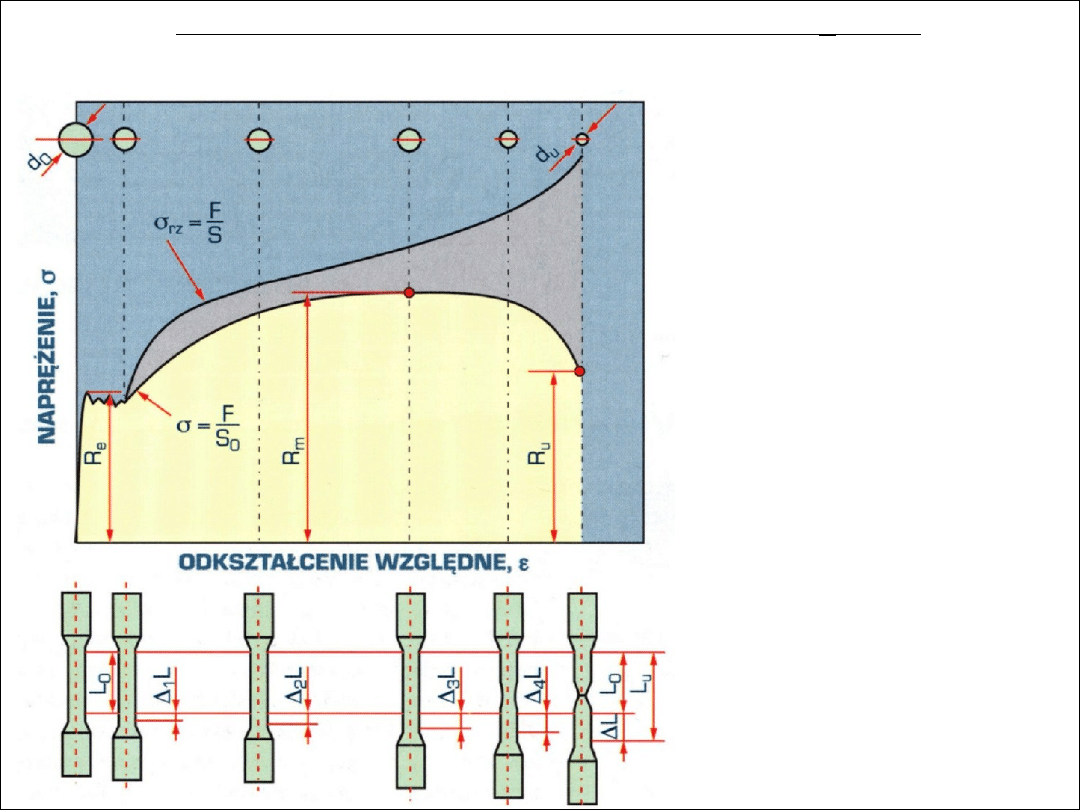
Rzeczywisty i umowny (inżynierski) wykres rozciągania
σ
= f (
ε
)
(przykład dla stali niskowęglowej z wyraźną granicą plastyczności)
H
R
eH
–
górna, R
eL
–
dolna [MPa]
R
0,2
–
umowna granica plastyczności,
(przy ε = 0,2%, gdy brak wyraźnej)
R
m
–
wytrzymałość na rozciąganie (F
m
/S
0
),
R
u
–
naprężenie zrywające (F
u
/S
u
),
R
e
–
fizyczna granica plastyczności (F
e
/S
0
)
A = (L
u
– L
0
)/L
0
-
wydłużenie [%]
Z = (d
0
– d
u
)/d
0
-
przewężenie [%]
E = Δ
σ
/Δ
ε
-
moduł Younga [MPa]
(w zakresie liniowo-sprężystym)
(+)
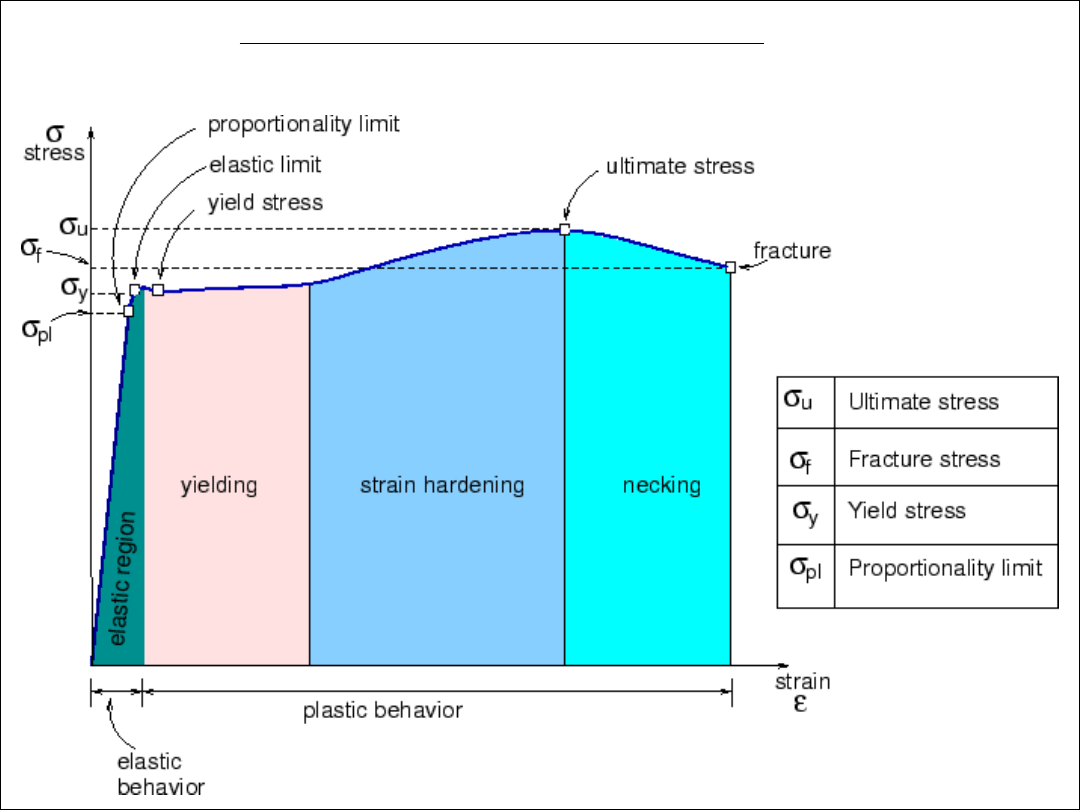
(www.shodor.org/~jingersoll/weave/tutorial/node4)
Charakterystyczne strefy wykresu rozciągania
(-+)
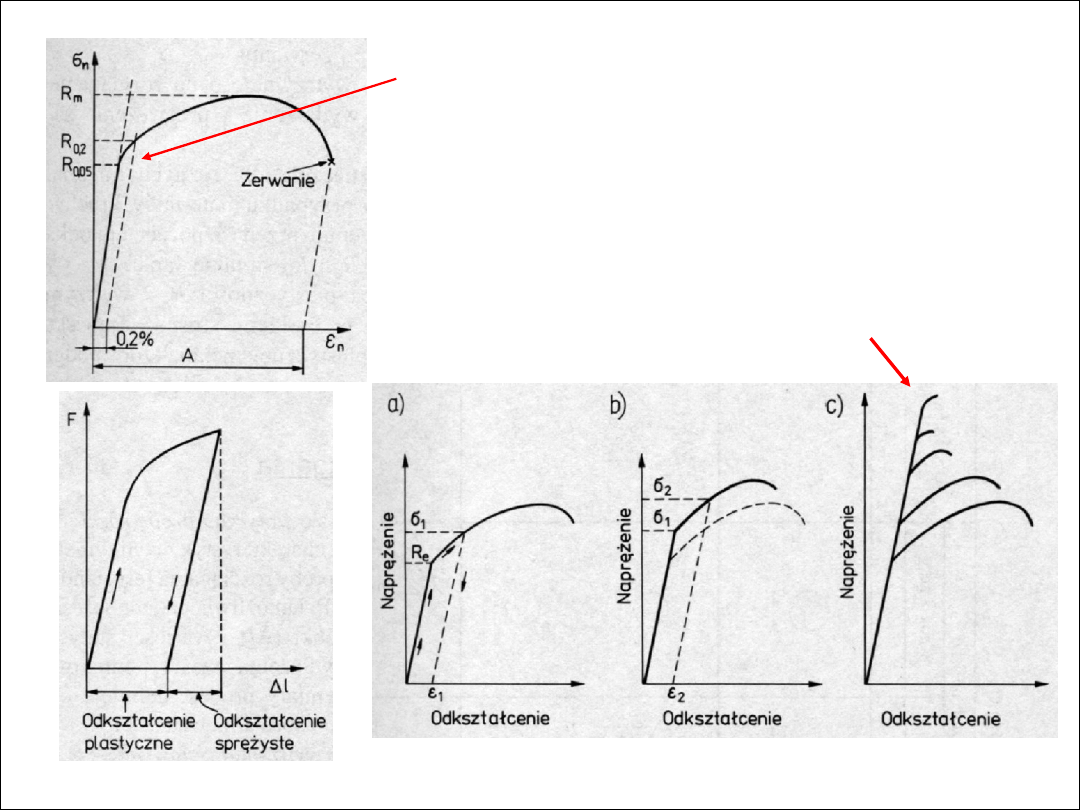
wyznaczanie umownej granicy sprężystości R
0,05
i plastyczności R
0,2
,
● umocnienie odkształceniowe - efekt wielokrotnego i przerywanego
rozciągania powyżej granicy plastyczności:
- wzrost granicy plastyczności oraz wytrzymałości,
- zmniejszenie wydłużenia do zerwania,
(M. Blicharski)
(+-)
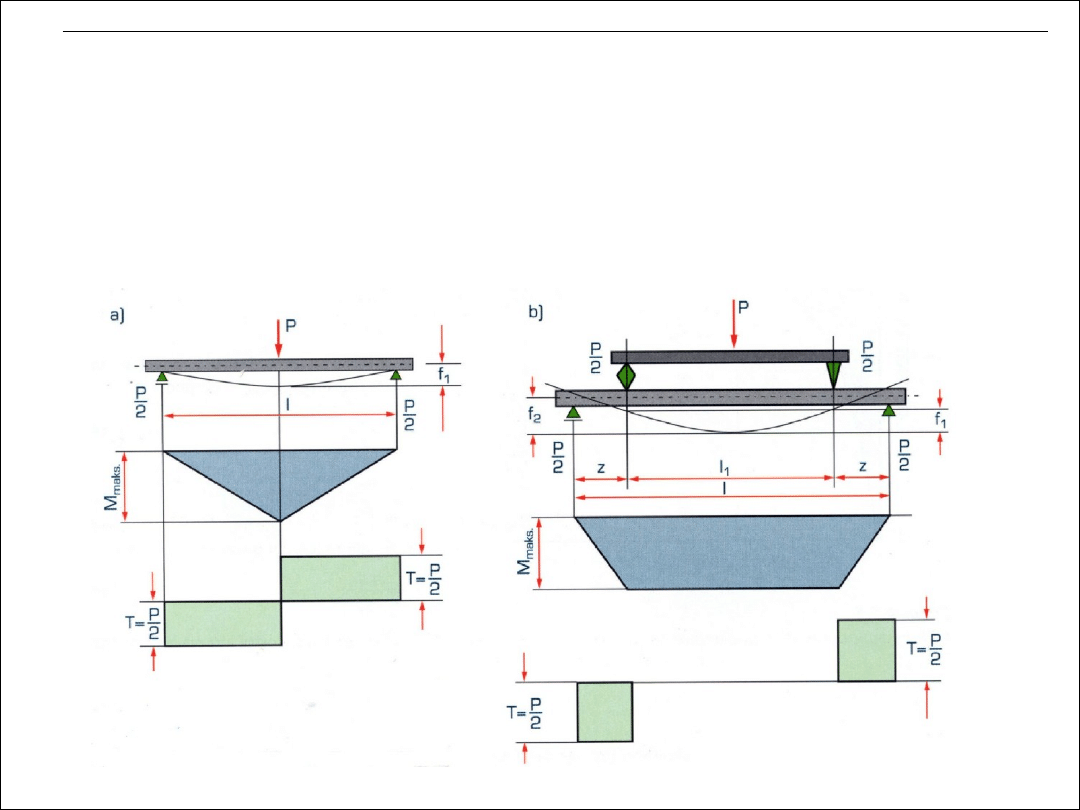
Badania właściwości materiałów kruchych i niezdolnych do odkształceń plastycznych:
● statyczna próba ściskania, np. materiały ceramiczne,
● statyczna próba zginania (zginanie trzy- lub czteropunktowe),
- pozwala oszacować wytrzymałość na rozciąganie, np. materiałów ceramicznych
(jedna strona zginanej belki jest rozciągana),
(-+)
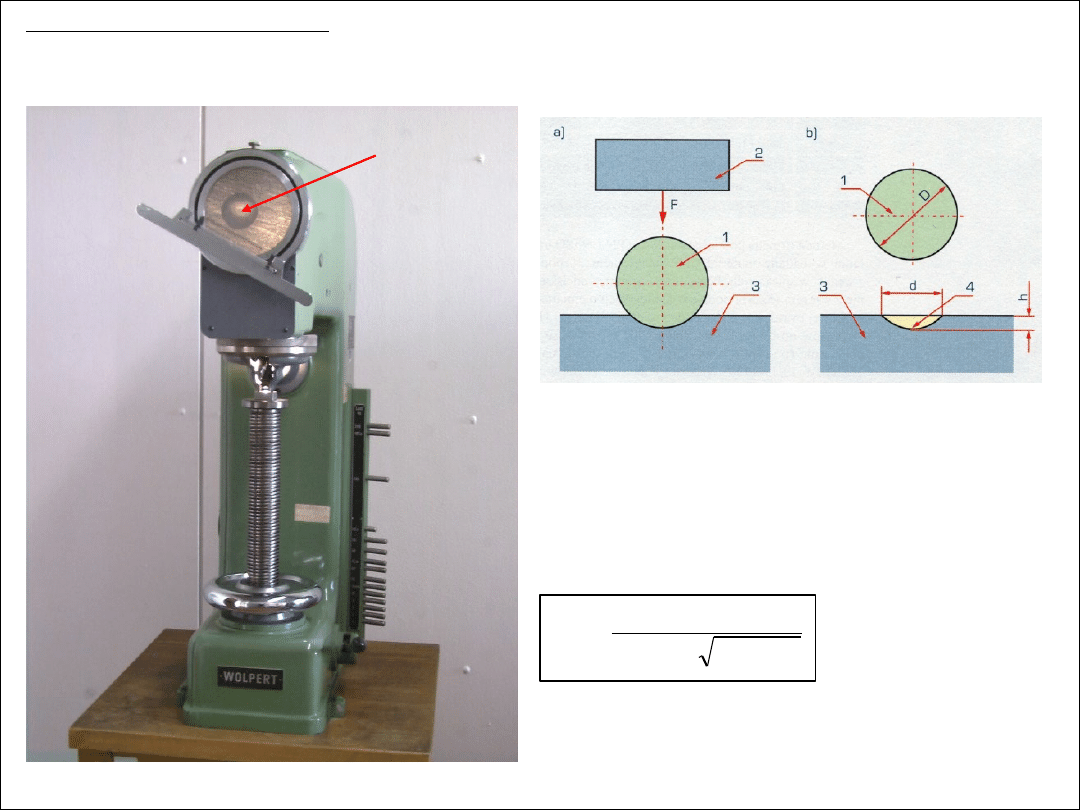
(www.gm.fh-koeln.de)
Statyczne próby twardości –
np. przez
pomiar
oporu materiału przeciw odkształceniu plastycznemu
● metoda Brinella –
polega na wciskaniu wgłębnika w badany materiał oraz pomiarze średnicy odcisku,
1- kulka o średnicy D [mm]
(stalowa lub z węglików spiekanych, D = 1
÷
10mm),
2- obciążenie F [N]
(10
÷
30 000 N, zależnie od twardości materiału),
3- badany materiał,
4- odcisk o średnicy d [mm],
2
2
(
204
,
0
d
D
D
D
F
HB
−
−
=
π
jednostki niemianowane,
np. 200HB
obraz odcisku
(+-)
(www.intertrade.com.cn)
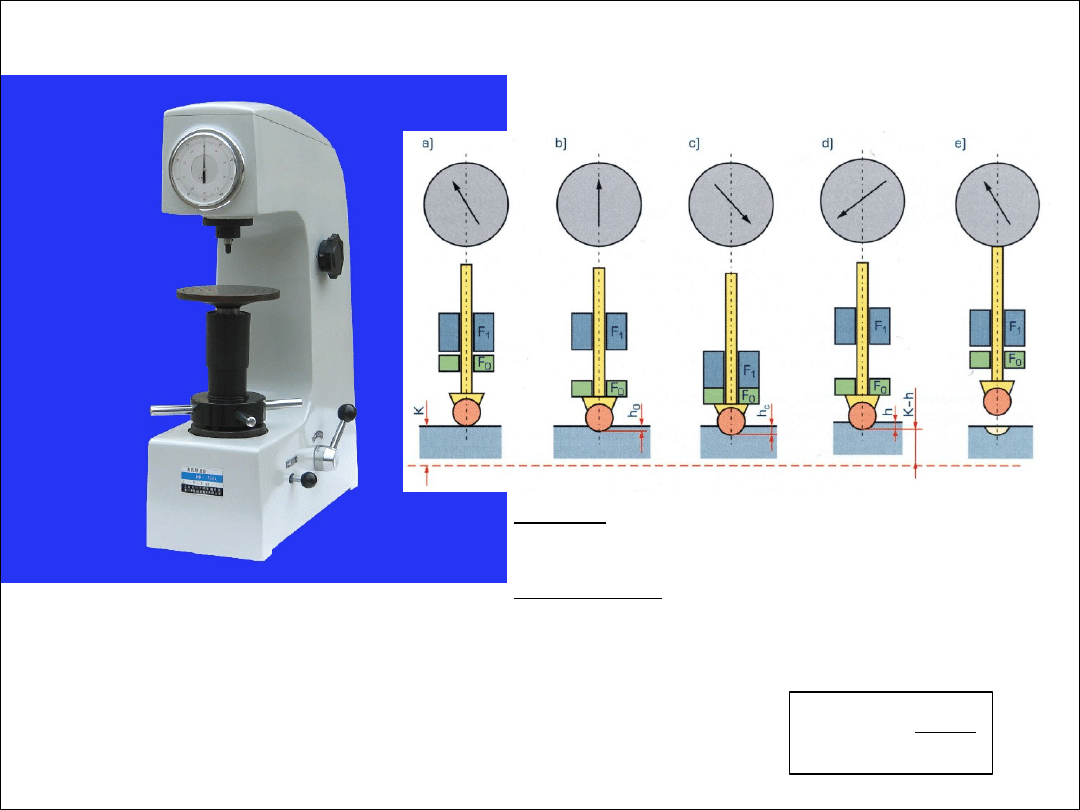
● metoda Rockwella -
polega na dwustopniowym wciskaniu wgłębnika w badany materiał
oraz pomiarze trwałego przyrostu głębokości odcisku po odciążeniu,
F
0
, F
1
– obciążenie wstępne oraz główne, [N],
h
0
, h
1
– głębokość odcisku przy obciążeniu wstępnym oraz głównym, [mm],
h – trwały przyrost głębokości odcisku (mierzony pod obciążeniem F
0
),
K – stała wyrażona w jednostkach podziałki (np. K=100 dla stożka),
wgłębnik:
- stożek diamentowy (dla materiałów twardych),
- kulka stalowa (dla materiałów miękkich),
wynik pomiaru:
nnHR oraz skala, np. 65HRC, 93HRB, 48HRK, itp.
002
,
0
h
K
HR
−
=
(-+)
obraz odcisku
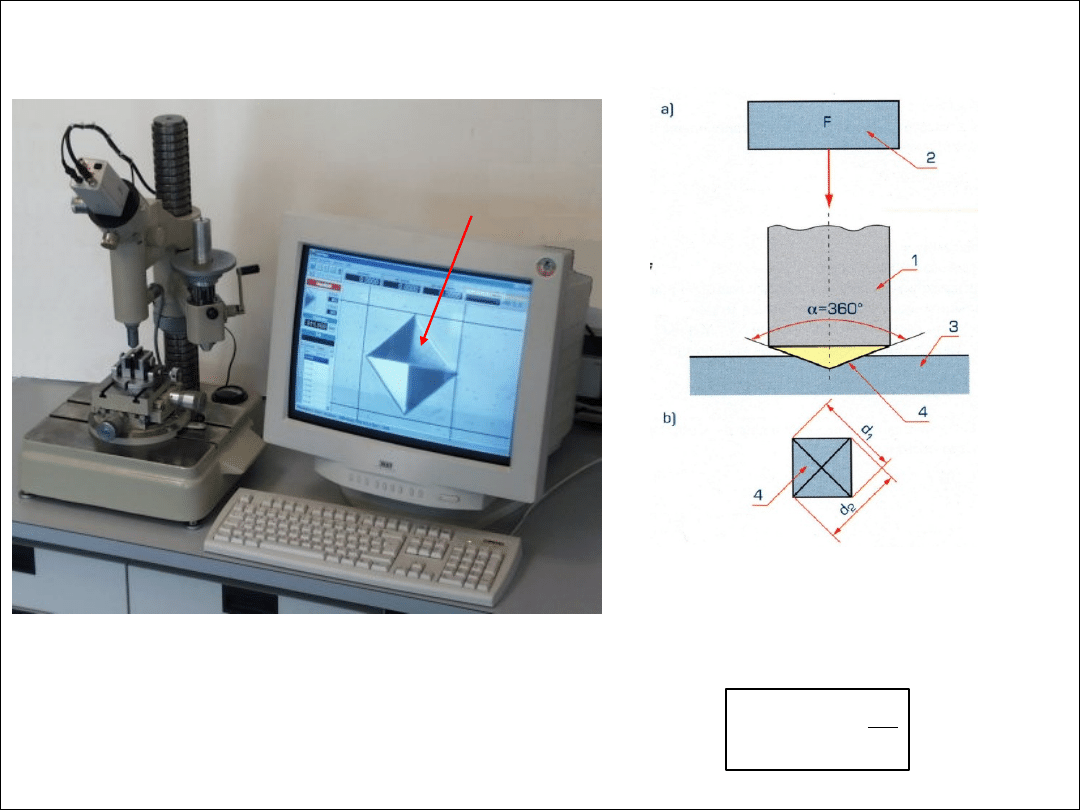
● metoda Vickersa –
polega na wciśnięciu w metal diamentowego ostrosłupa oraz pomiarze
przekątnych odcisku,
2
189
,
0
d
F
HV
=
d - średnia arytmetyczna przekątnych jednego
odcisku, [mm],
F - siła nacisku, [N],
- twardość Vickersa jest proporcjonalna do stosunku
obciążenia F do powierzchni bocznej trwałego odcisku,
- obciążenie F może wynosić od 0,2 do 100 N,
- wynik: np. 200HV30 , gdzie F = 30 N
(-+)
(L.A. Dobrzański)
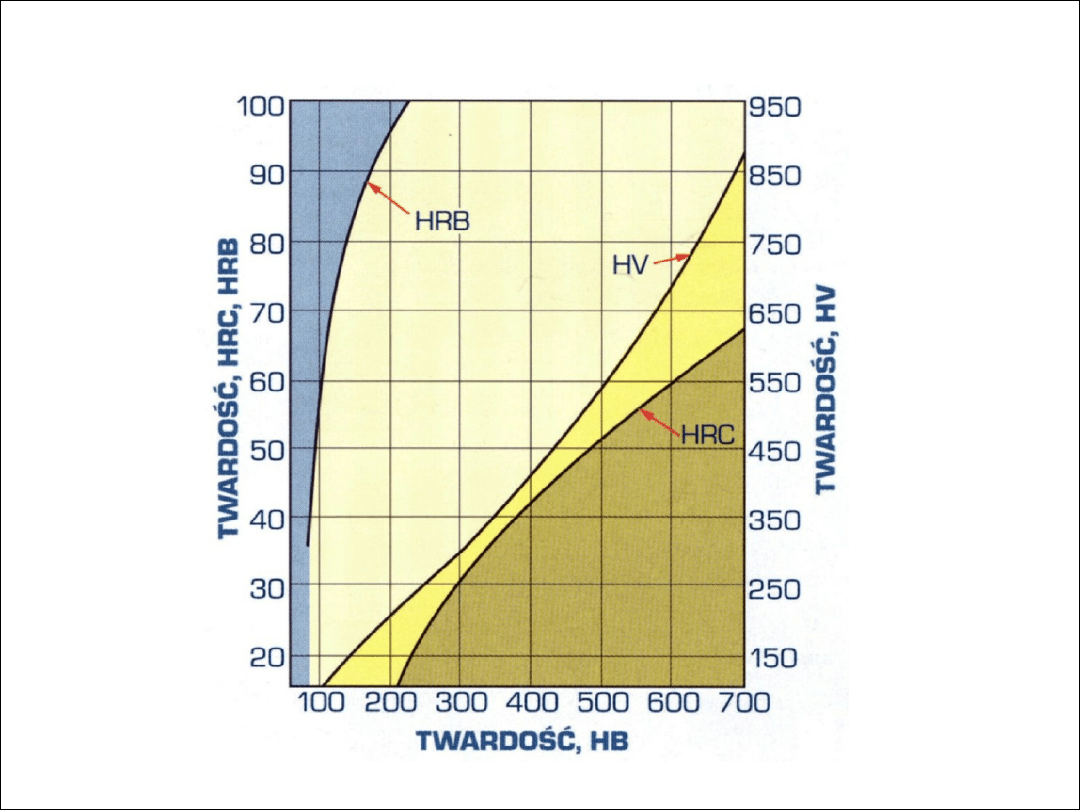
Porównanie wyników pomiaru twardości metodami Brinella, Rockwella i Vickersa.
(-)
(www.yasuda-seiki.co.jp)
(www.matsci.ucdavis.edu)
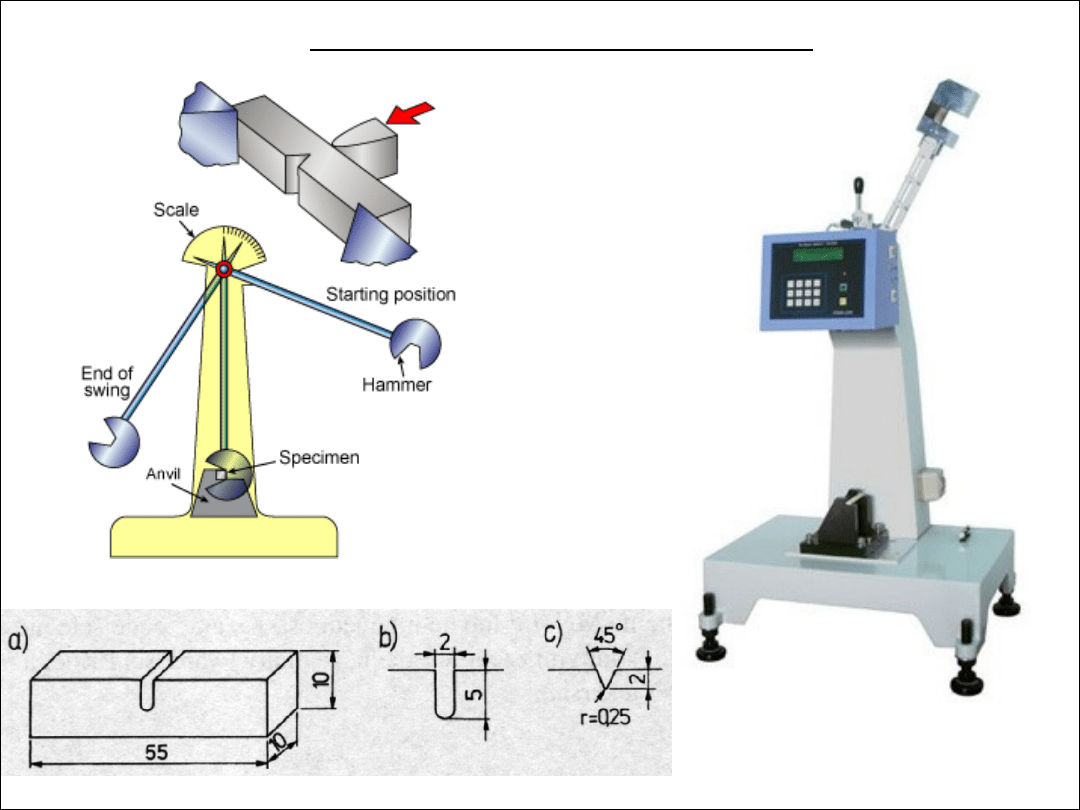
Pomiar udarności w próbie Charpy’ego
próbki - norma PN-EN
● wynikiem pomiaru jest
praca łamania [J]
(+)
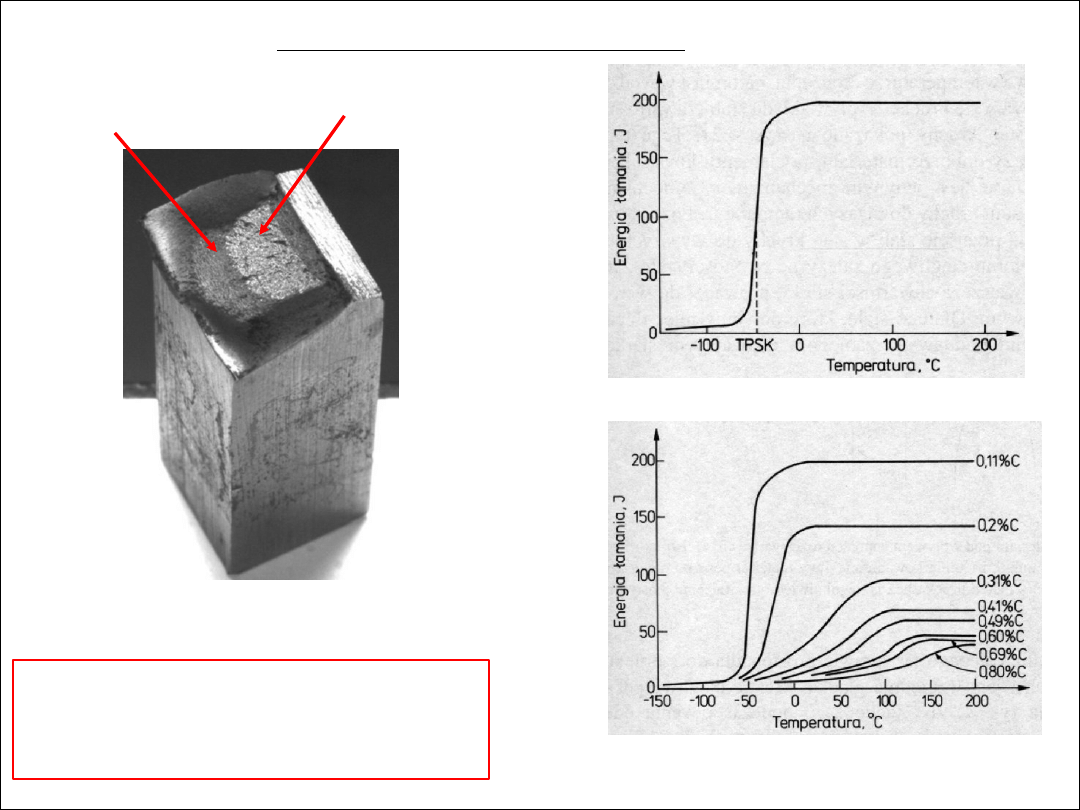
kruchy
ciągliwy
Analiza wyników badania udarności
● badania przełomu
- charakter przełomu (kruchy, ciągliwy, mieszany),
- udział powierzchni przełomu kruchego i ciągliwego,
● określanie temperatury przejścia w stan kruchy (T
PSK
)
● przykładowe badanie wpływu zawartości węgla w stali
na wartość temperatury T
PSK
przykład dla
stali 0,11% C
Udarność (praca łamania) ma istotne znaczenie
jako wskaźnik określający
ciągliwość materiału
(obciążenie dynamiczne oraz złożony stan
naprężenia na dnie karbu)
(www.matsci.ucdavis.edu)
(M. Blicharski)
p
rz
e
ło
m
k
ru
c
h
y
p
rz
e
ło
m
c
ią
g
li
w
y
(+-)
Podsumowanie
wskaźniki określające
„wytrzymałość”
materiału
wskaźniki określające
„ciągliwość”
materiału
R
e
lub
R
0,2
-
granica plastyczności,
R
m
-
wytrzymałość na rozciąganie
H -
twardość,
- pomiar twardości należy do wygodnych i tanich badań
nieniszczących (kontrola poprawności i jakości),
- wyniki H można wykorzystać do oszacowania R
m
lub R
e
,
- przykładowo dla stali (empirycznie):
R
m
[MPa] = (3,4
÷
3,6) HB
- H i R
m
często „wspólnie” opisują zachowanie się
materiału w warunkach dużych odkształceń
plastycznych (głęboki odcisk lub szyjka),
R
0,05
-
umowna granica sprężystości,
Najczęściej wysokim wartościom wskaźników wytrzymałościowych odpowiadają niskie wartości
wskaźników opisujących ciągliwość i odwrotnie - konieczność kompromisu w wyborze stanu materiału.
● brak jednoznacznej i ogólnie przyjętej definicji
(ang.: toughness, z ros.: wiązkość),
● najczęściej stosowane wyjaśnienia pojęcia:
- nie kruchość,
- odporność na pękanie
(często kruche pękanie w złożonym stanie naprężenia),
- zdolność do odkształceń plastycznych przed
wystąpieniem pęknięcia,
A -
wydłużenie (miara łagodna),
Z -
przewężenie (miara bardziej ostra),
K -
udarność (miara ostra),
K
Ic
-
odporność na pękanie (miara b. ostra),
T
PSK
–
temperatura przejścia w stan kruchy,
(+)